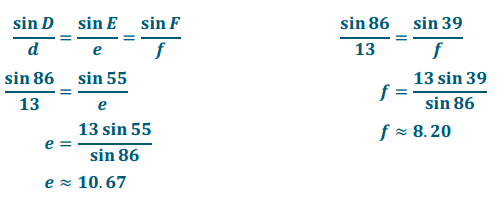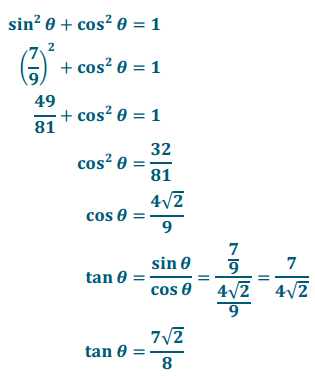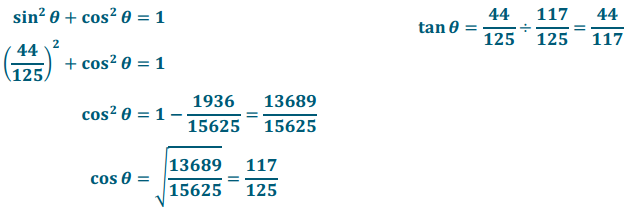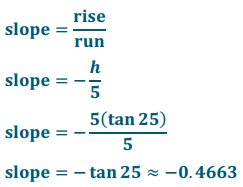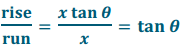Engage NY Eureka Math Geometry Module 2 Lesson 26 Answer Key
Eureka Math Geometry Module 2 Lesson 26 Exercise Answer Key
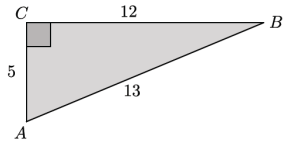
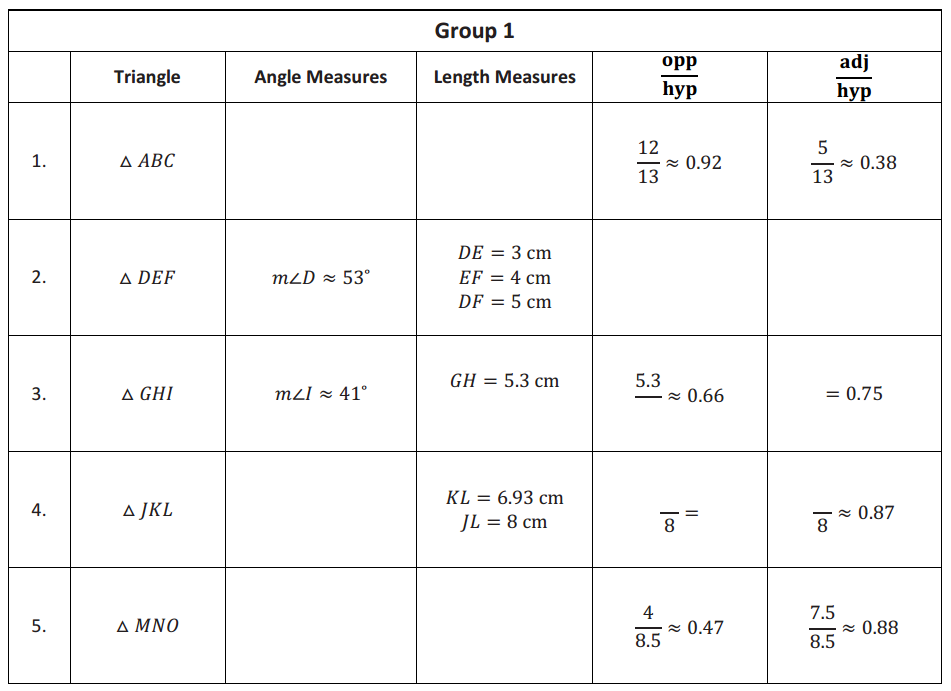
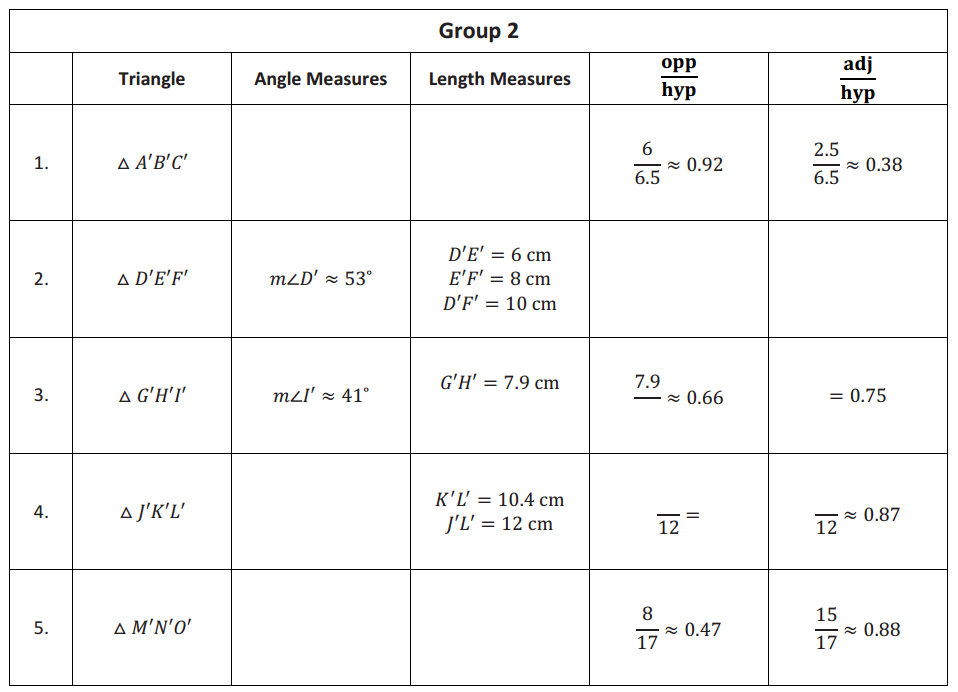
Exercise 1.
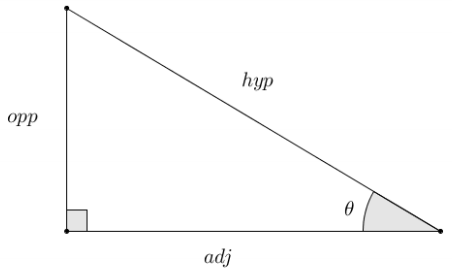
Identify the \(\frac{\text { opp }}{\text { hyp }}\) ratios for ∠A and ∠B.
Answer:
For ∠A: \(\frac{12}{13}\)
For ∠B: \(\frac{5}{13}\)
Exercise 2.
Identify the \(\frac{\text { adj }}{\text { hyp }}\) ratios for ∠A and ∠B.
Answer:
For ∠A: \(\frac{5}{13}\)
For ∠B: \(\frac{12}{13}\)
Exercise 3.
Describe the relationship between the ratios for ∠A and ∠B.
Answer:
The \(\frac{\text { opp }}{\text { hyp }}\) ratio for ∠A is equal to the \(\frac{\text { adj }}{\text { hyp }}\) ratio for ∠B.
The \(\frac{\text { opp }}{\text { hyp }}\) ratio for ∠B is equal to the \(\frac{\text { adj }}{\text { hyp }}\) ratio for ∠A.
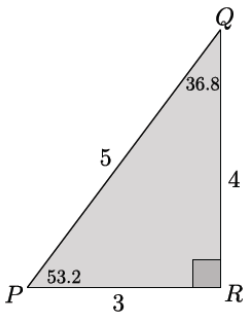
Exercise 4.
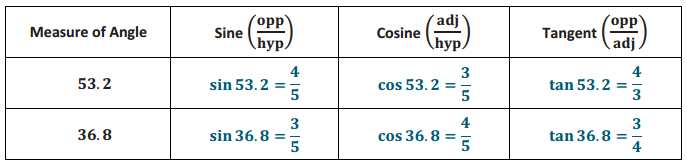
In ∆ PQR, m∠P = 53.2° and m∠Q = 36.8°. Complete the following table.
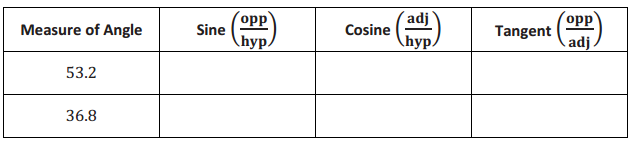

Answer:
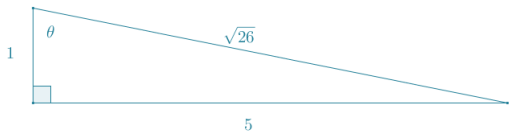
Exercise 5.
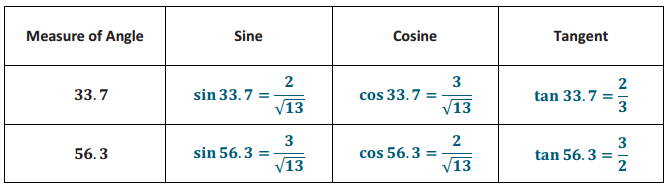
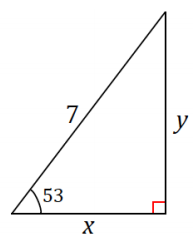
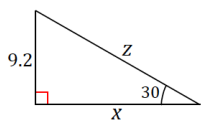
In the triangle below, m∠A = 33.7° and m∠B = 56.3°. Complete the following table.


Answer:
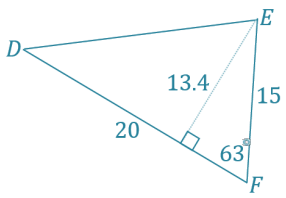
Exercise 6.
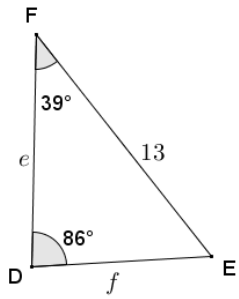
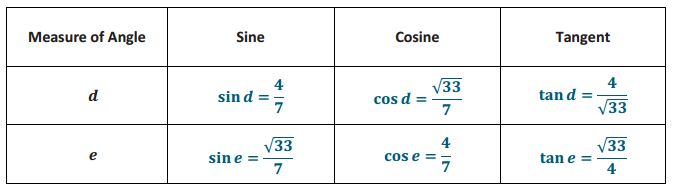
In the triangle below, let e be the measure of ∠E and d be the measure of ∠D. Complete the following table.

Answer:
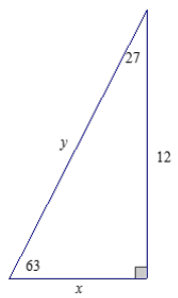
Exercise 7.
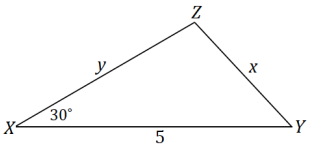
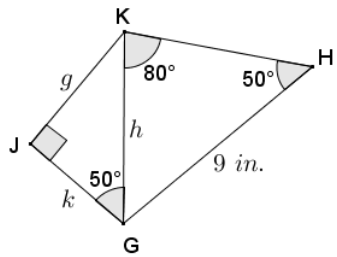
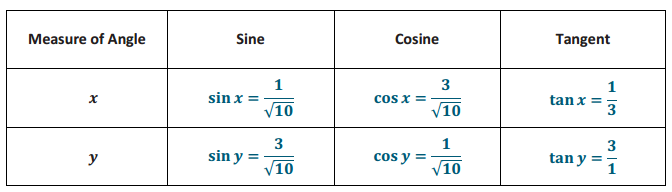
In the triangle below, let x be the measure of ∠X and y be the measure of ∠Y. Complete the following table.
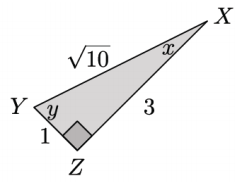
Answer:
Exercise 8.
Tamer did not finish completing the table below for a diagram similar to the previous problems that the teacher had on the board where p was the measure of ∠P and q was the measure of ∠Q. Use any patterns you notice from Exercises 1-4 to complete the table for Tamer.
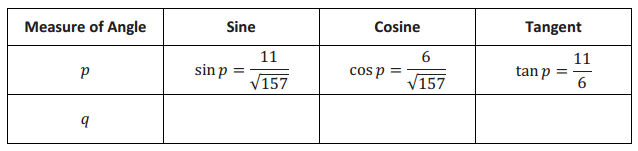
Answer:
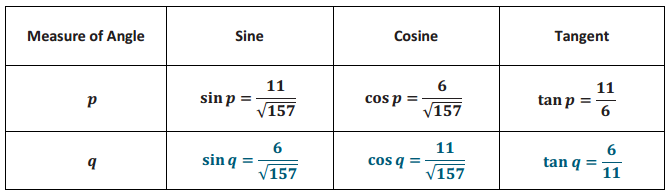
Exercise 9.
Explain how you were able to determine the sine, cosine, and tangent of ∠Q in Exercise 8.
Answer:
I was able to complete the table for Tamer by observing the patterns of previous problems. For example, I noticed that the sine of one angle was always equal to the ratio that represented the cosine of the other angle. Since I was given sin p, I knew the ratio \(\frac{11}{\sqrt{157}}\) would be the cos q. Similarly, cos p = sin q = \(\frac{6}{\sqrt{157}}\) Finally, I noticed that the tangents of the angles were always reciprocals of each other. Since i was given the tan p = \(\frac{11}{6}\) knew that the tan q must be equal to \(\frac{6}{11}\).
Eureka Math Geometry Module 2 Lesson 26 Problem Set Answer Key
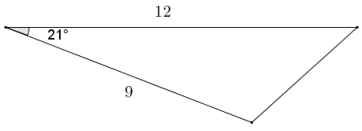
Question 1.
Given the triangle in the diagram, complete the following table.
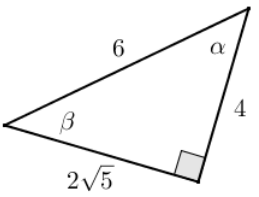

Answer:
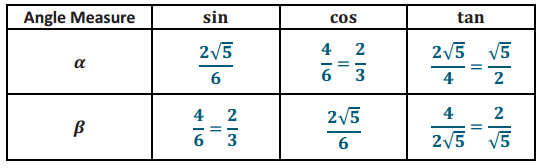
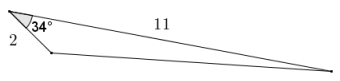
Question 2.
Given the table of values below (not in simplest radical form), label the sides and angles in the right triangle.


Answer:
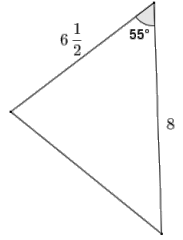
Question 3.
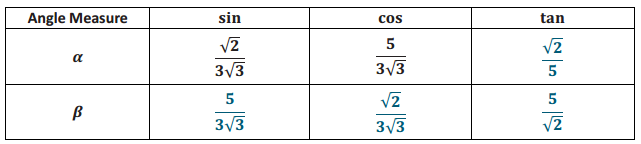
Given sin α and sin β, complete the missing values in the table. You may draw a diagram to help you.
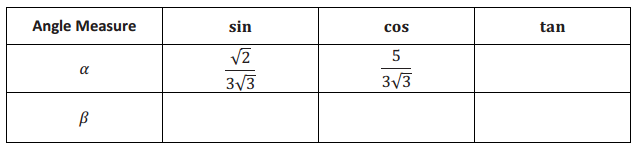
Answer:
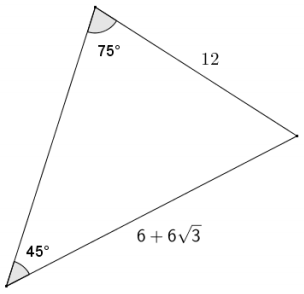
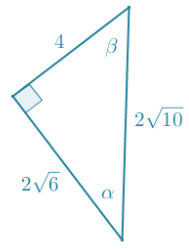
Question 4.
Given the triangle shown to the right, fill in the missing values in the table.
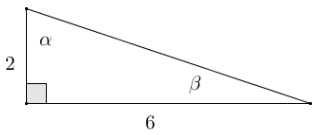

Answer:
Using the Pythagorean theorem:
hyp2 = 22 + 62
hyp2 = 4 + 36
hyp2 = 40
hyp = √40
hyp = 2√10

Question 5.
Jules thinks that if α and β are two different acute angle measures, then sin α ≠ sin β. Do you agree or disagree? Explain.
Answer:
I agree. If α and β are different acute angle measures, then either α > β or β > α. A right triangle with acute angle a cannot be similar to a right triangle with acute angle f? (unless α + β = 90) because the triangles fail the AA criterion. If the triangles are not similar, then their corresponding sides are not in proportion, meaning their within-figure ratios are not in proportion; therefore, sin α ≠ sin β. In the case where α + β = 90, the given right triangles are similar; however, a and fi must be alternate acute angles, meaning sin α = cos β, and sin β = cos α, but sin α ≠ sin β.
Question 6.
Given the triangle in the diagram, complete the following table.
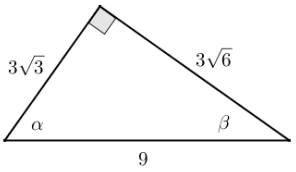

Answer:
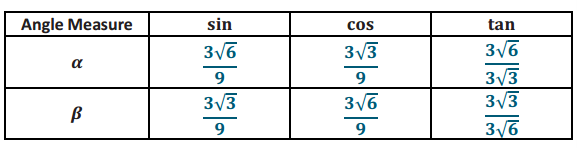
Rewrite the values from the table in simplest terms.

Answer:

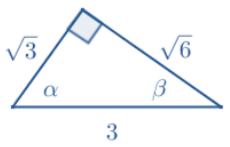
Draw and label the sides and angles of a right triangle using the values of the ratios sin and cos. How is the new triangle related to the original triangle?
Answer:
The triangles are similar by SSS criterion because the new triangle has sides that are \(\frac{1}{3}\) of the length of their corresponding sides in the original triangle.
Question 7.
Given tan α and cos β, in simplest terms, find the missing side lengths of the right triangle if one leg of the triangle has a length of 4. Draw and label the sides and angles of the right triangle.

Answer:
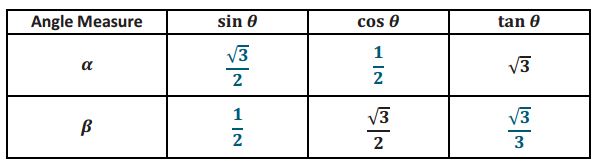
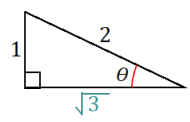
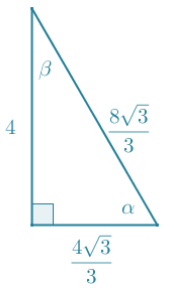
The problem does not specify which leg is 4, so there are two possible solutions to this problem. The values given in the table do not represent the actual lengths of the sides of the triangles; however, they do represent the lengths of the sides of a similar triangle, which is a 30 – 60 – 90 right triangle with side lengths 1, 2, and √3.
Case 1: The short leg of the right triangle is 4:

Case 2: The long leg of the right triangle is 4:
Question 8.
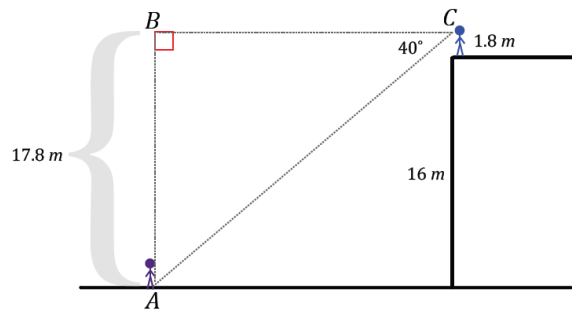
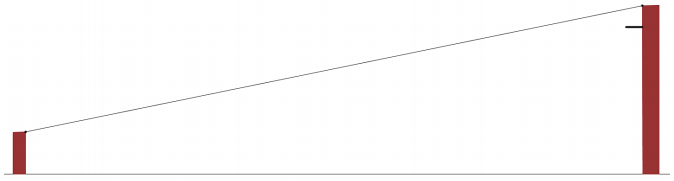
Eric wants to hang a rope bridge over a small ravine so that it is easier to cross. To hang the bridge, he needs to know how much rope Is needed to span the distance between two trees that are directly across from each other on either side of the ravine. Help Eric devise a plan using sine, cosine, and tangent to determine the approximate distance from tree A to tree B without having to cross the ravine.

Answer:
Student solutions will vary. Possible solution:
If Eric walks a path parallel to the ravine to a point P at a convenient distance from A, he could measure the angle formed by his line of sight to both trees. Using the measured angle and distance, he could use the value of the tangent ratio of the angle to determine the length of the opposite leg of the triangle. The length of the opposite leg of the triangle represents the distance between the two trees.
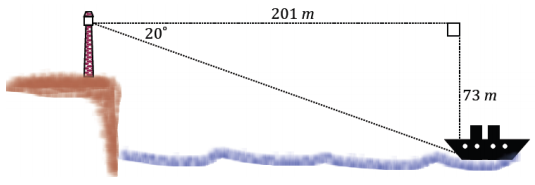
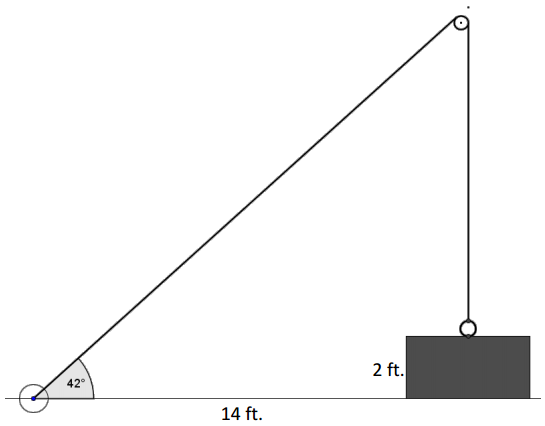
Question 9.
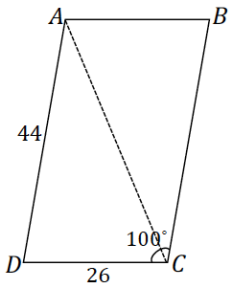
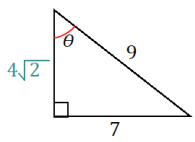
A fisherman is at point F on the open sea and has three favorite fishing locations. The locations are indicated by points A, B, and C. The fisherman plans to sail from F to A, then toB, then to C, and then back to F. If the fisherman is 14 miles from \(\overline{A C}\), find the total distance that he will sail.
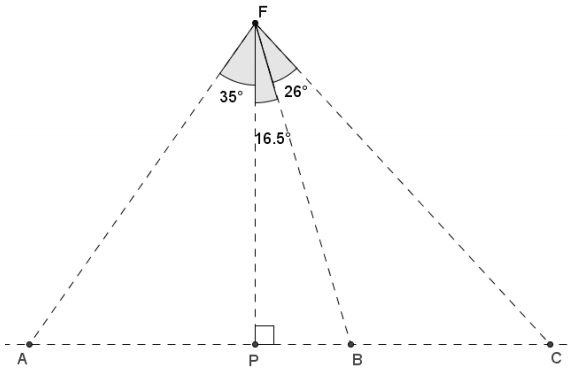
Answer:
FP = 14 and can be considered the adjacent side to the 35° angle shown in triangle APF.
Using cosine:
cos 35 = \(\frac{14}{A F}\)
AF = \(\frac{14}{\cos 35}\)
AF ≈ 17.09
Using tangent:
tan 35 = \(\frac{A P}{14}\)
AP = 14 tan 35
AP ≈ 9. 8029
\(\overline{P C}\) is the leg opposite angle PFC in triangle PFC and has a degree measure of 42.5.
Using tangent:
tan 42.5 = \(\frac{P C}{14}\)
PC = 14 tan 42.5
PC ≈ 12.8286
Using cosine:
cos 42.5 = \(\frac{14}{F C}\)
FC = \(\frac{14}{\cos 42.5}\)
FC ≈ 18. 9888
The total distance that the fisherman will sail:
distance = AF + AP + PC + FC
distance = \(\frac{14}{\cos 35}\) +14 tan 35 + 14 tan 42.5 + \(\frac{14}{\cos 42.5}\)
distance ≈ 58.7
The total distance that the fisherman will sail is approximately 58.7 miles.
Eureka Math Geometry Module 2 Lesson 26 Exit Ticket Answer Key
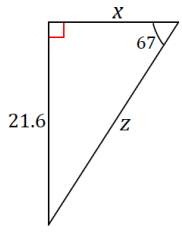
Question 1.
Given the diagram of the triangle, complete the following table.
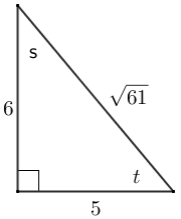
Answer:
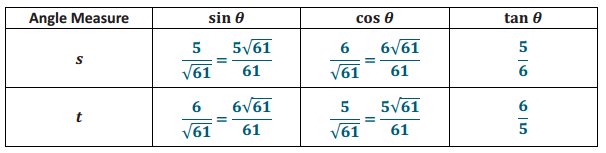
a. Which values are equal?
Answer:
sin s = cos t and cos s = sin t
b. How are tan s and tan t related?
Answer:
They are reciprocals: \(\frac{5}{6} \cdot \frac{6}{5}\) = 1.
Question 2.
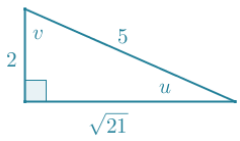
If u and y are the measures of complementary angles such that sin u = \(\frac{2}{5}\) and tan v = \(\frac{\sqrt{21}}{2}\) label the sides and angles of the right triangle In the diagram below with possible side lengths:
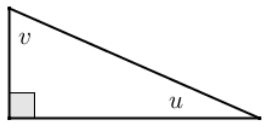
Answer:
A possible solution is shown below; however, any similar triangle having a shorter leg with length of 2x, longer leg with length of x√21, and hypotenuse with length of 5x, for some positive number x, is also correct.





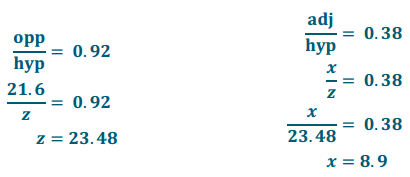

 Answer:
Answer: