Engage NY Eureka Math Geometry Module 4 Lesson 4 Answer Key
Eureka Math Geometry Module 4 Lesson 4 Exploratory Challenge Answer Key
Exploratory Challenge
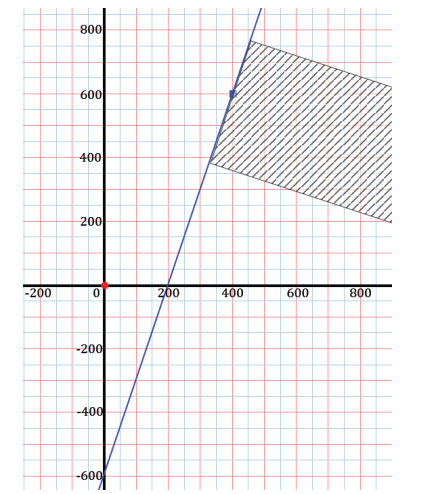
A search robot is sweeping through a flat plane in search of the homing beacon that is admitting a signal. (A homing beacon is a tracking device that sends out signals to identify the location). Programmers have set up a coordinate system so that their location is the origin, the positive x – axis is in the direction of east, and the positive y – axis is in the direction of north. The robot is currently 600 units south of the programmers’ location and is moving in an approximate northeast direction along the line y = 3x – 600.
Along this line, the robot hears the loudest “ping” at the point (400, 600). It detects this ping coming from approximately a southeast direction. The programmers have the robot return to the point (400, 600). What is the equation of the path the robot should take from here to reach the beacon?
Begin by sketching the location of the programmers and the path traveled by the robot on graph paper; then, shade the general direction the ping is coming from.
Answer:
A student response may look something like the following:
Eureka Math Geometry Module 4 Lesson 4 Example Answer Key
Example
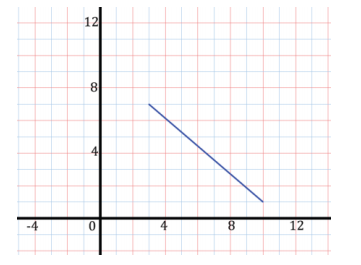
The line segment connecting (3, 7) to (10, 1) is rotated clockwise 90° about the point (3, 7).
a. Plot the segment.
Answer:
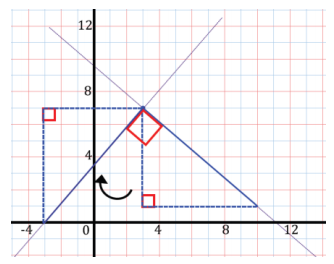
b. Where will the rotated endpoint land?
Answer:
( – 3, 0)
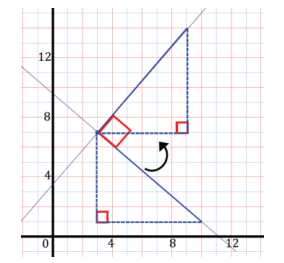
c. Now rotate the original segment 90° counterclockwise. Before using a sketch, predict the coordinates of the rotated endpoint using what you know about the perpendicular slope of the rotated segment.
Answer:
Eureka Math Geometry Module 4 Lesson 4 Exercise Answer Key
Opening Exercise
Write the equation of the line that satisfies the following conditions:
a. Has a slope of m = – \(\frac{1}{4}\) and passes through the point (0, – 5).
Answer:
y = – \(\frac{1}{4}\) x – 5
b. Passes through the points (1, 3) and ( – 2, – 1).
Answer:
y – 3 = \(\frac{4}{3}\) (x – 1) or y + 1 = \(\frac{4}{3}\) (x + 2)
Exercise
The point (a, b) is labeled below:
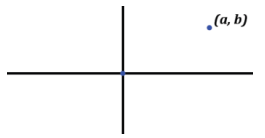
a. Using a and b, describe the location of (a, b) after a 90° counterclockwise rotation about the origin. Draw a rough sketch to justify your answer.
Answer:
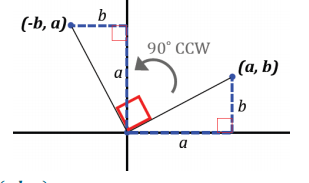
( – b, a)
b. If the rotation was clockwise about the origin, what is the rotated location of (a, b) in terms of a and b? Draw a rough sketch to justify your answer.
Answer:
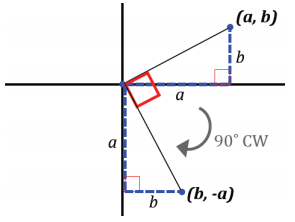
(b, – a)
c. What is the slope of the line through the origin and (a, b)? What is the slope of the perpendicular line through the origin?
Answer:
\(\frac{b}{a}\); – \(\frac{a}{b}\)
d. What do you notice about the relationship between the slope of the line through the origin and (a, b) and the slope of the perpendicular line?
Answer:
The slopes are negative reciprocals of each other. Their product is – 1.
Eureka Math Geometry Module 4 Lesson 4 Problem Set Answer Key
Question 1.
Find the new coordinates of point (0, 4) if it rotates:
a. 90° counterclockwise.
Answer:
( – 4, 0)
b. 90° clockwise.
Answer:
(4, 0)
c. 180° counterclockwise.
Answer:
(0, – 4)
d. 270° clockwise.
Answer:
( – 4, 0)
Question 2.
What are the new coordinates of the point ( – 3, – 4) if it is rotated about the origin:
a. Counterclockwise 90°?
Answer:
(4, – 3)
b. Clockwise 90°?
Answer:
( – 4, 3)
Question 3.
Line segment ST connects points S(7, 1) and T(2, 4).
a. Where does point T land if the segment is rotated 90˚ counterclockwise about S?
Answer:
(4, – 4)
b. Where does point T land if the segment is rotated 90° clockwise about S?
Answer:
(10, 6)
c.. What is the slope of the original segment?
Answer:
– \(\frac{3}{5}\)
d. What is the slope of the rotated segments?
Answer:
\(\frac{5}{3}\)
Question 4.
Line segment VW connects points V(1, 0) and W(5, – 3).
a. Where does point W land if the segment is rotated 90° counterclockwise about V?
Answer:
(4, 4)
b. Where does point W land if the segment is rotated 90° clockwise about V?
Answer:
( – 2, – 4)
c. Where does point V land if the segment is rotated 90° counterclockwise about W?
Answer:
(2, – 7)
d. Where does point V land if the segment is rotated 90° clockwise about W?
Answer:
(8, 1)
Question 5.
If the slope of a line is 0, what is the slope of a line perpendicular to it? If the line has slope 1, what is the slope of a line perpendicular to it?
Answer:
undefined; – 1
Question 6.
If a line through the origin has a slope of 2, what is the slope of the line through the origin that is perpendicular to it?
Answer:
– \(\frac{1}{2}\)
Question 7.
A line through the origin has a slope of \(\frac{1}{3}\). Carlos thinks the slope of a perpendicular line at the origin will be 3.
Do you agree? Explain why or why not.
Answer:
I disagree with Carlos. The slope of the perpendicular line would have a slope of – 3 because it should be the negative reciprocal of the original slope.
Question 8.
Could a line through the origin perpendicular to a line through the origin with slope \(\frac{1}{2}\) pass through the point ( – 1, 4)? Explain how you know.
Answer:
No, the equation of the line through the origin perpendicular to the line through the origin with slope \(\frac{1}{2}\) has an equation of y = – 2x. ( – 1, 4) is not a solution to this equation.
Eureka Math Geometry Module 4 Lesson 4 Exit Ticket Answer Key
Question 1.
If the line segment connecting point P(5, 2) to point R(3, 6) is rotated 90° counterclockwise about point R:
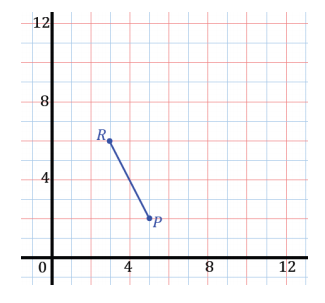
a. Where will point P land?
Answer:
(7, 8)
b. What is the slope of the original segment, \(\overline{P R}\)?
Answer:
– 2
c. What is the slope of the rotated segment? Explain how you know.
Answer:
The slope is \(\frac{1}{2}\); a 90° rotation means the segments are perpendicular, so the slopes are negative reciprocals of each other.