Hello students!!! Would you like to know what is meant by solid figures? If yes, then what are you waiting for you are on the right page. Start your preparation by using this page. In this article, the students of 9th grade can find the topics related to solid figures and their measurements. Usually, we can measure the solid figure in terms of total surface area, lateral surface area, and volume. So, we suggest you guys click on the below-mentioned links and learn in detail about the volume and surface area of the solid figures.
List of Solid Figures Concepts
- Volume and Surface Area of Cuboid
- Volume and Surface Area of Cube
- Volume and Surface Area of Cube and Cuboid
- Volume of Cuboid
- Volume of Cube
- Lateral Surface Area of a Cuboid
- Cross Section
- Cylinder
- Right Circular Cylinder
- Hollow Cylinder
- Problems on Right Circular Cylinder
What are Solid Figures?
Solid figures are nothing but three-dimensional geometric shapes such as cuboids, cubes, prisms, pyramids, spheres, etc. The 3D figures consist of faces, edges, and vertices. The flat part of a solid shape is known as the face. Each corner of the face is known as a vertex. The point where two faces meet is known as the edges. The solid figures contain three dimensions length, width, and height. Examples of solids figures are computers, dice, container, and so on.
Types of Solid Figures
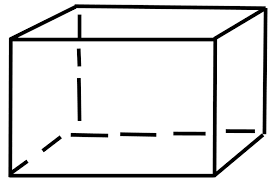
Cuboid: In geometry, a cuboid is a three-dimensional figure with six faces, 12 edges, and 8 vertices. A cuboid is a rectangular 3D box. The three dimensions of a cuboid are length, breadth, and height.
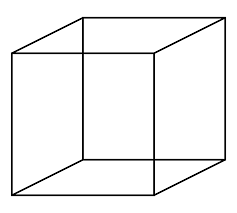
Cube: Cube is a type of solid figure which is bounded by six faces, 8 vertices, and 12 edges. It consists of three dimensions length, width, and height. And the difference between the cube and cuboid is that all the sides of the cube are equal.
Sphere: A sphere is a solid figure with no faces, no edges, and no vertices. It is a 3D figure. A sphere has one surface that is equidistant from the origin. An example of a sphere is the ball.

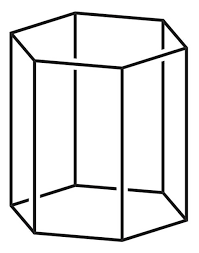
Prism: Prism is a 3D solid figure that consists of two equal ends, flat surfaces, and has an identical cross-section across its length. A prism has six vertices, 9 edges, and 5 faces.
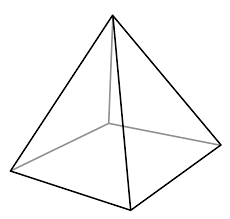
Pyramid: A pyramid is a solid figure with a flat base and all lateral faces as triangles. Types of pyramid are square pyramid, triangular pyramid, hexagonal pyramid, and pentagonal pyramid.
Cylinder: A cylinder is a solid three-dimensional figure with two parallel circular bases that are joined by the curved surface. The shape of a cylinder has no vertices, two edges, 2 flat faces, and one curved face. We can measure the cylinder using the total surface area, curved surface area, and volume of the cylinder.
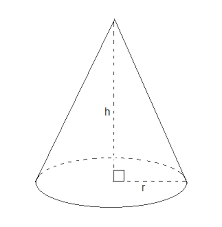
Cone: A cone is a three-dimensional geometric shape that narrows from the flat base to the point. The base of a cone is a circle. It has one face. An example of the cone is ice cream, funnel, party hat.
Also, Check:
Properties of Solid Shapes
1. Solid shapes or solid figures are three-dimensional geometric figures that means they have length, breadth, and height.
2. Solid figures have three dimensions.
3. They have the number of faces, edges, and vertices based on the figure.
Solid Figures Examples
Example 1.
Find the volume and surface area of a cuboid of length 5 cm, breadth 6 cm, and height 7 cm.
Solution:
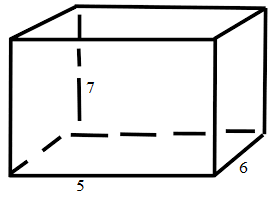
Given that
length= 5 cm
breadth = 6 cm
height = 7 cm
Volume of cuboid = V = l x b x h
= 5 x 6 x 7
= 210 cm³
Surface area of a cuboid = 2 ( lb + lh + bh)
= 2( 5×6 + 6×7 + 5×7)
=2(30 + 42 + 35)
=2(107)
= 142cm²
Thus the surface area of a cuboid is 142cm²
Example 2.
Find the volume of the sphere of radius 28 cm.
Solution:
Given that
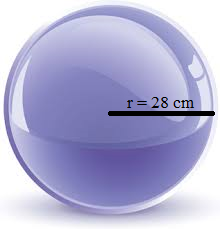
radius of the sphere = r = 28 cm
Volume of sphere = 4/3 πr³
= (4/3) × (22/7) × 28 × 28 × 28
= 4 × 22 × 28 × 28 x 4
= 275,968cm³
Thus the volume of the sphere is 275,968cm³
Example 3.
The base radius and height of a right circular cone is 7 cm and 24 cm. Find its curved surface area and volume
Solution:
Given that
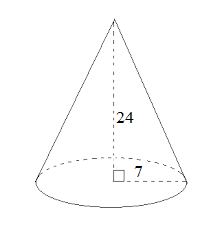
Radius = r = 7 cm
Height = h = 24 cm
Slant height = l = √ r² + h²
l = √7 × 7 + 24 × 24 cm
25 cm
Curved surface area = πrl
22/7 × 7 × 25 cm²
550 cm²
Total surface area = πrl + πr²
= (550 + 22/7 + 49) cm²
= (550 + 154) cm²
= 704 cm²
Volume = ⅓πr²h
= ⅓ × 22/7 × 49 × 24 cm³
= 1232 cm³
Thus the volume of a cone is 1232 cm³
Example 4.
A conical tent is 3 high and its base radius is 4 cm. Find the cost of the canvas required to make the tent at the rate of Rs 60 per unit.
Solution:
Given that
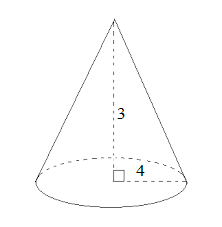
Radius = r = 3
Height = h = 4
Slant height = l = √r² + h²
= √ 9 + 16
= √25
= 5
Slant height of the tent is 5
Curved surface area = πrl
We know that π = 3.14
= 3.14 × 4 × 5
= 62.8
Therefore canvas required for making the tent = 62.8
Therefore cost of the canvas at 65 per m²
= 65 × 62.8
= 4082
Example 5.
The radius and height of the right circular cylinder are 7 cm and 10 cm. Find curved surface area, total surface area, and volume
Solution:
Given that
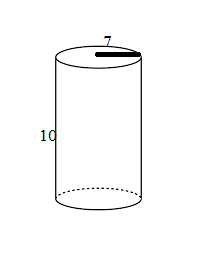
Radius = r = 7 cm
Height = h = 10 cm
The curved surface area of a circular cylinder = 2πrh
= 2 × 22/7 × 7 × 10 cm²
= 440 cm²
Total surface area of a circular cylinder = 2πrh + 2 πr²
= 2 × 22/7 × 7 × 10 + 2 × 22/7 × 7 × 7 cm²
= 440 cm² + 308 cm² = 748 cm²
Volume of a circular cylinder = πrh
= 22/7 × 7 × 10 cm²
= 1540 cm³
Thus the volume of the cylinder is 1540 cm³
Frequently Asked Questions on Solid Figures
1. What is meant by solid figures?
In geometry, the solid shapes are the objects that occupy space. Examples of solid shapes are cube, cone, cuboid, sphere, cylinder.
2. What is the measurement of a solid figure?
A solid figure has three dimensions while a plane figure has only two dimensions. The space enclosed by a solid figure is called its volume.
3. How do you represent solid figures?
Three-dimensional solid figures can be represented by the two-dimensional pattern of polygons that create them.
