Go through the enVision Math Common Core Grade 7 Answer Key Topic 8 Solve Problems Involving Geometry and finish your homework or assignments.
enVision Math Common Core 7th Grade Answers Key Topic 8 Solve Problems Involving Geometry
GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.

Question 1.
The number of square units that a figure covers is its _________.
Answer:
We know that,
The number of square units that a figure covers is its “Area”
Hence, from the above,
We can conclude that the best term to complete the given definition is the “Area”
Question 2.
The _________ of a triangle is the length of the perpendicular line segment from a vertex to the opposite side.
Answer:
We know that,
The “Height” of a triangle is the length of the perpendicular line segment from a vertex to the opposite side.
Hence, from the above,
We can conclude that the best term to complete the given definition is the “Height”
Question 3.
The _________ of a solid figure is the number of cubic units needed to fill it.
Answer:
We know that,
The “Volume” of a solid figure is the number of cubic units needed to fill it
Hence, from the above,
We can conclude that the best term to complete the given definition is the “Volume”
Question 4.
Any line segment that connects the center of a circle to a point on the circle is called a __________.
Answer:
We know that,
Any line segment that connects the center of a circle to a point on the circle is called a “Radius”
Hence, from the above,
We can conclude that the best term to complete the given definition is the “Radius”
Area and Volume
Find each measure.
Question 5.
Area of a triangle with a base 6 feet and height 9 feet
Answer:
It is given that
The base of the triangle is: 6 feet
The height of the triangle is: 9 feet
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
So,
A = \(\frac{1}{2}\) × 6 × 9
= \(\frac{54}{2}\)
= 27 feet²
Hence, from the above,
We can conclude that the area of the given triangle is: 27 feet²
Question 6.
The volume of a rectangular prism with length 4 inches, width 2 inches, and height 2 inches
Answer:
It is given that
The length of a rectangular prism is: 4 inches
The width of a rectangular prism is: 2 inches
The height of a rectangular prism is: 2 inches
Now,
We know that,
The volume of a rectangular prism (V) = Length × Width × Height
So,
V = 4 × 2 × 2
= 16 inches³
Hence, from the above,
We can conclude that the volume of the given rectangular prism is: 16 inches³
Measure Angles
Use a protractor to find the measure of each angle.
Question 7.
Answer:
To measure the angle, use “https://www.geogebra.org/calculator”
So,
The measured angle is:
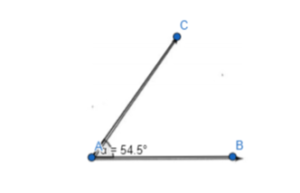
Hence, from the above,
We can conclude that the measured angle using the protractor is: 54.5°
Question 8.
Answer:
To measure the angle, use “https://www.geogebra.org/calculator”
So,
The measured angle is:
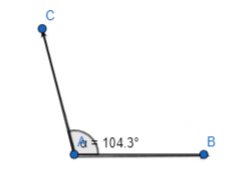
Hence, from the above,
We can conclude that the measured angle using the protractor is: 104.3°
Describe Characteristics of Shapes
Describe this figure using as many geometry terms as you can.
Question 9.
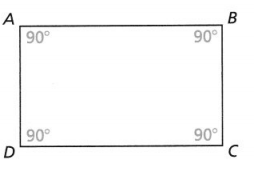
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
a. All the angles are 90°
b. The parallel sides are the same
c. The diagonals bisect each other
d. The lengths of the diagonals are equal
So,
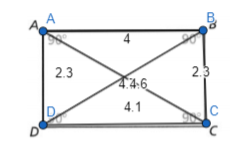
Hence, from the above,
We can conclude that the given figure is a “Rectangle”
Language Development
Fill in the word web to connect keywords you learn in this topic. A sample keyword and its connections are given.

PICK A PROJECT
PROJECT 8A
If you built a sculpture, what materials would you use?
PROJECT: CONSTRUCT A THREE-DIMENSIONAL SCULPTURE
PROJECT 8B
If you made a pizza, what kind of pizza would it be?
PROJECT: ANALYZE A PEPPERONI PIZZA
PROJECT 8C
What places have you visited where being a tour guide would be fun?
PROJECT: PLAN A GUIDED TOUR
PROJECT 8D
How could you determine which is a larger-a tall building or a wide building?
PROJECT: BUILD A SCALE MODEL
Lesson 8.1 Solve Problems Involving Scale Drawings
Explore It!
Calvin made a scale model of the plane shown.

I can… use the key in a scale drawing to find missing measures.
A. How can you represent the relationship between the model of the plane and the actual plane?
Answer:
The given figure is:

Now,
The representation of the relationship between the model of the plane and the actual plane is:
The actual diagram is an enlarged diagram of the scale diagram
So,
The scale factor = \(\frac{15 in.}{240 ft}\)
= \(\frac{1}{16}\)
Hence, from the above,
We can conclude that the actual diagram is 16 times larger than the scale diagram
B. What do you notice about the relationship between the model of the plane and the actual plane?
Answer:
We know that,
The relationship between the model of the plane and the actual plane can be given by a “Scale factor”
So,
The scale factor = \(\frac{15 in.}{240 ft}\)
= \(\frac{1}{16}\)
Hence, from the above,
We can conclude that the actual diagram is 16 times larger than the scale diagram
Focus on math practices
Look for Relationships If the model and the actual plane are to scale, what do you know about the relationship between all the other parts of the model and the actual plane, aside from the total length?
Answer:
If the model and the actual plane are to scale, then
All the other parts of the model and the actual plane, aside from the total length are also scaled
Essential Question
How do scale drawings and actual measurements represent proportional relationships?
Answer:
The “Scale factor” is the amount that an image is enlarged or shrunk. It is also called ‘k’ because k represents the multiplier between two proportional ratios and scale drawings represent proportional relationships
Try It!
What is the actual width, w, of the island if the width in the drawing is 2.5 inches?
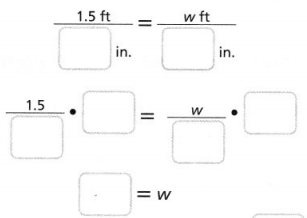
The actual width of the island is _______ feet.
Answer:
From Example 1,
It is given that,
Scale: 1 inch = 1.5 ft
Now,
\(\frac{1.5}{1}\) = \(\frac{w}{2.5}\)
w = \(\frac{1.5 × 2.5}{1}\)
w = 3.75 feet
Hence, from the above,
We can conclude that the actual width of the island is: 3.75 feet
Convince Me! How would the proportion for Example 1 change if the scale changed?
Answer:
For Example 1,
If the scale changed, then
The proportion would increase or decrease
Case 1:
If the scale changed to:
1 in = 2 ft
Then, the proportion will change like
\(\frac{2}{1}\) = \(\frac{x}{6}\)
x = \(\frac{6 × 2}{1}\)
x = 12 feet
So,
The actual width of the island is: 12 feet
Case 2:
If the scale changed to:
1 in = 1.25 ft
Then, the proportion will change like
\(\frac{1.25}{1}\) = \(\frac{x}{6}\)
x = \(\frac{6 × 1.25}{1}\)
x = 7.5 feet
So,
The actual width of the island is: 7.5 feet
Hence, from the above,
We can conclude that
If the scale increases, then the proportion also increases
If the scale decreases, then the proportion also decreases
Try It!
The scale drawing shown represents an existing barn. The shortest side of the barn measures 150 meters. If a new barn that is \(\frac{2}{3}\) its size replaces the existing barn, what will be the scale of this drawing to the new barn?

Answer:
It is given that
The scale drawing shown represents an existing barn. The shortest side of the barn measures 150 meters and a new barn that is \(\frac{2}{3}\) its size replaces the existing barn
Now,
The representation of the existing barn is:

Now,
The length of the shortest side for a new barn = \(\frac{2}{3}\) × 150
= 100 in.
So,
The scale factor for the shortest side for a new barn = \(\frac{150}{100}\)
= 1.5
Hence, from the above,
We can conclude that
The scale of the drawing to the new barn is 1: 1.5
KEY CONCEPT
The scale factor of a scale drawing is the ratio of an actual length, y, to the corresponding length, x, in the drawing. The ratio is the constant of proportionality, k, that relates the actual figure to the scale drawing. You can use a proportion or use an equation of the form y = kx to solve problems involving scale drawings.
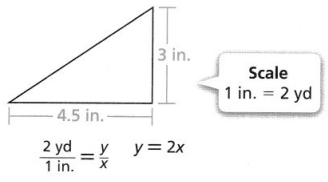
Do You Understand?
Question 1.
Essential Question How do scale drawings and actual measurements represent proportional relationships?
Answer:
The “Scale factor” is the amount that an image is enlarged or shrunk. It is also called “k” because k represents the multiplier between two proportional ratios and scale drawings represent proportional relationships
Question 2.
Generalize Describe the ratio of corresponding measures in scale drawings and the actual measures they represent?
Answer:
A scale drawing is a drawing that is to scale an original image. When an object is “to scale,” that means it is the same shape, but not the same size. It is also called k because k represents the multiplier between two proportional ratios and scale drawings represent proportional relationships.
Question 3.
Reasoning Mikayla is determining the actual distance between Harrisville and Lake Town using a map. The scale on her map reads. 1 inch = 50 miles. She measures the distance to be 4.5 inches and writes the following proportion:
\(\frac{1 \mathrm{in.}}{4.5 \mathrm{in.}}=\frac{50 \mathrm{mi}}{x \mathrm{mi}}\)
Explain why her proportion is equivalent to
\(\frac{50 \mathrm{mi}}{1 \text { in. }}=\frac{x \mathrm{mi}}{4.5 \mathrm{in} .}\)
Answer:
It is given that
Reasoning Mikayla is determining the actual distance between Harrisville and Lake Town using a map. The scale on her map reads. 1 inch = 50 miles. She measures the distance to be 4.5 inches
So,
The scale for the distance between Harrisville and Lake Town using a map is: 50: 1
Now,
Let the value that is equivalent to 4.5 inches be x miles
Now,
To find the value in miles that is equivalent to 4.5 inches,
We have to write
\(\frac{1 in.}{4.5 in.}\) = \(\frac{50 mi}{x mi}\)
Now,
Cross-Multiply the given equation
So,
\(\frac{50 mi}{1 in.}\) = \(\frac{x miles}{4.5 in.}\)
Hence, from the above,
We can conclude that the proportion is in the above form because of the cross-multiplication
Do You Know How?
Question 4.
What is the actual base length of the triangle depicted in the scale drawing?
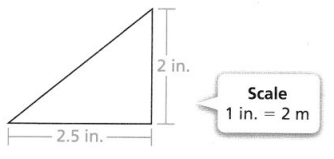
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The scale factor = \(\frac{2}{1}\)
So,
The actual base length of the given triangle = (The base length as depicted in the given triangle) × (Scale factor)
= 2.5 × \(\frac{2}{1}\)
= 2.5 × 2
= 5 m.
Hence, from the above,
We can conclude that
The actual base length of the triangle as depicted in the given scale drawing is: 5 m
Question 5.
What is the area of the actual square window shown in the scale drawing?
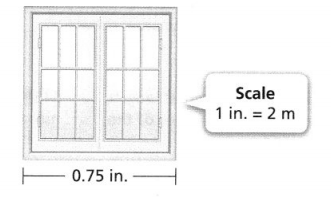
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
Scale factor = \(\frac{2}{1}\)
So,
The actual side length of the given square window = (The side length of the given square window) × (Scale factor)
= 0.75 × 2
= 15 m
Now,
We know that,
The area of a square = Side²
So,
The area of the actual square window = (Actual Side length of the given square window)²
= 15 m × 15 m
= 225 m²
Hence, from the above,
We can conclude that the area of the actual square window is: 225 m²
Question 6.
A distance of 30 miles on a map is represented by a 2-inch line. If the map is enlarged to 3 times its size, what will be the scale of the enlarged map?
Answer:
It is given that
A distance of 30 miles on a map is represented by a 2-inch line and the map is enlarged to 3 times its size
Now,
The scale distance on a map = \(\frac{Actual distance on a map}{Scale of a map}\)
= \(\frac{30}{2}\)
= 15 inches
Now,
The scale distance on the enlarged map = (The scale distance on a normal map) × 3
= 15 × 3
= 45 inches
So,
The scale of the enlarged map = \(\frac{45}{3}\)
= 15
Hence, from the above,
We can conclude that the scale of the enlarged map is: 1inch = 15 miles
Practice & Problem Solving
Leveled Practice For 7 and 8, fill in the boxes to find the actual measures.
Question 7.
On a map, 1 inch equals 5 miles. Two cities are 8 inches apart on the map.
What is the actual distance between the cities?
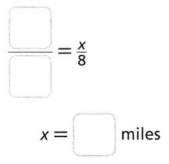
Answer:
It is given that
On a map, 1 inch equals 5 miles. Two cities are 8 inches apart on the map.
Now,
The scale factor from the given information is:
1 inch = 5 miles
So,
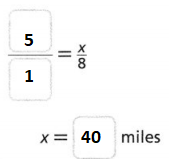
Hence, from the above,
We can conclude that
The actual distance between the cities is: 40 miles
Question 8.
Ryan makes a scale drawing of a banner for a school dance. He uses a scale of 1 inch = 3 feet, and the width of the drawing is 5 inches. What is the actual width, w, of the banner?
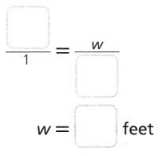
Answer:
It is given that
Ryan makes a scale drawing of a banner for a school dance. He uses a scale of 1 inch = 3 feet, and the width of the drawing is 5 inches
Now,
From the given information,
We can observe that
The actual width of the banner (w) = (The width of the drawing) × (Scale factor)
So,

Hence, from the above,
We can conclude that
The actual width (w) of the banner is: 15 feet
Question 9.
On a map, 1 inch equals 7.2 miles. Two houses are 1.5 inches apart on the map. What is the actual distance between the houses?
Answer:
It is given that
On a map, 1 inch equals 7.2 miles. Two houses are 1.5 inches apart on the map
So,
From the given information,
The scale factor = \(\frac{7.2}{1}\)
Now,
Let the actual distance between the houses be d
So,
\(\frac{7.2}{1}\) = \(\frac{d}{1.5}\)
d = 7.2 × 1.5
d = 10.80 miles
Hence, from the above,
We can conclude that
The actual distance between the houses is: 10.8 miles
Question 10.
The original blueprint for the Morenos’ living room has a scale of 2 inches = 5 feet. The family wants to use a new blueprint that shows the length of the living room to be 15 inches. If the width of the living room on the original blueprint is 6 inches and the length is 9.6 inches, what are the scale and the width of the new blueprint?
Answer:
It is given that
The original blueprint for the Morenos’ living room has a scale of 2 inches = 5 feet. The family wants to use a new blueprint that shows the length of the living room to be 15 inches and the width of the living room on the original blueprint is 6 inches and the length is 9.6 inches
Now,
The length of the new blueprint = (Scale factor) × (The length of the original blueprint)
= \(\frac{5}{2}\) × 9.6
= 5 × 4.8
= 24.0 inches
= 24 inches
The width of the new blueprint = (Scale factor) × (The width of the original blueprint)
= \(\frac{5}{2}\) × 6
= 5 × 3
= 15 inches
Now,
\(\frac{24}{15}\) = \(\frac{x}{1}\)
x = \(\frac{8}{3}\)
Hence, from the above,
We can conclude that
The scale factor for the new blueprint is:
3 inches = 8 feet
Question 11.
The scale for a drawing of the tennis court is 1 centimeter = 2 meters. What is the area of the actual tennis court?

Answer:
It is given that
The scale for a drawing of the tennis court is 1 centimeter = 2 meters.
Now,
The given figure is:

So,
The length of the actual tennis court = (Scale factor) × (The length of the scaled tennis court)
= 2 × 10
= 20 meters
So,
The width of the actual tennis court = (Scale factor) × (The width of the scaled tennis court)
= 2 × 5.5
= 11 meters
Now,
We know that,
The area of a rectangle = Length × Width
So,
The area of the actual tennis court = (The length of the actual tennis court) × (The width of the actual tennis court)
= 20 × 11
= 220 meters²
Hence, from the above,
We can conclude that the area of the actual tennis court is: 220 meters²
Question 12.
The scale for the drawing of a rectangular playing field is 2 inches = 5 feet.
a. Write an equation you can use to find the dimensions of the actual field, where x is a dimension of the scale drawing (in inches) and y is the corresponding dimension of the actual field (in feet).
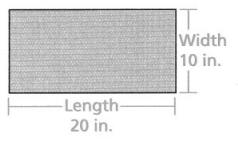
Answer:
It is given that
The scale for the drawing of a rectangular playing field is 2 inches = 5 feet.
Now,
The given figure is:

Now,
From the given information,
The scale factor = \(\frac{5}{2}\)
So,
The actual length of the rectangular playing field = (Scale factor) × (The length of the scaled rectangular playing field)
= \(\frac{5}{2}\) × 20
= 5 × 10
= 50 feet
The actual width of the rectangular playing field = (Scale factor) × (The width of the scaled rectangular playing field)
= \(\frac{5}{2}\) × 10
= 5 × 5
= 25 feet
So,
The scale factor for the actual rectangular playing field can be found out by:
\(\frac{50}{20}\) = \(\frac{x}{1}\) (or) \(\frac{25}{10}\) = \(\frac{x}{1}\)
x = \(\frac{5}{2}\)
Hence, from the above,
We can conclude that
The scale for the actual rectangular playing field is:
2 inches = 5 feet
b. What is the area of the field?
Answer:
From part (a),
We can observe that
The actual length of the rectangular playing field = (Scale factor) × (The length of the scaled rectangular playing field)
= \(\frac{5}{2}\) × 20
= 5 × 10
= 50 feet
The actual width of the rectangular playing field = (Scale factor) × (The width of the scaled rectangular playing field)
= \(\frac{5}{2}\) × 10
= 5 × 5
= 25 feet
So,
The area of the rectangular playing field = (Actual length) × (Actual width)
= 50 × 25
= 1,250 feet²
Hence, from the above,
We can conclude that
The area of the field is: 1,250 feet²
Question 13.
How many square feet of flooring are needed to cover the entire floor of Bedroom 1?
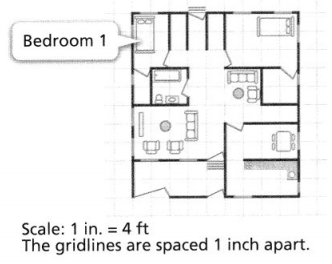
Answer:
Question 14.
The actual distance between Point A and Point B is 200 meters. A length of 1.9 feet represents this distance on a certain wall map. Point C and Point D are 3.8 feet apart on this map. What is the actual distance between Point C and Point D?
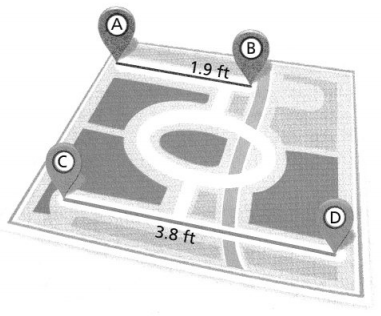
Answer:
It is given that
The actual distance between Point A and Point B is 200 meters. A length of 1.9 feet represents this distance on a certain wall map. Point C and Point D are 3.8 feet apart on this map
Now,
Let the actual distance between points C and D be x meters
So,
\(\frac{200}{x}\) = \(\frac{1.9}{3.8}\)
\(\frac{200}{x}\) = \(\frac{1}{2}\)
x = 200 × 2
x = 400 meters
Hence, from the above,
We can conclude that
The actual distance between points C and D is: 400 meters
Question 15.
Higher-Order Thinking A map of a highway has a scale of 2 inches equals 33 miles. The length of the highway on the map is 6 inches. There are 11 rest stops equally spaced on the highway, including one at each end. You are making a new map with a scale of 1 inch equals 30 miles. How far apart are the rest stops on the new map?
Answer:
It is given that
A map of a highway has a scale of 2 inches equals 33 miles. The length of the highway on the map is 6 inches. There are 11 rest stops equally spaced on the highway, including one at each end. You are making a new map with a scale of 1 inch equals 30 miles
So,
The actual length of the highway according to the scale of 2 in = 33 miles is:
The actual length of the highway = (Scale factor) × (The length of the highway on the map)
= \(\frac{33}{2}\) × 6
= 33 ×3
= 99 miles
The actual length of the highway according to the scale of 1 in = 30 miles is:
The actual length of the highway = (Scale factor) × (The length of the highway on the map)
= \(\frac{30}{1}\) × 6
= 30 ×6
= 180 miles
Now,
Let the number of stops on the highway with a scale of 1 in = 30 miles be x
So,
\(\frac{99}{11}\) = \(\frac{180}{x}\)
\(\frac{180}{x}\) = 9
x = \(\frac{180}{9}\)
x = 20 stops
Now,
The distance between the rest stops = \(\frac{30}{20}\)
= 1.5 feet
Hence, from the above,
We can conclude that
The distance between the rest stops on the new map are 1.5 feet
Assessment Practice
Question 16.
The original blueprint of a concrete patio has a scale of 2 inches = 3 feet.

Victoria wants to make a new blueprint of the patio with a length of 16.8 inches.
PART A
What is the scale for the new blueprint?
1 inch = _______ feet
Answer:
It is given that
The original blueprint of a concrete patio has a scale of 2 inches = 3 feet.
Now,
The given figure is:

Now,
From the given information,
Scale factor = \(\frac{3}{2}\)
So,
The length of the new blueprint = (Scale factor) × (The length of the original blueprint)
= \(\frac{3}{2}\) × 14
= 3 × 7
= 21 inches
Now,
\(\frac{14}{16.8}\) = \(\frac{21}{x}\)
x = 8.4 × 3
x = 25.2
Hence, from the above,
We can conclude that
The scale factor for the new blueprint is:
1 inch = 25.2 feet
PART B
What is the width, in inches, of the blueprint with the new scale?
Answer:
The given figure is:

So,
The width of the new blueprint = (Scale factor) × (The length of the original blueprint)
= \(\frac{3}{2}\) × 12
= 3 × 6
= 18 inches
Hence, from the above,
We can conclude that
The width (w) of the blueprint with the new scale is: 18 inches
Lesson 8.2 Draw Geometric Figures
Solve & Discuss It!
Students in the Art Club are designing a flag with the school’s mascot and emblem. The flag has four sides, with two sides that are twice as long as the other two sides. What shape could the flag be, and what dimensions could it have? Make and label a scale drawing as part of your answer.

I can… draw figures with given conditions.
Answer:
It is given that
Students in the Art Club are designing a flag with the school’s mascot and emblem. The flag has four sides, with two sides that are twice as long as the other two sides.
Now,
We know that,
A “Quadrilateral” is only a geometrical figure which has 4 sides
Now,
Let the length of the two sides be x cm
Let the length of the other two sides be 2x cm
Where,
x = 1, 2, 3,……….., n
Now,
Let the value of x be 2
Hence,
The representations of the flag are:

Make Sense and Persevere: Is there more than one shape that could represent the flag?
Answer:
Yes, there is more than one shape that could represent the flag
Now,
The representations of the flag are:

Hence,
From the above representation,
The different shapes of the flags are: Rectangle, Parallelogram, and Trapezium, and a Quadrilateral
Focus on math practices
Reasoning How did you decide what lengths to use for the four sides of the flag you drew? What lengths could the actual flag be, based on your drawing?
Answer:
It is given that
The flag has four sides, with two sides that are twice as long as the other two sides
Now,
Let the length of the two sides be x cm
Let the length of the other two sides be 2x cm
Where,
x = 1, 2, 3,……….., n
Now,
Based on the drawing that is present in part (a),
The actual lengths of the drawing are: 2 inches, 2 inches, 4 inches, and 4 inches
Essential Question
How can a shape that meets given conditions be drawn?
Answer:
Use the conditions that are given to draw a shape and based on that shape, determine the name of the shape and its dimensions
Try It!
Use a ruler and protractor to draw a quadrilateral with two equal sides that meet at a right angle, and two nonadjacent angles of the same measure. What is the name of the quadrilateral you drew?
The quadrilateral I drew is a ___________
Answer:
It is given that
Use a ruler and protractor to draw a quadrilateral with two equal sides that meet at a right angle, and two nonadjacent angles of the same measure.
Now,
The steps to draw the quadrilateral are:
Step 1:
Draw the line segment AB with a certain length i.e., AB = 4 cm
Step 2:
From B, make an angle of 90° with the same length as AB and draw a line segment BC
Step 3:
From C, make another angle of 90° and draw a line segment CD
Hence, from the above steps,
We can conclude that the quadrilateral drawn is: Square

Convince Me! Could you have drawn more than one shape that fits the given conditions? Explain.
Answer:
No, we can’t draw any shape other than the square that fits the above conditions
Try It!
a. Make a sketch to show another way Mr. Miller can arrange the desks to seat 10 people for lunch.
Answer:
The representation of the arrangement of desks to seating 10 people for lunch is:
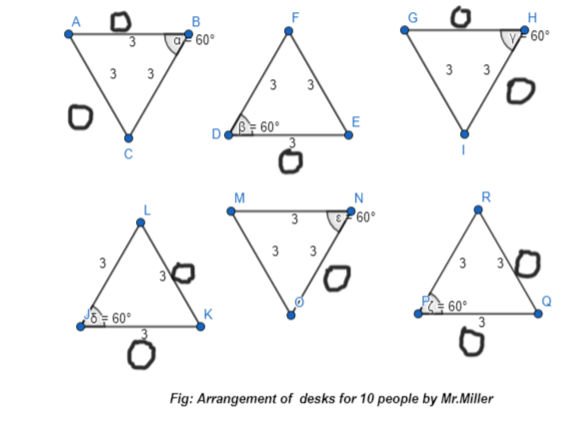
Hence, from the above arrangement,
We can conclude that Mr.Millercan arrange 6 desks in 2 rows to seat 10 people for lunch
b. Use geometry software to make a rhombus with a side length of 6 units and two angles that measure 45°.
Answer:
To draw a rhombus,
The geometry software we can use is: Geogebra
Now,
To draw a rhombus, the following steps have to be followed:
Step 1:
Draw a line segment AB with a length of 6 cm
Step 2:
From A, make an angle of 45° and join that segment and name it as AD
Step 3:
From D, draw a line segment DC = 6 cm
Step 4:
From C, make an angle of 45° and join A and C
Hence, from the above steps,
The representation of the rhombus is:
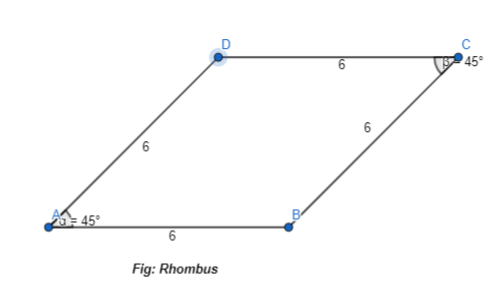
KEY CONCEPT
You can draw shapes that meet given conditions freehand, with a ruler and protractor, or with technology, The given conditions may include properties of geometric figures and relationships between parts of the figures.
Use Appropriate Tools Deciding how precise the drawing of the shape should be will help you choose the method you use to draw the shape.
Do You Understand?
Question 1.
Essential Question How can a shape that meets given conditions be drawn?
Answer:
Use the conditions that are given to draw a shape and based on that shape, determine the name of the shape and its dimensions
Question 2.
Use Appropriate Tools How can you decide whether to draw a shape freehand, with a ruler and protractor, or using technology?
Answer:
a. We will draw a shape freehand when there are not any measurements to draw a particular shape but only the name of the shape
b. We will draw a shape with a ruler when the measurements are specified for a particular shape
c. We will draw a shape with a protractor and a ruler when the measurements and an angle for a particular shape are specified
Question 3.
Construct Arguments Why can you draw more than one quadrilateral using four right angles?
Answer:
We know that,
A parallelogram is a quadrilateral with 2 pairs of opposite sides parallel. A rectangle is a special parallelogram that has 4 right angles. A square is a special rectangle that has all four sides congruent. The angle between these two sides could be a right angle
Hence, from the above,
We can conclude that we can draw more than one quadrilateral using four right angles
Do You Know How?
Question 4.
Draw, freehand, a quadrilateral with exactly one pair of parallel sides and at least one angle measuring 45°.
Answer:
The steps to draw a freehand quadrilateral with exactly one pair of parallel sides and at least one angle measuring 45° are:
Step 1:
Draw a line segment AB with a certain length
Step 2:
Mark an angle of 45° from point A using the protractor and join the segment and name it as BC
Step 3:
From B, draw a line segment such that the length of AB must not be equal to the line segment that is drawn from B and name it BC
Step 4 :
From C, draw a line segment named CDand the length of CD must be equal to the length of AB since they are 2 parallel sides
Step 5:
Join D and A and so we will get the desired quadrilateral
Question 5.
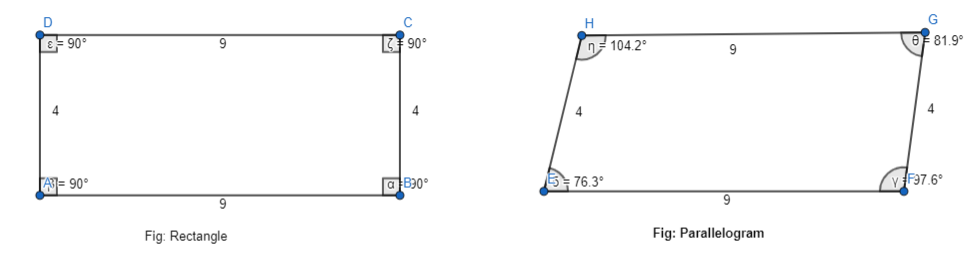
Use a ruler and protractor to draw a quadrilateral with four right angles, two side lengths each measuring 3 inches, and two side lengths each measuring 4 inches. What is the most descriptive name of the figure you drew?
Answer:
It is given that
Use a ruler and protractor to draw a quadrilateral with four right angles, two side lengths each measuring 3 inches, and two side lengths each measuring 4 inches
So,
By using the Geometry software,
The representation of the quadrilateral with the given specifications is:
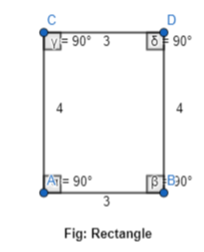
Hence, from the above,
We can conclude that the suitable name of the quadrilateral that was drawn using the given specifications is: Rectangle
Question 6.
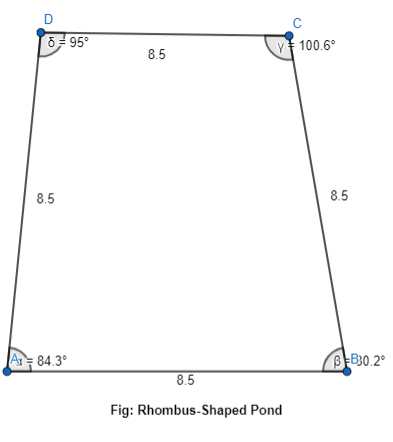
Use geometry software to draw a quadrilateral with two angles measuring 80° and two angles measuring 100°. What is the name of the figure you drew?
Answer:
It is given that
Use geometry software to draw a quadrilateral with two angles measuring 80° and two angles measuring 100°.
So,
The representation of the quadrilateral with the given specifications is:
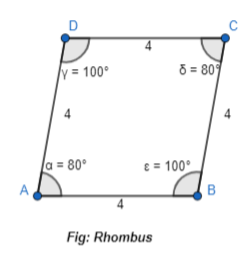
Now,
From the above figure,
We can observe that
a. All the angles are not equal to 90°
b. All the side lengths are equal
Hence, from the above,
We can conclude that the quadrilateral we were drawn using the given specifications is: Rhombus
Practice & Problem Solving
Question 7.
What quadrilaterals can you draw that have exactly four right angles?
Answer:
The quadrilaterals that we can draw that have exactly four right angles are:
a. Rectangle b. Square
Question 8.
A four-sided sandbox has more than two right angles, two side lengths of 2 feet, and two side lengths of 5 feet. What geometric shape best describes the shape of the sandbox?
Answer:
It is given that
A four-sided sandbox has more than two right angles, two side lengths of 2 feet, and two side lengths of 5 feet
So,
The representation of the sandbox with the given specifications is:
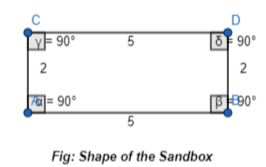
Now,
From the above figure,
We can observe that
a. All the angle measures are 90°
b. The parallel sides are of the same length
Hence, from the above,
We can conclude that the shape of the given sandbox is: Rectangle
Question 9.
What quadrilateral can you draw that has exactly one pair of parallel sides?
Answer:
The quadrilateral you can draw that has exactly one pair of parallel sides is: Trapezoid
Question 10.
A friend is building a 4-sided garden with two side lengths of 19 feet and exactly one right angle. What quadrilaterals could describe the garden?
Answer:
It is given that
A friend is building a 4-sided garden with two side lengths of 19 feet and exactly one right angle.
So,
From the above specifications,
The shape of the garden must be a rectangle
So,
The representation of the 4-sided garden with the given specifications is:
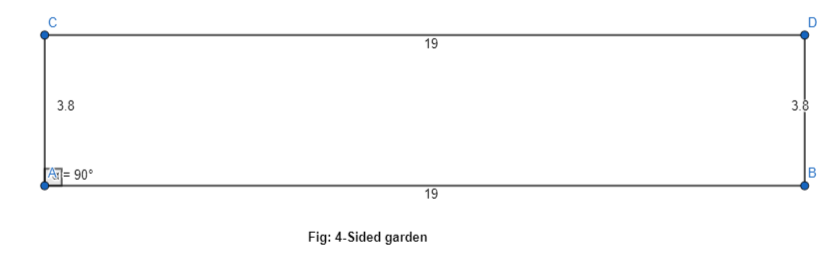
Hence, from the above,
We can conclude that the quadrilateral that could describe the garden is: Rectangle
Question 11.
What quadrilaterals can you draw that have two side lengths of 9 centimeters and two side lengths of 4 centimeters?
Answer:
The quadrilaterals that you can draw that have two side lengths of 9 cm and two side lengths of 4 cm are:
a. Rectangle (With all the angle measures 90°)
b. Parallelogram ( WIth all the angle measures not equal to 90°)
Hence,
The representation of the two quadrilateral with the given specifications is:
Question 12.
A park has a pond shaped like a quadrilateral with side lengths of 17 feet and no right angles. What other geometric shapes could describe the shape of the pond?
Answer:
It is given that
A park has a pond shaped like a quadrilateral with side lengths of 17 feet and no right angles
Now,
We know that,
A quadrilateral that has all the side lengths equal and no right angles is: Rhombus
So,
The shape of the pond is: Rhombus
Now,
We know that,
Any other geometric shape does not have all the equal side lengths other than the square but in the square, all the angle measures are 90°
Hence, from the above,
We can conclude that the shape of the pond is: Rhombus
 Scale: 1 cm = 2 feet
Scale: 1 cm = 2 feet
Question 13.
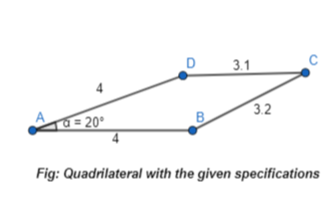
Draw a quadrilateral that has one angle measure of 20° and exactly one side length of 4 units.
Answer:
It is given that to draw a quadrilateral that has one angle measure of 20° and exactly one side length of 4 units.
Hence,
The representation of the quadrilateral with the given specifications by using the geometry software is:
Question 14.
Which of the following shapes are trapezoids that have side lengths of 7 inches and 5 inches and a right angle? Select all that apply.
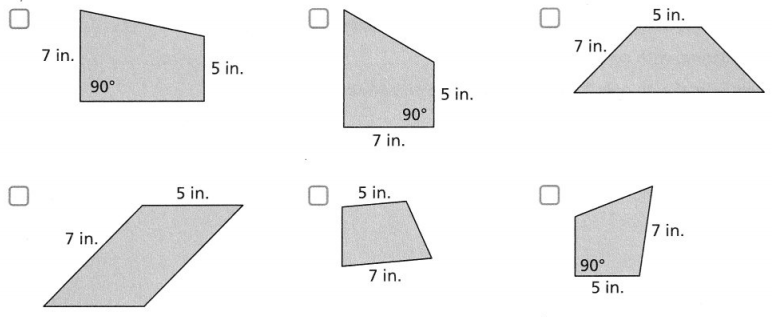
Answer:
We know that,
A right-angled Trapezoid has 2 adjacent right angles and a pair of parallel sides
Hence,
The Trapezoids that have represented by the given specifications are:
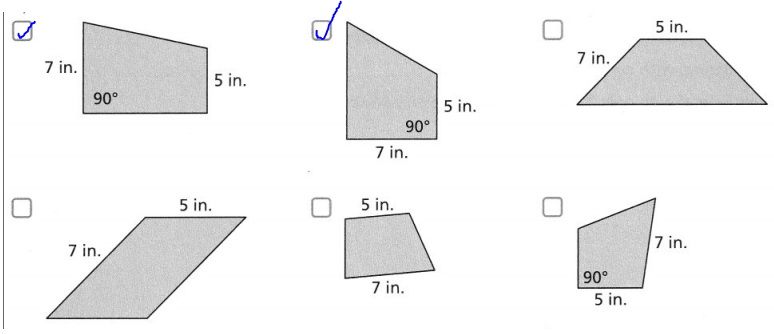
Question 15.
Using computer software, draw a quadrilateral with two sets of parallel sides and two angles measuring 135 degrees.
Answer:
It is given that
Draw a quadrilateral with two sets of parallel sides and two angles measuring 135 degrees.
Hence,
The representation of the quadrilateral with the given specifications by using the geometry software is:
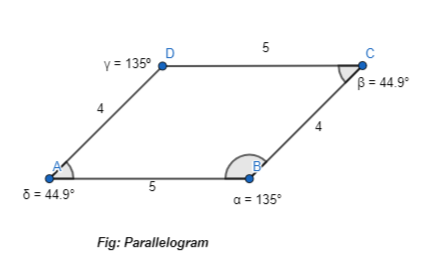
Question 16.
Higher-Order Thinking Draw a rhombus with side lengths of 6 units and angle measures of 100°, 80°, 100°, and 80°.
Answer:
It is given that
Draw a rhombus with side lengths of 6 units and angle measures of 100°, 80°, 100°, and 80°.
Hence,
The representation of a rhombus with the given specifications by using the geometry software is:

Assessment Practice
Question 17.
Thomas is painting a geometry mural. He is painting quadrilaterals that have at least 1 line of symmetry.
PART A
Which could be a quadrilateral that Thomas painted? Select all that apply.
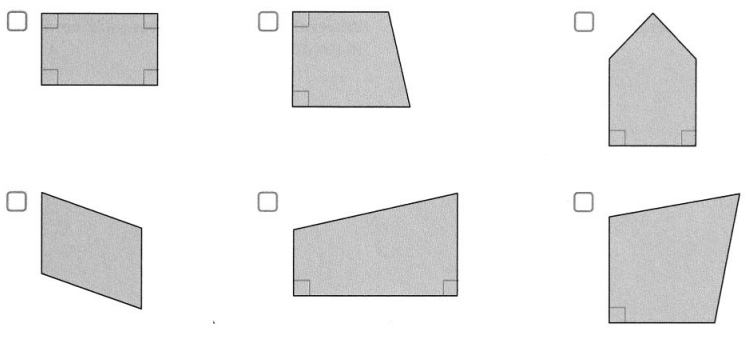
Answer:
It is given that
Thomas is painting a geometry mural. He is painting quadrilaterals that have at least 1 line of symmetry.
Now,
We know that,
The “Symmetry lines” are the lines that have equal side lengths
Hence, from the above,
The quadrilaterals that Thomas painted are:
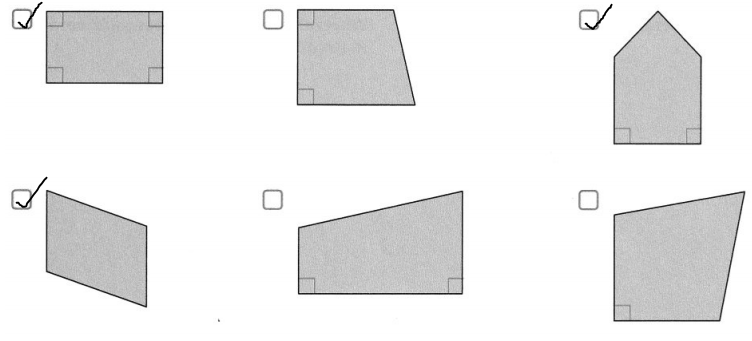
PART B
Which of the following figures can he also include in his painting?
A. quadrilateral with no equal sides
B. A quadrilateral with only 2 equal sides that are perpendicular to each other
C. A quadrilateral with 2 pairs of equal sides and 1 right angle
D. A quadrilateral with 2 pairs of parallel equal sides, with no right angles
Answer:
From part (a),
We can observe that the quadrilaterals that are included in Thomas painting have:
a. The equal sides and 1 right angle (or) more than one right angle
b. The equal pair of sides and no right angles
Hence, from the above,
We can conclude that the nature of figures that are included in Thomas paintings are: Option C and Option D
Lesson 8.3 Draw Triangles with Given Conditions
Solve & Discuss It!
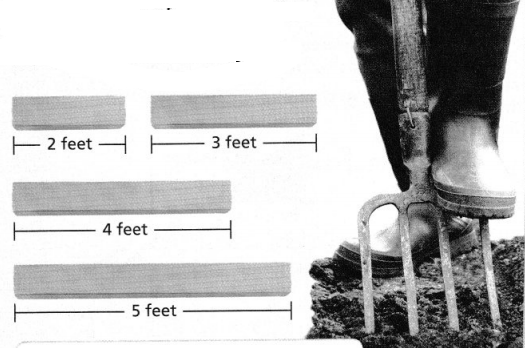
Kane has 4 pieces of wood available to build a triangle-shaped garden. Which pieces of wood can he use?
I can… draw triangles when given information about their side lengths and angle measures.
Answer:
It is given that
Kane has 4 pieces of wood available to build a triangle-shaped garden.
Now,
We know that,
To build a Triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the third side
Now,
The given pieces of wood are:
a. 2 feet b, 3 feet c. 4 feet d. 5 feet
So,
The possible combination of pieces of wood is:
a. (2, 3, 5) b. (2, 3, 4) c. (3, 4, 5) d. (2, 4, 5)
Now,
The possible combination of pieces of wood that allow to form a triangle-shaped garden is:
a. 2 + 3 !>[Not greater thhan] 5
b. 2 + 3 > 4
c. 3 + 4 > 5
d. 2 + 4 > 5
Hence, from the above,
We can conclude that the possible combinations of the pieces of wood that form a Triangle-shaped garden are:
a. (2 feet, 3 feet, 4 feet)
b. (3 feet, 4 feet, 5 feet)
c. (2 feet, 4 feet, 5 feet)
Make Sense and Persevere Try all possible combinations of three pieces of wood.
Answer:
We know that,
To build a Triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the third side
Now,
The given pieces of wood from part (a) are:
a. 2 feet b, 3 feet c. 4 feet d. 5 feet
So,
The possible combination of pieces of wood to form a triangle-shaped garden is:
a. (2, 3, 5) b. (2, 3, 4) c. (3, 4, 5) d. (2, 4, 5)
Now,
The possible combination of pieces of wood that allow to form a triangle-shaped garden is:
a. 2 + 3 !>[Not greater thhan] 5
b. 2 + 3 > 4
c. 3 + 4 > 5
d. 2 + 4 > 5
Hence, from the above,
We can conclude that the possible combinations of the pieces of wood that form a Triangle-shaped garden are:
a. (2 feet, 3 feet, 4 feet)
b. (3 feet, 4 feet, 5 feet)
c. (2 feet, 4 feet, 5 feet)
Focus on math practices
Use Structure Are there any combinations of three pieces of wood that will not create a triangle? Explain.
Answer:
Yes, there is a combination of three pieces of wood that will not create a triangle
Now,
From part (b),
We can observe that the combination of three pieces of wood that will not create a triangle is: (2, 3, 5)
Hence, from the above,
We can conclude that
The combination of three pieces of wood that will not create a triangle is: (2 feet, 3 feet, 5 feet)
Essential Question
How can you determine when it is possible to draw a triangle given certain conditions?
Answer:
The condition to draw a Triangle under the given conditions is:
The sum of the lengths of the two shortest sides must be greater than the length of the third side
Try It!
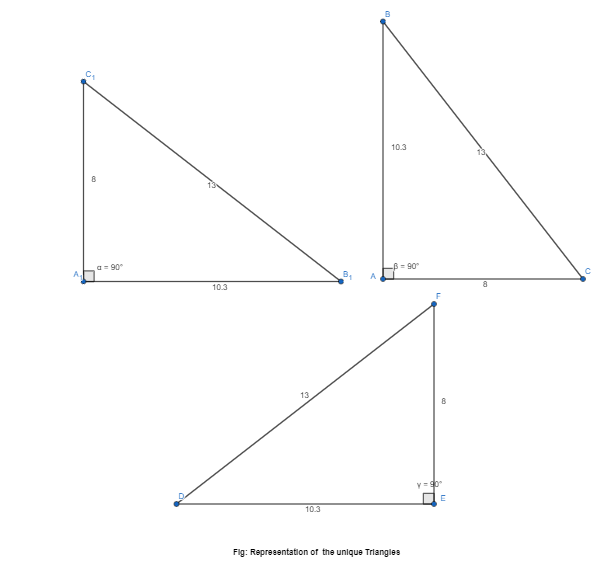
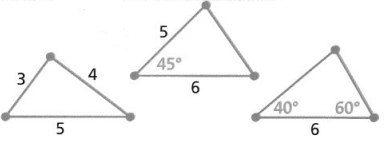
How many unique triangles can be drawn with given side lengths of 8 inches, 10.3 inches, and 13 inches?
_________ unique triangle(s) can be drawn with the given side lengths.
Answer:
The given side lengths are: 8 inches, 10.3 inches, and 13 inches
Now,
The representations of the given side lengths of the triangle in different positions are:
So,
From the above,
We can observe that the triangles with the same side lengths have the same shape and the same size, no matter how they are positioned
Hence, from the above,
We can conclude that “1 unique Triangle” can be drawn with the given side lengths
Convince Me! When two sides of a triangle are switched, why is it still considered the same triangle?
Answer:
When two sides of a triangle are switched, we are only switching their positions with their original side lengths.
So,
It is still considered the same triangle
Try It!
a. Write three side lengths that will form a triangle. Write three side lengths that will NOT form a triangle.
Answer:
We know that,
In order to construct a Triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the third side
Hence, from the above,
We can conclude that
The three side lengths that form a triangle are: 3 units, 4 units, and 5 units
The three side lengths that will not form a triangle are: 2 units, 3 units, and 5 units
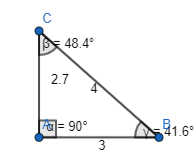
b. Can a triangle be drawn with a side length of 3 inches and angles at each end measuring 90° and 89°? Explain.
Answer:
It is given that
The side length of a triangle is: 3 inches
The angle measures of a triangle are 90° and 89°
Now,
We know that,
A triangle can only have 1 right angle
But,
The given triangle has 1 right angle and another almost right angle with a third angle measure 1°
Now,
The representation of the triangle with the given specifications will be like:
Hence, from the above,
We can conclude that
It is not possible to draw a triangle with a side length of 3 inches and angles at each end measuring 90° and 89°
Try It!
Can more than one triangle be drawn with two side lengths of 6 inches and a non-included angle of 60°? Explain.
Answer:
It is given that
The two side lengths of the triangle are: 6 inches and 6 inches
The non-included angle is: 60°
Now,
We know that,
As the two side lengths are the same, the triangle will be an “Isosceles Triangle”
So,
Besides the given angle measure, the other two angle measures must be the same
So,
The other two angle measures will be: 60° and 60° [ Since the first angle measure is 60° and the remaining angle measure is 120°]
So,
The representation of the triangle with the given specifications is:

Now,
From the above triangles,
We can observe that there is no change in shape irrespective of the same side lengths and the same non-included angle
Hence, from the above,
We can conclude that more than one triangle can not be drawn with two side lengths of 6 inches and a non-included angle of 60°
KEY CONCEPT
You can analyze given conditions of side lengths and angle measures to determine whether one unique triangle, more than one unique triangle, or no triangle can be drawn.
There is more than one possible triangle given these cases: all three angles, or two sides and a nonincluded angle.
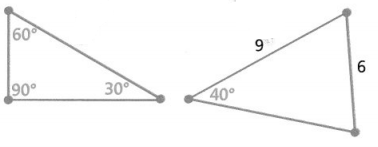
There is one unique triangle given these cases: all three sides, two sides and an included angle, or two angles and an included side.
Do You Understand?
Question 1.
Essential Question How can you determine when it is possible to draw a triangle given certain conditions?
Answer:
The condition to draw a Triangle under the given conditions is:
The sum of the lengths of the two shortest sides must be greater than the length of the third side
Question 2.
Look for Relationships What is the relationship between all triangles that can be drawn given the same three angle measures?
Answer:
If we have all the same three angle measures, then that triangle is known as an “Equilateral triangle”
So,
Whatever the turns, reflection, etc., we did, the shape of the equilateral triangle will not change
Hence, from the above,
We can conclude that a “Unique Triangle” can be formed if we draw a triangle will the same three angle measures
Question 3.
Why can there be only one way to draw a triangle if two sides and an included angle are given?
Answer:
It is possible to draw more than one triangle has the side lengths and angle measure as given. It depends on which line you start with, which end of the line you draw the angles, and whether they are above or below the line or not.
Hence, from the above,
We can conclude that because of the above, there is only one way to draw a triangle if two sides and an included angle are given
Do You Know How?
Question 4.
How many triangles can be drawn with side lengths 4 centimeters, 4.5 centimeters, and 9 centimeters? Explain.
Answer:
The given side lengths of a triangle are: 4 cm, 4.5 cm, and 9 cm
Now,
We know that,
In order to construct a triangle,
The sum of the length of the two shortest sides must be greater than the length of the third side
So,
4 + 4.5 > 9
8.5 >! 9
Hence, from the above,
We can conclude that the triangles can not be drawn for the given side lengths since the condition to form a triangle is not true for the given side lengths
Question 5.
Can more than one triangle be drawn with side lengths of 5 inches and 7 inches and an included angle with a measure of 50°? Explain.
Answer:
The given side lengths of a triangle are: 5 inches and 7 inches
The included angle of a triangle is: 50°
Now,
The representations of the triangles with the given specifications are:
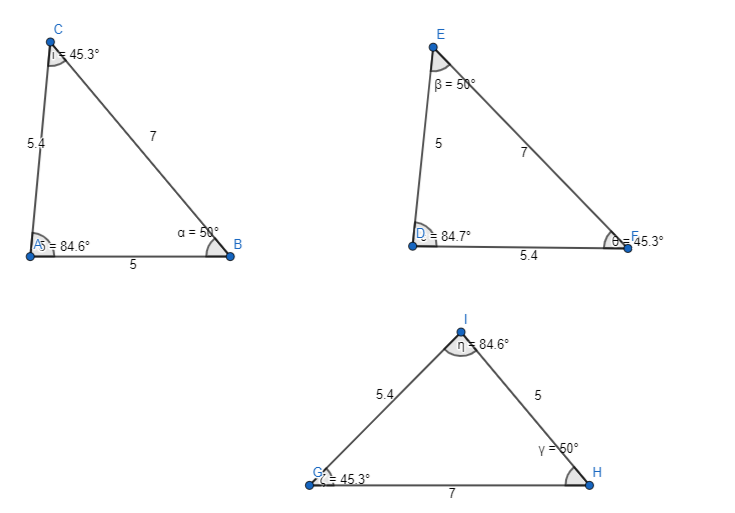
Now,
From the above,
We can observe that the triangle with the given specifications is the same even we turn the triangle to any degree
Hence, from the above,
We can conclude that
We can not draw more than one triangle with side lengths of 5 inches and 7 inches and an included angle with a measure of 50°
Question 6.
Sketch two different triangles that have angle measures of 45°, 45°, and 90°.
Answer:
The representation of the different triangles that have angle measures of 45°, 45°, and 90° are:

Practice & Problem Solving
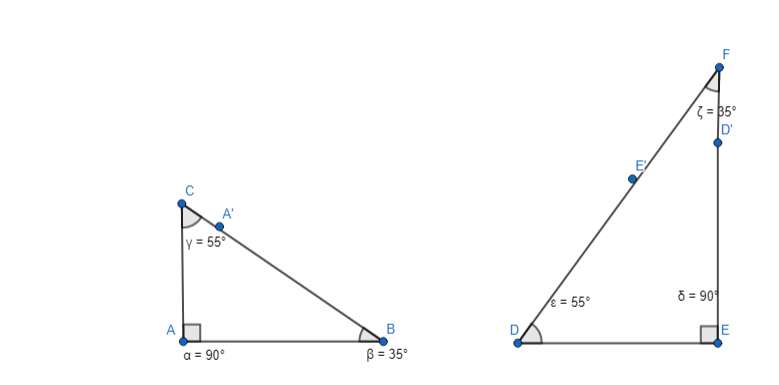
Question 7.
Draw two different triangles with angle measurements of 90°, 35°, and 55°.
Answer:
The representation of the two different triangles with angle measurements of 90°, 35°, and 55° is:
Question 8.
If you form a triangle from three given side lengths, will you always get one triangle or more than one triangle?
Answer:
If you form a triangle from three given side lengths, then you will not always get only one triangle
Ex:
The given side lengths of a triangle are: 3 cm, 4 cm, and 5 cm
Now,
We know that,
In order to construct a triangle,
The sum of the lengths of the two short sides must be greater than the length of the third side
So,
The possible combinations for forming a triangle are: (3, 4, 5), (3, 5, 4), (4, 3, 5), (5, 3, 4)
Question 9.
How can you make different-looking triangles given two of the angle measures and the included side lengths?
Answer:
Since the two angles are already given, therefore the value of the third angle is already fixed. That is, the third angle is the difference between 180° and the sum of the two angles. If the angles and the side lengths are given, then we can form any number of angles as long as the ratio of angles are consistent
Question 10.
If you form a triangle from two given angle measures and the length of the included side, will you always get one triangle or will you get more than one triangle?
Answer:
It is not always possible to construct a triangle from a given side length and two angles. If the two given angles add to more than 180°, then the sides of the triangle will diverge and never meet.
Question 11.
How can you make different triangles with the same angle measures?
Answer:
We can make different triangles with the same angle measures by making the sum of the angles consistent
Example:
The given angle measures are: 30°, 70°, 80°
Now,
The combination of different angle measures to make different triangles are:
a. 30°, 60° 90°
b. 40°, 50°, 90°
c. 40°, 60°, 80°
Question 12.
Given two side lengths of 15 units and 9.5 units, with a nonincluded angle of 75°, can you draw no triangles, only one triangle, or more than one triangle?
Answer:
The given side lengths are: 15 units and 9.5 units
The non-included angle is: 75°
Now,
The representation of the triangle with the given specifications are:
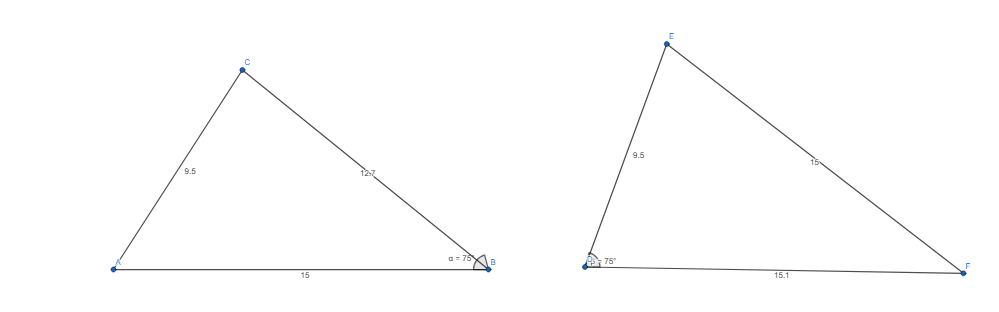
Now,
From the above,
We can observe that there is more than one triangle with the given specifications
Hence, from the above,
We can conclude that we can draw more than one triangle with the given specifications
Question 13.
A student was asked to form different triangles with angle measures of 90°, 30°, and 60°. She incorrectly said this triangle is the only triangle with angle measures of 90°, 30°, and 60°. What mistake might she have made?

Answer:
It is given that
A student was asked to form different triangles with angle measures of 90°, 30°, and 60°. She incorrectly said this triangle is the only triangle with angle measures of 90°, 30°, and 60°
Now,
We know that,
We can form any number of triangles as long as the sum of the angles is 180°
So,
The other combinations of the given angle measures are:
a. 30°, 60°, 90°
b. 40°, 60°, 80°
c. 30°, 50°, 100°
Hence, from the above,
We can conclude that the mistake done by her is:
She did not consider the other shapes of the triangles by adjusting the given angle measures
Question 14.
In triangle QRS, m∠QSR = 100°, m∠SQR = 45°, and QR = 4 units. In triangle XYZ, m∠XYZ = 100°, m∠ZXY = 45°, and XY = 4 units. Are triangles QRS and XYZ the same? Explain.
Answer:
Question 15.
You are asked to make a triangular sign using the given information about triangle WXY. In triangle WXY, m∠WXY = 45°, m∠YWX = 90°, and WX = 5 feet.
a. Which triangle is correct? Each square on the grid is equal to 1 square foot.
Answer:
It is given that
You are asked to make a triangular sign using the given information about triangle WXY. In triangle WXY, m∠WXY = 45°, m∠YWX = 90°, and WX = 5 feet.
So,
The representation of the triangle with the given specifications is:
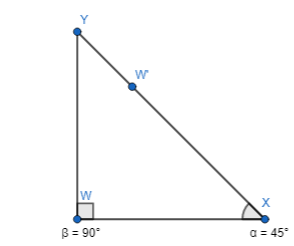
Hence, from the above,
We can conclude that Option B matches the given above figure
b. Explain why only one triangle can be formed with these three pieces of information.
Answer:
We know that,
It is not always possible to construct a triangle from a given side length and two angles. If the two given angles add to more than 180°, then the sides of the triangle will diverge and never meet.
Hence, from the above,
We can conclude that only one triangle can be formed by the given information in part (a)
Question 16.
Look for Relationships Two different triangles have side lengths of 13 and 16 units and a non-included angle of 50°. Explain how the triangles are different.
Answer:
It is given that
Two different triangles have side lengths of 13 and 16 units and a non-included angle of 50°
Now,
The representations of the triangle with the given specifications are: (Scale: 1 cm = 2 units)
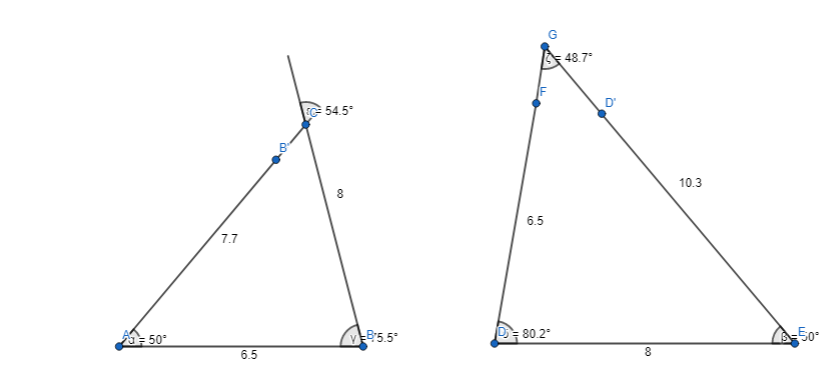
Now,
From the above,
We can observe that the angles are different for the two representations
Hence, from the above,
We can conclude that the representations of the triangles are different due to the remaining angle measures other than the non-included angle measure
Question 17.
Higher-Order Thinking Two triangles have side lengths of 12 units and 15 units and a non-included angle of 45°. Draw two different triangles with these conditions.
Answer:
It is given that
Two triangles have side lengths of 12 units and 15 units and a non-included angle of 45°
Hence,
The representation of the triangle with the given specifications are:
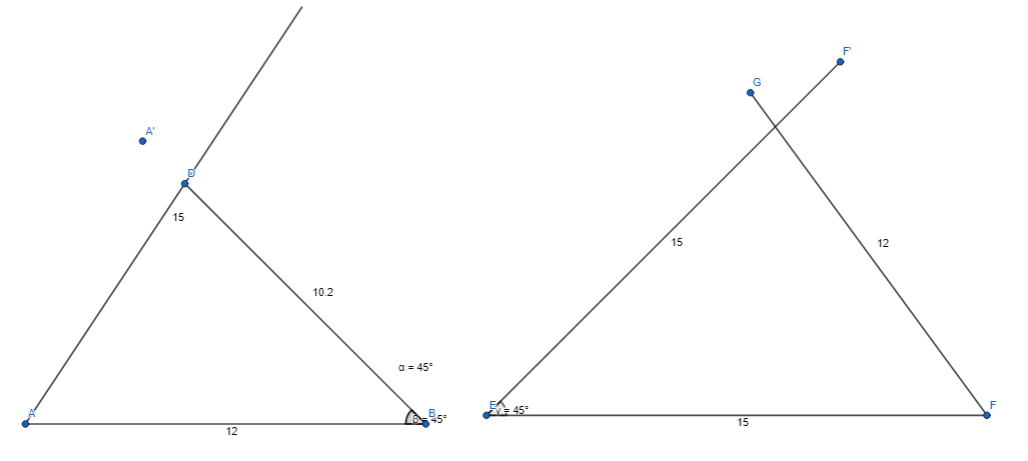
Question 18.
For triangle RST, RS is 12 centimeters, ST is 16 centimeters, and RT is 19 centimeters. How many triangles can be drawn with the given side lengths?
Answer:
It is given that
For triangle RST, RS is 12 centimeters, ST is 16 centimeters, and RT is 19 centimeters.
So,
The representation of the triangle with the given specifications is:
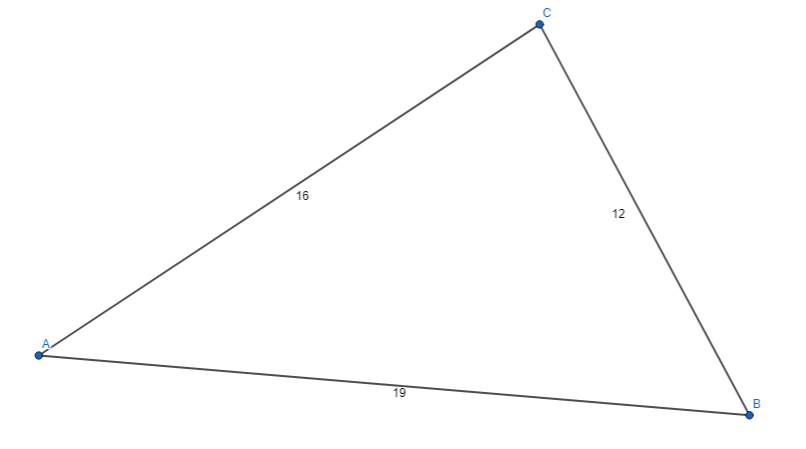
Hence, from the above,
We can conclude that only one triangle can be drawn with the given side lengths
Question 19.
A triangle has two side lengths of 8.5 centimeters and 9.5 centimeters. What is a possible length for the third side? Explain why this is a possible length.
Answer:
It is given that
A triangle has two side lengths of 8.5 centimeters and 9.5 centimeters.
Now,
We know that,
In order to construct a triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the longer side
Now,
Let the third side be x
Case 1:
8.5 + 9.5 > x
18 > x
x < 18
Case 2:
8.5 + x > 9.5
x > 9.5 – 8.5
x > 1
Hence, from the above,
We can conclude that the possible length of the third side must be: 1 < x < 18
Question 20.
Can a triangle be formed with side lengths of 4, 5, and 7 units?
Answer:
The given side lengths are: 4 units, 5 units, and 7 units
Now,
We know that,
In order to construct a triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the longer side
So,
4 + 5 > 7
9 > 7
Hence, from the above,
We can conclude that the triangle can be formed wit the given side lengths 4, 5, and 7 units
Assessment Practice
Question 21.
Which of the following combinations of side lengths would form a triangle? Select all that apply.
☐ 7 in., 10 in., 2.5 in.
☐ 4.5 ft, 8 ft, 5 ft
☐ 5 yd, 11 yds, 5 yd
☐ 12 in., 5 in., 9.5 in.
☐ 7 m, 7 m, 9 m
☐ 6 ft, 16 ft, 9 ft
Answer:
We know that,
In order to construct a triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the longer side
Hence,
The combinations of side lengths that would form a triangle are:

Question 22.
Which of the following combinations of side lengths would NOT form a triangle?
A. 7 cm, 10 cm, 13 cm
B. 10 ft, 13 ft, 15 ft
C. 10 yd, 11 yd, 13 yd
D. 10 in., 13 in., 23 in.
Answer:
We know that,
In order to construct a triangle,
The sum of the lengths of the two shortest sides must be greater than the length of the longer side
Hence,
The combinations of side lengths that would not form a triangle are:
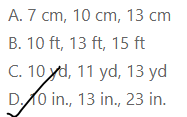
Question 23.
Draw a triangle that has exactly one line of symmetry.

Answer:
We know that,
The triangle, which has two equal sides, two equal angles and exactly one line of symmetry is known as the Isosceles Triangle. So, ΔABC is an Isosceles Triangle. Therefore, the triangle which has only one line of symmetry has been known as the Isosceles Triangle.
Hence,
The representation of the triangle that has exactly on the line of symmetry is:

Lesson 8.4 Solve Problems Using Angle Relationships
Explore It!
The intersecting skis form four angles.

I can… solve problems involving angle relationships.
A. List all the pairs of angles that share a ray.
Answer:
It is given that the intersecting skis form four angles.
Now,
The representation of the intersecting skies and the angles made by intersection are:

Hence, from the above figure,
We can conclude that the angles that share a ray are:
∠1, ∠2, ∠3, and ∠4
B. Suppose the measure of Z1 increases. What happens to the size of ∠2? ∠3?
Answer:
From the given figure,
We can observe that ∠1 and ∠2 are on the same side and they are known as “Adjacent angles”
We can observe that ∠1 and ∠3 are on the opposite sides of the ray and they are known as “Vertical angles”
Now,
We know that,
The sum of the adjacent angles is 180°
The angle measures of the vertical angles are the same
Hence, from the above,
We can conclude that
When the value of ∠1 increases, the value of ∠2 automatically decreases
When the value of ∠1 increases, the value of ∠3 also increases
C. How does the sum of the measures of ∠1 and ∠2 change when one ski moves? Explain.
Answer:
From the given figure,
We can observe that ∠1 and ∠2 lies on the same side of the ski and they are known as “Adjacent angles” (or) “Supplementary angles”
Now,
We know that,
The sum of the angle measures of adjacent angles is 180°
Hence, from the above,
We can conclude that the sum of the measures of ∠1 and ∠2 always remains constant even when one ski moves
Focus on math practices
Construct Arguments Why does the sum of all four angle measures stay the same when one of the skis moves?
Answer:
From the given figure,
We can observe that the intersecting skies form 4 angles
Now,
We know that,
The sum of the adjacent angles’ angle measures is 180°
The angle measures of the vertical angles are the same
So,
∠1 + ∠2 = 180° and ∠3 + ∠4 = 180°
∠1 = ∠3 and ∠2 = ∠4
So,
∠1 + ∠2 + ∠3 + ∠4 = 360°
So,
Even when we change one angle measure, the remaining angle measures will adjust their angle measures accordingly so that the sum of all the four angles remain the same i.e, 360°
Hence, from the above,
We can conclude that the sum of all four angle measures stay the same even when one of the skis moves
Essential Question
How are angles formed by intersecting lines related?
Answer:
When two lines intersect, the angles that are opposite each other are vertical angles. Recall that a linear pair is a pair of adjacent angles whose non-common sides are opposite rays. So, when two lines intersect, the angles that are on the same side of a line form a linear pair.
Try It!
∠MNQ and ∠PNR are vertical angles. What is the value of x?
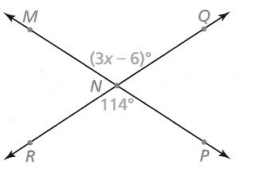
Vertical angles are __________, so the equation ___________ can be used to find x. The value of x is __________.
Answer:
It is given that ∠MNQ and ∠PNR are vertical angles
Now,
The given figure is:

Now,
We know that,
The angle measures of the vertical angles are the same
So,
(3x – 6)° = 114°
3x° = 114° + 6°
3x° = 120°
x° = \(\frac{120°}{3}\)
x° = 40°
Hence, from the above,
We can conclude that
Since the vertical angles are congruent, the equation (3x – 6)° = 114° can be used to find the value of x
Hence,
The value of x is: 40°
Convince Me! Why can you use an equation when solving for x in the diagram?
Answer:
The given figure is:

Now,
We know that,
The vertical angles are always congruent
So,
The angle measures of the vertical angles are also congruent
Now,
From the given figure,
We can observe that ∠MNQ and ∠PNR are vertical angles
So,
∠MNQ = ∠PNR
So,
(3x – 6)° = 114°
Hence, from the above,
We can conclude that we will use the equation to solve for x since the given angles are the vertical angles
Try It!
m∠1 is 4 times m∠2. ∠1 and ∠2 are complementary. ∠1 and ∠3 are vertical angles. ∠3 and ∠4 are supplementary. What are the measures of the four angles?
Answer:
It is given that
m∠1 is 4 times m∠2. ∠1 and ∠2 are complementary. ∠1 and ∠3 are vertical angles. ∠3 and ∠4 are supplementary
Now,
The given relation between ∠1 and ∠2 is:
∠2 = 4∠1
Now,
From the given information,
∠1 + ∠2 = 90°
∠1 + 4∠1 = 90°
5∠1 = 90°
∠1 = \(\frac{90°}{5}\)
∠1 = 18°
So,
∠2 = 4 ∠1
∠2 = 4 (18°)
∠2 = 72°
Now,
From the given information,
∠1 and ∠3 are vertical angles. ∠3 and ∠4 are supplementary
So,
∠1 = ∠3 = 18°
Now,
∠3 + ∠4 = 180°
∠4 = 180° – 18°
∠4 = 162°
Hence, from the above,
We can conclude that the measures of the four angles are:
∠1 = 18°, ∠2 = 72°, ∠3 = 18°, and ∠4 = 162°
KEY CONCEPT
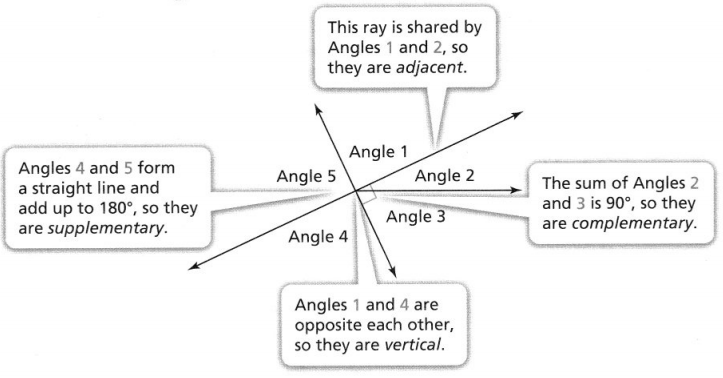
Do You Understand?
Question 1.
Essential Question How are angles formed by intersecting lines related?
Answer:
When two lines intersect, the angles that are opposite each other are vertical angles. Recall that a linear pair is a pair of adjacent angles whose non-common sides are opposite rays. So, when two lines intersect, the angles that are on the same side of a line form a linear pair.
Question 2.
Use Structure Can vertical angles also be adjacent angles? Explain.
Answer:
No, vertical angles can never be adjacent. Adjacent angles are the ones next to each other while vertical angles are opposite from each other.
Question 3.
Reasoning Do complementary and supplementary angles also have to be adjacent angles? Explain.
Answer:
Supplementary and complementary angles do not have to be adjacent, but they can be possible. Supplementary angles are two angles whose measures sum to 180 ° and complementary are the sum have to add up to 90 °
Do You Know How?
Use the diagram below for 4-6.
Answer:
The given figure is:

Question 4.
List two pairs of adjacent angles.
Answer:
From the given figure,
We can observe that
The two pairs of adjacent angles are:
a. ∠1 and ∠2 b. ∠3 and ∠4
Question 5.
List all pairs of vertical angles.
Answer:
From the given figure,
We can observe that
The pairs of vertical angles are:
∠1 and ∠3
Question 6.
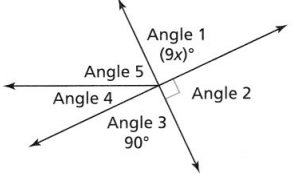
If ∠1 and ∠3 are the same measure, what is the value of x?
Answer:
From the given figure,
We can observe that
∠1 = 9x° and ∠3 = 90°
Now,
It is given that ∠1 and ∠3 are the same measure
So,
∠1 = ∠3
So,
9x° = 90°
x = \(\frac{90°}{9}\)
x = 10°
Hence, from the above,
We can conclude that the value of x is: 10°
Practice & Problem Solving
Question 7.
List each angle adjacent to ∠w.
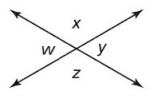
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The angles adjacent to ∠w are: ∠x and ∠z
Hence, from the above,
We can conclude that the angles adjacent to ∠w are: ∠x and ∠z
Question 8.
List two pairs of adjacent angles.
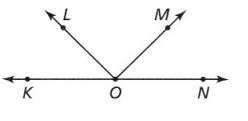
Answer:
The given figure is:

Now,
We know that,
The “Adjacent angles” are the angles that share the common vertex and common side
Now,
From the given figure,
We can observe that
The adjacent angles are: ∠KOL and ∠NOM
Hence, from the above,
We can conclude that the two pairs of adjacent angles are: ∠KOL and ∠NOM
Question 9.
Find the value of x.
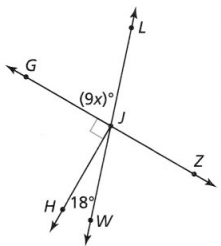
Answer:
The given figure is:

Now,
From the given figure,
We can observe that 9x° and 18° are the complementary angles
Now,
We know that,
The sum of the complementary angles is always 90°
So,
9x° + 18° = 90°
9x°= 90° – 18°
9x° = 72°
x = \(\frac{72°}{9}\)
x = 8°
Hence, from the above,
We can conclude that the value of x is: 8°
Question 10.
Find the value of x.
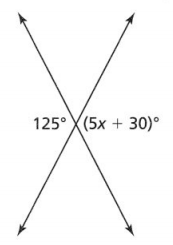
Answer:
The given figure is:

Now,
Fro the given figure,
We can observe that 125° and (5x + 30)° are vertical angles
Now,
We know that,
The vertical angles are always congruent
So,
(5x + 30)° = 125°
5x° = 125° – 30°
5x° = 95°
x = \(\frac{95°}{5}\)
x° = 19°
Hence, from the above,
We can conclude that the value of x is: 19°
Question 11.
∠1 and ∠2 are complementary angles. The measure of ∠1 is 42°. The measure of ∠2 is (3x)°. Find the value of x.
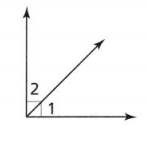
Answer:
It is given that
∠1 and ∠2 are complementary angles. The measure of ∠1 is 42°. The measure of ∠2 is (3x)°.
Now,
The given figure is:

Now,
We know that,
The sum of the complementary angles is always 90°
So,
∠1 + ∠2 = 90°
42°+ 3x° = 90°
3x° = 90° – 42°
3x° = 48°
x° = \(\frac{48°}{3}\)
x°= 16°
Hence, from the above,
We can conclude that the value of x is: 16°
Question 12.
Two streets form an intersection. ∠C and ∠D are supplementary angles. If the measure of ∠C is 128° and the measure of ∠D is two times the value of x, what is the value of x?

Answer:
It is given that
Two streets form an intersection. ∠C and ∠D are supplementary angles. The measure of ∠C is 128° and the measure of ∠D is two times the value of x
Now,
The given figure is:

Now,
We know that,
The sum of the supplemenatry angles is always 180°
So,
∠C + ∠D = 180°
128° + 2x° = 180°
2x° = 180° – 128°
2x° = 52°
x° = \(\frac{52°}{2}\)
x° = 26°
Hence, from the above,
We can conclude that the value of x is: 26°
Question 13.
If A and B are supplementary angles and ∠A is three times as large as ∠B, find the measures of ∠A and ∠B.
Answer:
It is given that
A and B are supplementary angles and ∠A is three times as large as ∠B
Now,
Let the value of ∠B be x°
So,
The value of ∠A will be: 3x°
Now,
We know that,
The sum of the supplementary angles is always 180°
So,
∠A + ∠B = 180°
So,
3x° + x° = 180°
4x° = 180°
x° = \(\frac{180°}{4}\)
x°= 45°
So,
∠B = 45°
∠A = 3x° = 3 (45°) = 135°
Hence, from the above,
We can conclude that the angle measures of ∠A and ∠B are 135° and 45° respectively
Question 14.
Higher-Order Thinking The measure of ∠DBE is (0.1x – 22)° and the measure of ∠CBE is (0.3x – 54)°. Find the value of x.
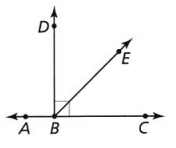
Answer:
It is given that
The measure of ∠DBE is (0.1x – 22)° and the measure of ∠CBE is (0.3x – 54)°
Now,
The given figure is:

Now,
From the given figure,
We can observe that ∠DBE and ∠CBE are the complementary angles
Now,
We know that,
The sum of the complementary angles is always 90°
So,
∠DBE + ∠CBE = 90°
(0.1x – 22)° + (0.3x – 54)° = 90°
0.4x° – 76° = 90°
0.4x°= 90° + 76°
0.4x° = 166°
4x° = 1,660°
x° = \(\frac{1,660°}{4}\)
x° = 415°
Hence, from the above,
We can conclude that the value of x is: 415°
Question 15.
Reasoning ∠1 and an angle that measures 50° are supplementary. Another angle that measures 50° and ∠3 is supplementary. Show that m∠1 and m∠3 are equal.
Answer:
It is give that
∠1 and an angle that measures 50° are supplementary. Another angle that measures 50° and ∠3 is supplementary
Now,
We know that,
The sum of the supplementary angles is always 180°
Now,
Let the unkown angle be ∠x
Now,
∠1 + ∠x = 180°
∠1 + 50° = 180°
∠1 = 180° – 50°
∠1 = 130°
Now,
∠x + ∠3 = 180°
∠3 + 50° = 180°
∠3 = 180° – 50°
∠3 = 130°
Hence, from the above,
We can conclude that
∠1 = ∠3
Assessment Practice
Question 16.
Using the diagram at the right, Martin incorrectly writes m∠b = 125° What mistake did Martin likely make? Find the correct measure of ∠b.
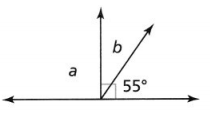
Answer:
It is given that
Martin incorrectly writes
m∠b = 125°
Now,
The given figure is:

Now,
From the give figure,
We can observe that ∠b and 55° are complementary angles
Now,
We know that,
The sum of complementary angles is always 90°
So,
Both the angles in the complementary angles must be acute angles i.e., the angle must be less than 90°
Now,
∠b + 55° = 90°
∠b = 90° – 55°
∠b = 35°
Hence, from the above,
We can conclude that
The mistake made by Martin is: Consideration of the angles as supplementary angles even though they are complementary angles
The correct measure of ∠b is: 35°
Question 17.
What is the measure, in degrees, of angle x?
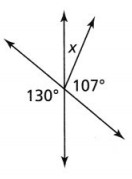
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
x° and 107° are adjacent angles
Now,
We know that,
The sum of the adjacent angles is always 180°
So,
x° + 107° = 180°
x° = 180° – 107°
x°= 73°
Hence, from the above,
We can conclude that the value of x is: 73°
Question 18.
What is the measure, in degrees, of the highlighted angle?
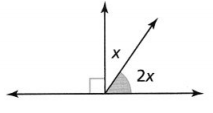
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
x° and 2x° are the supplementary angles
Now,
We know that,
The sum of the supplementary angles is always 180°
So,
x° + 2x° = 180°
3x° = 180°
x° = \(\frac{180°}{3}\)
x°= 60°
So,
2x° = 2 (60°) = 120°
Hence, from the above,
We can conclude that the value of the highlighted angle is: 120°
Lesson 8.5 Solve Problems Involving Circumference of a Circle
Explore It!
The distance around a circle and the distance across a circle are related.

I can… solve problems involving radius, diameter, and circumference of circles.
A. Use string to measure the distance across each circle. How many of these lengths does it take to go completely around the circle?
Answer:
We know that,
The distance around the circle is: Circumference
The distance across the circle is: Diameter
Now,
The complete length to go completely around the circle is given as:
Circumference = πd
Hence, from the above,
We can conclude that
The total length does it take to go completely around the circle = πd
Where
d is the diameter
B. Use the string and a ruler to measure the distance across the circle and the distance around the circle. Complete the table. Round each measurement to the nearest quarter inch.
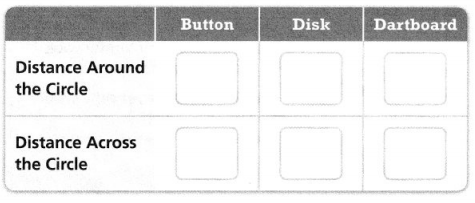
Answer:
C. What do you notice about the ratio of the distance around the circle to the distance across the circle for each circle?
Answer:
From the given table,
We can observe that the ratio of the circumference and the diameter is constant for all the circles
Hence, from the above,
We can conclude that the ratio of the distance around the circle to the distance across the circle for each circle is constant
Focus on math practices
Look for Relationships How can you estimate the distance around any circle when given the distance across the circle?
Answer:
We know that,
The distance around the circle is: Circumference
The distance across the circle is: Diameter
Now,
We know that,
The relationship between the distance around the circle and the distance across the circle is:
Distance around the circle = π × Distance across the circle
Hence, from the above,
We can conclude that
Circumference (C) = πd
Where,
d is the diameter
Essential Question
How is the circumference of a circle related to the length of its diameter?
Answer:
The relationship between the circumference of a circle and the diameter of the circle is:
Circumference (C) = πd
Where,
d is the diameter
Try It!
What is the circumference of the rim of a basketball hoop with a radius of 9 inches?
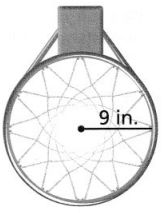
First, multiply the radius by __________ to get the diameter, __________ inches. Then, multiply the diameter by 3.14 (an approximation for π) to get a circumference of about __________ inches.
Answer:
The given figure is:

Now,
We know that,
The diameter of the rim (d) = 2 × Radius of the rim (r)
So,
d = 2 × 9
d = 18 in.
Now,
We know that,
Circumference (C) = πd
So,
C = 3.14 × 18
= 56.52 in.
Hence, from the above,
We can conclude that the circumference of the rim of a basketball hoop is about 56.52 in.
Convince Me! If the diameter is doubled, what happens to the circumference? Explain.
Answer:
We know that,
Circumference (C) = πd
So,
When the diameter is doubled,
Circumference (C) = π × 2d
Hence, from the above,
We can conclude that
If the diameter is doubled, then the circumference will also be doubled
Try It!
The circle has a circumference of 9.42 units. What is the area of the square? Use 3.14 for π. Explain how you found the answer.
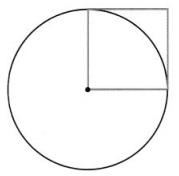
Answer:
It is given that the circle has a circumference of 9.42 units
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The radius of the circle = The side of the square
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
2πr = 9.42
r = \(\frac{9.42}{2π}\)
r = 1.5 units
So,
The side of the square is: 1.5 units
Now,
We know that,
The area of the square = Side²
So,
The area of the square = (1.5)²
= 2.25 units²
Hence, from the above,
We can conclude that the area of the square is: 2.25 units²
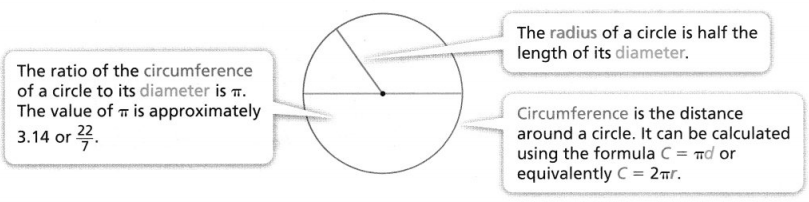
KEY CONCEPT
The parts of a circle and their relationships are summarized in the diagram below.
Do You Understand?
Question 1.
Essential Question How is the circumference of a circle related to the length of its diameter?
Answer:
The relationship between the circumference of a circle and the diameter of the circle is:
Circumference (C) = πd
Where,
d is the diameter
Question 2.
Construct Arguments Are there any circles for which the relationship between the diameter and circumference cannot be represented by π? Explain.
Answer:
We know that,
The circumference of a circle (C) = πd
Where,
d is the diameter
Now,
We will find the circumference of any circle (Semi circle, Quarter circle, etc.) from the above formula only with some modifications
Hence, from the above,
We can conclude that there are not any circles for which the relationship between the diameter and circumference cannot be represented by π
Question 3.
Be Precise Can you find the exact circumference of a circle when you multiply the diameter by \(\frac{22}{7}\)? Explain.
Answer:
No, we can not find the exact circumference of a circle when you multiply the diameter by \(\frac{22}{7}\) because the diameter will not always be the multiple of 7 so that the circumference will be an integer
Do You Know How?
Question 4.
What is the circumference of a circle with a radius of 5 inches?
Answer:
The given data is:
The radius of a circle (r) = 5 inches
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
C = 2 × 3.14 × 5
= 31.4 inches
Hence, from the above,
We can conclude that the circumference of the circle with the given radius is: 31.4 inches
Question 5.
What is the diameter of a circle with a circumference of 10.99 feet?
Answer:
The given data is:
The circumference of a circle (C) = 10.99 feet
Now,
We know that,
The circumference of a circle (C) = πd
So,
10.99 = 3.14 × d
d = \(\frac{10.99}{3.14}\)
d = 3.5 feet
Hence, from the above,
We can conclude that the diameter of the circle with the given circumference is: 3.5 feet
Question 6.
How many full revolutions does a car tire with a diameter of 25 inches make when the car travels one mile?

Answer:
It is given that
A car tire has a diameter of 25 inches
Now,,
We have to find the circumference of the tire and the speed of the car to find the number of revolutions
Now,
We know that,
The circumference of a circle (C) = πd
So,
C = 3.14 × 25
= 78.5 inches
So,
The circumference of the given car tire is: 78.5 inches
Now,
We know that,
1 mile = 5,280 feet
1 feet = 12 inches
So,
1 mile = 5,280 × 12
= 63,360 inches
Now,
We know that,
The number of revolutions the car tire can make = \(\frac{Speed of a car}{The circumference of a car tire}\)
= \(\frac{63,360}{78.5}\)
≅ 807 revolutions
Hence, from the above,
We can conclude that
The number of revolutions the given car tire can make with the given diameter is about 807 revolutions
Practice & Problem Solving
Question 7.
Find the circumference of the circle. Use π as part of the answer.
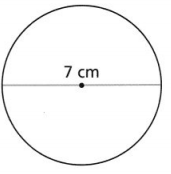
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The diameter of a circle (d) = 7 cm
Now,
We know that,
The circumference of a circle (C) = πd
So,
C = 7π cm
Hence, from the above,
We can conclude that the circumference of the circle with the given diameter in terms of π is: 7π cm
Question 8.
Find the circumference of the circle. Use 3.14 for π. Round to the nearest hundredth.
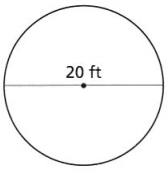
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The diameter of a circle (d) = 20 ft
Now,
We know that,
The circumference of a circle (C) = πd
So,
C = 3.14 × 20
= 62.80 ft
Hence, from the above,
We can conclude that the circumference of the circle with the given diameter is: 62.80 ft
Question 9.
Find the circumference of the circle. Use π as part of the answer.
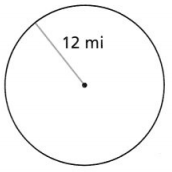
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of a circle (r) = 12 mi
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
C = 2π × 12
= 24π mi
Hence, from the above,
We can conclude that
The circumference of the circle with the given radius in terms of π is: 24π mi
Question 10.
Find the circumference of the circle. Use 3.14 for π. Round to the nearest hundredth.
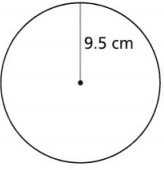
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of a circle (r) = 9.5 cm
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
C = 2 × 3.14 × 9.5
= 59.66 cm
Hence, from the above,
We can conclude that the circumference of the circle with the given radius is: 59.66 cm
Question 11.
Find the diameter of a circle with a circumference of 27 centimeters. Use 3.14 for π. Round to the nearest tenth.
Answer:
The given data is:
The circumference of a circle (C) = 27 cm
Now,
We know that,
The circumference of a circle (C) = πd
So,
27 = 3.14 × d
d = \(\frac{27}{3.14}\)
d = 8.59
d ≅ 9 cm
Hence, from the above,
We can conclude that the diameter of the circle with the given circumference is about 9 cm
Question 12.
The distance around a meteor crater is 9,687 feet. Find the diameter of the crater. Use \(\frac{22}{7}\) for π. Round to the nearest tenth.

Answer:
It is given that
The distance around a meteor crater is 9,687 feet
Now,
The given figure is:

Now,
From the above,
We can observe that the crater is in the form of a circle
Now,
We know that,
The distance around the circle is: Circumference
Now,
We know that,
The circumference of a circle (C) = πd
So,
9,687 = \(\frac{22}{7}\) × d
d = \(\frac{9,687 × 7}{22}\)
d = 3,082.2 feet
Hence, from the above,
We can conclude that the diameter of the crater for the given circumference of a crater is: 3,082.2 feet
Question 13.
Make Sense and Persevere The circumference of the inner circle is 44 feet. The distance between the inner circle and the outer circle is 3 feet. By how many feet is the circumference of the outer circle greater than the circumference of the inner circle? Use \(\frac{22}{7}\) for π. Round to the nearest hundredth of a foot.
Answer:
It is given that
The circumference of the inner circle is 44 feet. The distance between the inner circle and the outer circle is 3 feet
Now,
We know that,
The circumference of inner circle (c) = 2πr
So,
For inner circle:
44 = 2 × \(\frac{22}{7}\) × r
r = \(\frac{44 × 7}{22 × 2}\)
r = 7 feet
For outer circle:
The circumference of the outer circle (C) = 2π(R – r)
Where,
R is the radius of the outer circle
r is the radius of the inner circle
So,
C = 2 × \(\frac{22}{7}\) × (7 + 3)
C = 62.85 feet
So,
C – c = 62.85 – 44
= 18.85 feet
Hence, from the above,
We can conclude that the circumference of the outer circle is 18.85 feet greater than the circumference of the inner circle
Question 14.
Generalize What is the ratio of the radius to the circumference of any circle, using 3.14 for π?
Answer:
We know that,
The circumference of a circle (C) = 2πr
So,
\(\frac{C}{r}\) = 2π
\(\frac{C}{r}\) = 6.28
Hence, from the above,
We can conclude that the ratio of the radius to the circumference of any circle is: 6.28
Question 15.
What is the radius of a circle with a circumference of 26.69 centimeters?
Answer:
The given data is:
The circumference of a circle (C) = 26.69 cm
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
26.69 = 2 × 3.14 × r
r = \(\frac{26.69}{6.28}\)
r = 4.25 cm
Hence, from the above,
We can conclude that the radius of the circle with the given circumference is: 4.25 cm
Question 16.
Higher Order Thinking A unicycle wheel makes five rotations. The unicycle travels 37.94 feet. Find the diameter of the wheel in inches. Use 3.14 for π. Round to the nearest tenth of an inch.
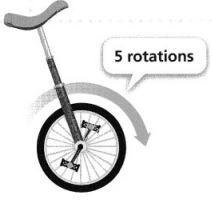
Answer:
It is given that
A unicycle wheel makes five rotations. The unicycle travels 37.94 feet
Now,
We know that,
The number of revolutions (or) rotations = \(\frac{The speed of the unicycle}{The circumference of the unicycle wheel}\)
So,
The circumference of the unicycle wheel = \(\frac{The speed of the unicycle}{The number of rotations}\)
3.14 × d = \(\frac{37.94}{5}\)
3.14 × d = 7.58
d = \(\frac{7.58}{3.14}\)
d = 2.41 feet
d = 2.41 × 12
d = 29 inches
Hence, from the above,
We can conclude that the diameter of the wheel in inches is: 29 inches
Assessment Practice
Question 17.
Camille drew the figure shown at the right. Which of the following is the best estimate of the perimeter of the figure?
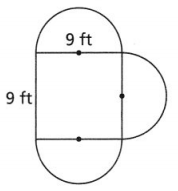
A. 36 feet
B. 81 feet
C. 45 feet
D. 50 feet
Answer:
Question 18.
A cabin on a Ferris wheel has traveled one-fourth of the circumference of the wheel, a distance of 117.75 feet. What is the radius, in feet, of the Ferris wheel? Use 3.14 for π.
Answer:
It is given that
A cabin on a Ferris wheel has traveled one-fourth of the circumference of the wheel, a distance of 117.75 feet
Now,
The circumference of the wheel (C) = 4 × 117.75
= 471 feet
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
471 = 2 × 3.14 × r
r = \(\frac{471}{6.28}\)
r = 75 feet
Hence, from the above,
We can conclude that the radius of the Ferris wheel is: 75 feet
Question 19.
The diagram shows a track composed of a rectangle with a semicircle on each end. The area of the rectangle is 7,200 square meters. What is the perimeter, in meters, of the track? Use 3.14 for π.
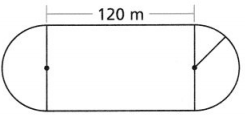
Answer:
It is given that
The diagram shows a track composed of a rectangle with a semicircle on each end. The area of the rectangle is 7,200 square meters.
Now,
The given figure is:

Now,
We know that,
The area of the rectangle (A) = Length × Width
So,
7,200 = 120 × Width
Width = \(\frac{7,200}{120}\)
Width = 60 m
So,
The radius of the semicircle (r) = \(\frac{Width of the rectangle}{2}\)
r = \(\frac{60}{2}\)
r = 30 m
Now,
We know that,
The perimeter of a rectangle = 2 (Length + Width)
The perimeter of a semicircle = r (π + 2)
Now,
The perimeter of a rectangle = 2 (120 + 60)
= 2 (180)
= 360 m
The perimeter of a semicircle = 30 (3.14 + 2)
= 154.2 m
So,
The perimeter of the track = The perimeter of a rectangle + 2 (The perimeter of a semicircle)
= 360 + 2 (154.2)
= 668.4 m
Hence, from the above,
We can conclude that the perimeter of the given track is: 668.4 m
Topic 8 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary How are adjacent angles and vertical angles alike? How are they different? Lesson 8-4
Answer:
We know that,
The adjacent angles and the vertical angles have the same vertex
We know that,
The sum of the adjacent angles is 180° (or) 90°
Question 2.
On a map, 1 inch equals 150 miles. The border between the two states is 5.5 inches long on the map. What is the actual length of the border? Lesson 8-1
Answer:
It is given that
On a map, 1 inch equals 150 miles. The border between the two states is 5.5 inches long on the map.
So,
The actual length of the border – (Scale factor) × (The border between the two states on the amp)
= 150 × 5.5
= 825 miles
Hence, from the above,
We can conclude that the actual length of the border is: 825 miles
In 3 and 4, use the figure to the right.

Question 3.
What is the measure of ∠BZD? Lesson 8-4
A. 58°
B. 148°
C. 32°
D. 90°
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
∠BZD = ∠BZC + ∠CZD
So,
∠BZD = 58° + 90°
∠BZD = 148°
Hence, from the above,
We can conclude that
The angle measure of ∠BZD is:

Question 4.
Find the value of x. Lesson 8-4
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
(2x)° + 58° = 180°
(2x)° = 180° – 58°
(2x)° = 122°
x = \(\frac{122°}{2}\)
x = 61°
Hence,f rom the above,
We can conclude that the value of x is: 61°
Question 5.
Pierce draws a circle with a radius of 3 centimeters. Gianna draws a circle with a radius that is twice as long as the radius of Pierce’s circle. How will the circumference of Gianna’s circle compare with the circumference of Pierce’s circle? Lesson 8-5
The circumference of Gianna’s circle is ___________ times the circumference of Pierce’s circle.
Answer:
It is given that
Pierce draws a circle with a radius of 3 centimeters. Gianna draws a circle with a radius that is twice as long as the radius of Pierce’s circle
So,
The radius of Pierce’s circle is: 3 cm
So,
The radius of Gianna’s circle = 2 × (Radius of Pierce’s circle)
= 2 × 3
= 6 cm
Now,
The circumference of Pierce’s circle (C) = 2πr
= 2 × π × 3
= 6π cm
Now,
The circumference of Gianna’s circle (C) = 2πr
= 2 × π × 6
= 12π cm
Now,
Let the number of times Gianna’s circumference is a number of times as Pierce’s circumference be x
So,
x × 6π = 12π
x = \(\frac{12π}{6π}\)
x = 2
Hence, from the above,
We can conclude that
The circumference of Gianna’s circle is 2 times the circumference of Pierce’s circle.
Question 6.
Draw a triangle with one side length of 5 units and another side length of 7 units. What additional piece of information will guarantee that only one triangle can be drawn? Lessons 8-2 and 8-3
Answer:
The representation of the triangle with the given side lengths is:
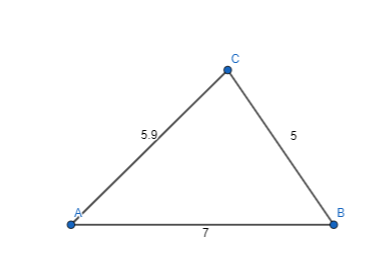
Now,
The additional information that will guarantee that only one triangle can be drawn is:
The angle between the two given side lengths i.e., an included angle
Topic 8 MID-TOPIC PERFORMANCE TASK
Mrs. Thomas has two rolls of garden edging that are each 96 inches long. She wants to make two new flower beds in her backyard. Each flower bed will be bordered by one roll of edging. One flower bed will be in the shape of a quadrilateral. The other will be in the shape of a triangle.
PART A
Mrs. Thomas decides to make a scale drawing of each flower bed using a scale of 1 centimeter = 5 inches. What will be the total length of each roll of edging in her scale drawings?
Answer:
It is given that
Mrs. Thomas has two rolls of garden edging that are each 96 inches long. She wants to make two new flower beds in her backyard. Each flower bed will be bordered by one roll of edging. One flower bed will be in the shape of a quadrilateral. The other will be in the shape of a triangle.
Mrs. Thomas decides to make a scale drawing of each flower bed using a scale of 1 centimeter = 5 inches.
Now,
From the given information,
Scale factor = \(\frac{5}{1}\)
So,
The total length of each roll of edging in her scale drawings = \(\frac{The total length of each roll of edging}{Scale factor}\)
= \(\frac{96 × 2}{5}\)
= 19.2 × 2
= 38.4 inches
Hence, from the above,
We can conclude that
The total length of each roll of edging in her scale drawings is: 38.4 inches
PART B
Mrs. Thomas wants the quadrilateral flower bed to have at least two 90° angles. Draw a possible plan for this flower bed using the scale from Part A. Make sure to use a complete roll of edging in the border. Label your drawing with all the angle measures and with the scaled length of each side. Name the shape of the flower bed you drew. What will be its actual dimensions?
Answer:
It is given that
Mrs. Thomas wants the quadrilateral flower bed to have at least two 90° angles
Now,
From part (a),
The scale is: 1 cm = 5 inches
So,
The representation of the quadrilateral flower bed with the scaled measurements is:
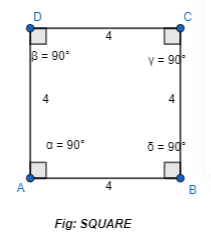
Now,
The actual dimensions of the given quadrilateral flower bed are:
The length of the quadrilateral flower bed = (Scaled length) × (Scale factor)
= 4 × 5
= 20 inches
Since the quadrilateral bed is a square bed, all the side lengths are equal
Hence, from the above,
We can conclude that
The shape of the flower bed is: Square
The actual dimensions of the flower bed are: 20 inches, 20 inches, 20 inches, 20 inches
PART C
Mrs. Thomas began to make a drawing for the triangular flower bed. In her drawing, the length of one side of the triangle is 4.8 centimeters, the length of the second side is 6.4 centimeters, and the included angle is a right angle. Use these measures and the scale from Part A to make a completed scale drawing. Label your drawing with all the angle measures to the nearest whole degree and with the scale length of each side. What will be the actual dimensions of this flower bed?
Answer:
It is given that
Mrs. Thomas began to make a drawing for the triangular flower bed. In her drawing, the length of one side of the triangle is 4.8 centimeters, the length of the second side is 6.4 centimeters, and the included angle is a right angle
Now,
From part (a),
The scale is: 1 cm = 5 inches
Now,
The representation of the triangular flower bed with the given specifications is:
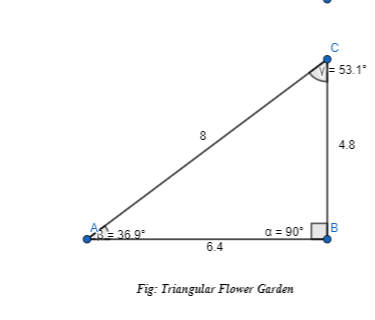
Now,
The actual dimensions of the triangular flower garden are:
The actual base length of the flower garden = (The scaled base length of the flower garden) × (Scale factor)
= 6.4 × 5
= 32.0
= 32 inches
The actual height of the flower garden = (The scaled height of the flower garden) × (scale factor)
= 4.8 × 5
= 24.0
= 24 inches
The actual hypotenuse length of the flower garden = (The scaled hypotenuse length of the flower garden) × (Scale factor)
= 8 × 5
= 40 inches
Hence, from the above,
We can conclude that
The actual dimensions of the flower garden are:
Base length: 32 inches
Height: 24 inches
Hypotenuse: 40 inches
Lesson 8.6 Solve Problems Involving Area of a Circle
Explore It!
Latoya cut a circle into 8 equal sections and arranged the pieces to form a shape resembling a parallelogram.
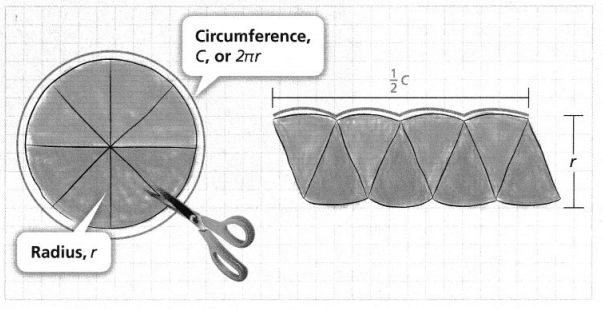
I can… solve problems involving the area of a circle.
A. How is the base length of the new shape related to the circumference of the circle?
Answer:
It is given that
Latoya cut a circle into 8 equal sections and arranged the pieces to form a shape resembling a parallelogram.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The base of the new figure is equal to half of the value of the circumference of the circle
Hence, from the above,
We can conclude that
The base of the new figure = \(\frac{1}{2}\) × Circumference of the circle
B. How is the height of the new shape related to the radius of the circle?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that the height of the new figure is equal to the radius of the circle
Hence, from the above,
We can conclude that
The height of the new figure = Radius of the circle
C. Since this new shape was made from a circle, use the information from the diagram and the formula for the area of the parallelogram, A= bh, to discover the formula for the area of a circle.
Answer:
It is given that
The area of the parallelogram (A) = bh
Where,
b is the Base of the parallelogram
h is the height of the parallelogram
But,
It is given that
The parallelogram is made from a circle
Now,
From part (a) and (b),
A = \(\frac{1}{2}\) × The circumference of a circle × Radius of a circle
A = \(\frac{1}{2}\) × 2πr × r
A = πr × r
A = πr²
Hence, from the above,
We can conclude that teh area of the circle that is derived fro the area of the parallelogram is: πr²
Focus on math practices
Look for Relationships The formula A = bh can be used to find a good estimate for the area of the cut-out diagram. What would happen to this estimate if the circle was cut into 100 sections? 1,000 sections?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The 8 parts of the circle made 4 parallelograms
So,
The relationship between the circles and parallelograms is:
The number of parallelograms = \(\frac{The number of parts of the circle}{2}\)
So,
For 100 pieces of the circle,
The number of parallelograms = \(\frac{100}{2}\)
= 50
For 1,000 pieces of the circle,
The number of parallelograms = \(\frac{1,000}{2}\)
= 500
Hence,
For 100 pieces of the circle,
The area of the parallelogram (A) = Base × Height [Since base = \(\frac{1}{2}\) × Circumference]
= 50r units²
For 1,000 pieces of the circle,
The area of the parallelogram (A) = Base × Height
= 500r units²
Essential Question
How can the area formula for a circle be used to solve problems?
Answer:
Area of a circle can be calculated by using the formulas:
a. Area = π × r2
where,
‘r’ is the radius.
b. Area = (π/4) × d2
where,
‘d’ is the diameter.
c. Area = C2/4π
where,
‘C’ is the circumference
Try It!
At a school play, there is a spotlight above the center of the floor that covers a lighted area with a radius of 7 feet. What is the area covered by the spotlight?

The area covered by the spotlight is about _________ square feet.
Answer:
It is given that
At a school play, there is a spotlight above the center of the floor that covers a lighted area with a radius of 7 feet
Now,
We know that,
The area of a circle (A) = πr²
So,
The area covered by the spotlight (A) = \(\frac{22}{7}\) × 7²
A = 154 feet²
Hence, from the above,
We can conclude that the area covered by the spotlight is: 154 square feet
Convince Me! If the diameter of a circle is given, how would you find the area?
Answer:
If the diameter of a circle is given, then
The area of a circle = (π/4) × d2
where,
‘d’ is the diameter.
Try It!
a. How far away can a person live from a radio station and hear its broadcast if the signal covers a circular area of 40,000 square miles? Write your answer as a whole number.
Answer:
It is given that
A person live from a radio station and hear its broadcast if the signal covers a circular area of 40,000 square miles
Now,
We have to find the diameter of a circle to find how far a person lives from a radio station
Now,
We know that,
The area of a circle (A) = πr²
So,
40,000 = 3.14 × r²
r² = \(\frac{40,000}{3.14}\)
r² = 12,738.85
r = 112.8
r ≈ 113 miles
So,
The diameter of a circle = 2 × The radius of a circle
= 2 × 113
= 226 miles
Hence, from the above,
We can conclude that the distance a person can live from a radio station and hear its broadcast is: 226 miles
b. What circular area is covered by the signal if the circumference is 754 miles?
Answer:
It is given that
The circumference of the circular signal is 754 miles
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
754 = 2 × 3.14 × r
r = \(\frac{754}{6.28}\)
r = 120 miles
Now,
The area of the circular signal (A) = πr²
So,
A = 3.14 × (120)²
A = 45,216 miles²
Hence, from the above,
We can conclude that teh circular area of the given signal is: 45,216 miles²
KEY CONCEPT
You can find the area, A, of a circle using the formula A = πr2, where r is the radius.
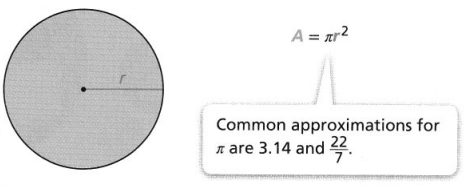
Do You Understand?
Question 1.
Essential Question How can the area formula for a circle be used to solve problems?
Answer:
Area of a circle can be calculated by using the formulas:
a. Area = π × r2
where,
‘r’ is the radius.
b. Area = (π/4) × d2
where,
‘d’ is the diameter.
c. Area = C2/4π
where,
‘C’ is the circumference
Question 2.
Be Precise
Is an area calculation exact when you use 3.14 or \(\frac{22}{7}\) as a value for π? Explain.
Answer:
The constant (pi) is not equal to either 22/7 or 3.14; these are only approximations to . The actual value of is the ratio of the circumference of a circle to its diameter, and is a transcendental number with infinitely many non-repeating decimal places
Question 3.
Use Structure if you know the diameter of a circle, how can you find the area?
Answer:
If you know the diameter of a circle, then
The area of a circle = (π/4) × d2
where,
‘d’ is the diameter.
Do You Know How?
For 4-7, use 3.14 for π.
Question 4.
What is the area of a circle with a radius of 8 inches?
Answer:
The given data is:
The radius of a circle is 8 inches
Now,
We know that,
The area of a circle (A) = πr²
So,
A = 3.14 × 8²
= 200.96 inches²
Hence, from the above,
We can conclude that the area of the circle with the given radius is: 200.96 inches²
Question 5.
What is the radius of a circle with an area of 28.26 square feet?
Answer:
The given data is:
The area of a circle is: 28.26 square feet
Now,
We know that,
The area of a circl (A) = πr²
So,
28.26 = 3.14 × r²
r² = \(\frac{28.26}{3.14}\)
r² = 9
r = 3 feet
Hence, from the above,
We can conclude that the radius of the circle with the given area is: 3 feet
Question 6.
What is the area of a circle with a circumference of 25.12 meters?
Answer:
The given data is:
The circumference of a circle is: 25.12 meters
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
25.12 = 2 × 3.14 × r
r = \(\frac{25.12}{6.28}\)
r = 4 meters
Now,
We know that,
The area of a circle (A) = πr²
So,
A = 3.14 × 4²
= 50.24 sq. meters
Hence, from the above,
We can conclude that the area of the circle with the given circmference is: 50.24 sq.meters
Question 7.
The diameter of a pizza is 12 inches. What is its area?

Answer:
It is given that
The diameter of a pizza is 12 inches.
Now,
The given figure is:

Now,
We know that,
Radius of a circle (r) = \(\frac{Diameter of a circle}{2}\)
r = \(\frac{12}{2}\)
r = 6 in.
Now,
We know that,
The area of a circle (A) = πr²
So,
A = 3.14 × 6²
= 113.04 in.²
Hence, from the above,
We can conclude that the area of the circle with the given diameter is: 113.04 in.²
Practice & Problem Solving
Question 8.
Find the area of the circle. Use 3.14 for π.

Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The radius of a circle (r) = 9 ft
Now,
We know that,
The arae of a circle (A) = πr²
So,
A = 3.14 × 9²
= 254.34 ft²
Hence, from the above,
We can conclude that teh arae of the circle with the given radius is: 254.34 feet²
Question 9.
Find the area of the circle. Use 3.14 for π.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The diameter of a circle is: 106 yd
Now,
We know that,
The radius of a circle (r) = \(\frac{The diameter of a circle}{2}\)
r = \(\frac{106}{2}\)
r = 53 yd
Now,
We know that,
The area of a circle (A) = πr²
So,
A = 3.14 × 53²
= 8,820.26 yd²
Hence, from the above,
We can conclude that the area of the circle with the given diameter is: 8,820.26 yd²
Question 10.
Jaylon created this stained-glass window. The upper two corners are quarter circles, each with a radius of 4 inches. Find the area of the window. Use 3.14 for π.
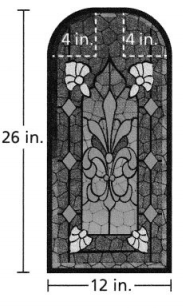
Answer:
It is given that
Jaylon created this stained-glass window. The upper two corners are quarter circles, each with a radius of 4 inches.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The stained glass window is made up of 2 quarter circles, 1 rectangle, and 1 square
Now,
We know that,
The area of a rectangle = Length × Width
The arae of a quarter circle = \(\frac{1}{4}\)πr²
The area of a square = Side × Side
Now,
The area of 2 quarter circles (A) = 2 × \(\frac{1}{4}\) × 3.14 × 4²
= 25.12 in.²
The area of the recatngle (A) = 12 × (26 – 4)
= 264 in.²
The area of the square that lies between the two quareter circles (A) = (12 – 8) × 4
= 16 in.²
So,
The area of the stained glass window = 25.12 + 264 + 16
= 305.12 in.²
Hence, from the above,
We can conclude that the area of the stained glass window is: 305.12 in.²
Question 11.
The circumference of a circle is 50.24 meters. What is the area of the circle? Use 3.14 for π.
Answer:
It is given that
The circumference of a circle is 50.24 meters
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
50.24 = 2 × 3.14 × r
r = \(\frac{50.24}{6.28}\)
r = 8 meters
Now,
We know that,
The area of a circle (A) = πr²
So,
A = 3.14 × 8²
= 200.96 meters²
Hence, from the above,
We can conclude that the area of the circle for the given circumference is: 200.96 meters²
Question 12.
Higher-Order Thinking A circular flower bed is 20 meters in diameter and has a circular sidewalk around it that is 3 meters wide. Find the area of the sidewalk in square meters. Use 3.14 for π. Round to the nearest whole number.
Answer:
It is given that
A circular flower bed is 20 meters in diameter and has a circular sidewalk around it that is 3 meters wide.
Now,
The area of the sidewalk is given as:
A = The area of a flower bed – The area of a sidewalk including the flower bed
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{20}{2}\)
r = 10 meters
Now,
The area of a flower bed (A) = πr²
So,
A = 3.14 × 10²
= 314 meters²
Now,
The area of a sidewalk including the flower bed (A) = 3.14 × (10 + 3)²
= 530.66 meters²
So,
The area of the sidewalk = 530.66 – 314
= 216.66 meters²
Hence, from the above,
We can conclude that the area of the sidewalk is: 216.66 meters²
Question 13.
A circular plate has a circumference of 16.3 inches. What is the area of this plate? Use 3.14 for π. Round to the nearest whole number.
Answer:
It is given that
A circular plate has a circumference of 16.3 inches
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
16.3 = 2 × 3.14 × r
r = \(\frac{16.3}{6.28}\)
r = 2.59 inches
Now,
We know that,
The area of the circular plate (A) = πr²
So,
A = 3.14 × (2.59)²
= 21.06
≈21 inches²
Hence, from the above,
We can conclude that the area of the circular plate for the given circumference is: 21 inches²
Question 14.
A water sprinkler sends water out in a circular pattern. How many feet away from the sprinkler can it spread water if the area formed by the watering pattern is 379.94 square feet?
Answer:
It is given that
A water sprinkler sends water out in a circular pattern and the area formed by the watering pattern is 379.94 square feet
Now,
We have to find the diameter to find how many feet away from the sprinkler can spread the water
Now,
We know that,
The area of a circle (A) = πr²
So,
379.94 = 3.14 × r²
r² = \(\frac{379.94}{3.14}\)
r² = 121
r = 11 feet
So,
Diameter (d) = 2 × Radius
d = 2 × 11
d = 22 feet
Hence, from the above,
We can conclude that the sprinkler can spread the water 22 feet away
Question 15.
The circumference of a circular rug is 24.8 meters. What is the area of the rug? Use 3.14 for π. Round your answer to the nearest tenth.
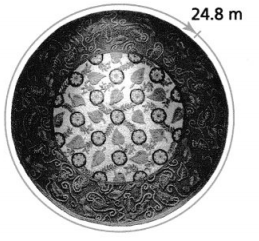
Answer:
It is given that
The circumference of a circular rug is 24.8 meters
Now,
The given figure is:

Now,
We know that,
The circumference of a circle (C) = 2πr
So,
24.8 = 2 × 3.14 × r
r = \(\frac{24.8}{6.28}\)
r = 3.94 m
Now,
The area of the circular rug (A) = πr²
So,
A = 3.14 × (3.94)²
= 48.7 m²
Hence, from the above,
We can conclude that the area of the circular rug for the given circumference to the nearest tenth is: 48.7 m²
Question 16.
Frank wants to find the area enclosed by the figure at the right. The figure has semicircles on each side of a 40-meter-by-40-meter square. Find the area enclosed by the figure. Use 3.14 for π.
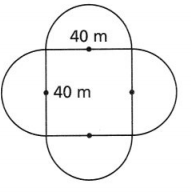
Answer:
It is given that
Frank wants to find the area enclosed by the figure at the right. The figure has semicircles on each side of a 40-meter-by-40-meter square.
Now,
The given figure is:

Now,
The area enclosed by the given figure = The area of the square + The area of the 4 semicircles
Now,
From the given figure,
We can observe that
The side of the square = 40 m
The diameter of the semi circle = 40 m
Now,
We know that,
The area of a square (A) = Side²
So,
A = 40²
= 1,600 m²
Now,
We know that,
The area of a semicircle (A) = \(\frac{1}{2}\)πr²
So,
A = \(\frac{1}{2}\) × 3.14 × \(\frac{1,600}{4}\)
= 628 m²
So,
The area enclosed bythe given figure (A) = 1,600 + 628
= 2,228 m²
Hence, from the above,
We can conclude that the area enclosed by the given figure is: 2,228 m²
Assessment Practice
Question 17.
Julia’s bedroom is 10 feet by 10 feet. She wants to place a circular rug in the corner of her room.
PART A
She places a rug with a radius of 2 feet in her room. How much of her bedroom floor, in square feet, is not covered by the rug? Use 3.14 for π. Round to the nearest tenth.
Answer:
It is given that
Julia’s bedroom is 10 feet by 10 feet. She wants to place a circular rug in the corner of her room.
So,
The diameter of the circular rug placed by Julia is: 10 feet
Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
r = \(\frac{10}{2}\)
r = 5 feet
So,
The space of bedroom floor that is not covered by the rug (C) = The space of the bedroom floor that is covered by the rug when the radius is 5 meters – The space of the bedroom floor that is covered by the rug when the radius is 2 meters
So,
C = 2π (5 – 2)
= 2 × 3.14 × 3
= 18.84 feet
Hence, from the above,
We can conclude that the space of bedroom floor that is not covered by the rug to the neares tenth is: 18.8 feet
PART B
Julia decides she wants a rug that covers about 50% of her floor. Which rug should she buy?
A. A rug with a radius of 5 feet
B. A rug with a diameter of 5 feet
C. A rug with a radius of 4 feet
D. A rug with a diameter of 4 feet
Answer:
It is given that Julia’s bedroom is 10 feet by 10 feet
So,
The diameter of the circular rug is: 10 feet
Now,
The rug covers the whole bedroom floor when the diameter is 10 feet
So,
When Julia decides to cover the bedroom floor only 50% with the rug,
Then, we have to find only the radius of the circular rug i.e., \(\frac{10}{2}\)
Hence, from the above,
We can conclude that option A matches the given situation

Question 18.
The circumference of a hubcap of a tire is 81.58 centimeters. Find the area, in square centimeters, of this hubcap. Use 3.14 as an approximation for π. Round your answer to the nearest whole centimeter.
Answer:
It is given that
The circumference of a hubcap of a tire is 81.58 centimeters.
Now,
We know that,
The circumference of a circle (C) = 2πr
So,
81.58 = 2 × 3.14 × r
r = \(\frac{81.58}{6.28}\)
r = 12.99 cm
Now,
The area of a circle (A) = πr²
So,
A = 3.14 × (12.99)²
= 529.8 cm²
≈ 530 cm²
Hence, from the above,
We can conclude that the area of the circular hubcap is about 530 cm²
3-Act Mathematical Modeling: Whole Lotta Dough
АСТ 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Construct Arguments Predict an answer to this Main Question. Explain your prediction.
Answer:
Question 4.
On the number line below, write a number that is too small to be the answer. Write a number that is too large.

Answer:
Question 5.
Plot your prediction on the same number line.
Answer:
ACT 2
Question 6.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 7.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 8.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 9.
What is your answer to the Main Question? Is it higher or lower than your prediction? Explain why.

Answer:
ACT 3
Question 10.
Write the answer you saw in the video.
Answer:
Question 11.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 12.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:
ACT 3 Extension
Question 13.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 14.
Reasoning Explain why your answer to the Main Question does not involve the symbol π.
Answer:
SEQUEL
Question 15.
Use Structure If the regular pizza costs $8.99, how much do you think the big pizza costs?
Answer:
Lesson 8.7 Describe Cross Sections
Solve & Discuss It!
How could Mrs. Mendoza divide the ream of paper equally between two art classes? She has a paper cutter to slice the paper if needed. What will the dimensions for each sheet of paper be once she has divided the ream? How many sheets will each class receive?

I can… determine what the cross-section looks like when a 3D figure is sliced.
Answer:
It is given that
Mrs. Mendoza has a paper cutter to slice the paper.
Now,
The given figure is:

Now,
From the given figure,
We can observe that,
A ream consists of 500 sheets
We can also observe that
The dimensions of the ream are:
Length of the ream: 8\(\frac{1}{2}\) inches
Width of the ream: 11 inches
Now,
From the given figure,
We can observe that
The shape of the ream is: Rectangle
Now,
We know that,
Even we cut a ream of paper, each sheet of paper has the same dimensions as a ream of paper
So,
The dimensions of each sheet of paper after Mrs. Mendoza divided the ream into 2 equal parts are:
Length: 8\(\frac{1}{2}\) inches
Width: 11 inches
Now,
The number of sheets of paper each class will get after dividing the ream = \(\frac{500}{2}\)
= 250 sheets
Hence, from the above,
We can conclude that
The number of sheets each class will receive is: 250
The dimensions of each sheet of paper once Mrs. Mendoza divided the ream is:
Length: 8\(\frac{1}{2}\) inches
Width: 11 inches
Focus on math practices
Use Structure How would the number of sheets of paper each class receives change if Mrs. Mendoza started with 300 sheets?
Answer:
It is given that
Mrs. Mendoza has 500 sheets of paper and she divided the sheets equally between the two classes
Now,
If Mrs. Mendoza started with 300 sheets of paper, then
The number of sheets divided by Mrs. Mendoza equally between the two classes = \(\frac{300}{2}\)
= 150
Hence, from the above,
We can conclude that the number of sheets each class receives when Mrs. Mendoza started with 300 sheets is: 150
Essential Question
How do the faces of a three-dimensional figure determine the two-dimensional shapes created by slicing the figure?
Answer:
A cross-section is a new face you see when you slice through a three-dimensional figure.
Example:
If you slice a rectangular pyramid parallel to the base, you get a smaller rectangle as the cross-section.
If you slice a rectangular pyramid parallel to the apex, you get a smaller triangle as the cross-section.
Try It!
Zachary made a vertical slice that was parallel to the left and right faces of a bread roll. What shape is the cross-section, and what are its dimensions?
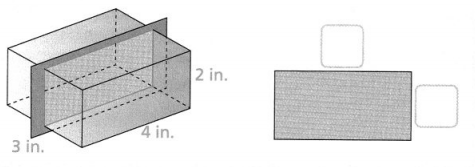
The shape of the cross section is a __________ that is __________ inches by ________ inches.
Answer:
It is given that
Zachary made a vertical slice that was parallel to the left and right faces of a bread roll
Now,
The given figure is:

Now,
From the given figure,
We can observe that
When Zachary made a vertical slice that was parallel to the left and right faces of a bread roll,
The shape of the cross-section Zachary can get is: Rectangle
Now,
The dimensions of the rectangle that we obtained by slicing is:
Length: 3 in.
Width: 2 in.
Hence, from the above,
We can conclude that
The shape of the cross-section is a “Rectangle” that is 3 inches × 2 inches.
Convince Me! What are the shapes of horizontal and vertical cross-sections of a rectangular prism, and how can you determine the dimensions of the cross-sections?
Answer:
The horizontal cross-section of a rectangular prism is: Rectangle
The vertical cross-section of a rectangular prism is: Rectangle
Now,
The dimensions of the cross-sections are:
a. One dimension of the cross-section will be the height of the prism.
b. Another dimension of the cross-section will be the length of the rectangle.
Try It!
Draw the cross-section that is created when a vertical plane intersects the top vertex and the shorter edge of the base of the pyramid shown. What is the area of the cross section?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The cross-section that is created when a vertical plane intersects the top vertex and the shorter edge of the base of the pyramid is: Triangle
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
A = \(\frac{1}{2}\) × 7 × 4
= 14 in.²
Hence, from the above,
We can conclude that the area of the cross-section is: 14 in.²
KEY CONCEPT
A cross section is the two-dimensional shape exposed when a three-dimensional figure is sliced. The shape and dimensions of a cross section in a rectangular prism are the same as the faces that are parallel to the slice.
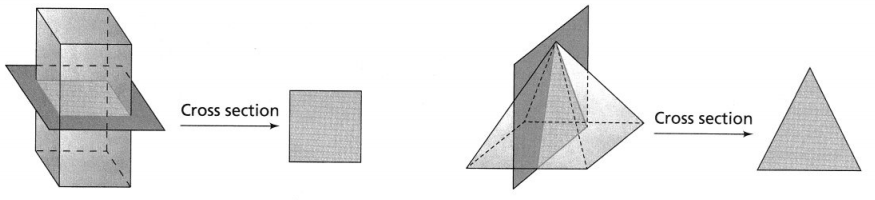
Do You Understand?
Question 1.
Essential Question How do the faces of a three-dimensional figure determine the two-dimensional shapes created by slicing the figure?
Answer:
A cross-section is a new face you see when you slice through a three-dimensional figure.
Example:
If you slice a rectangular pyramid parallel to the base, you get a smaller rectangle as the cross-section.
If you slice a rectangular pyramid parallel to the apex, you get a smaller triangle as the cross-section.
Question 2.
Generalize What are the shapes of the cross-sections that are parallel or perpendicular to the bases of a right rectangular prism?
Answer:
The shape of the cross-section that is parallel to the base of a right rectangular prism is: Rectangle
The shape of the cross-section that is perpendicular to the base of a right rectangular prism is: Triangle
Question 3.
Generalize What are the shapes of the horizontal cross-sections of a right rectangular pyramid? What are the shapes of vertical cross-sections through the vertex opposite the base?
Answer:
The shape of the horizontal cross-section of a right rectangular pyramid is: Rectangle
The shape of the vertical cross-section through the vertex that is opposite to the base is: Triangle
Do You Know How?
Question 4.
The divider in a desk drawer is a cross-section that is parallel to the front of the drawer. What is its shape, and what are its dimensions?
Answer:
It is given that
The divider in a desk drawer is a cross-section that is parallel to the front of the drawer
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The shape of the cross-section of the divider that is parallel in front of the door is: Rectangle
Now,
The dimensions of the cross-section of the divider are:
Length: 8 cm
Width: 5 cm
Hence, from the above,
We can conclude that
The shape of the cross-section of the divider is: Rectangle
The dimensions of the cross-section of the divider is:
Length: 8 cm
Width: 5 cm
Question 5.
Use the diagram to answer the questions.
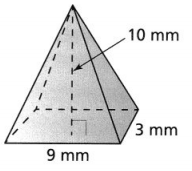
a. Draw the cross-section that is formed when the pyramid is sliced vertically through its vertex and its right face, perpendicular to its base.
Answer:
The given figure is:

Hence,
The cross-section that is formed when the pyramid is sliced vertically through its vertex and its right face that is perpendicular to its base is:
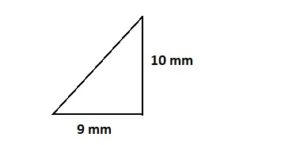
b. What is the area of this cross section?
Answer:
From part (a),
We can observe hat
The cross-section that is formed when the pyramid is sliced vertically through its vertex and its right face that is perpendicular to its base is:

Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
The area of the given cross-section (A) = \(\frac{1}{2}\) × 9 × 10
= 45 mm²
Hence, from the above,
We can conclude that the area of the given cross-section is: 45 mm²
Question 6.
What are the dimensions of the vertical cross section shown on this right rectangular prism?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that,
The vertical cross-section of the given right rectangular prism is: Rectangle
Now,
The dimensions of the vertical cross-section of the given right rectangular prism is:
Length: 5 in.
Width: 4 in.
Hence, from the above,
We can conclude that
The dimensions of the vertical cross-section shown on the given right rectangular prism is:
Length: 5 in.
Width: 4 in.
Question 7.
Be Precise Describe the cross section that is formed by a vertical plane, perpendicular to the base of the pyramid, that intersects the 9-in. edge and the top vertex of the pyramid shown.
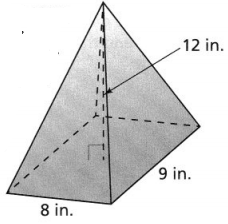
Answer:
The given figure is:

Hence,
The cross-section that is formed by a vertical plane, perpendicular to the base of the pyramid, that intersects the 9-in. edge and the top vertex of the given pyramid is:
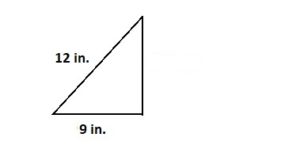
Question 8.
Mason is slicing butter for the meal he is preparing. Describe the vertical cross section when the knife slices through the butter, parallel to its sides.
Answer:
It is given that
Mason is slicing butter for the meal he is preparing
Now,
The given figure is:

Hence,
The vertical cross-section when the knife slices through the butter, parallel to its sides is:
Question 9.
a. Look for Relationships What are the dimensions of the vertical cross section?
Answer:
The given figure is:

Hence,
The dimensions of the vertical cross-section of the given figure is:
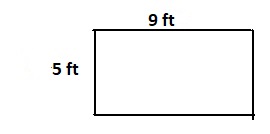
b. What would be the dimensions of a horizontal cross section?
Answer:
The given figure is:

Hence,
The horizontal cross-section of the given figure is:

Question 10.
Use the figure to the right.
a. Describe the cross section shown.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The horizontal cross-section of the given figure is: Rectangle
The vertical cross-section of the given figure is: Rectangle
Hence,
The dimensions of the horizontal cross-section of the given figure is:
Length: 4 ft
Width: 6 ft
The dimensions of the vertical cross-section of the given figure is:
Length: 11 ft
Width: 6 ft
b. Is it possible to have a horizontal cross section with different dimensions if you had the plane intersect the prism at another height? Explain.
Answer:
Yes, it is possible to have a horizontal cross section with different dimensions if you had the plane intersect the prism at another height
Now,
The given figure is:

Now,
From the given figure,
We can observe that
If we make a horizontal cross-section when another plane intersects the prism at another height, then
The dimensions of the new horizontal cross-section is:
Length: 11 ft
Width: 6 ft
Question 11.
Make Sense and Persevere The base of a right rectangular pyramid has a length of 12 centimeters, a width of 6 centimeters, and a height of 14 centimeters. Describe the cross-section formed by a horizontal plane that intersects the faces of the pyramid above the base.
Answer:
It is given that
The base of a right rectangular pyramid has a length of 12 centimeters, a width of 6 centimeters, and a height of 14 centimeters
Now,
We know that,
The horizontal cross-section of a right rectangular pyramid is: Rectangle
The vertical cross-section of a right rectangular pyramid is: Triangle
So,
The dimensions of the horizontal cross-section of the given right rectangular pyramid is:
Length: 12 cm
Width: 6 cm
Hence,
The representation of the horizontal cross-section of the given right rectangular pyramid is:

Question 12.
Higher Order Thinking Luis makes blocks from a painted piece of wood with dimensions of 27 inches × 24 inches × 1.5 inches. To make 72 blocks, the wood is cut into 3-inch squares. Draw two pictures showing the horizontal cross section and the vertical cross section of each block.
Answer:
It is given that
Luis makes blocks from a painted piece of wood with dimensions of 27 inches × 24 inches × 1.5 inches. To make 72 blocks, the wood is cut into 3-inch squares.
So,
The dimensions of each block is:
Length: \(\frac{27}{3}\) = 9 inches
Width: \(\frac{24}{3}\) = 8 inches
Height: \(\frac{1.5}{3}\) = 0.5 inches
Now,
It is given that the 72 blocks are cut into 3-inch squares
So,
The figure made by the given dimensions is: Cuboid
Now,
The vertical cross-section of the given cuboid is: Rectangle
The horizontal cross-section of the given cuboid is: Rectangle
Hence,
The representation of the vertical and horizontal cross-sections of the cuboid are:
Question 13.
Make Sense and Persevere The area of the cross section shown is 52 square yards. What is the length of the unknown side of the base of the pyramid?
Answer:
It is given that
The area of the cross-section shown is 52 square yards.
Now,
The given figure is:

Now,
From the above,
We can observe that the given figure is: Right Rectangular pyramid
Now,
We know that,
The vertical cross-section of the right rectangular pyramid is: Triangle
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
52 = \(\frac{1}{2}\) × x × 13
x = \(\frac{52 × 2}{13}\)
x = 8 yd
Hence, from the above,
We can conclude that the length of the unknown side of the base of the given pyramid is: 8 yd
Question 14.
A waiter slices a cake shaped like a square pyramid vertically through the top point.
a. Make Sense and Persevere Draw the cross section that is made by slicing the cake in this way.

Answer:
It is given that
A waiter slices a cake shaped like a square pyramid vertically through the top point.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
If we made the vertical cross-section of the given square pyramid, then
We will get the vertical cross-section as a Right triangle
Hence,
The representation of the vertical cross-section of the given square pyramid is:

b. What is the area of this cross section?
Answer:
From part (a),
We can observe that
The representation of the vertical cross-section of the given square pyramid is:

Now,
We know that,
In a right triangle,
(Hypotenuse)² = (Base)² + (Side)²
So,
In the given triangle,
18² = 14² + h²
h² = 18² – 14²
h = 11.3 inches
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
A = \(\frac{1}{2}\) × 14 × 11.3
= 79.19 yd²
Hence, from the above,
We can conclude that the area of the given cross-section is: 79.19 yd²
Question 15.
Miranda says that the triangle below represents the cross section of the rectangular pyramid shown.

What mistake might Miranda have made?
Answer:
It is given that
Miranda says that the triangle below represents the cross-section of the rectangular pyramid shown.
Now,
The given figure is:

Now,
We know that,
In a rectangular pyramid,
The vertical cross-section is: Triangle
The horizontal cross-section is: Rectangle
So,
According to the given information,
Miranda did not mention what type of cross-section she had drawn
Hence, from the above,
We can conclude that the mistake made by Miranda is:
She did not mention what type of cross-section she made
Assessment Practice
Question 16.
Estimate, to the nearest whole number, the number of vertical cross sections needed to equal the area of the base of the figure to the right. Explain how you made your estimate, and decide whether your estimate is higher or lower than the actual number.
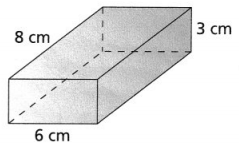
Answer:
The given figure is:

Now,
From the given figure,
We can observe that the given 3-d shape is: Cuboid
Now,
We know that,
The vertical cross-section of a cuboid is: Rectangle
The horizontal cross-section of a cuboid is: Rectangle
Now,
From the given figure,
The dimensions of a horizontal cross-section of the given figure is:
Length: 8 cm
Width: 6 cm
The dimensions of a vertical cross-section of the given figure is:
Length: 6 cm
Width: 3 cm
Now,
We know that,
The area of a rectangle = Length × Width
So,
The area of a horizontal cross-section of the given figure is:
A = 8 × 6 = 48 cm²
The area of a vertical cross-section of the given figure is:
A = 6 × 3 = 18 cm²
Hence, from the above,
We can conclude that
The number of vertical cross-sections < The area of the base of the given figure
Lesson 8.8 Solve Problems Involving Surface Area
Solve & Discuss It!
Alaya will paint the outside of a box in three different colors. Decide how she could paint the box. What is the total area that each color will cover?

I can… find the area and surface area of 2-dimensional composite shapes and 3-dimensional prisms.
Answer:
It is given that
Alaya will paint the outside of a box in three different colors
Now,
The given figure is:

Now,
From the given figure,
We can observe that the given figure is a “Cuboid” which has 6 faces
Now,
The different ways that Alaya can paint are:
a. She can paint all the faces of the box with the same color
b. She can paint the faces of the box with alternative colors i.e., 1 face is colored with 1 color, 2nd face is colored with 1 color, etc.
Now,
We know that,
The total surface area of a cuboid (A) = 2 (lw + wh + lh)
Where,
‘l’ is the length of the cuboid
‘w’ is the width of the cuboid
‘h’ is the height of the cuboid
Now,
From the given figure,
The length of the cuboid (l) is 32 in.
The width of the cuboid (w) is 16 in.
The height of the cuboid (h) is 14 in.
So,
A = 2 (32 × 16 + 16 × 14 + 32 × 14)
= 2 (512 + 224 + 448)
= 2,368 in.²
So,
The total surface area that each color will cover = \(\frac{2,368}{6}\)
= 394.66 in.²
Hence, from the above,
We can conclude that
The different ways that Alaya can paint are:
a. She can paint all the faces of the box with the same color
b. She can paint the faces of the box with alternative colors i.e., 1 face is colored with 1 color, 2nd face is colored with 1 color, etc.
The total area covered by each color is: 394.66 in.²
Make Sense and Persevere
What do you know about the faces of a rectangular prism?
Answer:
The facts about the rectangular prism are:
a. A rectangular prism is a polyhedron with two congruent and parallel bases.
b. Because of its cross-section along the length, it is said to be a prism.
c. A rectangular prism has 6 faces, 8 vertices, and 12 edges. Its base and top are always rectangles.
d. It has 3 dimensions They are length, width, and height.
Focus on math practices
Reasoning Trista paints each pair of opposite sides of the box with the same color. How many different areas does she need to find to determine the total area covered by each color? Explain.
Answer:
The given figure is:

Now,
It is given that
Trista paints each pair of opposite sides of the box with the same color
So,
Each color covers two opposite pairs of rectangles.
So,
With the help of each color,
We can determine the total area of the two opposite sides of the box
Hence, from the above,
We can conclude that
she needs to find 3 different areas to determine the total area covered by each color
Essential Question
How is finding the area of composite two-dimensional figures similar to finding the surface area of three-dimensional figures?
Answer:
To find the area of something, you start by multiplying the two dimensions together. To find the area of a rectangle, you multiply the length by the width. Although the area is a two-dimensional measurement, it can also be used with three-dimensional objects.
Try It!
This diagram shows the area of a room to be carpeted. What will be the area of the new carpet?
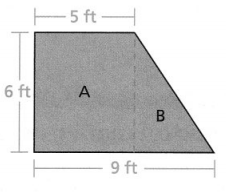
A = ________ = ________ ft2 B = _______ = _______ ft2
Total area = ______ + ______
The area of the new carpet is ________ square feet
Answer:
It is given that
The below diagram shows the area of a room to be carpeted.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The total area of a room that is carpeted = The area of a rectangle + The area of a triangle
Now,
From the given figure,
The dimensions of the rectangle are:
Length: 6 feet
Width: 5 feet
The dimensions of the triangle are:
Height: 6 feet
Base: 4 feet
Now,
We know that,
The area of a rectangle = Length × Width
= 6 × 5
= 30 feet²
Now,
We know that,
The area of a triangle = \(\frac{1}{2}\) × Base × height
= \(\frac{1}{2}\) × 6 × 4
= 12 feet²
So,
The area of the new carpet = 30 + 12
= 42 feet²
Hence, from the above,
We can conclude that the area of the new carpet is: 42 feet²
Convince Me! How does knowing the area of familiar shapes help find the total area of a composite shape?
Answer:
A composite figure is made up of simple geometric shapes. To find the area of a composite figure or other irregular-shaped figures, divide it into simple, non-overlapping figures. Find the area of each simpler figure, and then add the areas together to find the total area of the composite figure
Try It!
Hiromi is painting the front and back of a barn. Each can of paint covers 32 square feet. How many cans of paint does Hiromi need to cover the entire front and back of the barn?
Answer:
It is given that
Hiromi is painting the front and back of a barn. Each can of paint covers 32 square feet.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The total area of the barn (A) = The area of the front + The area of the back
= 2 (The area of the front) (or) 2 (The area of the back)
Now,
The front side of the barn is made up of a rectangle and a triangle
Now,
The area of the front side of the barn = The area of the rectangle + The area of the triangle
= Length × Width + \(\frac{1}{2}\) × Base × Height
= 11 × 12 + \(\frac{1}{2}\) × 12 × (15 – 11)
= 132 + 24
= 156 ft²
So,
The total area of the barn (A) = 2 × 156
= 312 ft²
Now,
The number of cans of paint does Hiromi need to cover the entire front and back of the barn = \(\frac{The total area of the barn}{The number of square feet each can covers}\)
= \(\frac{312}{32}\)
= 9.75
≅ 10 cans of paint
Hence, from the above,
We can conclude that Hiromi needs to cover 10 cans of paint to cover the entire front and back of the barn
KEY CONCEPT
The area of a two-dimensional composite figure is the sum of the areas of all the shapes that compose it. The surface area of a three-dimensional composite figure is the sum of the areas of all its faces.
Two-dimensional composite figure
Three-dimensional composite figure
Surface area of shape A + Surface area of shape B = Surface area of composite shape
Do You Understand?
Question 1.
Essential Question How is finding the area of composite two-dimensional figures similar to finding the surface area of three-dimensional figures?
Answer:
To find the area of something, you start by multiplying the two dimensions together. To find the area of a rectangle, you multiply the length by the width. Although the area is a two-dimensional measurement, it can also be used with three-dimensional objects.
Question 2.
Make Sense and Persevere Laine wants to determine the amount of fabric needed to cover a triangular prism-shaped box. She begins by measuring the dimensions of the box. Explain her next steps.
Answer:
It is given that
Laine wants to determine the amount of fabric needed to cover a triangular prism-shaped box. She begins by measuring the dimensions of the box
Now,
The next steps she has to follow are:
Step 1:
Divide the given triangular prism into the number of parts that have many faces as the given triangular prism has.
We know that,
The triangular prism has: 5 faces
So,
The number of smaller triangles are: 5
Step 2:
Find the area of each triangle
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
Step 3:
Add the areas of the 5 triangles to find the area of the given triangular prism
Hence, from the above,
We can conclude that the amount of fabric needed to cover a triangular prism is its total area
Question 3.
Use Structure Explain how you would find the surface area of the figure below.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that the given figure is made up of:
a. Rectangle b. Pentagon
So,
The total surface area of the given figure = Total area of the rectangle + Total area of the pentagon
Now,
From the given figure,
We can observe that
There are:
a. 5 Rectangles b. 2 Pentagons
Hence,
The total surface area of the given figure (A) = The area of 5 Rectangles + The area of 2 Pentagons
Do You Know How?
Question 4.
Paula is painting a henhouse. If a can of paint will cover 24 square feet, how many cans of paint does she need to buy? Explain the steps she might take to solve this problem.
Answer:
It is given that Paula is painting a henhouse
Now,
The representation of a henhouse is:

Now,
From the given figure,
We can observe that
The henhouse is made up of:
a. 5 Rectangles b. 4 Triangles
Now,
The steps that Paula might take to find the number of cans she needed to buy are:
Step 1:
Divide the henhouse into simple 2-d figures i.e, into rectangles and triangles
Step 2:
Find the areas of the 2-d figures
Step 3:
Find the total area of the henhouse by adding all the areas of 2-d figures
Step 4:
To find the number of cans Paula needed to buy,
The number of cans Paula needed to buy = \(\frac{The total area of the henhouse}{The area covered by 1 can of paint}\)
Hence, from the above,
We can conclude that
By following the above steps, Paula can solve her problem
Question 5.
Find the area of the composite figure. The two triangles have the same dimensions.
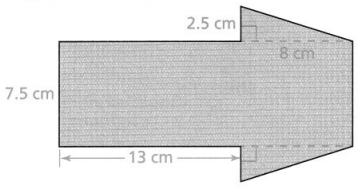
Answer:
The given figure is:

Now,
From the above figure,
We can observe that
The area of the composite figure (A) = The area of the 2 rectangles + The area of the 2 triangles
Now,
We know that,
The area of a rectangle (A) = Length × Width
The area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
A = (7.5 × 13) + (7.5 × 6) + 2 × \(\frac{1}{2}\) × 2.5 × 6
= 97.5 + 45 + 15
= 157.5 cm²
Hence, from the above,
We can conclude that the area of the composite figure is: 157.5 cm²
Question 6.
A stage block is being covered in carpet. The dimensions of the block are 2 feet by 3 feet by 6 feet. Every surface will need covering except for the surface touching the floor, which is 3 feet by 6 feet. How would you calculate the surface area that needs covering?
Answer:
It is given that
A stage block is being covered in carpet. The dimensions of the block are 2 feet by 3 feet by 6 feet. Every surface will need covering except for the surface touching the floor, which is 3 feet by 6 feet.
Now,
The surface area that needs covering = The total surface area – The surface area of the floor
Now,
From the given information,
We can say that the carpet is in the form of a rectangular prism
Now,
We know that,
The surface area of a rectangular prism (A) = 2 (lw + wh + lh)
Where,
‘l’ is the length
‘w’ is the width
‘h’ is the height
So,
The total surface area (A) = 2 (2 × 3 + 3 × 6 + 2 × 6)
= 2 (6 + 18 + 12)
= 72 feet²
Now,
From the given information,
We can observe that the floor is in the form of a rectangle
So,
The surface area of the floor (A) = 3 × 6
= 18 ft²
So,
The surface area that needs covering = The total surface area – The surface area of the floor
= 72 – 18
= 54 feet²
Hence, from the above,
We can conclude that the surface area that needs covering is: 54 feet²
Practice & Problem Solving
Leveled Practice In 7, fill in the boxes to solve.
Question 7.
Jacob is putting tiles on the sections of his yard labeled A, B, and C. What is the area of the parts that need tiles?
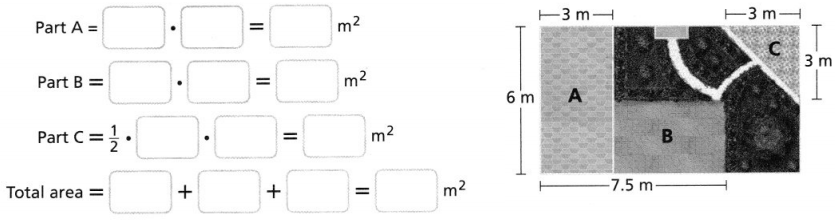
Answer:
It is given that
Jacob is putting tiles on the sections of his yard labeled A, B, and C.
Now,
From the given figure,
We can observe that the tiles are made up of parts named as:
A: Rectangle B: Rectangle C: Triangle
Now,
We know that,
The area of a rectangle (A) = Length × Width
The area of triangle A) = \(\frac{1}{2}\) × Base × Height
So,
The area of Part A:
A = 6 × 3 = 18 m²
The area of Part B:
A = 3 × 4.5 = 13.5 m²
The area of Part C:
A = \(\frac{1}{2}\) × 3 × 3 = 4.5 m²
So,
The total area of the tiles = The area of Part A + The area of Part B + The area of Part C
= 18 + 13.5 + 4.5
= 36 m²
Hence, from the above,
We can conclude that the area of the parts that need tiles is: 36 m²
Question 8.
What is the total area of the figure?

Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The area of the given figure (A) = The area of the rectangles + The area of a triangle
Now,
We know that,
The area of a rectangle (A) = Length × Width
The area of a triangle (A) = \(\frac{1}{2}\) ×Base × Height
So,
The area of the given figure (A) = 4 (4 × 9) + \(\frac{1}{2}\) × 9 × \(\sqrt{9² – 5²}\)
= 144 + 18.70
= 162.70 ft²
Hence, from the above,
We can conclude that the area of the given figure is: 162.70 ft²
Question 9.
Find the surface area of the prism.
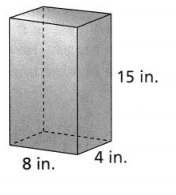
Answer:
The given figure is:

Now,
We know that,
The surface area of a rectangular prism = 2 (lw + wh + lh)
Where,
‘l’ is the length
‘w’ is the width
‘h’ is the height
So,
The area of the given prism (A) = 2 (15 × 4 + 4 × 8 + 15 × 8)
= 2 (60 + 32 + 120)
= 424 in.²
Hence, from the above,
We can conclude that the surface area of the given prism is: 424 in.²
Question 10.
Find the surface area of the triangular prism. The base of the prism is an isosceles triangle.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
For the given Triangular prism,
There are:
a. 2 Triangles b. 3 Paralleleograms
So,
The area of the triangular prism = The total area of the triangles + The total area of the parallelograms
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × height
The area of a parallelogram (A) = Base × Height
So,
The total area of the triangular prism (A) = 2 × \(\frac{1}{2}\) × 14 × 24 + 3 × 25 × 48
= 336 + 3,600
= 3,936 cm²
Hence, from the above,
We can conclude that the area of the given triangular prism is: 3,936 cm²
Question 11.
A block of wood has the shape of a triangular prism. The bases are right triangles. Find its surface area.
Answer:
It is given that
A block of wood has the shape of a triangular prism. The bases are right triangles
Now,
The given triangular prism is:

Now,
From the given triangular prism,
We can observe that
The triangular prism has:
a. 2 Right triangles b. 3 Parallelograms
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base × height
The area of a parallelogram (A) = Base × Height
So,
The total area of the triangular prism (A) = 2 × \(\frac{1}{2}\) × 1.5 × 2.5 + 3 × 2.5 × 15
= 3.75 + 112.5
= 116.25 in.²
Hence, from the above,
We can conclude that the area of the given triangular prism is: 116.25 in.²
Question 12.
A box has the shape of a rectangular prism. How much wrapping paper do you need to cover the box?

Answer:
It is given that A box has the shape of a rectangular prism
Now,
The given rectangular prism is:

Now,
To find the amount of wrapping paper you needed to cover the box,
We have to find the total area of the iven rectangular prism
Now,
We know that,
The surface area of a rectangular prism (A) = Length × Width × Height
So,
A = 16 × 3 × 15
= 720 in.²
Hence, from the above,
We can conclude that
The amount of wrapping paper you needed to cover the box is: 720 in.²
Question 13.
Higher-OrderThinking Find the surface area of the Rectangular Hexagonal prism. Show your work.

Answer:
The given rectangular hexagonal prism is:

Now,
From the given figure,
We can observe that
The total area of the rectangular hexagonal prism (A) = The area of the 2 cicles + The area of the 6 rectangles
Now,
We know that,
The area of a circle (A) = πr²
The area of a rectangle (A) = Length × Width
So,
A = 2 × 3.14 × (4.3)² + 6 × 14 × 5
= 116.11 + 420
= 536.11 cm²
Hence, from the above,
We can conclude that the area of the given rectangular hexagonal prism is: 536.11 cm²
Question 14.
A box has the shape of a rectangular prism with a height of 29 centimeters. If the height is increased by 0.7 centimeter, by how much does the surface area of the box increase?
Answer:
It is given that
A box has the shape of a rectangular prism with a height of 29 centimeters and the height is increased by 0.7 centimeters
Now,
The given rectangular prism is:

Now,
We know that,
The surface area of a rectangular prism (A) = Length × Width × Height
So,
A = 29 × 6.3 × 12
= 2,192.4 cm²
Now,
If the height of the given rectangular prism is increased by 0.7 cm, then
A = (29 + 0.7) × 6.3 × 12
= 2,245.32 cm²
So,
The amount of the surface area increased = 2,245.32 – 2,192.4
= 52.92 cm²
Hence, from the above,
We acn conclude that the amount of surface area increased when the height of the box increased by 0.7 cm is: 52.92 cm²
Question 15.
The base of a prism is an equilateral triangle with an area of 73.2 square centimeters. The area of each lateral face is 104 square centimeters. Riley incorrectly claims that the surface area is 250.4 square centimeters.
a. What is the correct surface area?
Answer:
It is given that
The base of a prism is an equilateral triangle with an area of 73.2 square centimeters. The area of each lateral face is 104 square centimeters. Riley incorrectly claims that the surface area is 250.4 square centimeters.
Now,
The total surface area (A) = The area of the base of the prism + The area of each lateral face
= 73.2 + 104
= 177.2 square cm
Hence, from the above,
We can conclude that the correct surface area is: 177.2 square cm
b. What could have been Riley’s error?
Answer:
The error done by Riley is:
a. She considered the bases of a prism to be 2 and the lateral face as 1
So,
The area she got is 250.4 square cm instead of 177.2 square cm
Assessment Practice
Question 16.
The bottom part of this block is a rectangular prism. The top part is a square pyramid. How much paper, in square centimeters, is needed to cover the block completely?
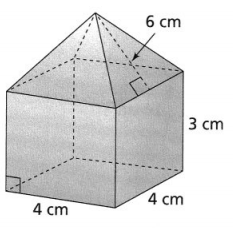
Answer:
It is given that
The bottom part of this block is a rectangular prism. The top part is a square pyramid
Now,
The given figure is:

Now,
From the above,
We can observe that
The area of the given block (A) = The area of the bottom part of the block + The area of the top part of the block
= Length × Width × Height + 5 × \(\frac{1}{2}\) × Base × Height
So,
A = 3 × 4 × 4 + 5 × \(\frac{1}{2}\) × 6 × 4
= 48 + 60
= 108 cm²
Hence, from the above,
We can conclude that
The amount of paper, in square centimeters, is needed to cover the block completely is: 108 cm²
Lesson 8.9 Solve Problems Involving Volume
Solve & Discuss It!
Volunteers at a food pantry pack boxes of soup into crates. How many boxes of soup will fill each crate? Show your work.
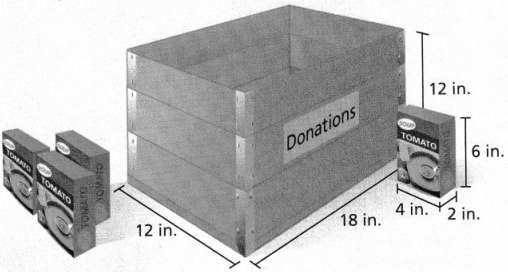
I can… use the area of the base of a three-dimensional figure to find its volume.
Answer:
It is given that
Volunteers at a food pantry pack boxes of soup into crates
Now,
The given figure is:

Now,
From the given figure,
We can observe that the boxes and crates are in the form of a cuboid
Now,
We know that,
The volume of a cuboid = Length × Width × Height
So,
The volume of the box = 4 × 2 × 6
= 48 in.³
The volume of the crate = 12 × 18 × 12
= 2,592 in.³
So,
The number of boxes of soup that will fill each crate = \(\frac{The volume of a crate}{The volume of a box}\)
= \(\frac{2,592}{48}\)
= 54 boxes
Hence, from the above,
We can conclude that the number of boxes of soup that will fill each crate is: 54 boxes
Look for Relationships How can you layer the soup boxes to cover the bottom of the crate?
Answer:
The given figure in part (a) is:

Now,
From the given figure in part (a),
We can observe that
We have to layer the soup boxes in the horizontal position to cover the bottom of the crate
Focus on math practices
Reasoning A supplier donated crates to the food pantry that are 15 inches long, instead of 18 inches long. All other dimensions are the same. What is the greatest number of boxes of soup that will fit in the donated crates? How will the volume of the soup vary from the total volume of the crate?
Answer:
It is given that
A supplier donated crates to the food pantry that are 15 inches long, instead of 18 inches long. All other dimensions are the same
Now,
The given figure is:

Now,
From the given figure,
We can observe that the boxes and crates are in the form of a cuboid
Now,
We know that,
The volume of a cuboid = Length × Width × Height
So,
The volume of the box = 4 × 2 × 6
= 48 in.³
The volume of the crate = 12 × 15 × 12
= 2,160 in.³
So,
The number of boxes of soup that will fill each crate = \(\frac{The volume of a crate}{The volume of a box}\)
= \(\frac{2,160}{48}\)
= 45 boxes
Hence, from the above,
We can conclude that the greatest number of boxes of soup that will fit in the donated crates is: 45 boxes
Essential Question
How does the formula for the volume of a prism help you understand what volume of a prism means?
Answer:
The formula for the volume of a prism is:
V=Bh
where,
B is the base area
h is the height.
Now,
The base of the prism is a rectangle
So,
The area of a rectangle = Length × Width
Hence, from the above,
We can conclude that
The formula for the volume of a prism is:
V = Length× Width × Height
Try It!
What is the volume of the triangular prism?
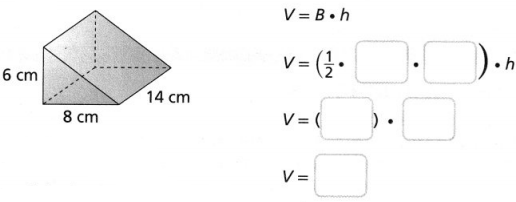
The volume of the prism is __________ cubic centimeters.
Answer:
The given figure is:
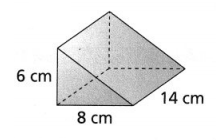
Now,
We know that,
The volume of a triangular prism (V) = Area of a triangle × Height
Now,
We know that,
The area of a triangle (A) = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
So,
The volume of a triangular prism (V) = \(\frac{1}{2}\) × 8 × 6 × 14
= 336 cm³
Hence, from the above,
We can conclude that the volume of the given triangular prism is: 336 cm³
Convince Me! What is the shape of the base of the figure? What are its dimensions? Explain.
Answer:
The given figure is:

Now,
From the given triangular prism,
We can observe that the shape of the base of the figure is: Triangle
Now,
From the given figure,
The dimensions of the base of the figure are:
The base of the triangle: 8 cm
The height of the triangle: 6 cm
Hence, from the above,
We can conclude that the dimensions of the base of the given figure is:
Base: 8 cm
Height: 6 cm
Try It!
Amber built a custom terrarium for her plants. What is the volume of the terrarium?
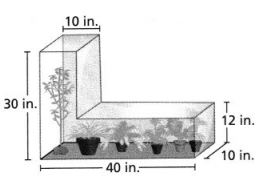
Answer:
It is given that
Amber built a custom terrarium for her plants.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The terrarium is made up of two rectangular prisms
Now,
We know that,
The volume of a rectangular prism (V) = Length × Width × Height
Now,
The volume of the first rectangular prism (V) = 30 × 10 × 10
= 3,000 in.³
The volume of the second rectangular prism (V) = 40 × 10 × 12
= 4,800 in.³
So,
The volume of the custom terrarium (V) = The volume of the first rectangular prism + The volume of the second rectangular prism
= 3,000 + 4,800
= 7,800 in.³
Hence, from the above,
We can conclude that the volume of the custom terrarium that was built by Amber is: 7,800 in.³
KEY CONCEPT
You can use formulas to solve problems involving the volume of three-dimensional figures.
Find the volume of a composite figure by finding the sum of the volumes of each solid figure.
You can use the formula V = Bh to find the volume or unknown dimension of a solid figure.
Do You Understand?
Question 1.
Essential Question How does the formula for volume of a prism help you understand what volume of a prism means?
Answer:
The formula for the volume of a prism is:
V=Bh
where,
B is the base area
h is the height.
Now,
The base of the prism is a rectangle
So,
The area of a rectangle = Length × Width
Hence, from the above,
We can conclude that
The formula for the volume of a prism is:
V = Length× Width × Height
Question 2.
Look for Relationships If you know the volume of a three-dimensional figure, how can you find a missing dimension of the figure?
Answer:
We know that,
The volume of any three-dimensional figure is:
V = Length × Width × Height
Now,
If we have any missing dimension in the figure that is related to the volume, then we will first multiply the known dimensions that are present with the unknown dimension and then divide the product of the known dimensions with the volume of the three-dimensional figure
Question 3.
Make Sense and Persevere How do you find the volume of a three-dimensional figure that can be decomposed into prisms?
Answer:
We know that,
A prism is a three-dimensional figure
We know that,
The volume of a prism (V) = Length × Width × Height
So,
If we have to find the volume of a three-dimensional figure that can be decomposed into prisms, then add all the volumes of the decomposed prisms
Do You Know How?
Question 4.
An aquarium has a regular hexagonal base with side lengths of 15 centimeters. When the hexagon is divided into six equal triangles, the height of each triangle is about 13 centimeters. If the aquarium is 50 centimeters tall, what is its volume?
Answer:
It is given that
An aquarium has a regular hexagonal base with side lengths of 15 centimeters. When the hexagon is divided into six equal triangles, the height of each triangle is about 13 centimeters and the aquarium is 50 centimeters tall
Now,
From the given information,
We can observe that the aquarium is in the form of a regular hexagonal prism
Now,
We know that,
The volume of any three-dimensional figure = Base area × Height
Where,
The base area for this is the area of the hexagon
Now,
We know that,
The area of the hexagon (B) = 6 × \(\frac{1}{2}\) × base × Height
= 6 × \(\frac{1}{2}\) × 15 × 13
= 585 cm²
So,
The volume of the given aquarium (V) = 585 × 50
= 29,250 cm³
Hence, from the above,
We can conclude that the volume of the given aquarium is: 29,250 cm³
Question 5.
A cheese box is shaped like a right triangular prism. The box is 6 inches long, 4 inches tall, and has a volume of 24 cubic inches. Can a cube of cheese that is 2.5 inches on each side fit inside the box? Explain.
Answer:
It is given that
A cheese box is shaped like a right triangular prism. The box is 6 inches long, 4 inches tall, and has a volume of 24 cubic inches.
Now,
We know that,
The volume of a right triangular prism (V) = Base area of a right triangle × Height
Now,
We know that,
Area of a triangle (A) = \(\frac{1}{2}\) × Base × Height
So,
24 = \(\frac{1}{2}\) × 6 × 4 × h
24 = 12 × h
h = \(\frac{24}{12}\)
h = 2 inches
Now,
From the above,
We can observe that
2 inches < 2.5 inches
Hence, from the above,
We can conclude that a cube of cheese that is 2.5 inches on each side does not fit inside the box
Question 6.
Ray made a toolbox with the dimensions shown to store garden tools. What is the volume of the toolbox?
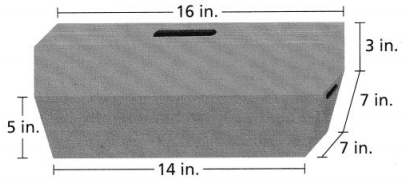
Answer:
It is given that
Ray made a toolbox with the dimensions shown to store garden tools.
Now,
The given figure is:

So,
The volume of the toolbox = (The volume of a cuboid) + (The volume of a trapezoidal prism)
Now,
We know that,
The volume of a cuboid (V) = Length × Width × Height
The volume of a trapezoidal prism (V) = (Area of a trapezoid) × (Height of the trapezoidal prism)
The area of a trapezoid (A) = [(b 1 + b 2 ) h] / 2
So,
The volume of the toolbox = (16 × 3 × 5) + [(7 + 7) × 5] ÷ 2 × 5
= (16 × 15) + \(\frac{70}{2}\) × 5
= 240 + 175
= 415 in.³
Hence, from the above,
We can conclude that
The volume of the toolbox is: 415 in.³
Practice & Problem Solving
Leveled Practice In 7-8, find the volume of each prism.
Question 7.
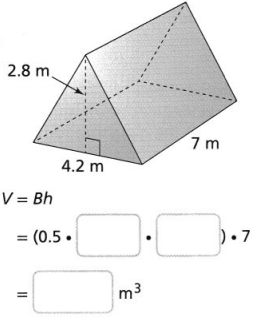
Answer:
The given figure is:
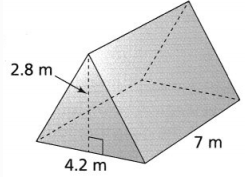
Now,
From the given figure,
We can observe that the given prism is a Right-triangular prism
So,
The volume of a right-triangular prism (V) = (Area of the right triangle) × Height
So,
The volume of the given prism is given as:
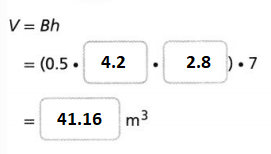
Hence, from the above,
We can conclude that
The volume of the given prism is: 41.16 m³
Question 8.
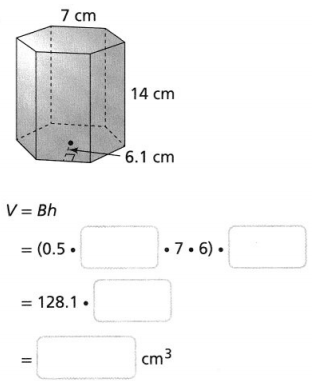
Answer:
The given figure is:
Now,
From the given figure,
We can observe that
The given figure is: Hexagonal prism
So,
The volume of the given prism (V) = (The area of a hexagon) × Height
Now,
We know that,
The area of a hexagon (A) = \(\frac{1}{2}\) × 6 × (Base of the triangle) × (Height of the triangle)
So,

Hence, from the above,
We can conclude that
The volume of the given prism is: 1,793.4 cm³
Question 9.
A tunnel for an amusement park ride has the shape of a regular hexagonal prism with dimensions shown. The prism has a volume of 3,572.1 cubic meters. Can two 8-meter cars connected by a 3-meter connector pass through the tunnel at the same time? Explain.
Answer:
It is given that
A tunnel for an amusement park ride has the shape of a regular hexagonal prism with dimensions shown. The prism has a volume of 3,572.1 cubic meters.
Now,
The given figure is:

Now,
From the given information,
We can say that
The volume of a regular hexagonal prism (V) = (Area of a hexagon) × (Height of a prism)
Now,
We know that,
The area of a hexagon (A) = \(\frac{1}{2}\) × 6 × (Base of the triangle) × (Height of the triangle)
So,
3,572.1 = 6 × \(\frac{1}{2}\) × 7 × 8.1 × h
3,572.1 = 170.1 × h
h = \(\frac{3,572.1}{170.1}\)
h = 21 m
Now,
The area of the tunnel = 8 × 3
= 24 m²
So,
24 > 21
Hence, from the above,
We can conclude that the two 8-meter cars connected by a 3-meter connector can’t pass through the tunnel at the same time
Question 10.
A volume of 185.5 cubic feet of concrete was used to make the section of a skateboard ramp shown. How long is the ramp?

Answer:
It is given that
A volume of 185.5 cubic feet of concrete was used to make the section of a skateboard ramp shown.
Now,
The given figure is:

Now,
We know that,
The volume of a rectangular prism (V) = Length × Width × Height
Now,
Let the length of the skateboard ramp be x ft
So,
The volume of a skateboard ramp (V) = 4 × 7 × x
185.5 = 28 × x
x = \(\frac{185.5}{28}\)
x = 6.62
x ≈ 7 ft
Hence, from the above,
We can conclude that the length of the ramp is about 7 ft
Question 11.
Make Sense and Persevere A small cube has a volume of 64 cubic feet. A larger cube has sides that are three times as long as the small cube. How long are the sides of each cube?
Answer:
It is given that
A small cube has a volume of 64 cubic feet. A larger cube has sides that are three times as long as the small cube
Now,
We know that,
The volume of a cube (V) = Side³
So,
For a small cube,
Side³ = 64
Side = \(\sqrt[3]{64}\)
Side = 4 feet
Now,
According to the given information,
The side of a larger cube = 3 × (The side of a small cube)
= 3 × 4
= 12 feet
Hence, from the above,
We can conclude that
The side length of a small cube is: 4 feet
The side length of a larger cube is: 12 feet
Question 12.
What is the volume of the regular hexagonal prism, to the nearest cubic centimeter?

Answer:
The given figure is:

Now,
We know that,
The volume of a regular hexagonal prism (V) = (Area of a hexagon) × (Height of the prism)
Now,
We know that,
Area of a hexagon (A) = \(\frac{1}{2}\) × 6 × (Base of the triangle) × (Height of the triangle)
So,
The volume of the given prism (V) = 6 × \(\frac{1}{2}\) × 9 × 10.4 × 24
= 6,739.2
≈ 6,740 cm³
Hence, from the above,
We can conclude that the volume of the given regular hexagonal prism is: 6,740 cm³
Question 13.
A mailbox has the dimensions shown What is the volume of the mailbox?

Answer:
The given figure is:

Now,
From the given mailbox,
We can observe that
The mailbox is the combination of a right triangular prism and a regular prism
Now,
We know that,
The volume of a right triangular prism (V) = (Area of a right triangle) × (The height of a prism)
The volume of a regular prism (V) = Length × Width × Height
Now,
We knwo that,
The area of a right triangle (A) = \(\frac{1}{2}\) × (Base of a triangle) × (Height of a triangle)
So,
The volume of the given mailbox (V) = (\(\frac{1}{2}\) × 2 × 8 × 8) + (8 × 8 × 12)
= 64 + 768
= 832 in.³
Hence, from the above,
We can conclude that the volume of the given mailbox is: 832 in.³
Question 14.
Use Structure A glass bead has the shape of a prism with a rectangular prism removed. What is the volume of the glass that forms the bead?
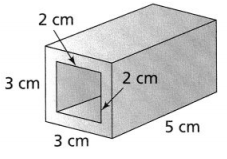
Answer:
It is given that
A glass bead has the shape of a prism with a rectangular prism removed.
Now,
The given figure is:

Now,
The volume of the glass that forms the bead (V) = (The volume of the glass bead that has the shape of a prism) + (The volume of a rectangular pris that is removed)
= (2 × 2 × 5) + (3 × 3 × 5)
= 20 + 45
= 65 cm³
Hence, from the above,
We can conclude that
The volume of the glass that forms the bead is: 65 cm³
Question 15.
Higher Order Thinking A cake has two layers. Each layer is a regular hexagonal prism. A slice removes one face of each prism, as shown.

a. What is the volume of the slice?
Answer:
b. What is the volume of the remaining cake?
Answer:
Assessment Practice
Question 16.
The area of the top of the box shown is 60 square centimeters. What is the volume, in cubic centimeters, of the box?
Answer:
It is given that
The area of the top of the box shown is 60 square centimeters
Now,
The given figure is:

So,
The volume of the given box (V) = 60 × 2 × 5
= 600 cm³
Hence, from the above,
We can conclude that
The volume of the given box is: 600 cm³
Question 17.
Which of the following freezers is the best buy in terms of dollars per cubic foot?
A. Freezer A has an interior of 1 foot by 1 foot by 5 feet and sells for $499.99.
B. Freezer B has two sections of 3 cubic feet each and sells for $629.99.
C. Freezer C has interior dimensions of 1.5 feet by 1.5 feet by 4 feet and sells for $849.99.
D. Freezer D has 3 sections of 1.5 cubic feet each and sells for $444.99.
Answer:
We now that,
To know which Freezer is best,
We have to find the volume of the given Freezer and see whether for the high volume of Freezer, the cost of the Freezer is low or not
Now,
For Freezer A,
Volume (V) = 1 × 1 × 5 = 5 ft³
The ratio in terms of dollars per cubic foot = \(\frac{499.99}{5}\)
= 100
For Freezer B,
Volume (V) = 3 + 3 = 6 ft³
The ratio in terms of dollars per cubic foot = \(\frac{629.99}{6}\)
= 105
For freezer C,
Volume (V) = 1.5 ×1.5 × 4
= 2.25×4
= 9.00
= 9 ft³
The ratio in terms of dollars per cubic foot = \(\frac{849.99}{9}\)
= 94
For Freezer D,
Volume (V) = 1.5 + 1.5 + 1.5 = 4.5 ft³
The ratio in terms of dollars per cubic foot = \(\frac{444.99}{4.5}\)
= 99
Hence, from the above,
We can conclude that
The freezers that is the best buy in terms of dollars per cubic foot are:

Topic 8 Review
Topic Essential Question
How can geometry be used to solve problems?
Answer:
You can use this field of mathematics to help you solve problems by drawing your problem and separating it out into geometric shapes. To do this, you divide your shape into smaller, common geometric shapes such as squares, rectangles, triangles, and circles and use the appropriate formulas for each
Vocabulary Review
Complete each definition, and then provide an example of each vocabulary word.


Answer:

Use Vocabulary in Writing
Shawna drew this picture of three intersecting lines. Use vocabulary terms to explain how she could determine the value of x.
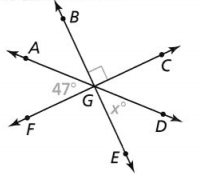
Answer:
Shawna drew this picture of three intersecting lines
Now,
The given figure is:

Now,
From the given figure,
We can observe that
47° and x° are the vertical angles
Now,
We know that,
The vertical angles have the same angle measures
So,
x° = 47°
Hence, from the above,
We can conclude that the value of x is: 47°
Concepts and Skills Review
Lesson 8.1 Solve Problems involving Scale Drawings
Quick Review
In a scale drawing, the scale is a ratio that relates each drawing length to the actual length it represents. To find unknown lengths, you can use the scale to write a proportion.
Example
A blueprint of a room is drawn to a scale of 2 inches = 7 feet. The actual length of one wall is 56 feet. What is the length of this wall on the blueprint?
Answer:
Use the scale to write a proportion.
\(\frac{2 \text { in. }}{7 \mathrm{ft}}=\frac{x \text { in. }}{56 \mathrm{ft}}\)
56 feet = 7 feet x 8, so multiply 2 inches by 8
x = 2 inches x 8 = 16 inches
The length in the blueprint is 16 inches.
Practice
Use the scale drawing to answer the questions.

Question 1.
What is the actual area of the meeting room in square yards?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
Scale factor = \(\frac{3}{1}\)
So,
The actual length of the meeting room = (Scale factor) × (The length of the scale drawing)
= 3 × 4
= 12 yd
So,
The actual width of the meeting room = (Scale factor) × (The width of the scale drawing)
= 3 × 1.5
= 4.5 yd
So,
The actual area of the meeting room = (The actual length of the meeting room) × (The actual width of the meeting room)
= 12 × 4.5
= 54.0
= 54 yd²
Hence, from the above,
We can conclude that
The actual area of the meeting room is: 54 yd²
Question 2.
John decides to make a new scale drawing of the meeting room. He wants the length of the room in the new drawing to be 8 inches. What is the new scale for the drawing?
Answer:
It is given that
John decides to make a new scale drawing of the meeting room. He wants the length of the room in the new drawing to be 8 inches
Now,
From Question 1,
The actual length of the meeting room = (Scale factor) × (The length of the scale drawing)
= 3 × 4
= 12 yd
So,
\(\frac{1}{8}\) = \(\frac{12}{x}\)
x = 96
So,
The new scale for the drawing is:
8 inches = 96 yd
Divide by 8 on both sides
1 inch = 12 yd
Hence, from the above,
We can conclude that
The new scale for the drawing is:
1 inch = 12 yd
Lesson 8.2 Draw Geometric Figures
Quick Review
You can classify a quadrilateral as a trapezoid, a rectangle, a square, or a parallelogram based on its side lengths, side relationships, and angle measures.
Example
Draw a quadrilateral with exactly two perpendicular sides and one angle measuring 120°. What is the name of the figure you drew?
Answer:
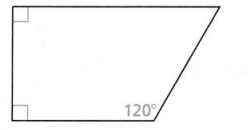
The figure has exactly one pair of parallel sides, so it is a trapezoid.
Practice
Question 1.
Draw a quadrilateral with two pairs of parallel sides, with one side measuring 5 centimeters, one side measuring 3 centimeters, and one angle measuring 45°. What is the name of the figure you drew?
Answer:
The representation of the quadrilateral with two pairs of parallel sides, with one side measuring 5 centimeters, one side measuring 3 centimeters, and one angle measuring 45° is:
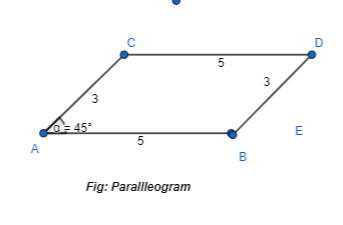
Now,
From the figure,
We can observe that
a. The side lengths of the parallel sides are the same
b. The angle measures are not 90°
Hence, from the above,
We can conclude that
The quadrilateral with the given specifications is called: parallelogram
Question 2.
What quadrilaterals can you draw that have two angles measuring 115° and two angles measuring 65°?
Answer:
It is given that the two angles measuring 115° and two angles measuring 65°
So,
The representation of the quadrilateral that has two angles measuring 115° and two angles measuring 65° is:
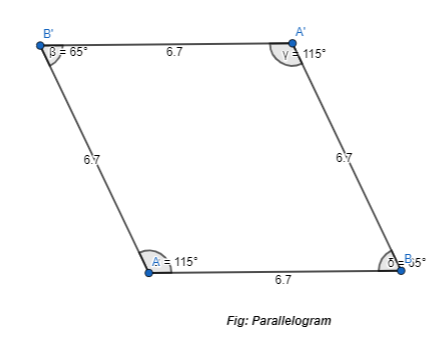
Hence, from the above,
We can conclude that
The quadrilateral that you can draw with the same opposite angle measures is: Parallelogram
Lesson 8.3 Draw Triangles with Given Conditions
Quick Review
When you are given certain conditions for a triangle, it may be possible to draw one triangle, more than one triangle, or no triangle.
Example
How many triangles can be drawn with side lengths of 3 inches, 5 inches, and 6 inches?
Answer:
No matter how you position the sides, the triangle has the same shape and size. There is only one way to draw a triangle with these side lengths.
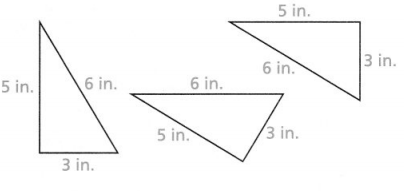
Practice
Question 1.
Can more than one triangle be drawn with side lengths of 4 centimeters and 2 centimeters and an included angle of 50°? Explain.
Answer:
It is given that
one triangle is drawn with side lengths of 4 centimeters and 2 centimeters and an included angle of 50°
So,
The representations of the triangles with the given specifications are:
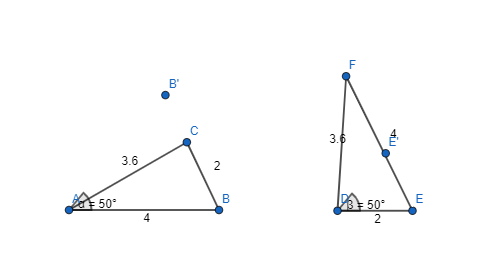
Now,
From the above triangles,
We can observe that both the representations of the triangles are the same
Hence, from the above,
We can conclude that more than one triangle can not be drawn from the given specifications
Question 2.
When given angle measures of 25°, 65°, and 90°, is it impossible to draw a triangle, possible to draw only one triangle, or possible to draw more than one triangle? Explain.
Answer:
We know that,
There is more than one triangle possible for the below cases:
a. Three different angle measures
b. Two sides and an included triangle
Now,
In this question,
Three different angle measures are given
Hence, from the above,
We can conclude that it is impossible to draw more than one triangle
Lesson 8-4 Solve Problems Using Angle Relationships
Quick Review
Angles that have a common vertex and a common side but no common interior points are adjacent angles. Supplementary angles are angles with a sum of 180°. Complementary angles are angles with a sum of 90°. When two lines intersect, the angles that have no side in common are called vertical angles. Vertical angles are equal.
Example
List all pairs of vertical angles in this figure.
Answer:
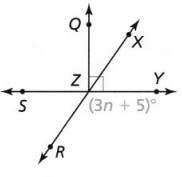
There are two pairs of vertical angles:
• ∠SZR and ∠XZY
• ∠SZX and ∠RZY
Practice
Use the figure from the example.

Question 1.
Name a pair of complementary angles.
Answer:
The given figure is:

Now,
We know that,
The complementary angles are the angles that have the angle measure of 90°
Hence, from the above,
We can conclude that
The pair of Complementary angles are: ∠QZX and ∠XZY
Question 2.
The measure of ∠XZY is 55°. Which other angle has a measure of 55°? Explain.
Answer:
It is given that the angle measure of ∠XZY is: 55°
Now,
The given figure is:

Now,
From the given figure,
We can observe that
There are two pairs of vertical angles:
a. ∠SZR and ∠XZY
b. ∠SZX and ∠RZY
Now,
We know that,
The vertical angles are the angles that have the same angle measures
Hence, from the above,
We can conclude that
The other angles that have a measure of 55° are: ∠SZR, ∠SZX, and ∠RZY
Question 3.
Use the information from Problem 2. Find the value of n.
Answer:
The given figure is:

Now,
From problem 2,
We can observe that
∠SZR and ∠RZY are the adjacent angles
So,
According to the given information,
(3n + 5)° + 55° = 180°
3n° = 180° – 60°
3n° = 120°
n = \(\frac{120°}{3}\)
n = 40°
Hence, from the above,
We can conclude that the value of n is: 40°
Lesson 8.5 Solve Problems Involving Circumference of a Circle
Quick Review
The distance around a circle is called its circumference. The number a (pi) is the ratio of the circumference of any circle to its diameter. So when you know the diameter, d, of a circle, or its radius, r, you can determine its circumference, C, with the formula C = πd or C = 2πr.
Example
What is the circumference of a circle with a radius of 6 meters? Use 3.14 for π.
Answer:
C = 2πr
C = 2π(6)
C ≈ 2(3.14)(6)
C = 37.68
The circumference is about 37.68 meters.
Practice
Question 1.
The length of the minute hand of a clock is 14 inches. What is the length of the path traced by the outer tip of the minute hand in one hour? Use \(\frac{22}{7}\) for π.
Answer:
It is given that
The length of the minute hand of a clock is 14 inches
So,
The length of the path traced by the outer tip of the minute hand in one hour = 2π × (The length of the minute hand of a clock)
= 2 × \(\frac{22}{7}\) × 14
= 88 inches
Hence, from the above,
We can conclude that
The length of the path traced by the outer tip of the minute hand in one hour is: 88 inches
Question 2.
The circumference of a bicycle tire is 126.5 centimeters. What is the diameter of the tire? Use 3.14 for a. Round to the nearest tenth as needed.
Answer:
It is given that
The circumference of a bicycle tire is 126.5 centimeters
Now,
We know that,
The circumference of a bicycle tire (C) = πd
Where,
d is the diameter of the bicycle tire
So,
According to the given information,
126.5 = 3.14 × d
d = \(\frac{126.5}{3.14}\)
d = 40.28
d ≈ 40.3 centimeters
Hence, from the above,
We can conclude that
The diameter of the tire is: 40.3 centimeters
Lesson 8.6 Solve Problems involving Area of a Circle
Quick Review
The area, A, of a circle can be found using the formula A = πr2, where r is the radius. You can use 3.14 or \(\frac{22}{7}\) as an approximation for π.
Example
The diameter of the logo at the center of a basketball court is 10 feet. What is the area of the logo? Use 3.14 for π.
Answer:
The radius of a circle is half the diameter. So the radius of the logo is half of 10 feet, or 5 feet. Substitute the radius into the circle area formula.
A = πr2
A = π(5)2
A ≈ 3.14(25)
A = 78.5
The area of the logo is about 78.5 square feet.
Practice
Question 1.
Jessie wants to paint the top of the table shown. What is the approximate area that she will paint? Use 3.14 for it. Round to the nearest whole number of inches.

Answer:
It is given that
Jessie wants to paint the top of the table shown.
Now,
The given figure is:

Now,
We know that,
Radius (r) = \(\frac{Diameter}{2}\)
So,
r = \(\frac{78}{2}\)
r = 39 in
Now,
We know that,
The area of a circle (A) = πr²
So,
The area of the top of table (A) = 3.14 × 39²
= 4,775.94 in²
≈ 4,776 in²
Hence, from the above,
We can conclude that the approximate area that she will paint is: 4,776 in.²
Question 2.
What is the diameter of a circle with an area of 113.04 square centimeters? Use 3.14 for π.
Answer:
It is given that
The area of a circle is: 113.04 square centimeters
Now,
We know that,
The area of a circle (A) = πr²
So,
113.04 = 3.14 × r²
r² = \(\frac{113.04}{3.14}\)
r² = 36
r = 6 cm
Now,
We know that,
Diameter (d) = 2 × Radius (r)
So,
d = 2 × 6
d = 12 cm
Hence, from the above,
We can conclude that
The diameter of the given circle is: 12 cm
Question 3.
The distance around a circular park is 88 yards. What is the area of the park? Use \(\frac{22}{7}\) for π.
Answer:
It is given that
The distance around a circular park is 88 yards
Now,
We know that,
Circumference (C) = 2πr
So,
88 = 2 × \(\frac{22}{7}\) × r
r = \(\frac{7 × 88}{2 × 22}\)
r = 14 yards
Now,
We know that,
Area of a circle (A) = πr²
So,
The area of the circular park (A) = \(\frac{22}{7}\) × 14²
= 616 yards²
Hence, from the above,
We can conclude that the area of the given circular park is: 616 yards²
Lesson 8.7 Describe Cross Sections
Quick Review
A cross section is the two-dimensional shape exposed when a three-dimensional figure is sliced. Recognizing the shape of a cross section can help in solving some problems.
Example
Muffins are packed in two layers in a box with a piece of cardboard placed between. What shape is the cardboard and what are its dimensions?
Answer:

The cardboard lies on a cross section shaped like a rectangle that is 15 inches long and 10 inches wide.
Practice
Question 1.
The figure shows a vertical cross-section of a right rectangular pyramid. What shape is the cross-section and what is its area?
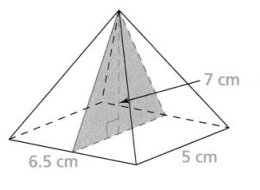
Answer:
It is given that
The figure shows a vertical cross-section of a right rectangular pyramid
Now,
The given figure is:

Now,
From the above figure,
We can observe that
The vertical cross-section of the given pyramid is: Right triangle
Now,
We know that,
The area of a right triangle (A) = \(\frac{1}{2}\) × (Base of the triangle) × (Height of the triangle)
So,
The area of the vertical cross-section (A) = \(\frac{1}{2}\) × 7 × 5
= 17.5 cm²
Hence, from the above,
We can conclude that
The shape of the cross-section is: Right triangle
The area of the cross-section is: 17.5 cm²
Question 2.
Zach wants to slice the pyramid along a horizontal plane that intersects the pyramid above its base. Describe the cross section that would be formed.
Answer:
It is given that
Zach wants to slice the pyramid along a horizontal plane that intersects the pyramid above its base
Now,
The given figure is:

Hence, from the above,
We can conclude that
The shape of the horizontal plane when the pyramid is intersected is: Rectangle
Lesson 8.8 Solve Problems involving Surface Area
Quick Review
A composite figure is the combination of two or more geometric shapes. The surface area of a two- and a three-dimensional composite figure will be the sum of the areas of all the shapes, or faces.
Example
The figure shows the plan for a kitchen countertop. What is the area of the countertop?
Answer:
(3 • 8) + (3 • 2) + \(\frac{1}{2}\)(3 • 3) = 24 + 6 + 4.5 = 34.5
The area of the countertop is 34.5 ft2.
Practice
Question 1.
Kara wants to paint the four outside walls of her dog’s house. She will not paint the roof or the door on the front of the house. What is the area of the surface that Kara needs to paint?
Answer:
It is given that
Kara wants to paint the four outside walls of her dog’s house. She will not paint the roof or the door on the front of the house.
Now,
The given figure is:

Now,
The area of the dog’s house that Kara needed to paint (A) = (The total area of the dog’s house) – (The area of the front of the house)
= ([\(\frac{1}{2}\) × 4 × 4] + [7 × 3]) – (\(\frac{1}{2}\) × 4 × 4)
= 29 – 8
= 21 ft²
Hence, from the above,
We can conclude that
The area of the surface that Kara needs to paint is: 21 ft²
Lesson 8.9 Solve Problems involving Volume
Quick Review
You can find the volume, V, of a prism using the formula V = Bh. In this formula, B represents the area of the base of the prism and h represents the height of the prism. Volume is measured in cubic units.
If the volume of a prism is known, you may be able to use this formula to find an unknown dimension of the prism. You also can use this formula to solve problems involving volumes of composite figures that are made up of two or more prisms.
Example
Rhonda received a package in a box shaped like a rectangular prism. What is the volume of the box?
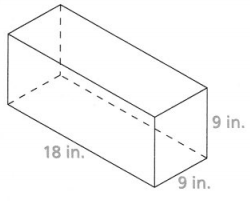
Answer:
Find the area of the rectangular base.
A = 9(18) = 162 in.2
Find the volume of the prism.
V = Bh
V= 162(9)
V= 1,458 in.3
Practice
Question 1.
Holly has a gift box that is shaped like a regular hexagonal prism. What is the volume of the box?
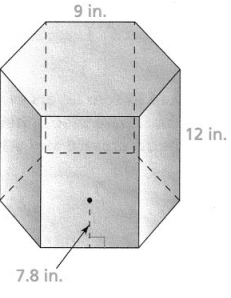
Answer:
It is given that
Holly has a gift box that is shaped like a regular hexagonal prism
Now,
The given figure is:

Now,
We know that,
The volume of a regular hexagonal prism (V) = (Area of a hexagon) × (Height of the regular hexagonal prism)
The area of a hexagon (A) = 6 × \(\frac{1}{2}\) × (Base of a triangle}{Height of a triangle}
So,
V = 6 × \(\frac{1}{2}\) × 7.8 × 12 × 9
= 2,527.2 in.³
Hence, from the above,
We can conclude that
The volume of the given regular hexagonal prism is: 2,527.2 in.³
Question 2.
A designer is planning a trail mix box that is shaped like a rectangular prism. The front of the box must have the width and height shown. The volume of the box must be 162 cubic inches. What must be the depth, d, of the box?
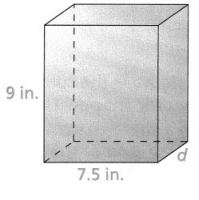
Answer:
It is given that
A designer is planning a trail mix box that is shaped like a rectangular prism. The front of the box must have the width and height shown. The volume of the box must be 162 cubic inches.
Now,
The given figure is:

Now,
We know that,
The volume of a rectangular prism (V) = Length × Width × Height
So,
162 = 9 × 7.5 × d
162 = 67.5 × d
d = \(\frac{162}{67.5}\)
d = 2.4 in.
Hence, from the above,
We can conclude that
The depth of the box is 2.4 in.
Question 3.
A building that is used for storage has the dimensions shown. What is the volume of the building?
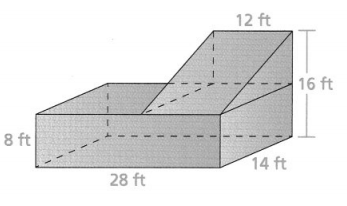
Answer:
It is given that
A building that is used for storage has the dimensions shown
Now,
The given figure is:

So,
The volume of the building (V) = (8 × 28 ×14) + (12 × 16 × 14)
= 3,136 + 2,688
= 5,824 ft³
Hence, from the above,
We can conclude that
The volume of the building is: 5,824 ft³
Topic 8 Fluency Practice
Pathfinder
Shade a path from START to FINISH. Follow the answers to the problems so that each answer is greater than the one before. You can only move up, down, right, or left.
I can… use the percent equation to solve problems.
START
