Go through the enVision Math Common Core Grade 8 Answer Key Topic 7 Understand and Apply the Pythagorean Theorem and finish your homework or assignments.
enVision Math Common Core 8th Grade Answers Key Topic 7 Understand And Apply The Pythagorean Theorem
Topic Essential Question
How can you use the Pythagorean Theorem to solve problems?
Answer:
The Pythagorean Theorem is used to calculate the steepness of slopes of hills or mountains. A surveyor looks through a telescope toward a measuring stick a fixed distance away, so that the telescope’s line of sight and the measuring stick form a right angle.
3-ACT MATH OOO

Go with the Flow
You may have noticed that when you double the base and the height of a triangle, the area is more than doubled. The same is true for doubling the sides of a square or the radius of a circle. So what is the relationship? Think about this during the 3-Act Mathematical Modeling lesson.

Topic 7 enVision STEM Project
Did You Know?
Over two billion people will face water shortages by 2050 according to a 2015 United Nations Environment Program report.
Rainwater can be collected and stored for use in irrigation, industrial uses, flushing toilets, washing clothes and cars, or it can be purified for use as everyday drinking water.
This alternative water source reduces the use of fresh water from reservoirs and wells.

Using water wisely saves money on water and energy bills and extends the life of supply and wastewater facilities.

Roofs of buildings or large tarps are used to collect rainwater.
A rainwater collection system for a building roof that measures 28 feet by 40 feet can provide 700 gallons of water-enough water to support two people for a year—from a rainfall of 1.0 inch.

Even a 5 foot by 7-foot tarp can collect 2 gallons of water from a rainfall total of only 0.1 in.
The rainwater harvesting market is expected to grow 5% from 2016 to 2020.

Your Task: Rainy Days

Rainwater collection is an inexpensive way to save water in areas where it is scarce. One inch of rain falling on a square roof with an area of 100 ft² collects 62 gallons of water that weighs over 500 pounds. You and your classmates will research the necessary components of a rainwater collection system. Then you will use what you know about right triangles to design a slanted roof system that will be used to collect rainwater.
Answer:
It is given that
Rainwater collection is an inexpensive way to save water in areas where it is scarce. One inch of rain falling on a square roof with an area of 100 ft² collects 62 gallons of water that weighs over 500 pounds
Now,
The necessary components of a rainwater collection system are:
A) Catchments B) Coarse mesh C) Gutters D) Conduits E) First-flushing F) Filter G) Storage facility H) Recharge Structures
Topic 7 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
cube root
diagonal
isosceles triangle
perimeter
right triangle
square root
Question 1.
The __________ of a number is a factor that when multiplied by itself gives the number.
Answer:
We know that,
The “Square root” of a number is a factor that when multiplied by itself gives the number
Hence, from the above,
We can conclude that the best term to complete the given definition is a “Square root”
Question 2.
A _________ is a line segment that connects two vertices of a polygon and is not the side.
Answer:
We know that,
A “Diagonal” is a line segment that connects two vertices of a polygon and is not the side
Hence, from the above,
We can conclude that the best term to complete the given definition is a “Diagonal”
Question 3.
The _________ of a figure is the distance around it.
Answer:
We know that,
The “Perimeter” of a figure is the distance around it
Hence, from the above,
We can conclude that the best term to complete the given definition is the “Perimeter”
Question 4.
A ___________ is a triangle with one right angle.
Answer:
We know that,
A “Right triangle” is a triangle with one right angle
Hence, from the above,
We can conclude that the best term to complete the given definition is a “Right angle”
Simplify Expressions with Exponents
Simplify the expression.
Question 5.
32 + 42
Answer:
The given expression is: 32 + 42
So,
32 + 42
= (3 × 3) + (4 × 4)
= 9 + 16
= 25
Question 6.
22 + 52
Answer:
The given expression is: 22 + 52
So,
2² + 52
= (2 × 2) + (5 × 5)
= 4 + 25
= 29
Question 7.
102 – 82
Answer:
The given expression is: 102 – 82
So,
102 – 82
= (10 × 10) – (8 × 8)
= 100 – 64
= 36
Square Roots
Determine the square root.
Question 8.
\(\sqrt {81}\)
Answer:
The given expression is: \(\sqrt{81}\)
Hence,
\(\sqrt{81}\) = 9
Question 9.
\(\sqrt {144}\)
Answer:
The given expression is: \(\sqrt{144}\)
Hence,
\(\sqrt{144}\) = 12
Question 10.
\(\sqrt {225}\)
Answer:
The given expression is: \(\sqrt{225}\)
Hence,
\(\sqrt{225}\) = 15
Distance on a Coordinate Plane
Determine the distance between the two points.
Question 11.
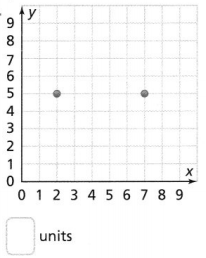
Answer:
The given graph is:

From the given graph,
The given points are: (2, 5), (7, 5)
Now,
Compare the given points with (x1, y1), (x2, y2)
We know that,
Distance between 2 points = √(x2 – x1)2 + (y2 – y1)2
= √(7 – 2)2 + (5 – 5)2
= \(\sqrt{5²}\)
= 5 units
Hence, from the above,
We can conclude that the distance between the given points is: 5 units
Question 12.
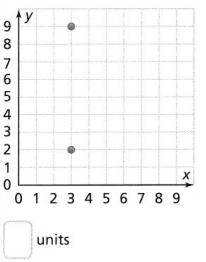
Answer:
The given graph is:

From the given graph,
The given points are: (3, 2), (3, 9)
Now,
Compare the given points with (x1, y1), (x2, y2)
We know that,
Distance between 2 points =√(x2 – x1)2 + (y2 – y1)2
= √(3 – 3)2 + (9 – 2)2
= \(\sqrt{7²}\)
= 7 units
Hence, from the above,
We can conclude that the distance between the given points is: 7 units
Language Development
Complete the word map using key terms, examples, or illustrations related to the Pythagorean Theorem and its Converse.


Answer:


Topic 7 PICK A PROJECT
PROJECT 7A
Where would you like to bike ride in your neighborhood?
PROJECT: PLAN A METRIC CENTURY RIDE

PROJECT 7B
What designs have you seen on kites?
PROJECT: BUILD A KITE

PROJECT 7C
What buildings in your community have unusual shapes as part of their structure or design?
PROJECT: MAKE A SCRAPBOOK

PROJECT 7D
What geometric designs have you noticed on your clothes?
PROJECT: DESIGN A FABRIC TEMPLATE

3-ACT MATH
3-Act Mathematical Modeling: Go with the Flow

АСТ 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Make a prediction to answer this Main Question.
_________ % will fit in the third square.
Answer:
Question 4.
Construct Arguments Explain how you arrived at your prediction.
Answer:
ACT 2
Question 5.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 6.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 7.
Model With Math
Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 8.
What is your answer to the Main Question? Does it differ from your prediction? Explain.
Answer:
АСТ 3
Question 9.
Write the answer you saw in the video.
Answer:
Question 10.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 11.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.

Answer:
Act 3
Extension
Reflect
Question 12.
Model with Math
Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 13.
Reason Abstractly How did you represent the situation using symbols? How did you use those symbols to solve the problem?

Answer:
SEQUEL
Question 14.
Construct Arguments Explain why you can use an area formula when the problem involves comparing volumes.

Answer:
Lesson 7.1 Understand the Pythagorean Theorem
Explain It!
Kelly drew a right triangle on graph paper. Kelly says that the sum of the areas of squares with side lengths a and b is the same as the area of a square with side length c.
I can… use the Pythagorean Theorem to find unknown sides of triangles.
A. Do you agree with Kelly? Explain.
Answer:
It is given that
Kelly drew a right triangle on graph paper. Kelly says that the sum of the areas of squares with side lengths a and b is the same as the area of a square with side length c.
We know that,
According to the Pythagorean theorem,
Hypotenuse² = Side length 1² + Side length 2²
So,
From the given graph,
We can observe that
Side length 1 is: a
Side length 2 is: b
The hypotenuse is: c
So,
c² = a² + b²
Hence, from the above,
We can conclude that we can agree with Kelly
B. Sam drew a different right triangle with side lengths a = 5, b = 12, and c = 13. Is the relationship Kelly described true for Sam’s right triangle? Explain.
Answer:
It is given that
Sam drew a different right triangle with side lengths a = 5, b = 12, and c = 13
Now,
From part (a),
The relation according to Kelly is:
c² = a² + b²
So,
13² = 12² + 5²
169 = 144 + 25
169 = 169
Hence, from the above,
We can conclude that the relationship Kelly described is true for Sam’s right-angled triangle
Focus on math practices
Generalize Kelly draws another right triangle. What would you expect to be the relationship between the areas of the squares drawn on each side of the triangle? Explain.
Answer:
It is given that Kelly draws another right triangle
Hence,
If in a triangle, the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right.”
Essential Question
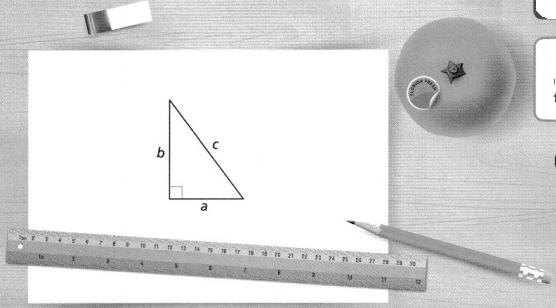
How does the Pythagorean Theorem relate to the side lengths of a right triangle?
Answer:
The Pythagorean equation relates the sides of a right triangle in a simple way so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides but less than their sum.
Try It!
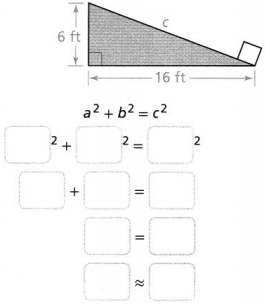
A right triangle has side lengths 15 centimeters, 25 centimeters, and 20 centimeters. How can you use the Pythagorean Theorem to write an equation that describes how the side lengths are related?
a2 + b2 = c2
_______2 + ________2 = _________2
_________ + _________ = ________
Answer:
It is given that
A right triangle has side lengths 15 centimeters, 25 centimeters, and 20 centimeters.
We know that,
According to the Pythagorean Theorem,
The hypotenuse has the greatest length in the right triangle
Now,
Let the hypotenuse be c
Let the other two sides be a and b
So,
From the given information,
c = 25 centimeters, a = 15 centimeters,and b = 20 centimeters
So,
According to the Pythagorean Theorem,
25² = 15² + 20²
625 = 225 + 400
625 = 625
Hence, from the above,
We can conclude that we proved how the Pythagorean Theorem relates to the lengths of the right triangle
Convince Me!
How do you know that the geometric proof of the Pythagorean Theorem shown above can be applied to all right triangles?
Answer:
It can be proven using the law of cosines or as follows: Let ABC be a triangle with side lengths a, b, and c, with a2 + b2 = c2. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle. This proof of the converse makes use of the Pythagorean theorem itself.
Try It!
A right triangle has a hypotenuse length of 32 meters. It has one leg with a length of 18 meters. What is the length of the other leg? Express your answer as a square root.
Answer:
It is given that
A right triangle has a hypotenuse length of 32 meters. It has one leg with a length of 18 meters.
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the legs
Now,
Let the other leg be x
So,
32² = 18² + x²
x² = 32² – 18²
x² = 1024 – 324
x² = 700
x = \(\sqrt{700}\)
Hence, from the above,
We can conclude that the length of the other leg is: \(\sqrt{700}\)
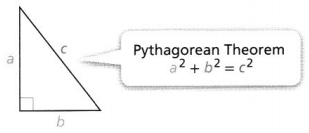
KEY CONCEPT
The Pythagorean Theorem is an equation that relates the side lengths of a right triangle, a2 + b2 = c2, where a and b are the legs of a right triangle and c is the hypotenuse.
Do You Understand?
Question 1.
Essential Question How does the Pythagorean Theorem relate to the side lengths of a right triangle?
Answer:
The Pythagorean equation relates the sides of a right triangle in a simple way so that if the lengths of any two sides are known the length of the third side can be found. Another corollary of the theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides but less than their sum.
Question 2.
Use Structure A side of each of the three squares forms a side of a right triangle.
Would any three squares form the sides of a right triangle? Explain.

Answer:
It is given that
A side of each of the three squares forms a side of a right triangle.
Now,
We know that,
The length of all the sides in a square is equal
Now,
From the given figure,
We can observe that
Each side of a square from the three squares form a right triangle
Hence, from the above,
We can conclude that the three squares form the sides of a right triangle
Question 3.
Construct Arguments Xavier said the missing length is about 18.5 units. Without calculating, how can you tell that Xavier solved incorrectly?
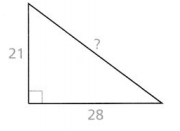
Answer:
It is given that
Xavier said the missing length is about 18.5 units
Now,
We know that,
According to the Pythagorean Theorem,
The length of the hypotenuse is the greatest
Now,
The given right triangle is:

So,
According to the Pythagorean Theorem,
The length of the missing side should be greater than 21 and 26
Hence, from the above,
We can conclude that Xavier calculated incorrectly
Do You Know How?
Question 4.
A right triangle has leg lengths of 4 inches and 5 inches. What is the length of the hypotenuse? Write the answer as a square root and round to the nearest tenth of an inch.
Answer:
It is given that
A right triangle has leg lengths of 4 inches and 5 inches
Now,
We know that,
According to the Pythagorean theorem,
c² = a²+ b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
c² = 4² + 5²
c² = 16 + 25
c² = 41
c = \(\sqrt{41}\)
c = 6.4 inches
Hence, from the above,
We can conclude that the length of the hypotenuse is: 6.4 inches
Question 5.
Find the missing side length to the nearest tenth of afoot.
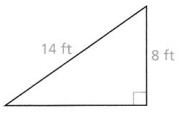
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean theorem,
c² = a²+ b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
14² = 8² + b²
b²= 14² – 8²
b² = 196 – 64
b² = 132
b = \(\sqrt{132}\)
b = 11.5 feet
Hence, from the above,
We can conclude that the length of the missing side is: 11.5 feet
Question 6.
Find the missing side length to the nearest tenth of a millimeter.
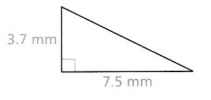
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean theorem,
c² = a²+ b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
c² = (3.7)² + (7.5)²
c² = 13.69 + 56.25
c² = 69.94
c = \(\sqrt{69.94}\)
c = 8.4 mm
Hence, from the above,
We can conclude that the length of the missing side is: 8.4 mm
Practice & Problem Solving
Leveled Practice In 7 and 8, find the missing side length of each triangle.
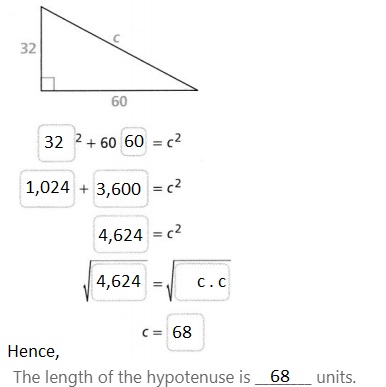
Question 7.
The length of the hypotenuse is ________ units.
Answer:
Question 8.
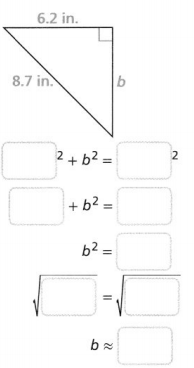
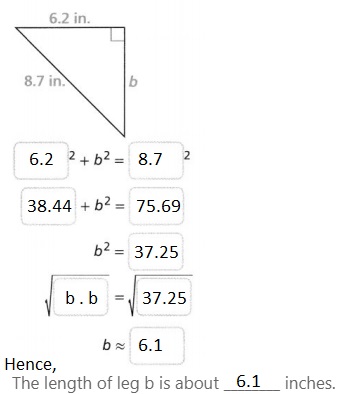
The length of leg b is about ________ inches.
Answer:
Question 9.
What is the length of the hypotenuse of the triangle when x = 15? Round your answer to the nearest tenth of a unit.
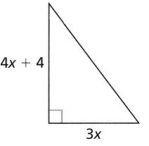
Answer:
The given right angle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
c² = (3x)² + (4x + 4)²
Now,
When x = 15,
c² = (3 × 15)² + (4 × 15 + 4)²
c² = 45² + 64²
c² = 2,025 + 4,096
c² = 6,121
c = \(\sqrt{6,121}\)
c = 78.2 units
Hence, from the above,
We can conclude that the length of the hypotenuse when x= 15 is: 78.2 units
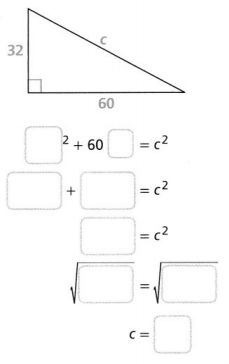
Question 10.
What is the length of the missing side rounded to the nearest tenth of a centimeter?
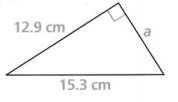
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a²+ b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
a² = (12.9)² + (15.3)²
a² = 166.41 + 234.09
a² = 400.5
a = \(\sqrt{400.5}\)
a = 20 cm
Hence, from the above,
We can conclude that the length of the side a is: 20 cm
Question 11.
Use the Pythagorean Theorem to find the unknown side length of the right triangle.
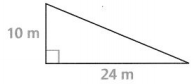
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a²+ b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
c² = (10)² + (24)²
c² = 100 + 576
c² = 676
c = \(\sqrt{676}\)
c = 26 m
Hence, from the above,
We can conclude that the length of the side a is: 26 m
Question 12.
What is the length of the unknown leg of the right triangle rounded to the nearest tenth of afoot?
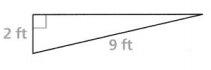
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
9² = 2² + b²
b² = 9² – 2²
b² = 81 – 4
b² = 77
b = \(\sqrt{77}\)
b = 8.8 foot
Hence, from the above,
We can conclude that the length of the unknown leg is: 8.8 foot
Question 13.
A student is asked to find the length of the hypotenuse of a right triangle. The length of one leg is 32 centimeters, and the length of the other leg is 26 centimeters. The student incorrectly says that the length of the hypotenuse is 7.6 centimeters.
a. Find the length of the hypotenuse of the right triangle to the nearest tenth of a centimeter.
Answer:
It is given that
A student is asked to find the length of the hypotenuse of a right triangle. The length of one leg is 32 centimeters, and the length of the other leg is 26 centimeters. The student incorrectly says that the length of the hypotenuse is 7.6 centimeters.
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
c² = 32² + 26²
c² = 1,024 + 676
c² = 1,700
c = \(\sqrt{1,700}\)
c = 41.2 centimeters
Hence, from the above,
We can conclude that the length of the hypotenuse of a right triangle is: 41.2 centimeters
b. What mistake might the student have made?
Answer:
It is given that
The student incorrectly says that the length of the hypotenuse is 7.6 centimeters.
But,
From part (a),
The length of the hypotenuse is: 41.2 centimeters
Hence, from the above,
We can conclude that the mistake the student might make is the misinterpretation of the length of the hypotenuse
Question 14.
Find the length of the unknown leg of the right triangle.
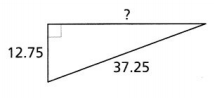
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
(37.25)² = (12.25)² + b²
b² = (37.25)² – (12.25)²
b² = 1,387.56 – 150.06
b² = 1,237.5
b = \(\sqrt{1,237.5}\)
b = 35.17 units
Hence, from the above,
We can conclude that the length of the unknown leg is: 35.17 units
Question 15.
Higher-Order Thinking A right triangle has side lengths 12 centimeters and 14 centimeters. Name two possible side lengths for the third side, and explain how you solved for each.
Answer:
It is given that
A right triangle has side lengths of
12 centimeters and 14 centimeters.
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
Now,
Let the length of the third side be x
So,
The possible lengths of the third side may be:
x < 12 centimeters and x > 14 centimeters
Hence, from the above,
We can conclude that the two possible side lengths for the third side are:
x < 12 centimeters and x > 14 centimeters
Assessment Practice
Question 16.
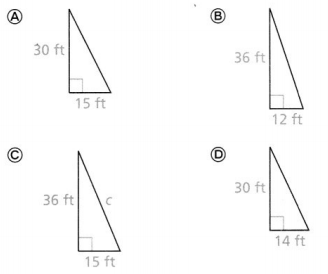
Which right triangle has a hypotenuse that is about 39 feet long?
Answer:
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
For Options A and D:
A) c² = 30² + 15² D) c² = 30² + 14²
= 33.54 ft = 33.10 ft
For Options B and C:
B) c² = 36² + 12² C) c² = 36² + 15²
= 37.94 ft = 39 ft
Hence, from the above,
We can conclude that Option C matches the given situation
Question 17.
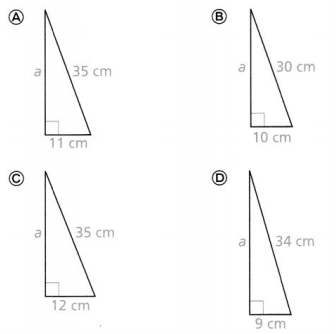
Which right triangle does NOT have an unknown leg length of about 33 cm?
Answer:
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the hypotenuse
a and b are the lengths of the legs
So,
For Options A and D:
A) b² = 35² – 11² D) b² = 34² – 9²
= 33.22 cm = 32.78 cm
For Options B and C:
B) b² = 30² – 10² C) b² = 35² – 12²
= 28.28 cm = 32.87 cm
Hence, from the above,
We can conclude that Option B matches the given situation
Lesson 7.2 Understand the Converse of the Pythagorean Theorem
Solve & Discuss It!
Kayla has some straws that she will use for an art project. She wants to glue three of the straws onto a sheet of paper, without overlapping, to make the outline of a right triangle. Which three straws could Kayla use to make a right triangle? Explain.

I can… use the Converse of the Pythagorean Theorem to identify right triangles.
Answer:
It is given that
Kayla has some straws that she will use for an art project. She wants to glue three of the straws onto a sheet of paper, without overlapping, to make the outline of a right triangle.
Now,
We know that,
The converse of the Pythagorean Theorem states that if the square of the third side of a triangle is equivalent to the sum of its two shorter sides, then it must be a right triangle i.e.,
If c² = a²+ b², then the given triangle is a right triangle
So,
From the given straws,
we can observe that
The straws numbered 3, 4, and 5 can be glued to make the outline of a right triangle
The straws numbered 5, 12, and 13 can be glued to make the outline of a right triangle
Hence, from the above,
We can conclude that there are 2 pairs of straws i.e., (3, 4, 5) and (12, 5, 13) to make the outline of a right triangle
Look for Relationships
How could you use the Pythagorean Theorem to determine whether the lengths form a right triangle?
Answer:
According to the converse of the Pythagorean Theorem,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Focus on math practices
Use Structure Could Kayla use the straws that form a right triangle to make a triangle that is not a right triangle? Explain.
Answer:
From the given straws,
We can observe that the pair (6, 7, 4) can’t form a right triangle but (3, 4, 5) can form a right triangle
Hence, from the above,
We can conclude that Kayla can use the straws that form a right triangle to make a triangle that is not a right triangle
Essential Question
How can you determine whether a triangle is a right triangle?
Answer:
We can determine the triangle is a right triangle by using the converse of the Pythagorean Theorem
Hence,
According to the converse of the Pythagorean Theorem,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Try It!
A triangle has side lengths 4 inches, 5 inches, and 7 inches. Is the triangle a right triangle?

Is a2 + b2 equal to c2? _______
Is the triangle a right triangle? _________
Answer:
It is given that
A triangle has side lengths 4 inches, 5 inches, and 7 inches.
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
So,
c² = a² + b²
Where,
c is the hypotenuse that has the longest side length
a and b are the lengths of the legs
So,
7² = 4² + 5²
49 = 16 + 25
49 = 41
So,
49 ≠ 41
Hence, from the above,
We can conclude that
c² ≠ a²+ b²
The given triangle is not a right triangle
Convince Me!
Explain the proof of the Converse of the Pythagorean Theorem in your own words.
Answer:
The converse of the Pythagorean Theorem is:
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Try It!
A triangle has side lengths 10 feet, \(\sqrt {205}\) feet, and \(\sqrt {105}\) feet. Is this a right triangle? Explain.
Answer:
It is given that
A triangle has side lengths 10 feet, \(\sqrt {205}\) feet, and \(\sqrt {105}\) feet.
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b², then
The given triangle is a right triangle
We know that,
c is the length of the hypotenuse that has the longest side in a right triangle
So,
(\(\sqrt{205}\))² =(\(\sqrt{105}\))² + 10²
205 = 105 + 100
205 = 205
So,
c² = a² + b²
Hence, from the above,
We can conclude that the triangle with the given side lengths is a right triangle
Try It!
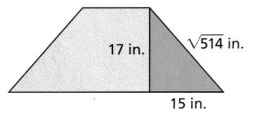
A triangle is inside a trapezoid. Is the triangle a right triangle? Explain.
Answer:
It is given that a triangle is inside a trapezoid
Now,
The given trapezoid is:

From the given trapezoid,
The sides of the triangle are: 17 in., 15 in., \(\sqrt{514}\) in.
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then, the given triangle is a right triangle
So,
(\(\sqrt{514}\))² = 17² + 15²
514 = 289 + 225
514 = 514
So,
c² = a² + b²
Hence, from the above,
We can conclude that the triangle that is in the trapezoid is a right triangle
KEY CONCEPT
The Converse of the Pythagorean Theorem states that if the sum of the squares of the lengths of two sides of a triangle is equal to the square of the length of the third side, the triangle is a right triangle.

Do You Understand?
Question 1.
Essential Question How can you determine whether a triangle is a right triangle?
Answer:
We can determine the triangle is a right triangle by using the converse of the Pythagorean Theorem
Hence,
According to the converse of the Pythagorean Theorem,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Question 2.
Construct Arguments A triangle has side lengths of 3 centimeters, 5 centimeters, and 4 centimeters. Abe used the Converse of the Pythagorean Theorem to determine whether it is a right triangle.
32 + 52 \(\underline{\underline{?}}\) 42
9 + 25 \(\underline{\underline{?}}\) 16
34 ≠ 16
Abe concluded that it is not a right triangle. Is Abe correct? Explain.
Answer:
It is given that
A triangle has side lengths of 3 centimeters, 5 centimeters, and 4 centimeters
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then, the triangle is a right triangle
We know that,
The hypotenuse has the length of the longest side
So,
5²= 3² + 4²
25 = 9 + 16
25 = 25
So,
c² = a² + b²
Hence, from the above,
We can conclude that the given triangle is a right triangle and Abe is not correct
Question 3.
Use Structure When you are given three side lengths for a triangle, how do you know which length to substitute for a, b, or c in the Pythagorean Theorem?
Answer:
First, we will find the squares of all lengths, then we will check which two squares of sides are equal to the square of the third side as per Pythagoras theorem. Hence the two sides would according be a and b and the third side will become c
Do You Know How?
Question 4.
Is the triangle a right triangle? Explain.
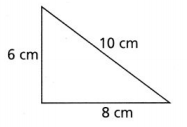
Answer:
The given triangle is:

We know that,
According to the converse of the Pythagorean Theorem,
If c² = a² + b²,
then, the triangle is a right triangle
So,
10² = 6² + 8²
100 = 36 + 64
100 = 100
So,
c² = a² + b²
Hence, from the above,
We can conclude that the given triangle is a right triangle
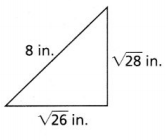
Question 5.
Is the triangle a right triangle? Explain.
Answer:
The given triangle is:

We know that,
According to the converse of the Pythagorean Theorem,
If c² = a² + b²,
then, the triangle is a right triangle
So,
8² = (\(\sqrt{26}\))² + (\(\sqrt{28}\))²
64 = 26 + 28
64 = 54
So,
c² ≠ a² + b²
Hence, from the above,
We can conclude that the given triangle is not a right triangle
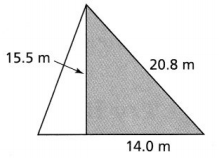
Question 6.
Is the purple triangle a right triangle? Explain.
Answer:
The given triangle is:

We know that,
According to the converse of the Pythagorean Theorem,
If c² = a² + b²,
then, the triangle is a right triangle
So,
(20.8)² = 14² + (15.5)²
432.64 = 196 + 240.25
432.64 = 436.25
So,
c² ≠ a² + b²
Hence, from the above,
We can conclude that the purple triangle is not a right triangle
Practice & Problem Solving
Leveled Practice In 7 and 8, determine whether each triangle is a right triangle.
Question 7.
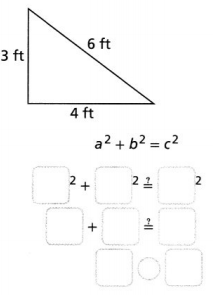
Is the triangle a right triangle? ________
Answer:
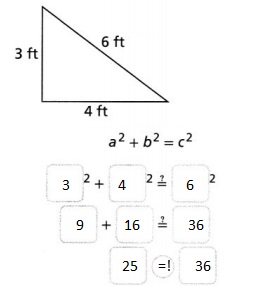
Hence, from the above,
We can conclude that the given triangle is not a right triangle
Question 8.

Is the triangle a right triangle? _________
Answer:
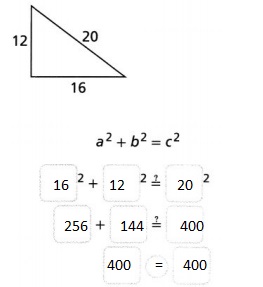
Hence, from the above,
We can conclude that the given triangle is a right triangle
Question 9.
Can the sides of a right triangle have lengths 5, 15, and \(\sqrt {250}\)? Explain.
Answer:
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then, the triangle is a right triangle
The hypotenuse has the longest side length
So,
(\(\sqrt{250}\))² = 5² + 15²
250 = 25 + 225
250 = 250
Hence, from the above,
We can conclude that the sides of a right triangle have lengths 5, 15, and \(\sqrt {250}\)
Question 10.
Is ∆PQR a right triangle? Explain.

Answer:
The given triangle is:

We know that,
According to the converse of the Pythagorean Theorem,
If c² = a² + b²,
then, the triangle is a right triangle
So,
(6.25)² = (3.75)² + 5²
39.0625 = 14.0625 + 25
39.0625 = 39.0625
So,
c² = a² + b²
Hence, from the above,
We can conclude that ΔPQR is a right triangle
Question 11.
The green triangle is set inside a rectangle. Is the green triangle a right triangle? Explain.
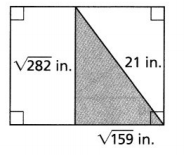
Answer:
It is given that
The green triangle is set inside a rectangle
Now,
The given figure is:

We know that,
According to the converse of the Pythagorean Theorem,
If c² = a² + b²,
then, the triangle is a right triangle
So,
21² = (\(\sqrt{282}\))² + (\(\sqrt{159}\))²
441 = 282 + 159
441 = 441
So,
c² = a² + b²
Hence, from the above,
We can conclude that the given green triangle is a right triangle
Question 12.
The side lengths of three triangles are shown. Which of the triangles are right triangles?
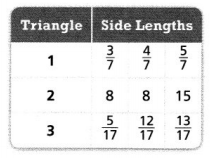
Answer:
It is given that
The side lengths of the three triangles are shown in the table
Now,
The given table is:

Now,
We know that,
According to the converse of the Pythagorean Theorem,
If c² = a² + b²,
then, the triangle is a right triangle
So
For Triangle 1,
(\(\frac{5}{7}\))² = (\(\frac{3}{7}\))² + (\(\frac{4}{7}\))²
25 = 16 + 9
25 = 25
For Triangle 2,
15² = 8² + 8²
225 = 64 + 64
225 = 128
For Triangle 3,
(\(\frac{13}{17}\))² = (\(\frac{12}{17}\))² + (\(\frac{5}{17}\))²
169 = 144 + 25
169 = 169
So,
The condition
c² = a² + b²
is true for the Triangles 1 and 3
Hence, from the above,
We can conclude that Triangle 1 and Triangle 3 is a right triangle
Question 13.
Construct Arguments Three students draw triangles with the side lengths shown. All three say that their triangle is a right triangle. Which students are incorrect? What mistake might they have made?
Student 1: 22, 33, 55
Student 2: 44, 33, 77
Student 3: 33, 44, 55
Answer:
It is given that
Three students draw triangles with the side lengths shown. All three say that their triangle is a right triangle.
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then, the triangle is a right triangle
Now,
For student 1,
55² = 33² + 22²
3,025 = 1,089 + 484
3,025 = 1,573
For student 2,
77²= 44² + 33²
5,929 = 1,936 + 1,089
5,929 = 3,025
For student 3,
55² = 44² + 33²
3,025 = 1,936 + 1,089
3,025 = 3,025
So,
The condition
c² = a² + b²
is false for the side lengths of the triangles that are drawn by students 1 and 2
Hence, from the above,
We can conclude that student 1 and student 2 are incorrect
Question 14.
Model with Math
∆JKL is an isosceles triangle. Is KM the height of ∆JKL? Explain.

Answer:
It is given that
ΔJKL is an isosceles triangle
Now,
To find whether KM is the height of ΔJKL,
Find out whether ΔKLM is a right triangle or not
Now,
The given triangle is:

Now,
We know that,
According to the converse of the Pythagorean Theorem,
c² = a²+ b²
So,
From ΔKLM,
(\(\sqrt{340}\))² = 13² + 14²
340 = 169 + 196
340 = 365
So,
c² ≠ a² + b²
So,
ΔKLM is not a right triangle
Hence, from the above,
We can conclude that KM is not the height of ΔJKL
Question 15.
Higher-Order Thinking The side lengths of three triangles are given.
Triangle 1: \(\sqrt{229}\) units, \(\sqrt{225}\) units, 22 units
Triangle 2: \(\sqrt{11 \frac{1}{3}}\) units, \(\sqrt{13 \frac{2}{3}}\) units, 5 units
Triangle 3: 16 units, 17 units, \(\sqrt{545}\) units
a. Which lengths represent the side lengths of a right triangle?
Answer:
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²
then, the triangle is a right triangle
Now,
For Triangle 1,
(\(\sqrt{229}\))² = (\(\sqrt{225}\))² + 22²
229 = 225 + 484
229 = 709
For Triangle 2,
(\(\sqrt{\frac{41}{3}}\))² + (\(\sqrt{\frac{34}{3}}\))² = 5²
\(\frac{41}{3}\) + \(\frac{34}{3}\) = 25
25 = 25
For Triangle 3,
(\(\sqrt{545}\))² = 16² + 17²
545 = 256 + 289
545 = 545
So,
The condition
c² = a²+ b²
is true for triangle 2 and triangle 3
Hence, from the above,
We can conclude that Triangle 2 and Triangle 3 represent the side lengths of a triangle
b. For any triangles that are not right triangles, use two of the sides to make a right triangle.
Answer:
Assessment Practice
Question 16.
Which shaded triangle is a right triangle? Explain.
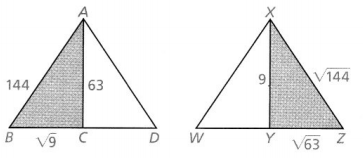
Answer:
The given figure is:

Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a²+ b²,
then the triangle is a right triangle
Now,
For ΔABC,
144² = 63² + (\(\sqrt{9}\))²
20,736 = 3,969 + 9
20,736 = 3,978
For ΔXYZ,
(\(\sqrt{144}\))² = (\(\sqrt{63}\))² + 9²
144 = 63 + 81
144 = 144
So,
The condition c² = a²+ b² is true for the shaded triangle XYZ
Hence, from the above,
We can conclude that the shaded triangle ΔXYZ is a right triangle
Question 17.
Which triangle is a right triangle?
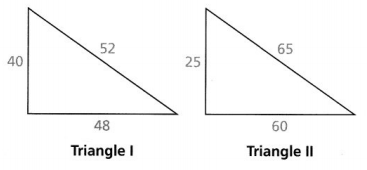
A. Triangle I only
B. Triangle II only
C. Triangle I and Triangle II
D. Neither Triangle I nor Triangle II
Answer:
The given triangles are:

Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then the triangle is a right triangle
Now,
For Triangle I,
52² = 40² + 48²
2,704 = 1,600 + 2,304
2,704 = 3,904
For Triangle II,
65² = 60² + 25²
4,225 = 3,600 + 625
4,225 = 4,225
Hence, from the above,
We can conclude that Triangle II only is a right triangle
Topic 7 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary How are the hypotenuse and the legs of a right triangle related? Lesson 7-1
Answer:
The relation between the sides and angles of a right triangle is the basis for trigonometry. The side opposite the right angle is called the hypotenuse. The sides adjacent to the right angle are called legs
Question 2.
Given that ∆QPR has side lengths of 12.5 centimeters, 30 centimeters, and 32.5 centimeters, proves ∆QPR is a right triangle. Lesson 7-2
Answer:
It is given that
∆QPR has side lengths of 12.5 centimeters, 30 centimeters, and 32.5 centimeters
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then, the triangle is a right triangle
So,
(32.5)² = (12.5)² + 30²
1,056.25 = 156.25 + 900
1,056.25 = 1,056.25
So,
The condition
c² = a² + b²
is true for the given side lengths of a triangle
Hence, from the above,
We can conclude that ΔQPR is a right triangle
Question 3.
Ella said that if she knows the lengths of just two sides of any triangle, then she can find the length of the third side by using the Pythagorean Theorem. Is Ella correct? Explain. Lesson 7-1
Answer:
Ella said that if she knows the lengths of just two sides of any triangle, then she can find the length of the third side by using the Pythagorean Theorem.
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the legs
Now,
If we know a and b, then we can find c
If we know b and c, then we can find a
If we know a and c, then we can find b
Hence, from the above,
We can conclude that Ella is correct
Question 4.
Find the unknown side length. Round to the nearest tenth. Lesson 7-1
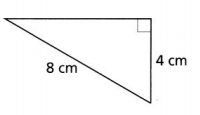
Answer:
The given triangle is:

From the given triangle,
We can observe that it is a right triangle
So,
Now,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the legs
Now,
8² = 4² + b²
64 = 16 + b²
b² = 64 – 16
b² = 48
b = \(\sqrt{48}\)
b = 6.9 cm
Hence, from the above,
We can conclude that the length of the unknown side is: 6.9 cm
Question 5.
The height of a shed is 6 m. A ladder leans against the shed with its base 4.5 m away, and its top just reaching the roof. What is the length of the ladder? Lesson 7-1
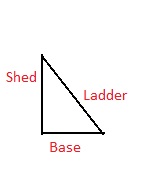
Answer:
It is given that
The height of a shed is 6 m. A ladder leans against the shed with its base 4.5 m away, and its top just reaching the roof.
Now,
From the given figure,
We can observe that the ladder looks like the hypotenuse of a right triangle for the shed
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the legs
In this situation,
c is the length of the ladder
a is the height of the shed
b is the length of the base
So,
c² = 6² + (4.5)²
c² = 36 + 20.25
c² = 56.25
c = \(\sqrt{56.25}\)
c = 7.5 m
Hence, from the above,
We can conclude that the length of the ladder is: 7.5 m
Question 6.
Select all the sets of lengths that could represent the sides of a right triangle. Lesson 7-2
☐ 5 cm, 10 cm, 15 cm
☐ 7 in., 14 in., 25 in.
☐ 13 m, 84 m, 85 m
☐ 5 ft, 11 ft, 12 ft
☐ 6ft, 9 ft, \(\sqrt {117}\) ft
Answer:
Let the given options be named as A, B, C, D, and E
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse and has the longest length
a and b are the legs
So,
A)
15² = 5² + 10²
225 = 25 + 100
225 ≠ 125
B)
25² = 7² + 14²
625 = 49 + 196
625 ≠ 245
C)
85² = 84² + 13²
7,225 = 7,056 + 169
7,225 = 7,225
D)
12² = 11² + 5²
144 = 121 + 25
144 ≠ 146
E)
(\(\sqrt{117}\))² = 6² + 9²
117 = 36 + 81
17 = 117
Hence, from the above,
We can conclude that the side lengths present in options C and E represent the side lengths of a right triangle
Topic 7 MID-TOPIC PERFORMANCE TASK
Javier is standing near a palm tree. He holds an electronic tape measure near his eyes and finds the three distances shown.
PART A
Javier says that he can now use the Pythagorean Theorem to find the height of the tree. Explain. Use vocabulary terms in your explanation.
Answer:
It is given that
Javier says that he can now use the Pythagorean Theorem to find the height of the tree
Now,
According to the Pythagorean Theorem,
In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. The sides of this triangle have been named Perpendicular (The height of the tree), Base, and Hypotenuse.
PART B
Find the height of the tree. Round to the nearest tenth. Show your work.

Answer:
From the given figure,
We can observe that
To find the height of the tree, we have to find the perpendicular distances of the two right triangles
Now,
Let x be the perpendicular height of the first right triangle
Let y be the perpendicular height of the second right triangle
So,
The height of the tree = x + y
Now,
The side lengths of the first right triangle are: 25 ft, 7 ft, x ft
Now,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the side lengths
So,
25² = 7² + x²
x² = 625 – 49
x² = 576
x = \(\sqrt{576}\)
x = 24 ft
Now,
The side lengths of the second right triangle are: 9 ft, 7ft, y ft
So,
9² = 7² + y²
y² = 81 – 49
y² = 32
y = \(\sqrt{32}\)
y = 5.6 ft
So,
The height of the tree = 24 + 5.6
= 29.6 ft
Hence, from the above,
We can conclude that the height of the tree to the nearest tenth is: 29.6 ft
PART C
Javier moves backward so that his horizontal distance from the palm tree is 3 feet greater. Will the distance from his eyes to the top of the tree also be 3 feet greater? Explain.
Answer:
Yes it will be greater, he is moving back 3 feet so what you are doing is taking the leg (a²) and multiplying it by 3. Once you do, you see triangle 1 has double and so did triangle 2. Triangle 2 was originally 5.6 (rounded to 6) then went up to 26.1. Triangle 1 was originally 24 and went up to 74.7 (or 75)
Step-by-step explanation:
For Triangle 1 (when multiplied by 3):
We know that,
a² + b² = c²
7² + b² = 27²
49 + b² = 729
b² = 680
b = \(\sqrt{680}\)
b = 26.1 ft
For Triangle 2:
We know that,
a² + b² = c²
7² + b² =75²
b² = 5576
b = \(\sqrt{5,576}\)
b = 74.7 ft
PART D
Could Javier change his horizontal distance from the tree so that the distance from his eyes to the top of the tree is only 20 feet? Explain.
Answer:
Yes, Javier can change his horizontal distance from the tree so that the distance from his eyes to the top of the tree is only 20 feet by moving forward 5 ft
Lesson 7.3 Apply the Pythagorean Theorem to Solve Problems
Solve & Discuss It!
Carlos is giving his friend in another state a new umbrella as a gift. He wants to ship the umbrella in a box he already has. Which box can Carlos use to ship the umbrella? Explain.
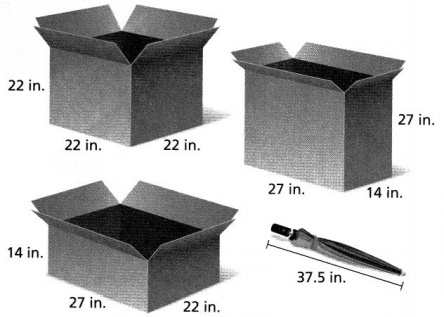
I can… use the Pythagorean Theorem to solve problems.
Answer:
It is given that
Carlos is giving his friend in another state a new umbrella as a gift. He wants to ship the umbrella in a box he already has.
Now,
From the given figure,
We can observe that the umbrella is 37.5 inches long.
Now,
If you observe, each box doesn’t have 37 inches wide, however, they are tridimensional figures, which means they have a certain height.
So,
The smaller box is too small to fit the umbrella.
But,
The medium box is perfect because it has 27 inches wide and 27 inches in height, which is enough to fit the umbrella. These are the best dimensions to send the umbrella.
Hence, from the above,
We can conclude that the box that can be used by Carlos to ship the umbrella has the dimensions 27 in × 14 in × 27 in
Make Sense and Persevere
How will the umbrella fit inside any of the boxes?
Answer:
We know that,
The box is a 3-d figure
So,
To fit the whole umbrella in the box, we have to put it in a diagonal manner i.e., like the hypotenuse of a right triangle
Focus on math practices
Construct Arguments Tim says that the diagonal of any of the boxes will always be longer than the sides. Is Tim correct? Explain.
Answer:
We know that,
If we consider a square or any 2-d figure or any 3-d figure that consists of 1 right angle,
then, the diagonal will divide a figure into 2 right triangles
We know that,
We can apply the Pythagorean Theorem for any right triangle
We know that,
In a right triangle,
The hypotenuse is the longest side
We know that,
The hypotenuse in a right triangle is considered as a diagonal in a figure that consists of 1 right angle
Hence, from the above,
We can conclude that Tim is correct
Essential Question
What types of problems can be solved using the Pythagorean Theorem?
Answer:
The Pythagorean theorem is a way of relating the leg lengths of a right triangle to the length of the hypotenuse, which is the side opposite the right angle. Even though it is written in these terms, it can be used to find any of the sides as long as you know the lengths of the other two sides
Try It!
What is the length of the diagonal, d, of a rectangle with length 19 feet and width 17 feet?
leg2 + leg2 = hypotenuse2
______ 2 + _______2 = d2
______ + _______ = d2
_______ = d2
________ ≈ d
Answer:
It is given that a rectangle has a length of 19 feet and a width of 17 feet
Now,
We know that,
In a rectangle,
If a diagonal is drawn, then it divides the rectangle into 2 right angles
So,
According to the Pythagorean Theorem,
d² = a² + b²
Where,
d is the diagonal or hypotenuse
a and b are the lengths of the legs
So,
d²= 19² + 17²
d² = 361 + 289
d² = 650
d = \(\sqrt{650}\)
d = 25.4 ft
Hence, from the above,
We can conclude that the length of the diagonal is: 25.4 ft
Convince Me!
If the rectangle were a square, would the process of finding the length of the diagonal change? Explain.
Answer:
We know that,
For any figure i.e., either 2-d figure or 3-d figure with 1 right angle, the diagonal will divide that figure into 2 right angles
We know that,
We will use the Pythagorean Theorem to find the length of any unknown side in the right triangle
Hence, from the above,
We can conclude that even if the rectangle were a square, the process of finding the length of the diagonal will not change
Try It!
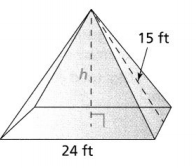
A company wants to rent a tent that has a height of at least 10 feet for an outdoor show. Should they rent the tent shown at the right? Explain.
Answer:
It is given that
A company wants to rent a tent that has a height of at least 10 feet for an outdoor show.
Now,
The given figure is:

Now,
To find whether the tent should be rented or not,
We have to find the value of h
We can also observe that the triangle that contains the value of h is a right triangle
Now,
The base of the right triangle = \(\frac{24}{2}\)
= 12 ft
Now,
The side lengths of the right triangle are: h, 15 ft, 12 ft
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
So,
15² = 12² + h²
h² = 225 – 144
h² = 81
h = \(\sqrt{81}\)
h = 9 ft
But,
The given height of the tent is: 10 ft
So,
9 ft < 10 ft
Hence, from the above,
We can conclude that the company should not rent the tent
KEY CONCEPT
You can use the Pythagorean Theorem and its converse to solve problems involving right triangles.
Do You Understand?
Question 1.
Essential Question What types of problems can be solved using the Pythagorean Theorem?
Answer:
The Pythagorean theorem is a way of relating the leg lengths of a right triangle to the length of the hypotenuse, which is the side opposite the right angle. Even though it is written in these terms, it can be used to find any of the sides as long as you know the lengths of the other two sides
Question 2.
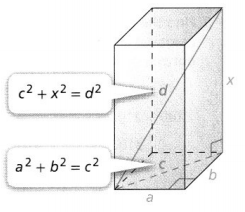
Look for Structure How is using the Pythagorean Theorem in a rectangular prism similar to using it in a rectangle?
Answer:
We know that,
The rectangular prism and the rectangle have at least 1 right angle
We know that,
If a 3-d or 2-d figure has 1 right angle, then the diagonal of that figure divides the figure into the right triangles
So,
If we have the right triangle, then we can use the Pythagorean Theorem irrespective of the overall shape of the figure
Question 3.
Construct Arguments Glen found the length of the hypotenuse of a right triangle using \(\sqrt{a^{2}+b^{2}}\). Gigi used \(\sqrt{(a+b)^{2}}\). Who is correct? Explain.
Answer:
It is given that
Glen found the length of the hypotenuse of a right triangle using \(\sqrt{a^{2}+b^{2}}\). Gigi used \(\sqrt{(a+b)^{2}}\).
Now,
We know that,
We can use the Pythagorean Theorem only for the right triangles
The condition for a triangle to become the right triangle is:
Hypotenuse² = Side² + Side²
c² = a² + b²
Hence, from the above,
We can conclude that Glen is correct
Do You Know How?
Question 4.
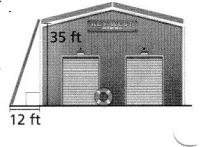
You are painting the roof of a boathouse. You are going to place the base of a ladder 12 feet from the boathouse. How long does the ladder need to be to reach the roof of the boathouse?
Answer:
It is given that
You are painting the roof of a boathouse. You are going to place the base of a ladder 12 feet from the boathouse.
Now,
From the figure,
We can observe that the roof of a boathouse, ladder, and the base form a right triangle
So,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the height of the boathouse
a is the length of the base
b is the length of the ladder
So,
35² = 12² + b²
b² = 1,225 – 144
b² = 1,081
b = \(\sqrt{1,081}\)
b = 32.9 ft
Hence, from the above,
We can conclude that the length of the ladder that is needed to reach the roof of the boathouse is: 32.9 ft
Question 5.
A box-shaped like a right rectangular prism measures 5 centimeters by 3 centimeters by 2 centimeters. What is the length of the interior diagonal of the prism to the nearest hundredth?
Answer:
It is given that
A box-shaped like a right rectangular prism measures 5 centimeters by 3 centimeters by 2 centimeters.
So,
The dimensions of a rectangular prism is: 5 cm × 3 cm × 2 cm
So,
The length of the rectangular prism is: 5 cm
The width of the rectangular prism is: 3 cm
The height of the rectangular prism is: 2 cm
Now,
We know that,
The length of the diagonal of the prism = \(\sqrt{Length^{2} + Width^{2} + Height^{2}}\)
So,
The length of the diagonal of the rectangular prism = \(\sqrt{5^{2} + 3^{2} + 2^{2}}\)
= \(\sqrt{25 + 9 + 4}\)
= \(\sqrt{38}\)
= 6.16 cm
Hence, from the above,
We can conclude that the length of the interior diagonal of the rectangular prism is: 6.16 cm
Question 6.
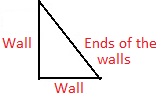
A wall 12 feet long makes a corner with a wall that is 14 feet long. The other ends of the walls are about 18.44 feet apart. Do the walls form a right angle? Explain.
Answer:
It is given that
A wall 12 feet long makes a corner with a wall that is 14 feet long. The other ends of the walls are about 18.44 feet apart
Now,
The given figure is:

From the given figure,
We can observe that the given situation forms the right triangle
Now,
We know that,
According to the Pythagorean Therem,
c² = a² + b²
So,
c² = 12² + 14²
c² = 144 + 196
c² = 340
c = \(\sqrt{340}\)
c = 18.44 feet
Hence, from the above,
We can conclude that the walls form a right angle
Practice & Problem Solving
Leveled Practice In 7 and 8, use the Pythagorean Theorem to solve.
Question 7.
You are going to use an inclined plane to lift a heavy object to the top of a shelving unit with a height of 6 feet. The base of the inclined plane is 16 feet from the shelving unit. What is the length of the inclined plane? Round to the nearest tenth of a foot.
The length of the inclined plane is about ________ feet.
Answer:

Question 8.
Find the missing lengths in the rectangular prism.
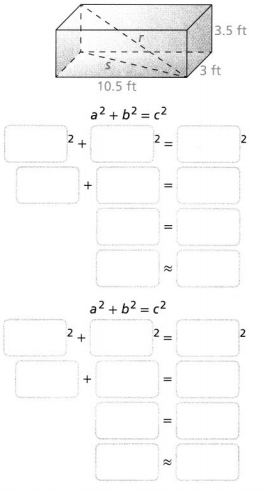
Answer:

Question 9.
A stainless steel patio heater is shaped like a square pyramid. The length of one side of the base is 19.8 inches. The slant height is 92.8 inches. What is the height of the heater? Round to the nearest tenth of an inch.
Answer:
It is given that
A stainless steel patio heater is shaped like a square pyramid. The length of one side of the base is 19.8 inches. The slant height is 92.8 inches
Now,
We know that,
The slant height is nothing but a length of the diagonal
Now,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the slant height
a is the length of the base of the steel patio heater
b is the height of the heater
So,
(92.8)² = (19.8)² + b²
b² = 8,611.84 – 392.04
c² = 8,219.8
c = \(\sqrt{8,219.8}\)
c = 90.6 inches
Hence, from the above,
We can conclude that the height of the heater is: 90.6 inches
Question 10.
Reasoning What is the measurement of the longest line segment in a right rectangular prism that is 16 centimeters long, 9 centimeters wide, and 7 centimeters tall? Round to the nearest tenth of a centimeter.
Answer:
It is given that
A right rectangular prism is 16 centimeters long, 9 centimeters wide, and 7 centimeters tall
So,
The dimensions of a right rectangular prism are: 16 cm × 9 cm × 7 cm
So,
The length of the right rectangular prism is: 16 cm
The width of the right rectangular prism is: 9 cm
The height of the right rectangular prism is: 7 cm
We know that,
The longest line segment in any 2-d or 3-d figure is a “Diagonal”
Now,
We know that,
The length of the diagonal of the right rectangular prism = \(\sqrt{Length^{2} + Width^{2} + Height^{2}}\)
So,
The length of the diagonal of the right rectangular prism = \(\sqrt{16^{2} + 9^{2} + 7^{2}}\)
= \(\sqrt{256 + 49 + 81}\)
= \(\sqrt{386}\)
= 19.64 cm
Hence, from the above,
We can conclude that the length of the longest line segment in the right rectangular prism is: 19.64 cm
Question 11.
Felipe is making triangles for a stained glass window. He made the design shown but wants to change it. Felipe wants to move the purple triangle to the corner. The purple piece has side lengths of 4.5 inches, 6 inches, and 7 inches. Can the purple piece be moved to the corner? Explain.

Answer:
It is given that
Felipe is making triangles for a stained glass window. He made the design shown as above but wants to change it. Felipe wants to move the purple triangle to the corner. The purple piece has side lengths of 4.5 inches, 6 inches, and 7 inches.
Now,
From the given figure,
We can observe that
If the purple figure is moving to the corner, then one side of the purple figure will become a right angle
So,
Now,
We have to find whether the purple figure will be a right triangle or not if it moves to a corner
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²,
then, the triangle is a right triangle
We know that,
The hypotenuse has the longest side length
So,
7² = 4.5² + 6²
49 = 20.25 + 36
49 = 56.25
So,
The condition
c² = a² + b²
is false
Hence, from the above,
We can conclude that the purple figure should not
Question 12.
a. What is the longest poster you could fit in the box? Express your answer to the nearest tenth of an inch.

Answer:
The given figure is:

From the given figure,
We can observe that there will be two longest sides for two pairs of different side lengths
we know that,
The longest side is nothing but a diagonal
Now,
The two pairs of side lengths are: (20, 12, x), and (8, 12, y)
Where,
x and y are the lengths of the longest sides
Now,
We know that
Since the figure consists of the right triangles,
According to the Pythagorean Theorem,
c² = a² + b²
So,
x² = 20² + 12²
x² = 400 + 144
x² = 544
x = \(\sqrt{544}\)
x = 23.32 in.
So,
y² = 12² + 8²
y² = 144 + 64
y² = 208
y = \(\sqrt{208}\)
y = 14.42 in.
Hence, from the above,
We can conclude that the longest poster that you can fit in the box is: 23.32 in.
b. Explain why you can fit only one maximum-length poster in the box, but you can fit multiple 21.5-inch posters in the same box.

Answer:
It is given that
you can fit multiple 21.5-inch posters in the same box.
Now,
From part (a),
We can observe that the length of the longest poster that can fit into the box is: 23.32 in.
So,
21.5 in. < 23.32 in.
Hence, from the above,
We can conclude that since the given size of the posters is less than the maximum length of the poster,
We can fit multiple 21.5-inch posters in the same box instead of 1 poster that is of the maximum length
Question 13.
The corner of a room where two walls meet the floor should be at a right angle. Jeff makes a mark along each wall. One mark is 3 inches from the corner. The other is 4 inches from the corner. How can Jeff use the Pythagorean Theorem to see if the walls form a right angle?
Answer:
It is given that
The corner of a room where two walls meet the floor should be at a right angle. Jeff makes a mark along each wall. One mark is 3 inches from the corner. The other is 4 inches from the corner.
Now,
To see whether the walls form a right angle or not,
We have to see whether the length along the walls is greater than the lengths of the marks from the corners
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length along the walls
a is the length of one mark from the corner
b is the length of another mark from the corner
So,
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = \(\sqrt{25}\)
c = 5
So,
From the above value,
We can observe that
c > a and c > b
Hence, from the above,
We can conclude that the walls form a right angle
Question 14.
Higher-Order Thinking It is recommended that a ramp have at least 6 feet of horizontal distance for every 1 foot of vertical rise along an incline. The ramp shown has a vertical rise of 2 feet. Does the ramp show match the recommended specifications? Explain.

Answer:
It is given that
It is recommended that a ramp have at least 6 feet of horizontal distance for every 1 foot of vertical rise along an incline. The ramp shown has a vertical rise of 2 feet
Now,
6 feet of horizontal distance for every 1 foot,
The ramp shown has a vertical rise of 5 feet.
So,
The rate of change (m) ≤ \(\frac{1 foot}{6 feet}\)
Convert both to a single unit of inches
We know that,
1 foot = 12 inches
So,
m ≤ \(\frac{12 inches}{72 inches}\)
Divide by 4 into both sides
m ≤ \(\frac{4 inches}{18 inches}\)
Now,
For a ramp that has a vertical distance of 2 feet and the same horizontal distance
m = \(\frac{12 inches}{24 inches}\)
m = \(\frac{4 inches}{6 inches}\)
So,
The rate of change when the vertical distance is 6 feet > The rate of change when the vertical distance is 2 feet
Hence, from the above,
We can conclude that the ramp shown above matched the given specifications
Assessment Practice
Question 15.
A machine in a factory cuts out triangular sheets of metal. Which of the triangles are right triangles? Select all that apply.
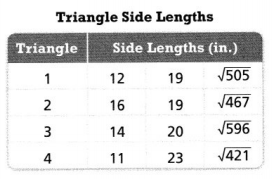
☐ Triangle 1
☐ Triangle 2
☐ Triangle 3
☐ Triangle 4
Answer:
It is given that
A machine in a factory cuts out triangular sheets of metal.
Now,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²
then, the triangle is a right triangle
Now,
For Triangle 1,
(\(\sqrt{505}\))² = 12² + 19²
505 = 505
For Triangle 2,
(\(\sqrt{467}\))² = 16² + 19²
467 ≠ 617
For Triangle 3,
(\(\sqrt{596}\))² = 14² + 20²
596 = 596
For Triangle 4,
(\(\sqrt{421}\))² = 11² + 23²
421 ≠ 650
Hence, from the above,
We can conclude that Triangle 1 and Triangle 3 are the right triangles
Question 16.
What is the length b, in feet, of the rectangular plot of land shown?
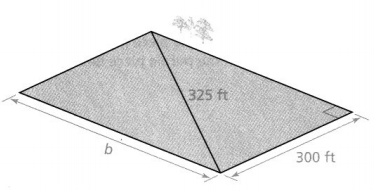
Answer:
It is given that the given figure is a rectangular plot of land
We know that,
In a rectangle,
The opposite sides are equal and the angles are all 90°
So,
A diagonal forms 2 right triangles in a rectangle
Now,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the length of the diagonal
a is the width
b is the length
Now,
325² = 300² + b²
b²= 1,05,625 – 90,000
b² = 15,625
b = \(\sqrt{15,625}\)
b = 125 ft
Hence, from the above,
We can conclude that the length of b is: 125 ft
Lesson 7.4 Find Distance in the Coordinate
Explore It!
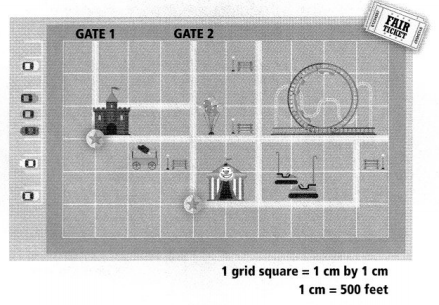
Thomas and Jim are outside the haunted castle ride and want to get to the clown tent in time for the next show.
I can… use the Pythagorean Theorem to find the distance between two points in the coordinate plane.
A. How can you represent the starred locations on a coordinate plane?
Answer:
It is given that
Thomas and Jim are outside the haunted castle ride and want to get to the clown tent in time for the next show.
Now,
The given route of the castle is:

Now,
From the given figure,
To represent the route in the coordinate plane,
The given scale is:
X-axis: 1 cm = 500 feet
Y-axis: 1 cm = 500 feet
Now,
From the given figure,
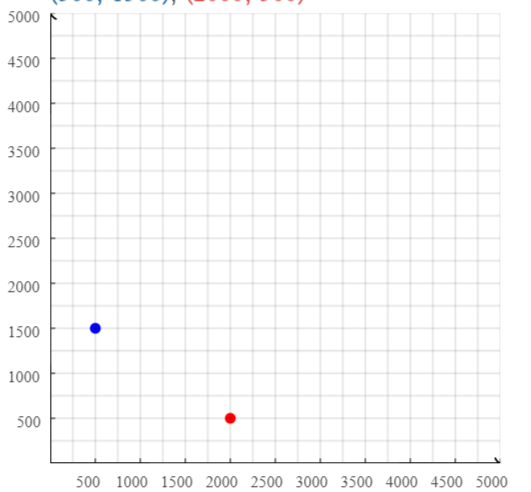
The coordinates of the starred locations can be:
The coordinates of the haunted house are: (500, 1,500),
The coordinates of the clown tent are: (2,000, 500)
Hence,
The representation of the starred locations in the coordinate plane is:
B. Jim says that the marked yellow paths show the shortest path to the tent. Write an expression to represent this and find the distance Jim walks from the haunted mansion to the clown tent.
Answer:
From part (a),
We know that,
The coordinates of the haunted house are: (500, 1,500),
The coordinates of the clown tent are: (2,000, 500)
Now,
We know that
The linear equation in the slope-intercept form is:
y = mx + b
Where,
m is the slope
b is the initial value (or) y-intercept
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
Slope (m) = y2 – y1 / x2 – x1
So,
Slope (m) = \(\frac{500 – 1,500}{2,000 – 500}\)
Slope (m) = –\(\frac{1,000}{1,500}\)
Slope (m) = –\(\frac{2}{3}\)
So,
The equation in the slope-intercept form is:
y = –\(\frac{2}{3}\)x + b
So,
3y = -2x + 3b
Now,
Substitute (500, 1,500) or (2,000, 500) in the above equation
So,
1,500 = -4000 + 3b
3b = 5,500
So,
The equation that represents the shortest path to the tent is:
3y = -2x + 5,500
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the haunted mansion and the clown tent = \(\sqrt{(2,000 – 500)^{2} + (500 – 1,500)^{2}}\)
= \(\sqrt{1,500^{2} + 1,000^{2}}\)
= \(\sqrt{2,250,000 + 1,000,000}\)
= 1,802.77 feet
Hence, from the above,
We can conclude that
The equation that represents the shortest path to the clown tent is:
3y = -2x + 5,500
The distance between the haunted mansion and the clown tent is: 1,802.77 feet
Focus on math practices
Construct Arguments Why is the distance between two nonhorizontal and nonvertical points always greater than the horizontal or vertical distance?
Answer:
Let us consider a coordinate plane
Now,
When we draw either a horizontal line or the vertical line,
We can observe that the length will be constant
But,
When we draw non-vertical and non-horizontal lines,
We can observe that the lengths are unknown and not constant
Hence, from the above,
We can conclude that the distance between two nonhorizontal and nonvertical points always greater than the horizontal or vertical distance
Essential Question
How can you use the Pythagorean Theorem to find the distance between two points?
Answer:
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the side lengths or lengths of the legs
Now,
Graphically,
The terms of the Pythagorean Theorem can be expressed as:
c is the distance between two points
a and b are the points
So,
c = \(\sqrt{a^{2} + b^{2}}\)
Try It!
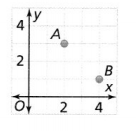
What is the distance between points A and B?
The distance between point A and point B is about ________ units.
Answer:
The given graph is:

The representation of the graph in the coordinate plane is:
From the given graph,
The coordinates of A are: (2, 3)
The coordinates of B are: (4, 1)
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points A and B = \(\sqrt{(4 – 2)^{2} + (1 – 3)^{2}}\)
= \(\sqrt{2^{2} + 2^{2}}\)
= \(\sqrt{4 + 4}\)
= 2.83 units
Hence, from the above,
We can conclude that the distance between points A and B is about 2.83 units
Convince Me!
Why do you need to use the Pythagorean Theorem to find the distance between points A and B?
Answer:
The representation of points A and B in the coordinate plane are:

Now,
When we observe the graph,
We can see that A and B can form a right triangle
Now,
We know that,
The Pythagorean Theorem is only applicable to the right triangles
So,
According to the Pythagorean Theorem,
c² = a² + b²
c = \(\sqrt{a^{2} + b^{2}}\)
where,
c is the distance between points A and B
A and B are the given points
Try It!
Find the perimeter of ∆ABC with vertices (2, 5), (5, -1), and (2, -1).
Answer:
It is given that
∆ABC with vertices (2, 5), (5, -1), and (2, -1)
Now,
The names of the vertices are:
A (2, 5), B (5, -1), and C (2, -1)
We know that,
The perimeter of a triangle is the sum of all the side lengths of a triangle
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
In ∆ABC,
AB and BC are the side lengths
Ac is the hypotenuse
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points A and B = \(\sqrt{(5 – 2)^{2} + (-1 – 5)^{2}}\)
= \(\sqrt{3^{2} + 6^{2}}\)
= \(\sqrt{9 + 36}\)
= 6.70 units
The distance between the points B and C (BC) = \(\sqrt{(2 – 5)^{2} + (-1 + 1)^{2}}\)
= \(\sqrt{3^{2} + 0^{2}}\)
= \(\sqrt{9 + 0}\)
= 3 units
The distance between the points A and C (AC) = \(\sqrt{(2 – 2)^{2} + (-1 – 5)^{2}}\)
= \(\sqrt{0^{2} + 6^{2}}\)
= \(\sqrt{0 + 36}\)
= 6 units
So,
The perimeter of ∆ABC = AB + BC + AC
= 6 + 3 + 6.70
= 15.7 units
Hence, from the above,
We can conclude that the perimeter of ∆ABC is about 15.7 units
Try It!
What are the coordinates, to the nearest tenth, of the third vertex in an isosceles triangle that has one side length of 2 and two side lengths of 5, with vertices at (1, 0) and (1, 2)? The third vertex is in the first quadrant.
Answer:
It is given that
An isosceles triangle that has one side length of 2 and two side lengths of 5, with vertices at (1, 0) and (1, 2)
Now,
Let the third vertex be (x, y)
Now,
The given vertices are:
A (1, 0), B (1, 2), and C (x, y)
It is also given that
BC = 2 units, and AC = 5 units
We know that,
An isosceles triangle has any 2 equal side lengths
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points A and B = \(\sqrt{(2 – 0)^{2} + (1 – 1)^{2}}\)
= \(\sqrt{2^{2} + 0^{2}}\)
= \(\sqrt{4 + 0}\)
= 4 units
The distance between the points B and C = \(\sqrt{(x – 1)^{2} + (y – 2)^{2}}\)
Squaring on both sides
So,
BC² = (x – 1)² + (y – 2)²
The distance between the points A and C = \(\sqrt{(x – 1)^{2} + (y – 0)^{2}}\)
Squaring on both sides
So,
BC² = (x – 1)² + y²
So,
(x – 1)² + (y – 2)² = 4 —– (1)
(x – 1)² + y² = 25 —— (2)
So,
From eq (1) and eq (2),
25 – y² + (y – 2)² = 4
-y² + y² – 4y + 4 = -21
-4y = -25
y = \(\frac{25}{4}\)
So,
(x – 1)² = |25 – (\(\frac{25}{4}\))²|
x = \(\frac{19}{4}\)
Hence, from the above,
We can conclude that the third vertex is: (\(\frac{19}{4}\), \(\frac{25}{4}\))
KEY CONCEPT
You can use the Pythagorean Theorem to find the distance between any two points, P and Q, on the coordinate plane.

Do You Understand?
Question 1.
Essential Question How can you use the Pythagorean Theorem to find the distance between two points?
Answer:
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the side lengths or lengths of the legs
Now,
Graphically,
The terms of the Pythagorean Theorem can be expressed as:
c is the distance between two points
a and b are the points
So,
c = \(\sqrt{a^{2} + b^{2}}\)
Question 2.
Model with Math
Can you use a right triangle to represent the distance between any two points on the coordinate plane? Explain.
Answer:
Derived from the Pythagorean Theorem, the distance formula is used to find the distance between two points in the plane. We know that,
According to the Pythagorean Theorem,
a²+b²=c²
where,
a and b are the lengths of the legs adjacent to the right angle
c is the length of the hypotenuse.
Question 3.
Generalize How does the fact that the points are on opposite sides of the y-axis affect the process of finding the distance between the two points?
Answer:
The fact that the points are on opposite sides of the y-axis affects the process of finding the distance between the two points because We need to find the distance between the two points by adding the distances from each of them to the y-axis.
Do You Know How?
In 4-6, use the coordinate plane below.
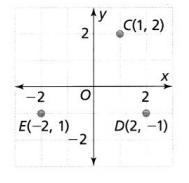
Answer:
The given coordinate plane is:

From the given coordinate plane,
The given points are:
C (1, 2), D (2, -1), and E (-2, 1)
Question 4.
Find the distance between points C and D. Round to the nearest hundredth.
Answer:
Compare the points C and D with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points C and D = \(\sqrt{(2 – 1)^{2} + (-1 – 2)^{2}}\)
= \(\sqrt{1^{2} + 3^{2}}\)
= \(\sqrt{1 + 9}\)
= 3.16 units
Hence, from the above,
We can conclude that the distance between points C and D is: 3.16 units
Question 5.
Find the perimeter of ∆CDE.
Answer:
We know that,
The “Perimeter” is defined as the sum of all the side lengths
So,
The perimeter of ∆CDE = CD + DE + CE
So,
The distance between the points C and D = \(\sqrt{(2 – 1)^{2} + (-1 – 2)^{2}}\)
= \(\sqrt{1^{2} + 3^{2}}\)
= \(\sqrt{1 + 9}\)
= 3.16 units
The distance between the points D and E = \(\sqrt{(-2 – 2)^{2} + (1 + 1)^{2}}\)
= \(\sqrt{4^{2} + 2^{2}}\)
= \(\sqrt{16 + 4}\)
= 4.47 units
The distance between the points C and E = \(\sqrt{(-2 – 1)^{2} + (1 – 2)^{2}}\)
= \(\sqrt{3^{2} + 1^{2}}\)
= \(\sqrt{1 + 9}\)
= 3.16 units
So,
The perimeter of ∆CDE = 3.16 + 4.47 + 3.16
= 10.79 units
Hence, from the above,
We can conclude that the perimeter of ∆CDE is: 10.79 units
Question 6.
Point B is plotted on the coordinate plane above the x-axis. ∆BDE is equilateral. What are the coordinates of point B to the nearest hundredth?
Answer:
It is given that
Point B is plotted on the coordinate plane above the x-axis. ∆BDE is equilateral.
Now,
Let the unknown vertex be B (x, y)
So,
The given points are:
B (x, y), D (2, -1), and E (-2, 1)
It is given that ΔBDE is equilateral
So,
BD = DE = EB
BD² = DE² = EB²
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points B and D = \(\sqrt{(x – 2)^{2} + (y – 1)^{2}}\)
Squaring on both sides
So,
BD² = (x – 2)² + (y + 1)²
The distance between the points D and E = \(\sqrt{(1 + 1)^{2} + (-2 – 2)^{2}}\)
= \(\sqrt{2^{2} + 4^{2}}\)
= \(\sqrt{4 + 16}\)
= 4.47 units
The distance between the points E and B = \(\sqrt{(x + 2)^{2} + (y – 1)^{2}}\)
Squaring on both sides
So,
EB² = (x + 2)² + (y – 1)²
Now,
(x – 2)² + (y + 1)² = 4.47 —- (1)
(x + 2)² + (y – 1)² = (x – 2)² + (y + 1)²
x² + 2x + 4 + y² + 1 – 2y = x² + 4 – 4x + y² + 1 + 2y
2x + 4 + 1 – 2y = 4 – 4x + 1 + 2y
6x + 5 = 4y + 5
6x = 4y
3x = 2y
x = \(\frac{2}{3}\)y
Now,
From eq (1),
x² + 4 – 4x + y² + 1 + 2y = 4.47
x² + y² -4x + 2y = -0.47
(\(\frac{2}{3}\)y)² + y² – 4 (\(\frac{2}{3}\))y + 2y = -0.47
4y² + 15y + 4.23 = 0
So,
y = -0.30 (or) y = -3.44
So,
x = \(\frac{2}{3}\) (-0.30) (or) x = \(\frac{2}{3}\) (-3.44)
x = -0.2 (or) x = -2.29
Hence, from the above,
We can conclude that the coordinates of point B are: (-0.2, -0.30) or (-2.29, -3.44)
Practice & Problem Solving
Question 7.
Leveled Practice Use the Pythagorean Theorem to find the distance between points P and Q.
Label the length, in units, of each leg of the right triangle.
The distance between point P and point Q is __________ units.
Answer:
From the given coordinate plane,
There are only 2 vertices
Let the third vertex be R(x, y) and the coordinates of R can be found from the coordinate plane
Now,
From the given coordinate plane,
The vertices are:
P (3, 2), Q (9, 10), and R (9, 2)
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points Q and R = \(\sqrt{(9 – 9)^{2} + (10 – 2)^{2}}\)
= \(\sqrt{0^{2} + 8^{2}}\)
= \(\sqrt{0 + 64}\)
= 8 units
The distance between the points P and R = \(\sqrt{(9 – 3)^{2} + (2 – 2)^{2}}\)
= \(\sqrt{0^{2} + 6^{2}}\)
= \(\sqrt{0 + 36}\)
= 6 units
Now,
From the given coordinate plane,
We can observe that P, Q, R form the right triangle
So,
According to the Pythagorean Theorem,
PQ² = QR² + PR²
PQ² = 8² + 6²
PQ² = 64 + 36
PQ² = 100
PQ = \(\sqrt{100}\)
PQ = 10 units
Hence, from the above,
We can conclude that the length of PQ is: 10 units
Question 8.
Find the perimeter of triangle QPR. Round to the nearest hundredth.
Answer:
From the coordinate plane,
The vertices of ΔPQR are:
P (-5, -2), Q (2, -2), and R (-1, 3)
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points P and Q = \(\sqrt{(2 + 5)^{2} + (2 – 2)^{2}}\)
= \(\sqrt{0^{2} + 7^{2}}\)
= \(\sqrt{0 + 49}\)
= 7 units
The distance between the points Q and R = \(\sqrt{(-1 – 2)^{2} + (3 + 2)^{2}}\)
= \(\sqrt{3^{2} + 5^{2}}\)
= \(\sqrt{9 + 25}\)
= 5.83 units
The distance between the points P and R = \(\sqrt{(1 – 5)^{2} + (-3 – 2)^{2}}\)
= \(\sqrt{4^{2} + 5^{2}}\)
= \(\sqrt{16 + 25}\)
= 6.40 units
So,
The perimeter of ΔPQR = PQ + QR + PR
= 7 + 5.83 + 6.40
= 19.23 units
Hence, from the above,
We can conclude that the perimeter of ΔPQR is: 19.23 units
Question 9.
Determine whether the triangle is equilateral, isosceles, or scalene.
Answer:
We know that,
On the basis of the side lengths,
Scalene Triangle – All the side lengths are different
Equilateral Triangle – All the side lengths are the same
Isosceles Triangle – Any two of the side lengths are the same
So,
From Exercise 8,
We can observe that all the side lengths are different
Hence, from the above,
We can conclude that ΔPQR is a scalene Triangle
Question 10.
You walk along the outside of a park starting at point P. Then you take a shortcut represented by \(\overline{P Q}\) on the graph.

a. What is the length of the shortcut in meters? Round to the nearest tenth of a meter.
Answer:
It is given that
You walk along the outside of a park starting at point P. Then you take a shortcut represented by \(\overline{P Q}\) on the graph.
Now,
From the given figure,
We can observe that
The vertices are:
P (0, 0), Q (40, 85), and R (40, 0)
The shortest path is represented as PQ
Now,
Compare the points P and Q with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points P and Q = \(\sqrt{(40 – 0)^{2} + (85 – 0)^{2}}\)
= \(\sqrt{40^{2} + 85^{2}}\)
= \(\sqrt{1,600 + 7,225}\)
= 93.9 m
Hence, from the above,
We can conclude that the length of the shortest path is: 93.9 meters
b. What is the total length of your walk in the park? Round to the nearest tenth of a meter.
Answer:
We know that,
The total length is nothing but the “Perimeter”
So,
The perimeter of the given triangle = PQ + QR + PR
Now,
The distance between the points P and Q = \(\sqrt{(40 – 0)^{2} + (85 – 0)^{2}}\)
= \(\sqrt{40^{2} + 85^{2}}\)
= \(\sqrt{1,600 + 7,225}\)
= 93.9 m
The distance between the points Q and R = \(\sqrt{(40 – 40)^{2} + (85 – 0)^{2}}\)
= \(\sqrt{0^{2} + 85^{2}}\)
= \(\sqrt{0 + 7,225}\)
= 85 m
The distance between the points P and R = \(\sqrt{(40 – 0)^{2} + (0 – 0)^{2}}\)
= \(\sqrt{0^{2} + 40^{2}}\)
= \(\sqrt{0 + 1,600}\)
= 40 m
So,
The total length of your walk in the park = PQ + QR + PR
= 93.9 + 85 + 40
= 218.9 meters
Hence, from the above,
We can conclude that the total length of your walk in the park is: 218.9 meters
Question 11.
Suppose a park is located 3.6 miles east of your home. The library is 4.8 miles north of the park. What is the shortest distance between your home and the library?
Answer:
It is given that
A park is located 3.6 miles east of your home. The library is 4.8 miles north of the park
So,
The representation of the above situation is:
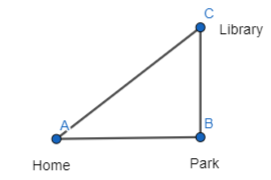
Now,
According to the Pythagorean Theorem,
(The shortest distance between home and library)² = (The distance from home to park)² + (he distance from park to library)²
(The shortest distance between home and library)² = 3.6² + 4.8²
(The shortest distance between home and library)² = 12.96 + 23.04
The shortest distance between home and library = 6
Hence, from the above,
We can conclude that the shortest distance between home and library is: 6 miles
Question 12.
Use Structure Point B has coordinates (2, 1). The x-coordinate of point A is -10. The distance between point A and point B is 15 units. What are the possible coordinates of point A?
Answer:
It is given that
Point B has coordinates (2, 1). The x-coordinate of point A is -10. The distance between point A and point B is 15 units
Now,
Let the coordinates of A be:
(x, y) = (-10, y)
Now,
Compare the points A and B with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points A and B = \(\sqrt{(-10 – 2)^{2} + (y – 1)^{2}}\)
15 = \(\sqrt{12^{2} + (y – 1)^{2}}\)
15 = \(\sqrt{144 + (y – 1)^{2}}\)
Now,
Squaring on both sides
So,
144 + (y – 1)² = 225
(y 1)² = 225 – 144
(y – 1)² = 81
y – 1 = \(\sqrt{81}\)
y – 1 = 9 (or) y – 1 = -9
y = 9 + 1 (or) y = -9 + 1
y = 10 (or) y = -8
Hence, from the above,
We can conclude that the possible coordinates of A are: (-10, 10), and (-10, -8)
Question 13.
Higher-Order Thinking ∆EFG and ∆HIJ have the same perimeter and side lengths. The coordinates are E(6, 2), F(9, 2), G(8, 7), H(0, 0), and I(0, 3). What are the possible coordinates of point J?
Answer:
It is given that
∆EFG and ∆HIJ have the same perimeter and side lengths. The coordinates are E(6, 2), F(9, 2), G(8, 7), H(0, 0), and I(0, 3)
So,
According to the side lengths,
EF = HI, FG = IJ, and GE = JH
So,
EF² = HI², FG²= JI², and GE² = JH²
Now,
Let the unknown vertex be J (x, y)
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points E and F = \(\sqrt{(9 – 6)^{2} + (2 – 2)^{2}}\)
= \(\sqrt{3^{2} + 0^{2}}\)
= \(\sqrt{9 + 0}\)
= 3 units
The distance between the points F and G = \(\sqrt{(8 – 9)^{2} + (7 – 2)^{2}}\)
= \(\sqrt{1^{2} + 5^{2}}\)
= \(\sqrt{1 + 25}\)
= 5.09 units
The distance between the points G and E = \(\sqrt{(8 – 6)^{2} + (7 – 2)^{2}}\)
= \(\sqrt{2^{2} + 5^{2}}\)
= \(\sqrt{4 + 25}\)
= 5.38 units
Now,
The distance between the points H and I = \(\sqrt{(0 – 0)^{2} + (3 – 0)^{2}}\)
= \(\sqrt{3^{2} + 0^{2}}\)
= \(\sqrt{9 + 0}\)
= 3 units
The distance between the points I and J = \(\sqrt{(x – 0)^{2} + (y – 3)^{2}}\)
5.09 = \(\sqrt{x^{2} + (y – 3)^{2}}\)
Squaring on both sides
So,
x² + (y – 3)² = 25.90 units
The distance between the points J and H = \(\sqrt{(x – 0)^{2} + (y – 0)^{2}}\)
5.38 = \(\sqrt{x^{2} + y^{2}}\)
Squaring on both sides
So,
x² + y² = 28.94 units
Now,
28.94 – y² + (y – 3)² = 25.90
y² + 9 – 6y – y² = 25.90 – 28.94
9 – 6y = -3.04
-6y = -3.04 – 9
6y = 12.04
y = 2
Now,
Substitute the value of y in eq 2
x² + 4 = 28.94
x² = 24.94
x = 4.99 (or) x = -4.99
Hence, from the baove,
We can conclude that the missing vertex is: J (4.99, 2) or J (-4.99, 2)
b. Explain why there can be different possibilities for the coordinates for point J.
Answer:
Assessment Practice
Question 14.
Find the distance, in units, between P and R. Round to the nearest tenth.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The points are:
P (5, 10), and R (12, 14)
Now,
Compare the points P and R with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points P and R = \(\sqrt{(14 – 10)^{2} + (12 – 5)^{2}}\)
= \(\sqrt{4^{2} + 7^{2}}\)
= \(\sqrt{16 + 49}\)
= 8.1 units
Hence, from the above,
We can conclude that the distance between P and R is: 8.1 units
Question 15.
Find the distance, in units, between A(1, 5) and B(5.5, 9.25). Round to the nearest tenth.
Answer:
The given points are:
A (1, 5), and B (5.5, 9.25)
Now,
Compare the points A and B with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points A and B = \(\sqrt{(9.25 – 5)^{2} + (5.5 – 1)^{2}}\)
= \(\sqrt{4.25^{2} + 4.5^{2}}\)
= \(\sqrt{18.06 + 20.25}\)
= 6.2 units
Hence, from the above,
We can conclude that the distance between points A and B is: 6.2 units
Topic 7 REVIEW
Topic Essential Question
How can you use the Pythagorean Theorem to solve problems?
Answer:
Step 1:
Draw a right triangle and then read through the problems again to determine the length of the legs and the hypotenuse. Step 2:
Use the Pythagorean Theorem (a2 + b2 = c2) to write an equation to be solved.
Step 3:
Simplify the equation by distributing and combining like terms as needed.
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.
Vocabulary
The converse of the Pythagorean Theorem
hypotenuse
leg
proof
Pythagorean Theorem

Answer:

Use Vocabulary in Writing
All faces of the figure are rectangles. Explain how to find the length of d. Use vocabulary terms in your description.
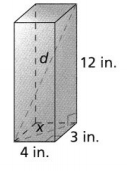
Answer:
The given figure is:

From the given figure,
We can observe that there are 2 right triangles
Now,
For the first right triangle,
The given side lengths are:
a = 3, b = 4, and c = x
Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
So,
x² = 3² + 4²
x² = 9 + 16
x² = 25
x = \(\sqrt{25}\)
x = 5
Now,
For the second right triangle,
a = 5, b = 12, and c = d
So,
d² = 5² + 12²
d² = 25 + 144
d² = 169
d = \(\sqrt{169}\)
d = 13
Hence, from the above,
We can conclude that the length of d is: 13 units
Concepts and Skills Review
Lesson 7.1 Understand the Pythagorean Theorem
Quick Review
The Pythagorean Theorem states that, in a right triangle, the sum of the squares of the lengths of the legs, a and b, is equal to the square of the length of the hypotenuse, c. So, a2 + b2 = c2.
Example
Find the length of the hypotenuse of a triangle with legs of 7 meters and 24 meters.
Answer:
Substitute 7 for a and 24 for b. Then solve for c.
a2 + b2 = c2
49 + 576 = c2
\(\sqrt {625}\) = C
The length of the hypotenuse is 25 meters.
Practice
Question 1.
Find the length of the hypotenuse.
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the side lengths
So,
c² = 12² + 5²
c² = 144 + 25
c² = 169
c = \(\sqrt{169}\)
c = 13
Hence, from the above,
We can conclude that the length of the hypotenuse is: 13 cm
Question 2.
Find the unknown side length. Round to the nearest tenth.
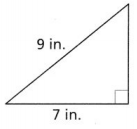
Answer:
The given right triangle is:

Now,
We know that,
According to the Pythagorean Theorem,
c² = a² + b²
Where,
c is the hypotenuse
a and b are the side lengths
So,
9² = 7² + b²
b² = 81 – 49
b² = 32
b = \(\sqrt{32}\)
b = 5.65
Hence, from the above,
We can conclude that the length of the hypotenuse is: 5.65 in.
Lesson 7.2 Understand the Converse of the Pythagorean Theorem
Quick Review
For a triangle with side lengths a, b, and c, if a2 + b2 = c2, then the triangle is a right triangle by the Converse of the Pythagorean Theorem.
Example
Is a triangle with side lengths of 8 m, 15 m, and 17 m a right triangle? Explain.
Answer:
Substitute 8 for a, 15 for b, and 17 for c.
a2 + b2 \(\underline{\underline{?}}\) c2
82 + 152 \(\underline{\underline{?}}\) 172
289 = 289 ✓
Because a2 + b2 = c2, the triangle is a right triangle.
Practice
Question 1.
Is the triangle a right triangle? Explain.

Answer:
The given triangle is:

Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²
then, the given triangle is a right triangle
So,
Now,
37² = 35² + 12²
1,369 = 1,225 + 144
1,369 = 1,369
So,
The condition c² = a² + b² is true
Hence, from the above,
We can conclude that the given triangle is a right triangle
Question 2.
A triangle has side lengths of 1.5 inches, 2 inches, and 3 inches. Is the triangle a right triangle? Explain.
Answer:
It is given that
A triangle has side lengths of 1.5 inches, 2 inches, and 3 inches
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²
then, the given triangle is a right triangle
We know that,
The longest side is the hypotenuse
So,
Now,
3² = (1.5)² + 2²
9 = 2.25 + 4
9 = 6.25
So,
The condition c² = a² + b² is false
Hence, from the above,
We can conclude that the given triangle is not a right triangle
Question 3.
A triangle has side lengths of 9 feet, 40 feet, and 41 feet. Is the triangle a right triangle? Explain
Answer:
It is given that
A triangle has side lengths of 9 feet, 40 feet, and 41 feet
Now,
We know that,
According to the converse of the Pythagorean Theorem,
If
c² = a² + b²
then, the given triangle is a right triangle
We know that,
The longest side is the hypotenuse
So,
Now,
41² = 40² + 9²
1,681 = 1,600 + 81
1,681 = 1,681
So,
The condition c² = a² + b² is true
Hence, from the above,
We can conclude that the given triangle is a right triangle
Lesson 7.3 Apply the Pythagorean Theorem to Solve Problems
Quick Review
The Pythagorean Theorem can be used to find unknown side lengths of an object that is shaped like a right triangle. It also can be used to find diagonal measures in certain two-dimensional and three-dimensional objects.
Example
A shipping box is 20 inches long along the diagonal of its base. Each diagonal of the box is 29 inches long. How tall is the box?
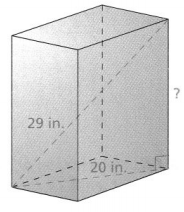
Answer:
Substitute 20 for a and 29 for c. Then solve for b.
a2 + b2 = c2
202 + b2 = 292
400 + b2 = 841
b = \(\sqrt {441}\)
The height of the shipping box is 21 inches.
Practice
Question 1.
A basketball court is in the shape of a rectangle that is 94 feet long and 50 feet wide. What is the length of a diagonal of the court? Round to the nearest tenth.
Answer:
It is given that
A basketball court is in the shape of a rectangle that is 94 feet long and 50 feet wide
We know that,
By drawing a diagonal in the rectangle, it will become 2 right triangles
The diagonal will be the hypotenuse of the right triangle
Now,
We know that,
According to the Pythagorean Theorem,
c² = a²+ b²
Where,
c is the length of the diagonal
a and b are the side lengths
So,
c² = 94²+ 50²
c²= 8,836 + 2,500
c² = 11,336
c = \(\sqrt{11,336}\)
c = 106.4 feet
hence, from the above,
We can conclude that the length of the diagonal is: 106.4 feet
Question 2.
A packaging box for a metal rod is 7.5 inches along a diagonal of the base. The height of the box is 18 inches. What is the length of a diagonal of the box?
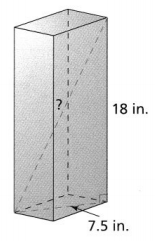
Answer:
It is given that
A packaging box for a metal rod is 7.5 inches along a diagonal of the base. The height of the box is 18 inches.
Now,
From the given figure,
We can observe that it looks like a right triangle
Now,
We know that,
According to the Pythagorean Theorem,
c² = a²+ b²
Where,
c is the length of the diagonal
a and b are the side lengths
So,
c² = 18² + (7.5)²
c²= 324 + 56.25
c² = 380.25
c = \(\sqrt{380.25}\)
c = 19.5 inches
Hence, from the above,
We can conclude that the length of the diagonal of the box is: 19.5 inches
Lesson 7.4 Find Distance in the Coordinate Plane
Quick Review
The Pythagorean Theorem can be used to find the distance between any two points on the coordinate plane.
Example
Find the distance between the two points on the coordinate plane. Round to the nearest tenth.

Answer:
Draw a right triangle. Determine the lengths of its legs.
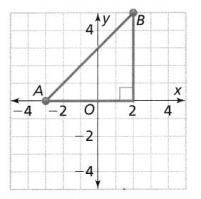
The length of the horizontal leg is 5 units.
The length of the vertical leg is 5 units.
Use the relationship a2 + b2 = c2. Substitute 5 for a and 5 for b. Then solve for C.
a2 + b2 = -2
52 + 52 = c2
25 + 25 = c2
50 = c2
\(\sqrt {50}\) = C
7.1 ≈ c
The distance between the two points is about 7.1 units.
Practice
Question 1.
Points C and D represent the location of two parks on a map. Find the distance between the parks if the length of each unit on the grid is equal to 25 miles. Round to the nearest mile.
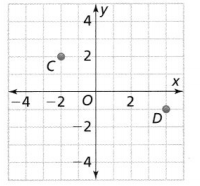
Answer:
It is given that
Points C and D represent the location of two parks on a map
Now,
The given coordinate plane is:

From the given coordinate plane,
The points are:
C (-2, 2), and D (4, -1)
Now,
Compare the points C and D with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points C and D = \(\sqrt{(-1 – 2)^{2} + (4 + 2)^{2}}\)
= \(\sqrt{3^{2} + 6^{2}}\)
= \(\sqrt{9 + 36}\)
= 6.70 units
It is given that the length of each unit in the grid is: 25 miles
So,
The distance between the points C and D = 6.25 × 25
= 156.25 miles
Hence, from the above,
We can conclude that the distance between points C and D is: 156.25 miles
Question 2.
Find the perimeter of ∆ABC. Round to the nearest tenth.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔABC are:
A (1, 2), B (7, 9), and C (7, 2)
We know that,
The perimeter of a triangle is the sum of all the side lengths of a triangle
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
From the given coordinate plane,
We know that,
In ∆ABC,
AC and BC are the side lengths
AB is the hypotenuse
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points A and C = \(\sqrt{(2 – 2)^{2} + (7 – 1)^{2}}\)
= \(\sqrt{0^{2} + 6^{2}}\)
= \(\sqrt{36 + 0}\)
= 6 units
The distance between the points B and C (BC) = \(\sqrt{(7 – 7)^{2} + (-2 + 9)^{2}}\)
= \(\sqrt{0^{2} + 7^{2}}\)
= \(\sqrt{0 + 49}\)
= 7 units
The distance between the points A and B (AB) = \(\sqrt{(9 – 2)^{2} + (7 – 1)^{2}}\)
= \(\sqrt{7^{2} + 6^{2}}\)
= \(\sqrt{49 + 36}\)
= 9.21 units
So,
The perimeter of ∆ABC = AB + BC + AC
= 6 + 7 + 9.21
= 22.2 units
Hence, from the above,
We can conclude that the perimeter of ∆ABC is about 22.2 units
Question 3.
Triangle JKL is an equilateral triangle with two of its vertices at points J and K. What are the coordinates of point L? Round to the nearest tenth as needed.
Answer:
It is given that
Triangle JKL is an equilateral triangle with two of its vertices at points J and K
Now,
The given coordinate plane is:

Now,
From the given coordinate plane,
The two vertices of ΔJKL are:
J (3, 2), K (9, 2)
Now,
Let the third vertex be L (x, y)
We know that,
In an equilateral triangle, all the side lengths are the same
So,
JK = KL = JL
JK² = KL² = JL²
So,
Now,
Compare the given points with (x1, y1), (x2, y2)
Now,
We know that,
The distance between two points = √(x2– x1) + (y2 – y1)²
So,
The distance between the points J and K = \(\sqrt{(9 – 3)^{2} + (2 – 2)^{2}}\)
= \(\sqrt{0^{2} + 6^{2}}\)
= \(\sqrt{36 + 0}\)
= 6 units
The distance between the points K and L = \(\sqrt{(x – 9)^{2} + (y – 2)^{2}}\)
6= \(\sqrt{(x – 9)^{2} + (y – 2)^{2}}\)
Squaring on both sides
So,
(x – 9)² + (y – 2)² = 36
The distance between the points J and L = \(\sqrt{(x – 3)^{2} + (y – 2)^{2}}\)
6= \(\sqrt{(x – 3)^{2} + (y – 2)^{2}}\)
Squaring on both sides
So,
(x – 3)² + (y – 2)² = 36
Now,
(x – 9)² + 36 – (x – 3)² = 36
(x – 9)² = (x – 3)²
x² + 81 – 18x = x² + 9 – 6x
18x – 6x = 81 – 9
12x = 72
x = \(\frac{72}{12}\)
x = 6
So,
Substitute the value of x in eq (2)
(6 – 3)² + (y – 2)² = 36
(y – 2)² = 36 – 9
y – 2 = \(\sqrt{27}\)
y = 7.2
Hence, from the above,
We can conclude that the third vertex is: L (6, 7.2)
Topic 7 Fluency Practice
Riddle Rearranging
Solve each equation. Then arrange the answers in order from least to greatest. The letters will spell out the answer to the riddle below.
I can… solve multistep equations.

Why did the coffee shop server love the job? Because there were so

Answer:
The Ascending order of the solutions of the equations is:
M < N < Y < P < A < E < R < K < S