Go through the enVision Math Common Core Grade 8 Answer Key Topic 6 Congruence and Similarity and finish your homework or assignments.
enVision Math Common Core 8th Grade Answers Key Topic 6 Congruence And Similarity
Topic Essential Question
How can you show that two figures are either congruent or similar to one another?
Answer:
When two line segments have the same length, we can say that they are congruent. When two figures have the same shape and size, we can say that the two figures are congruent. These two triangles are congruent. We can also say that their side lengths are the same and that their angle measures are the same
3-ACT MATH

Tricks of the Trade
All kinds of objects in nature have symmetry: beehives, pine cones, butterflies, and snowflakes, to name a few. If you look closely, you will start to see patterns left and right. Think about this during the 3-Act Mathematical Modeling lesson.

Topic 6 ënVision STEM Project
Did You Know?
Trees provide wood for cooking and heating for half of the world’s population.

As trees grow, carbon dioxide is removed from the atmosphere for photosynthesis. Forests are called “carbon sinks” because one acre of forest absorbs six tons of carbon dioxide and puts out four tons of oxygen.

Trees provide lumber for buildings, tools, and furniture. Other products include rubber, sponges, cork, paper, chocolate, nuts, and fruit.
About 30% of the land is covered by forests.

Forests are now being managed to preserve wildlife and old-growth forests, protect biodiversity, safeguard watersheds, and develop recreation, as well as extract timber.
Forests also need to be managed to prevent raging wildfires, invasive species, overgrazing, and disease.

Your Task: Forest Health
The proper management of forests is a growing science. You and your classmates will learn about forest health indicators and use what you know about similar triangles and ratios to gather and interpret data in order to assess the health of a forest.

Topic 6 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
adjacent angles
complementary angles
supplementary angles
vertical angles
Question 1.
_________ have a sum of 90°.
Answer:
We know that,
The “Complementary angles” have a sum of 90°
Hence, from the above,
We can conclude that the best term to complete the given definition is: Complementary angles
Question 2.
_________ share the same ray.
Answer:
We know that,
The “Adjacent Angles” share the same ray
Hence, from the above,
We can conclude that the best term to complete the given definition is: Adjacent angles
Question 3.
_________ are pairs of opposite angles made by intersecting lines.
Answer:
We know that,
The “Vertical Angles” are pairs of opposite angles made by intersecting lines
Hence, from the above,
We can conclude that the best term to complete the given definition is: Vertical angles
Question 4.
__________ have a sum of 180°
Answer:
We know that,
The “Supplementary Angles” have a sum of 180°
Hence, from the above,
We can conclude that the best term to complete the given definition is: Supplementary angles
Multiplying Real Numbers
Simplify the expression.
Question 5.
5 × 2 = ________
Answer:
The given expression is:
5 × 2
Hence, from the above,
We can conclude that
5 × 2 = 10
Question 6.
6 × \(\frac{1}{2}\) = ________
Answer:
The given expression is:
6 × \(\frac{1}{2}\)
So,
6 × \(\frac{1}{2}\)
= \(\frac{6}{2}\)
= 3
Hence, from the above,
We can conclude that
6 × \(\frac{1}{2}\) = 3
Question 7.
12 × \(\frac{1}{3}\) = ________
Answer:
The given expression is:
12 × \(\frac{1}{3}\)
So,
12 × \(\frac{1}{3}\)
= \(\frac{12}{3}\)
= 4
Hence, from the above,
We can conclude that
12 × \(\frac{1}{3}\) = 4
Identifying Points on a Coordinate Plane
Name the location of the point.
Answer:
The given coordinate plane is:

From the given coordinate plane,
We can observe that
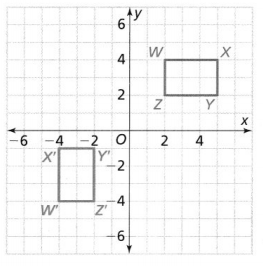
Question 8.
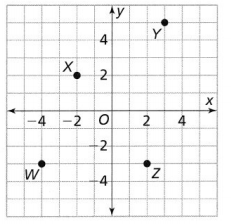
point W
Answer:
From the given coordinate plane,
We can observe that point W lies where both the x-axis and y-axis are negative
Hence, from the above,
We can conclude that point W lies in the third quadrant
Question 9.
point X
Answer:
From the given coordinate plane,
We can observe that point X lies where the x-axis is negative and the y-axis is positive
Hence, from the above,
We can conclude that point X lies in the second quadrant
Question 10.
point Y
Answer:
From the given coordinate plane,
We can observe that point Y lies where both the x-axis and y-axis are positive
Hence, from the above,
We can conclude that point Y lies in the first quadrant
Question 11.
point Z
Answer:
From the given coordinate plane,
We can observe that point Z lies where the x-axis is positive and the y-axis is negative
Hence, from the above,
We can conclude that point Z lies in the fourth quadrant
Supplementary Angles
The angles are supplementary. Find the missing angle measure.
Question 12.
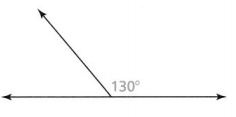
Answer:
The given figure is:

We know that,
The sum of the supplementary angles is: 180°
Now,
Let the missing angle measure be: x°
So,
x° + 130° = 180°
x° = 180° – 130°
x° = 50°
Hence, from the above,
We can conclude that the missing angle measure is: 50°
Question 13.
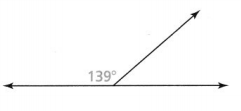
Answer:
The given figure is:

We know that,
The sum of the supplementary angles is: 180°
Now,
Let the missing angle measure be: x°
So,
x° + 139° = 180°
x° = 180° – 139°
x° = 41°
Hence, from the above,
We can conclude that the missing angle measure is: 41°
Language Development
Complete the graphic organizer with an illustration for each transformation. Write either congruent or similar to make the given statement true.


Answer:

Topic 6 PICK A PROJECT
PROJECT 6A
How might an artist use mathematics?
PROJECT: WRITE A BIOGRAPHY

PROJECT 6B
What geometric shapes do you see around you?
PROJECT: RECORD A VIDEO ABOUT SIMILAR FIGURES

PROJECT 6C
What different types of bridges have you crossed?
PROJECT: BUILD A MODEL OF A TRUSS BRIDGE

PROJECT 6D
What shapes tessellate?
PROJECT: DESIGN A TESSELLATION

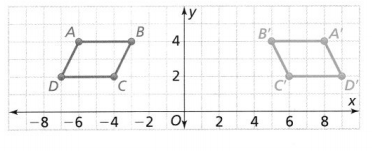
Lesson 6.1 Analyze Translations
Solve & Discuss It!
Ashanti draws a trapezoid on the coordinate plane and labels it in Figure 1. Then she draws Figure 2. How can she determine whether the figures have the same side lengths and the same angle measures?
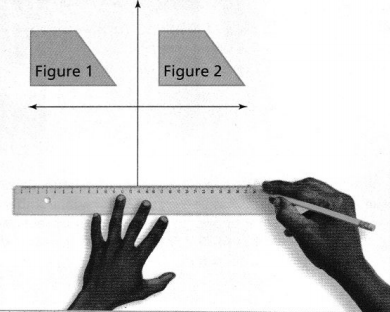
I can… translate two-dimensional figures.
Answer:
It is given that
Ashanti draws a trapezoid on the coordinate plane and labels it in Figure 1. Then she draws Figure 2.
The given figure is:

From the figure,
We can observe that the first figure was translated or moved to the right by some units and became a second figure
We know that,
A “Translation” is a transformation that moves every point in a figure the same distance in the same direction
We know that,
The pre-image and image in the “Translation” are similar
We know that,
Two figures are said to be similar if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal.
Hence, from the above,
We can conclude that by using the “Translation” property, she can determine whether the figures have the same side lengths and the same angle measures
Focus on math practices
Be Precise How do you know that the method you described shows whether the side lengths and angle measures are equal? Explain.
Answer:
We know that,
A “Translation” is a transformation that moves every point in a figure the same distance in the same direction
We know that,
The pre-image and image in the “Translation” are similar
We know that,
Two figures are said to be similar if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal.
Essential Question
How does a translation affect the properties of a two-dimensional figure?
Answer:
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
Try It!
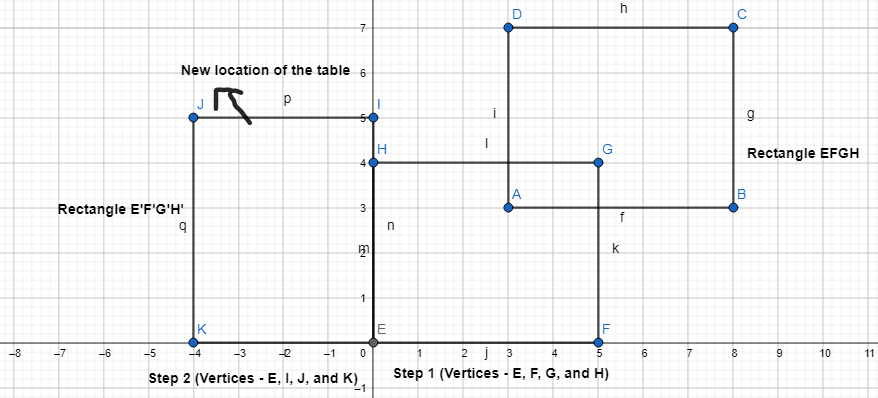
The clients also want the small table below the window moved 5 feet to the right. Where should the architect place the small table? Draw the new location of the table on the plan.
Answer:
It is given that
The clients also want the small table below the window moved 5 feet to the right
Now,
The original plan is:
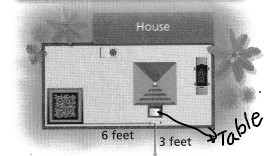
From the above plan,
We can observe that the window is at most right
So,
When we move the table,
The new location of the table will be below the window
Hence,
The location of the table on the new plan is:

Convince Me!
An equilateral triangle with side lengths 5 inches is translated 3 units down and 2 units right. Describe the shape and dimensions of the translated figure.
Answer:
It is given that
An equilateral triangle with side lengths 5 inches is translated 3 units down and 2 units right.
We know that,
In an equilateral triangle, all the side lengths are equal
Now,
Let the dimensions of an equilateral triangle be (x1, y1), (x2, y2), and (x3, y3)
So,
The dimensions of the translated figure are: (x1 + 2, y1 – 3), (x2 + 2, y2 – 3), and (x3 + 2, y3 – 3)
Now,
Let us suppose the dimensions of an equilateral to be:
(1, 1), (1, 6), and (5, 3)
So,
The dimensions of the translated equilateral triangle are:
(3, -2), (3, 3), and (7, 0)
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way
So,
The shape of the translated figure remains the same as the original figure
Hence,
The representation and shape of the original and translated equilateral triangles are:
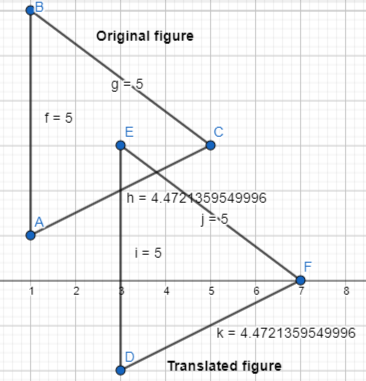
Try It!
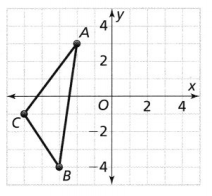
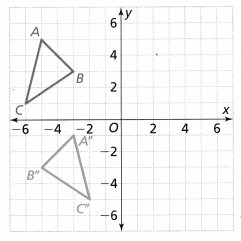
Triangle ABC is translated 5 units right and 1 unit down. Graph and label the image A’ B’C’. If m∠A = 30° in ΔABC, then what is m∠A in ΔA’B’C’?
Answer:
The given figure is:

From the given figure,
The dimensions of ΔABC are:
A (-2, 3), B (-3, -4), and C (-5, -1)
Now,
Let the dimensions of an equilateral triangle be (x1, y1), (x2, y2), and (x3, y3)
So,
The dimensions of the translated figure are: (x1 + 5, y1 – 1), (x2 + 5, y2 – 1), and (x3 + 5, y3 – 1)
So,
The dimensions of the translated triangle (A’B’C’) are:
A (3, 2), B (2, -5), and C (0, -2)
We know that,
A translated figure has the same shape as the original shape i.e, the lengths and the angles of the translated figure are also the same as the original figure
So,
m∠A in Triangle ABC = m∠A in Triangle A’B’C’ = 30°
Hence,
The representation of the original and translated triangles are:
KEY CONCEPT
A translation, or slide, is a transformation that moves Preimage to every point of a figure the same distance and the same direction.
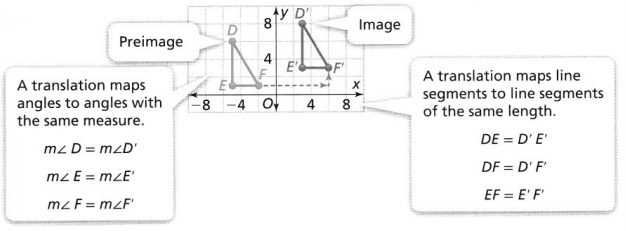
Do You Understand?
Question 1.
Essential Question How does a translation affect the properties of a two-dimensional figure?
Answer:
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
Question 2.
Construct Arguments Triangle L’M’N’ is the image of triangle LMN after a translation. How are the side lengths and angle measures of the triangles related? Explain.
Answer:
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
Hence, from the above,
We can conclude that
The side lengths and the angle measures of Triangle L’M’N’ is the same as The side lengths and the angle measures of Triangle LMN
Question 3.
Generalize Sanjay determined that one vertex of a figure was mapped to its image by translating the point 2 units left and 7 units down. What is the rule that maps the other vertices of the figure to their images?
Answer:
It is given that
Sanjay determined that one vertex of a figure was mapped to its image by translating the point 2 units left and 7 units down
Now,
Now,
Let the dimensions of any vertex of the given be (x, y)
So,
The dimensions of any vertex of the translated figure are: (x – 2, y + 7)
Hence, from the above,
We can conclude that
The rule that maps the other vertices of the figure to their images is: (x – 2, y – 7)
Do You Know How?
In 4-6, use the coordinate plane.
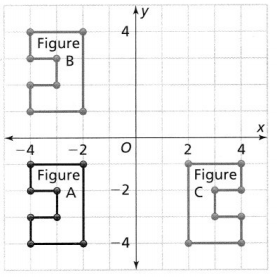
Question 4.
Which figure is a translation of Figure A? Explain
Answer:
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
So,
When we observe the coordinate plane,
We can see that A and C have the same shape i.e., have the same length and the same angle
Hence, from the above,
We can conclude that
Figure C is a translation of Figure A
Question 5.
Graph the translation of Figure A 3 units right and 4 units up.
Answer:
From the given coordinate plane,
The dimensions of Figure A are:
(-2, -1), (-4, -1), (-4, -2), (-3, -2), (-3, -3), (-4, -3), (-4, -4), and (-2, -4)
So,
The rule that maps the vertices of the given figure to their images is: (x + 3, y + 4)
So,
The vertices of the image are:
(1, 3), (-1, 3), (-1, 2), (0, 2), (0, 1), (-1, 1), (-1, 0), and (1, 0)
Hence,
The representation of Figure A and its translated figure is:
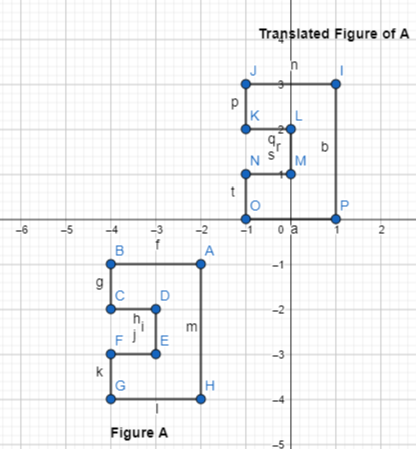
Question 6.
Describe the translation needed to move Figure B to the same position as the image from Item 5.
Answer:
From the given coordinate plane,
The dimensions of figure B are:
(-2, 4), (-4, 4), (-4, 3), (-3, 3), (-3, 2), (-4, 2), (-4, 1), and (-2, 1)
Hence,
The translation needed to move figure B to the same position as the image from Item 5 is:
The X-axis: Translate 3 units right
The Y-axis: Translate 1 unit down
Practice & Problem Solving
Question 7.
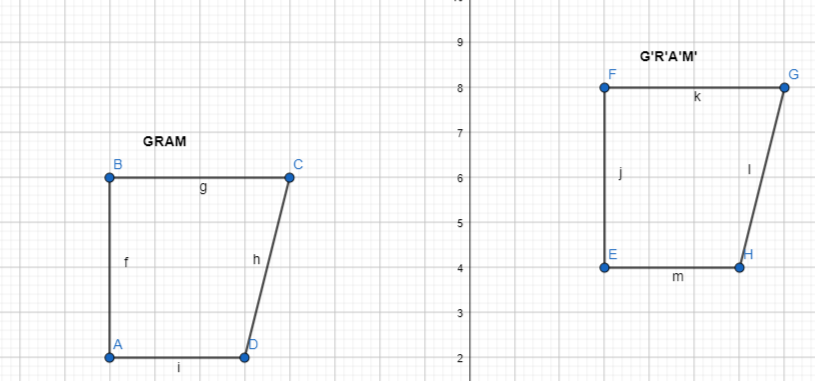
Graph G’R’A’M’, the image of GRAM after a translation 11 units right and 2 units up.
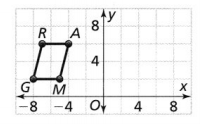
Answer:
The given coordinate plane is:

From the given coordinate plane,
The dimensions of GRAM are:
G (-8, 2), R (-8, 6), A (-4, 6), and M (-5, 2)
So,
After a translation of 11 units right and 2 units up,
The dimensions of G’R’A’M’ are:
G’ (-8 + 11, 2 + 2), R’ (-8 + 11, 6 + 2), A’ (-4 + 11, 6 + 2), and M’ (-5 + 11, 2 + 2)
So,
G’ (3, 4), R’ (3, 8), A’ (7, 8), and M’ (6, 4)
Hence,
The representation of GRAM and its image G’R’A’M’ is:
Question 8.
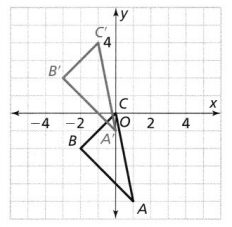
∆A’ B’ C’ is a translation of ∆ABC. Describe the translation.
Answer:
The given coordinate plane is:

From the coordinate plane,
The dimensions of ΔABC are:
A (1, -5), B (-2, -2), and C (0, 0)
Now,
The dimensions of ΔA’B’C’ are:
A’ (0, -1), B’ (-3, 2), and C’ (-1, 4)
So,
By observing the dimensions of ΔABC and ΔA’B’C’,
The translation between ΔABC and ΔA’B’C is:
The x-axis: Translate 1 unit left
The y-axis: Translate 4 units up
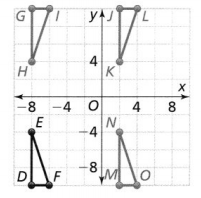
Question 9.
Which triangle is the image of ∆DEF after a translation? Describe the translation.
Answer:
The given figure is:

We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
So,
From the given figure,
We can observe that
ΔMNO has the same shape as ΔDEF
So,
The image of ΔDEF is: ΔMNO
Now,
The dimensions of ΔDEF are:
D (-8, -10), F (-6, -10), and E (-8, -4)
Now,
The dimensions of ΔMNO are:
M (2, -10), O (4, -10), and N (2, -4)
So,
By observing the dimensions of ΔDEF and ΔMNo,
The translation between ΔDEF and ΔMNO is:
The x-axis: Translate 10 units right
The y-axis: No Translation required
Question 10.
The vertices of figure QRST are translated 3 units left and 11 units down to form figure Q’R’S’T’. Explain the similarities and differences between the two figures.
Answer:
It is given that
The vertices of figure QRST are translated 3 units left and 11 units down to form figure Q’R’S’T’.
Hence,
The similarities between figure QRST and figure Q’R’S’T’ are:
a. The two figures have the same side length
b. The two figures have the same angle measure
c. The two figures have the same shape
The differences between figure QRST and figure Q’R’S’T’ are:
a. Different dimensions of the vertices of QRST and Q’R’S’T’
b. Different positions of figure QRST and figure Q’R’S’T’
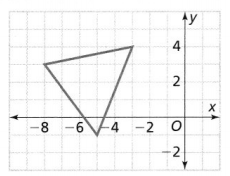
Question 11.
Graph the image of the given triangle after a translation of 3 units right and 2 units up.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The dimensions of the given triangle are:
(-3, 4), (-5, -1), and (-8, 3)
Now,
After a translation 3 units right and 2 units up,
The dimensions of the given triangle are:
(-3 + 3, 4 + 2), (-5 + 3, -1 + 2), and (-8 + 3, 3 + 2)
(0, 6), (-2, 1), and (-5, 5)
Hence,
The representation of the given triangle and its image is:
Question 12.
Quadrilateral P’Q’R’ S’ is the image of quadrilateral PQRS after a translation.
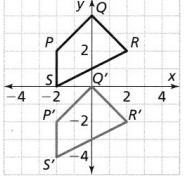
Answer:
It is given that
Quadrilateral P’Q’R’ S’ is the image of quadrilateral PQRS after a translation.
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
a. If the length of side PQ is about 2.8 units, what is the length of side P’ Q’?
Answer:
It is given that
The length of the side PQ is about 2.8 units
Hence, from the above,
We can conclude that the length of side P’Q’ is also about 2.8 units
b. If m∠R = 75°, what is m∠R’?
Answer:
It is given that
m∠R = 75°
Hence, from the above,
We can conclude that
m∠R’ = 75°
Question 13.
Higher-Order Thinking A farmer has a plot of land shaped like the figure in the graph. There is another identical plot of land 120 yards east and 100 yards north of the original plot.
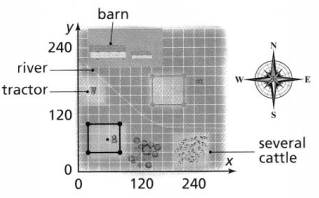
a. Draw the image after the given translation.
Answer:
It is given that
A farmer has a plot of land shaped like the figure in the graph. There is another identical plot of land 120 yards east and 100 yards north of the original plot.
Now,
The given plot of land is:

Now,
From the given plot of land,
The dimensions of land are:
(0, 0), (0, 300), (300, 0), and (300, 300)
Now,
After the translation of 120 units right and 100 units up,
The dimensions of the identical plot are:
(0 + 120, 0 + 100), (0 + 120, 300 + 100), (300 + 120, 0 + 100), and (300 + 120, 300 + 100)
(120, 100), (120, 400), (420, 100), and (420, 400)
Hence,
The representation of the plot and its image after the translation is:
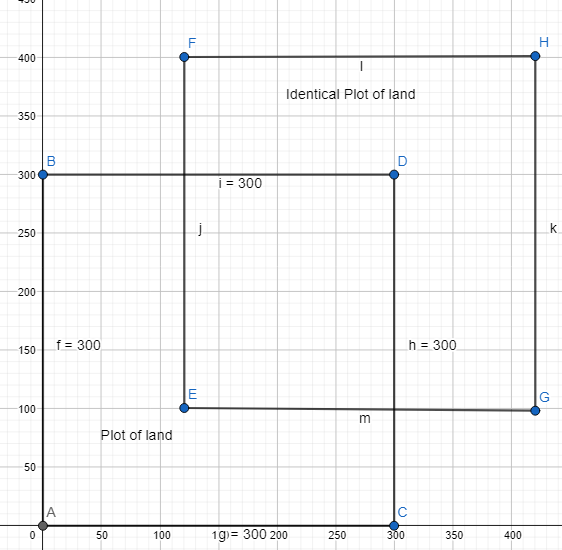
b. Find the combined area of the 2 plots in square yards.
Answer:
From part (a),
We can observe that the shape of the plot of land and its identical is like a square
We know that,
The square has the equal side lengths
Now,
From part (a),
We can observe that the side length of the plot of land and its identical is: 300 yards
Now,
We know that,
The area of square = Side²
So,
The area of the plot of land = 300²
= 90,000 yard²
The area of the identical plot of land = 300²
= 90,000 yard²
So,
The combined area of the 2 plots = 90,000 + 90,000
= 1,80,000 yard²
Hence, from the above,
We can conclude that the combined area of the 2 plots is: 1,80,000 yard²
Assessment Practice
Question 14.
What is true about the preimage of a figure and its image created by a translation? Select all that apply.
☐ Each point in the image moves the same distance and direction from the preimage.
☐ Each point in the image has the same x-coordinate as the corresponding point in the preimage.
☐ Each point in the image has the same y-coordinate as the corresponding point in the preimage.
☐ The preimage and the image are the same size.
☐ The preimage and the image are the same shape.
Answer:
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
Hence,
The statements that are true about the preimage of a figure and its image created by a translation are:

Question 15.
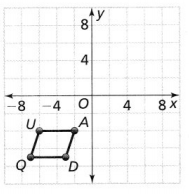
The vertices of parallelogram QUAD are Q(-7, -7), U(-6, -4), A(-2,-4), and D(-3, -7).
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The dimensions of the parallelogram QUAD are:
Q (-7, -7), U (-6, -4), A (-2, -4), and D (-3, -7)
Now,
After the translation of 11 units right and 9 units up,
The dimensions of the parallelogram QUAD are:
Q’ (-7 + 11, -7 + 9), U’ (-6 + 11, -4 + 9), A’ (-2 + 11, -4 + 9), and D’ (-3 + 11, -7 + 9)
Q’ (4, 2), U’ (5, 5), A’ (9, 5), and D’ (8, 2)
PART A
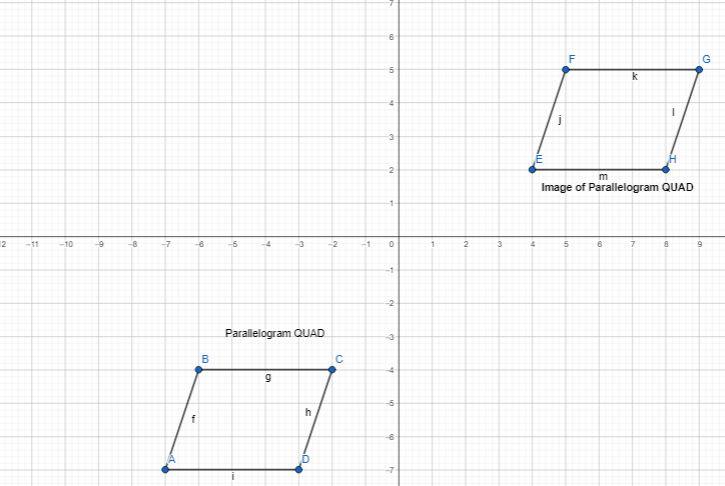
Graph and label the image of QUAD after a translation 11 units right and 9 units up.
Answer:
The representation of the parallelogram QUAd and its image is:
PART B
If m∠U = 110°, what is m∠ U’?
Answer:
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
Hence, from the above,
We can conclude that
m∠U’ = 110°
PART C
If the length of side UA is 4 units, what is the length of side U’ A’?
Answer:
We know that,
When you translate something in geometry, you’re simply moving it around. You don’t distort it in any way. If you translate a segment, it remains a segment, and its length doesn’t change. Similarly, if you translate an angle, the measure of the angle doesn’t change.
Hence, from the above,
We can conclude that
The length of the side U’ A’ is: 4 units
Lesson 6.2 Analyze Reflections
Solve & Discuss It!
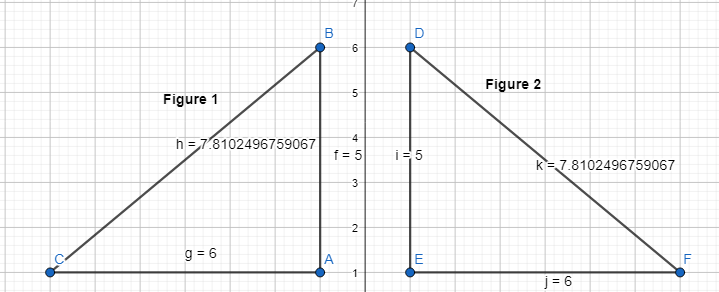
Dale draws a triangle on grid paper and labels it in Figure 1. Then using his pencil as a guide, he draws another triangle directly on the opposite side of the pencil so that the vertical side is now one square to the right of the pencil instead of one square to the left of the pencil. He labels this triangle in Figure 2. How are the figures the same? How are they different?
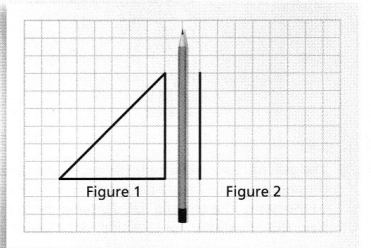
I can… reflect two-dimensional figures.
Answer:
Dale draws a triangle on grid paper and labels it in Figure 1. Then using his pencil as a guide, he draws another triangle directly on the opposite side of the pencil so that the vertical side is now one square to the right of the pencil instead of one square to the left of the pencil. He labels this triangle in Figure 2.
Hence,
The representation of Figure 1 and Figure 2 is:
So,
From the above representation,
The similarities between Figure 1 and Figure 2 are:
a. Both the figures have the same side lengths
b. Both the figures have the same angle measures
c. Both the figures have the same size
d. Both the figures have the same distance
The differences between Figure 1 and Figure 2 are:
a. The positions of both figures are different
b. The orientations of both figures are different
c. The directions of both the figures are different
Look for Relationships
What do you notice about the size, shape, and direction of the two figures?
Answer:
The similarities between Figure 1 and Figure 2 are:
a. Both the figures have the same side lengths
b. Both the figures have the same angle measures
c. Both the figures have the same size
d. Both the figures have the same distance
The differences between Figure 1 and Figure 2 are:
a. The positions of both figures are different
b. The orientations of both figures are different
c. The directions of both the figures are different
Focus on math practices
Reasoning Dale draws a line in place of his pencil and folds the grid paper along the line. How do the triangles align when the grid paper is folded? Explain.
Answer:
It is given that
Dale draws a line in place of his pencil and folds the grid paper along the line
Now,
The representation of Figure 1 and Figure 2 are:

Now,
From the given figure,
We can observe that the two triangles will stack on each other when the grid paper is folded i.e.,
a. The vertical side of figure 2 is on top of the vertical side of figure 1
b. The base of figure 2 is on top of the base of figure 1
c. The hypotenuse of figure 2 is on top of the hypotenuse of figure 1
Essential Question
How does a reflection affect the properties of a two-dimensional figure?
Answer:
When the reflection takes place along the x-axis,
The values of x will remain constant and the values of y will have a sign change
Ex:
When (x, y) and (-x, y) reflects along the x-axis,
The reflection of (x, y) will become (x, -y)
The reflection of (-x, y) will become (-x, -y)
When the reflection takes place along the y-axis,
The values of y will remain constant and the values of x will have a sign change
Ex:
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
Try It!
While updating the design, the architect accidentally clicked on the chair and reflected it across the centerline. Draw the new location of the chair on the plan.
Answer:
It is given that
While updating the design, the architect accidentally clicked on the chair and reflected it across the centerline.
Hence,
The representation of the new location of the chair is:

Convince Me!
How do the preimage and image compare after a reflection?
Answer:
A reflection is a transformation that turns a figure into its mirror image by flipping it over a line. The line of reflection is the line that a figure is reflected over. If a point is on the line of reflection then the image is the same as the preimage. Otherwise,
the image is not the same as the preimage. Images are always congruent to preimages
Try It!
Quadrilateral KLMN has vertices at K(2, 6), L(3, 8), M(5, 4), and N(3, 2). It is reflected across the y-axis, resulting in quadrilateral K’L’M’N’. What are the coordinates of point N’?
Answer:
It is given that
Quadrilateral KLMN has vertices at K(2, 6), L(3, 8), M(5, 4), and N(3, 2). It is reflected across the y-axis, resulting in quadrilateral K’L’M’N’
Now,
We know that,
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
So,
The reflection of N (3, 2) i.e., the coordinates of N’ is: (-3, 2)
Hence, from the above,
We can conclude that the coordinates of N’ are: (-3, 2)
Try It!
Polygon ABCDE is reflected across the line x = -2. Graph and label the image A’B’C’D’E’. Is m∠A= M∠A? Explain.
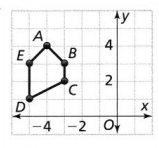
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of polygon ABCDE are:
A (-4, 4), B (-3, 3), C (-3, 2), D (-5, 1), and E (-5, 3)
It is given that polygon ABCDE is reflected along x = -2 i.e., alone the x-axis
We know that,
When (x, y) and (-x, y) reflects along the y-axis,
The reflection of (x, y) will become (x, -y)
The reflection of (-x, y) will become (-x, -y)
So,
The vertices of the reflection of polygon ABCDE i..e, A’B’C’D’E’ are:
A’ (-4, -4), B’ (-3, -3), C’ (-3, -2), D’ (-5, -1), and E’ (-5, -3)
We know that,
In reflection,
The side lengths and the angle measures in the image and the preimage are the same
Hence,
The representation of polygon ABCDE and its reflection polygon A’B’C’D’E’ is:
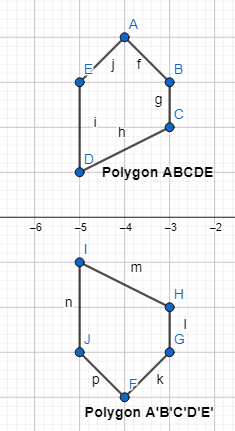
Hence,
m ∠A = M ∠A
KEY CONCEPT
A reflection, or flip, is a transformation that flips a figure across a line of reflection. The preimage and image are the same distance from the line of reflection but on opposite sides. They have the same size and shape but different orientations.
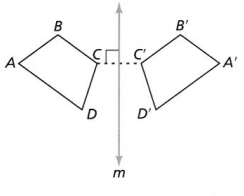
Do You Understand?
Question 1.
Essential Question How does a reflection affect the properties of a two-dimensional figure?
Answer:
When the reflection takes place along the x-axis,
The values of x will remain constant and the values of y will have a sign change
Ex:
When (x, y) and (-x, y) reflects along the x-axis,
The reflection of (x, y) will become (x, -y)
The reflection of (-x, y) will become (-x, -y)
When the reflection takes place along the y-axis,
The values of y will remain constant and the values of x will have a sign change
Ex:
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
Question 2.
Generalize What do you notice about the corresponding coordinates of the preimage and image after a reflection across the x-axis?
Answer:
When the reflection takes place along the x-axis,
The values of x will remain constant and the values of y will have a sign change
Ex:
When (x, y) and (-x, y) reflects along the x-axis,
The reflection of (x, y) will become (x, -y)
The reflection of (-x, y) will become (-x, -y)
Question 3.
Construct Arguments Jorge said the y-values would stay the same when you reflect a preimage across the line y = 5 since the y-values stay the same when you reflect a preimage across the y-axis. Is Jorge correct? Explain.
Answer:
It is given that
Jorge said the y-values would stay the same when you reflect a preimage across the line y = 5 since the y-values stay the same when you reflect a preimage across the y-axis.
Now,
We know that,
When the reflection takes place along the y-axis,
The values of y will remain constant and the values of x will have a sign change
Ex:
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
Hence, from the above,
We can conclude that Jorge is correct
Do You Know How?
Question 4.
Is AX’ Y’ Z’ a reflection of AXYZ across line g?
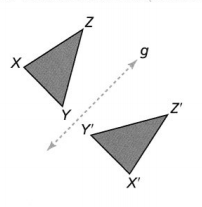
Answer:
The given figure is:

Now,
From the given figure,
We can observe that ΔXYZ is reflected across the line g i.e., y-axis
We know that,
When the reflection takes place along the y-axis,
The values of y will remain constant and the values of x will have a sign change
Ex:
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
So,
From the figure,
We can observe that
The negative x-coordinates of the vertices of ΔXYZ became the positive x -coordinates for Δ X’Y’Z’
Hence, from the above,
We can conclude that ΔX’Y’Z’ is the reflection of ΔXYZ across the line g
Use the coordinate grid below for 5 and 6.
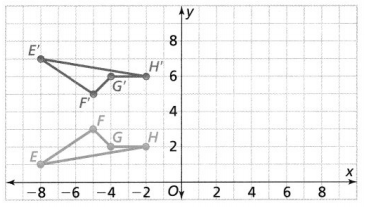
Question 5.
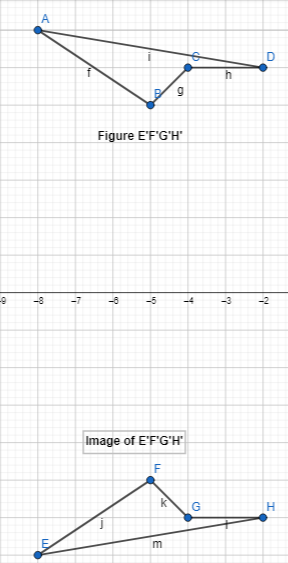
Describe the reflection of figure EFGH.
Answer:
The given coordinate plane is:

From the given coordinate plane,
We can observe that
The reflection of figure EFGH is: Figure E’F’G’H’
Now,
We can observe that
The reflection of the figure EFGH takes place across the x-axis
So,
The x-coordinates of the vertices of the reflection of the figure EFGH will be constant and only y-coordinates will have a change in value
Hence,
The figure EFGH will flip i.e., top becomes down and vice-versa to form a reflection i.e., figure E’F’G’H’
Question 6.
Draw the image that would result from a reflection of figure E’F’G’H across the line x = -1.
Answer:
The given coordinate plane is:

Now,
From the reflection of EFGH i.e., figure E’F’G’H’,
We can observe that the vertices of the figure E’F’G’H’ are:
E’ (-8, 7), F’ (-5, 5), G’ (-4, 6), and H’ (-2, 6)
Now,
To form the image of the figure E’F’G’H’,
We need to reflect the figure E’F’G’H’ across the y-axis
When the reflection takes place along the x-axis,
The values of x will remain constant and the values of y will have a sign change
Ex:
When (x, y) and (-x, y) reflects along the x-axis,
The reflection of (x, y) will become (x, -y)
The reflection of (-x, y) will become (-x, -y)
So,
The vertices for the image of the figure E’F’G’H’ are:
E’ (-8, -7), F’ (-5, -5), G’ (-4, -6), and H’ (-2, -6)
Hence,
The representation of the figure E’F’G’H’ and its image is:
Practice & Problem Solving
Question 7.
Leveled Practice Trapezoid ABCD is shown. Draw the reflection of trapezoid ABCD across the y-axis.
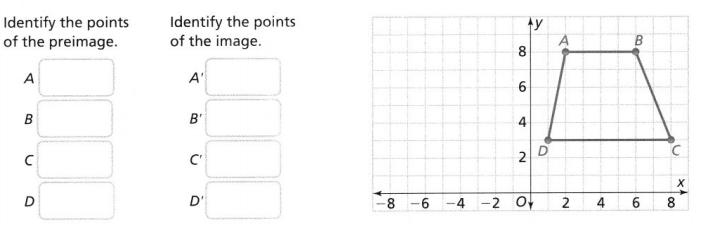
Plot the points and draw trapezoid A’ B’C’D’.
Answer:
From the given trapezoid ABCD,
The vertices are:
A (2, 8), B (6, 8), C (8, 3), and D (1, 3)
It is given that
Draw the reflection of trapezoid ABCD across the y-axis i.e., y is constant
Now,
We know that,
When the reflection takes place along the y-axis,
The values of y will remain constant and the values of x will have a sign change
Ex:
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
So,
The vertices for the reflection of trapezoid ABCD are:
A’ (-2, 8), B (-6, 8), C’ (-8, 3), and D (-1, 3)
So,
The points of the preimage and image are:

Hence,
The representation of trapezoid A’B’C’D’ is:
Question 8.
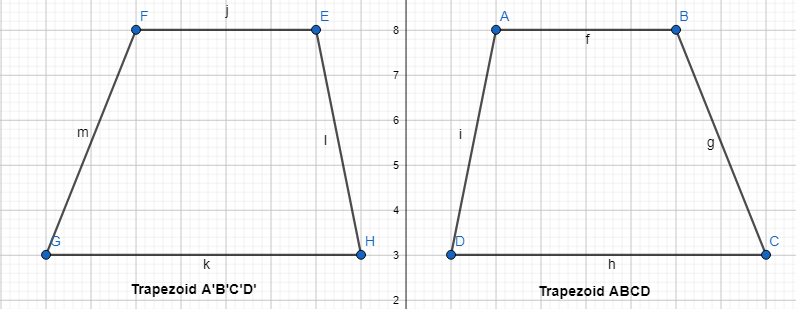
Reasoning is triangle A’ B’C’a reflection of triangle ABC across the line? Explain.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that the reflection of ΔABC takes place across the y-axis
Now,
When the reflection takes place along the y-axis,
The values of y will remain constant and the values of x will have a sign change
Ex:
When (x, y) and (x, -y) reflects along the y-axis,
The reflection of (x, y) will become (-x, y)
The reflection of (x, -y) will become (-x, -y)
So,
From the vertices of ΔABC,
The x-coordinates are negative and the y-coordinates are positive
So,
For the reflection of ΔABC along the y-axis,
The x-coordinates will have to become positive and the y-coordinates will be positive as in the vertices of ΔABC
Hence, from the above,
We can conclude that ΔA’B’C’ is the reflection of ΔABC across the given line
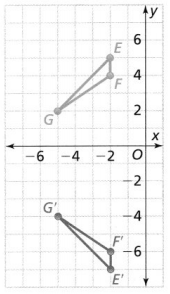
Question 9.
Your friend gives you the graph of quadrilateral ABCD and its image, quadrilateral A’B’C’D’. What reflection produces this image?
Answer:
It is given that
Your friend gives you the graph of quadrilateral ABCD and its image, quadrilateral A’B’C’D’
Now,
The quadrilateral ABCD and its image quadrilateral A’B’C’D’ is:

Now,
From the given figure,
We can observe that
The quadrilateral ABCD and its image will have the same y-coordinates but the x-coordinates are different
We know that,
When the reflection takes place across the y-axis,
The y-coordinates are the same for the image and the preimage
The x-coordiantes have sign changes with the same values for the image and the preimage
Hence, from the above,
We can conclude that the reflection across the y-axis produces the image quadrilateral A’B’C’D’
Question 10.
Construct Arguments Your friend incorrectly says that the reflection of ∆EFG to its image ∆E’ F’G’ is a reflection across the y-axis.
a. What is your friend’s mistake?
Answer:
The given coordinate plane is:

From the above figure,
We can observe that
For the vertices of the given figure,
The x-coordinates remain the same whereas the y-coordinates are different
We know that,
When the reflection takes place across the x-axis,
The x-coordinates of the preimage and the image are the same
The y-coordinates of the preimage and the image will have sign change with the same values
Hence, from the above,
We can conclude that the reflection of ΔEFG takes pace across the x-axis instead of across the y-axis
b. What is the correct description of the reflection?
Answer:
From the given figure,
We can observe that
For the vertices of the given figure,
The x-coordinates remain the same whereas the y-coordinates are different
We know that,
When the reflection takes place across the x-axis,
The x-coordinates of the preimage and the image are the same
The y-coordinates of the preimage and the image will have sign change with the same values
Hence, from the above,
We can conclude that the reflection of ΔEFG to its image ΔE’F’G’ takes pace across the x-axis
Question 11.
Make Sense and Persevere The vertices of ∆ABC are A(-5, 5), B(-2,5), and C(-2, 3). If ∆ ABC is reflected across the line y = -1, find the coordinates of the vertex C’
Answer:
It is given that
The vertices of ∆ABC are A(-5, 5), B(-2,5), and C(-2, 3) and ∆ ABC is reflected across the line y = -1
We know that,
When the reflection takes place across the y-axis,
The y-coordinates of the preimage and the image are the same
The x-coordinates of the preimage and the image will have sign change with the same values
So,
The reflection of the vertex C (-2, 3) is: (2, 3)
Hence, from the above,
We can conclude that the coordinates of the vertex C’ i.e., the reflection of the vertex C is: (2, 3)
Question 12.
Higher Order Thinking What reflection of the parallelogram ABCD results in image A’B’C’D?
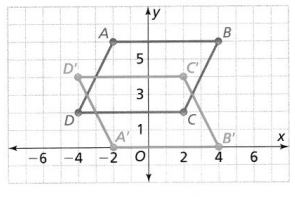
Answer:
The given figure is:

From the given figure,
We can observe that the parallelogram ABCD and its reflection A’B’C’D’ are parallel to the x-axis
Now,
We can observe that,
For both the parallelogram ABCD and its reflection A’B’C’D’,
The x-coordinates are changing but the y-coordinates remain the same
Now,
We know that,
When the reflection takes place across the y-axis,
The y-coordinates of the preimage and the image are the same
The x-coordinates of the preimage and the image will have sign change with the same values
Hence, from the above,
We can conclude that the reflection across the y-axis of the parallelogram ABCD results in image A’B’C’D
Assessment Practice
Question 13.
∆JAR has vertices J(4, 5), A6, 4), and R(5,2). What graph shows ∆JAR and its image after a reflection across the line y = 1?
PART A
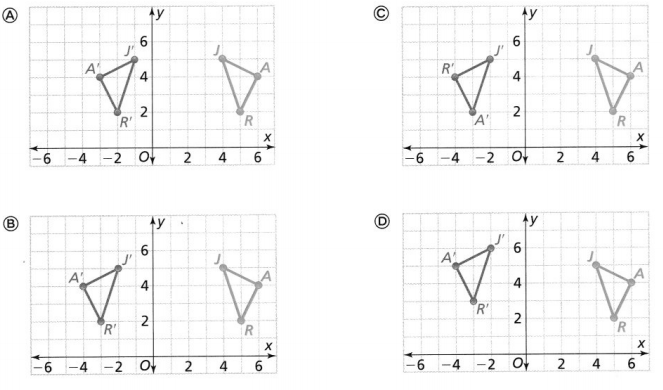
Answer:
It is given that
∆JAR has vertices J(4, 5), A6, 4), and R(5,2)
Now,
We know that,
The reflection across the y-axis is:
The y -coordinates are the same
The x-coordinates will have sign changes with the same value
So,
The reflection of the vertices of ΔJAR is:
J’ (-4, 5), A’ (-6, 4), and R (-5, 2)
Hence,f rom the above,
We can conclude that option D matches with the given vertices of the reflection i.e., ΔJ’A’R’
PART B
The measure of ∠A = 90°. What is m∠A’?
Answer:
We know that,
In Reflection,
The side lengths and the angle measures of the preimage and the image are the same
Hence, from the above,
We can conclude that
∠A = ∠A’ = 90°
Lesson 6.3 Analyze Rotations
Explain It!
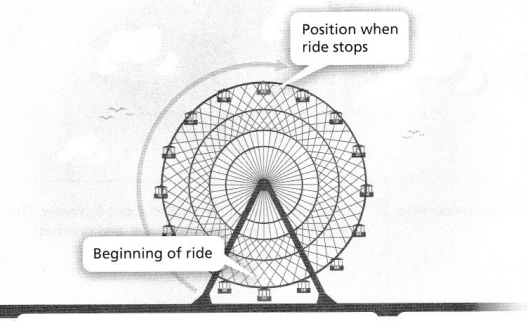
Maria boards a car at the bottom of the Ferris wheel. She rides to the top, where the car stops. Maria tells her friend that she completed \(\frac{1}{4}\) of the turn before the car stopped.
I can… rotate a two-dimensional figure.
A. Do you agree with Maria? Explain.
Answer:
It is given that
Maria boards a car at the bottom of the Ferris wheel. She rides to the top, where the car stops. Maria tells her friend that she completed \(\frac{1}{4}\) of the turn before the car stopped.
Now,
We know that,
From the given figure,
The Ferris wheel looks like a circle
We know that
The total angle measure of a circle (Ferris wheel) is: 360°
But,
It is given that
Maria tells her friend that she completed \(\frac{1}{4}\) of the turn before the car stopped
But, from the figure,
We can observe that she completed the \(\frac{1}{2}\) of the ride
Hence, from the above,
We can conclude that we can’t agree with Maria
B. How could you use angle measures to describe the change in position of the car?
Answer:
We know that,
From the given figure,
The Ferris wheel looks like a circle
We know that
The total angle measure of a circle (Ferris wheel) is: 360°
So,
The starting position of the car in terms of angle measure is given as 0°
The \(\frac{1}{2}\) of the position of the car in terms of angle measure = \(\frac{360°}{2}\)
= 180°
Hence, from the above,
We can conclude that
In terms of angle measures,
The starting position of the car is: 0°
The \(\frac{1}{2}\) of the car is: 180°
Focus on math practices
Construct Arguments How can you describe Maria’s change in position when her car returns to the position at which she began the ride?
Answer:
We know that,
The starting position of the car is: 0°
The \(\frac{1}{2}\) of the car is: 180°
Now,
If Maria’s car returns to the position at which she began the ride, then
Maria has completed the Ferris wheel (or) Maria returned back from her previous \(\frac{1}{2}\) of the position of the car
Hence,
In terms of angle measures,
The change in Maria’s position when her car returns to the position at which she began the ride is: 360° (or) -180°
Here,
-180° represents that Maria returned back from her previous \(\frac{1}{2}\) of the position of the car
Essential Question
How does rotation affect the properties of a two-dimensional figure?
Answer:
When you rotate a two-dimensional figure, you are just moving it.
Ex:
If you rotate a rectangle, then it will remain a rectangle, just moved wherever you move it. This is similarly the same with an angle and aside length, the measure of the angle and the side length won’t change.
Try It!
The architect continues to rotate the umbrella in a counterclockwise direction until it is in its original position. What is the angle of this rotation?
Answer:
It is given that
The architect continues to rotate the umbrella in a counterclockwise direction until it is in its original position.
Now,
We know that,
If any figure rotates until it comes to its original position again, then that means the figure completed a full cycle (or) revolution and the angle of the full cycle is: 360°
Hence, from the above,
We can conclude that the architect continues to rotate the umbrella for 360° in a counterclockwise direction until it is in its original position
Convince Me!
How does an image compare to its preimage after a -45° rotation?
Answer:
Try It!
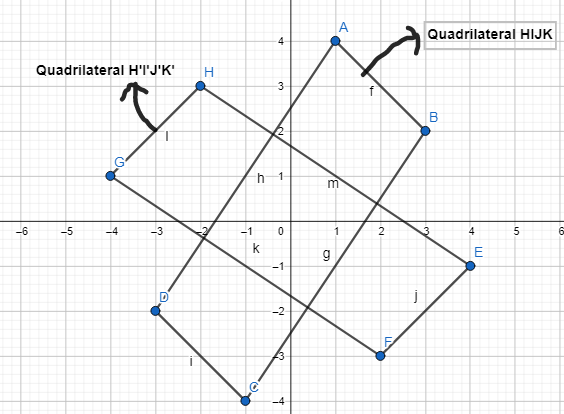
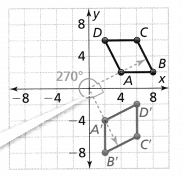
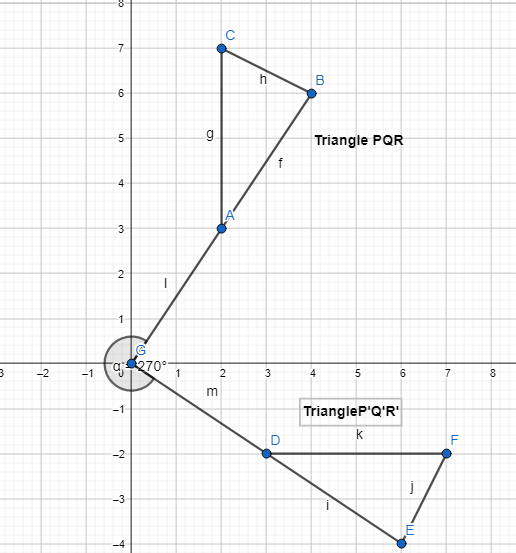
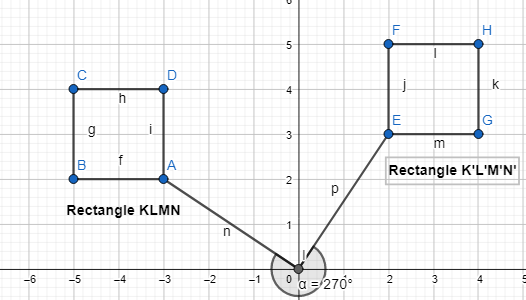
The coordinates of the vertices of quadrilateral HIJK are H(1,4), I(3, 2), J(-1,-4), and K(-3, -2). If quadrilateral HIJK is rotated 270° about the origin, what are the vertices of the resulting image, quadrilateral H’I’I’K?
Answer:
It is given that
The coordinates of the vertices of quadrilateral HIJK are H(1,4), I(3, 2), J(-1,-4), and K(-3, -2)
Now,.
We know that,
The change in the x and y-coordinates for the given angle of rotation is:
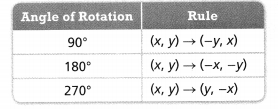
Now,
It is given that to rotate the quadrilateral HIJK 270° about the origin to form the quadrilateral H’I’J’K’
So,
The vertices of the quadrilateral H’I’J’K’ are:
H’ (4, -1), I’ (2, -3), J’ (-4, 1), K’ (-2, 3)
Hence,
The representation of the quadrilateral HIJK and its image H’I’J’K’ is:
Try It!
Describe the rotation that maps ∆FGH to ∆FG’H’.
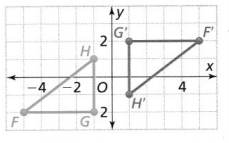
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔFGH are:
F (-5, -2), G (-1, -2), and H (-1, 1)
The vertices of ΔF’G’H’ are:
F’ (5, 2), G’ (1, 2), and H’ (1, -1)
Now,
To find the rotation that maps ΔFGH through ΔF’G’H’, the following steps are:
Step 1:
Draw rays from the origin through point G and point G’
Step 2:
Measure the angle formed by the rays
So,
The representation of ΔFGH and its image ΔF’G’H’ with its angle of rotation is:
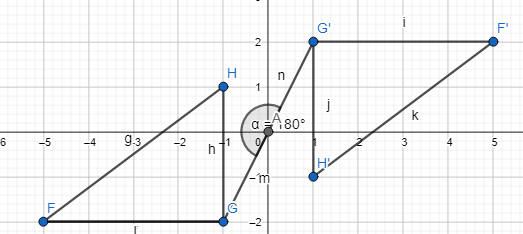
Hence, from the above,
We can conclude that the angle of rotation that maps ΔFGH through ΔF’G’H’ is: 180°
KEY CONCEPT
A rotation is a transformation that turns a figure about a fixed point called the center of rotation. The angle of rotation is the number of degrees the figure is rotated. The x- and y-coordinates change in predictable ways when rotated.

Do You Understand?
Question 1.
Essential Question How does rotation affect the properties of a two-dimensional figure?
Answer:
When you rotate a two-dimensional figure, you are just moving it.
Ex:
If you rotate a rectangle, then it will remain a rectangle, just moved wherever you move it. This is similarly the same with an angle and aside length, the measure of the angle and the side length won’t change.
Question 2.
Reasoning If a preimage is rotated 360 degrees about the origin how can you describe its image?
Answer:
We know that,
To complete the full cycle i.e., to a preimage to return to its original position, the angle measure is: 360°
Hence, from the above,
We can conclude that
If a preimage is rotated 360° about the origin, then the image and the preimage are the same
Question 3.
Construct Arguments In Example 3, side AB is parallel to side DC. How are side A’ B’ and side D’ C’ related? Explain.
Answer:
In Example 3,
The given two-dimensional figure is a parallelogram
We know that,
In a parallelogram, the opposite sides have the same side lengths
So,
Now,
It is given that
In parallelogram ABCD,
AB is parallel to CD
So,
In parallelogram A’B’C’D’,
A’B’ is parallel to C’D’ since these two sides are just the images of the sides AB and CD
Hence, from the above,
We can conclude that A’B’ is parallel to C’D’
Do You Know How?
Question 4.
The coordinates of the vertices of rectangle ABCD are A(3,-2), B(3, 2), C(-3, 2), and D(-3,-2).
a. Rectangle ABCD is rotated 90° about the origin. What are the coordinates of the vertices of rectangle A’B’C’D’?
Answer:
It is given that
The coordinates of the vertices of rectangle ABCD are A(3,-2), B(3, 2), C(-3, 2), and D(-3,-2).
Now,
We know that,
The change in the x and y-coordinates for the given angle of rotation is:

Now,
It is given that to rotate the rectangle ABCD 90° about the origin to form the rectangle A’B’C’D’
So,
The vertices of the rectangle A’B’C’D’ are:
A’ (2, 3), B’ (-2, 3), C’ (-2, -3), and D’ (2, -3)
Hence,
The representation of the rectangle ABCD and its image rectangle A’B’C’D’ is:
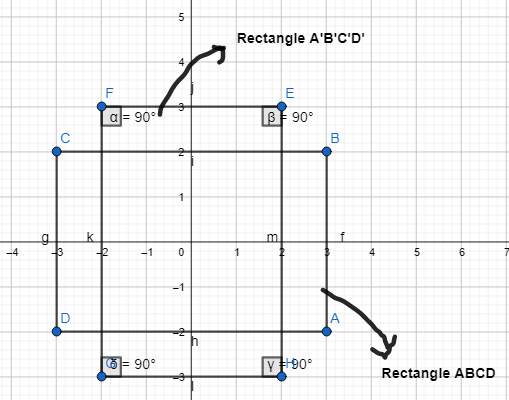
b. What are the measures of the angles of A’B’C’D’?
Answer:
From part (a),
We can observe that all the angles of the rectangle A’B’C’D’ are the same
Hence, from the above,
We can conclude that the angle measures of the rectangle A’B’C’D’ are:
∠A = 90°, ∠B = 90°, ∠C = 90°,and ∠D = 90°
Question 5.
Describe the counterclockwise rotation that maps ∆QRS to ∆Q’R’S.
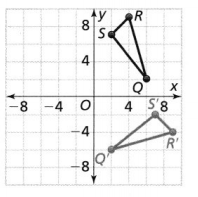
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔQRS are:
Q (6, 2), R (4, 9), and S (2, 7)
The vertices of ΔQ’R’S’ are:
Q’ (2, -6), R’ (9, -4), and S’ (7, -2)
Now,
To find the rotation that maps ΔQRS through ΔQ’R’S’, the following steps are:
Step 1:
Draw rays from the origin through point Q and point Q’
Step 2:
Measure the angle formed by the rays
So,
The representation of ΔQRS and its image ΔQ’R’S’ with its angle of rotation is:
Hence, from the above,
We can conclude that the angle of rotation that maps ΔQRS through ΔQ’R’S’ is: 90°
Practice & Problem Solving
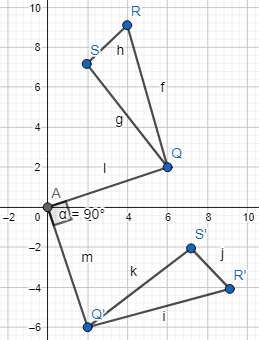
Question 6.
What is the angle of rotation about the origin that maps △ΡQR to △Ρ’ Ο’ R’?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔPQR are:
P (3, 3), Q (5, 3), and R (5, 7)
The vertices of ΔP’Q’R’ are:
P’ (-3, 3), Q’ (-3, 5), and S’ (-7, 5)
Now,
To find the rotation that maps ΔPQR through ΔP’Q’R’, the following steps are:
Step 1:
Draw rays from the origin through point P and point P’
Step 2:
Measure the angle formed by the rays
So,
The representation of ΔPQR and its image ΔP’Q’R” with its angle of rotation is:
Hence, from the above,
We can conclude that the angle of rotation that maps ΔPQR through ΔP’Q’R’ is: 90°
Question 7.
Is △X’ Y’Z’ a rotation of △XYZ? Explain.
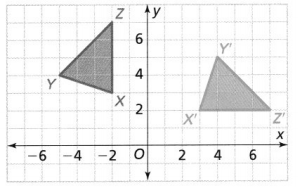
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔXYZ are:
X (-2, 3), Y (-5, 4), and Z (-2, 7)
The vertices of ΔX’Y’Z’ are:
X’ (3, 2), Y’ (4, 5), and Z’ (7, 2)
Now,
To find the angle of rotation,
Compare the x and y-coordinates of ΔXYZ and ΔX’Y’Z’
So,
(x, y) before rotation ——-> (y, -x) after rotation
We know that,

Hence, from the above,
We can conclude that ΔX’Y’Z’ is a rotation of ΔXYZ
Question 8.
△PQR is rotated 270° about the origin. Graph and label the coordinates of P’, Q’, and R’.
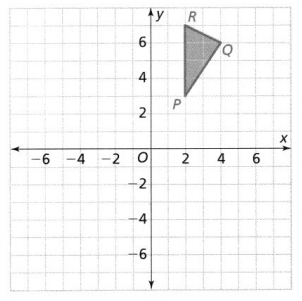
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔPQR are:
P (2, 3), Q (4, 6), and R (2, 7)
It is given that
Rotate ΔPQR 270° at the origin
We know that,

So,
The vertices of ΔP’Q’R’ when the angle of rotation is 270° are:
P’ (3, -2), Q’ (6, -4), and R’ (7, -2)
Hence,
The representation of ΔPQR and its image ΔP’Q’R’ is:
Question 9.
Is △P’ Q’R’a 270° rotation of △PQR about the origin? Explain.
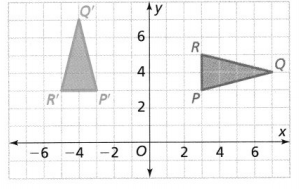
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔPQR are:
P (3, 3), Q (7, 4), and R (3, 5)
The vertices of ΔP’Q’R’ are:
P’ (-3, 3), Q’ (-4, 7), and R’ (-5, 3)
Now,
To find the angle of rotation,
Compare the x and y-coordinates of ΔPQR and ΔP’Q’R’
So,
(x, y) before rotation ——-> (-y, x) after rotation
We know that,

Hence, from the above,
We can conclude that ΔP’Q’R’ is a rotation of ΔPQR
Question 10.
Reasoning Explain why any rotation can be described by an angle between 0° and 360°.
Answer:
If you rotate an object 360°, it’s like the object never moved because the object would still be in the same spot as if you didn’t move it.
Hence,
Any rotation can be described by an angle of 0° to 360°
Question 11.
Rotate rectangle KLMN 270° about the origin.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of rectangle KLMN are:
K (-3, 2), L (-5, 2), M (-5, 4), and N (-3, 4)
It is given that
Rotate rectangle KLMN 270° at the origin
We know that,

So,
The vertices of rectangle K’L’M’N’ when the angle of rotation is 270° are:
K’ (2, 3), L’ (2, 5), M’ (4, 5), and N’ (4, 3)
Hence,
The representation of rectangle KLMN and its image rectangle K’L’M’N’ is:
Question 12.
Higher-Order Thinking An architect is designing a new windmill with four sails. In her sketch, the sails’ center of rotation is the origin, (0, 0), and the tip of one of the sails, point Q, has coordinates (2, -3). She wants to make another sketch that shows the windmill after the sails have rotated 270° about their center of rotation. What would be the coordinates of?
Answer:
It is given that
An architect is designing a new windmill with four sails. In her sketch, the sails’ center of rotation is the origin, (0, 0), and the tip of one of the sails, point Q, has coordinates (2, -3). She wants to make another sketch that shows the windmill after the sails have rotated 270° about their center of rotation
So,
We have to rotate point Q 270° about the origin
We know that,

So,
When we rotate any point 270° about the origin,
(x, y) before rotation ——–> (y, -x)
So,
The representation of point Q after representation is: (-3, -2)
Hence,
The representation of point Q and its image Q’ is:
Assessment Practice
Question 13.
A rotation about the origin maps △TRI to △T’ R’I’.
PART A
Which graph shows an angle you could measure to find the angle of rotation about the origin?
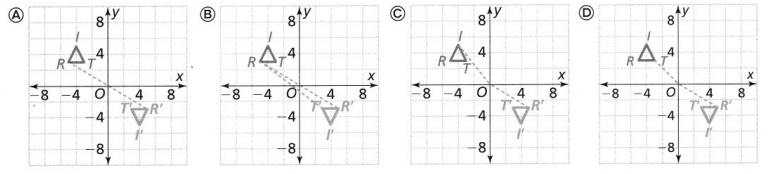
Answer:
It is given that
A rotation about the origin maps △TRI to △T’ R’I’
Now,
We know that,
We can find the angle of rotation only when the vertex maps with its image but not with any other images
Hence, from the above,
We can conclude that option A matches the given situation
PART B
What is the angle of rotation about the origin?
A. 90°
B. 180°
C. 270°
D. 360°
Answer:
From part (a),
When we observe option A,
The vertices of ΔTRI are:
T (-3, 3), R (-5, 3), and I (-4, 5)
The vertices of ΔT’R’I’ are:
T’ (3, -3), R’ (5, -3), and I’ (4, -5)
We know that,

So,
When we compare the vertices of ΔTRI and ΔT’R’I’,
We can observe that
(x, y) before rotation ———–> (-x, -y) after rotation
Hence, from the above,
We can conclude that the angle of rotation about the origin is: 180°
Lesson 6.4 Compose Transformations
Solve & Discuss It!
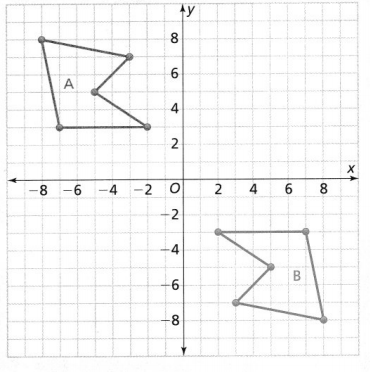
How can you map Figure A onto Figure B?
I can… describe and perform a sequence of transformations.
Answer:
The given figure is:

Now,
The steps to obtain Figure B from Figure A are:
Step 1:
Reflect Figure A across the x-axis
Step 2:
Reflect the figure that we obtained in Step 1 across the y-axis
Hence,
The representation of the mapping of Figure A and Figure B using the above steps is:
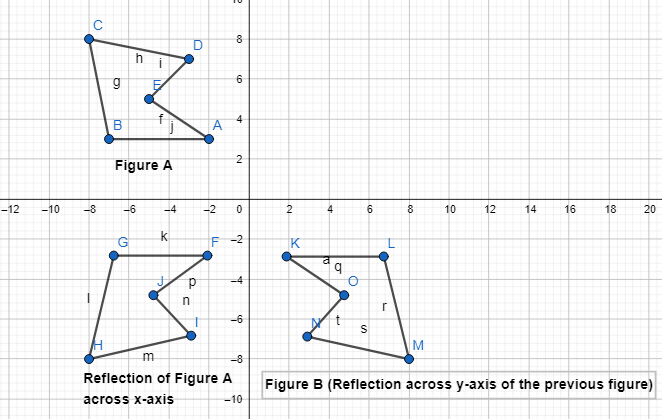
Focus on math practices
Look for Relationships Is there another transformation or sequence of transformations that will map Figure A to Figure B?
Answer:
Yes, there are another sequence of transformations that will map Figure A to figure B
Now,
The steps to obtain Figure B from Figure A are:
Step 1:
Reflect Figure A across the y-axis
Step 2:
Reflect the figure that we obtained in Step 1 across the x-axis
Hence,
The representation of the mapping of Figure A and Figure B using the above steps is:
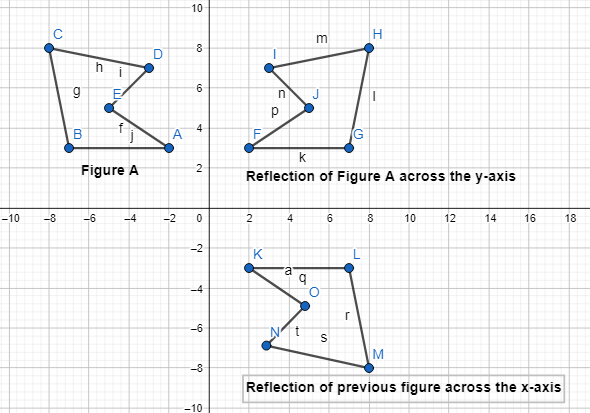
Essential Question
How can you use a sequence of transformations to map a preimage to its image?
Answer:
Mathematical transformations involve changing an image in some prescribed manner. There are four main types of transformations They are:
A) Translation B) Rotation C) Reflection D) Dilation
Try It!
Ava decided to move the cabinet to the opposite wall. What sequence of transformations moves the cabinet to its new position?

Answer:
It is given that
Ava decided to move the cabinet to the opposite wall
So,
From the figure,
We can observe that
To move the cabinet wall to the opposite wall, the following sequences of transformations have to be followed:
Step 1:
Translate the cabinet 8 units down
Step 2:
Rotate the cabinet 360° counterclockwise
Hence, from the above,
We can conclude that
The new position of the cabinet is:
Convince Me!
Ava decides that she would like the chairs to be placed directly across from the couch. What is a sequence of transformations that she can use to move the chairs to their new positions?
Try It!
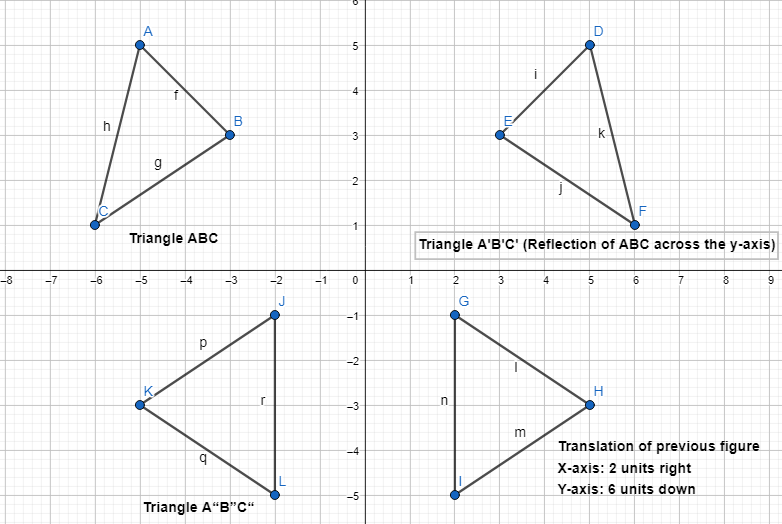
What is another sequence of transformations that maps △ABC onto △A” B” C”?
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔABC are:
A (-5, 5), B (-3, 3), and C (-6, 1)
Now,
Another sequence of transformations that maps ΔABC onto ΔA”B” C” is:
Step 1:
Draw ΔABC and make its reflection across the y-axis and name it ΔA’B’C’
Step 2:
Translate ΔA’B’C’ 2 units to the right and 6 units down
Step 3:
Reflect the figure we obtained in step 2 across the y-axis
Hence, from the above,
We can conclude that
The representation of another sequence of transformations that maps ΔABC onto ΔA”B” C” is:
KEY CONCEPT
You can use a sequence of two or more transformations to map a preimage to its image.
You can map △ABC onto △Α” Β” C” by translation of 3 units right followed by a 90° clockwise rotation about the origin.
Do You Understand?
Question 1.
Essential Question How can you use a sequence of transformations to map a preimage to its image?
Answer:
Mathematical transformations involve changing an image in some prescribed manner. There are four main types of transformations They are:
A) Translation B) Rotation C) Reflection D) Dilation
Question 2.
Make Sense and Persevere A preimage is rotated 180° about the origin and then rotated 180° about the origin again. Compare the preimage and image.
Answer:
It is given that
A preimage is rotated 180° about the origin and then rotated 180° about the origin again
Now,
When the preimage is rotated 180° and again 180°
The image will be the same as the preimage
Hence, from the above,
We can conclude that
When a preimage is rotated 180° about the origin and then rotated 180° about the origin again, the preimage and the image will be the same
Question 3.
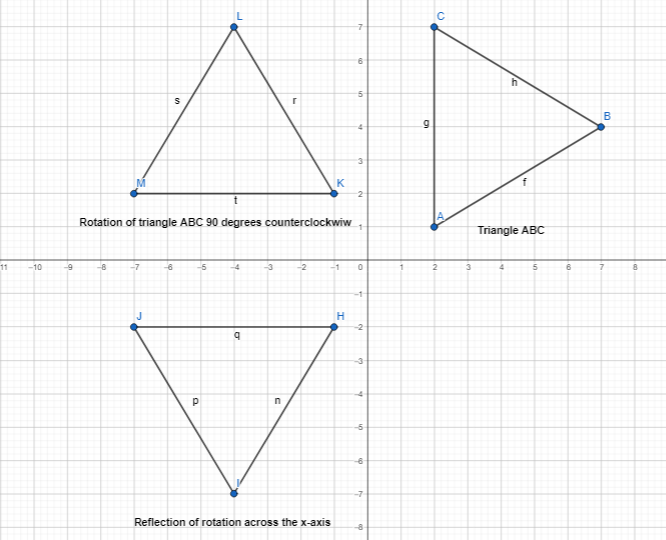
Reasoning A figure ABC, with vertices A(2, 1), B(7, 4), and C(2, 7), is rotated 90° clockwise about the origin, and then reflected across the x-axis. Describe another sequence that would result in the same image.
Answer:
It is given that
A figure ABC, with vertices A(2, 1), B(7, 4), and C(2, 7), is rotated 90° clockwise about the origin, and then reflected across the x-axis
So,
The steps for another sequence of transformations that would result in the same image as the given situation is:
Step 1:
Draw the given vertices of Triangle ABC
Step 2:
Rotate Triangle ABC 90° counterclockwise
Step 3:
Reflect the image that we obtained in step 2 across the x-axis so that we will get the same image as in the given situation
Hence,
The representation of another sequence of transformations is:
Do You Know How?
In 4-6, use the diagram below.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of Figure WXYZ are:
W (2, 4), X (5, 4), Y (5, 2), and Z (2, 2)
The vertices of Figure W’X’Y’Z’ are:
W’ (-4, -4), X’ (-4, -1), Y’ (-2, -1), and Z’ (-2, -4)
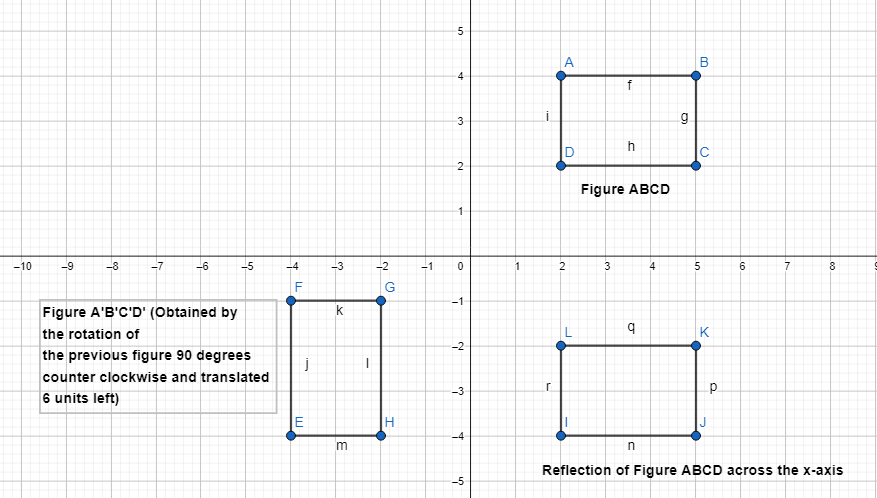
Question 4.
Describe a sequence of transformations that maps rectangle WXYZ onto rectangle W’X’Y’Z’.
Answer:
The steps that we have to follow to obtain the given sequence of transformations that maps rectangle WXYZ onto rectangle W’X’Y’Z’ are:
Step 1:
Draw rectangle WXYZ
Step 2:
Reflect rectangle WXYZ across the x-axis
Step 3:
Rotate the image we obtained in step 2 90° counterclockwise
Step 4:
Translate the image we obtained in step-3 6 units left so that we can obtain rectangle W’X’Y’Z’
Hence,
The representation of the sequence of transformations for the given situation is:
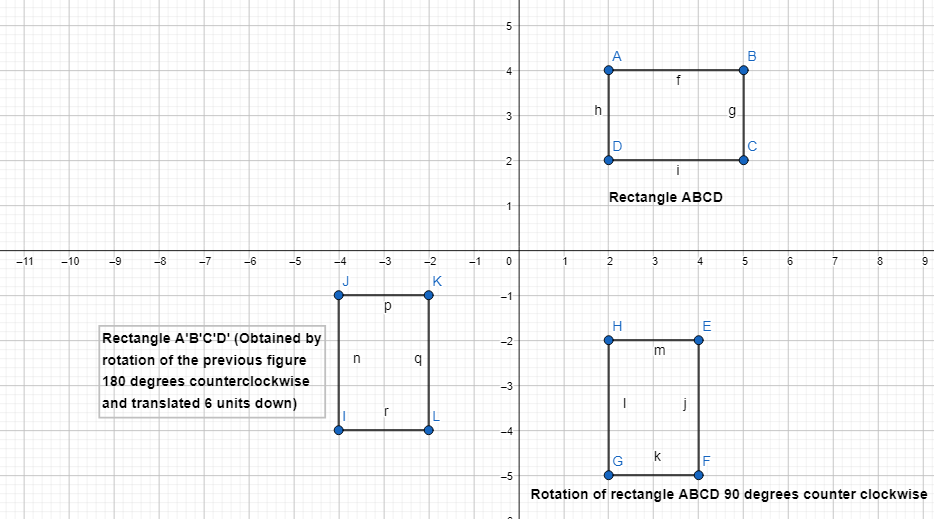
Question 5.
Describe another way that you could map rectangle WXYZ onto W’X’Y’Z’.
Answer:
The steps for another way of transformations that maps rectangle WXYZ onto W’X’Y’Z’ are:
Step 1:
Draw Rectangle WXYZ
Step 2:
Rotate rectangle WXYZ 90° counterclockwise
Step 3:
Rotate the image we obtained in step-2 180° counterclockwise
Step 4:
Translate the image we obtained in step 3 6 units down so that we can obtain rectangle W’X’Y’Z’
Hence,
The representation of another sequence of transformations is:
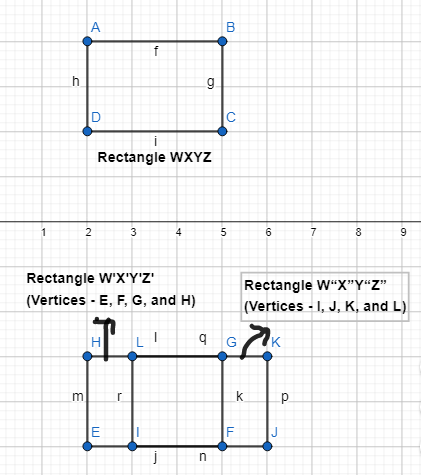
Question 6.
Draw the image of rectangle WXYZ after a reflection across the line y = 1 and a translation 1 unit right. Label the image W” X” Y” Z”.
Answer:
The vertices of rectangle WXYZ are:
W (2, 4), X (5, 4), Y (5, 2), and Z (2, 2)
After the reflection across the line y = 1,
The vertices of rectangle WXYZ are:
W’ (2, -5), X’ (5, -5), Y’ (5, -3), and Z’ (2, -3)
After the translation of 1 unit right,
The vertices of rectangle WXYZ are:
W” (3, -5), X” (6, -5), Y” (6, -3), and Z” (3, -3)
Hence,
The representation of rectangle WXYZ and its image W”X” Y”Z” after the above sequence of transformations is:
Practice & Problem Solving
Question 7.
Leveled Practice Describe a sequence of transformations that maps △QRS onto △TUV.
A translation ________ units left and ________ units down, followed by a _________ across the ________.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔQRS are:
Q (3, 4), R (7, 4), and S (6, 9)
The vertices of ΔTUV are:
T (0, 0), U (-4, 0), and V (-3, 5)
Now,
In order to obtain the vertices of ΔTUV, the following transformations we have to follow are:
Step 1:
Translate the vertices of ΔQRS 3 units left and 4 units down
Step 2:
Reflect the image we obtained in step 1 across the x-axis in order to get the vertices of ΔTUV
Hence, from the above,
We can conclude that
A translation of 3 units left and 4 units down, followed by a reflection across the x-axis
Question 8.
Model with Math
A family moves a table, shown as rectangle EFGH, by translating it 3 units left and 3 units down followed by a 90° rotation about the origin. Graph E’ F’G’H’ to show the new location of the table.
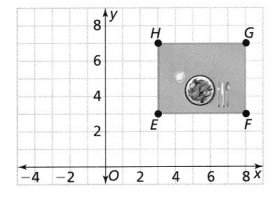
Answer:
It is given that
A family moves a table, shown as rectangle EFGH, by translating it 3 units left and 3 units down followed by a 90° rotation about the origin
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of rectangle EFGH are:
E (3, 3), F (8, 3), G (8, 7), and H (3, 7)
Now,
To obtain rectangle E’F’G’H’,
The following series of transformations are:
Step 1:
By translating 3 units left and 3 units down,
The vertices of rectangle EFGH will become:
E (3 – 3, 3 – 3), F (8 – 3, 3 – 3), G (8 – 3, 7 – 3), and H (3 – 3, 7 – 3)
E (0, 0), F (5, 0), G (5, 4), and H (0, 4)
Step 2:
Rotate the vertices we obtain in step 1 90° counterclockwise about the origin
We know that,
When we rotate a point 90° counterclockwise about the origin,
(x, y) before rotation ——> (-y, x) after rotation
So,
The vertices of rectangle E’F’G’H’ are:
E’ (0, 0), F’ (0, 5), G’ (-4, 5), and H’ (-4, 0)
Hence,
The representation of the new location of the table is:
Question 9.
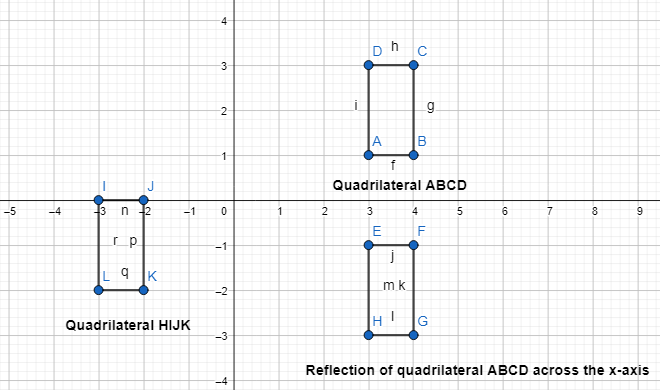
Describe a sequence of transformations that maps quadrilateral ABCD to quadrilateral HIJK.
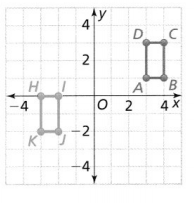
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of quadrilateral ABCD are:
A (3, 1), B (4, 1), C (4, 3), and D (3, 3)
The vertices of quadrilateral HIJK are:
H (-3, 0), I (-2, 0), J (-2, -2), and K (-3, -2)
Now,
The series of transformations that maps quadrilateral ABCD onto quadrilateral HIJK are:
Step 1:
Draw quadrilateral ABCD
Step 2:
Reflect quadrilateral ABCD across the x-axis
So,
The vertices of quadrilateral ABCD are:
A (3, -1), B (4, -1), C (4, -3), and D (3, -3)
Step 3:
Translate 6 units left and 1 unit up
So,
The vertices that we obtained in step 2 will become (The vertices of quadrilateral HIJK):
H (-3, 0), I (-2, 0), J (-2, -2), and K (-3, -2)
Hence,
The representation of the series of transformations that map quadrilateral ABCD onto quadrilateral HIJK are:
Question 10.
Map △QRS to △Q’R’ S’with a reflection across the y-axis followed by a translation 6 units down.
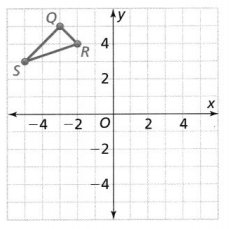
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔQRS are:
Q (-3, 5), R (-2, 4), and S (-5, 3)
Now,
The series of transformations that maps ΔQRS to ΔQ’R’S’ as given above are:
Step 1:
Reflect the vertices of ΔQRS along the y-axis
So,
Q (3, 5), R (2, 4), and S (5, 3)
Step 2:
Translate the vertices that we obtain in step-1 6 units down so that we can obtain the vertices of ΔQ’R’S’
So,
Q’ (3, 5 – 6), R’ (2, 4 – 6), and S’ (5, 3 – 6)
Q’ (3, -1), R’ (2, -2), and S’ (5, -3)
Hence,
The representation of the series of transformations for the given situation is:
Question 11.
Higher-Order Thinking A student says that he was rearranging furniture at home and he used a glide reflection to move a table with legs from one side of the room to the other. Will a glide reflection result in a functioning table? Explain.
Answer:
It is given that
A student says that he was rearranging furniture at home and he used a glide reflection to move a table with legs from one side of the room to the other.
We know that,
A glide reflection is a sequence of translation and reflection
Now,
From the given situation,
We can observe that the table is moving from one room to the other
So,
The “Translation” occurs
Now,
After moving he will rearrange the table in the room
So,
A “Reflection” may take place
Hence, from the above,
We can conclude that a glide reflection result in a functioning table
Assessment Practice
Question 12.
PART A
Which sequence of transformations maps rectangle ABCD onto rectangle A’ B’C’D?
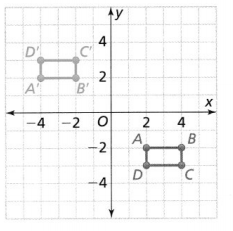
A. translation 6 units down, reflection across the x-axis
B. reflection across the x-axis, translation 6 units right
C. reflection across the x-axis, translation 6 units left
D. translation 6 units left, reflection across the y-axis
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of rectangle ABCD are:
A (2, -2), B (4, -2), C (4, -3), and D (2, -3)
The vertices of rectangle A’B’C’D’ are:
A’ (-4, 2), B’ (-2, 2), C’ (-2, 3), and D’ (-4, 3)
So,
The sequence of transformations that maps rectangle ABCD to rectangle A’B’C’D’ is:
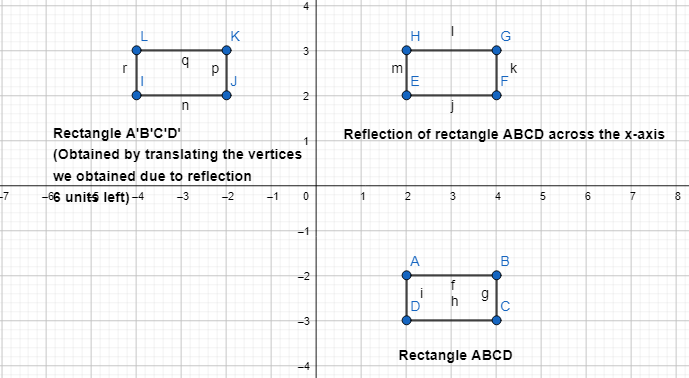
Hence, from the above,
We can conclude that option C matches the given situation
PART B
Describe a sequence of transformations that maps A’B’C’ D’ onto ABCD.
Answer:
The sequence of transformations that maps A’B’C’D’ onto ABCD is:
Step 1:
Draw the rectangle ABCD
So,
The vertices of rectangle ABCD are:
A (2, -2), B (4, -2), C (4, -3), and D (2, -3)
Step 2:
Reflect rectangle ABCD across the x-axis
So,
The vertices of rectangle ABCD are:
A (2, 2), B (4, 2), C (4, 3), and D (2, 3)
Step 3:
Translate the vertices that we obtained in step 2 6 units left so that we can obtain rectangle A’B’C’D’
So,
A’ (2 – 6, 2), B’ (4 – 6, 2), C’ (4 – 6, 3), and D’ (2 – 6, 3)
So,
A’ (-4, 2), B’ (-2, 2), C’ (-2, 3), and D’ (-4, 3)
Question 13.
PART A
Which figures are the image of Figure A after a reflection across the x-axis and a translation of 4 units right?
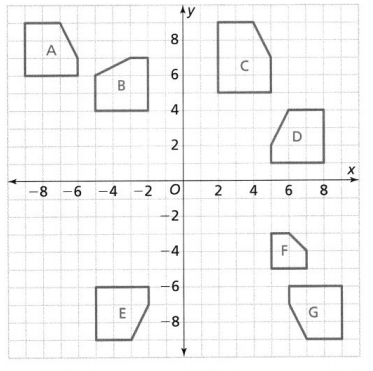
A. Figure B
B. Figure C
C. Figure D
D. Figure E
Answer:
We know that,
A “Reflection” is called a “Flip” but the reflection does not affect the shape and length of the figure
So,
From the given figures,
When we observe Figures A and B,
We can say that Figure B is a reflection of A because the shape and length is the same
But,
when we observe the other figures,
We have different shapes and lengths between the preimage and the image
Hence, from the above,
We can conclude that
Figure B is the image of Figure A after a reflection across the x-axis and a translation of 4 units right
PART B
Which figure can be transformed into Figure G after a rotation 90° about the origin, then a translation 13 units right and 4 units down?
A. Figure B
B. Figure D
C. Figure E
D. Figure F
Answer:
From the given figures,
We have to obtain
The coordinates of Figure G are:
(6, -6), (9, -6), (9, -9), (7, -9), and (6, -5)
We know that,
When a point rotates 90° about the origin,
(x, y) before rotation ——-> (-y, x) after rotation
Now,
For the translation of 13 units right and 4 units down,
The vertices will be like: (x + 13, y – 4)
Hence, from the above,
We can conclude that option A matches the given situation
3-ACT MATH
3-Act Mathematical Modeling: Tricks of the Trade

ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.

Answer:
Question 3.
Make a prediction to answer this Main Question.
Answer:
Question 4.
Construct Arguments Explain how you arrived at your prediction.
Answer:
ACT 2
Question 5.
What information in this situation would be helpful to know? How would you use that information?

Answer:
Question 6.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 7.
Model with Math Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 8.
What is your answer to the Main Question? Does it differ from your prediction? Explain.

Answer:
ACT 3
Question 9.
Write the answer you saw in the video.
Answer:
Question 10.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?
Answer:
Question 11.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:
ACT 3 Extension
Reflect
Question 12.
Model with Math Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?

Answer:
Question 13.
Make Sense and Persevere When did you struggle most while solving the problem? How did you overcome that obstacle?
Answer:
SEQUEL
Question 14.
Be Precise Find another optical illusion online involving shapes that look different but are the same. Explain how you know the shapes are the same.
Answer:
Lesson 6.5 Understand Congruent Figures
Solve & Discuss It!
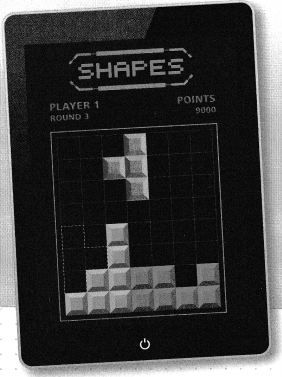
Simone plays a video game in which she moves shapes into empty spaces. After several rounds, her next move must fit the blue piece into the dashed space. How can Simone move the blue piece to fit in the space?
I can… use a sequence of translations, reflections, and rotations to show that figures are congruent.
Answer:
It is given that
Simone plays a video game in which she moves shapes into empty spaces. After several rounds, her next move must fit the blue piece into the dashed space.
Now,
From the given figure,
We can observe that
The blue piece and the dashed piece are the reflections of each other
Hence,
Simone move the blue piece to fit in the space by the translation followed by reflection
Reasoning
How can you use what you know about sequences of transformations to move the piece?
Answer:
From the given figure,
We can observe that
The blue piece should be moved to the place of the dashed space and it will be possible only due to the “Translation”
But,
We can observe that it does not fit into the dashed space.
So,
Reflect the blue piece that it can fit into the dashed piece
Hence, from the above,
We can conclude that the sequence of transformations we can use to move the transformation are:
a. Translation b. Reflection
Focus on math practices
Construct Arguments How do you know that the piece that fits into the space is the same as the original blue shape? Explain.
Answer:
We know that,
In the reflection,
a. The shape of the preimage and the image are the same
b. The length of the preimage and the image are the same
c. The orientation of the image and the preimage are different
Hence, from the above,
We can conclude that
Due to the properties of the reflection,
We know that the piece that fits into space is the same as the original shape
Essential Question
How does a sequence of translations, reflections, and rotations result in congruent figures?
Answer:
If we copy one figure on tracing paper and move the paper so the copy covers the other figure exactly, then that suggests they are congruent. We can prove that two figures are congruent by describing a sequence of translations, rotations, and reflections that move one figure onto the other so they match up exactly.
Try It!
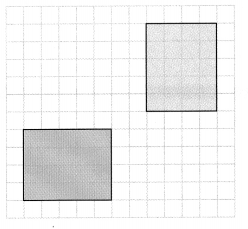
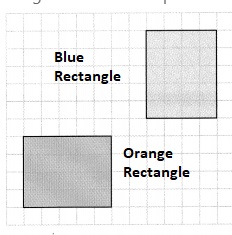
How can you determine whether the orange and blue rectangles are congruent?
Answer:
The given coordinate plane is:
From the given coordinate plane,
We can observe that
The blue rectangle has a length of 6 units and a width of 5 units
The orange rectangle has a length of 5 units and a width of 6 units
Now,
We can say that
We can obtain the orange rectangle by rotating the blue rectangle
We know that,
Rotations, reflections, and translations are isometric. That means that these transformations do not change the size of the figure. If the size and shape of the figure is not changed, then the figures are congruent
Hence, from the above,
We can conclude that the orange and blue rectangles are congruent
Convince Me!
Quadrilateral PQRS is congruent to quadrilateral P’ Q’R’S. What do you know about how these figures relate?
Answer:
It is given that
Quadrilateral PQRS is congruent to quadrilateral P’ Q’R’S
We know that,
When the two figures are congruent,
a. The shapes of the two figures are the same
b. The lengths of the two figures are the same
c. The angle measures of the two figures are the same
Hence,
In Quadrilateral PQRS and Quadrilateral P’Q’R’S’, the two figures are said to be congruent when
a. PQ = P’Q’ and RS = R’S’
b. ∠P = ∠P’, ∠Q = ∠Q’, ∠R = ∠R’, and ∠S = ∠S’
Try It!
Are the figures congruent? Explain.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of Figure 1 are:
(1, 5), (3, 7), (3, 5), and (2, 3)
The vertices of Figure 2 are:
(6, 3), (8, 3), (10, 2), and (8, 1)
Now,
Find out whether Translation, Reflection, and Rotation is possible between 2 figures or not
So,
The representation of Figure 1 and Figure 2 are:
Now,
From the given figures,
We can observe that none of the transformations is possible
Hence, from the above,
We can conclude that the two figures are not congruent
KEY CONCEPT
Two-dimensional figures are congruent if there is a sequence of translations, reflections, and rotations that maps one figure onto the other.
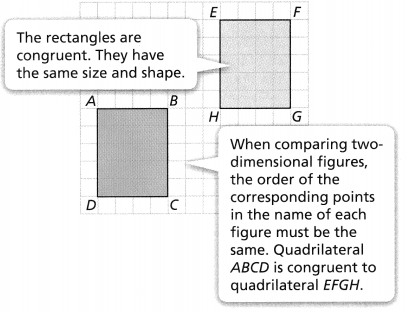
Do You Understand?
Question 1.
Essential Question How does a sequence of translations, reflections, and rotations result in congruent figures?
Answer:
If we copy one figure on tracing paper and move the paper so the copy covers the other figure exactly, then that suggests they are congruent. We can prove that two figures are congruent by describing a sequence of translations, rotations, and reflections that move one figure onto the other so they match up exactly.
Question 2.
Reasoning Does a sequence of transformations have to include a translation, a reflection, and a rotation to result in congruent figures? Explain.
Answer:
Rotations, reflections, and translations are isometric. That means that these transformations do not change the size of the figure. If the size and shape of the figure is not changed, then the figures are congruent
Question 3.
Construct Arguments Is there a sequence of reflections, rotations, and translations that makes the preimage and image not only congruent, but identical in orientation? Explain.
Answer:
We know that,
In the reflection,
The orientation of the preimage and the image will differ
Hence, from the above,
We can conclude that
There is a sequence of reflections, rotations, and translations that makes the preimage and image only congruent but not identical in orientation
Do You Know How?
Question 4.
A rectangle with an area of 25 square centimeters is rotated and reflected in the coordinate plane. What will be the area of the resulting image? Explain.
Answer:
It is given that
A rectangle with an area of 25 square centimeters is rotated and reflected in the coordinate plane.
We know that,
In a sequence of transformations like Translation, Rotation, and Reflection,
The shapes and side lengths of the image and the preimage are the same
Since the side lengths are the same, the area will also be the same
Hence, from the above,
We can conclude that the area of the image will also be 25 square centimeters
In 5 and 6, use the coordinate grid below.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔABC are:
A (1, 4), B (2, 2), and C (5, 2)
The vertices of ΔDEF are:
D (9, 9), E (8, 7), and F (5, 7)
The vertices of ΔGHI are:
G (6, 6), H (8, 5), and I (8, 1)
Question 5.
Is △ABC ≅ △DEF? Explain.
Answer:
To find whether ΔABC is congruent to ΔDEF or not,
Step 1:
Reflect Triangle ABC across the x-axis
Step 2:
Translate the image that we obtained in step-1 10 units right and 5 units up
So,
The representation of step 1 and step 2 is:
Hence, from the above,
We can observe that the vertices we obtained in step 2 are the same as ΔDEF
Hence,
ΔABC is congruent to ΔDEF
Question 6.
Is △ABC ≅ △GHI? Explain.
Answer:
The representation of △ABC and △GHI is:
From the above,
We can observe that △ABC and △GHI do not have the same size
We know that,
In order to be 2 figures congruent,
a. The sizes of the figures would be the same
b. The shapes of the figures would be the same
c. The side lengths of the figures should be the same
Hence, from the above,
We can conclude that
△ABC is not congruent to △GHI
Practice & Problem Solving
Question 7.
△Q’R’ S’ is the image of △QRS after a reflection across the y-axis and a translation 6 units down. Is the image the same size and shape as the preimage?
△QRS and △Q’R’S’ _________ the same size and shape.
Answer:
It is given that
△Q’R’ S’ is the image of △QRS after a reflection across the y-axis and a translation 6 units down
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔQRS are:
Q (-3, 5), R (-2, 4), and S (-5, 3)
The vertices of ΔQ’R’S’ are:
Q’ (3, -1), R’ (2, -2), and S’ (5, -3)
Now,
Step 1:
After a reflection of ΔQRS across the y-axis,
The vertices of ΔQRS will be:
Q (3, 5), R (2, 4), and S (5, 3)
Step 2:
After a translation of 6 units down,
The vertices that we obtained in Step 1 are:
Q’ (3, 5 – 6), R’ (2, 4 – 6), and S’ (5, 3 – 6)
Q’ (3, -1), R’ (2, -2), and S’ (5, -3)
So,
The vertices of ΔQ’R’S’ we obtained from the coordinate plane and the vertices of ΔQ’R’S’ we obtained after the sequence of transformations are the same
Hence, from the above,
We can conclude that △QRS and △Q’R’S’ have the same size and shape and the image (ΔQ’R’S’) is the same size and shape as the preimage (ΔQRS)
Question 8.
Is △DEF ≅ △D’ E’F’? Explain.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔDEF are:
D (5, 5), E (6, 3), and F (2, 4)
The vertices of ΔD’E’F’ are:
D’ (-2, -1), E’ (-3, 1), and F’ (1, 0)
So,
The representtaion of the sequence of transformations of ΔDEF to show it is congruent to ΔD’E’F’ is:
Hence, from the above,
We can conclude that ΔDEF is congruent to ΔD’E’F’
Question 9.
Construct Arguments Describe a way to show that quadrilateral ABCD is congruent to quadrilateral A’B’C’D’.
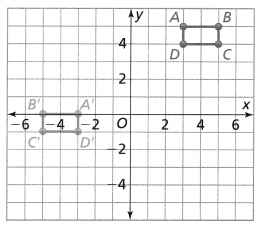
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of quadrilateral ABCD are:
A (3, 5), B (5, 5), C (5, 4), and D (3, 4)
The vertices of quadriateral A’B’C’D’ are:
A’ (-3, 0), B’ (-5, 0), C’ (-5, -1), and D’ (-3, -1)
So,
The representtaion of the transformation of sequences that shows quadrilateral ABCd is congruent to quadrilateral A’B’C’D’ is:
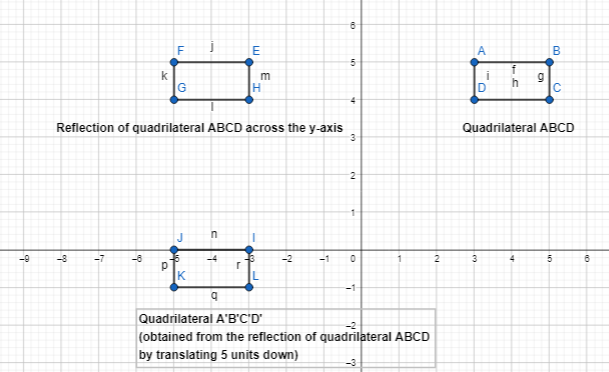
Hence, from the above,
We can conclude that quadrilateral ABCD is congruent to quadrilateral A’B’C’D’
Question 10.
You are making two triangular flags for a project and need the flags to be the same shape and size. △XYZ and △X’Y’Z’ are the flags you have drawn. Are the flags the same shape and size? Explain.
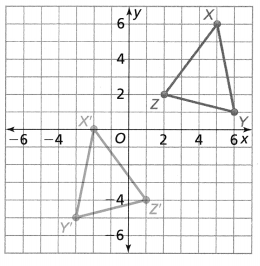
Answer:
It is given that
You are making two triangular flags for a project and need the flags to be the same shape and size. △XYZ and △X’Y’Z’ are the flags you have drawn.
Now,
The given coordinate plane is:

From the given coordiate plane,
The vertices of ΔXYZ are:
X (5, 6), Y (6, 1), and Z (2, 2)
he vertices of ΔX’Y’Z’ are:
X’ (-2, 0), Y’ (-3, -5), and Z’ (1, -4)
So,
The representtaion of the sequence of transformation to find whether two flags have the same size and the same shape or not is:
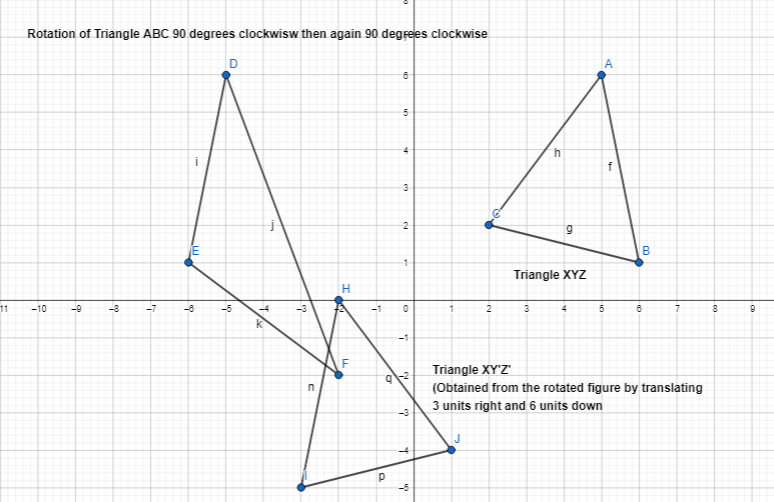
Question 11.
Which two triangles are congruent? Describe the sequence of transformations that maps one figure onto the other.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔABC are:
A (-3, 2), B (-2, 7), and C (-7, 4)
The vertices of ΔQRS are:
Q (4, 7), R (2, 2), and S (7, 2)
The vertices of ΔXYZ are:
X (-2, -7), Y (-2, -3), and Z (-7, -5)
The vertices of ΔDEF are:
D (7, -5), E (2, -2), and F (2, -7)
Now,
We know that,
The two figures are said to be congruent when
a. The 2 figures have the same size i.e., the same length and the same angle measure
b. The 2 figures have the same shape
So,
The figures that are congruent to each other are represented as:
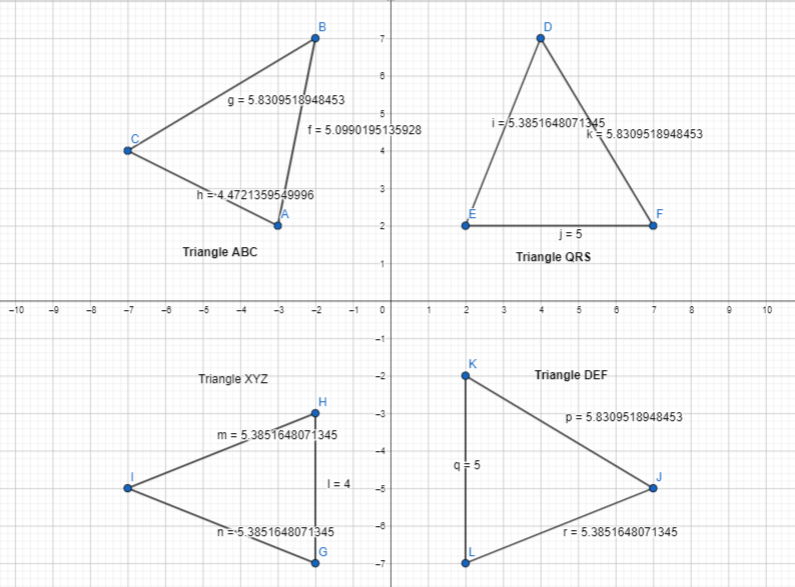
So,
From the above,
We can say that ΔQRS and ΔDEf are congruent
Hence,
The sequence of Transformations to show ΔQRS and ΔDEF are congruent is:
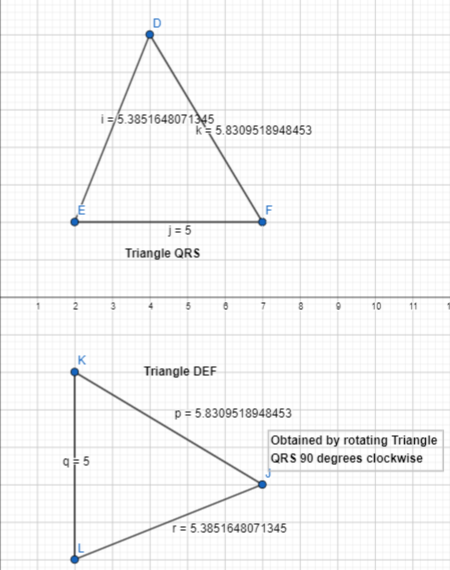
Question 12.
Is △LMN ≅ △XYZ? Explain.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔLMN are:
L (7, 9), M (9, 5), and N (6, 5)
The vertices of ΔXYZ are:
X (2, 2), Y (5, 4), and Z (5, 1)
Now,
We know that,
The two figures are said to be congruent when
a. The 2 figures have the same size i.e., the same length and the same angle measure
b. The 2 figures have the same shape
So,
The sequence of transformations to find whether ΔLMN is congruent to ΔXYZ is:
Hence, from the above,
We can conclude that ΔLMN is not congruent to ΔXYZ since they don’t have the same side lengths
Question 13.
Higher-Order Thinking A student was asked to describe a sequence of transformations that maps △DEF onto △D’ E’F’, given that △DEF ≅ △D’ E’F’. She incorrectly said the sequence of transformations that maps △DEF onto △D’ E’F’ is a reflection across the x-axis, followed by a translation of 6 units right and 4 units up. What mistake did the student likely make?
Answer:
It is given that
A student was asked to describe a sequence of transformations that maps △DEF onto △D’ E’F’, given that △DEF ≅ △D’ E’F’. She incorrectly said the sequence of transformations that maps △DEF onto △D’ E’F’ is a reflection across the x-axis, followed by a translation of 6 units right and 4 units up
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔDEF are:
D (4, 5), E (5, 1), and F (1, 2)
The vertices of ΔD’E’F’ are:
D’ (-2, -1), E’ (-1, 3), and F’ (-5, 2)
Now,
The correct sequence of Transformations to show ΔDEF and ΔD’E’F’ are congruent is:
Hence, from the above,
We can conclude that the mistake done by a student is the interchange of the sequence of Transformations
Hence,
The correct sequence of Transformations is:
Translation of 6 units left and 4 units down followed by the reflection across the x-axis
Assessment Practice
Question 14.
PART A
How can you determine whether △DEF ≅ △D’ E’ F?
A. Determine whether a sequence of rotations maps △DEF onto △D’E’F’.
B. Determine whether a sequence of transformations maps △DEF onto △D’ E’F’.
C. Determine whether a sequence of translations maps △DEF onto △D’ E’F’.
D. Determine whether a sequence of reflections maps △DEF onto △D’ E’F’.
Answer:
We know that,
If we want to find whether the given figures are congruent or not, then
We have to determine whether a sequence of transformations maps ΔDEF onto ΔD’E’F’
Hence, from the above,
We can conclude that option A matches the given situation
PART B
Is △DEF ≅ △D’ E’ F? Explain.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔDEF are:
D (5, 5), E (6, 3), and F (2, 4)
The vertices of ΔD’E’F’ are:
D’ (-2, -1), E’ (-3, 1), and F’ (1, 0)
So,
The representation of the sequence of transformations to find out whether ΔDEf and ΔD’E’F’ are congruent or not is:
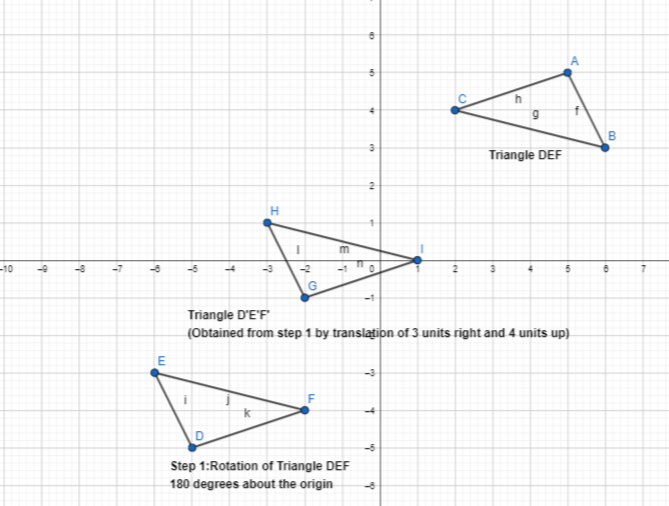
Hence, from the above,
We can conclude that ΔDEF is congruent to ΔD’E’F’
Topic 6 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary Describe three transformations where the image and preimage have the same size and shape. Lesson 6-1, Lesson 6-2, and Lesson 6-3
Answer:
We know that,
There are four types of transformations. They are:
a. Translation
b. Reflection
c. Rotation
d. Translation
Now,
Some transformations keep the pre-image and image congruent. Congruent means that they are the same size and shape or that they have the same measurements. They make not have the same orientation
Hence,
Three of the four transformations that preserve the size and shape of the pre-image are: Translation, Rotation, and Reflections
For 2-6, use the figures below.
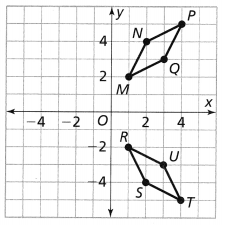
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of the quadrilateral MNPQ are:
M (1, 2), N (2, 4), P (4, 5), and Q (3, 3)
The vertices of the quadrilateral RSTU are:
R (1, -2), S (2, -4), T (4, -5), and U (3, -3)
Question 2.
What are the coordinates of each point after quadrilateral RSTU is rotated 90° about the origin? Lesson 6-3
Answer:
We know that,
When any point is rotated 90° about the origin,
(x, y) before rotation ——–> (-y, x) after rotation
Hence,
After 90° rotation about the origin,
The coordinates of each point of the quadrilateral RSTU will become:
R (2, 1), S (4, 2), T (5, 4), and U (3, 3)
Question 3.
What are the coordinates of each point after quadrilateral MNPQ is translated 2 units right and 5 units down? Lesson 6-1
Answer:
We know that,
When the translation occurs,
(x, y) before Translation ——-> (x + h, y + k) after Translation
Where,
h is the translation on the x-axis
k is the translation on the y-axis
We will take the positive value of h when the translation occurs on the right side of the x-axis
We will take the negative value of h when the translation occurs on the left side of the x-axis
We will take the positive value of k when the translation occurs on the top side of the y-axis
We will take the negative value of k when the translation occurs on the down side of the y-axis
Hence,
After the Translation of 2 units right and 5 units down,
The coordinates of each point of the quadrilateral MNPQ will become:
M (1 + 2, 2 – 5), N (2 + 2, 4 – 5), P (4 + 2, 5 – 5), and Q (3 + 2, 3 – 5)
M (3, -3), N (4, -1), P (6, 0), and Q (5, -2)
Question 4.
What are the coordinates of each point after quadrilateral MNPQ is reflected across the x-axis and then translated into 3 units left? Lessons 6-2 and 6-4
Answer:
We know that,
The vertices of the quadrilateral MNPQ are:
M (1, 2), N (2, 4), P (4, 5), and Q (3, 3)
So,
After the vertices of the quadrilateral, MNPQ reflected across the x-axis,
The vertices of the quadrilateral MNPQ will become:
M (1, -2), N (2, -4), P (4, -5), and Q (3, -3)
Now,
After the Translation of 3 units left,
The vertices of the quadrilateral MNPQ will become:
M (1 – 3, -2), N (2 – 3, -4), P (4 – 3, -5), and Q (3 – 3, -3)
M (-2, -2), N (-1, -4), P (1, -5), and Q (0, -3)
Hence, from the above,
We can conclude that the coordinates of each point after quadrilateral MNPQ is reflected across the x-axis and then translated into 3 units left are:
M (-2, -2), N (-1, -4), P (1, -5), and Q (0, -3)
Question 5.
Which series of transformations maps quadrilateral MNPQ onto quadrilateral RSTU? Lesson 6-4
A. reflection across the x-axis, translation 4 units down
B. reflection across the y-axis, translation 4 units down
C. rotation 180° about the origin, and then reflection across the x-axis
D. rotation 180° about the origin, and then reflection across the y-axis
Answer:
The representation of the series of transformations that maps the quadrilateral MNPQ onto the quadrilateral RSTU is:
Hence, from the above,
We can conclude that option A matches the given situation
Question 6.
Is quadrilateral MNPQ congruent to quadrilateral RSTU? Explain. Lesson 6-5
Answer:
We know that,
The 2 figures are said to be congruent only when:
a. The shapes of the 2 figures are the same
b. The sizes of the 2 figures are the same (Side lengths, and Angle measures)
Now,
From the above,
We can observe that the side lengths are not the same
Hence, from the above,
We can conclude that the quadrilateral MNPQ is not congruent to the quadrilateral RSTU
Topic 6 MID-TOPIC PERFORMANCE TASK
A tessellation is a design in a plane that uses one or more congruent figures, with no overlaps and no gaps, to cover the entire plane. A tessellation of an equilateral triangle is shown.
PART A
Explain how the tessellation of an equilateral triangle is formed using reflections.
Answer:
We know that,
When you cut a shape out of paper, then flip it over, the flipped shape looks like a mirror image of the original shape. So a tessellation made with this technique is called a “Reflection tessellation”
Now,
See if the figure will fit together with no gaps. The answer is yes, the figures will tessellate because it is made up of two shapes that do tessellate
PART B
Explain how the tessellation of an equilateral triangle is formed using rotations.
Answer:
We know that
A “Rotational tessellation” is a pattern where the repeating shapes fit together by rotating 90 degrees
Now,
See if the figure will fit together with no gaps. The answer is yes, the figures will tessellate because it is made up of two shapes that do tessellate
PART C
Which of the regular polygon(s) below can be tessellated using a series of transformations?
Answer:
We know that,
Equilateral triangles, squares, and regular hexagons are the only regular polygons that will tessellate. Therefore, there are only three regular tessellations.
Hence, from the above,
We can conclude that square and pentagon can be tessellated by using a series of transformations
Lesson 6.6 Describe Dilations
Solve & Discuss It!
A landscape architect designs a small splash pad represented by △ABC. Then she decides to make the splash pad larger as shown by △ADE. How are the splash pad designs alike? How are they different?

I can… dilate two-dimensional figures
Answer:
It is given that
A landscape architect designs a small splash pad represented by △ABC. Then she decides to make the splash pad larger as shown by △ADE.
Now,
The given landscape architect is:

Now,
From the given landscape architect,
We can observe that the difference in the splash designs
Hence, from the above landscape architect,
We can conclude that
The splash designs are alike in:
a. Shape b. Angle measures c. Orientation
The splash designs are different in:
a. Side lengths
Look for Relationships
How can you use what you know about scale drawings to compare and contrast the designs?
Answer:
A dilation is a transformation that results in an image with the same shape, angle measures, and orientation as the preimage, but different side lengths.
We know that,
When the scale factor is greater than 1, the dilation is a reduction.
When the scale factor is between 0 and 1, the dilation is an enlargement.
Focus on math practices
Reasoning Paul wants to make two square picnic tables. One table will have side lengths that are \(\frac{1}{2}\) of the lengths of the second table. How do the tablets compare? Explain.
Answer:
It is given that
Paul wants to make two square picnic tables. One table will have side lengths that are \(\frac{1}{2}\) of the lengths of the second table
So,
The size of the tables are in the ratio of \(\frac{1}{2}\) : 1
So,
The size of the tables are in the ratio of 1:2
Hence, from the above,
We can conclude that the side lengths of one table are 2 times the side lengths of the second table
Essential Question
What is the relationship between a preimage and its image after a dilation?
Answer:
After dilation, the pre-image and image have the same shape but not the same size.
In terms of Sides:
In dilation, the sides of the pre-image and the corresponding sides of the image are proportional.
Try It!
F’G’ H’I’ is the image of FGHI after a dilation with center at the origin. What is the scale factor?
The ratio of a side length in FGHI to a corresponding side length in F’GH’I’is: \(\frac{}{}\)
The scale factor is __________.
Answer:
It is given that
F’G’ H’I’ is the image of FGHI after a dilation with center at the origin.
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of FGHI are:
F (1, 1), G (1, 2), H (2, 2), and I (2, 1)
The vertices of F’G’H’I’ are:
F’ (5, 5), G’ (5, 10), H’ (10, 10), and I’ (10, 5)
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
The ratio of a side length in FGHI to a corresponding side length in F’GH’I’is:
\(\frac{Side length of F’G’}{Side length of FG}\) (or) \(\frac{Side length of H’I’}{Side length of HI}\)
= \(\frac{0 + 5}{0 + 1}\) (or) \(\frac{0 + 5}{0 + 1}\)
= 5
So,
The scale factor is: 5
Hence, from the above,
We can conclude that
The ratio of a side length in FGHI to a corresponding side length in F’GH’I’is: \(\frac{5}{1}\)
The scale factor is 5.
Convince Me!
Quadrilateral WXYZ is the image of quadrilateral FGHI after a dilation with center at the origin and a scale factor of 3.5. What are the coordinates of the vertices of quadrilateral WXYZ?
Answer:
It is given that
Quadrilateral WXYZ is the image of quadrilateral FGHI after a dilation with center at the origin and a scale factor of 3.5
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of FGHI are:
F (1, 1), G (1, 2), H (2, 2), and I (2, 1)
It is given that
The scale factor is: 3.5
So,
The vertices of the quadrilateral WXYZ are:
W ( 1 × 3.5, 1 ×3.5), X (1 × 3.5, 2 × 3.5), Y (2 × 3.5, 2 × 3.5), and Z (2 × 3.5, 1 × 3.5)
So,
W (3.5, 3.5), X (3.5, 7), Y (7, 7), and Z (7, 3.5)
Hence, from the above,
We can conclude that
The coordinates of the vertices of quadrilateral WXYZ are:
W (3.5, 3.5), X (3.5, 7), Y (7, 7), and Z (7, 3.5)
Try It!
A dilation maps point L(3, 6) to its image L’ (2, 4). Complete the dilation of figure LMN and label the image L’M’N’. What is the scale factor? What is the length of side M’N’?
Answer:
It is given that
A dilation maps point L(3, 6) to its image L’ (2, 4). Complete the dilation of figure LMN and label the image L’M’N’
Now,
The given coordinate plane is:

From the coordinate plane,
The vertices of ΔLMN are:
L (3, 6), M (3, 3), and N (6, 3)
It is given that the image of L is: L’ (2, 4)
Now,
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
The scale factor = \(\frac{Side length of L’}{Side length of L}\)
= \(\frac{4 – 2}{6 – 3}\)
= \(\frac{2}{3}\)
So,
The scale factor is: \(\frac{2}{3}\)
Now,
The coordinates of M’ = The coordinates of M × \(\frac{2}{3}\)
= (3, 3) × \(\frac{2}{3}\)
= (3 × \(\frac{2}{3}\), 3 × \(\frac{2}{3}\))
= (2, 2)
The coordinates of N’ = The coordinates of N × \(\frac{2}{3}\)
= (6, 3) × \(\frac{2}{3}\)
= (6 × \(\frac{2}{3}\), 3 × \(\frac{2}{3}\))
= (4, 2)
Now,
Compare M’ and N’ with (x 1, y 1), (x 2, y 2 )
We know that,
The distance between 2 points = √(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
So,
The side length of M’N’ = √(4 – 2 ) 2 + (2 – 2 )2
= 2 units
Hence, from the above,
We can conclude that
The scale factor is: \(\frac{2}{3}\)
The side length of M’N’ is: 2 units
KEY CONCEPT
A dilation is a transformation that results in an image with the same shape, angle measures, and orientation as the preimage, but different side lengths.
When the scale factor is greater than 1, the dilation is an enlargement.
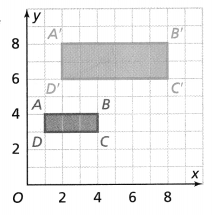
When the scale factor is between 0 and 1, the dilation is a reduction.
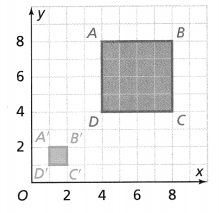
Do You Understand?
Question 1.
Essential Question What is the relationship between a preimage and its image after a dilation?
Answer:
After dilation, the pre-image and image have the same shape but not the same size.
In terms of Sides:
In dilation, the sides of the pre-image and the corresponding sides of the image are proportional.
Question 2.
Generalize When will a dilation be a reduction? When will it be an enlargement?
Answer:
When the scale factor is greater than 1, the dilation is an enlargement.

When the scale factor is between 0 and 1, the dilation is a reduction.

Question 3.
Reasoning Flora draws a rectangle with points at (12, 12), (15, 12), (15,9), and (12, 9). She dilates the figure with center at the origin and a scale factor of \(\frac{3}{4}\). what is the measure of each angle in the image? Explain.
Answer:
It is given that
Flora draws a rectangle with points at (12, 12), (15, 12), (15,9), and (12, 9). She dilates the figure with center at the origin and a scale factor of \(\frac{3}{4}\)
So,
The vertices for the image of the given rectangle = (x × \(\frac{3}{4}\), y × \(\frac{3}{4}\))
So,
The vertices for the image of the given rectangle wil be:
( 12 × \(\frac{3}{4}\), 12 × \(\frac{3}{4}\)), (15 × \(\frac{3}{4}\), 12 × \(\frac{3}{4}\)), (15 × \(\frac{3}{4}\), 9 × \(\frac{3}{4}\)), and (12 × \(\frac{3}{4}\), 9 × \(\frac{3}{4}\))
= (9, 9), (11.25, 9), (11.25, 6.75), and (9, 6.75)
Now,
We know that,
In dilation,
a. The preimage and image are the same in shape, orientation, and angle measures
b. the preimage and the image are different in size and the side lengths
So,
The representation of the angle measures in the preimage and image of the given rectangle is:
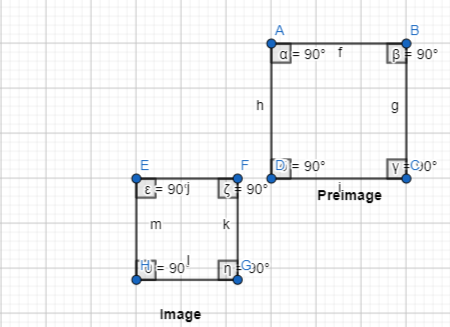
Hence, from the above,
We can conclude that the measure of each angle in the image is: 90°
Do You Know How?
In 4-6, use the coordinate grid below.
Answer:
The given coordinate plane is:

From the coordinate plane,
The vertices of Figure 1 are:
(4, 4), (6, 8), and (8, 4)
The vertices of Figure 2 are:
(2, 2), (3, 4), and (4, 2)
The vertices of Figure 3 are:
(1, 1), (1.5, 2), and (2, 1)
Question 4.
Figure 3 is the image of Figure 1 after a dilation with a center at the origin. What is the scale factor? Explain.
Answer:
It is given that
Figure 3 is the image of Figure 1 after a dilation with a center at the origin
Now,
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
Scale factor = \(\frac{4}{1}\) (or) \(\frac{6}{1.5}\) (or) \(\frac{8}{2}\)
= 4
Hence, from the above,
We can conclude that the scale factor is “4” so that Figure 3 is the image of Figure 1
Question 5.
What are the coordinates of the image of Figure 2 after a dilation with center at the origin and a scale factor of 3?
Answer:
We know that,
The vertices of Figure 2 are:
(2, 2), (3, 4), and (4, 2)
So,
With a scale factor of 3,
The vertices of Figure 2 will become:
(2 × 3, 2 × 3), (3 × 3, 4 × 3), and (4 × 3, 2 × 3)
= (6, 6), (9, 12), and (12, 6)
Hence, from the above,
We can conclude that the coordinates of the image of Figure 2 after a dilation at the origin and a scale factor of 3 are:
(6, 6), (9, 12), and (12, 6)
Question 6.
Which figures represent a dilation with a scale factor of \(\frac{1}{2}\)?
Answer:
We know that,
The vertices of Figure 1 are:
(4, 4), (6, 8), and (8, 4)
The vertices of Figure 2 are:
(2, 2), (3, 4), and (4, 2)
The vertices of Figure 3 are:
(1, 1), (1.5, 2), and (2, 1)
Now,
If we consider Figure 2 as the preimage and Figure 1 as the image, then
Scale factor = \(\frac{2}{4}\) (or) \(\frac{3}{6}\) (or) \(\frac{4}{8}\)
= \(\frac{1}{2}\)
If we consider Figure 3 as the preimage and Figure 2 as the image, then
Scale factor = \(\frac{1}{2}\) (or) \(\frac{1.5}{3}\) (or) \(\frac{2}{4}\)
= \(\frac{1}{2}\)
Hence, from the above,
We can conclude that (Figure 2, Figure 1) and (Figure 3, Figure 2) represent a dilation with a scale factor of \(\frac{1}{2}\)
Practice & Problem Solving
Question 7.
Leveled Practice Draw the image of △DEF after a dilation with center (0, 0) and scale factor of 2.
Find the coordinates of each point in the original figure.
D(____, (____) E(____, (____) F(____, (____)
Multiply each coordinate by _______.
Find the coordinates of each point in the image:
D'(____, (____) E'(____, (____) F'(____, (____)
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔDEF are:
D (0, 0), E (2, 0), and F (0, 2)
Now,
With a scale factor of 2,
Multiply each coordinate with 2
The coordinates of ΔDEF will become:
D (0 × 2, 0 × 2), E (2 × 2, 0 × 2), and F (0 × 2, 2 × 2)
D (0, 0), E (4, 0), and F (0, 4)
So,
The coordinates of the points for the image of ΔDEF are:
D’ (0, 0), E’ (4, 0), and F’ (0, 4)
Hence,
The representation of ΔDEF and its image ΔD’E’F’ is:
Question 8.
Find the scale factor for the dilation shown.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of Figure DEFG are:
D (0, 0), E (5, 0), F (5, 6), and G (0, 6)
The vertices of Figure D’E’F’G’ are:
D’ (0, 0), E’ (15, 0), G’ (15, 18), and H’ (0, 18)
Now,
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
Scale factor = \(\frac{15}{5}\) (or) \(\frac{18}{6}\)
= 3
Hence, from the above,
We can conclude that
The scale factor for the given dilation is: 3
Question 9.
Critique Reasoning For the dilation with center (0, 0) shown on the graph, your friend says the scale factor is \(\frac{5}{2}\). What is the correct scale factor? What mistake did your friend likely make?
Answer:
It is given that
For the dilation with center (0, 0) shown on the graph, your friend says the scale factor is \(\frac{5}{2}\)
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔABC are:
A (0, 5), B (-5, 0), and C (5, -5)
The vertices of ΔA’B’C’ are:
A’ (0, 2), B’ (-2, 0), C’ (2, -2)
Now,
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
Scale factor = \(\frac{2}{5}\) (or) \(\frac{-2}{-5}\)
= \(\frac{2}{5}\)
Hence, from the above,
We can conclude that
The correct scale factor is: \(\frac{2}{5}\)
The mistake done by your friend is:
The consideration of the scale factor as \(\frac{Length of the preimage}{length of the image}\) instead of \(\frac{Length of the image}{Length of the preimage}\)
Question 10.
The smaller figure is the image of dilation of the larger figure. The origin is the center of dilation. Tell whether the dilation is an enlargement or a reduction. Then find the scale factor of the dilation.
Answer:
It is given that
The smaller figure is the image of dilation of the larger figure. The origin is the center of dilation
Now,
The given coordinate plane is:

From the given coordinate plane,
The coordinates of each point of the preimage are:
(3, 6), (15, 6), (15, 18), and (3, 18)
The coordinates of each point of the image are:
(1, 2), (5, 2), (5, 6), and (1, 6)
Now,
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
Scale factor = \(\frac{1}{3}\) (or) \(\frac{2}{6}\) (or) \(\frac{5}{15}\) (or) \(\frac{6}{18}\)
= \(\frac{1}{3}\)
Now,
Since the scale factor is less than 1, the dilation is a reduction
Hence, from the above,
We can conclude that
The given dilation is a reduction
The scale factor is: \(\frac{1}{3}\)
Question 11.
Higher-Order Thinking Q’R’S’T’ is the image of QRST after a dilation with center at the origin.
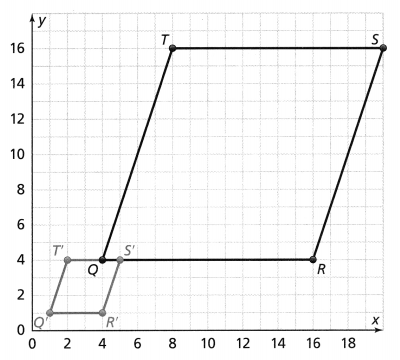
Answer:
It is given that
Q’R’S’T’ is the image of QRST after a dilation with center at the origin
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of the parallelogram QRST are:
Q (4, 4), R (16, 4), S (20, 16), and T (8, 16)
The vertices of the parallelogram Q’R’S’T’ are:
Q’ (1, 1), R’ (4, 1), S’ (5, 4), and T’ (2, 4)
a. Find the scale factor.
Answer:
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
Scale factor = \(\frac{4}{1}\) (or) \(\frac{16}{4}\) (or) \(\frac{20}{5}\) (or) \(\frac{8}{2}\)
= 4
Hence, from the above,
We can conclude that the scale factor is: 4
b. Find the area of each parallelogram. What is the relationship between the areas?
Answer:
We know that,
Area of the parallelogram = Base × Height
Now,
the representation of the side lengths of the parallelogram QRST and its dilation Q’R’S’T’ is:
So,
The area of the parallelogram QRST = 12.6 × 12
= 151.2 square units
The area of the parallelogram Q’R’S’T’ = \(\frac{The area of the parallelogram QRST}{4}\)
= 37.8 square units
Hence, from the above,
We can conclude that
The area of the parallelogram QRST is: 151.2 sq. units
The area of the parallelogram Q’R’S’T’ is: 37.8 sq. units
The relationship between the two areas is:
The area of the parallelogram Q’R’S’T’ = \(\frac{The area of the parallelogram QRST}{4}\)
Assessment Practice
Question 12.
Triangle PQR is the image of △JKL after a dilation. Is the dilation an enlargement or a reduction? Explain.
A. An enlargement, because the image is larger than the original figure
B. An enlargement, because the image is smaller than the original figure
C. A reduction, because the image is smaller than the original figure
D. A reduction, because the image is larger than the original figure
Answer:
It is given that
Triangle PQR is the image of △JKL after a dilation
Now,
From the given figure,
We can observe that ΔPQR is larger than ΔJKL
So,
We can say that the dilation is an enlargement
Hence, from the above,
We can conclude that option A matches with the given situation
Question 13.
Rectangle QUAD has coordinates Q(0, 0), U(0, 3), A(6, 3), and D(6, 0). Q’U’ A’D’ is the image of QUAD after a dilation with center (0, 0) and a scale factor of 6. What are the coordinates of point D’? Explain.
Answer:
It is given that
Rectangle QUAD has coordinates Q(0, 0), 4(0, 3), A6, 3), and D(6, 0). Q’U’ A’D’ is the image of QUAD after a dilation with center (0, 0) and a scale factor of 6.
So,
With a scale factor of 6,
The vertices of the rectangle QUAD will become:
Q (0 × 6, 0 × 6), U (0 × 6, 3 × 6), A (6 × 6, 3 × 6) and D (6 × 6, 0 × 6)
= Q (0, 0), U (0, 18), A (36, 18), and D (6, 0)
So,
After a dilation,
The vertices of the rectangle QUAD will become the vertices of the rectangle Q’U’A’D’
So,
The vertices of the rectangle Q’U’A’D’ are:
Q’ (0, 0), U’ (0, 18), A’ (36, 18), and D’ (36, 0)
Hence, from the above,
We can conclude that the coordinates of point D’ are: (36, 0)
Lesson 6.7 Understand Similar Figures
Solve & Discuss It!
Andrew draws the two figures shown on a coordinate plane. How are the two figures alike? How are they different? How do you know?
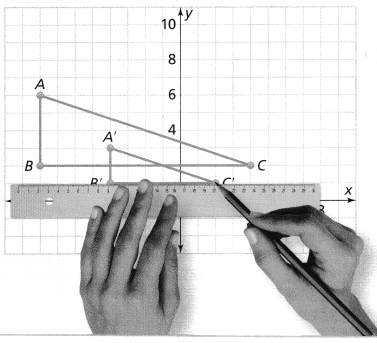
I can… use a sequence of transformations, including dilations, to show that figures are similar.
Answer:
It is given that
Andrew draws the two figures shown on a coordinate plane
Now,
The given figures are:

From the above,
We can observe that
ΔABC is the preimage
ΔA’B’C’ is the image
We can also observe that
The image is smaller than the image since the transformation we used when drawing the image is a “Dilation”
Hence,
Since the transformation we used is a “Dilation”,
The two figures are similar in terms of:
a. Shape b. Size c. Orientation d. Angle measures
The two figures are different in terms of:
a. Side lengths
Look for Relationships
Is △ABC a preimage of △A’B’C’? How do you know?
Answer:
The given figures are:

From the given figures,
We can clearly observe that the transformation called “Dilation” takes place
Since the dilation takes place,
We can conclude that ΔABC is a preimage of ΔA’B’C’
Focus on math practices
Reasoning How can you use the coordinates of the vertices of the triangles to identify the transformation that maps △ABC to △A’B’C’? Explain.
Answer:
The given figures are:

Now,
Fro the given figures,
We know that a transformation called a “Dilation” takes place
So,
We know that,
The “Scale factor” is the ratio of a length in the image to the corresponding length in the preimage
So,
Scale factor = [altex]\frac{The x-coordinate (or) y-coordinate that maps A’ or B’ or C’}{The x-coordinate (or) y-coordinate that maps A or B or C}[/latex}
Hence, from the above,
We can conclude that
By using the “Scale factor”, the coordinates of the vertices of the triangles can be used to identify the transformation that maps △ABC to △A’B’C’
Essential Question
How are similar figures related by a sequence of transformations?
Answer:
Two figures are similar if and only if one figure can be obtained from the other by a single transformation, or a sequence of transformations, including translations, reflections, rotations, and/or dilations. Similarity transformations preserve shape, but not necessarily size, making the figures “similar”
Try It!
Is △ΑΒC similar to △A’ B’ C?
The triangles _________ similar.
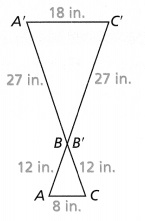
Answer:
The given figures are:

Now,
If we want to find the 2 triangles are similar or not, find the scale factor and find whether they have the same shape or not
If the scale factor for 2 triangles is the same, then those triangles are similar
Now,
We know that,
The scale factor is defined as the distance from this center point to a point on the preimage and also the distance from the center point to a point on the image
Now,
For AB and A’B’,
Scale factor = \(\frac{27}{12}\)
= \(\frac{9}{4}\)
For BC and B’C’,
Scale factor = \(\frac{27}{12}\)
= \(\frac{9}{4}\)
For AC and A’C’,
Scale factor = \(\frac{18}{8}\)
= \(\frac{9}{4}\)
Since the scale factor is equal for all the corresponding sides
We can conclude that ΔABC is similar to ΔA’B’C’
Convince Me!
What sequence of transformations shows that △ABC is similar to △A’ B’C’?
Answer:
The sequence of Transformations that shows ΔABC is similar to ΔA’B’C’ is:
a. Rotation b. Dilation c. Translation
Try It!
a. Graph the image of JKL after a reflection across the line x = 1 followed by dilation with a scale factor of \(\frac{1}{2}\) and center of dilation point J’.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔJKL are:
J (-2, -4), K (-4, 0), and L (-2, 1)
The vertices of ΔPQR are:
P (-4, 2), Q (4, 6), and R (6, 2)
Now,
After the reflection of ΔJKL across the line x = 1,
J (-1, 4), K (-3, 0), and L (-1, -1)
So,
With a scale factor of \(\frac{1}{2}\),
The vertices of ΔJKL will become:
J (-1, 4) × \(\frac{1}{2}\), K (-3, 0) × \(\frac{1}{2}\), and L (-1, -1) × \(\frac{1}{2}\)
So,
J’ (-0.5, 2), K’ (-1.5, 0), and L’ (-0.5, -0.5)
Hence,
The representation of the image of JKL after a reflection across the line x = 1 followed by dilation with a scale factor of \(\frac{1}{2}\) and center of dilation point J’ is:
b. Is △JKL similar to △PQR?
Answer:
We know that,
The vertices of ΔJKL are:
J (-2, -4), K (-4, 0), and L (-2, 1)
The vertices of ΔPQR are:
P (-4, 2), Q (4, 6), and R (6, 2)
Now,
Step 1:
Rotate the vertices of ΔJKL 270° about the origin
We know that,
(x, y) before 270° rotation —-> (y, -x) after 270° rotation
So,
The vertices of ΔJKL will be:
J (-4, 2), K (0, 4), and L (1, 2)
Step 2:
Dilate the vertices of ΔJKL we obtained in step 1 by a scale factor of 2
So,
The vertices of ΔJKL will be:
J (-8, 4), K (0, 8), and L (2, 4)
Step 3:
Translate the vertices of ΔJKL we obtained in step 2 by 4 units right and 2 units down
So,
The vertices of ΔJKL will become:
P (-4, 2), Q (4, 6), and R (6, 2)
So,
The representation of the sequence of transformations is:
Hence, from the above,
We can conclude that ΔJKL is similar to ΔPQR
KEY CONCEPT
Two-dimensional figures are similar if there is a sequence of rotations, reflections, translations, and dilations that maps one figure onto the other.
Do You Understand?
Question 1.
Essential Question How are similar figures related by a sequence of transformations?
Answer:
Two figures are similar if and only if one figure can be obtained from the other by a single transformation, or a sequence of transformations, including translations, reflections, rotations, and/or dilations. Similarity transformations preserve the shape, but not necessarily size, making the figures “similar”
Question 2.
Be Precise How do the angle measures and side lengths compare in similar figures?
Answer:
Matching sides of two or more polygons are called corresponding sides, and matching angles are called corresponding angles. If two figures are similar, then the measures of the corresponding angles are equal and the ratios of the lengths of the corresponding sides are proportional.
Question 3.
Generalize Does a given translation, reflection, or rotation, followed by a given dilation, always map a figure to the same image as that same dilation followed by that same translation, reflection, or rotation? Explain.
Answer:
We know that,
The images formed by reflection, translation, and rotation have the same shape and size whereas dilation has the same shape but a different size
In the same way,
The image formed by dilation has the same shape but a different size whereas the image formed by reflection, translation, and rotation has the same shape and size as the image formed in dilation
Hence, from the above,
We can conclude that
The translation, reflection, or rotation, followed by a given dilation, always map a figure to the same image as that same dilation followed by that same translation, reflection, or rotation
Do You Know How?
Question 4.
Is trapezoid ABCD – trapezoid EFGH? Explain.
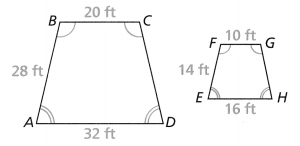
Answer:
The given figures are:

From the given figures,
We can observe that
The corresponding angles i.e., the opposite angles are equal
Now,
The ratio of the side lengths of the corresponding figures = \(\frac{32}{16}\) (or) \(\frac{28}{14}\) (or) \(\frac{20}{10}\)
= 2
So,
The ratio of the side lengths of the corresponding figures are the same
Now,
We know that,
Two figures are said to be similar if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal. This common ratio is called the scale factor
Hence, from the above,
We can conclude that
Trapezoid ABCD – Trapezoid EFGH
Use the graph for 5 and 6.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔABC are:
A (-4, -2), B (-1, -2), and C (-3, -3)
The vertices of ΔDEF are:
D (9, -5), E (6, -8), and F (1, -5)
Question 5.
△ABC is dilated by a factor of 2 with a center of dilation at point C, reflected across the x-axis, and translated 3 units up. Graph the resulting similar figure.
Answer:
We know that,
The vertices of ΔABC are:
A (-4, -2), B (-1, -2), and C (-3, -3)
So,
Step 1:
After dilation by a factor of 2:
Multiply all the coordinates of each point by 2
So,
The vertices of ΔABC are:
A (-8, -4), B (-2, -4), and C (-6, -6)
Now,
With a dilation at point C,
Add all the coordinates of each point with -3
So,
The vertices of ΔABC are:
A (-11, -7), B (-5, -7), and C (-9, -9)
Step 2:
When the vertices of ΔABC that we obtained in step 1 reflects across the x-axis,
The vertices of ΔABC will be:
A (-11, 7), B (-5, 7), and C (-9, 9)
Step 3:
When the vertices of ΔABC we obtained in step 2 translated by 3 units up,
Add all the y-coordinates of each point with 3
So,
The vertices of ΔABC will be:
A (-11, 10), B (-5, 10), and C (-9, 12)
Hence,
The representation of all the steps is:
Question 6.
Is △ABC similar to △DEF? Explain.
Answer:
We know that,
The vertices of ΔABC are:
A (-4, -2), B (-1, -2), and C (-3, -3)
The vertices of ΔDEF are:
D (9, -5), E (6, -8), and F (1, -5)
We know that,
Two figures are said to be similar if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal
So,
The representation of ΔABC and ΔDEF are:
From the above,
We can observe that the ratio of the corresponding side lengths are not in the same proportion
Hence, from the above,
We can conclude that ΔABC is not similar to ΔDEF
Practice & Problem Solving
Question 7.
Leveled Practice RSTU and VXYZ are quadrilaterals. Given RSTU ~ VXYZ, describe a sequence of transformations that maps RSTU to VXYZ.
• reflection across the ________
• translation ______ unit(s) left and _______ unit(s) up
• dilation with center (0,0) and a scale factor of ________
Answer:
The given coordinate plane is:

From the coordinate plane,
The vertices of the quadrilateral VXYZ are:
V (-2, -1), X (-3, 0), Y (-2, 2), and Z (-1, 0)
The vertices of the quadrilateral RSTU are:
R (3, 0), S (6, 3), T (3, 9), and U (0, 3)
Now,
Step 1:
Reflect the vertices of the quadrilateral VXYZ across the y-axis
So,
The vertices of the quadrilateral VXYZ will be:
V (2, -1), X (3, 0), Y (2, 2), and Z (1, 0)
Step 2:
Dilate the vertices of the quadrilateral VXYZ with a scale factor of 3
So,
Multiply all the coordinates of all the vertices of the quadrilateral VXYZ by 3
So,
The vertices of the quadrilateral VXYZ will be:
V (6, -3), X (9, 0), Y (6, 6), and Z (3, 0)
Step 3:
Translate the vertices of the quadrilateral VXYZ 3 units left and 3 units up
So,
The vertices of the quadrilateral VXYZ will become:
R (3, 0), S (6, 3), T (3, 9), and U (0, 3)
Hence,
The sequence of Transformations that map the quadrilateral VXYZ onto the quadrilateral RSTU is:
Question 8.
Reasoning Is △MNO similar to △PQO? Explain.
Answer:
The given coordinate plane is:

From the coordinate plane,
The vertices of ΔMNO are:
M (6, 6 ), N (0, 6), and O (0, 0)
The vertices of ΔPQO are:
P (-12, -9), Q (0, -9), and O (0, 0)
We know that,
Two figures are said to be similar if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent, and the ratios of the lengths of their corresponding sides are equal
So,
The representation of ΔMNO and ΔPQO are:
From the above,
We can observe that
a. The ratio of the corresponding side lengths are not in the same proportion
b. The angle measures are not the same
Hence, from the above,
We can conclude that ΔMNO is not similar to ΔPQO
Question 9.
△PQR is dilated by a scale factor of 2 with a center of dilation (0, 0) and rotated 180° about the origin. Graph the resulting similar △XYZ.
Answer:
It is given that
△PQR is dilated by a scale factor of 2 with a center of dilation (0, 0) and rotated 180° about the origin.
Now,
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔPQR are:
P (2, 2), Q (4, 2), and R (3, 4)
Now,
Step 1:
Dilation of ΔPQR by a scale factor of 2:
Multiply all the coordinates of each point of ΔPQR by 2
So,
The vertices of ΔPQR will be:
P (4, 4), Q (8, 4), and R (6, 8)
Step 2:
Rotation of 180° counterclockwise about the origin:
We know that,
(x, y) before rotating 180° ——- > (-x, -y) after rotating 180°
So,
The vertices of ΔPQR that we obtained in step 1 will become:
X (-4, -4), Y (-8, -4), and Z (-6, -8)
Hence,
The graph of the resulting ΔXYZ is:
Question 10.
Describe a sequence of transformations that shows that quadrilateral RSTU is similar to quadrilateral VXYZ.
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of the quadrilateral VXYZ are:
V (-5, -5), X (-5, -1), Y (-1, -1), and Z (-1, -5)
The vertices of the quadrilateral RSTU are:
R (-16, -14), S (-16, -6), T (-8, -6), and U (-8, -14)
Now,
Step 1:
Translate the quadrilateral VXYZ 3 units left and 2 units down
So,
The vertices of the quadrilateral VXYZ will be:
V (-8, -7), X (-8, -3), Y (-4, -3), and Z (-4, -7)
Step 2:
Dilate the vertices of the quadrilateral VXYZ we obtained in step 1 by a scale factor of 2
So,
The vertices of the quadrilateral VXYZ will be:
R (-16, -14), S (-16, -6), T (-8, -6), and U (-8, -14)
Hence,
The sequence of Transformations that shows the quadrilateral VXYZ is similar to the quadrilateral RSTU is:
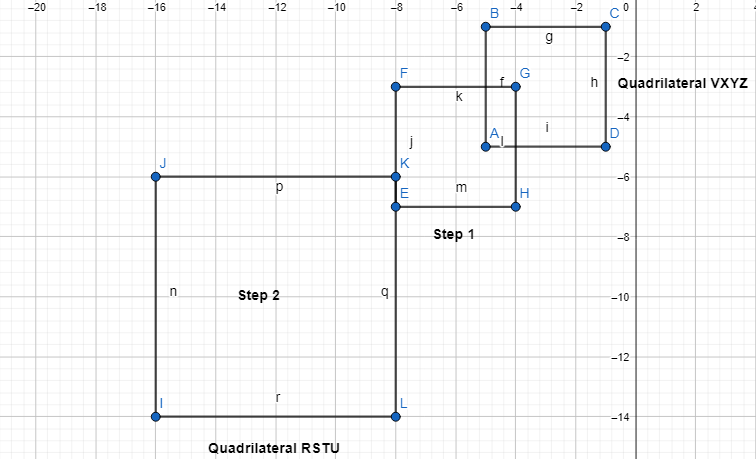
Question 11.
Construct Arguments Is △PQR similar to △XYZ? Explain.
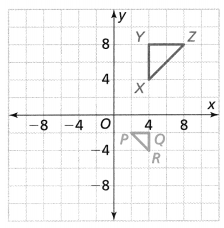
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔXYZ are:
X (4, 4), Y (4, 8), and Z (8, 8)
The vertices of ΔPQR are:
P (2, -2), Q (4, -2), and R (4, -4)
Now,
Step 1:
Rotate ΔXYZ 270° about the origin
We know that,
(x, Y) before 270° rotation —— > (y, -x) after 270° rotation
So,
The vertices of ΔXYZ will become:
X ( 4, -4), Y (8, -4), and Z (8, -8)
Step 2:
Dilate ΔXYZ with a scale factor of \(\frac{1}{2}\)
So,
The vertices of ΔXYZ that we obtained in step 1 will become:
P (2, -2), Q (4, -2), and R (4, -4)
So,
After the sequence of Rotation and Dilation of ΔXYZ,
We obtained the vertices of ΔPQR
Hence, from the above,
We can conclude that ΔPQR is similar to ΔXYZ
Question 12.
Higher-Order Thinking Given △JKL ~ △XYZ, find two possible coordinates for missing point Y. For each coordinate chosen, describe a sequence of transformations, including a dilation, that will map △JKL to △XYZ.
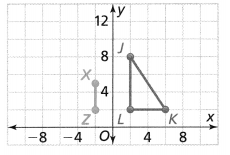
Answer:
It is given that
Given △JKL ~ △XYZ
Now,
The given coordinate plane is:

From the coordinate plane,
The vertices of ΔJKL are:
J (2, 8), K (6, 2), and L (2, 2)
The vertices of ΔXYZ are:
X (-2, 5), Y (x, y), and Z (-2, 2)
Now,
Step 1:
Reflect ΔJKL across the y-axis
So,
The vertices of ΔJKL will be:
J (-2, 8), K (-6, 2), and L (-2, 2)
Step 2:
Dilate the vertices of ΔJKL that we obtained in step by a scale factor of \(\frac{1}{2}\)
So,
The vertices of ΔJKL will be:
(-1, 4), K (-3, 1), and L (-1, 1)
Step 3:
Translate the vertices of ΔJKL that we obtained in step 2 by 1 unit left and 1 unit up
So,
The vertices of ΔJKL will become:
X (-2, 5), Y (-4, 2), and Z (-2, 2)
Hence, from the above,
We can conclude that the coordinates for the missing point Y are: (-4, 2)
Assessment Practice
Question 13.
Rajesh is making pennants in preparation for a school soccer game. He wants the pennants to be similar triangles. Which of these triangles could he use for the pennants?
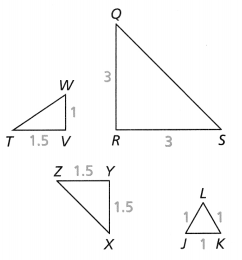
A. △QRS and △TVW
B. △QRS and △XYZ
C. △TVW and △JKL
D. △TVW and △XYZ
Answer:
It is given that
Rajesh is making pennants in preparation for a school soccer game. He wants the pennants to be similar triangles.
Now,
If we want to find which of the triangles are similar, find the scale factor and find whether they have the same shape or not
If the scale factor for 2 triangles is the same, then those triangles are similar
Now,
We know that,
The scale factor is defined as the distance from this center point to a point on the preimage and also the distance from the center point to a point on the image
Now,
For ΔQRS and ΔTVW,
Scale factor = \(\frac{3}{1}\) (or) \(\frac{3}{1.5}\)
= 3 (or) 2
For ΔQRS and ΔXYZ,
Scale factor = \(\frac{3}{1.5}\) (or) \(\frac{3}{1.5}\)
= 2
Hence from the above,
We can conclude that ΔQRS and ΔXYZ are similar triangles and he can use these triangles for the pennants
Question 14.
Determine whether the following pairs of triangles are similar or not similar.
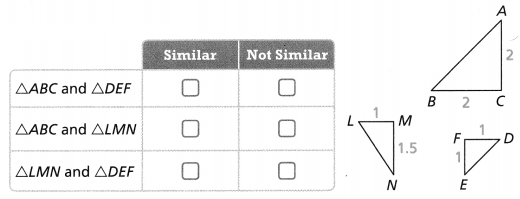
Answer:
If we want to find which of the triangles are similar, find the scale factor and find whether they have the same shape or not
If the scale factor for 2 triangles is the same, then those triangles are similar
Now,
We know that,
The scale factor is defined as the distance from this center point to a point on the preimage and also the distance from the center point to a point on the image
Now,
For ΔABC and ΔDEF,
Scale factor = \(\frac{2}{1}\) (or) \(\frac{2}{1}\)
= 2
For ΔABC and ΔLMN,
Scale factor = \(\frac{2}{1.5}\) (or) \(\frac{2}{1}\)
= 1.33 (or) 2
For ΔDEF and ΔLMN,
Scale factor = \(\frac{1}{1}\) (or) \(\frac{1.5}{1}\)
= 1 (or) 1.5
Hence from the above,
We can conclude that ΔABC and ΔDEF are similar triangles
Lesson 6.8 Angles, Lines, and Transversals
Solve & Discuss It!
Draw two parallel lines. Then draw a line that intersects both lines. Which angles have equal measures?
I can… identify and find the measures of angles formed by parallel lines and a transversal.
Answer:
Let a and b be the two parallel lines and the line that is intersecting the parallel lines is a “Transversal”
So,
The representation of the parallel lines along with the transversal is:
Now,
From the above,
The angles that have equal measures are:
Corresponding angles:
∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, and ∠4 = ∠8
Alternate Interior angles:
∠4 = ∠6, ∠3 = ∠5
Alternate Exterior angles:
∠1 = ∠7, ∠2 = ∠8
Vertically Opposite Angles:
∠1 = ∠7, ∠2 = ∠8
Use Appropriate Tools
What tools can you use to determine which angles have equal measures?
Answer:
The tools that can be used to determine which angles have equal measures are:
a. Pencil b. Scale c. Protractor d. Setsquare
Focus on math practices
Reasoning What properties or definitions can you use to describe which angles have equal measures?
Answer:
The definitions that you can use to describe which angles have equal measures are:
Corresponding angles:
Corresponding angles are angles that are in the same position relative to lines intersected by a transversal
Alternate Interior angles:
When two parallel lines are crossed by a transversal, the pair of angles formed on the inner side of the parallel lines, but on the opposite sides of the transversal are called alternate interior angles
Alternate Exterior angles:
Alternate exterior angles are the pair of angles that lie on the outer side of the two parallel lines but on either side of the transversal line
Essential Question
What are the relationships among angles that are created when a line intersects two parallel lines?
Answer:
If two parallel lines are cut by a third line, the third line is called the transversal.
So,
The relationships among angles that are created when a line intersects two parallel lines are :
(1) Corresponding angles
(2) Vertically Opposite angles
(3) Alternate interior angles
(4) Alternate exterior angles
Try It!
Which angles are congruent to ∠8?



Which angles are supplementary to ∠8?




Answer:
The given transversal is:

We know that,
The angle relationships that have equal angle measures are:
a. Corresponding angles b. Vertically opposite angles c. Alternate interior angles d. Alternate exterior angles
We know that,
The angle relationships that have supplementary angle measures are:
a. Adjacent angles
Hence, from the above,
We can conclude that
The angles that are congruent to ∠8 are: ∠4, ∠6 and ∠2
The angles that are supplementary to ∠8 are: ∠7, ∠1, ∠2, and ∠6
Convince Me!
Use what you know about other angle relationships to explain why ∠4 and ∠5 are supplementary angles.
Answer:
The given transversal is:

Now,
From the given Transversal,
We can observe that
∠4 and ∠5 are consecutive interior angles
Now,
We know that,
The sum of the consecutive interior angles is always equal to 180°
The angles that have the sum 180° are also called “Supplementary angles”
Hence, from the above,
We can conclude that ∠4 and ∠5 are supplementary angles
Try It!
What are the measures of ∠7 and ∠2? Explain.
Answer:
The given transversal is:

Now,
From the given transversal,
We can observe that
∠4 and 99° are the corresponding angles
∠4 and ∠2 are alternate interior angles
∠5 and ∠7 are vertical angles
∠4 and ∠5 are supplementary angles
So,
Now,
∠4 = 99°
Now,
∠4 + ∠5 = 180°
∠5 = 180° – 99°
∠5 = 81°
Now,
∠2 = 99°
∠7 = 81°
Hence, from the above,
We can conclude that
The values of ∠7 and ∠2 are: 81° and 99° respectively
Try It!
In the figure, a || b. What is the value of x?
Answer:
It is given that a || b
Now,
The given transversal is:

From the given transversal,
We can observe that
59° and (x + 12)° are consecutive exterior angles
Now,
We know that,
The sum of the angles of consecutive exterior angles is: 180°
So,
59°+ (x + 12)° = 180°
x + 71° = 180°
x = 180° – 71°
x = 109°
Hence, from the above,
We can conclude that the value of x is: 109°
KEY CONCEPT
If parallel lines are intersected by a transversal, then
• Corresponding angles are congruent.
• Alternate interior angles are congruent.
• Same-side interior angles are supplementary.
Do You Understand?
Question 1.
Essential Question What are the relationships among angles that are created when a line intersects two parallel lines?
Answer:
If two parallel lines are cut by a third line, the third line is called the transversal.
So,
The relationships among angles that are created when a line intersects two parallel lines are :
(1) Corresponding angles
(2) Vertically Opposite angles
(3) Alternate interior angles
(4) Alternate exterior angles
Question 2.
When parallel lines are cut by a transversal, how can you use a translation to describe how angles are related?
Answer:
Let a and b be the parallel lines
Now,
The given transversal is:
Now,
When the parallel lines are cut by a transversal,
The relation between angles is:
Corresponding angles:
∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, and ∠4 = ∠8
Alternate Interior angles:
∠4 = ∠6, ∠3 = ∠5
Alternate Exterior angles:
∠1 = ∠7, ∠2 = ∠8
Vertically Opposite Angles:
∠1 = ∠7, ∠2 = ∠8
Consecutive Interior angles:
∠4 + ∠5 = 180°, ∠3 + ∠6 = 180°
Consecutive Exterior angles:
∠1 + ∠8 = 180°, ∠7 + ∠2 = 180°
Question 3.
How many angles are created when two parallel lines are cut by a transversal? How many different angle measures are there?
Answer:
When two parallel lines are cut by a transversal, the number of angles created are: 8
Now,
The different angle measures are:
a. Corresponding angles
b. Alternate Interior angles
c. Alternate Exterior angles
d. Vertical angles
e. Consecutive interior angles
f. Consecutive exterior angles
g. Adjacent angles
Question 4.
Use Structure How can you use angle measures to tell whether two lines are parallel?
Answer:
The ways to prove two lines are parallel using angle measures are:
a. If corresponding angles are congruent.
b. If alternate interior angles are congruent.
c. If consecutive, or same side, interior angles are supplementary.
d. If alternate exterior angles are congruent.
Do You Know How?
In 5-7, use the figure below.
Question 5.
Which angles are congruent to ∠8?
Answer:
The given transversal is:

Now,
We know that,
The angle relationships that have equal angle measures are:
a. Corresponding angles b. Vertically opposite angles c. Alternate interior angles d. Alternate exterior angles
Hence, from the above,
We can conclude that
The angles that are congruent to ∠8 are: ∠2, ∠4, and ∠6
Question 6.
If m∠4 = 70°, what is m∠6? Explain.
Answer:
The given transversal is:

Now,
From the given transversal,
We can observe that
∠4 and ∠6 are alternate interior angles
We know that,
The alternate interior angles are congruent
Hence, from the above,
We can conclude that
∠4 = ∠6 = 70°
Question 7.
If m∠1 = 95°, write an equation that could be used to find the measure of ∠8. Find m∠8.
Answer:
The given transversal is:

Now,
From the given transversal,
We can observe that
∠1 and ∠8 are consecutive exterior angles
Now,
We know that,
The sum of the consecutive exterior angle measures is 180°
So,
∠1 + ∠8 = 180°
∠8 = 180° – ∠1
∠8 = 180° – 95°
∠8 = 85°
Hence, from the above,
We can conclude that the measure of ∠8 is: 85°
Question 8.
What must x equal if line a is parallel to line b?
Answer:
It is given that line a is parallel to line b
Now,
The given transversal is:

Now,
From the given transversal,
We can observe that
(2x + 35)° and 103° are the corresponding angles
We know that,
The corresponding angles are congruent
So,
(2x + 35)° = 103°
2x° = 103° – 35°
2x° = 68°
x° = \(\frac{68°}{2}\)
x° = 34°
Hence, from the above,
We can conclude that the value of x is: 34°
Practice & Problem Solving
Question 9.
If p || q, what is the value of u?
Answer:
The given transversal is:

From the given transversal,
We can observe that
u and 148° are vertically opposite angles
Now,
We know that.
The vertically opposite angles are always congruent
Hence, from the above,
We can conclude that the value of u is: 148°
Question 10.
Are ∠K and ∠B corresponding angles? Explain.
Answer:
The given transversal is:

Now,
We know that,
Corresponding angles are angles that are in the same position relative to lines intersected by a transversal
So,
From the given transversal,
We can observe that
∠B is internal and ∠K is external. They are equals if the two intersected lines by the transversal are parallel
Hence, from the above,
We can conclude that
∠K and ∠B are called “Corresponding angles” only when m || n
Question 11.
Streets A and B run parallel to each other. The measure of ∠6 is 155°. What is the measure of ∠4?
Answer:
It is given that
Streets A and B run parallel to each other. The measure of ∠6 is 155°
Now,
The given representation of streets A and B are:

Now,
From the given representation,
We can observe that
∠4 and ∠6 are consecutive interior angles
We know that,
The sum of consecutive interior angles is always equal to 180°
So,
∠4 + ∠6 = 180°
∠4 = 180° – ∠6
∠4 = 180° – 155°
∠4 = 25°
Hence, from the above,
We can conclude that the measure of ∠4 is: 25°
Question 12.
Reasoning The figure shows the design of a rectangular windowpane. The four horizontal lines are parallel. The measure of ∠6 is 53°. What is the measure of ∠12? Write and solve an equation to find the answer.
Answer:
It is given that
The figure shows the design of a rectangular windowpane. The four horizontal lines are parallel. The measure of ∠6 is 53°
Now,
The representation of the rectangular windowpane is:

Now,
From the given representation,
We can observe that
∠6 and ∠12 are consecutive interior angles
We know that,
The sum of consecutive interior angles is: 180°
so,
∠6 + ∠12 = 180°
∠12 = 180° – ∠6
∠12 = 180° – 53°
∠12 = 127°
Hence, from the above,
We can conclude that the angle measure of ∠12 is: 127°
Question 13.
In the figure, m || n. If m∠8 is (4x + 7)° and m∠2 is 107°, what is the value of x? Explain.
Answer:
It is given that
m || n and m∠8 is (4x + 7)° and m∠2 is 107°
Now,
The given transversal is:

From the given transversal,
We can observe that
∠2 and ∠8 are vertically opposite angles
We know that,
The vertically opposite angles are always congruent
So,
∠2 = ∠8
107° = (4x + 7)°
4x° = 107°- 7°
4x° = 100°
x° = \(\frac{100°}{4}\)
x° = 25°
Hence, from the above,
We can conclude that the value of x is: 25°
Question 14.
For the given figure, can you conclude m || n? Explain.
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
74° and 74° are alternate interior angles
Now,
We know that,
The Converse of the Alternate Interior Angles Theorem states that if two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel
Hence, from the above,
We can conclude that m || n since the alternate interior angles are congruent
Question 15.
Line m is parallel to line n. Find the value of x and each missing angle measure.
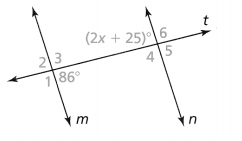
Answer:
It is given that line m is parallel to n
Now,
The given transversal is:

From the given transversal,
We can observe that
(2x + 25)° and 86° are vertically opposite angles
We know that,
The vertically opposite angles are always congruent
So,
(2x + 25)° = 86°
2x° = 86°- 25°
2x°= 61°
x° = \(\frac{61°}{2}\)
x° = 30.5°
So,
The value of x is: 30.5°
Now,
We can observe that
∠1 and 86° are supplementary angles
∠1 and ∠3 are vertical angles
∠2 and ∠3 are supplementary angles
(2x + 25)° and ∠6 are supplementary angles
∠6 and ∠4 are vertical angles
∠4 and ∠5 are supplementary angles
So,
∠1 + 86° = 180°
∠1 = 180° – 86°
∠1 = 94°
∠1 = ∠3 = 94°
∠2 + ∠3 = 180°
∠2 = 180° – ∠3
∠2 = 180° – 94°
∠2 = 86°
Now,
(2x + 25)° + ∠6 = 180°
2 (30.5)° + ∠6 = 180° – 25°
∠6 = 155° – 61°
∠6 = 94°
∠ 6 = ∠4 = 94°
∠4 + ∠5 = 180°
∠5 = 180° – ∠4
∠5 = 180° – 94°
∠5 = 96°
Hence, from the above,
We can conclude that
The value of x is: 30.5°
The missing angle measures are:
∠1 = ∠3 = 94°; ∠4 = ∠6 = 94°; ∠2 = 86°; ∠5 = 96°
Question 16.
Higher Order Thinking
a. Find the value of x given that r || s.
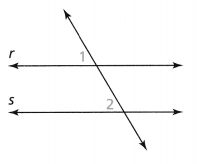
m∠1 = (63 – x)°
m∠2 = (72 – 2x)°
Answer:
It is given that r || s
Now,
The given transversal is:

From the given transversal,
We can observe that
∠1 and ∠2 are corresponding angles
So,
∠1 = ∠2
So,
(63 – x)° = (72 – 2x)°
2x° – x°= 72° – 63°
x° = 9°
Hence, from the above,
We can conclude that the value of x is: 9°
b. Find m∠1 and m∠2.
Answer:
From part (a),
We can observe that the value of x is: 9°
So,
∠1 = (63 – x)°
∠1 = 63° – 9°
∠1 = 56°
∠2 = (72 – 2x)°
∠2 = 72° – 2 (9)°
∠2 = 72° – 18°
∠2 = 54°
Hence, from the above,
We can conclude that
The values of ∠1 and ∠2 are: 56° and 54° respectively
Question 17.
Find the measures of ∠b and ∠d given that m || n.
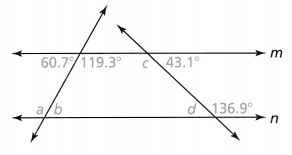
Answer:
It is given that m || n
Now,
The given transversal is:

From the given transversal,
We can observe that
∠b and 119.3° are supplementary angles
So,
∠b + 119.3° = 180°
∠b = 180° – 119.3°
∠b = 70.7°
Now,
∠d and 136.9° are supplementary angles
So,
∠d + 136.9° = 180°
∠d = 180° – 136.9°
∠d = 43.1°
Hence, from the above,
We can conclude that
The values of ∠b and ∠d are 70.7° and 43.1° respectively
Assessment Practice
Question 18.
In the figure, g || p. Which angles are alternate interior angles? Select all that apply.
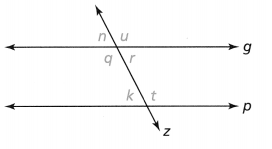
☐ ∠q and ∠r
☐ ∠q and ∠t
☐ ∠q and ∠k
☐ ∠r and ∠t
☐ ∠r and ∠k
☐ ∠u and ∠9
Answer:
It is given that g || p
Now,
The given transversal is:

From the given transversal,
We can observe that
∠r and ∠k are alternate interior angles
∠q and ∠t are alternate interior angles
Hence, from the above,
We can conclude that
The alternate interior angles are:
Question 19.
In the figure, p || q. On a recent math test, Jacob incorrectly listed the value of w as 101.
PART A
Find the value of w.
Answer:
It is given that p || q
Now,
The given transversal is:

From the given transversal,
We can observe that
79° and ∠w are the corresponding angles
Hence, from the above,
We can conclude that the value of ∠w is: 79°
PART B
What mistake did Jacob likely make?
Answer:
We know that,
The corresponding angles are always congruent
Hence,
The mistake that Jacob likely made is:
Jacob considers ∠w and 101° the corresponding angles
Lesson 6.9 Interior and Exterior Angles of Triangles
Solve & Discuss It!
Nell cuts tile to make a decorative strip for a kitchen backsplash. She must cut the tiles precisely to be congruent triangles. She plans to place the tiles between two pieces of molding, as shown. What is m∠2? Explain.
I can… find the interior and exterior angle measures of a triangle.
Answer:
It is given that
Nell cuts tile to make a decorative strip for a kitchen backsplash. She must cut the tiles precisely to be congruent triangles. She plans to place the tiles between two pieces of molding, as shown
Now,
The representation of the decorative strip for a kitchen backsplash is:
Now,
From the given representation,
We can observe that
∠1 of second congruent triangle = ∠1 of the first congruent triangle
∠3 of second congruent triangle = ∠3 of the third congruent triangle
Now,
We know that,
The sum of all the adjacent angles in a transversal is 180°
So,
∠1 + ∠2 + ∠3 = 180°
From the given representation,
∠1 = ∠3 = 65°
So,
∠2 = 180° – (65° + 65°)
∠2 = 180° – 130°
∠2 = 50°
Hence, from the above,
We can conclude that the value of ∠2 is: 50°
Model with Math
How can you use your knowledge of parallel lines and transversals to solve the problem?
Answer:
The representation of the above problem in the form of parallel lines and transversals is:
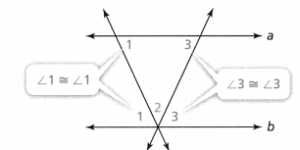
Now,
From the above figure,
We can observe that
According to the alternate interior angles theorem,
∠1 of second congruent triangle = ∠1 of the first congruent triangle
∠3 of second congruent triangle = ∠3 of the third congruent triangle
Now,
We know that,
The sum of all the adjacent angles in a transversal is 180°
Focus on math practices
Reasoning What assumption(s) did you need to make to find m∠2? Explain why your assumption(s) is reasonable.
Answer:
The assumptions you need to find ∠2 are:
a. ∠1 of the second congruent triangle = ∠1 of the first congruent triangle
b. ∠3 of the second congruent triangle = ∠3 of the third congruent triangle
c. The sum of all the adjacent angles in a transversal is 180°
Essential Question
How are the interior and exterior angles of a triangle related?
Answer:
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Try It!
Find the unknown angle measure in the triangle at the right.
Answer:
The given triangle is:

Now,
We know that,
The sum of all the interior angles in a triangle is: 180°
Now,
Let x° be the unknown angle measure
So,
68° + 40° + x° = 180°
x° = 180° – 108°
x° = 72°
Hence, from the above,
We can conclude that the value of the unknown angle measure is: 72°
Convince Me!
Could a triangle have interior angle measures of 23°, 71°, and 96°? Explain.
Answer:
The given interior angle measures of a triangle are 23°, 71°, and 96°
Now,
We know that,
The sum of all the interior angles in a triangle is: 180°
So,
23° + 71° + 96° = 180°
94° + 96° = 180°
190° ≠ 180°
Hence, from the above,
We can conclude that a triangle could not have given interior angle measures
Try It!
What is the measure of the exterior angle shown?
Answer:
The given triangle is:

Now,
From the given figure,
We can observe that
(7x – 1)° and (8x + 8)° are interior angle measures
16x° is an exterior angle measure
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
So,
16x° = (7x – 1)° + (8x + 8)°
16x° = 15x° + 7°
16x° – 15x° = 7°
x° = 7°
So,
16x° = 16 (7)°
= 112°
Hence, from the above,
We can conclude that the exterior angle measure of the given triangle is: 112°
KEY CONCEPT
The sum of the measures of the interior angles of a triangle is 180°.
m∠1 + m∠2 + m∠3 = 180°
The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
m∠2 + m∠3 = m∠4
Do You Understand?
Question 1.
Essential Question How are the interior and exterior angles of a triangle related?
Answer:
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Question 2.
Reasoning Maggie draws a triangle with a right angle. The other two angles have equal measures. What are the possible values of the exterior angles for Maggie’s triangle? Explain.
Answer:
It is given that
Maggie draws a triangle with a right angle. The other two angles have equal measures
Now,
We know that,
The sum of the interior angles in a triangle is: 180°
Now,
Let the unknown two angle measures be x°
So,
90° + x° + x° = 180°
2x° = 180° – 90°
2x°= 90°
x° = \(\frac{90°}{2}\)
x° = 45°
So,
The two unknown angle measures are 45° and 45°
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Now,
Let the exterior angle measure be y°
So,
y° = 45° + 45°
y° = 90°
Hence, from the above,
We can conclude that the possible value for the exterior angle measure of Maggie’s triangle is: 90°
Question 3.
Brian draws a triangle with interior angles of 32° and 87°, and one exterior angle of 93°. Draw the triangle. Label all of the interior angles and the exterior angle.
Answer:
It is given that
Brian draws a triangle with interior angles of 32° and 87°, and one exterior angle of 93°
Now,
We know that,
The sum of all the interior angles in a triangle is 180°
Now,
Let the unknown interior angle measure be: x°
So,
x°+ 32° + 87° = 180°
x° = 180° – 119°
x° = 61°
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
Now,
Let the unknown exterior angle measure be y°
So,
From the given interior angle measures,
y° = 61° + 32°
So,
In a triangle,
The interior angle measures are 61°, 32°, and 87°
The exterior angle measure is: 93°
Hence,
The representation of the interior angles and the exterior angle of a triangle is:
Do You Know How?
Use the diagram below for 4 and 5. Assume that a || b.
Question 4.
What are the measures of ∠1 and ∠2? Explain.
Answer:
It is given that a || b
Now,
The given transversal is:

From the given transversal,
We can observe that
∠1 and 37.3° are vertically opposite angles
So,
∠1 = 37.3°
Now,
We know that,
The sum of all the interior angles in a triangle is 180°
So,
∠1 + 79.4° + ∠2 = 180°
37.3° + 79.4° + ∠2 = 180°
∠2 = 180° – 116.7
∠2 = 63.3°
Hence, from the above,
We can conclude that the measures of ∠1 and ∠2 are 37.3° and 63.3° respectively
Question 5.
What are the measures of ∠3 and ∠4? Explain.
Answer:
It is given that a || b
Now,
The given transversal is:

Now,
From the given transversal,
We can observe that
∠3 and ∠4 are the exterior angles
Now,
∠3 = ∠2 + 79.4°
∠3 = 63.3° + 79.4°
∠3 = 132.7°
Now,
∠4 = ∠1 + 79.4°
∠4 = 37.3° + 79.4°
∠4 = 116.7°
Hence, from the above,
We can conclude that the values of ∠3 and ∠4 are: 132.7° and 116.7°
Question 6.
In △ABC, M∠A = x°, m∠B = (2x)°, and m∠C = (6x + 18)°. What is the measure of each angle?
Answer:
It is given that
In ΔABC,
The angle measures of all the interior angles are:
∠A = x°, ∠B = 2x°, and ∠C = (6x + 18)°
Now,
We know that,
The sum of all the interior angles in a triangle is 180°
So,
x° + 2x° + 6x° + 18° = 180°
9x°= 180° – 18°
9x° = 162°
x° = \(\frac{162°}{9}\)
x° = 18°
So,
∠A = 18°
∠B = 2 (18°) = 36°
∠C = (6x + 18)° = 6 (18°) + 18° = 126°
Hence, from the above,
We can conclude that the measure of each angle is: 18°, 36°, and 126°
Practice & Problem Solving
Question 7.
Leveled Practice For the figure shown, find m∠1.
Angle 1 is an _________ angle of the triangle.
m∠1 is equal to the sum of its ___________.
m∠1 = _______° + _______°
m∠1 = _______°
Answer:
The given triangle is:

Now,
From the given triangle,
We can observe that
∠1 is the exterior angle
59° and 56° are the interior angle measures
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
So,
∠1 = 59° + 56°
∠1 = 115°
Hence, from the above,
We can conclude that the value of ∠1 is: 115°
Question 8.
Find m∠1 and m∠2.
Answer:
The given triangle is:

From the given triangle,
We can observe that
There are 2 triangles and ∠1 is the exterior angle for the second triangle
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
So,
For the first triangle,
138° = ∠1 + 18°
∠1 = 138° – 18°
∠1 = 120°
For the second triangle,
∠1 = ∠2 + 85°
120° = ∠2 + 85°
∠2 = 120° – 85°
∠2 = 35°
Hence, from the above,
We can conclude that the values of ∠1 and ∠2 are: 120° and 35°
Question 9.
In △ABC, what is m∠c?
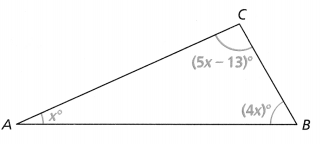
Answer:
The given triangle is:

Now,
We know that,
The sum of all the interior angles in a triangle is: 180°
So,
x° + (4x)° + (5x – 13)° = 180°
(10x – 13)° = 180°
10x° = 180° + 13°
10x° = 193°
x° = \(\frac{193°}{10}\)
x° = 19.3°
So,
∠C = (5x – 13)°
∠C = 5 (19.3)° – 13°
∠C = 96.5° – 13°
∠C = 83.5°
Hence, from the above,
We can conclude that the value of ∠C is: 83.5°
Question 10.
In the figure, m∠1 = (8x + 7)°, m∠2 = (4x + 14)°, and m∠4 = (13x + 12)°. Your friend incorrectly says that m∠4 = 51°. What is m∠4? What mistake might your friend have made?
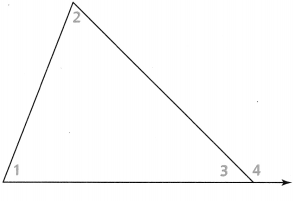
Answer:
It is given that
In the given figure, m∠1 = (8x + 7)°, m∠2 = (4x + 14)°, and m∠4 = (13x + 12)°. Your friend incorrectly says that m∠4 = 51°
Now,
The given figure is:

From the given figure,
We can observe that
∠1, ∠2, and ∠3 are the interior angles
∠4 is an exterior angle
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
The sum of all the interior angles in a triangle is 180°
So,
∠1 + ∠2 + ∠3 = 180°
∠4 = ∠1 + ∠2
So,
(13x + 12)° = (8x + 7)° + (4x + 14)°
13x° + 12° = 12x° + 21°
13x° – 12x° = 21°- 12°
x°= 9°
So,
∠4 = (13x + 12)°
∠4 = 13 (9)° + 12°
∠4 = 117° + 12°
∠4 = 129°
Hence, from the above,
We can conclude that
The value of ∠4 is: 120°
The mistake mightyour friend has made is:
He considered ∠4 as an interior angle and he subtracted the value of ∠4 from 180°
Question 11.
What is m∠1?
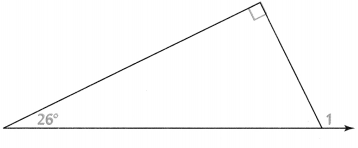
Answer:
The given triangle is:

Now,
From the given triangle,
We can observe that
∠1 is an exterior angle
26° and 90° are interior angles
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
So,
∠1 = 26° + 90°
∠1 = 116°
Hence, from the above,
We can conclude that the value of ∠1 is: 116°
Question 12.
Higher Order Thinking Given that m∠1 = (16x)°, m∠2 = (8x + 21)°, and m∠4 = (25x + 19)°, what is an expression for m∠3? What is m∠3?
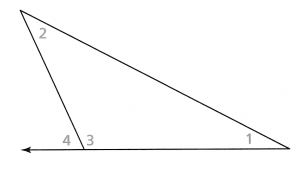
Answer:
It is given that
Given that m∠1 = (16x)°, m∠2 = (8x + 21)°, and m∠4 = (25x + 19)°, what is an expression for m∠3
Now,
The given triangle is:

From the given figure,
We can observe that
∠1, ∠2, and ∠3 are the interior angles
∠4 is an exterior angle
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
The sum of all the interior angles in a triangle is 180°
So,
∠1 + ∠2 + ∠3 = 180°
∠4 = ∠1 + ∠2
So,
(25x + 19)° = (16x)° + (8x + 21)°
25x° + 19° = 24x° + 21°
25x° – 24x° = 21°- 19°
x°= 2°
So,
∠3 = 180° – (16 (2)° + 8 (2)° + 21°)
∠3 = 180° – 69°
∠3 = 111°
Hence, from the above,
We can conclude that
The value of ∠3 is: 111°
Question 13.
A ramp attached to a building is being built to help with deliveries. The angle that the bottom of the ramp makes with the ground is 37.2°. Find the measure of the other acute angle.
Answer:
It is given that
A ramp attached to a building is being built to help with deliveries. The angle that the bottom of the ramp makes with the ground is 37.2°
Now,
The representation of the ramp is:

From the above,
We can observe that the ramp is in the form of a right triangle
Now,
We know that,
The sum of all the interior angles in a triangle is: 180°
So,
37.2° + 90° + x° = 180°
127.2° + x° = 180°
x°= 180° – 127.2°
x°= 62.8°
Hence, from the above,
We can conclude that the measure of the other acute angle is: 62.8°
Assessment Practice
Question 14.
The measure of ∠F is 110°. The measure of ∠E is 100°. What is the measure of ∠D?
A. 150°
B. 80°
C. 70°
D. 30°
Answer:
It is given that
The measure of ∠F is 110°. The measure of ∠E is 100°
Now,
The given transversal is:

From the given transversal,
We can observe that
∠A and ∠D are the vertical angles
Now,
We know that,
The sum of the adjacent angles is: 180°
So,
∠F + ∠C = 180°
∠B + ∠E = 180°
So,
∠C = 180° – ∠F
∠C = 180°- 110°
∠C = 70°
Now,
∠B = 180° – ∠E
∠B = 180° – 100°
∠B = 80°
Now,
We know that,
The sum of all the interior angles in a triangle is: 180°
So,
∠A + ∠B + ∠C = 180°
70° + 80°+ ∠A = 180°
∠A = 180° – 150°
∠A = 30°
So,
∠D = 30°
Hence, from the above,
We can conclude that the measure of ∠D is: 30°
Question 15.
In the figure, m∠1 = (3x + 12)°, m∠2 = (3x + 18)° and m∠3 = (7x + 10)°. What is m∠3 in degrees?
Answer:
It is given that
m∠1 = (3x + 12)°, m∠2 = (3x + 18)° and m∠3 = (7x + 10)°
Now,
The given triangle is:

From the given triangle,
We can observe that
∠1 and ∠2 are the interior angles
∠3 is an exterior angle
Now,
We know that,
An exterior angle of a triangle is equal to the sum of the two opposite interior angles. The sum of exterior angle and interior angle is equal to 180 degrees.
So,
∠3 = ∠1 + ∠2
(7x + 10)° = (3x + 12)° + (3x + 18)°
(7x + 10)° = (6x + 30)°
7x° – 6x° = 30° – 10°
x° = 20°
So,
∠3 = 7 (20)° + 10°
∠3 = 140° + 10°
∠3 = 150°
Hence, from the above,
We can conclude that the measure of ∠3 is 150°
Lesson 6.10 Angle-Angle Triangle Similarity
Explore It!
Justin made two flags for his model sailboat.
I can… use angle measures to determine whether two triangles are similar.
A. Draw and label triangles to represent each flag.
Answer:
It is given that
Justin made two flags for his model sailboat
Hence,
The representation of triangles that represent each flag is:
B. How are the side lengths of the triangles related?
Answer:
The representation of triangles that represent each flag is:

From the given triangles,
We can observe that,
After dilation,
Flag A and Flag B have different side lengths that are divided (or) multiplied by some value of scale factor and the sizes of Flag A and Flag B are different
Hence, from the above,
We can conclude that
After dilation transformation,
The side lengths of Flag A is greater than the side lengths of Flag B
C. How are the angle measurements of the triangles related?
Answer:
The representation of triangles that represent each flag is:

From the given triangles,
We can observe that the apex vertex of Flag A is 46° and the base vertices of Flag B are 67° and 67°
Now,
We know that,
The sum of all the angles in a triangle is 180°
So,
For Flag B,
Let the unknown angle measure be x°
So,
67° + 67° + x° = 180°
x° = 180° – 134°
x° = 46°
So,
For Flag B,
The apex vertex is: 46°
Now,
When we observe two triangles,
The apex vertex of Flag A and Flag B is the same
Hence, from the above,
We can conclude that the corresponding angle measurements for Flag A and Flag B are the same
Focus on math practices
Reasoning Justin makes a third flag that has sides that are shorter than the sides of the small flag. Two of the angles for each flag measure the same. Are the third angles for each flag the same measure? Explain.
Answer:
It is given that
Justin makes a third flag that has sides that are shorter than the sides of the small flag. Two of the angles for each flag measure the same
So,
Two of the angles for each flag are 67° and 67°
Since two angle measures are the same for all the flags, the remaining third angle measure will also be the same
Hence, from the above,
We can conclude that the third angles for each flag have the same measure
Essential Question
How can you use angle measures to determine whether two triangles are similar?
Answer:
The Angle-Angle (AA) Criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.
∠A ≅ ∠D and B ≅ ∠E,
So,
△ABC – △DEF.
Try It!
Is △ΧΥΖ ~ △LMN?
m∠X = _______
m∠N = ________
The triangles ________ similar.
Answer:
The given triangles are:

Now,
For ΔXYZ:
We know that,
The sum of all the angles in a triangle is: 180°
So,
∠X + ∠Y + ∠Z = 180°
∠X = 180° – 92° – 42°
∠X = 180° – 134°
∠X = 46°
For ΔLMN:
We know that,
The sum of all the angles in a triangle is: 180°
So,
∠L + ∠M + ∠N = 180°
∠N = 180° – 92° – 53°
∠N = 180° – 148°
∠N = 32°
Now,
To find whether the given triangles are similar or not,
Find out the angle measures of the corresponding sides
So,
For ΔXYZ and ΔLMN,
∠X = ∠L, ∠Y = ∠M, ∠Z = ∠N
But,
We can observe that
∠X ≠ ∠L
Hence, from the above,
We can conclude that
Since the angle measure of the corresponding sides are not the same,
ΔXYZ is not similar to ΔLMN
Convince Me!
Use what you know about transformations and parallel lines to explain why the Angle-Angle Criterion is true for all triangles.
Try It!
If QR || YZ, is △XYZ ~ △XRQ? Explain.
Answer:
It is given that QR || YZ
Now,
The given figure is:

Now,
We know that,
Since the lines are parallel, the angles that corresponding to the sides will also be the same
Hence,
According to the Side – Side criterion,
ΔXYZ is similar to ΔXRQ
Try It!
Find the value of x if the two triangles are similar. Explain.
Answer:
The given triangles are:

It is given that two triangles are similar
So,
According to Angle – Angle criterion,
(15x)° = 90°
So,
x° = \(\frac{90°}{15}\)
x° = 6°
Hence, from the above,
We can conclude that the value of x is: 6°
KEY CONCEPT
The Angle-Angle (AA) Criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

∠A ≅ ∠D and B ≅ ∠E, so △ABC – △DEF.
Do You Understand?
Question 1.
Essential Question How can you use angle measures to determine whether two triangles are similar?
Answer:
The Angle-Angle (AA) Criterion states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar triangles.

∠A ≅ ∠D and B ≅ ∠E,
So,
△ABC – △DEF.
Question 2.
Construct Arguments Claire says that the AA Criterion should be called the AAA Criterion. Explain why Claire might say this. Do you agree? Explain.
Answer:
It is given that
Claire says that the AA Criterion should be called the AAA Criterion.
Now,
We know that
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Now,
AAA criterion may be reformulated as the AAA (angle-angle-angle) similarity theorem
According to the AAA criterion,
Two triangles have their corresponding angles equal if and only if their corresponding sides are proportional.
So,
From the above two criterions’ statements,
We can observe that the definition of both the criteria are the same
Hence, from the above,
We can conclude that you can agree with Clara
Question 3.
Reasoning Which triangle pairs below are always similar? Explain.
Two right triangles
Two isosceles right triangles
Two equilateral triangles
Answer:
The given pairs of triangles are:
a. Two right triangles
b. Two isosceles right triangles
c. Two equilateral triangles
Now,
We know that,
Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion
Hence, from the above,
We can conclude that
The triangle pairs that are similar are:
a. Two isosceles right triangles
b. Two equilateral triangles
Do You Know How?
Question 4.
Are the two triangles similar? Explain.
Answer:
The given triangles are:

From the given triangles,
We can observe that the apex angle measure in the first triangle is 44° and the apex angle measure in the second triangle is 46°
Now,
We know that
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
So,
44° ≠ 46°
Hence, from the above,
We can conclude that the two triangles are not similar
Question 5.
Is △QRS ~ △QLM? Explain.
Answer:
The given triangles are:

Now,
From the given triangles,
We can observe that
∠R from ΔQRS = ∠L from ΔQLM
Now,
We know that
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
So,
90° = 90°
Hence, from the above,
We can conclude that ΔQRS is similar to ΔQLM
Question 6.
Are the triangles similar? What is the value of x?
Answer:
The given triangles are:

Now,
From the given triangles,
We can observe that
The apex angle of the smaller triangle and the apex angle of the larger triangle is the same
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
So,
The given two triangles are similar
Now,
According to AAA criterion,
(4x)° and 76° are alternate angles
Now,
We know that,
The alternate angles are always congruent
So,
(4x)° = 76°
x° = \(\frac{76°}{4}\)
x° = 19°
Hence, from the above,
We can conclude that the value of x is: 19°
Practice & Problem Solving
Question 7.
Is △XYZ ~ △XTU?
Answer:
The given triangles are:

Now,
We know that,
The sum of all the angles in a triangle is: 180°
So,
In ΔXTU,
103° + ∠T + 48° = 180°
∠T = 180° – 151°
∠T = 29°
Now,
∠T in ΔXTU and ∠Y in ΔXYZ are not the same
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Hence, from the above,
We can conclude that
ΔXTU and ΔXYZ are not similar
Question 8.
For what value of x are △RST and △NSP similar? Explain.
Answer:
The given triangles are:

Now,
For the given triangles to be equal,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
So,
∠T in ΔRST = ∠P in ΔNSP
So,
(x + 19)° = (2x)°
2x° – x°= 19°
x° = 19°
Hence, from the above,
We can conclude that the value of x so that ΔRSt and ΔNSP are similar is: 19°
Question 9.
Is △FGH ~ △JIH? Explain.
Answer:
The given triangles are:

Now,
We know that,
The sum of all the angles in a triangle is equal to 180°
So,
In ΔJIH,
∠J + ∠I + ∠H = 180°
∠J = 180° – (43° + 35°)
∠J = 180° – 78°
∠J = 102°
So,
From the given triangles,
We can observe that
∠J in ΔJIH and ∠F in ΔFGH are not the same
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Hence, from the above,
We can conclude that ΔRST and ΔJIH are not similar
Question 10.
Are △RST and △NSP similar? Explain.
Answer:
The given triangles are:

Now,
For the given triangles to be equal,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
So,
∠T in ΔRST = ∠P in ΔNSP
So,
(x + 15)° = (2x)°
2x° – x°= 15°
x° = 15°
Hence, from the above,
We can conclude that the value of x so that ΔRSt and ΔNSP are similar is: 15°
Question 11.
Contruct Arguments Describe how to use angle relationships to decide whether any two triangles are similar.
Answer:
According to AA criterion,
If two pairs of corresponding angles in a pair of triangles are congruent, then the triangles are similar. We know this because if two angle pairs are the same, then the third pair must also be equal. When the three angle pairs are all equal, the three pairs of sides must also be in proportion.
Question 12.
Higher Order Thinking Are the triangles shown below similar? Explain.
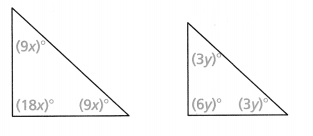
Answer:
The given triangles are:

Now,
From the given triangles,
We can observe that
The angle measures for the smaller triangle can be obtained by dividing the angle measures of the larger triangle by 3
But,
We know that,
The angle measures must be equal for both the triangles with the proportionate side lengths
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Hence, from the above,
We can conclude that the given triangles are not similar
Assessment Practice
Question 13.
Which of the following statements are true? Select all that apply.
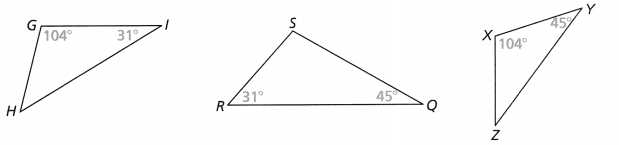
☐ △XYZ ~ △SQR
☐ △XYZ ~ △QSR
☐ △XYZ ~ △GHI
☐ △GIH ~ △SRQ
☐ △ZXY ~ △GIH
☐ △GHI ~ △SRQ
Answer:
The given triangles are:

Now,
From the given triangles,
We can observe that
∠I in ΔGIH or ΔHIG is equal to ∠R in ΔQRS or ΔSRQ
∠G in ΔGIH or ΔGHI is equal to ∠X in ΔXYZ or ΔXZY
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Hence, from the above,
We can conclude that
a. △GIH ~ △SRQ
b. △XYZ ~ △GHI
Question 14.
Is △GHI ~ △QRS? Explain your reasoning.
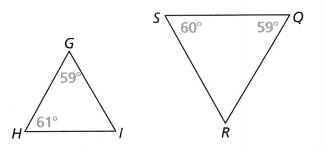
Answer:
The given triangles are:

Now,
From the given triangles,
We can observe that
∠G in ΔGHi and ∠Q in ΔQRS are the same
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Hence, from the above,
We can conclude that ΔGHI and ΔQRS are similar
Topic 6 REVIEW
Topic Essential Question
How can you show that two figures are either congruent or similar to one another?
Answer:
When the two figures are congruent,
a. The shapes and sizes of the two figures are the same
b. The side lengths and the angle measures are the same
c. The orientation is not the same
When the two figures are similar,
a. The shapes and orientations are the same
b. The sizes may are not the same
c. The angle measures are the same but the side lengths are different
Vocabulary Review
Complete each sentence by matching each vocabulary word to its definition. Assume pairs of lines are parallel.
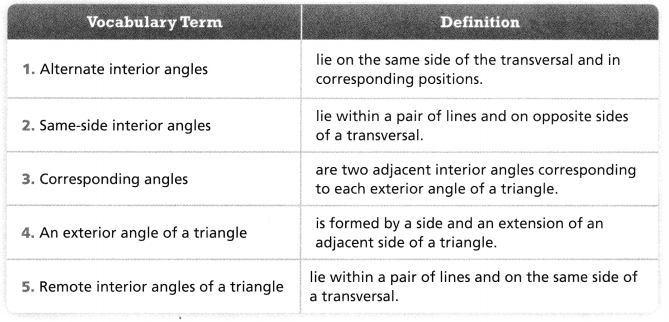
Answer:
Use Vocabulary in Writing
Describe a way to show that △ABC is congruent to △DEF Use vocabulary terms from this Topic in your description.
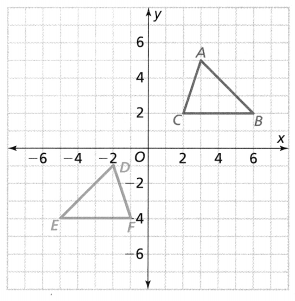
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of ΔABC are:
A (3, 5), B (6, 2), and C (2, 2)
The vertices of ΔDEF are:
D (-2, -1), E (-5, -4), and F (-1, -4)
Now,
The sequence of transformations to show ΔABC is congruent to ΔDEF is:
Step 1:
Reflect the vertices of ΔABC across the y-axis
Step 2:
Translate the image we obtained in step 1 by 1 unit right and 6 units down so that we can obtain the vertices of ΔDEF
Hence,
The representation of the sequence of transformations to show ΔABC is congruent to ΔDEF is:
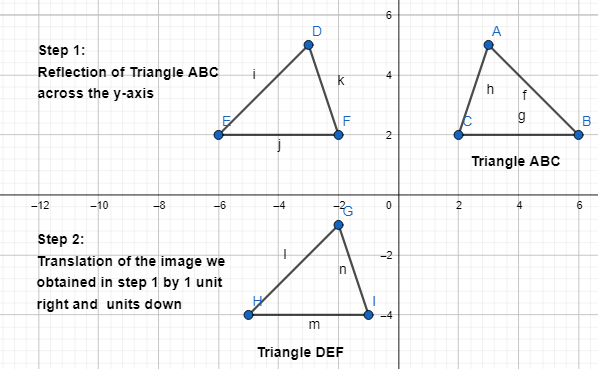
Concepts and Skills Review
Lesson 6.1 Analyze Translations
Quick Review
A translation is a transformation that maps each point of the preimage the same distance and in the same direction.
Example
Translate △XYZ 5 units right and 3 units up.
Answer:
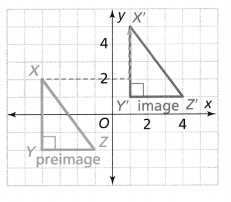
Practice
Question 1.
Draw the image after a translation 3 units left and 2 units up.
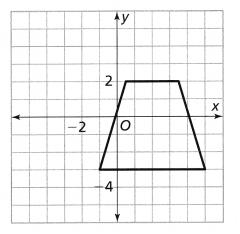
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of the preimage are:
(-1, -3), (0.5, 2), (3.5, 2), and (5, -3)
Now,
After the translation of 3 units left and 2 units up,
The vertices of the image will become:
(-1 – 3, -3 + 2), (0.5 – 3, 2 + 2), (3.5 – 3, 2 + 2), and (5 – 3, -3 + 2)
(-4, -1), (-2.5, 4), (0.5, 4), and (2, -1)
Hence,
The representation of the preimage and the image is:
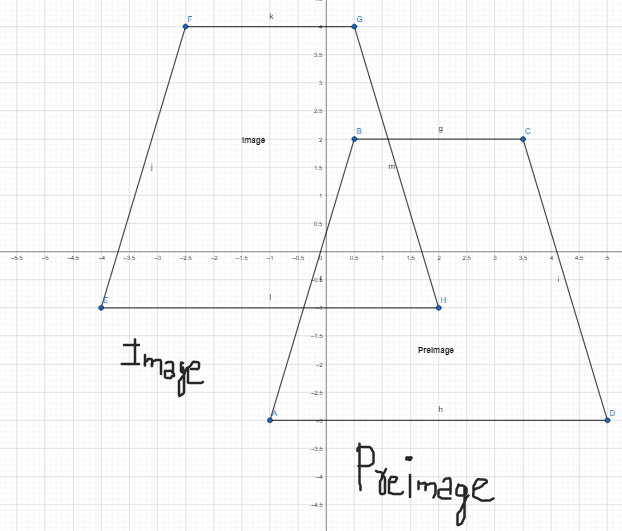
Lesson 6.2 Analyze Reflections
Quick Review
Reflected figures are the same distance from the line of reflection but on opposite sides.
Example
What are the coordinates of the image of △ABC after a reflection across the y-axis?
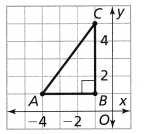
Answer:
Use the rule (x, y) → (-x, y).
A (-4, 1) → A'(4, 1)
B (-1, 1) → B'(1, 1)
C (-1, 5) → C'(1, 5)
Practice
Use the figure.
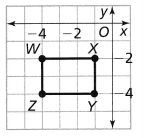
Question 1.
What are the coordinates of the image of rectangle WXYZ after a reflection across the X-axis?
Answer:
The given coordinate plane is:

From the given coordinate plane,
The vertices of the rectangle WXYZ are:
W (-4, -2), X (-1, -2), Y (-1, -4), and Z (-4, -4)
Now,
We know that,
If a point reflects across the x-axis,
The x-coordinate will be the same but the y-coordinate will change the sign
So,
(x, y) before reflection —– > (x, -y) after reflection
Hence,
The vertices of the rectangle WXYZ after reflection across the x-axis will become:
W’ (-4, 2), X’ (-1, 2), Y’ (-1, 4), and Z’ (-4, 4)
Hence,
The representation of the rectangle WXYZ (Preimage) and the rectangle W’X’Y’Z’ (Image) is:
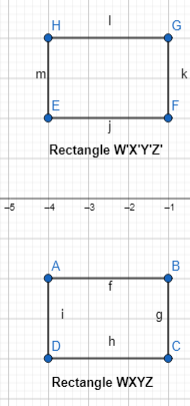
Question 2.
What are the coordinates of the image of WXYZ after a reflection across the y-axis?
Answer:
We know that,
The vertices of the rectangle WXYZ are:
W (-4, -2), X (-1, -2), Y (-1, -4), and Z (-4, -4)
Now,
We know that,
If a point reflects across the y-axis,
The y-coordinate will be the same but the x-coordinate will change the sign
So,
(x, y) before reflection —– > (-x, y) after reflection
Hence,
The vertices of the rectangle WXYZ after reflection across the y-axis will become:
W’ (4, -2), X’ (1, -2), Y’ (1, -4), and Z’ (4, -4)
Hence,
The representation of the rectangle WXYZ (Preimage) and the rectangle W’X’Y’Z’ (Image) is:
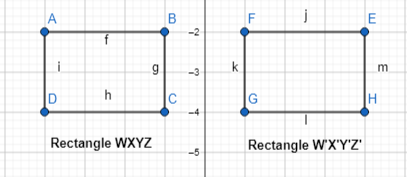
Lesson 6.3 Analyze Rotations
Quick Review
A rotation turns a figure about a fixed point, called the center of rotation. The angle of rotation is the number of degrees the figure is rotated.
Example
What are the coordinates of the image of △ABC after a 90° rotation about the origin?
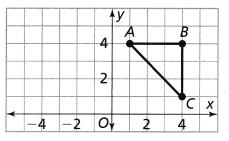
Answer:
Use the rule (x, y) → (-y, x).
A(1, 4) → A'(-4, 1)
B(4, 4) → B'(-4, 4)
C(4, 1) → C'(-1, 4)
Practice
Use the figure.
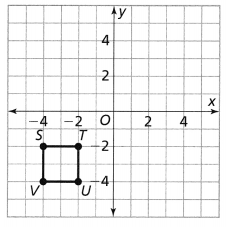
Question 1.
What are the coordinates of the image of quadrilateral STUV after a 180° rotation about the origin?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of the quadrilateral STUV are:
S (-4, -2), T (-2, -2), U (-2, -4), and V (-4, -4)
Now,
We know that,
When any point rotates 180° counterclockwise about the origin,
(x, y) before rotating 180° —– > (-x, -y) after rotating 180°
So,
The vertices of the quadrilateral STUV after the rotation of 180° are:
S’ (4, 2), T (2, 2), U (2, 4), and V (4, 4)
Hence,
The representation of the quadrilateral STUV after the rotation of 180° is:
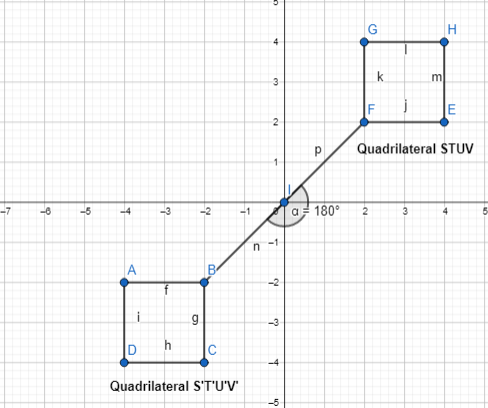
Question 2.
What are the coordinates of the image of quadrilateral STUV after a 270° rotation about the origin?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of the quadrilateral STUV are:
S (-4, -2), T (-2, -2), U (-2, -4), and V (-4, -4)
Now,
We know that,
When any point rotates 270° counterclockwise about the origin,
(x, y) before rotating 270° —– > (y, -x) after rotating 270°
So,
The vertices of the quadrilateral STUV after the rotation of 270° are:
S’ (-2, 4), T (-2, 2), U (-4, 2), and V (-4, 4)
Hence,
The representation of the quadrilateral STUV after the rotation of 180° is:
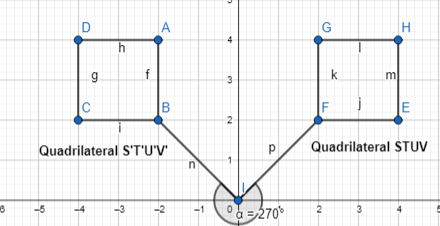
Lesson 6.4 Compose Transformations
Quick Review
To compose a sequence of transformations, perform one transformation, and then use the resulting image to perform the next transformation.
Example
How can you use a sequence of transformations to map Figure A onto Figure B?
Answer:
Translate Figure A 3 units up, and then reflect Figure A across the y-axis.
Practice
Question 1.
Translate rectangle ABCD 5 units down, and then reflect it across the y-axis.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of the rectangle ABCD are:
A (-5, 4), B (-1, 4), C (-1, 2), and D (-5, 2)
Now,
The sequence of transformations to draw the image of the rectangle ABCD is:
Step 1:
Translate the rectangle ABCD 5 units down
So,
The vertices of the rectangle ABCD are:
A (-5, 4 – 5), B (-1, 4 – 5), C (-1, 2 – 5), and D (-5, 2 -5)
A (-5, -1), B (-1, -1), C (-1, -3), and D (-5, -3)
Step 2:
Reflect the vertices that we obtained in step 1 across the y-axis
Now,
We know that,
If a point reflects across the y-axis,
The y-coordinate will be the same but the x-coordinate will change the sign
So,
(x, y) before reflection —– > (-x, y) after reflection
So,
The vertices of the rectangle ABCD are:
A (5, -1), B (1, -1), C (1, -3), and D (5, -3)
Hence,
The representation of the sequence of transformations to represent the rectangle ABCD and its image is:
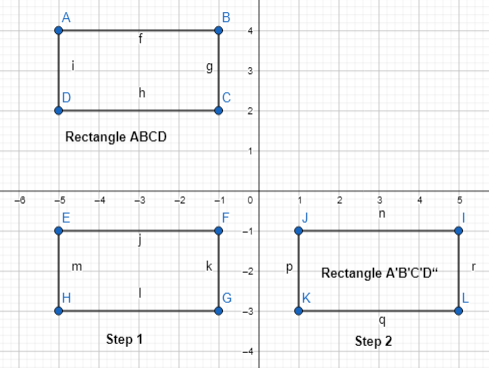
Lesson 6.5 Understand Congruent Figures
Quick Review
Two figures are congruent if a sequence of transformations maps one figure onto the other.
Example
How can you determine if Figure A is congruent to Figure B?
Answer:
Reflect Figure A across the y-axis, and then translate Figure A 6 units up and 1 unit left.
Practice
Question 1.
Is quadrilateral A congruent to quadrilateral B? Explain.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of quadrilateral A are:
(1, 1), (2, 4), (4, 4), and (5, 1)
The vertices of quadrilateral B are:
(-5, -4), (-4, -1), (-3, -1), and (-2, -4)
Now,
We know that,
The two figures are said to be congruent when
a. The shapes and sizes of the figures must be the same
b. The side lengths of the 2 figures must be the same
c. The angle measures must be the same
So,
The representation of the quadrilateral A and the quadrilateral B is:
Hence, from the above,
We can conclude that quadrilateral A and quadrilateral B are not congruent side their side lengths are not the same
Lesson 6.6 Describe Dilations
Quick Review
A dilation results in an image that is the same shape but not the same size as the preimage.
Example
What dilation maps WXYZ to W’X’Y’Z?
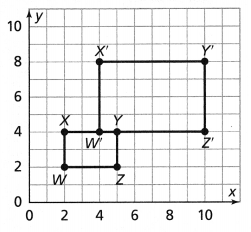
Answer:
A dilation with center at the origin and a scale factor of 2 maps WXYZ to W’X’Y’Z’.
Practice
Use the figure.
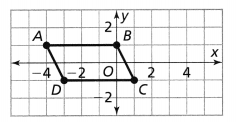
Question 1.
What are the coordinates of the image of parallelogram ABCD after a dilation with center (0, 0) and a scale factor of 3?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of the parallelogram ABCD are:
A (-4, 1), B (0, 1), C (1, -1), and D (-3, -1)
Now,
After a dilation with center (0, 0) and a scale factor of 3,
The vertices of the parallelogram must be multiplied with 3
So,
A (-4, 1) × 3, B (0, 1) × 3, C (1, -1) × 3, and D (-3, -1) × 3
A’ (-12, 3), B’ (0, 3), C’ (3, -3), and D’ (-9, -3)
Hence, from the above,
We can conclude that the coordinates for the image of the parallelogram ABCD after a dilation with center (0, 0) and a scale factor of 3 is:
A’ (-12, 3), B’ (0, 3), C’ (3, -3), and D’ (-9, -3)
Question 2.
What are the coordinates of the image of parallelogram ABCD after a dilation with center (0, 0) and a scale factor of \(\frac{1}{2}\)?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of the parallelogram ABCD are:
A (-4, 1), B (0, 1), C (1, -1), and D (-3, -1)
Now,
After a dilation with center (0, 0) and a scale factor of \(\frac{1}{2}\),
The vertices of the parallelogram must be multiplied with \(\frac{1}{2}\)
So,
A (-4, 1) × \(\frac{1}{2}\), B (0, 1) × \(\frac{1}{2}\), C (1, -1) × \(\frac{1}{2}\), and D (-3, -1) × \(\frac{1}{2}\)
A’ (-2, 0.5), B’ (0, 0.5), C’ (0.5, -0.5), and D’ (-1.5, -0.5)
Hence, from the above,
We can conclude that the coordinates for the image of the parallelogram ABCD after a dilation with center (0, 0) and a scale factor of \(\frac{1}{2}\) is:
A’ (-2, 0.5), B’ (0, 0.5), C’ (0.5, -0.5), and D’ (-1.5, -0.5)
Lesson 6.7 Understand Similar Figures
Quick Review
Two-dimensional figures are similar if there is a sequence of translations, reflections, rotations, and dilations that maps one figure onto the other figure. Similar figures have the same shape, congruent angles, and proportional side lengths.
Example
Is rectangle ABCD ~ rectangle A’B’C’D?
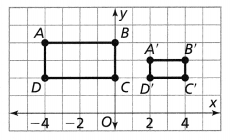
Answer:
All the angles are right angles.
\(\frac{A B}{A^{\prime} B^{\prime}}=\frac{B C}{B^{\prime} C^{\prime}}=\frac{C D}{C^{\prime} D^{\prime}}=\frac{A D}{A^{\prime} D^{\prime}}=\frac{2}{1}\) = 2
The figures have congruent angle measures and proportional side lengths, so they are similar.
Practice
Use the figure.
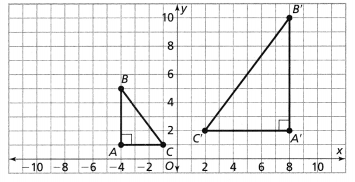
Question 1.
Is △ABC similar to △A’B’C’ ? Explain.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The vertices of ΔABC are:
A (-4, 1) B (-4, 5), and C (-1, 1)
The vertices of ΔA’B’C’ are:
A’ (8, 2), B’ (8, 10), and C’ (2, 2)
Now,
The sequence of transformations to find whether △ABC is similar to △A’B’C’ or not is:
Step 1:
Reflect the vertices of △ABC across the y-axis
Step 2:
Dilate the vertices of △ABC we obtained in step 1 with center (0, 0) and a scale factor of 2
Hence,
The representation of the sequence of transformations to represent that △ABC is similar to △A’B’C’ is:
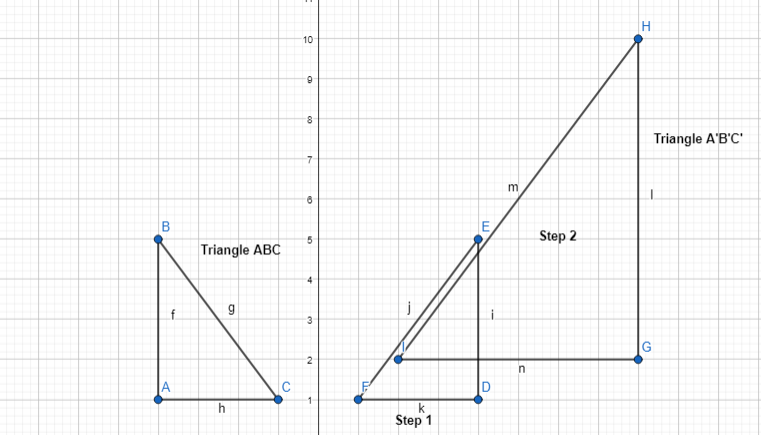
Question 2.
What sequence of transformations shows that △ABC is similar to △A’B’C’?
Answer:
The sequence of transformations that shows △ABC is similar to △A’B’C’ is:
Step 1:
Reflect the vertices of △ABC across the y-axis
Step 2:
Dilate the vertices of △ABC we obtained in step 1 with center (0, 0) and a scale factor of 2
Lesson 6.8 Angles, Lines, and Transversals
Quick Review
When parallel lines are intersected by a transversal, corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary.
Example
If m || n, what is the value of x?
Answer:
m∠3 = 45° (5x + 25)°
45+ (5x + 25) = 180 – n
x = 22
Practice
In the figure, a || b. What is the value of x?
Answer:
It is given that a || b
Now,
The given transversal is:

Now,
From the given transversal,
We can observe that
(3x + 9)° and 129° are alternate angles
Now,
We know that,
The alternate angles are always congruent
So,
(3x + 9)° = 129°
3x° = 129° – 9°
3x° = 120°
x° = \(\frac{120°}{3}\)
x°= 40°
Hence, from the above,
We can conclude that the value of x is: 40°
Lesson 6.9 Interior and Exterior Angles of Triangles
Quick Review
The sum of the measures of the interior angles of a triangle is 180°. The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
Example
Find the missing angle measure.
Answer:
x + 40 = 100, so x = 60
Practice
Question 1.
Find the missing angle measure.
Answer:
The given triangle is:

Now,
From the given triangle,
The angle measures are 48°, 102°
Let the unknown angle measure be x°
Now,
We know that,
The sum of all the angles in a given triangle is equal to 180°
So,
48°+ 102° + x° = 180°
x° = 180° – 150°
x° = 30°
Hence, from the above,
We can conclude that the missing angle measure is: 30°
Question 2.
Find the value of x.
Answer:
The given triangle is:

Now,
We know that,
The angle measure of an exterior angle is equal to the sum of the remote interior angles that is opposite to the given exterior angle
So,
3x° + 2x° = 115°
5x° = 115°
x° = \(\frac{115°}{3}\)
x° = 23°
Hence, from the above,
We can conclude that the value of x is: 23°
Lesson 6-10 Angle-Angle Triangle Similarity
Quick Review
By the AA Criterion, if two angles in one triangle are congruent to two angles in another triangle, then the triangles are similar.
Example
Is △ABC ~ △DEF? Explain.
Answer:
m∠B = 180° – 90° – 37° = 53°
m∠A = m∠D = 90° and m∠B = m∠E = 53°
Because two angles of the triangles are congruent, the triangles are similar by the AA Criterion.
Practice
Question 1.
AB || XY. Is △ABC ~ △XYC? Explain.
Answer:
It is given that AB || XY
Now,
The given triangles are:

Now,
From the given triangles,
We can observe that
∠A in ΔABC = ∠X in ΔXYC
Now,
We know that,
AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other
Hence, from the above,
We can conclude that ΔABC is similar to ΔXYC
Question 2.
Find the values of x and y given that △ABC is similar to △MNC.
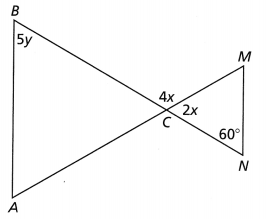
Answer:
It is given that ΔABC is similar to ΔMNC
Now,
The given triangles are:

Now,
We know that,
The sum of adjacent angles is equal to 180°
So,
4x° + 2x° = 180°
6x° = 180°
x° = \(\frac{180°}{6}\)
x° = 30°
Now,
Since ∠N = 60°,
∠A = 60° (By AA criterion)
Now,
We know that,
The sum of all the interior angles in a triangle is equal to 180°
So,
5y° + 60° + 30° = 180°
5y° = 180° – 90°
5y° = 90°
y° = \(\frac{90°}{5}\)
y° = 18°
Hence, from the above,
We can conclude that the values of x and y are: 30° and 18° respectively
Topic 6 Fluency Practice
Crisscrossed
Solve each equation. Write your answers in the cross-number puzzle below. Each digit, negative sign, and decimal point of your answer goes in its own box.

I can… solve multistep equations. © 8.EE.C.7b
