Trigonometry is a branch of mathematics that deals with the relationship between the angles, sides of a right-angled triangle. It was invented by the Greek mathematician named Hipparchus. From this page, you can learn about the basics of trigonometry such as trigonometric ratios(sine, cosine, tangent, secant, cotangent, cosecant), functions, tables, formulas, and more example questions.
Trigonometry Definition
Trigonometry is one of the branches of mathematics. The word trigonometry is derived from the Latin words Trigon means triangle and Metron means to measure. It is the study of the relationship between the sides and angles of a right-angled triangle. It is useful to measure the missing side or angle of a right-angle triangle. The quick links to get important topics regarding trigonometry are here.
- Measurement of Trigonometric Angles
- Sexagesimal System
- Circular System
- Radian is a Constant Angle
- Relation between Sexagesimal and Circular
- Conversion from Sexagesimal to Circular System
- Conversion from Circular to Sexagesimal System
The three basic trigonometric functions are sine, cosine, tangent and the remaining three functions are cotangent, secant, and cosecant. The basics of trigonometry are covered in the following sections.
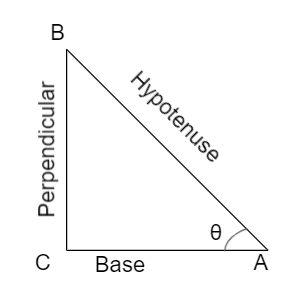
In a right-angled triangle, we have the following three sides.
- Perpendicular: It is the side opposite to the angle θ.
- Base: This is the adjacent side to the angle θ.
- Hypotenuse: This is the side opposite to the right angle.
Trigonometric Ratios | Trigonometry Functions
The trigonometric ratios of a right-angled triangle are called trigonometric functions. The six trigonometric ratios are sin, cos, tan, cot, sec, cosec. These ratios are evaluated in the case of a right-angled triangle. The important functions are calculated using the below formulas.
- Sine function = sin = \(\frac { Perpendicular }{ Hypotenuse } \)
- Cosine function = cos = \(\frac { Base }{ Hypotenuse } \)
- Tangent function = tan = \(\frac { Perpendicular }{ Base } \)
- Cotangent function = cot = \(\frac { Base }{ Perpendicular } \)
- Secant function = sec = \(\frac { Hypotenuse }{ Base } \)
- Cosecant function = cosec = \(\frac { Hypotenuse }{ Perpendicular } \)
Trigonometric Table
Check the table for common angles which are used to solve the trigonometric problems involving these ratios.
| Angles | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin θ | 0 | \(\frac { 1 }{ 2 } \) | \(\frac { 1 }{ √2 } \) | \(\frac { √3 }{ 2 } \) | 1 |
| cos θ | 1 | \(\frac { √3 }{ 2 } \) | \(\frac { 1 }{ √2 } \) | \(\frac { 1 }{ 2 } \) | 0 |
| tan θ | 0 | \(\frac { 1 }{ √3 } \) | 1 | √3 | ∞ |
| cot θ | ∞ | √3 | √2 | \(\frac { 1 }{ √3 } \) | 1 |
| sec θ | 1 | \(\frac { 2 }{ √3 } \) | √2 | 2 | ∞ |
| cosec θ | ∞ | 2 | 1 | \(\frac { 2 }{ √3 } \) | 0 |
Trigonometry Angles
Trigonometric angles are the angles in right-angled triangles which are different trigonometric functions. The most used angles in trigonometry are 0°, 30°, 45°, 60°, 90°. The trigonometric values for these angles can be observed directly in the table. The important angles in trigonometry are 180°, 270°, 360°. The trigonometry angles can be defined as:
- θ = sin-1 (\(\frac { Perpendicular }{ Hypotenuse } \))
- θ = cos-1 (\(\frac { Base }{ Hypotenuse } \))
- θ = tan-1 (\(\frac { Perpendicular }{ Base } \))
Unit Circle and Trigonometric Values
Unit circle can be used to calculate the values of basic trigonometric functions (sine, cosine, tangent). The below-given circle shows how trigonometric ratios like sin, cos can be represented in a unit circle.
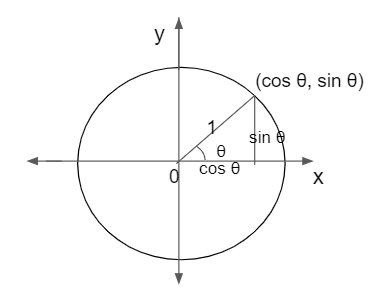
For suppose the length of the perpendicular is y and base is x. The length of the hypotenuse is the radius of the unit circle. Therefore, the trigonometry ratios are as follows:
- sin θ = y/1 = y
- cos θ = x/1 = x
- tan θ = y/x
Trigonometric Formulas
The trigonometric identities or formulas are the equations which are true for right-angled triangles. Few special trigonometric identities are here:
- Pythagorean Identities
- sin²θ + cos²θ = 1
- tan²θ + 1 = sec²θ
- cot²θ + 1 = cosec²θ
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ – sin²θ
- tan 2θ = 2 tan θ / (1 – tan²θ)
- cot 2θ = (cot²θ – 1) / 2 cot θ
- Sum and Difference Identities
- For angles x and y, we have the following relationships:
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
- tan(x + y) = \(\frac { tan(x) + tan(y) }{ 1 – tan(x)tan(y) } \)
- sin(x – y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- tan(x – y) = \(\frac { tan(x) – tan(y) }{ 1 + tan(x)tan(y) } \)
- If A, B, C are angles and a, b , c are the sides of the triangle, then
- Sine Laws
- \(\frac { a }{ sinA } \) = \(\frac { b }{ sinB } \) = \(\frac { c }{ sinC } \)
- Cosine Laws
- c² = a² + b² – 2ab cos C
- a² = b² + c² – 2bc cos A
- b² = a² + c² – 2ac cos B
- Sine Laws
Euler’s formula
eix = cos x + i sin x
Where x is the angle and i is the imaginary number.
sin x = \(\frac { eix – e-ix }{ 2i } \)
cos x = \(\frac { eix + e-ix }{ 2 } \)
tan x = \(\frac { eix – e-ix }{ i(eix + e-ix) } \)
Applications of Trigonometry
Some of the applications of trigonometry are provided here.
- It is useful to measure the height of the mountains, find the distance of long rivers, etc.
- Its applications are in various fields like oceanography, meteorology, seismology, astronomy, physical sciences, navigation, acoustics, electronics, etc.
Basics of Trigonometry
There are 3 basic functions in trigonometry. They are sine, cosine and tangent. Based on these 3 functions other three functions derived are cotangent, secant and cosecant. The formulas of these functions are listed here.
If θ is the angle in a right-angled triangle, then
sin θ = \(\frac { Perpendicular }{ Hypotenuse } \)
cos θ = \(\frac { Base }{ Hypotenuse } \)
tan θ = \(\frac { Perpendicular }{ Base } \)
cot θ = \(\frac { 1 }{ tan θ } \)
sec θ = \(\frac { 1 }{ cos θ } \)
cosec θ = \(\frac { 1 }{ sin θ } \)
The perpendicular side is the side opposite to the angle θ
The base is the adjacent side to the angle θ
The hypotenuse is the side opposite to the right angle.
Problems & Solutions on Trigonometry
Problem 1:
A man observed a pole of height 75 ft. According to his measurement, the pole cast a 15 ft long shadow. Find the angle of elevation of the sun from the tip of the shadow using trigonometry.
Solution:
Let x be the angle of elevation of sun.
tan x = \(\frac { 75 }{ 15 } \) = 5
x = tan-1(5)
= 78.69 degrees
Therefore, the angle of elevation of the sun from the tip of the shadow is 78.69 degrees.
Problem 2:
Two friends started climbing a pyramid-shaped hill. The first person climbs 315 m and finds that the angle of depression as 72.3 degrees from his starting point. How high is he from the ground?
Solution:
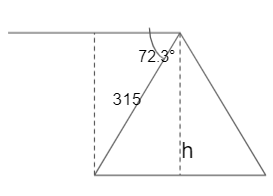
Let h be the height above the ground.
sin 72.3° = \(\frac { h }{ 315 } \)
0.953 = \(\frac { h }{ 315 } \)
h = 300.195 m
The man is 300.195 m above the ground.
FAQ’s on Trigonometry
1. What is the basics of trigonometry?
Trigonometry basics deal with the measurement of angles and sides of a right-angled triangle. The basic trigonometric ratios are sine, cosine, tangent, cotangent, secant and cosecant.
2. What are 6 basic trigonometry functions?
The 6 important trigonometry functions are sine function, cosine function, tangent function, cotangent function, secant function, and cosecant function.
3. Is trigonometry SOH CAH TOA?
We use the SOH CAH TOA technique to memorize the relationship between trigonometric ratios.
- SOH: Sine = \(\frac { Perpendicular }{ Hypotenuse } \)
- CAH = Cosine = \(\frac { Base }{ Hypotenuse } \)
- TOA = Tangent = \(\frac { Perpendicular }{ Base } \)
