Trigonometry deals with the relationship between the sides and angles of a right-angled triangle. An angle is the rotation of a ray from the initial point to the terminal point. Two basic units of angle measurement are radians and degrees. Check the below sections to know more details about the measurement of trigonometric angles & solved questions.
What is Trigonometric Angle?
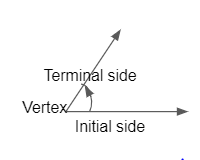
An angle is defined as the rotation of a ray from an initial point to a terminal point. The commonly used terms in angles are listed here.
- Vertex: Point of rotation
- Initial side: The original ray
- Terminal side: The final position of the ray after rotation
- Positive angle: The direction of rotation is anticlockwise
- Negative angle: The direction of rotation is clockwise
Measurement of Trigonometric Angles
The angle measurement is the amount of rotation performed by the initial side to obtain the terminal side. Generally, we use degrees or radians to measure a trigonometric angle. A complete revolution is divided by 360 units is called degrees. It means, if the angle rotation is (1/360)th of the revolution, then the angle is measured of one degree. Half of the revolution is 180°, one complete revolution is 360°.
- Angle θ is said to be acute angle if 0° ≤ θ < 90°
- Angle θ is said to be right angle if θ = 90°
- Angle θ is said to be obtuse angle if 90° < θ < 180°
- Angle θ is said to be a straight angle if θ = 180°
- Angle θ is said to be reflex angle if 180° < θ < 360°
Angle Measurement in Radians
Radian angle measurement is difficult than degree measurement. Let us take a circle with a radius of 1 unit. The angle subtended by an arc at the centre of the circle has a measure of 1 radian. The full circle in radians is π. The conversion between revolutions, degrees and radians is provided here.
| Degrees | Radians | Revolutions |
|---|---|---|
| 0 | 0 | 0 |
| 30 | π/6 | 1/12 |
| 45 | π/4 | 1/8 |
| 60 | π/3 | 1/6 |
| 90 | π/2 | 1/4 |
| 120 | 2π/3 | 1/3 |
| 135 | 3π/4 | 3/8 |
| 180 | π | 1/2 |
| 225 | 5π/4 | 5/8 |
| 270 | 3π/2 | 3/4 |
| 315 | 7π/4 | 7/8 |
| 360 | 2π | 1 |
Trigonometrical Angles on Quadrants
Geometrical angles are always positive. There is no use of negative words. But the measure of angles in trigonometry is formed by the revolution of a straight line about a fixed point. The trigonometrical angle may have any positive or negative value.
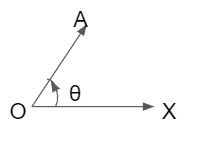
Let OX be a fixed-line and OA is a revolving line whose initial position coincides with OX. The angle formed by ∠XOA is called trigonometrical angle.
If OA revolves about O in the anticlockwise direction from initial to the final position, then ∠XOA = θ formed by the generating line OA is called a trigonometrical positive angle. If the generating line OA revolves about O in the clockwise direction from initial to the final position, then ∠XOA = α formed by OA is called trigonometrical negative angle

The above coordinate geometry has 4 regions XOY, YOX’, X’OY’, Y’OX and they are called first, second, third and fourth quadrants. The rays OA, OB, OC< OD describe the angles ∠XOA, ∠XOB, ∠XOC and ∠XOD in four quadrants. Each angle is positive as the angle is formed in the clockwise direction.
The measure of each angle is 0 < ∠XOA < 90°, 90° < ∠XOB < 180°, 180° < ∠XOC < 270° and 270° < ∠XOD < 360°.
Example:
Consider the measure of an angle in trigonometry 2770°.
2770° = 7 x 360° + 180° + 70°. So, the angle of magnitude 2770° is described by the revolving line.
