Eureka Math Geometry Module 2 Lesson 19 Answer Key

Engage NY Eureka Math Geometry Module 2 Lesson 19 Answer Key

Eureka Math Geometry Module 2 Lesson 19 Opening Exercise Answer Key

Show x: y = x’: y’ is equivalent to x: x’ = y: y’.

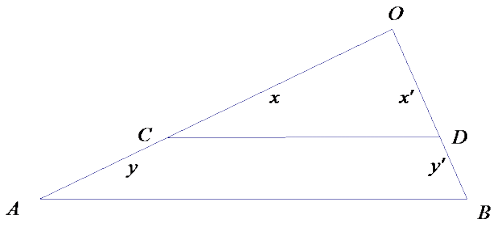
Answer:

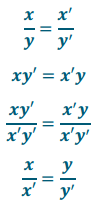
Eureka Math Geometry Module 2 Lesson 19 Exercise Answer Key

Exercise 1.

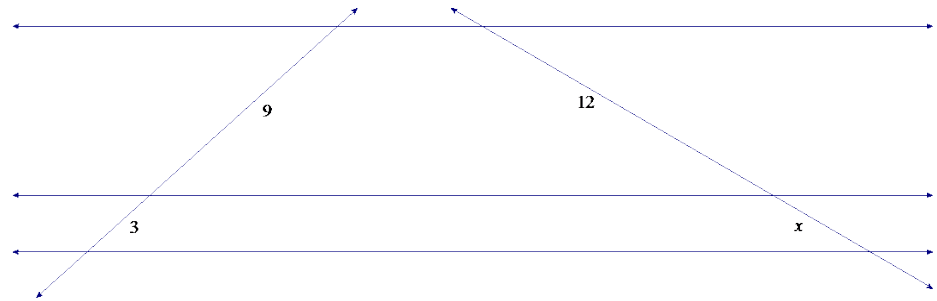
Answer:
x = 4

Exercise 2.

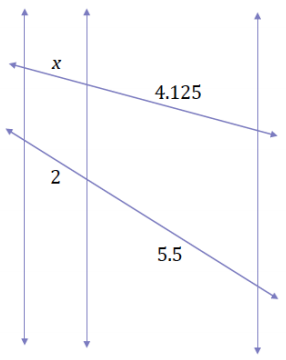
Answer:
x = 1.5

Eureka Math Geometry Module 2 Lesson 19 Problem Set Answer Key

Question 1.
Given the diagram shown, \(\overline{A D}\|\overline{G J}\| \overline{L O} \| \overline{Q T}\) and \(\overline{A Q}\|\overline{B R}\| \overline{C S} \| \overline{D T}\) Use the additional information given in each part below to answer the questions:

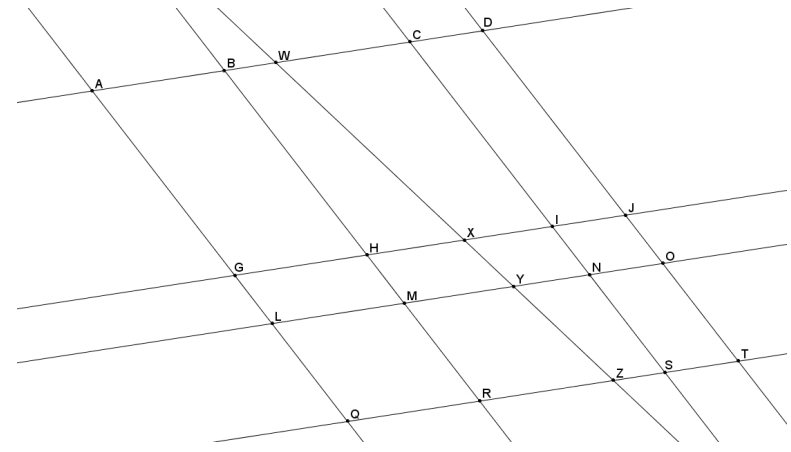
a. If GL = 4, what is HM?
Answer:
GHML forms a parallelogram since opposite sides are parallel, and opposite sides of a parallelogram are equal in length; therefore, HM = GL = 4.

b. If GL = 4, LQ = 9, and XV = 5, what is YZ?
Answer:
Parallel lines cut transversals proportionally; therefore, it is true that = \(\frac{G L}{L Q}=\frac{X Y}{Y Z}\), and likewise YZ = \(\frac{L Q}{G L}\) (XV).
YZ = \(\frac{9}{4}\)(5)
YZ= 11\(\frac{1}{4}\)

c. Using information from part (b), If CI = 18, what is WX?
Answer:
By the same argument used in part (a), IN = GL = 4. Parallel lines cut transversals proportionally; therefore, it is true that \(\frac{C I}{I N}=\frac{W X}{X Y}\), and likewise WX = \(\frac{C I}{I N}\)(XY).
WX = \(\frac{18}{4}\)(5)
WX = 22\(\frac{1}{2}\)

Question 2.
Use your knowledge about families of parallel lines to find the coordinates of point P on the coordinate plane below.

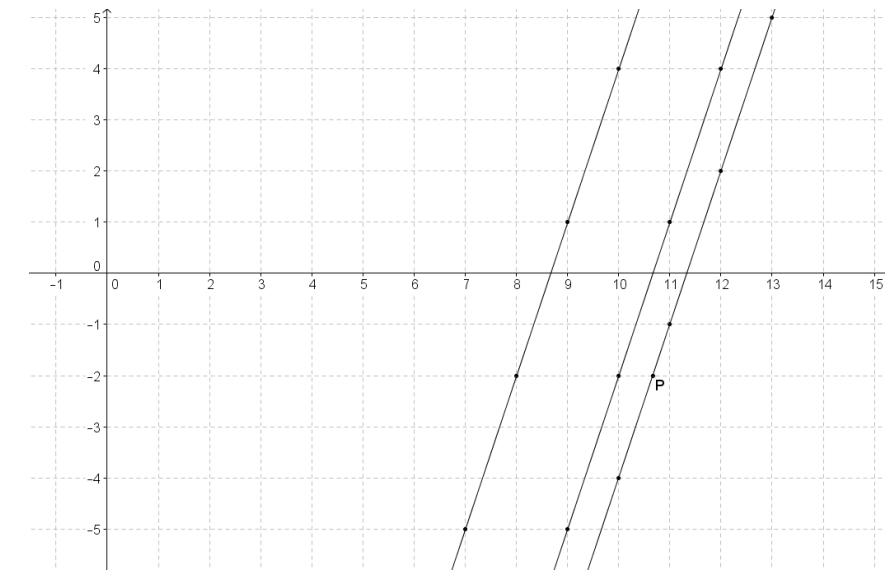
Answer:
The given lines on the coordinate plane are parallel because they have the same slope m = 3. First, draw a horizontal transversal through points (8, -2) and (10, -2) and a second transversal through points (10,4) and (10, -4). The transversals intersect at (10, -2). Parallel lines cut transversals proportionally, so using horizontal and vertical distances, \(\frac{6}{2}=\frac{2}{x}\), where x represents the distance from point (10, -2) to P.
x = \(\frac{2}{6}\)(2)
x = \(\frac{4}{6}=\frac{2}{3}\)
Point P is \(\frac{2}{3}\) unit more than 10, or 10\(\frac{2}{3}\), so the coordinates of point Pare (1o\(\frac{2}{3}\), -2).

Question 3.
ACDB and FCDE are both trapezoids with bases \(\overline{A B}, \overline{F E}\), and \(\overline{C D}\). The perimeter of trapezoid ACDB is 24\(\frac{1}{2}\). If the ratio of AF: FC is 1: 3, AB = 7, and ED = 5\(\frac{5}{8}\), find AF, FC, and BE.

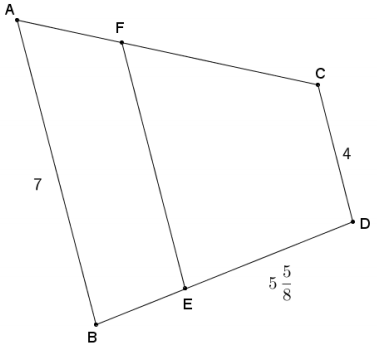
Answer:

Question 4.
Given the diagram and the ratio of a: b is 3: 2, answer each question below:

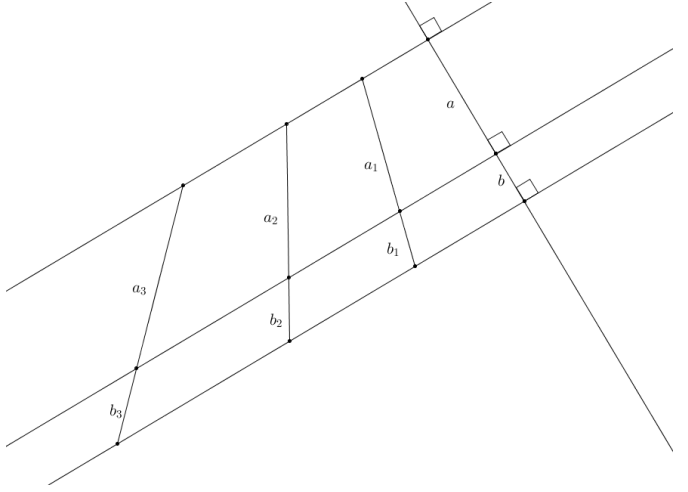
a. Write an equation for a_n in terms of b_n.
Answer:
a_n = \(\frac{3}{2}\)b_n

b. Write an equation for b_n in terms of a_n.
Answer:
b_n = \(\frac{2}{3}\)a_n

c. Use one of your equations to find b₁ in terms of a if a₁ = 1.2(a).
Answer:
b_n = \(\frac{2}{3}\)a_n
b₁ = \(\frac{2}{3}\left(\frac{12}{10} a\right)\)
b₁ = \(\frac{4}{5}\)a

d. What is the relationship between b₁ and b?
Answer:
Using the equation from parts (a) and (c), a = \(\frac{3}{2}\)b, so b₁ = \(\frac{4}{5}\left(\frac{3}{2} b\right)\); thus, b1 = \(\frac{6}{5}\)b.

e. What constant, c, relates b1 and b? Is this surprising? Why or why not?
Answer:
The constant relating b1 and b is the same constant relating a1 to a, c = \(\frac{12}{10}\) = 1.2.

f. Using the formula a_n = c · a_{n – 1}, find a₃ in terms of a.
Answer:

g. Using the formula b_n = c · b_n-1, find b₃ in terms of b.
Answer:
b₃ = \(\frac{216}{125}\)b

h. Use your answers from parts (f) and (g) to calculate the value of the ratio of a₃: b₃.
Answer:

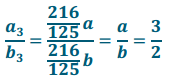
Question 5.
julius wants to try to estimate the circumference of the earth based on measurements made near his home. He cannot find a location near his home where the sun Is straight overhead. Will he be able to calculate the circumference of the earth? If so, explain and draw a diagram to support your claim.
Answer:
Note to the teacher: This problem is very open-ended, requires critical thinking, and may not be suitable for all students. The problem may be scaffolded by providing a diagram with possible measurements that Julius made based on the description in the student solution below.

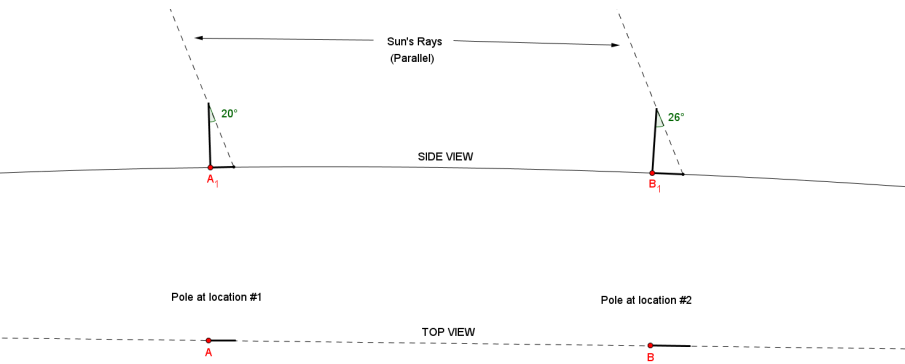
Possible solution: If Julius can find two locations such that those locations and their shadows lie in the same straight path, then the difference of the shadows’ angles can be used as part of the 360° in the earth’s circumference. The distance between those two locations corresponds with that difference of angles.

Eureka Math Geometry Module 2 Lesson 19 Exit Ticket Answer Key

Question 1.
Given the diagram shown, \(\overline{A G}\) || \(\overline{B H}\) || \(\overline{C I}\), AB = 6.5 cm, GH = 7.5 cm, and HI = 18 cm. Find BC.

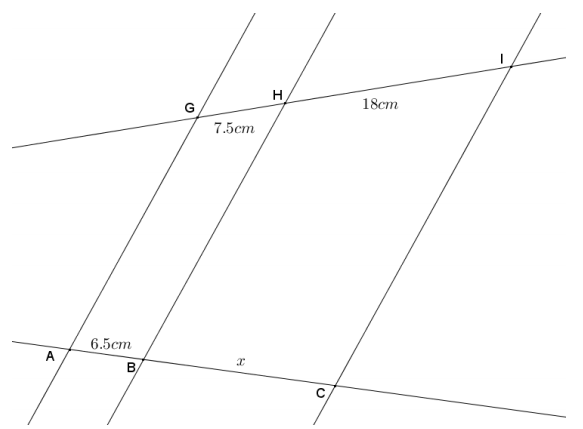
Answer:

Question 2.
Martin the Martian lives on Planet Mart. Martin wants to know the circumference of Planet Mart, but it is too large to measure directly. He uses the same method as Eratosthenes by measuring the angle of the sun’s rays in two locations. The sun shines on a flagpole in Martinsburg, but there is no shadow. At the same time, the sun shines on a flagpole in Martville, and a shadow forms a 10° angle with the pole. The distance from Martville to Martinsburg is 294 miles. What is the circumference of Planet Mart?
Answer:
The distance from Martinsburg to Martville makes up only 10° of the total rotation about the planet. There are 360° in the complete circumference of the planet, and 36 · 10° = 360°, so 36 294 miles = 10584 miles.
The circumference of planet Mart is 10,584 miles.