Engage NY Eureka Math Geometry Module 2 End of Module Assessment Answer Key
Eureka Math Geometry Module 2 End of Module Assessment Answer Key
Question 1.
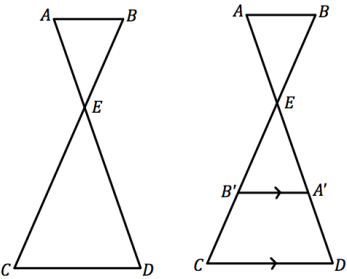
In the figure below, rotate ∆EAB about E by 180° to get ∆E\(A^{\prime} B^{\prime}\). If \(\overline{A^{\prime} B^{\prime}} \| \overline{C D}\), prove that ∆EAB – ∆EDC.
Answer:
Triangles EAB and E\(A^{\prime} B^{\prime}\). are congruent since a 180° rotation is a rigid motion. Since \(\overline{A^{\prime} B^{\prime}} \| \overline{C D}\), m∠E\(B^{\prime} A^{\prime}\) = m∠ECD, and m∠\(B^{\prime}\)E\(A^{\prime}\) = m∠CED. So, △E\(A^{\prime} B^{\prime}\) ~ △EDC by AA similarity criteria, and △EAB ~ △EDC by the transitive property of similarity
Question 2.
Answer the following questions based on the diagram below.
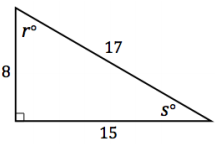
a. Find the sine and cosine values of angles r and s. Leave the answers as fractions.
sin r°=
sin s°=
cos r°=
cos s°=
tan r°=
tan s°=
Answer:
sin r°= \(\frac{15}{17}\)
sin s°= \(\frac{8}{17}\)
cos r°= \(\frac{8}{17}\)
cos s°= \(\frac{15}{17}\)
tan r°= \(\frac{15}{8}\)
tan s°= \(\frac{8}{15}\)
b. Why is the sine of an acute angle the same value as the cosine of its complement?
Answer:
By definition, sine is the ratio of the opposite side: hypotenuse and cosine is the ratio of the adjacent side: hypotenuse; since the opposite side of an angle is the adjacent side of its complement, sinθ = cos(90 – θ).
c. Determine the measures of the angles to the nearest tenth of a degree in the right triangles below.
i. Determine the measure of ∠a.
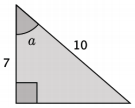
Answer:
m∠a ≈ 45.6°
ii. Determine the measure of ∠b.
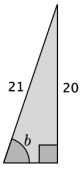
Answer:
m∠b ≈ 72.2°
iii. Explain how you were able to determine the measure of the unknown angle in part (i) or part (ii).
Answer:
For part (i), students should state that they had to use arccos to determine the unknown angle because the information given about the side lengths included the side adjacent to the unknown angle and the hypotenuse.
For part (ii), students should state that they had to use arcsin to determine the unknown angle because the information given about the side lengths included the side opposite to the unknown angle and the hypotenuse.
d. A ball is dropped from the top of a 45 ft. building. Once the ball is released, a strong gust of wind blew the ball off course, and it dropped 4 ft. from the base of the building.
i. Sketch a diagram of the situation.
Answer:
Sample sketch shown below.
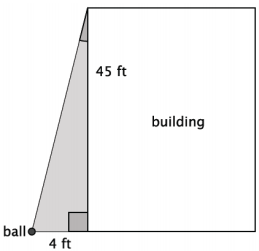
ii. By approximately how many degrees was the ball blown off course? Round your answer to the nearest whole degree.
Answer:
The wind blew the ball about 5˚ off course.
Question 3.
A radio tower is anchored by long cables called guy wires, such as \(\overline{A B}\) in the figure below. Point A is 250 m from the base of the tower, and m∠BAC = 59°.
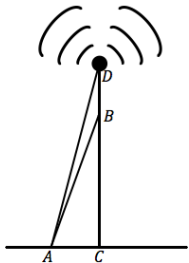
a. How long is the guy wire? Round to the nearest tenth.
Answer:
cos 59 = \(\frac{250}{A B}\)
AB = \(\frac{250}{\cos 59}\)
AB ≈ 485.4
The guy wire is approximately 485.4 meters.
b. How far above the ground is it fastened to the tower?
Answer:
tan 59 = \(\frac{B C}{250}\)
BC = 250 tan 59
BC ≈ 416.1
It is fastened approximately 416.1 meters above the ground.
c. How tall is the tower, \(\overline{D C}\), if m∠DAC = 71°?
Answer:
tan 71 = \(\frac{D C}{250}\)
DC = 250 tan 71
DC ≈ 726.1
The tower is approximately 726.1 meters tall.
Question 4.
The following problem is modeled after a surveying question developed by a Chinese mathematician during the Tang dynasty in the seventh century C.E.
A building sits on the edge of a river. A man views the building from the opposite side of the river. He measures the angle of elevation with a handheld tool and finds the angle measure to be 45°. He moves 50 feet away from the river and remeasures the angle of elevation to be 30°.
What is the height of the building? From his original location, how far away is the viewer from the top of the building? Round to the nearest whole foot.
Answer:
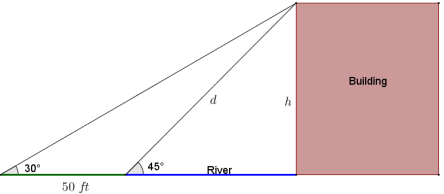
The angle of depression from the top of the building to the man’s original spot is also 45°, and the angle of depression to his final position is 60°, so the difference of the angles is 15°. Let d represent the distance from the man’s position at the edge of the river to the top of the building, and let h represent the height of the building in feet.
Using the law of sines:
\(\frac{\sin 30}{d}=\frac{\sin 15}{50}\)
d = \(\frac{50 \sin 30}{\sin 15}\) ≈ 96.6
The distance d is approximately 96.6 feet.
By the Pythagorean theorem, the distance d = h√2.
50 \(\frac{\sin 30}{\sin 15}\) = h√2
\(\frac{25}{\sin 15(\sqrt{2})}\) = h
h ≈ 68.3
The distance from the viewer to the top of the building is approximately 97 ft., and the height of the building is approximately 68 ft.
Question 5.
Prove the Pythagorean theorem using similar triangles. Provide a well-labeled diagram to support your justification.
Answer:
A right triangle ABC has side lengths a, b, and c. An altitude is drawn from C to the opposite side, dividing c into lengths x and c – x. Since the altitude from C divides the triangle into smaller similar right triangles by the AA criterion, then:
\(\frac{a}{x}=\frac{c}{a}\)
a2 = cx
\(\frac{b}{c-x}=\frac{c}{b}\)
b2 = c(c – x)
a2 + b2 = cx + c(c – x) = c2
a2 + b2 = c2
Question 6.
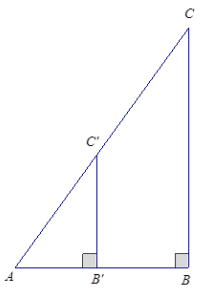
In right triangle ABC with ∠B a right angle, a line segment \(B^{\prime} C^{\prime}\) connects side \(\overline{A B}\) with the hypotenuse so that ∠A\(B^{\prime} C^{\prime}\) is a right angle as shown. Use facts about similar triangles to show why cos \(C^{\prime}\) = cos C.
Answer:
By the AA criterion, △ABC ~ △A\(B^{\prime} C^{\prime}\). Let r be the scale factor of the similarity
transformation. Then, \(B^{\prime} C^{\prime}\) = r . BC, and A\(C^{\prime}\) = r . AC. Thus,
cos \(C^{\prime}\) = \(\frac{B^{\prime} C^{\prime}}{A C^{\prime}}=\frac{r \cdot B C}{r \cdot A C}=\frac{B C}{A C}\) = cos C
cos \(C^{\prime}\) = cos C
Question 7.
Terry said, “I will define the zine of an angle x as follows. Build an isosceles triangle in which the sides of equal length meet at angle x. The zine of x will be the ratio of the length of the base of that triangle to the length of one of the equal sides.” Molly said, “Won’t the zine of x depend on how you build the isosceles triangle?”
a. What can Terry say to convince Molly that she need not worry about this? Explain your answer.
Answer:
Isosceles triangles with vertex angle x are similar to each other; therefore, the value of zine x, the ratio of the length of the base of that triangle to the length of one of the equal sides, is the same for all such triangles.
b. Describe a relationship between zine and sin.
Answer:
zine x = 2 sin \(\frac{1}{2}\)x