Engage NY Eureka Math Geometry Module 5 Lesson 8 Answer Key
Eureka Math Geometry Module 5 Lesson 8 Exercise Answer Key
Opening Exercise
Given circle A with \(\overline{B C}\) ⊥ \(\overline{D E}\), FA = 6, and AC = 10. Find BF and DE. Explain your work.
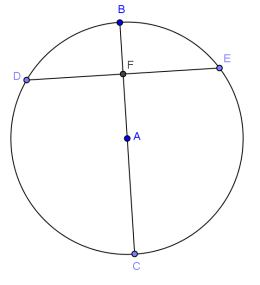
Answer:
BF = 4, DE = 16.
\(\overline{A B}\) is a radius with a measure of 10. If FA = 6, then BF = 10 – 6 = 4.
Connect \(\overline{A D}\) and \(\overline{A E}\). In △DAE, AD and AE are both equal to 10. Both △DFA and △EFA are right triangles and congruent, so by the Pythagorean theorem,
DF = FE = 8, making DE = 16.
Exercises
Exercise 1.
Given circle A with \(m \widehat{B C}\) = 54° and ∠CDB ≅ ∠DBE, find \(m \widehat{D E}\). Explain your work.

Answer:
\(m \widehat{D E}\) = 54°. m∠CAB = 54° because the central angle has the same measure as its subtended arc. m∠CDB is 27° because an inscribed angle has half the measure of the central angle with the same inscribed arc. Since ∠CDB is congruent to ∠DBE, \(m \widehat{D E}\) is 54° because it is double the angle inscribed in it.
Exercise 2.
If two arcs in a circle have the same measure, what can you say about the quadrilateral formed by the four endpoints? Explain.
Answer:
If the arcs are congruent, their endpoints can be joined to form chords that are parallel (\(\overline{B C}\) ∥\(\overline{D E}\)).
The chords subtending the congruent arcs are congruent (\(\overline{B D}\) ≅ \(\overline{C E}\)).
A quadrilateral with one pair of opposite sides parallel and the other pair of sides congruent is an isosceles trapezoid.
Exercise 3.
Find the angle measure of \(\widehat{C D}\) and \(\widehat{E D}\).
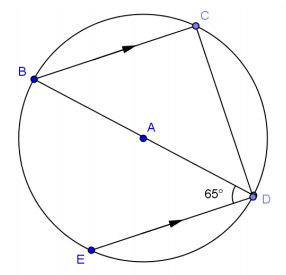
Answer:
\(m \widehat{C D}\) = 130°, \(m \widehat{E D}\) = 50°
Exercise 4.
\(m \widehat{C B}\) = \(m \widehat{E D}\) and \(m \widehat{B C}\) : \(m \widehat{B D}\) : \(m \widehat{E C}\) = 1 : 2 : 4. Find the following angle measures.
a. m∠BCF
Answer:
45°
b. m∠EDF
Answer:
90°
c. m∠CFE
Answer:
135°
Exercise 5.
\(\overline{B C}\) is a diameter of circle A. \(m \widehat{B D}\) : \(m \widehat{D E}\) : \(m \widehat{E C}\) = 1 : 3 : 5. Find the following arc measures.
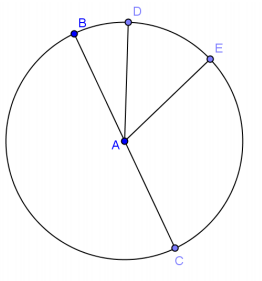
a. \(m \widehat{B D}\)
Answer:
20°
b. \(m \widehat{D E C}\)
Answer:
160°
c. \(m \widehat{E C B}\)
Answer:
280°
Eureka Math Geometry Module 5 Lesson 8 Problem Set Answer Key
Question 1.
Find the following arc measures.
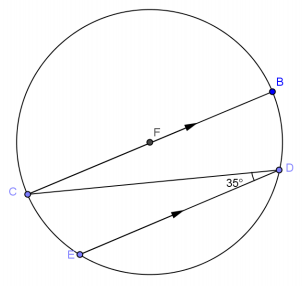
a. \(m \widehat{C E}\)
Answer:
70°
b. \(m \widehat{B D}\)
Answer:
70°
c. \(m \widehat{E D}\)
Answer:
40°
Question 2.
In circle A, \(\overline{B C}\) is a diameter, \(m \widehat{C E}\) = \(m \widehat{E D}\), and m∠CAE = 32°.
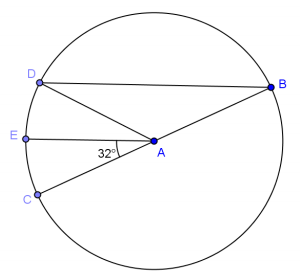
a. Find m∠CAD.
Answer:
64°
b. Find m∠ADC.
Answer:
58°
Question 3.
In circle A, (\(\overline{B C}\) is a diameter, 2\(m \widehat{C E}\) = \(m \widehat{E D}\), and \(\overline{B C}\) ∥ \(\overline{D E}\). Find m∠CDE.
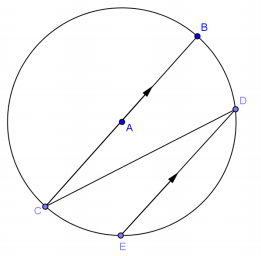
Answer:
22.5°
Question 4.
In circle A, \(\overline{B C}\) is a diameter and \(m \widehat{C E}\) = 68°.
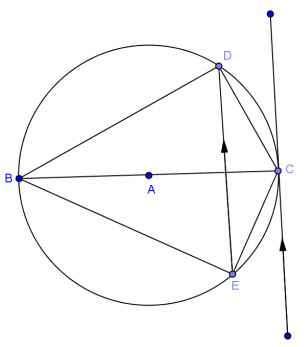
a. Find \(m \widehat{C D}\).
Answer:
68°
b. Find m∠DBE.
Answer:
68°
c. Find m∠DCE.
Answer:
112°
Question 5.
In the circle given, \(\widehat{B C}\) ≅ \(\widehat{E D}\). Prove \(\overline{B E}\) ≅ \(\overline{D C}\).

Answer:
Join \(\overline{C E}\).
BC = ED (congruent arcs have chords equal in length)
m∠CBE = m∠EDC (angles inscribed in same arc are equal in measure) m∠BCE = m∠DEC (angles inscribed in congruent arcs are equal in measure)
△BCE≅ △DEC (AAS)
\(\overline{B E}\) ≅ \(\overline{D C}\)(corresponding sides of congruent triangles are congruent)
Question 6.
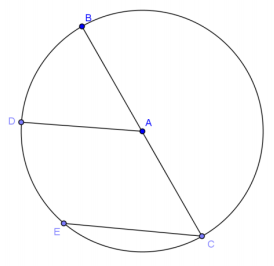
Given circle A with \(\overline{A D}\) ∥ \(\overline{C E}\), show (\(m \widehat{B D}\) ≅ \(\widehat{D E}\).
Answer:
Join \(\overline{B D}\), \(\overline{D E}\), \(\overline{A E}\).
AC = AE = AD = AB (radii)
∠AEC ≅ ∠ACE, ∠AED ≅ ∠ADE, ∠ADB ≅ ∠ABD (base angles of isosceles triangles are congruent)
∠AEC ≅ ∠EAD (alternate interior angles are congruent)
m∠ADE + m∠DEA + m∠EAD = 180° (sum of angles of a triangle)
3m∠AED = 180° (substitution)
m∠AED = 60°; △BAD ≅ △DAE ≅ △EAC (SAS)
BD = DE (corresponding parts of congruent triangles)
\(m \widehat{B D}\) ≅ \(m \widehat{D E}\) (arcs subtended by congruent chords)
Question 7.
In circle A, \(\overline{A B}\) is a radius, \(m \widehat{B C}\) ≅ \(m \widehat{B D}\), and m∠CAD = 54°. Find m∠ABC. Complete the proof.
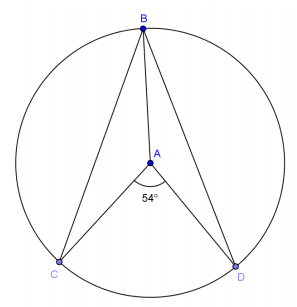
BC = BD _____________________
m∠________ = m∠_______ _____________________
m∠BAC + m∠CAD + m∠BAD = ___________
2m∠________ + 54° = 360° ________
m∠BAC = ________
AB = AC ________
m∠________ = m∠ ________ __________________
2m∠ABC + m∠BAC = ________ Sum of ____________________
m∠ABC = ________
Answer:
BC = BD Chords of congruent arcs
m∠BAC = m∠BAD Angles inscribed in congruent arcs are equal in measure.
m∠BAC + m∠CAD + m∠BAD = 360°
2m∠BAC + 54° = 360° Circle
m∠BAC = 153°
AB = AC Radii
m∠ABC = m∠ACB Base angles of isosceles
2m∠ABC + m∠BAC = 180° Sum of angles of a triangle equal 180°
m∠ABC = 13.5°
Eureka Math Geometry Module 5 Lesson 8 Exit Ticket Answer Key
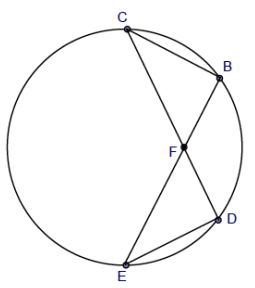
Question 1.
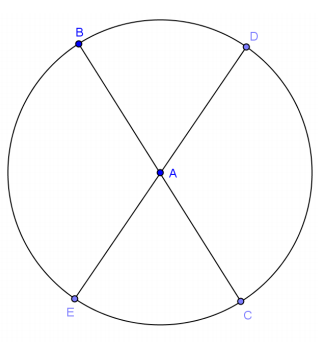
Given circle A with radius 10, prove BE = DC.
Answer:
m∠BAE = m∠DAC (vertical angles are congruent)
\(m \widehat{B E}\) = \(m \widehat{D C}\) (arcs are equal in degree measure to their inscribed central angles)
BE = DC (chords are equal in length if they subtend congruent arcs)
Question 2.
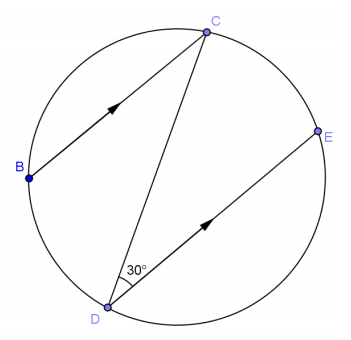
Given the circle at right, find \(m \widehat{B D}\).
Answer:
60°