Engage NY Eureka Math Geometry Module 5 Lesson 17 Answer Key
Eureka Math Geometry Module 5 Lesson 17 Example Answer Key
Example 1.
If we graph all of the points whose distance from the origin is equal to 5, what shape will be formed?
Answer:
By definition, the set of all points in the plane whose distance from the origin is 5 units is called a circle.
Example 2.
Let’s look at another circle, one whose center is not at the origin. Shown below is a circle with center (2, 3) and radius 5.
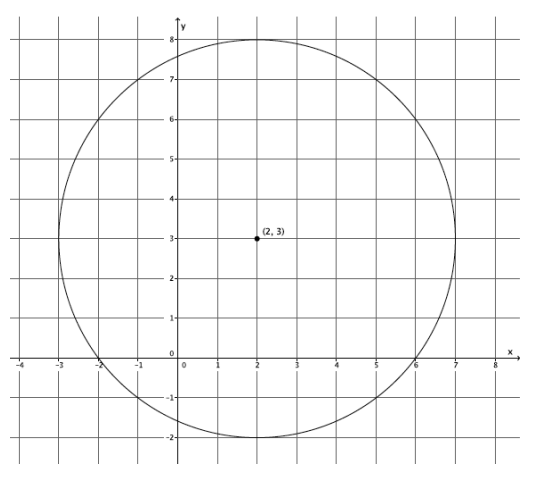
Answer:
→ Both of the circles have a radius of 5, but their centers are different, which makes the points that comprise the circles different.
→ Are the circles congruent? Is there a sequence of basic rigid motions that would take this circle to the origin? Explain.
→ Yes, the circles are congruent because both have a radius equal to 5. We could map one circle onto the other using a translation. For example, we could translate the circle with center at (2, 3) to the origin by translating along a vector from point (2, 3) to point (0, 0).
→ What effect does the translation have on all of the points from the circle above?
Show the circles side by side. Provide time for students to discuss this with partners.
→ Each x – coordinate is decreased by 2, and each y – coordinate is decreased by 3.
The effect that translation has on the points can be expressed as the following. Let (x, y) be any point on the circle with center (2, 3). Then, the coordinates of all of the points (x, y) after the translation are ((x – 2), (y – 3)).
→ Since the radius is equal to 5, we can locate any point (x, y) on the circle using the Pythagorean theorem as we did before.
(x – 2)2 + (y – 3)2 = 52
The solutions to this equation are all the points of a circle whose radius is 5 and center is at (2, 3).
→ What do the numbers 2, 3, and 5 represent in the equation above?
The 2 and 3 represent the location of the center (2, 3), and the 5 is the radius.
→ Assume we have a circle with radius 5 whose center is at (a, b). What is an equation whose graph is that circle?
Provide time for students to discuss this in pairs.
The circle with radius 5 and center at (a, b) is given by the graph of the equation
(x – a)2 + (y – b)2 = 52.
→ Assume we have a circle with radius r whose center is at (a, b). What is an equation whose graph is that circle?
Provide time for students to discuss this in pairs.
The circle with radius r and center at (a, b) is given by the graph of the equation
(x – a)2 + (y – b)2 = r2.
The last equation, (x – a)2 + (y – b)2 = r2, is the general equation for any circle with radius r and center (a, b).
Eureka Math Geometry Module 5 Lesson 17 Exercise Answer Key
Exercises 1–2
Exercise 1.
What is the length of the segment shown on the coordinate plane below?
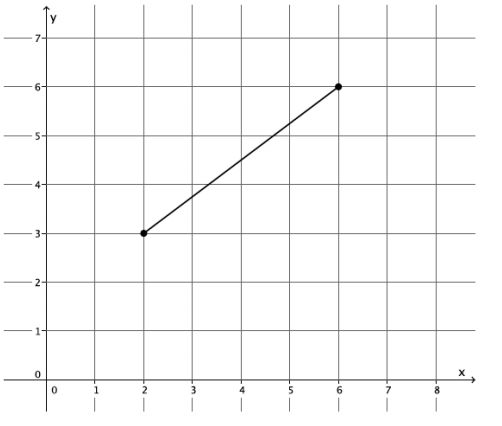
Answer:
Students may use the Pythagorean theorem or the distance formula to determine the length of the segment to be 5 units.
Exercise 2.
Use the distance formula to determine the distance between points (9, 15) and (3, 7).
Answer:
\(\sqrt{(9 – 3)^{2} + (15 – 7)^{2}}\) = d
\(\sqrt{36 + 64}\) = d
10 = d
Exercises 3–11
Exercise 3.
Write an equation for the circle whose center is at (9, 0) and has radius 7.
Answer:
(x – 9)2 + y2 = 49
Exercise 4.
Write an equation whose graph is the circle below.
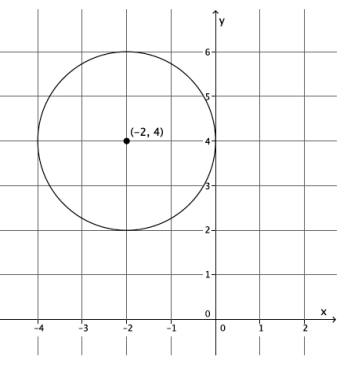
Answer:
(x + 2)2 + (y – 4)2 = 4
Exercise 5.
What is the radius and center of the circle given by the equation (x + 12)2 + (y – 4)2 = 81?
Answer:
The radius is 9, and the center is ( – 12, 4).
Exercise 6.
Petra is given the equation (x – 15)2 + (y + 4)2 = 100 and identifies its graph as a circle whose center is ( – 15, 4) and radius is 10. Has Petra made a mistake? Explain.
Answer:
Petra did not identify the correct center. The general form for the equation of a circle is given by (x – a)2 + (y – b)2 = r2, where (a, b) is the center and r is the radius. Petra noted the value of a as – 15 when it is really 15, and the value of b as 4 when it is really – 4. Therefore, Petra should have identified the center as (15, – 4). The radius was identified correctly.
Exercise 7.
a. What is the radius of the circle with center (3, 10) that passes through (12, 12)?
Answer:
(x – 3)2 + (y – 10)2 = r2
(12 – 3)2 + (12 – 10)2 = r2
81 + 4 = r2
\(\sqrt{85}\) = r
b. What is the equation of this circle?
Answer:
(x – 3)2 + (y – 10)2 = 85
Exercise 8.
A circle with center (2, – 5) is tangent to the x – axis.
a. What is the radius of the circle?
r = 5
b. What is the equation of the circle?
Answer:
(x – 2)2 + (y + 5)2 = 25
Exercise 9.
Two points in the plane, A( – 3, 8) and B(17, 8), represent the endpoints of the diameter of a circle.
a. What is the center of the circle? Explain.
Answer:
(7, 8); the midpoint of the diameter
b. What is the radius of the circle? Explain.
Answer:
10; the distance from one endpoint to the center
c. Write the equation of the circle.
Answer:
(x – 7)2 + (y – 8)2 = 100
Exercise 10.
Consider the circles with the following equations:
x2 + y2 = 25 and
(x – 9)2 + (y – 12)2 = 100.
a. What are the radii of the circles?
Answer:
The radii are 5 and 10.
b. What is the distance between the centers of the circles?
Answer:
d = \(\sqrt{(9 – 0)^{2} + (12 – 0)^{2}}\)
d = 15
c. Make a rough sketch of the two circles to explain why the circles must be tangent to one another.
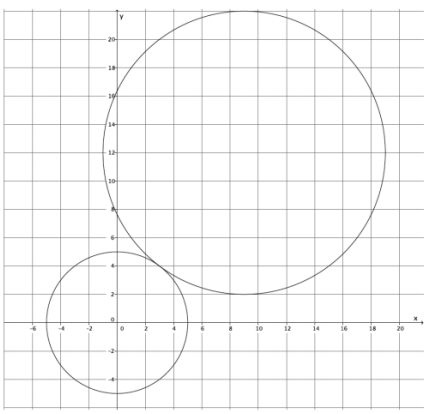
Answer:
The circles must be tangent because there is just one point that is common to both graphs (or there is only one solution that satisfies both equations), i.e., (3, 4).
Exercise 11.
A circle is given by the equation (x2 + 2x + 1) + (y2 + 4y + 4) = 121.
a. What is the center of the circle?
Answer:
The center is at ( – 1, – 2).
b. What is the radius of the circle?
Answer:
The radius is 11.
c. Describe what you had to do in order to determine the center and the radius of the circle.
Answer:
I had to factor each of the trinomials to get the equation in the proper form in order to identify the center of the circle. To get the radius, I had to take the square root of 121.
Eureka Math Geometry Module 5 Lesson 17 Problem Set Answer Key
Question 1.
Write the equation for a circle with center (\(\frac{1}{2}\), \(\frac{3}{7}\)) and radius \(\sqrt{13}[/latex.
Answer:
(x – [latex]\frac{1}{2}\))2 + (y – \(\frac{3}{7}\))2 = 13
Question 2.
What is the center and radius of the circle given by the equation x2 + (y – 11)2 = 144?
Answer:
The center is located at (0, 11), and the radius is 12.
Question 3.
A circle is given by the equation x2 + y2 = 100. Which of the following points are on the circle?
a. (0, 10)
Answer:
This point is on the circle.
b. ( – 8, 6)
Answer:
This point is on the circle.
c. ( – 10, – 10)
Answer:
This point is not on the circle.
d. (45, 55)
Answer:
This point is not on the circle.
e. ( – 10, 0)
Answer:
This point is on the circle.
Question 4.
Determine the center and radius of each circle.
a. 3x2 + 3y2 = 75
Answer:
The center is at (0, 0), and the radius is 5.
b. 2(x + 1)2 + 2(y + 2)2 = 10
Answer:
The center is at ( – 1, – 2), and the radius is √5.
c. 4(x – 2)2 + 4(y – 9)2 – 64 = 0
Answer:
The center is at (2, 9), and the radius is 4.
Question 5.
A circle has center ( – 13, π) and passes through the point (2, π).
a. What is the radius of the circle?
Answer:
(x + 13)2 + (y – π)2 = r2
(2 + 13)2 + (π – π)2 = r2
152 = r2
15 = r
b. Write the equation of the circle.
Answer:
(x + 13)2 + (y – π)2 = 225
Question 6.
Two points in the plane, A(19, 4) and B(19, – 6), represent the endpoints of the diameter of a circle.
a. What is the center of the circle?
Answer:
(19, – 1)
b. What is the radius of the circle?
Answer:
5
c. Write the equation of the circle.
Answer:
(x – 19)2 + (y + 1)2 = 25
Question 7.
Write the equation of the circle shown below.
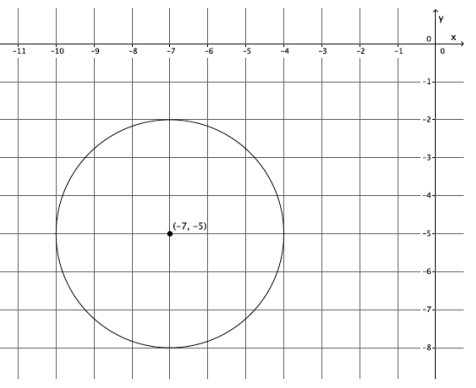
Answer:
(x + 7)2 + (y + 5)2 = 9
Question 8.
Write the equation of the circle shown below.
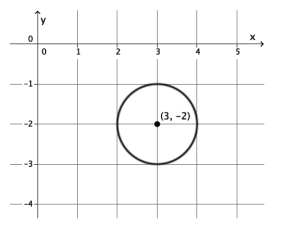
Answer:
(x – 3)2 + (y + 2)2 = 1
Question 9.
Consider the circles with the following equations:
x2 + y2 = 2 and
(x – 3)2 + (y – 3)2 = 32.
a. What are the radii of the two circles?
Answer:
The radii are \(\sqrt{2}\) and \(\sqrt{32}\).
b. What is the distance between their centers?
Answer:
\(\sqrt{32}\) – \(\sqrt{2}\) = 4\(\sqrt{2}\) – \(\sqrt{2}\) = 3\(\sqrt{2}\)
c. Make a rough sketch of the two circles to explain why the circles must be tangent to one another.
Answer:

The circles must be tangent because there is just one point that is common to both graphs (or there is only one solution that satisfies both equations), i.e., ( – 1, – 1).
Eureka Math Geometry Module 5 Lesson 17 Exit Ticket Answer Key
Question 1.
Describe the circle given by the equation (x – 7)2 + (y – 8)2 = 9.
Answer:
The circle has a center at (7, 8) and a radius of 3.
Question 2.
Write the equation for a circle with center (0, – 4) and radius 8.
Answer:
x2 + (y + 4)2 = 64
Question 3.
Write the equation for the circle shown below.
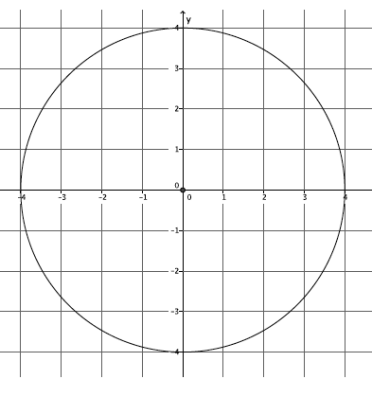
Answer:
x2 + y2 = 16
Question 4.
A circle has a diameter with endpoints at (6, 5) and (8, 5). Write the equation for the circle.
Answer:
(x – 7)2 + (y – 5)2 = 1