Engage NY Eureka Math Geometry Module 3 Lesson 12 Answer Key
Eureka Math Geometry Module 3 Lesson 12 Example Answer Key
Use your knowledge about the volumes of cones and cylinders to find a volume for a solid hemisphere of radius R.
Answer:
→ We have determined that the volume of H U S is equal to the volume of T. What is the volume of S?
Vol(S) = \(\frac{1}{3}\) × area of base × height
Vol(S) = \(\frac{1}{3}\) πR3
→ What is the volume of T?
Vol(T) = area of base × height
Vol(T) = πR3
→ Set up an equation and solve for Vol(H).
Vol(H) + \(\frac{1}{3}\) πR3 = πR3
Vol(H) = \(\frac{2}{3}\)πR3
→ What does \(\frac{2}{3}\)πR3 represent?
The Vol(H), or the volume of a hemisphere with radius R
→ Then, what is the volume formula for a whole sphere?
Twice the volume of a solid hemisphere or \(\frac{4}{3}\)πR3
→ The volume formula for a sphere is V = \(\frac{4}{3}\)πR3
Eureka Math Geometry Module 3 Lesson 12 Opening Exercise Answer Key
Picture a marble and a beach ball. Which one would you describe as a sphere? What differences between the two could possibly impact how we describe what a sphere is?

Answer:
Answers vary; some students may feel that both are spheres. Some may distinguish that one is a solid while the other is hollow. Share out responses before moving to the definition of sphere.
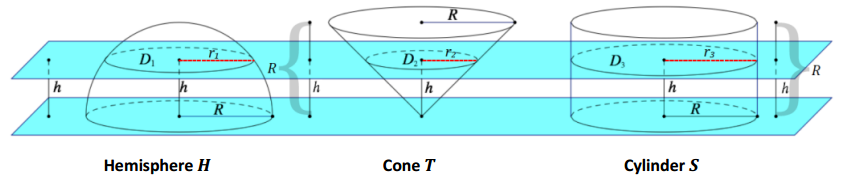
→ The solids are aligned above a base plane that contains the bases of the hemisphere and cylinder and the vertex of the cone; the altitude of the cone is perpendicular to this plane.
→ A cross-sectional plane that is distance h from the base plane intersects the three solids. What is the shape of each cross-section? Sketch the cross-sections, and make a conjecture about their relative sizes (e.g., order smallest to largest, and explain why).
Each cross-section is in the shape of a disk. It looks like the cross-section of the cone will be the smallest, the cross-section of the cylinder will be the largest, and the cross-section of the hemisphere will be between the sizes of the other two.
→ Let D1, D2, D3 be the cross-sectional disks for the solid hemisphere, the cone, and the cylinder, respectively.
→ Let r1, r2, r3 be the radii of D1, D2, D3, respectively.
→ Our first task in order to accomplish our objective is to find the area of each cross-sectional disk. Since the radii are all of different lengths, we want to try and find the area of each disk in terms of R and h, which are common between the solids.
→ Examine the hemisphere more closely in Figure 1.
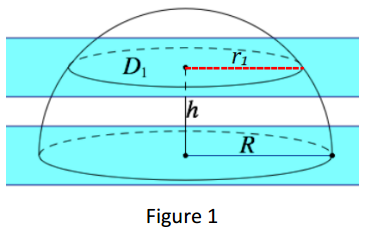
→ What is the area formula for disk D1 in terms of r1?
Area(D1) = πr12
→ How can we find r1 in terms of h and R?
Allow students time to piece together that the diagram they need to focus on looks like the following figure. Take student responses before confirming with the solution.
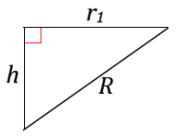
By the Pythagorean theorem: .
r12 + h2 = R2 hemisphere.
r1 = \(\sqrt{R^{2}-h^{2}}\)
→ Once we have r1, substitute it into the area formula for disk D1.
The area of D1:
Area(D1) = πr12
Area(D1) = π\(\left(\sqrt{R^{2}-h^{2}}\right)^{2}\)
Area(D1) = πR2 – πh2
→ Let us pause and summarize what we know so far. Describe what we have shown so far.
We have shown that the area of the cross-sectional disk of the hemisphere is πR2 – πh2
Record this result in the classroom.
→ Continuing on with our goal of finding the area of each disk, now find the radius r2 and the area of D2 in terms of R and h. Examine the cone more closely in Figure 2.
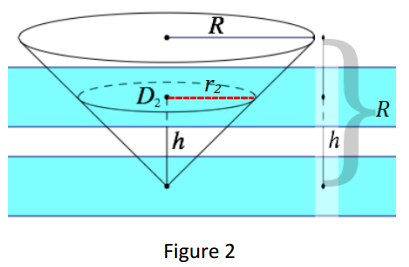
If students require a prompt, remind them that both the radius and the height of the cone are each length R.
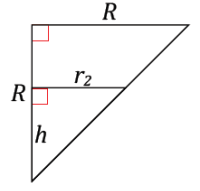
By using similar triangles:
\(\frac{r_{2}}{h}=\frac{R}{R}\) = 1, or r2 = h
The area of D2:
Area(D2) = πr22 = πh2
→ Let us pause again and summarize what we know about the area of the cross-section of the cone. Describe what we have shown.
We have shown that the area of the cross-sectional disk of the hemisphere is πR2 – πh2.
Record the response next to the last summary.
→ Lastly, we need to find the area of disk D3 in terms of R and h. Examine the cone more closely in Figure 3.

→ In the case of this cylinder, will h play a part in the area formula of disk D3? Why?
The radius r3 is equal to R, so the area formula will not require h this time.
The area of D3:
Area(D3) = πR2
Write all three areas on the board while asking the following questions:
→ What do you now know about the three areas of the cross-sections?
Area(D1) = πR2 – πh2
Area(D2) = πh2
Area(D3) = πR2
→ Do you notice a relationship between the areas of D1, D2, D3? What is it?
The area of D3 is the sum of the areas of D1 and D2.
Area(D1) + Area(D2) = Area(D3)
(πR2 – πh2) + πh2 = πR2
→ Then, let us review two key facts: (1) The three solids all have the same height; (2) at any given height, the sum of the areas of the cross-sections of the hemisphere and cone are equal to the cross-section of the cylinder.
Eureka Math Geometry Module 3 Lesson 12 Exercise Answer Key
Exercise 1.
Find the volume of a sphere with a diameter of 12 cm to one decimal place.
Answer:
V = \(\frac{4}{3}\)π(6)3
V = \(\frac{4}{3}\)π(216)
V ≈ 904.8
The volume of the sphere is approximately 904.8 cm3.
Exercise 2.
An ice cream cone is 11 cm deep and 5 cm across the opening of the cone. Two hemisphere-shaped scoops of ice cream, which also have diameters of 5 cm, are placed on top of the cone. If the ice cream were to melt into the cone, would it overflow?
Answer:
Volume(cone) = \(\frac{1}{3} \pi\left(\frac{5}{2}\right)^{2}\) · (11) Volume(ice cream) = \(\frac{4}{3} \pi\left(\frac{5}{2}\right)^{3}\)
Volume(cone) ≈ 72 Volume(ice cream) ≈ 65.4
The volume the cone can hold is roughly 72 cm3. The volume of ice cream is roughly 65.4 cm3.
The melted ice cream will not overflow because there is significantly less ice cream than there is space in the cone.
Exercise 3.
Bouncy rubber balls are composed of a hollow rubber shell 0.4” thick and an outside diameter of 1. 2”. The price of the rubber needed to produce this toy is $0. 035/in3.
a. What is the cost of producing 1 case, which holds 50 such balls? Round to the nearest cent.
Answer:
The outer shell of the ball is 0.4” thick, so the hollow center has a diameter of 0.8” and, therefore, a radius of 0.4”.
The volume of rubber in a ball is equal to the difference of the volumes of the entire sphere and the hollow center.
V = [\(\frac{4}{3}\)π(0.6)3] – [\(\frac{4}{3}\)π(0.4)3]
V = \(\frac{4}{3}\)π[(0.6)3 – (0.4)3]
V = \(\frac{4}{3}\)π[0.152]
V ≈ 0.6367
The volume of rubber needed for each individual ball is approximately 0.6367 in3. For a case of 50 rubber balls, the volume of rubber required is \(\frac{4}{3}\)π[0. 152] · 50 ≈ 31.8, or 31.8 in3.
Total cost equals the cost per cubic inch times the total volume for the case.
Total cost = [0.035] · [\(\frac{4}{3}\)π[0. 152] · 50]
Total cost ≈ 1.11
The total cost for rubber to produce a case of 50 rubber balls is approximately $1. 11.
b. If each ball is sold for $0. 10, how much profit is earned on each ball sold?
Answer:
Total sales = (selling price). (units sold)
Total sales = (0. 1)(50)
Total sales = 5
The total sales earned for selling the case of rubber balls is $5.
Profit earned = (total sales) – (expense)
Profit earned = (5) – (1.11)
Profit earned = 3.89
The total profit earned after selling the case of rubber balls is $3. 89.
Profit per unit = \(\frac{3.89}{50}\)
Profit per unit = 0.0778
The profit earned on the sale of each ball is approximately $0.08.
Extension:

→ The volume formula for a solid sphere can be used to find the surface area of a sphere with radius R.
→ Cover the sphere with non-overlapping regions with area A1, A2, A3, …, An.
→ For each region, draw a “cone” with the region for a base and the center of the sphere for the vertex (see image).
One says “cone” since the base is not flat but rather a piece of a sphere. However, it is an approximation of a cone.
→ The volume of the cone with base area A1 and height equal to the radius R is approximately
Volume(A1) ≈ \(\frac{1}{3}\) · A1 · R.
→ How is the volume of the sphere related to the volume of the cones? Explain and then show what you mean in a formula.
The volume of the sphere is the sum of the volumes of these “cones.”
\(\frac{4}{3}\)πR3 ≈ \(\frac{1}{3}\) · (A1 + A2 + ··· + An) · R
→ Let S be the surface area of the sphere. Then, the sum is A1 + A2 + ··· + An = S. We can rewrite the last approximation as
\(\frac{4}{3}\)πR3 ≈ \(\frac{1}{3}\) · S · R
Remind students that the right-hand side is only approximately equal to the left-hand side because the bases of these “cones” are slightly curved, and R is not the exact height.
→ As the regions are made smaller, and we take more of them, the “cones” more closely approximate actual cones. Hence, the volume of the solid sphere would actually approach \(\frac{1}{3}\) · S · R as the number of regions approaches ∞.
→ Under this assumption, we will use the equal sign instead of the approximation symbol:
\(\frac{4}{3}\)πR3 ≈ \(\frac{1}{3}\) · S · R
→ Solving for S, we get
S = 4πR2.
→ Thus, the formula for the surface area of a sphere is
Surface Area = 4πR2.
Eureka Math Geometry Module 3 Lesson 12 Problem Set Answer Key
Question 1.
A solid sphere has volume 36π. Find the radius of the sphere.
Answer:
\(\frac{4}{3}\)πr3 = 36π
r3 = 27
r = 3
Therefore, the radius is 3 units.
Question 2.
A sphere has surface area 16π. Find the radius of the sphere.
Answer:
4.2πr2 = 16π
r2 = 4
r = 2
Therefore, the radius is 2 units.
Question 3.
Consider a right circular cylinder with radius r and height h. The area of each base is πr2. Think of the lateral surface area as a label on a soup can. If you make a vertical cut along the label and unroll it, the label unrolls to the shape of a rectangle.
a. Find the dimensions of the rectangle.

Answer:
2πr by h

b. What is the lateral (or curved) area of the cylinder?
Answer:
Lateral Area = length × width
Lateral Area = 2πrh
Question 4.
Consider a right circular cone with radius r, height h, and slant height l (see Figure 1). The area of the base is πr2. Open the lateral area of the cone to form part of a disk (see Figure 2). The surface area Is a fraction of the area of this disk.

a. What is the area of the entire disk in Figure 2?
Answer:
Area = πl2
b. What is the circumference of the disk in Figure 2?
Answer:
Circumference = 2πl
The length of the arc on this circumference (i.e., the arc that borders the green region) is the circumference of the base of the cone with radius r or 2πr. (Remember, the green region forms the curved portion of the cone and closes around the circle of the base.)
c. What is the ratio of the area of the disk that is shaded to the area of the whole disk?
Answer:
\(\frac{2 \pi r}{2 \pi l}=\frac{r}{l}\)
d. What is the lateral (or curved) area of the cone?
Answer:
\(\frac{r}{l}\) × πl2 = πrl
Question 5.
A right circular cone has radius 3 cm and height 4 cm. Find the lateral surface area.
Answer:
By the Pythagorean theorem, the slant height of the cone is 5 cm.
The lateral surface area in cm2 is πrl = π3 · 5 = 15π. The lateral surface area is 15π cm2.
Question 6.
A semicircular disk of radius 3 ft. is revolved about its diameter (straight side) one complete revolution. Describe the solid determined by this revolution, and then find the volume of the solid.
Answer:
The solid is a solid sphere with radius 3 ft. The volume in ft3 is \(\frac{4}{3}\)π33 = 36π. The volume is 36π ft3.
Question 7.
A sphere and a circular cylinder have the same radius, r, and the height of the cylinder is 2r.
a. What is the ratio of the volumes of the solids?
Answer:
The volume of the sphere is \(\frac{4}{3}\)πr3, and the volume of the cylinder is 2πr3, so the ratio of the volumes is the following:
\(\frac{\frac{4}{3} \pi r^{3}}{2 \pi r^{3}}=\frac{4}{6}=\frac{2}{3}\)
The ratio of the volume of the sphere to the volume of the cylinder is 2: 3.
b. What is the ratio of the surface areas of the solids?
Answer:
The surface area of the sphere is 4πr2, and the surface area of the cylinder is 2(πr2) + (2πr · 2r) = 6πr2,
so the ratio of the surface areas is the following:
\(\frac{4 \pi r^{2}}{6 \pi r^{2}}=\frac{4}{6}=\frac{2}{3}\).
The ratio of the surface area of the sphere to the surface area of the cylinder is 2:3.
Question 8.
The base of a circular cone has a diameter of 10 cm and an altitude of 10 cm. The cone is filled with water. A sphere is lowered into the cone until it just fits. Exactly one-half of the sphere remains out of the water. Once the sphere is removed, how much water remains in the cone?
Answer:

Question 9.
Ten has an aquarium that is a cube with edge lengths of 24 inches. The aquarium is \(\frac{2}{3}\) full of water. She has a supply of ball bearings, each having a diameter of \(\frac{3}{4}\) inch.
a. What is the maximum number of ball bearings that Ten can drop into the aquarium without the water overflowing?
Answer:
24 in. × 24 in. × 24 in. = 13824 in3
The volume of the cube is 13.824 in3.
24in. × 24in. × 18 in. 10368 in3
The volume of water in the cube is 10.368 in3.
13824 in3 – 10368 in3 – 3456 in3
The remaining volume in the aquarium is 3,456 in3.

The volume of one boll bearing is \(\frac{9}{128}\)π in3 or approximately 0.221 in3.
\(\frac{3456}{\frac{9}{128} \pi}=\frac{49152}{\pi}\) ≈ 15645.6
Ten can drop 15.645 balI bearings into the aquarium without the water overflowing. If she drops in one more, the water (theoretically without considering a meniscus) will overflow.
b. Would your answer be the same if the aquarium were \(\frac{2}{3}\) full of sand? Explain.
Answer:
Ir, the original problem, the water vnlI fill the gaps between the bail bearings as they ore dropped in; however, the sand will not fill the gaps unless the mixture of sand and boll bearings is continuously stirred.
c. If the aquarium were empty, how many ball bearings would fit on the bottom of the aquarium if you arranged them in rows and columns, as shown in the picture?
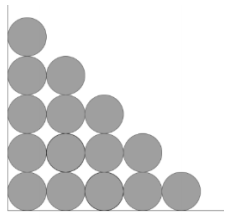
Answer:
The length and width of the aquarium are 24 inches, and 24 inches divided into \(\frac{3}{4}\) inch intervals is 32, so each row and column would contain 32 bearings. The total number of bearings in a single layer would be 1,024.
d. How many of these layers could be stacked inside the aquarium without going over the top of the aquarium? How many bearings would there be altogether?
Answer:
The aquarium is 24 inches high as well, so there could be 32 layers of bearings for a total of 32,768 bearings.
e. With the bearings still in the aquarium, how much water can be poured into the aquarium without overflowing?
Answer:
(32768) (\(\frac{9}{128}\)) ≈ 7238. 229 474
The total volume of the ball bearings is approximately 7238.229474 in3.
13824 – 7238. 229474 = 6585.770 526
The space between the ball bearings has a volume of 6585.770526 in3.
6585. 770 526 × 0. 004 329 = 28. 509 800 61
With the bearings in the aquarium, approximately 28.5 gallons of water could be poured in without overflowing the tank.
f. Approximately how much of the aquarium do the ball bearings occupy?
Answer:
A little more than half of the space.
Question 10.
Challenge: A hemispherical bowl has a radius of 2 meters. The bowl is filled with water to a depth of 1 meter. What is the volume of water in the bowl? (Hint: Consider a cone with the same base radius and height and the
cross-section of that cone that lies 1 meter from the vertex.)
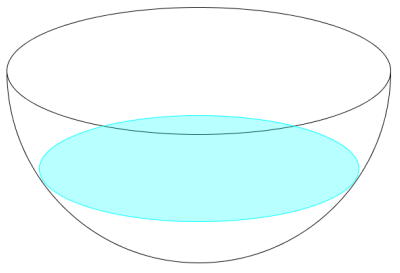
Answer:
The volume of a hemisphere with radius 2 is equal to the difference of the volume of a circular cylinder with radius 2 and height 2 and the volume of a circular cone with base radius 2 and height 2. The cross-sections of the circular cone and the hemisphere taken at the same height h from the vertex of the cone and the circular face of the hemisphere have a sum equal to the base of the cylinder.
Using Cavalieri’s principle, the volume of the water that remains in the bowl can be found by calculating the volume of the circular cylinder with the circular cone removed, and below the cross-section at a height of 1 (See diagram right).

Question 11.
Challenge: A certain device must be created to house a scientific Instrument. The housing must be a spherical shell, with an outside diameter of 1 m. It will be made of a material whose density is 14 g/cm3. It will house a sensor inside that weighs 1.2 kg. The housing, with the sensor inside, must be neutrally buoyant, meaning that its density must be the same as water. Ignoring any air inside the housing, and assuming that water has a density of 1 g/cm3, how thick should the housing be made so that the device is neutrally buoyant? Round your answer to the nearest tenth of a centimeter.
Answer:

Question 12.
Challenge: An inverted, conical tank has a circular base of radius 2 m and a height of 2 m and is full of water. Some of the water drains into a hemispherical tank, which also has a radius of 2 m. Afterward, the depth of the water in the conical tank is 80 cm. Find the depth of the water in the hemispherical tank.
Answer:
Total volume of water:
V = \(\frac{1}{3}\)π(2)2(2)
V = \(\frac{8}{3}\)π; the total volume of water is \(\frac{8}{3}\)π m3.
The cone formed when the water level is at 80 cm (0.8 m) is similar to the original cone; therefore, the radius of that cone is also 80 cm.
The volume of water once the water level drops to 80 cm:
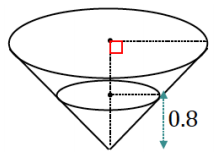
V = \(\frac{1}{3}\)π(0.8)2(0.8 m)
V = \(\frac{1}{3}\)π(0. 512)
The volume of water in the cone water once the water level drops to 80 cm is
\(\frac{1}{3}\)π(0. 512) m3.
The volume of water that has drained into the hemispherical tank:
V = [\(\frac{8}{3}\)π – \(\frac{1}{3}\)π(0. 512)]
V = \(\frac{1}{3}\)π[8 – (0.512)]
V = \(\frac{1}{3}\)π[7. 488]
V = 2.496π
The volume of water in the hemispherical tank is 2. 496π m3.
The pool of water that sits in the hemispherical tank is also hemispherical.
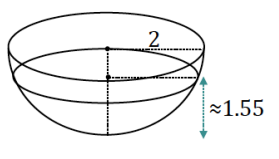
2.496π = \(\left(\frac{1}{2}\right) \frac{4}{3}\)πr3
r3 = 2.496\(\left(\frac{3}{2}\right)\)
r3 = 3.744
r ≈ 1.55
The depth of the water in the hemispherical tank is approximately 1.55 m.
Eureka Math Geometry Module 3 Lesson 12 Exit Ticket Answer Key
Question 1.
Snow globes consist of a glass sphere that is filled with liquid and other contents. If the inside radius of the snow globe is 3 in., find the approximate volume of material in cubic inches that can fit inside.

Answer:
Volume = \(\frac{4}{3}\)πR3
Volume = \(\frac{8}{3}\)π · 33
Volume = 36π ≈ 113.1
The snow globe can contain approximately 113.1 in3 of material.
Question 2.
The diagram shows a hemisphere, a circular cone, and a circular cylinder with heights and radii both equal to 9.

a. Sketch parallel cross-sections of each solid at height 3 above plane P.
Answer:
See the diagram above.
b. The base of the hemisphere, the vertex of the cone, and the base of the cylinder lie in base plane P. Sketch parallel cross-sectional disks of the figures at a distance h from the base plane, and then describe how the areas of the cross-sections are related.
Answer:
The cross-sectional disk is \(\frac{1}{3}\) of the distance from plane P to the base of the cone, so its radius is also \(\frac{1}{3}\) of the radius of the cone’s base. Therefore, the radius of the disk is 3, and the disk has area 9π.
The area of the cross-sectional disk in the cylinder is the same as the area of the cylinder’s base since the disk is congruent to the base. The area of the disk in the cylinder is 81π.
Area(cylinder disk) = Area(hemisphere disk) + Area(cone disk)
81π = Area(hemisphere disk) + 9π
72π = Area(hemisphere disk)
The area of the disk in the hemisphere at height 3 above plane P is 72π or approximately 226.2.