Engage NY Eureka Math Geometry Module 2 Lesson 15 Answer Key
Eureka Math Geometry Module 2 Lesson 15 Exercise Answer Key
Exercise 1.
Draw two triangles of different sizes with two pairs of equal angles. Then, measure the lengths of the corresponding sides to verify that the ratio of their lengths is proportional. Use a ruler, compass, or protractor, as necessary.
Answer:
Students’ work will vary. Verify that students have drawn a pair of triangles with two pairs of equal angles and have shown via direct measurement that the ratios of corresponding side lengths are proportional.
Exercise 2.
Are the triangles you drew in Exercise 1 similar? Explain.
Answer:
Yes, the triangles are similar. The converse of the theorem on similar triangles states that when we have two triangles ∆ ABC and ∆ A’B’C’ with corresponding angles that are equal and corresponding side lengths that are proportional, then the triangles are similar.
Exercise 3.
Why is it that you only need to construct triangles where two pairs of angles are equal but not three?
Answer:
If we are given the measure of two angles of a triangle, then we also know the third measure because of the triangle sum theorem. All three angles must add to 180°, so showing two pairs of angles are equal in measure is just like showing all three pairs of angles are equal in measure.
Exercise 4.
Why were the ratios of the corresponding sides proportional?
Answer:
Since the triangles are similar, we know that there exists a similarity transformation that maps one triangle onto another. Then, corresponding sides of similar triangles must be in proportion because of what we know about similarity, dilation, and scale factor. Specifically, the length of a dilated segment is equal to the length of the original segment multiplied by the scale factor. For example,
\(\frac{A^{\prime} B^{\prime}}{A B}\) = r and A’B’ = rAB.
Exercise 5.
Do you think that what you observed will be true when you construct a pair of triangles with two pairs of equal angles? Explain.
Answer:
Accept any reasonable explanation. Use students’ responses as a springboard for the Opening discussion and the presentation of the AA criterion for similarity.
Exercise 6.
Draw another two triangles of different sizes with two pairs of equal angles. Then, measure the lengths of the corresponding sides to verify that the ratio of their lengths is proportional. Use a ruler, compass, or protractor, as necessary.
Answer:
Students’ work will vary. Verify that they have drawn a pair of triangles with two pairs of equal angles and have shown via direct measurement that the ratios of corresponding side lengths are proportional.
Exercise 7.
Are the triangles shown below similar? Explain. If the triangles are similar, identify any missing angle and side length measures.
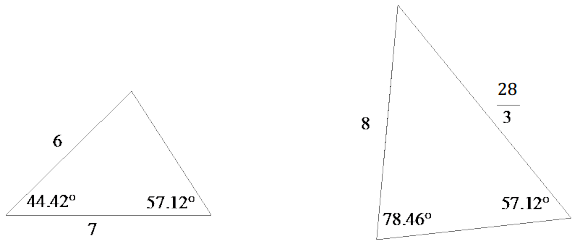
Answer:
Yes, the triangles are similar because they have two pairs of equal corresponding angles. By the AA criterion, they must be similar. The angle measures and side lengths are shown below.
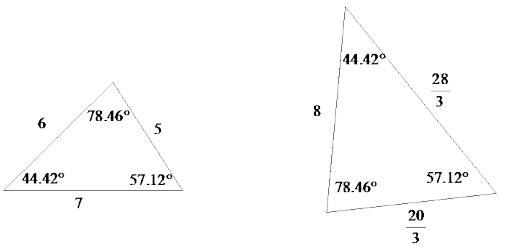
Exercise 8.
Are the triangles shown below similar? Explain. If the triangles are similar, identify any missing angle and side length measures.
Answer:
The triangles are not similar because they have just one pair of corresponding equal angles. By the triangle sum theorem, m∠C = 60° and m∠D = 61°. Since similar triangles must have equal corresponding angles, we can conclude that the triangles shown are not similar.
Exercise 9.
The triangles shown below are similar. Use what you know about similar triangles to find the missing side lengths x and y.
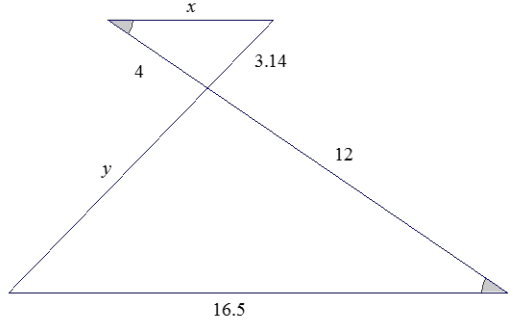
Answer:
\(\frac{12}{4}=\frac{16.5}{x}\)
12x = 66
x = 5.5
\(\frac{12}{4}=\frac{y}{3.14}\)
37.68 = 4y
9.42 = y
Side length x is 5.5 units, and side length y is 9.42 units.
Exercise 10.
The triangles shown below are similar. Write an explanation to a student, Claudia, of how to find the lengths of x and y.
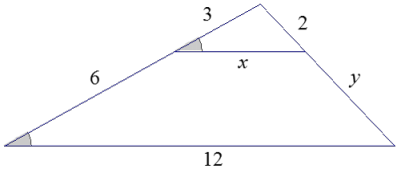
Answer:
Claudia,
We are given that the triangles are similar; therefore, we know that they have equal corresponding angles and corresponding sides that are equal in ratio. For that reason, we can write \(\frac{3}{9}=\frac{2}{2+y}\), which represents two pairs of corresponding sides of the two triangles. We can solve for y as follows:
\(\frac{3}{9}=\frac{2}{2+y}\)
6 + 3y = 18
3y = 12
y = 4
We can solve for x in a similar manners We begin by writing two pairs of corresponding sides as equal ratios, making sure that one of the ratios contains the length x.
\(\frac{x}{12}=\frac{3}{9}\)
9x = 36
x = 4
Therefore, side length x is 4 units, and side length y is 4 units.
Eureka Math Geometry Module 2 Lesson 15 Problem Set Answer Key
Question 1.
In the figure to the right, ∆ LMN ~ ∆ MPL.
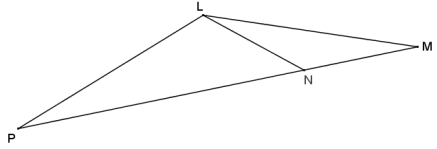
a. Classify ∆ LMP based on what you know about similar triangles, and justify your reasoning.
Answer:
By the given similarity statement, M and P are corresponding vertices; therefore, the angles at M and P must be congruent. This means that ∆ LMP is an isosceles triangle by base ∠‘s converse.
b. If m∠P = 20°, find the remaining angles in the diagram.
Answer:
m∠M = 20°, m∠MLN = 20°, m∠MNL = 140°, m∠NLP = 120°, m∠MLP = 140°, and m∠LNP = 40°.
Triangle MNL is also isosceles.
Question 2.
In the diagram below, ∆ ABC ~ ∆ AFD. Determine whether the following statements must be true from the given information, and explain why.
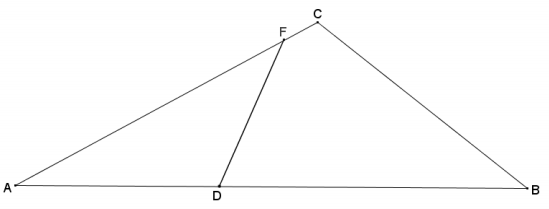
a. ∆ CAB ~ ∆DAF
Answer:
This statement is true because corresponding vertices are the same as in the given similarity statement but are listed in a different order.
b. ∆ ADF ~ ∆ CAB
Answer:
There is no information given to draw this conclusion.
C. ∆ BCA ~ ∆ ADF
Answer:
There is no information given to draw this conclusion.
d. ∆ ADF ~ ∆ ACB
Answer:
This statement is true because corresponding vertices are the same as in the given similarity statement but are listed in a different order.
Question 3.
In the diagram below, D is the midpoint of \(\overline{A B}\), F is the midpoint of \(\overline{B C}\), and E is the midpoint of \(\overline{A C}\). Prove that ∆ ABC ~ ∆ FED.
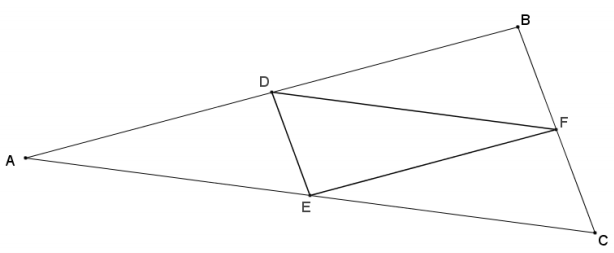
Answer:

Question 4.
Use the diagram below to answer each part.
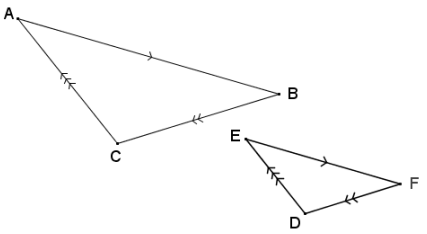
a. If \(\overline{A C}\|\overline{E D}, \overline{A B}\| \overline{E F}\), and \(\overline{C B} \| \overline{D F}\), prove that the triangles are similar.
Answer:
By extending all sides of both triangles, there are several pairs of parallel lines cut by parallel transversals.
Using corresponding angles within parallel lines and transitivity, ∆ ABC ~ ∆ EFD by the AA criterion for proving similar triangles.
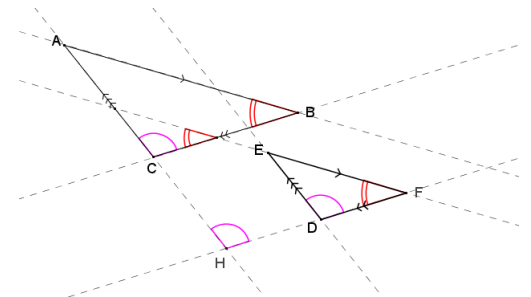
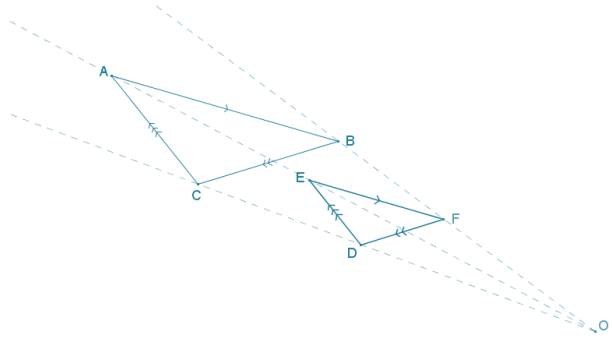
b. The triangles are not congruent. Find the dilation that takes one to the other.
Answer:
Extend lines joining corresponding vertices to find their intersection O, which is the center of dilation.
Question 5.
Given trapezoid ARDE, and \(\overline{A B}\) || \(\overline{E D}\), prove that ∆ AFB ~ ∆ DEF.
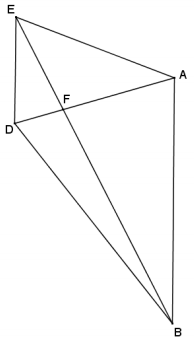
Answer:
From the given information, ∠EDA ≅ ∠DAB by alternate interior ∠‘s, \(\overline{A B}\) || \(\overline{E D}\) (by the same argument, ∠DEB ≅ ∠ABE). Furthermore, ∠EFD ≅ ∠BFA because vertical angles are congruent. Therefore, ∆ AFB ~ ∆ DEF by the AA criterion for proving similar triangles.
Eureka Math Geometry Module 2 Lesson 15 Exit Ticket Answer Key
Question 1.
Given the diagram to the right, \(\overline{U X} \perp \overline{V W}\), and \(\overline{W Y} \perp \overline{U V}\). Show that ∆ UXV ~ ∆ WYV.
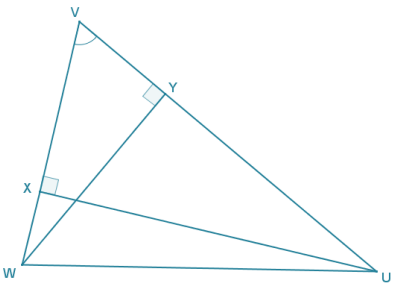
Answer:
By the definition of perpendicular lines, ∠WYV and ∠UXV are right angles, and all right angles are congruent, so ∠WYV ≅ ∠UXV. Both ∆ UXV and ∆ WYV share ∠V, and by the reflexive property ∠V ≅ ∠V. Therefore, by the AA criterion for proving similar triangles, ∆ UXV ~ ∆ WYV.
Question 2.
Given the diagram to the right and \(\overline{D E}\) || \(\overline{K L}\). find FE and FL.
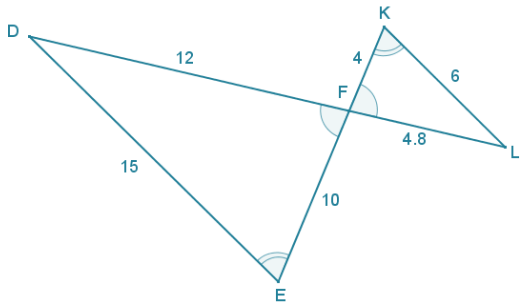
Answer:
By alternate interior ∠‘s, \(\overline{D E}\) || \(\overline{K L}\), it follows that ∠K ≅ ∠E (and by a similar argument, ∠D ≅ ∠L). ∠DFE and ∠KFL are vertically opposite angles and therefore congruent. By AA criterion for proving similar triangles, ∆ DFE ~ ∆ LFK. Therefore,

Using the relationship of similar triangles, EF = 10, and LF = 4.8.