Engage NY Eureka Math Geometry Module 2 Lesson 27 Answer Key
Eureka Math Geometry 2 Module 2 Lesson 27 Example Answer Key
If α and β are the measurements of complementary angles, then we are going to show that sin α = cos β.
In right triangle ABC, the measurement of acute angle ∠A is denoted by α, and the measurement of acute angle ∠B is denoted by β?.
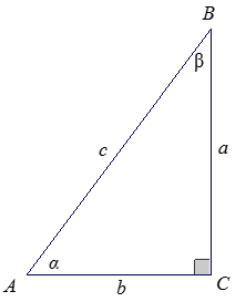
Determine the following values in the table:
Answer:

What can you conclude from the results?
Answer:
Since the ratios for sin α and cos β are the same, sin α = cos β, and the ratios for cos α and sin β are the same; additionally, cos α = sin β. The sine of an angle is equal to the cosine of its complementary angle, and the cosine of an angle is equal to the sine of its complementary angle.
→ Therefore, we conclude for complementary angles α and β that sin α = cos β, or in other words, when 0 < 6 < 90 that sin(90 – θ) = cos θ, and sin θ = cos (90 – θ). Any two angles that are complementary can be realized as the acute angles in a right triangle. Hence, the co- prefix in cosine is a reference to the fact that the cosine of an angle is the sine of its complement.
Example 2.
What is happening to a and b as θ changes? What happens to sin θ and cos θ?
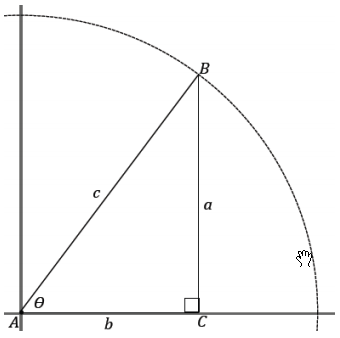
Answer:
→ There are values for sine and cosine commonly known for certain angle measurements. Two such angle measurements are when θ = 0° and θ = 90°.
→ To better understand sine and cosine values, imagine a right triangle whose hypotenuse has a fixed length c of 1 unit. We illustrate this by imagining the hypotenuse as the radius of a circle, as in the image.
→ What happens to the value of the sine ratio as θ approaches 0°? Consider what is happening to the opposite side, a.
With one end of the meter stick fixed at A, rotate it like the hands of a clock, and show how a decreases as θ decreases. Demonstrate the change in the triangle for each case.
As θ gets closer to 0°, a decreases. Since sin θ = the value of sin θ is also approaching 0.
→ Similarly, what happens to the value of the cosine ratio as θ approaches 0°? Consider what is happening to the adjacent side, b.
As θ gets closer to 0°, b increases and becomes closer to 1. Since cos θ = \(\frac{b}{1}\) the value of cos θ is approaching 1.
→ Now, consider what happens to the value of the sine ratio as θ approaches 90°. Consider what is happening to the opposite side, a.
As θ gets closer to 90°, a increases and becomes closer to 1. Since sin θ = \(\frac{a}{1}\) the value of sin θ is also approaching 1.
→ What happens to the value of the cosine ratio as θ approaches 90°? Consider what is happening to the adjacent side, b.
As θ gets closer to 90°, b decreases and becomes closer to 0. Since cos θ = \(\frac{b}{1}\) the value of cos θ is approaching 0.
→ Remember, because there are no right triangles with an acute angle of 0° or of 90°, in the above thought experiment, we are really defining sin 0 = 0 and cos 0 = 1.
→ Similarly, we define sin 90 = 1 and cos 90 = 0; notice that this falls in line with our conclusion that the sine of an angle is equal to the cosine of its complementary angle.
Example 3
There are certain special angles where it is possible to give the exact value of sine and cosine. These are the angles that measure 0°, 30°, 45°, 60°, and 90°; these angle measures are frequently seen.
You should memorize the sine and cosine of these angles with quick recall just as you did your arithmetic facts.
a. Learn the following sine and cosine values of the key angle measurements.

We focus on an easy way to remember the entries In the table. What do you notice about the table values?
Answer:
The entries for cosine are the same as the entries for sine but ¡n the reverse order.
This is easily explained because the pairs (0, 90), (30, 60), and (45, 45) are the measures of complementary angles.
So, for instance, sin 30 = cos 60.
The sequence 0, \(\frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}\), 1 may be easier to remember as the sequence \(\frac{\sqrt{0}}{2}, \frac{\sqrt{1}}{2}, \frac{\sqrt{2}}{2}, \frac{\sqrt{3}}{2}, \frac{\sqrt{4}}{2}\).
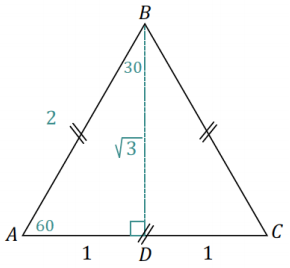
b. ∆ ABC is equilateral, with side length 2; D is the midpoint of side \(\overline{A C}\). Label all side lengths and angle measurements for ∆ ABD. Use your figure to determine the sine and cosine of 30 and 60.
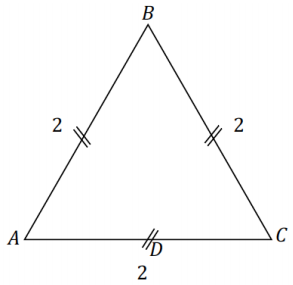
Answer:
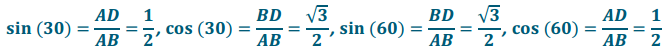
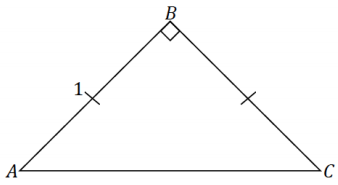
c. Draw an isosceles right triangle with legs of length 1. What are the measures of the acute angles of the triangle? What is the length of the hypotenuse? Use your triangle to determine sine and cosine of the acute angles.
Answer:
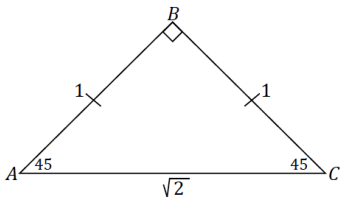
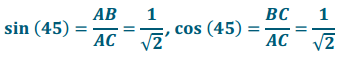
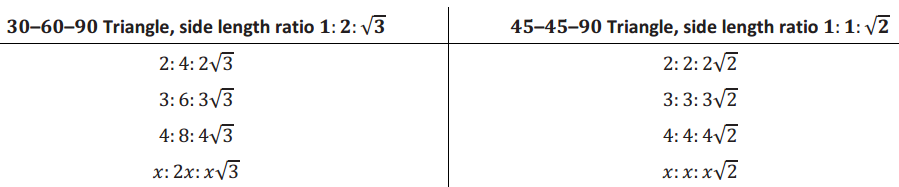
Parts (b) and (c) demonstrate how the sine and cosine values of the mentioned special angles can be found. These triangles are common to trigonometry; we refer to the triangle in part (b) as a 30-60-90 triangle and the triangle in part (c) as a 45-45-90 triangle.
Eureka Math Geometry Module 2 Lesson 27 Exercise Answer Key
Exercise 1.
Consider the right triangle ABC so that ∠C is a right angle, and the degree measures of ∠A and ∠B are α and β, respectively.
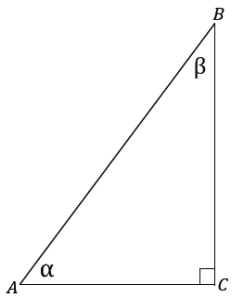
a. Find α + β.
Answer:
90°
b. Use trigonometric ratios to describe \(\frac{B C}{A B}\) two different ways.
Answer:
sin ∠A = \(\frac{B C}{A B}\), cos ∠B = \(\frac{B C}{A B}\)
c. Use trigonometric ratios to describe \(\frac{A C}{A B}\) two different ways.
Answer:
sin ∠B = \(\frac{A C}{A B}\), cos∠A = \(\frac{A C}{A B}\)
d. What can you conclude about sin α and cos β?
Answer:
sin α = cos β
e. What can you conclude about cos α and sin β?
Answer:
cos α = sin β
Exercise 2.
Find values for θ that make each statement true.
a. sin θ = cos (25)
Answer:
θ = 65
b. sin 80 = cos θ
Answer:
θ = 10
c. sin θ = cos (θ + 10)
Answer:
θ = 40
d. sin(θ – 45) = cos(θ)
Answer:
θ = 67.5
Exercise 3.
For what angle measurement must sine and cosine have the same value? Explain how you know.
Answer:
Sine and cosine have the same value for θ = 45. The sine of an angle is equal to the cosine of its complement.
Since the complement of 45 is 45, sin 45 = cos 45.
Exercise 4.
Find the missing side length in the triangle.
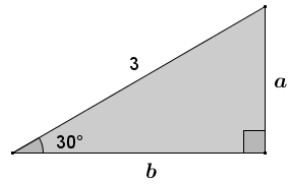
Answer:
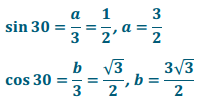
Exercise 5.
Find the missing side length in the triangle.
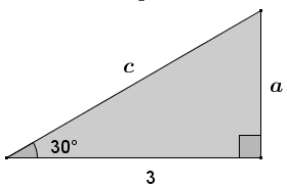
Answer:
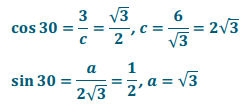
Eureka Math Geometry Module 2 Lesson 27 Problem Set Answer Key
Question 1.
Find the value of θ that makes each statement tr
a. sin θ = cos(θ + 38)
Answer:
cos(90 – θ) = cos(θ + 3θ)
90 – θ = θ + 3θ
52 = 2θ
26 = θ
b. cos θ = sin(θ – 30)
Answer:
sin(90 – θ) = sin(θ – 30)
90 – θ = θ – 30
120 = 2θ
60 = θ
c. sin θ = cos(3θ + 20)
Answer:
cos(90 – θ) = cos(3θ + 20)
90 – θ = 3θ + 20
70 = 4θ
17.5 = θ
d. sin(\(\frac{\theta}{3}\) + 10) = cos θ
Answer:
sin (\(\frac{\theta}{3}\) + 10) = sin(90 – θ)
\(\frac{\theta}{3}\) + 10 = 90 – θ
\(\frac{4 \theta}{3}\) = 80
θ = 60
Question 2.
a. Make a prediction about how the sum sin 30 + cos 60 will relate to the sum sin 60 + cos 30.
Answer:
Answers will vary; however, some students may believe that the sums will be equal. This is explored in Problems 3 through 5.
b. Use the sine and cosine values of special angles to find the sum: sin 30 + cos 60.
Answer:
sin 30 = \(\frac{1}{2}\) and cos 60 = \(\frac{1}{2}\) Therefore, sin 30+ cos 60 = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1.
Alternative strategy:
cos 60° = sin (90 – 60)° = sin 30°
sin 300 + cos 60° = sin 30° + sin 30° = 2(sin 30°) = 2 (\(\frac{1}{2}\)) = 1
c. Find the sum: sin 60 + cos 30.
Answer:
sin 60 = \(\frac{\sqrt{3}}{2}\) and cos30 = \(\frac{\sqrt{3}}{2}\) Therefore, sin 60 + cos 30 = \(\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\) = √3.
d. Was your prediction a valid prediction? Explain why or why not.
Answer:
Answers will vary.
Question 3.
Langdon thinks that the sum sin 30 + sin 30 is equal to sin 60. Do you agree with Langdon? Explain what this means about the sum of the sines of angles.
Answer:
I disagree. Explanations may vary. It was shown in the solution to Problem 3 that sin 30 + sin 30 = 1, and it is known that sin 60 = \(\frac{\sqrt{3}}{2}\) ≠ 1. This shows that the sum of the sines of angles is not equal to the sine of the sum of the angles.
Question 4.
A square has side lengths of 7√2. Use sine or cosine to find the length of the diagonal of the square. Confirm your answer using the Pythagorean theorem.
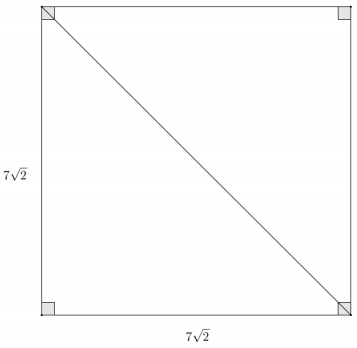
Answer:
The diagonal of a square cuts the square into two congruent 45 – 45 – 90 right triangles. Let d represent the length of the diagonal of the square:
cos 45 = \(\frac{\sqrt{2}}{2}\)
\(\frac{\sqrt{2}}{2}=\frac{7 \sqrt{2}}{d}\)
d√2 = 14√2
d = 14
Confirmation using Pythagorean theorem:
(7√2)2 + (7√2)2 = hyp2
98 + 98 = hyp2
196 = hyp2
√196 = hyp
14 = hyp
Question 5.
Given an equilateral triangle with sides of length 9, find the length of the altitude. Confirm your answer using the Pythagorean theorem.
Answer:
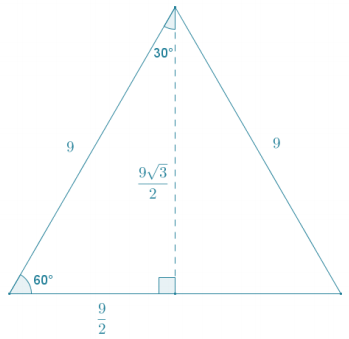
An altitude drawn within an equilateral triangle cuts the equilateral triangle into two congruent 30 – 60 – 90 right triangles. Let h represent the length of the altitude:
sin 60 = \(\frac{\sqrt{3}}{2}\)
\(\frac{\sqrt{3}}{2}=\frac{h}{9}\)
9√3 = 2h
\(\frac{9 \sqrt{3}}{2}\) = h
The altitude of the triangle has a length of \(\frac{9 \sqrt{3}}{2}\).
Confirmation using Pythagorean theorem:
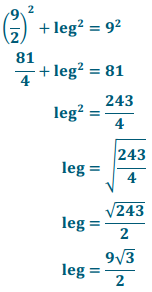
Eureka Math Geometry Module 2 Lesson 27 Exit Ticket Answer Key
Question 1.
Find the values for θ that make each statement true.
a. sin θ = cos 32
Answer:
θ = 90 – 32
θ = 58
b. cos θ = sin(θ + 20)
Answer:
sin(90 – θ) = sin(θ + 20)
90 – θ = θ + 20
70 = 2θ
35 = θ
Question 2.
∆ LMN is a 30-60-90 right triangle. Find the unknown lengths x and y.
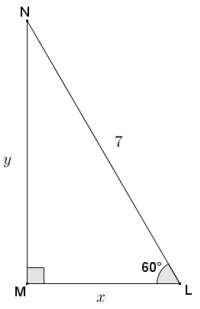
Answer:
