Engage NY Eureka Math Geometry Module 3 Lesson 7 Answer Key
Eureka Math Geometry Module 3 Lesson 7 Example Answer Key
Example 1.
In the following triangular pyramid, a plane passes through the pyramid so that it is parallel to the base and results in the cross-section ∆ A’B’C’. If the area of ∆ ABC is 25 mm2, what is the area of ∆ A’B’C’?
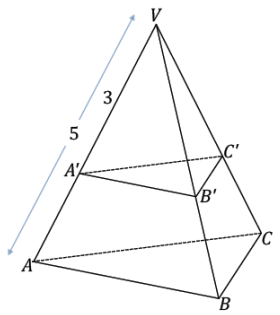
Answer:
→ Based on the fact that the cross-section is parallel to the base, what can you conclude about \(\overline{A B}\) and \(\overline{A^{\prime} B^{\prime}}\)?
They must be parallel.
→ Since \(\overline{A B}\) || \(\overline{A^{\prime} B^{\prime}}\), by the triangle side splitter theorem, we can conclude that \(\overline{A^{\prime} B^{\prime}}\) splits ∆ ABV proportionally. Then, a dilation maps A to A’ and B to B’ by the same scale factor. What is the center and scale factor k of this dilation?
The center must be V, and the scale factor must be k = \(\frac{3}{5}\)
→ What does the dilation theorem tell us about the length relationship between \(\overline{A B}\) and \(\overline{A^{\prime} B^{\prime}}\)?
A’B’ = \(\frac{3}{5}\)AB
→ Furthermore, since the cross-section is parallel to the base, what conclusions can we draw about the relationship between \(\overline{B C}\) and \(\overline{B^{\prime} C^{\prime}}\), and\(\overline{A C}\) and \(\overline{A^{\prime} C^{\prime}}\)?
\(\overline{B C}\) || \(\overline{B^{\prime} C^{\prime}}\) and \(\overline{A B}\) || \(\overline{A^{\prime} B^{\prime}}\), and, just as with \(\overline{A B}\) and \(\overline{A^{\prime} B^{\prime}}\), a dilation with center V and the scale factor k = \(\frac{3}{5}\)maps B to B’ and C to C’. B’C’ = \(\frac{3}{5}\)BC and A’C’ = \(\frac{3}{5}\)AC.
→ If each of the lengths of ∆ A’B’C’ is \(\frac{3}{5}\) the corresponding lengths of ∆ ABC, what can be concluded about the relationship between ∆ A’B’C’ and ∆ ABC?
The triangles are similar by the SSS similarity criterion.
→ What is the relationship between the areas of these similar figures?
Area(∆ A’B’C’) = \(\left(\frac{3}{5}\right)^{2}\) Area (∆ ABC)
→ Find the area of ∆ A’B’C’.
Area (∆ A’B’C’) = \(\left(\frac{3}{5}\right)^{2}\) (25)
Area(∆ A’B’C’) = \(\frac{9}{25}\)(25) = 9; the area of ∆ A’B’C’ is 9 mm2.
Based on what we knew about the cross-section of the pyramid, we were able to determine that the cross section is in fact similar to the base and use that knowledge to determine the area of the cross-section.
Example 2.
In the following triangular pyramid, a plane passes through the pyramid so that it is parallel to the base and results in the cross-section ∆ A’B’C’. The altitude from V is drawn; the intersection of the altitude with the base is X, and the intersection of the altitude with the cross-section is X’. If the distance from X to V is 18 mm, the distance from X’ to V is 12 mm, and the area of t ∆’B’C’ is 28 mm2, what is the area of ∆ ABC?

Answer:
Allow students time to wrestle with the question in partner pairs or small groups. Triangles ∆ AVX and ∆ A’V’X’ can be shown to be similar by the AA Similarity. The argument to show that the cross-section is similar to the base is the same as that presented in Example 1. The difference here is how to determine the scale factor of the dilation. Since the corresponding sides of the right triangles are proportional in length, the scale factor is k = \(\frac{V X^{\prime}}{V X}=\frac{2}{3}\). The area of the base can be calculated as follows:
Area(∆ A’B’C’) = \(\left(\frac{2}{3}\right)^{2}\) Area(∆ ABC)
28 = \(\left(\frac{2}{3}\right)^{2}\) Area(∆ ABC)
Area(∆ ABC) = 63
The area of ∆ ABC is 63 mm2.
Before moving to either the Extension or Exercise 1, have a brief conversation on how a cone can be generated from rotating a right triangle about either leg of the triangle.
Extension:
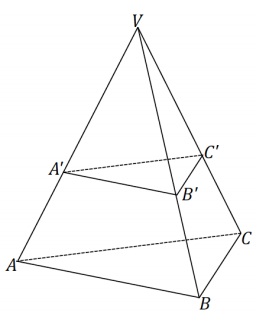
Answer:
→ Look at plane ABV. Can you describe a dilation of this plane that would take \(\overline{A B}\) to \(\overline{A^{\prime} B^{\prime}}\)? Remember to specify a center and a scale factor.
The dilation would have center V and scale factor k = \(\frac{A^{\prime} V}{A V}=\frac{B^{\prime} V}{B V}\).
→ Do the same for plane BCV.
The scale factor for this dilation would also be k = \(\frac{B^{\prime} V}{B V}=\frac{C^{\prime} V}{C V}\)
→ What about plane CAV?
The scale factor is still k = \(\frac{C^{\prime} V}{C V}=\frac{A^{\prime} V}{A V}\).
→ Since corresponding sides are related by the same scale factor, what can you conclude about triangles ∆ ABC and ∆ A’B’C’?
∆ ABC ~ ∆ A’B’ C’ by the SSS similarity criterion.
→ How can this result be used to show that any pyramid (i.e., those with polygonal bases rather than those with triangular bases) has cross-sections similar to the base?
Whatever polygon represents the base of the pyramid, we can cut the pyramid up into a bunch of triangular regions. Then, the cross-section will be a bunch of triangles that are similar to the corresponding triangles in the base. So, the cross-section as a whole is similar to the base.
→ Observe that while we’ve only proven the result for pyramids, it does generalize for general cones, just as we suspected when we discussed dilations.
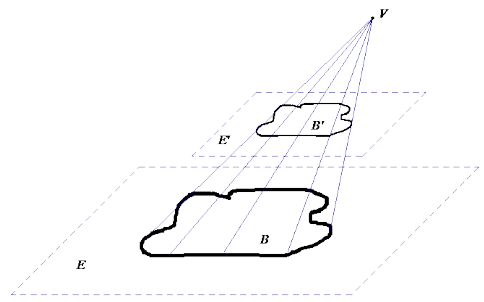
Answer:
→ Since B’ ~ B, we know that Area(B’) = k2 Area(B), where k is the scale factor of the dilation.
→ How can we relate the scale factor to the height of the general cone?
Allow students a moment to consider before continuing.
→ Draw an altitude for the cone, and let Q and Q’ be the points where it intersects planes E and E’, respectively. Call the distance between V and Q as h and the distance between V and Q’ as h’.
→ Choose a point P in B, and draw PV. Let P’ be the intersection of this segment with E’.
→ Consider plane PQV. What is the scale factor taking \(\overline{P Q}\) to \(\overline{P^{\prime} Q^{\prime}}\)?
→ A dilation with scale factor k = \(\frac{h^{\prime}}{h}\) and center V maps B to B’.
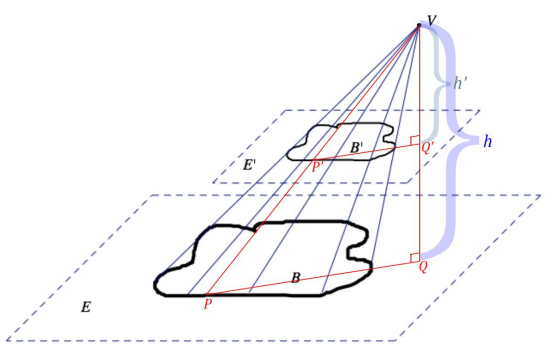
→ Use this scale factor to compare the Area(B’) to the Area(B).
The area of the similar region should be the area of the original figure times the square of the scale
factor: Area (B’) = \(\left(\frac{h^{\prime}}{h}\right)^{2}\) Area(B).
Example 3.
GENERAL CONE CROSS-SECTION ThEOREM: If two general cones have the same base area and the same height, then cross sections for the general cones the same distance from the vertex have the same area.
State the theorem in your own words.

Answer:
The theorem is saying that if two cones have the same base area and the same height, then cross-sections of both solids that are the same height from the vertex should have the same area.
Use the space below to prove the general cone cross-section theorem.
Answer:
→ Let the bases of the cones B and C in Figure 8 be such that (1) Area(B) = Area(C), (2) the height of each cone is h, and (3) the distance from each vertex to B’ and to C’ are both h’.
→ How can we show that Area(B’) = Area(C’)?
Area(B’) = \(\left(\frac{h^{\prime}}{h}\right)^{2}\) Area(B)
Area(C’) = \(\left(\frac{h^{\prime}}{h}\right)^{2}\) Area(C)
→ Since Area(B) = Area(C), then Area(B’) = Area(C’).
Eureka Math Geometry Module 3 Lesson 7 Opening Exercise Answer Key
Group the following images by shared properties. What defines each of the groups you have made?
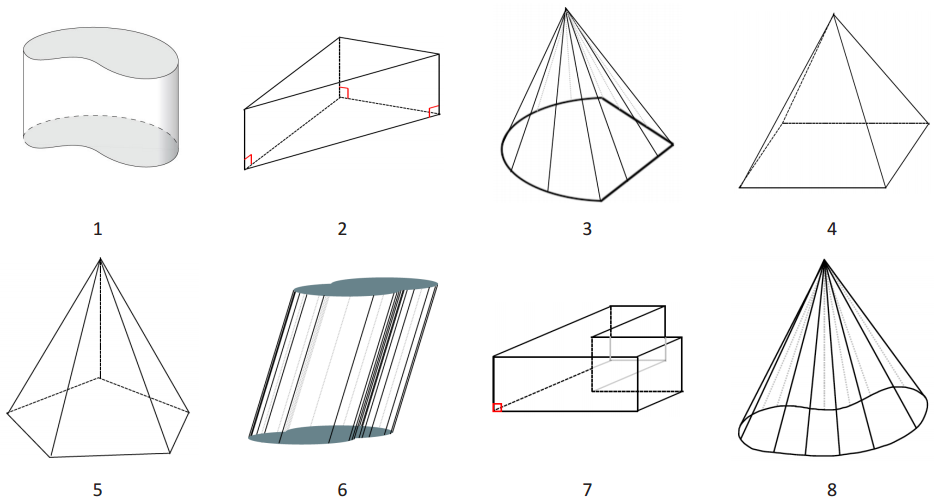
Answer:
Group A: General cylinders, images 1 and 6
Group B: Prisms, images 2 and 7
Group C: Figures that come to a point with a polygonal base, images 4 and 5.
Group D: Figures that come to a point with a curved or semi-curved region as a base, images 3 and 8.
RECTANGULAR PYRAMID: Given a rectangular region B in a plane E and a point V not in E, the rectangular pyramid with base B and vertex V is the collection of all segments VP for any point P in B.
GENERAL CONE: Let B be a region in a plane E and V be a point not in E. The cone with base B and vertex V is the union of all \(\overline{V P}\) for all points P in B (See Figures 1 and 2).

Answer:
→ You have seen rectangular pyramids before. Look at the definition again, and compare and contrast it with the definition of general cone.
→ The definitions are essentially the same. The only difference is that a rectangular pyramid has a rectangular base. A general cone can have any region for a base.
→ Much like a general cylinder, a general cone is named by its base.
→ A general cone with a disk as a base is called a circular cone.
→ A general cone with a polygonal base is called a pyramid. Examples of this include a rectangular pyramid or a triangular pyramid.
→ A general cone whose vertex lies on the perpendicular line to the base and that passes through the center of the base is a right cone (or a right pyramid if the base is polygonal). Figure 4 shows a right rectangular pyramid, while Figure 3 shows a rectangular pyramid that is not right.
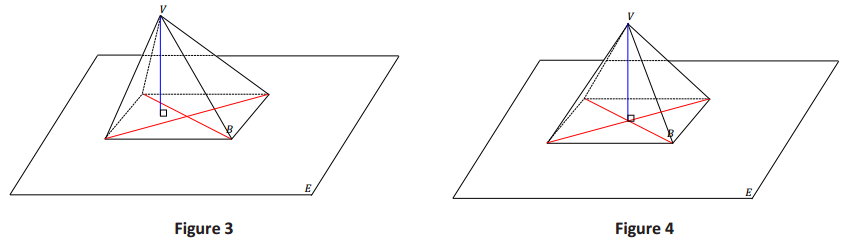
Answer:
→ A right circular cone has been commonly referred to as a cone since the elementary years; we will continue to use cone to refer to a right circular cone.
For pyramids, in addition to the base, there are lateral faces and edges.
→ Name a lateral face and edge in Figure 5, and explain how you know it is a lateral face.
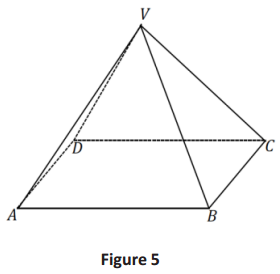
Answer:
→ The triangular region AVB is defined by a side of the base, AB, and vertex V and is an example of a lateral face.
→ The segments \(\overline{A V}, \overline{B V}, \overline{C V},\) and \(\overline{D V}\)are all lateral edges.
Once the definitions of general cone and rectangular pyramid have been discussed, begin the discussion on how the cross-section is similar to the base.
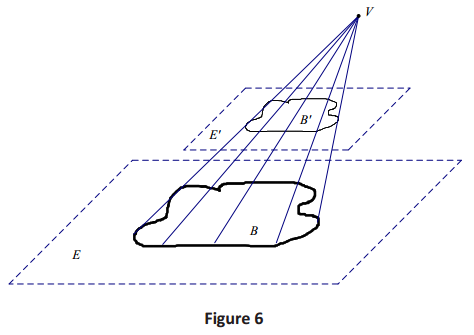
Answer:
→ Observe the general cone in Figure 6. The plane E’ is parallel to E and is between the point V and the plane E. The intersection of the general cone with E’ gives a cross-section B’.
→ We can show the existence of a dilation that maps B to B’; this similarity [ base.) transformation would imply that the cross-section is similar to the base.
→ We have only studied dilations in two dimensions, or in the plane, but it turns out that dilations behave similarly in three-dimensional space.
→ A dilation of three-dimensional space with center O and scale factor r is defined the same way it is in the
plane. The dilation maps O to itself and maps any other point X to the point X’ on ray OX so that OX’ = r · OX.
Emphasize that students already knew that a dilation is thought of as two points at a time: the center and a point being dilated. This still holds true in three dimensions.
A visual may help establish an intuitive sense of what a dilation of a three-dimensional figure looks like. This can be easily done using interactive white board software that commonly includes images of prisms. By enlarging and reducing the image of a prism, students can get a feel of what is happening during the dilation of a 3D figure. Snapshots are provided below.
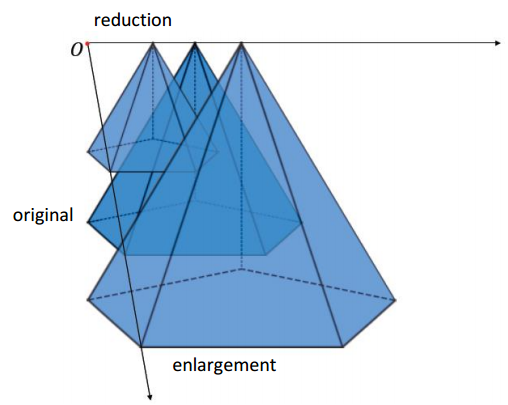
Eureka Math Geometry Module 3 Lesson 7 Exercise Answer Key
Exercise 1.
The area of the base of a cone is 16, and the height is 10. Find the area of a cross-section that is distance S from the vertex.
Answer:
Area(cross-section) = \(\left(\frac{5}{10}\right)^{2}\) · 16 = 4; the area of the cross-section that is a distance 5 from the vertex is 4 units2.
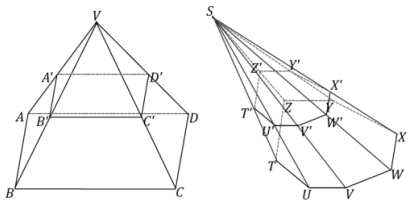
Exercise 2.
The following pyramids have equal altitudes, and both bases are equal in area and are coplanar. Both pyramids’ cross- sections are also coplanar. If BC = 3√2 and B’C’ = 2√3, and the area of TUVWXYZ Is 30 unIts2, what is the area of cross-section A’B’C’D’?
Answer:
\(\left(\frac{2 \sqrt{3}}{3 \sqrt{2}}\right)^{2}\) · 30 = 20; the area of the cross-section A’B’C’D’ is 20 units2.
Eureka Math Geometry Module 3 Lesson 7 Problem Set Answer Key
Question 1.
The base of a pyramid has area 4. A cross-section that lies in a parallel plane that is distance of 2 from the base plane has an area of 1. Find the height, h, of the pyramid.
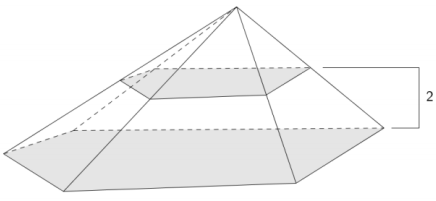
Answer:
The cross-section is similar to the base with scale factor r, and the areas of the similar slices are related by the square of the scale factor, r2.
r2 4 = 1
r2 = \(\frac{1}{4}\)
r = \(\frac{1}{2}\)
The scale factor of the cross-section is \(\frac{1}{2}\).
Let h’ be the distance from the cross-section (or slice) to the vertex. Then
h’ = h – 2, and the heights of the slices are also related by the scale factor, so
\(\frac{h-2}{h}\) = \(\frac{1}{2}\)
h = 2(h – 2)
h = 2h – 4
h = 4.
The height of the pyramid is 4 units.
Question 2.
The base of a pyramid is a trapezoid. The trapezoidal bases have lengths of 3 and 5, and the trapezoid’s height is 4. Find the area of the parallel slice that is three-fourths of the way from the vertex to the base.
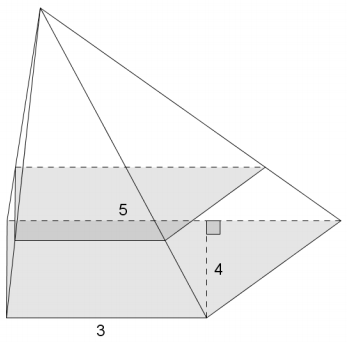
Answer:
The area of the trapezoidal base:
Area = \(\frac{1}{2}\)(b1 + b2)h
Area = \(\frac{1}{2}\)(3 + 5) · 4
Area = 16.
The area of the base of the pyramid is 16 units2.
Let h be the height of the pyramid. The distance from the vertex to the given slice is \(\frac{3}{4}\)h. The slice is similar to the base with scale factor \(\frac{\frac{3}{4} h}{h}\), or \(\frac{3}{4}\)
The areas of similar figures are related by the square of the
scale factor relating their dimensions, so \(\left(\frac{3}{4}\right)^{2}\) · 16, or 9.
Therefore, the area of the slice is 9 units2.
Question 3.
A cone has base area 36 cm2. A parallel slice 5 cm from the vertex has area 25 cm2. Find the height of the cone.
Answer:
Let h be the cone’s height in centimeters.
\(\left(\frac{5}{h}\right)^{2}\) · 36 = 25
\(\left(\frac{5}{h}\right)^{2}=\frac{25}{36}\)
\(\frac{5}{h}=\frac{5}{6}\)
h = 6
The cone has height 6 cm.
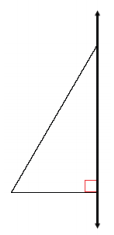
Question 4.
Sketch the figures formed if the triangular regions are rotated around the provided axis:
a.
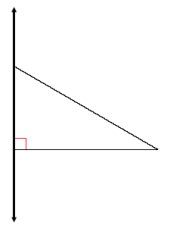
Answer:
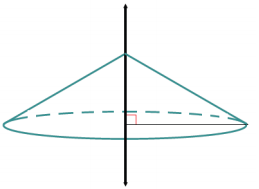
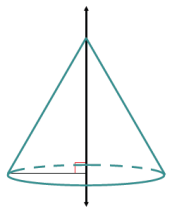
b.
Answer:
Question 5.
Liza drew the top view of a rectangular pyramid with two cross-sections as shown in the diagram and said that her diagram represents one, and only one, rectangular pyramid. Do you agree or disagree with Liza? Explain.
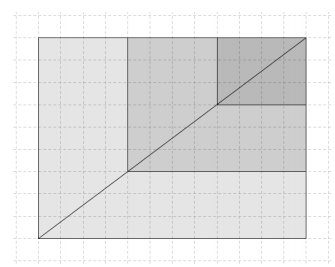
Answer:
Liza’s statement is not valid. As shown, the top cross-section has dimensions that are \(\frac{1}{3}\) the corresponding lengths of the base, and the lower cross-section has dimensions that are \(\frac{2}{3}\) the corresponding lengths of the base; therefore, the cross-sections are \(\frac{1}{3}\) and \(\frac{2}{3}\) of the distance from the vertex to the base, respectively. However, since no information was given about the distance between cross-sections or the height of the pyramid, the only conclusion we can draw is that the distance between each given consecutive cross-section is \(\frac{1}{3}\) the height of the pyramid.
Question 6.
A general hexagonal pyramid has height 10 in. A slice 2 in. above the base has area 16 in2. Find the area of the base.
Answer:
Let A be the area of the base in square inches. Two inches above the base is \(\frac{4}{5}\) from the vertex.
\(\left(\frac{4}{5}\right)^{2}\) A = 16
A = 25
The base has area 25 in2.
Question 7.
A general cone has base area 3 units2. Find the area of the slice of the cone that is parallel to the base and \(\frac{2}{3}\) of the way from the vertex to the base.
Answer:
Let h represent the height of the cone. Then, the distance from the vertex to the slice of the cone is \(\frac{2}{3}\) h. The slice is similar to the base with a scale factor of \(\frac{\frac{2}{3} h}{h}\), or \(\frac{2}{3}\). The area of the slice is equal to the area of the base times the square of the scale factor.
Area(slice) = \(\left(\frac{2}{3}\right)^{2}\) · 36
Area(slice) = \(\frac{4}{9}\) · 36
Area(slice) = 16
The area of the slice of the cone is 16 units2.
Question 8.
A rectangular cone and a triangular cone have bases with the same area. Explain why the cross-sections for the cones halfway between the base and the vertex have the same area.
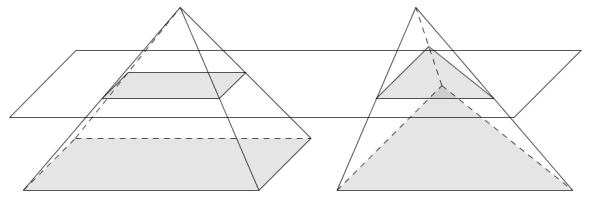
Answer:
Let A be the area of the bases. The cross-sections are each similar to the base with scale factor \(\frac{1}{2}\). So, each has area \(\frac{1}{4}\)A. Thus, they are equal.
Question 9.
The following right triangle is rotated about side AB. What is the resulting figure, and what are its dimensions?
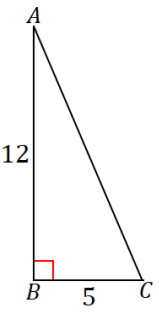
Answer:
The resulting figure is a circular cone with radius 5 and height 12.
Eureka Math Geometry Module 3 Lesson 7 Exit Ticket Answer Key
The diagram below shows a circular cone and a general pyramid. The bases of the cones are equal in area, and the solid have equal heights.
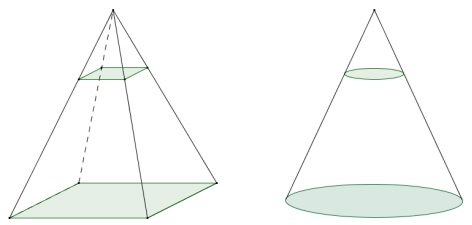
a. Sketch a slice in each cone that is parallel to the base of the cone and \(\frac{2}{3}\) closer to the vertex than the base plane.
Answer:
b. If the area of the base of the circular cone is 616 units2, find the exact area of the slice drawn in the pyramid.
Answer:
The distance from the slice to the vertex is \(\frac{1}{3}\) the height of the cone, so the scale factor from the base to the slice is \(\frac{1}{3}\). The areas of the planar regions are related by the square of the scale factor, or \(\frac{1}{9}\).
Area(slice) = \(\frac{1}{9}\)(Area(base))
Area(slice) = \(\frac{1}{9}\)(616)
Area(slice) = \(\frac{616}{9}\)
If two cones have the same base area and the same height, then cross-sections for the cones the same distance from the vertex have the same area, so the area of the slice from the pyramid is \(\frac{616}{9}\) unit2.