Engage NY Eureka Math Geometry Module 3 Lesson 10 Answer Key
Eureka Math Geometry Module 3 Lesson 10 Example Answer Key
a. The following triangles have equal areas: Area(∆ ABC) = Area(∆ A’B’C’) = 15 units2. The distance between ![]() and is
and is ![]() . Find the lengths of \(\overline{D E}\) and \(\overline{D^{\prime} E^{\prime}}\).
. Find the lengths of \(\overline{D E}\) and \(\overline{D^{\prime} E^{\prime}}\).
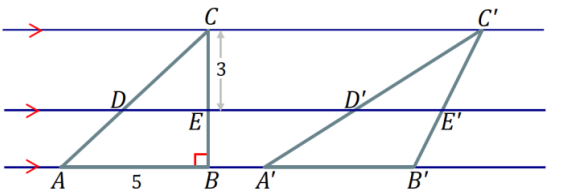
Answer:

b. Joey says that if two figures have the same height and the same area, then their cross-sectional lengths at each height will be the same. Give an example to show that joey’s theory is incorrect.
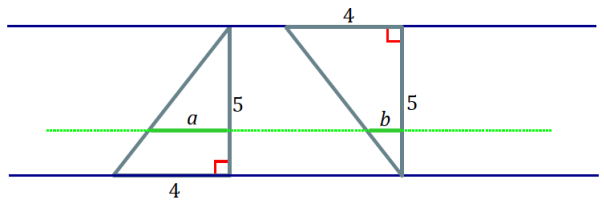
Answer:
Though both triangles have the same height and the same area, their cross-sectional lengths, represented here by a and b, are not the same.
Discussion
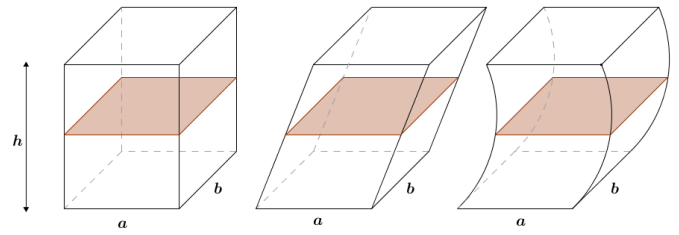
CAVALIERI’S PRINCIPLE: Given two solids that are included between two parallel planes, if every plane parallel to the two planes intersects both solids in cross-sections of equal area, then the volumes of the two solids are equal.
→ Consider how Cavalieri’s principle is related to the principle of parallel slices. Explain each principle in your own words and how they are related.
Provide time for a Quick Write with the last statement as the prompt: Consider how Cavalier’s principle is related to the principle of parallel slices. Explain each principle in your own words and how they are related. Ask students to simply think for 30 seconds and write for another 90 seconds. Share out ideas as a whole group afterward.
Just as the same cross-sectional length at any given height of two regions with equal altitudes implies that the two regions are of equal area, cross-sections (i.e., regions, not lengths) of equal areas at every height of two solids of equal altitudes imply that the solids have equal volumes. Students should notice the parallel between the two principles for two dimensions and three dimensions.
After the Quick Write, refer to Figure 4 when asking the following question. In the demonstration and regarding the anecdote on Cavalieri, students are introduced to Cavalieri’s principle in the context of stacks of items that are identical. They should consider solids whose lateral edges are not necessarily perpendicular to the bases (see Figure 4).
→ Assuming that two solids do meet the criteria of Cavalieri’s principle-that is, both solids have the same altitude and have cross-sections of equal area at every height-does it imply that both solids are of the same type? In other words, does the principle only work if we compare two triangular prisms or two cylinders? Does the principle apply if the two solids are different (e.g., one is a cylinder, and one is a triangular prism), or if one solid is a right solid, while the other is an oblique solid? Why?
Allow students time in partners to discuss before sharing out responses as a whole class. Students’ answers may vary. Some might believe that Cavalieri’s principle only holds when the solids being compared are of the same type; others may have arguments for why the principle holds regardless of the types of solids being compared. Once students share out a few ideas, proceed with the explanation below.
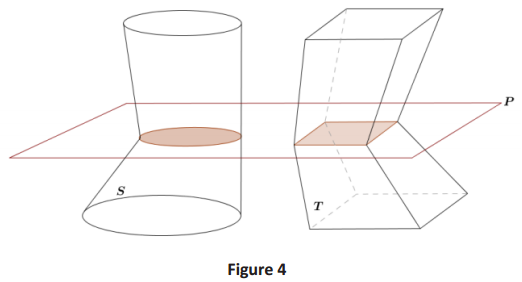
→ Cavalieri’s principle holds true regardless of the types of solids being compared, as long as the criteria of the principle are met. The volume of a solid can be approximated by right prisms, as we saw in Lesson 8.
→ Then, if we took multiple cross-sections of each solid, all at the same heights, we would build corresponding prisms of equal volumes, and so the total volume of each solid must be the same.
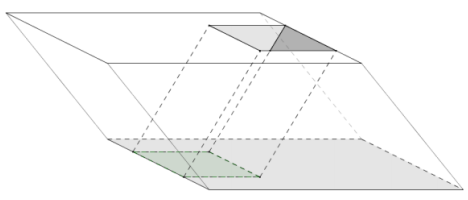
→ Let’s look at a visual example. In Figure 5 we have two different types of solids: one right square pyramid and one oblique trapezoidal pyramid. The two solids meet the criteria of Cavalieri’s principle because both are equal height, and the green cross-sections, taken at the same height, are equal in area. Does Cavalieri’s principle hold? Do the two solids have the same volume?
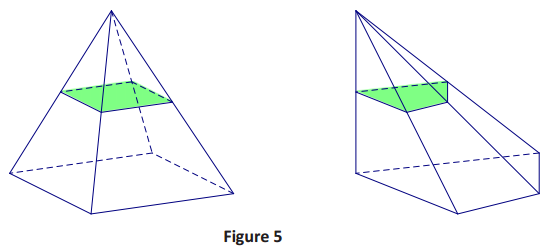
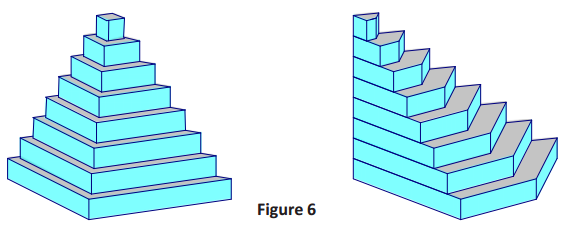
→ The images in Figure 6 approximate the volumes of the solids in Figure 5. Each volume is approximated by eight right prisms. Each corresponding prism has a base equal in area and equal in height to the other. What can we conclude about the relative volumes of the two solids?
Since each of the corresponding pairs of prisms has the same volume, the total volumes of each solid must be equal to each other.
→ Compare these images with the image of the red, green, and blue regions broken into small rectangles. These eight prisms approximate the volume of the cone in the same way that the small rectangles approximated the area of the red, green, and blue regions.
→ Imagine if instead of eight prisms, there were loo or 1,000. What happens to the approximation of the volume as the number of prisms increases?
The approximation is refined as the number of cross-sections increases.
→ In fact, as we increase the number of prisms, the height of each prism used for the approximation approaches 0, meaning that they more and more closely resemble cross-sections.
At this point, ask students to summarize what has been covered so far in this discussion. The following points succinctly capture what students should share:
→ Cavalieri’s principle is for solids, while the principle of parallel slices in the plane is for planar regions.
→ Cavalieri’s principle says that if two solids have the same altitude (i.e., if bases of both solids lie in the same parallel planes) and the cross-sections of both solids are equal in area at any height, then the solids are equal in volume.
→ Furthermore, it is worth making the point that Cavalieri’s principle holds for any two solids as long as its criteria are met. We should not think of the principle holding for two solids that look alike or happen to both be of the same type.
→ Finally, the reason the principle holds for any two solids that meet its criteria is because the volume of each solid can be approximated by right prisms built over cross-sections for any given height. Since we know the area of each solid’s cross-section is the same at any given height, the volume of the prisms built over each cross-section must be the same as well.
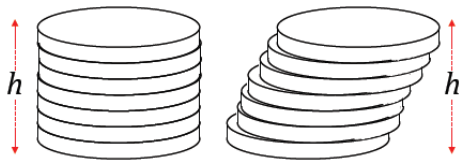
→ Recall a question we first posed in Lesson 6. In reference to two stacks of cards or coins of equal height, we asked whether the volume of the stack was different based on whether we had a right cylinder or oblique cylinder.
→ We can now answer this question: Are the two volumes different? Why?
By Cavalieri’s principle, each cross-section between two stacks of cards or coins is the same, and the heights of each solid are the same, so the two volumes are equal.
→ Prior to this lesson, we had established the volume formula for general right prisms (this of course captures figures with polygonal, circular, and irregular bases) is area of base × height.
→ Now, we can use Cavalieri’s principle to show the volume formula of any cylinder (i.e., not just general right cylinders as studied so far), is area of base × height. Why? Explain in terms of two cylinders that have identical bases, but one is oblique, and the other is right.
If two general cylinders have the same heights and have identical bases, then the cross-section of both are identical at any given height, regardless of whether one is oblique and the other is right. The prisms built over corresponding cross-sections are equal in volume, so the total volumes of the two figures are the same, and therefore we can use the volume formula area of base × height for any general cylinder.
Eureka Math Geometry Module 3 Lesson 10 Opening Exercise Answer Key
The bases of the following triangular prism T and rectangular prism R lie in the same plane. A plane that Is parallel to the bases and also a distance 3 from the bottom base intersects both solids and creates cross-sections T’ and R’.
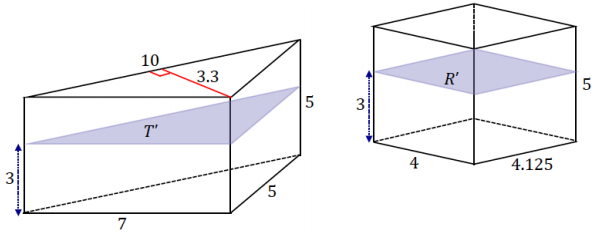
a. Find Area(T’).
Answer:
Area(T’) = 16.5
b. Find Area(R’).
Answer:
Area(R’) = 16.5
c. Find Vol(T).
Answer:
Vol(T) = 82.5
d. Find Vol(R).
Answer:
Vol(R)= 82.5
e. If a height other than 3 were chosen for the cross-section, would the cross-sectional area of either solid change?
Answer:
No, the areas of the cross-sections of both solids at any given height are the same.
Discussion
→ By the end of this lesson, we are going to be able to draw a few more conclusions regarding the Opening Exercise.
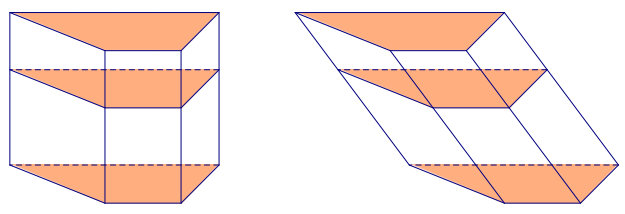
→ Take a look at Figure 1. Do you notice anything special regarding the red, green, and blue regions?
Take any student observations; the fact that the areas are the same may or may not come up as a guess.
Discussion
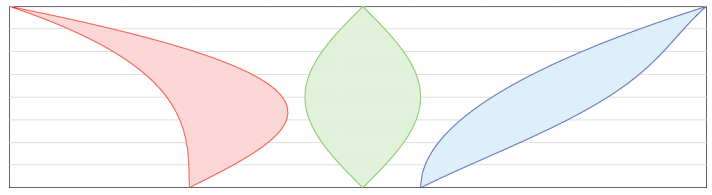
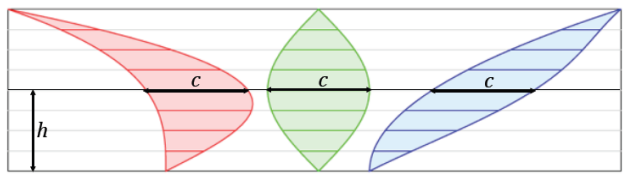
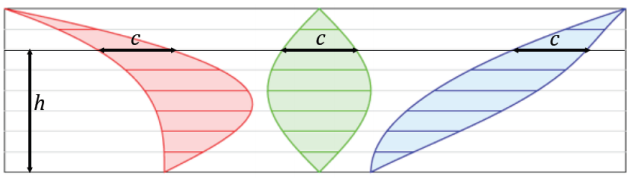
→ Examine Examples 1 and 2. Each has the cross-sectional length of the red, green, and blue regions marked at a particular height. In each example, the cross-sectional length is the same.
Explain what is meant by cross-sectional length: A cross-sectional length is the horizontal distance across a region. As an alternative, have students actually measure each cross-sectional length.
→ What would you conjecture this means for the area of the regions in relation to each other?
Example 1.
Example 2.
→ It turns out that the area of the red, green, and blue regions is the same by the following principle:
PRINCIPLE OF PARALLEL SLICES IN THE PLANE: If two planar figures of equal altitude have identical cross-sectional lengths at each height, then the regions of the figures have the same area.
→The reason this principle is true is because the regions can be approximated by rectangles, and two figures with identical cross-sectional lengths can be approximated using congruent rectangles.
→ That is, the same rectangles that approximate the red region can be used to approximate the green region, which can also be used to approximate the blue region, as shown below.
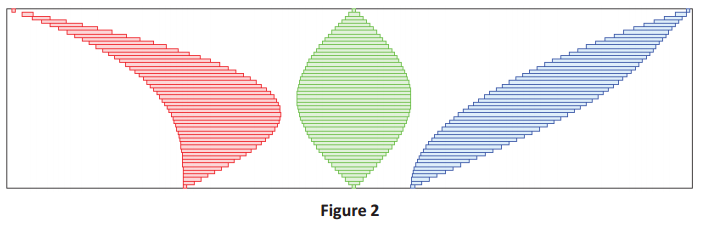
→ Consider the red, green, and blue regions broken up into rectangles in this way in Figure 2. Imagine we created such a region out of little plastic (green) rectangles. Now, picture pushing the top third of the rectangles over to the left without disturbing the bottom two-thirds of the rectangles. Other than moving the rectangles over, no change has been made to them. This rearranged version of the green region now looks like the red region. Since we can do this no matter how thin our slices are, we must conclude that the areas of the red and green regions are equal. We can make a similar argument in order to re-create the blue region.
Eureka Math Geometry Module 3 Lesson 10 Problem Set Answer Key
Question 1.
Use the principle of parallel slices to explain the area formula for a parallelogram.
Answer:
Every slice of a parallelogram made parallel to a side has the same length as that side, which is also true in a rectangle. Since each figure has the same height, and the lengths of their slices at each level are equal in length, it follows that the figures have the same area. The area of a rectangle is the product of its length and width; therefore, the area of the parallelogram is the product of the length of a side times the distance between it and the opposite side.
Question 2.
Use the principle of parallel slices to show that the three triangles shown below all have the same area.
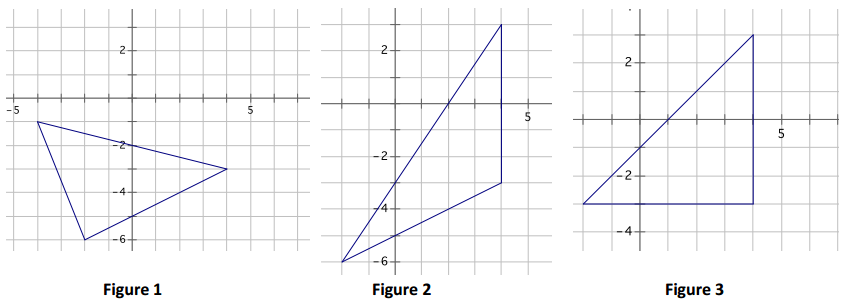
Answer:
The triangle in Figure 1 shares points at (-2, -6) and (4, -3) with the triangle in Figure 2, which has slope of \(\frac{1}{2}\). If you slide the vertex at (-4, -1) along a parallel line of slope \(\frac{1}{2}\) to (4,3), the height of the triangle does not change, and the triangle, therefore, has the same area. By parallel slices, the triangle in Figure 1 has the same area as the triangle in Figure 2.
The triangles in Figure 2 and Figure 3 share the side between points at (4, -3) and (4, 3), which is vertical. If we slide the vertex at (-2, -6) in Figure 2 vertically to (-2, -3), the height of the triangle again does not change and it, therefore, has the same area. Again, by the principle of parallel slices, the areas of the triangles in Figures 2 and 3 are the same.
Question 3.
An oblique prism has a rectangular base that is 16 in. × 9 in. A hole in the prism is also the shape of an oblique prism with a rectangular base that is 3 in. wide and 6 in. long, and the prism’s height is 9 in. (as shown in the diagram). Find the volume of the remaining solid.
Answer:
Volume of the large prism:
16 in. · 9 in. · 9 in. = 1296 in3
Volume of the prism-shaped hole:
3 in. · 6in. · 9 in. = 162 in3
Volume of the remaining solid:
1296 in3 – 162 in3 = 1134 in3
Question 4.
An oblique circular cylinder has height 5 and volume 45π. Find the radius of the circular base.
Answer:
Volume = πr2 · 5
45π = πr2 · S
r2 = 9
r = 3
The radius of the circular base is 3.
Question 5.
A right circular cone and a solid hemisphere share the same base. The vertex of the cone lies on the hemisphere. Removing the cone from the solid hemisphere forms a solid. Draw a picture, and describe the cross-sections of this solid that are parallel to the base.
Answer:
The base plane intersects the solid in a circle. A plane through the vertex of the cone meets the solid in a single point. Cross-sections arising from intermediate planes are regions between concentric circles in the plane.
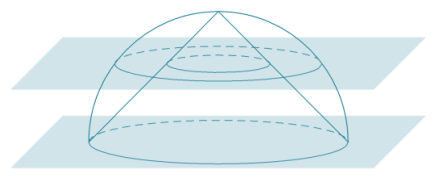
Question 6.
Use Cavalieri’s principle to explain why a circular cylinder with a base of radius 5 and a height of 10 has the same volume as a square prism whose base is a square with edge length 5√π and whose height is also 10.
Answer:
The area of the base of the circular cylinder:
Area = π · r2
Area = π · 52 = 25π
The area of the base of the square prism:
Area = length · width
Area = (5√π) · (5√π)
Area = 25π
The bases of the two cylinders have the same areas, and their heights are given as the same. Given that both solids are cylinders, every slice made parallel to the bases of the solids will have equal area; thus, the volume of each solid is the area of its base times its height, or 250π.
Eureka Math Geometry Module 3 Lesson 10 Exit Ticket Answer Key
Question 1.
Morgan tells you that Cavalieri’s principle cannot apply to the cylinders shown below because their bases are different. Do you agree or disagree? Explain.
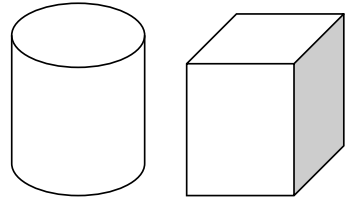
Answer:
Even though the bases are not the same geometric figure, Cavalieri’s principle may still apply because It is based on parallel slices with equal areas. If the areas of the bases are the same and the heights of the cylinders are the same, then the volumes of the cylinders are equal.
Question 2.
A triangular prism has an isosceles right triangular base with a hypotenuse of √32 and a prism height of 15. A square prism has a height of 15, and its volume is equal to that of the triangular prism. What are the dimensions of the square base?

Answer:
If the volumes of the solids are the same and their heights are the same, then the areas of the parallel cross-sections (or bases) must be the same since the area of all parallel slices In a prism are congruent.
√32 = 4√2
The legs of the Isosceles right triangular base are length 4.
The area of the base of the triangular prism B:
Bt = \(\frac{1}{2}\) · 4 · 4.
Bt = 8.
The area of the base of the triangular prism must be equal to B, and being a square, its sides, x, must be equal in length, making the area of the square base x2:
x2 = 8
x = √8 = 2√2.
The lengths of the sides of the square base are 2√2.