Engage NY Eureka Math Geometry Module 2 Lesson 2 Answer Key
Eureka Math Geometry Module 2 Lesson 2 Example Answer Key
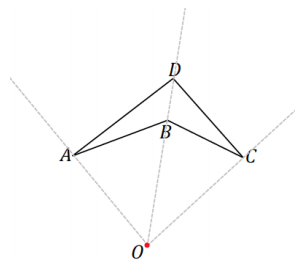
Create a scale drawing of the figure below using the ratio method about center 0 and scale factor r = \(\frac{1}{2}\).
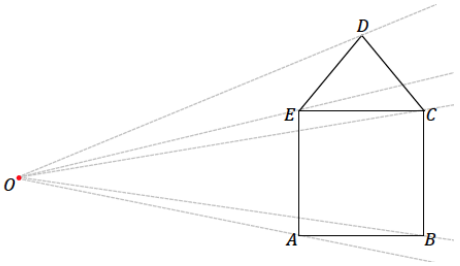
Step 1. Draw a ray beginning at O through each vertex of the figure.
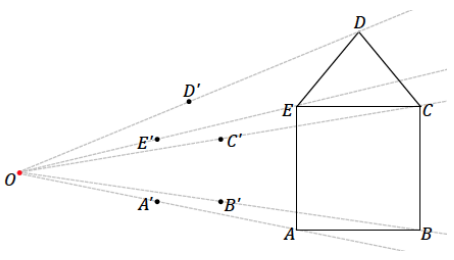
Step 2. Dilate each vertex along the appropriate ray by scale factor r = \(\frac{1}{2}\). Use the ruler to find the midpoint between O and D and then each of the other vertices. Label each respective midpoint with prime notation (e.g., D’).
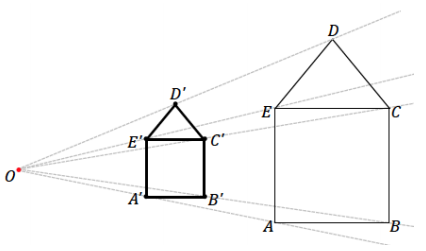
Step 3. Join vertices in the way they are joined in the original figure (e.g., segment A’B’ corresponds to segment AB).
Answer:
Step 1. Draw a ray beginning at O through each vertex of the figure.
Step 2. Dilate each vertex along the appropriate ray by scale factor r = \(\frac{1}{2}\). Use the ruler to find the midpoint between O and D and then each of the other vertices. Label each respective midpoint with prime notation (e.g., D’).
Step 3. Join vertices in the way they are joined in the original figure (e.g., segment A’B’ corresponds to segment AB).
Example 2.
a. Create a scale drawing of the figure below using the ratio method about center O and scale factor r = 3.
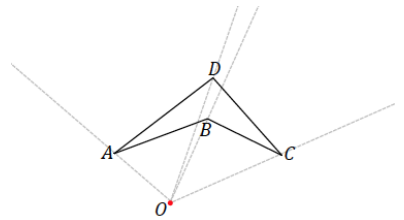
Step 1. Draw a ray beginning at O through each vertex of the figure.
Step 2. Use your ruler to determine the location of A’ on \(\overrightarrow{O A}\); A’ should be three times as far from O as A.
Determine the locations of B’ and C’ in the same way along the respective rays.
Step 3. Draw the corresponding line segments (e.g., segment A’B’ corresponds to segment AB).
Answer:
Step 1. Draw a ray beginning at O through each vertex of the figure.
Step 2. Use your ruler to determine the location of A’ on \(\overrightarrow{O A}\); A’ should be three times as far from O as A.
Determine the locations of B’ and C’ in the same way along the respective rays.
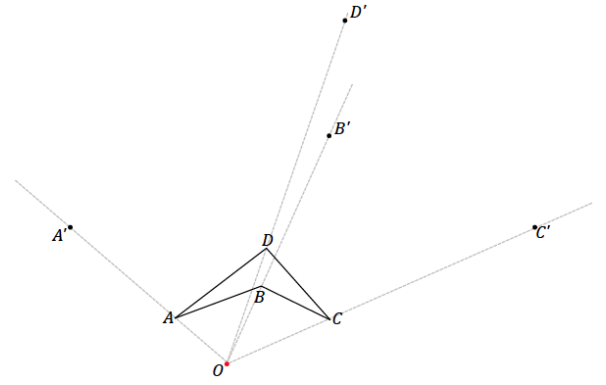
Step 3. Draw the corresponding line segments (e.g., segment A’B’ corresponds to segment AB).

b. Locate a point X so that It lies between endpoints A and B on segment AB of the original figure in part (a). Use the ratio method to locate X’ on the scale drawing in part (a).
Answer:
Sample response:
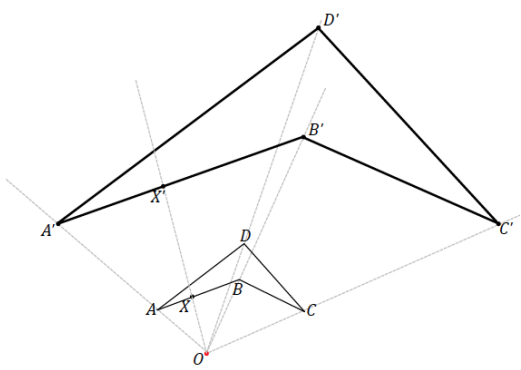
c. Imagine a dilation of the same figure as in parts (a) and (b). What if the ray from the center passed through two distinct points, such as B and D? What does that imply about the locations of B’ and D’?
Answer:
Both B’ and D’ also lie on the same ray.
Eureka Math Geometry Module 2 Lesson 2 Opening Exercise Answer Key
Based on what you recall from Grade 8, describe what a dilation is.
Answer:
Student responses will vary; students may say that a dilation results in a reduction or an enlargement of the original figure or that corresponding side lengths are proportional in length, and corresponding angles are equal in measure. The objective is to prime them for an in-depth conversation about dilations; take one or two responses and move on.
Eureka Math Geometry Module 2 Lesson 2 Exercise Answer Key
Exercise 1.
Create a scale drawing of the figure below using the ratio method about center O and scale factor r = \(\frac{3}{4}\) Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and the corresponding angles are equal in measurement.

Answer:
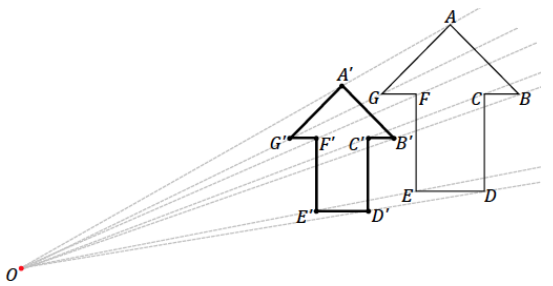
Verification of the reduced figure should show that the length of each segment In the scale drawing is \(\frac{3}{4}\) the length of each segment in the original figure (e.g., A’G’ = \(\frac{3}{4}\) (AG)). The angle measurements are as follows (when an angle could be interpreted as having two possible measurements, the smaller one was selected in all cases): m∠A = 90°,
m∠B = 45°, m∠C = 90°, m∠D = 90°, m∠E = 90°, m∠F = 90°, and m∠G = 45°.
Exercise 2.
∆ A’B’C’ is a scale drawing of ∆ ABC drawn by using the ratio method. Use your ruler to determine the location of the center O used for the scale drawing.
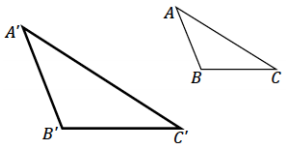
Answer:
Exercise 3.
Use the figure below with center O and a scale factor of r = \(\frac{5}{2}\) create a scale drawing. Verify that the resulting figure is In fact a scale drawing by showing that corresponding side lengths are in constant proportion and that the corresponding angles are equal in measurement.
Answer:
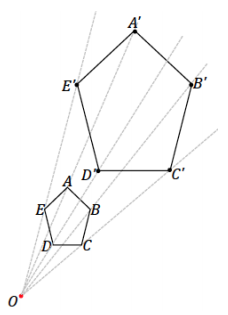
Verification of the enlarged figure should show that the length of each segment in the scale drawing is 2. 5 times the
length of each segment in the original figure (e.g., A’B’ = 2. 5(AB)). The angle measurements are m∠A = 94°, m∠B = 118°, m∠C = 105°, m∠D = 105°, and m∠E = 118°.
Exercise 4.
Summarize the steps to create a scale drawing by the ratio method. Be sure to describe all necessary parameters to use the ratio method.
Answer:
To use the ratio method to create a scale drawing, the problem must provide a polygonal figure, a center O, and a scale factor. To begin the ratio method, draw a ray that originates at O and passes through each vertex of the figure. We are dilating each vertex along its respective ray. Measure the distance between O and a vertex and multiply it by the scale factor. The resulting value is the distance away from O at which the scaled point will be located. Once all the vertices are dilated, they should be joined in the same way as they are joined in the original figure.
Exercise 5.
A clothing company wants to print the face of the Statue of Liberty on a T-shirt. The length of the face from the top of the forehead to the chin is 17 feet, and the width of the face Is 10 feet. Given that a medium-sized T-shirt has a length of 29 inches and a width of 20 inches, what dimensions of the face are needed to produce a scaled version that will fit on the T-shirt?
a. What shape would you use to model the face of the statue?
Answer:
Answers may vary. Students may say triangle, rectangle, or circle.
b. Knowing that the maximum width of the T-shirt is 20 inches, what scale factor is needed to make the width of the face fit on the shirt?
Answer:
Answers may vary. Sample response shown below.
\(\frac{20}{120}=\frac{1}{6}\)
The width of the face on the T-shirt will need to be scaled to \(\frac{1}{6}\) the size of the statue’s face.
c. What scale factor should be used to scale the length of the face? Explain.
Answer:
Answers may vary. Students should respond that the scale factor Identified in part (b) should be used for the length.
To keep the length of the face proportional to the width, a scale factor of \(\frac{1}{6}\) should be used.
d. Using the scale factor identified in part (c), what is the scaled length of the face? Will it fit on the shirt?
Answer:
Answers may vary.
\(\frac{1}{6}\)(204) = 34
The scaled length of the face would be 34 inches. The length of the shirt is only 29 inches, so the face will not fit on the shirt.
e. Identify the scale factor you would use to ensure that the face of the statue was in proportion and would fit on the T-shirt. Identify the dimensions of the face that will be printed on the shirt.
Answer:
Answers may vary. Scaling by a factor of \(\frac{1}{7}\) produces dimensions that are still too large to fit on the shirt. The largest scale factor that could be used is \(\frac{1}{8}\) producing a scaled width of 15 inches and a scaled length of 25.5 inches.
f. The T-shirt company wants the width of the face to be no smaller than 10 inches. What scale factors could be used to create a scaled version of the face that meets this requirement?
Answer:
Scale factors of \(\frac{1}{8}, \frac{1}{9}, \frac{1}{10}, \frac{1}{11}\) or \(\frac{1}{12}\) could be used to ensure the width of the face is no smaller than 10 inches.
g. If It costs the company $0. 005 for each square inch of print on a shirt, what is the maximum and minimum costs for printing the face of the Statue of Liberty on one T-shirt?
Answer:
The largest scaled face would have dimensions 15 × 25.5, meaning the print would cost approximately $1.91 per shirt. The smallest scaled face would have dimensions 10 × 17, meaning the print would cost $0.85 per shirt.
Exercise 6.
Create your own scale drawing using the ratio method. In the space below:
a. Draw an original figure.
b. Locate and label a center of dilation O.
c. Choose a scale factor r.
d. Describe your dilation using appropriate notation.
e. Complete a scale drawing using the ratio method.
Show all measurements and calculations to confirm that the new figure Is a scale drawing. The work here will be your answer key.
Next, trace your original figure onto a fresh piece of paper. Trade the traced figure with a partner. Provide your partner with the dilation information. Each partner should complete the other’s scale drawing. When finished, check all work for accuracy against your answer key.
Answer:
Answers will vary. Encourage students to check each other’s work and to discover the reason for any discrepancies found between the author’s answers and the partner’s answers.
Eureka Math Geometry Module 2 Lesson 2 Problem Set Answer Key
Question 1.
Use the ratio method to create a scale drawing about center O with a scale factor of r = \(\frac{1}{4}\). Use a ruler and protractor to verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and the corresponding angles are equal in measurement.
Answer:
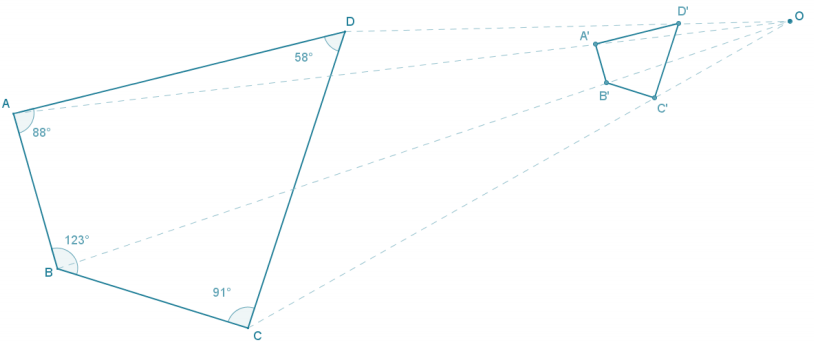
The measurements in the figure are m∠A = 88°, m∠B = 123°, m∠C = 91°, and m∠D = 58°. All side-length measurements of the scale drawing should be in the constant ratio of 1:4.
Question 2.
Use the ratio method to create a scale drawing about center O with a scale factor of r = 2. Verify that the resulting figure is in fact a scale drawing by showing that corresponding side lengths are in constant proportion and that the corresponding angles are equal in measurement.
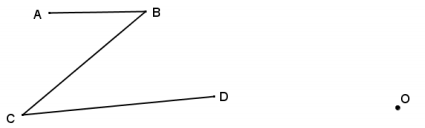
Answer:
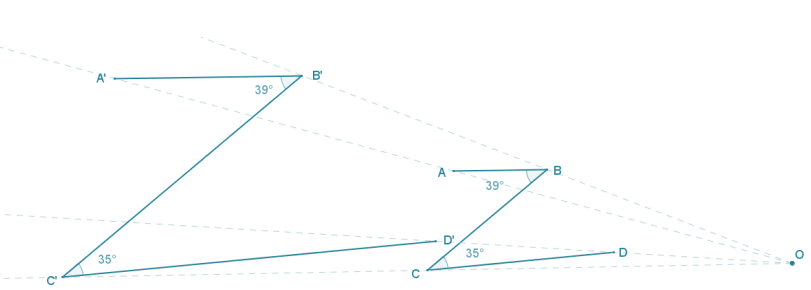
The measurements in the figure are m∠B = 39° and m∠C = 35°. All side-length measurements of the scale drawing should be in the constant ratio of 2: 1.
Question 3.
Use the ratio method to create two scale drawings: D0,2 and Dp,2. Label the scale drawing with respect to center O as ∆ A’B’C’ and the scale drawing with respect to center P as ∆ A”B”C”.
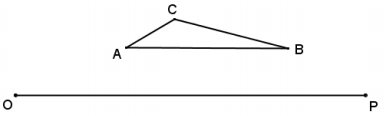
Answer:
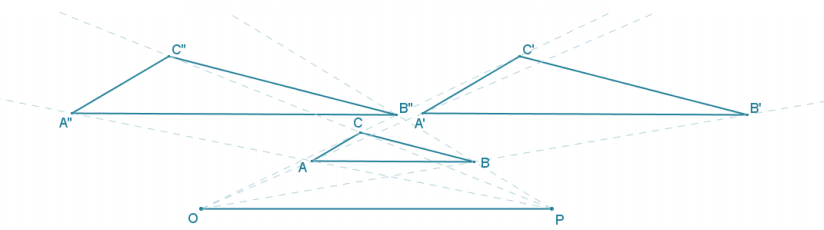
What do you notice about the two scale drawings?
Answer:
They are both congruent since each was drawn with the same scale factor.
What rigid motion can be used to map ∆ A’B’C’ onto ∆ A”B”C”?
Answer:
Answers may vary. For example, a translation by vector \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{A}^{\prime \prime}}\) is acceptable.
Question 4.
Sara found a drawing of a triangle that appears to be a scale drawing. Much of the drawing has faded, but she can see the drawing and construction lines in the diagram below. If we assume the ratio method was used to construct ∆ A’B’C’ as a scale model of ∆ ABC, can you find the center O, the scale factor r, and locate ∆ ABC?
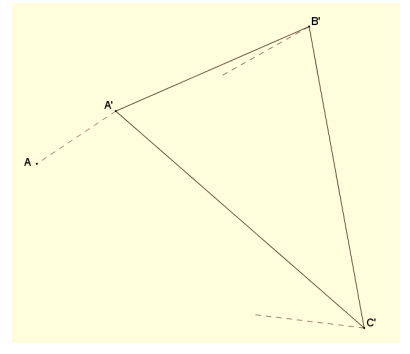
Answer:
Extend ray A’A and the partial ray drawn from either B’ or C’. The point where they intersect is center O. \(\frac{O A^{\prime}}{O A}=\frac{3}{2}\); the scale factor is \(\frac{3}{2}\). Locate B\(\frac{2}{3}\) of the distance from O to B’ and C\(\frac{2}{3}\) of the way from O to C’. Connect the vertices to show original ∆ ABC.
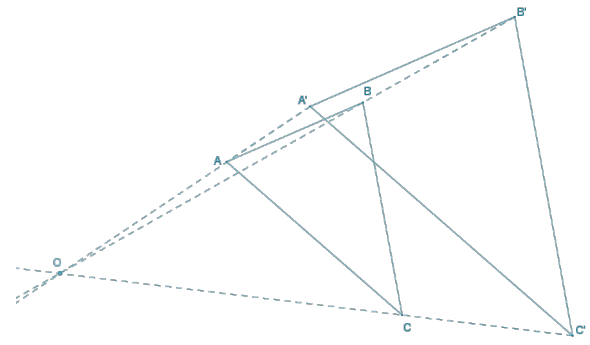
Question 5.
Quadrilateral A”B”C”D” is one of a sequence of three scale drawings of quadrilateral ABCD that were all constructed using the ratio method from center O. Find the center O, each scale drawing in the sequence, and the scale factor for each scale drawing. The other scale drawings are quadrilaterals A’B’C’D’ and A”B”C”D”.
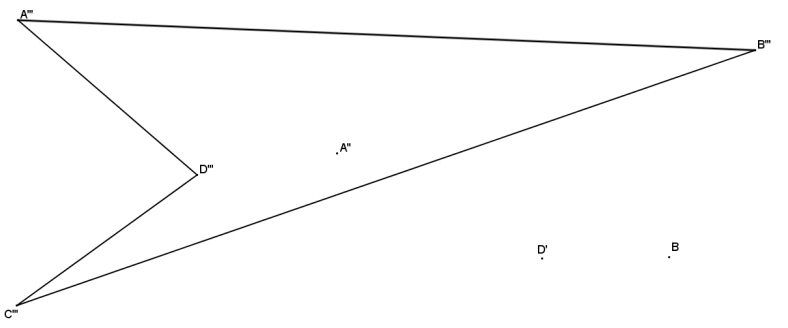
Answer:
Note to the teacher: One option is to simplify this diagram by joining vertices D” and B”, forming a triangle.
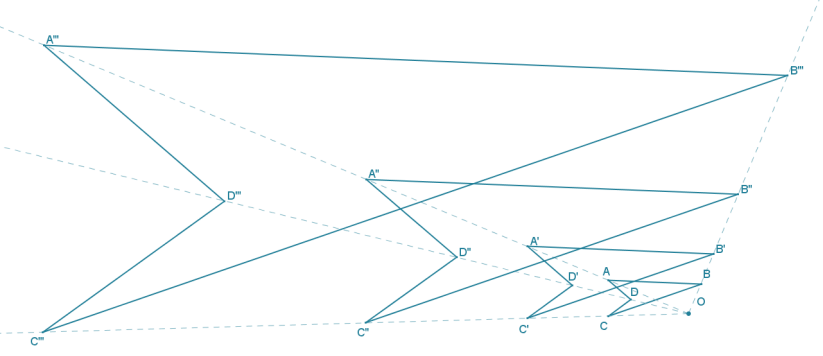
Each scale drawing is created from the same center point, so the corresponding vertices of the scale drawings should align with the center O. Draw any two of \(\overline{\boldsymbol{A}^{\prime \prime \prime} \boldsymbol{A}^{\prime \prime}}, \overline{\boldsymbol{D}^{\prime \prime \prime} \boldsymbol{D}^{\prime}}\) or \(\overline{\boldsymbol{B}^{\prime \prime \prime} \boldsymbol{B}}\) to find center O at their intersection.
The ratio of OA”: OA is 4: 1, so the scale factor of figure A”B”C”D” is 4.
The ratio of OD’: OD is 2: 1, so the scale factor of figure A’B’C’D’ is 2.
The ratio of OB”’: OB is 8: 1, so the scale factor of figure A”’B”’C”’D”’ is 8.
Question 6.
Maggie has a rectangle drawn in the corner of an 8\(\frac{1}{2}\)inch by 11-inch sheet of printer paper as shown in the diagram. To cut out the rectangle, Maggie must make two cuts. She wants to scale the rectangle so that she can cut it out using only one cut with a paper cutter.
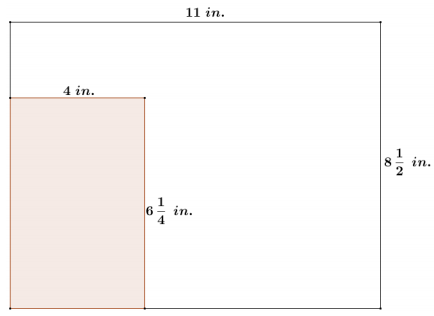
Answer:
a. What are the dimensions of Maggie’s scaled rectangle, and what is its scale factor from the original rectangle?
Answer:
If the rectangle is scaled from the corner of the paper at which it currently sits, the maximum height of the rectangle will be
8\(\frac{1}{2}\) inches.
k = \(\frac{8 \frac{1}{2}}{6 \frac{1}{4}}=\frac{34}{25}\)
The scale factor to the enlarged rectangle is \(\frac{34}{25}\)
y = \(\frac{34}{25}\)(4)
y = \(\frac{136}{25}\) = 5.44
Using the scale factor, the width of the scaled rectangle is 5.44 inches.
b. After making the cut for the scaled rectangle, is there enough material left to cut another identical rectangle? If so, what is the area of scrap per sheet of paper?
Answer:
The total width of the sheet of paper is 11 inches, which is more than 2(5.44) = 10.88 inches, so yes, there is enough material to get two identical rectangles from one sheet of paper. The resulting scrap strip measures 8\(\frac{1}{2}\) inches by 0. 12 inches, giving a scrap area of 1.02 in2 per sheet of paper.
Eureka Math Geometry Module 2 Lesson 2 Exit Ticket Answer Key
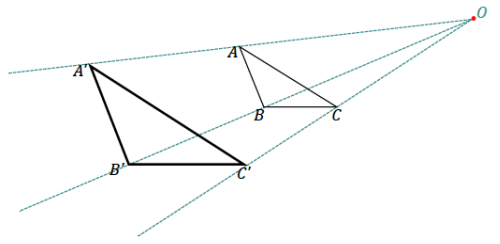
One of the following images shows a well-scaled drawing of ∆ ABC done by the ratio method; the other image is not a well-scaled drawing. Use your ruler and protractor to make the necessary measurements and show the calculations that determine which is a scale drawing and which is not.
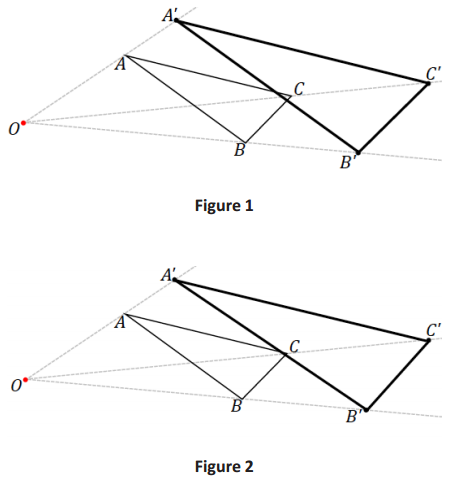
Answer:
Figure 1 shows the true scale drawing.
∆ ABC angle measurements: m∠A = 22°, m∠B = 100°, m∠C = 58°, which are the same for ∆ A’B’C’ in Figure 1. The value of the ratios of OA’: 0A, OB’: OB, and OC’: OC are the same.
∆ A’B’C’ in Figure 2 has angle measurements m∠A’ = 20°, m∠B’ = 99°, m∠C’ = 61°, and the value of the ratios of OA’: OA, OB’: OB, and OC’: OC are not the same.