Prasanna

Arithmetic Mean is commonly referred to as an average. The Arithmetic Mean in Statistics is nothing but adding the numbers in a given data set and then dividing by the total number of items within that set. In this article, we have shared the three essential types of Word Problems on Arithmetic Mean (average).

Check out this free average word problems pdf and try to solve all the questions based on the arithmetic mean (average), weighted average, and average speed. For your reference and best practice sessions, we have listed out a few arithmetic mean problems with answers so learn well and score the best grades in exams.

Read Similar Articles:

• Mean
• Mean of the Tabulated Data

How to Solve (Average) Arithmetic Mean Word Problems?

In order to calculate the various word problems on arithmetic mean, we have to follow some basic steps;

1. Firstly, collect the data from the question.
2. Find Sum of the observations and the total number of observations.
3. Now, put the values in the given arithmetic mean formula ie., Arithmetic Mean (Average) = (Sum of the observations)/(Number of observations)
4. Finally, you will get the required result for the given word problem on calculating the arithmetic mean.

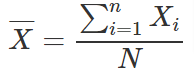Where Sum of Observations = Average x Number of Observation

Worked-out Arithmetic Mean Problems with Answers PDF

Example 1:
The marks scored by 7 students in a maths class test are 21, 23, 25, 27, 29, 31, 33. Find the arithmetic mean.
Solution:
Mean = Sum of the marks of students /number of students
= 21 + 23 + 25 + 27 + 29 + 31+ 33 / 7
= 189/7
= 27
Hence, mean of marks is 27.

Example 2: 
A cycle race was formed by 5 participants in the times provided below. What is the average time for this cycle race? 3.8 hr, 4.7 hr, 5.7 hr, 3.1 hr, 4.9 hr
Solution:
Given participates are 5 and its times are 3.8 hr, 4.7 hr, 5.7 hr, 3.1 hr, 4.9
Now, add the times  3.8 + 4.7 + 5.7 + 3.1 + 4.9
The formula to calculate the Arithmetic mean or Average is Sum of observations/ Number of observations
Mean = 3.8 + 4.7 + 5.7 + 3.1 + 4.9 / 5
= 22.2 / 5
= 4.44

Example 3: 
Find the mean of the first 10 odd numbers?
Solution:
Given that first 10 odd numbers ie., 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Mean = Sum of the 10 odd numbers / total count of odd number
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 / 10
= 100/ 10
= 10.

Example 4:
If the arithmetic mean of 12 observations 26, 10, 14, 16, x, 17, 9, 11, 12, 19, 28, 20 is 22. Find the missing observation.
Solution: 
Given observations are 26, 10, 14, 16, x, 17, 9, 11, 12, 19, 28, 20, Total observations = 12 and Arithmetic mean = 22
Arithmetic Mean (Average) = (Sum of the observations)/(Number of observations)
22 = 26 + 10 + 14 + 16 + x + 17 + 9 + 11 + 12 + 19 + 28 +20 / 12
22 = 182 + x / 12
182 + x = 22 x 12
182 + x = 264
x = 264 – 182
x = 82
Hence, the missing observation is 82.

Example 5: 
The mean of 20 numbers was found to be 18. Later on, it was detected that a number 46 was misread as 26. Find the correct mean of given numbers.
Solution:
Given that the calculated mean of 20 numbers = 18
Hence, calculated sum of these numbers = (18 x 20) = 360
Correct sum of these numbers = [360 – (wrong item) + (correct item)]
=[360 – 46 + 26]
= 340.
Therefore, the correct mean = 340/20 = 18.

Example 6: 
Yash chose to do running and Zumba to be fit. He spent 40 hours doing Zumba and running in 10 days. On average, how much money did he spend on doing running and Zumba every day?
Solution:
No. of hours Yash spent on doing running and Zumba = 40 hours
No. of hours Yash spent on doing running and Zumba in 10 days = 40/10 = 4 hours
Hence, Yash spent 4 hours doing running and Zumba.

Statistics and Statistical Data is the study of the collection, organization, analysis, interpretation, and presentation of numerical data by the theory of probability, especially with methods for drawing inferences about characteristics of a population from examination of a random sample.

Nearly 2000 years ago, the study of statistics has begun. Now, it holds an essential position in the fields of economics, business, industry, and all branches of science. Students will come to use both statistics and data in scholarly research. Learn more about the statistical data, statistical data analysis from the further sections & enhance your subject knowledge.

What is Statistical Data in Math?

The study of statistical data starts with collecting data. On the basis of a method of collection, the data may be divided into two categories.

(i) Primary Data: If the researcher collects the data by personal observation and is only liable for their truth then the data is known as primary data.

(ii) Secondary Data: If the auditor prepares the data on the basis of information given by different sources like correspondence or publications then the data is called secondary data.

Types of Statistical Data Analysis

There are two widely utilized statistical methods under the techniques of statistical data analysis and they are as such:

1. Descriptive Statistics

This type of statistical data is a form of data analysis that is primarily used to explain, show, or summarize data from a sample in an expressive way. For instance, mean, median, standard deviation, and variance.

In short, it aims to describe the relationship between variables in a sample or population and provides a summary in the form of mean, median, and mode.

2. Inferential Statistics

In order to make conclusions from the data sample by using the null and alternative hypotheses, we use this method. And, also it is included with a probability distribution, correlation testing, and regression analysis.

In short, inferential statistics utilize a random sample of data, interpreted from a population, to make and describe inferences about the whole population

Difference Between Descriptive Statistics and Inferential Statistics

The given table make you understand the factual differences between descriptive statistics and inferential statistics;

S.No	Descriptive Statistics	Inferential Statistics
1	Related with specifying the target population.	Make inferences from the sample & also make them generalize as per the population.
2	Arrange, analyze and reflect the data in a meaningful mode.	Correlate, test, and anticipate future outcomes.
3	The final results are described in the form of charts, tables, and graphs.	Concluding results are the probability scores.
4	Describes the earlier acknowledged data.	It helps in making conclusions regarding the population which is over the data available.
5	Measures of central tendency (mean, median, mode), Spread of data (Range, standard deviation, etc.) are the Deployed tool.	Hypothesis testing, Analysis of variance, etc. are the Deployed tools.

FAQs on Data and Statistics in Maths

1. What is sample or representative data?

A representative sample or representative data is a subset of a population that attempts to correctly match the characteristics of the larger group in the field of study. The relevant data is very large then we use samples. For instance, an auditorium of 20 students with 15 males and 5 females could generate a representative sample that might include 4 students: two males and two females.

2. What is Statistical Data Analysis?

Statistics include data acquisition, data interpretation, and data validation, and statistical data analysis is the way of managing various statistical operations, i.e. thorough quantitative research that endeavors to quantify data and implements some sort of statistical analysis.

3. What are the 4 Basics Steps for Statistical Data Analysis?

For analyzing any problem by using the statistical data analysis includes four basic steps;

1. Defining the problem
2. Accumulating the data
3. Analyzing the data
4. Reporting the outcomes

There are several examples of linear equations in real life. Real-Life Problems are turned into mathematical statements to form linear equations and solve them using different methods. In this article, we have mentioned various models of Problems on Application of Linear Equations for your reference. Practice them and learn how to solve the Applications of Linear Equations Questions with the examples listed.

How to Convert a Real-Life Problem into Linear Equations?

Follow the steps mentioned below to change a real-life problem into a linear equation and solve it easily. They are as under

• Read the given statement carefully and write it in the form of an algebraic expression.
• Determine the unknown quantity to be found.
• Use the conditions and frame an equation to find the unknown variable.
• Solve the equation.
• Verify if the value obtained meets the given conditions or not.

Read Similar Articles:

• Linear Equation in One Variable
• Solution of a Linear Equation in One Variable

Applications of Linear Equations Problems with Solutions

Example 1.
The Sum of Two Numbers is 60. One Number is Thrice another Number. Find the Numbers?
Solution:
Let the numbers be x
One Number is thrice the other number 3x
Sum of two numbers = 60
x+3x=60
4x=60
x=15
Other Number = 4x
=4*15
=60

Example 2.
If a car travels from city A to city B in 6 hours and covers a distance of 900 kms, find the speed of the car?
Solution:
Let us consider the speed of car be ‘s’
Given time t = 6 hrs
We know s = d/t
s=900/6
=150 km/hr
therefore, Speed of the Car = 150km/hr

Example 3.
A daughter is one-sixth of her mother’s age at present. If after 4 years, the daughter becomes one-half of her mother’s age. Then, calculate their present ages?
Solution:
Let us take x and y as the present ages of the mother and daughter.
Now, at present daughter is one-third of her mother’s age
So, y = x/6 or x= 6y ————————-(1)
After 4years, so we add 5 to the present ages.
(y + 4) = 1/2 (x + 4)
Or, 2y + 8 = x + 4 ————————-(2)
Substituting x = 3y from equation (1) to equation (2) we get,
2y + 8 = 3y +4
3y – 2y = 8 – 4
Hence, y = 4
Now, x = 6y
So, x = 6 x 4 = 24
Hence, x = 24.
Hence the present age of the mother is 24, and that of the daughter is 4.

Example 4.
Find the number whose one-third is less than the one-seventh by 4?
Solution:
Let the unknown number be x
According to the problem, one-third of x is less than the one-seventh of x by 4
Therefore, x/3 – x/7 = 4
Multiplying both sides by 20 (LCM of denominators 4 and 5 is 20)
7x – 3x = 4*21
4x = 84
x=21
Therefore, the unknown number is 21.

In the earlier topics, we have discussed in detail Linear Equations in One Variable. Now we will try to expand your knowledge on the concept and deal with the method of solving linear equation in one variable. Solving a Linear Equation in One Variable refers to finding the Solution of Linear Equation in One Variable. Check out Solved Examples for finding the solution of linear equation in one variable and learn the related concept.

Also, Check: Solution of a Linear Equation in One Variable

How to Solve Linear Equations in One Variable?

Follow the simple steps listed below and learn the rules for solving linear equations in one variable clearly. They are along the lines

• Observe the linear equation carefully.
• Identify the quantity you need to find out.
• Split the equation into two parts i.e. L.H.S and R.H.S and later check the terms containing constants and variables.
• Shift all the constants to R.H.S of the equation and variables to the L.H.S of an equation.
• Do the needful and perform arithmetic operations on both sides of the equation to get the value of the variable.

Examples on Methods of Solving Linear Equation in One Variable

Example 1.
Solve 2x – 6 = 30?
Solution:
Given 2x – 6 = 30
Transfering constants to one side and variables to one side we have 2x=30+6
2x=36
x=36/2 =18
Thus the value of the variable x is 18

Example 2.
Solve 4x – 32 = 16 – 2x?
Solution:
Given 4x – 32 = 16 – 2x
Since there are variables on both sides let us move them to one side to find their value.
4x+2x=16+32
6x=48
x=48/6 =8
Thus, the value of the variable x is 8

Example 3.
The sum of the two numbers is 30. The numbers are such that one of them is 5 times the other number. Find the numbers?
Solution:
Let One Number be x
Another Number is 5 times x = 5x
Sum of Two Numbers =30
x+5x=30
6x=30
x=30/6=5
5x=5*5=25
Therefore, numbers are 5, 25

Example 4.
A mother is 3 times older than his daughter. If the sum of ages of both mother and daughter is 48 years. Then find the age of both of them?
Solution:
Let the age of the daughter be ‘x’ years.
Then, mother’s age = 3x years.
It is given that sum of their ages is 48 years.
So, x + 3x = 48
4x = 48
x = 12.
So, daughter’s age = 12 years.
Mother’s age =3x = 36 years.
 

A Linear Equation is a mathematical statement including one variable in it. Usually to solve variables in a linear equation number of equations should be equal to the number of variables. It is the same with Linear Equations in one variable you need only one equation to find the variable in it.  This article of ours covers everything on the solution of a linear equation definition, types of solutions of linear equations, how to solve a linear equation in one variable with examples.

What is the Solution of a Linear Equation?

Solution of a Linear Equation is nothing but the points at which the lines or planes denoting the linear equations meet. The solution set of a system of linear equations is nothing but the set of values to the variables of all possible solutions.

Types of Solutions of Linear Equations

A System of Linear Equations has 3 types of solutions. We have listed all of them with enough explanatory diagrams for your reference.

Unique Solution of System of Linear Equations

Unique Solution of System of Linear Equations tells us that there is only one point and on substituting which L.H.S is equal to R.H.S. In the Case of Simultaneous Linear Equations in Two Variables unique solution is an ordered pair(x,y) that satisfies both equations.

No Solution

The System of Linear Equations has no solution when the lines don’t intersect or meet at any point, graphs of linear equations are parallel.

Infinite Solutions

A System of Linear Equations has infinite solutions if there exist infinite solutions for a solution set for which L.H.S and R.H.S become equal, or the graph includes straight lines overlapping each other.

How to Solve a Linear Equation in One Variable?

Follow the step-by-step process listed below for solving a linear equation in one variable. They are along the lines

• Go through the given linear equation carefully.
• Figure out the quantity you need to find out.
• Simply split the equation into two parts as L.H.S and R.H.S
• Identify the terms having constants and variables.
• Transfer all the constants to R.H.S of Equation and Variables to L.H.S of the equation.
• Perform Algebraic Operations on both sides to determine the value of the variable.

Linear Equations in One Variable Questions

Example 1.
Solve x +15 = 32?
Solution:
Given x +15 = 32
Let us transfer the constants and variables on the R.H.S and L.H.S
x=32-15
=17

Example 2.
Solve 3x+60=6x-30?
Solution:
Given 3x+60=6x-30
Transfering the constants and variables to their respective sides we can write 60+30=6x-3x
90=3x
x=90/3
x=30

Example 3.
The sum of the two numbers is 48. If one number is 5 times the other, find the numbers?
Solution:
Let the number be x
Since the other number is 5 times the other = 5x
Given Sum of 2 Numbers = 48
x+5x=48
6x=48
x=48/6 =8
Other Number =5x =5*8=40

Example 4.
Sam loves to collect ¢5 and ¢10 coins in his piggy bank. He knows that the total sum in his piggy bank is ¢90, and it has 4 times as many two-cent coins as five-cent coins in it. He wants to know the exact number of ¢5 and ¢10 coins in his piggy bank. Can you help him find the count?
Solution:

Let the number of ¢5 coins be x.
The number of ¢10 coins will be 4x.
Total amount = 5x + 10(4x)
Thus, 5x + 10(4x) = 90
5x + 40x = 90
45x = 90
x = 90/45=2

Therefore, sam has 2 coins ¢5 of and 20 coins of ¢10.

Linear Equations in One Variable is a basic equation that can be expressed in the form ax+b=0 in which a, b are integers and x is a variable. Linear Equation in One Variable has a single solution for it. In this article, we have covered everything like Definition, Standard Form of Linear equation in One Variable, How to Solve Linear Equation in One Variable with enough Examples.

See More: Solving Linear Equations

What is meant by Linear Equations in One Variable?

A Linear Equation is a kind of equation in which the degree of each variable in the equation is one. Linear Equations in One Variable has only one Variable in it and has only one solution to it. When we draw it on a graph it appears to be a straight line in the horizontal or vertical direction.

Example of Linear Equation in One Variable 5x+20=45

Standard Form of a Linear Equation in One Variable

The Standard Form of a Linear Equation in One Variable is ax + b = 0 Where a is the coefficient of x and b is the constant term. We need to segregate the coefficient and constant term to get the solution of the linear equation.

How to Solve Linear Equations in One Variable?

Follow the simple steps listed below to solve linear equations in one variable. They are as under

• Initially, place the constant term on one side and the coefficient term on another side by either adding or subtracting on both sides of the equation.
• Simplify or reduce the constant terms
• Isolate the variable on one side by either multiplying or dividing it into both sides of the equation.
• Simplify and note down the answer.

How to Frame Linear Equation in One Variable using Word Problem?

Go through the simple steps and learn how to frame a linear equation in one variable from a given word problem. They are as follows

• First of all, read the given data carefully and make a note of the required quantities separately.
• Mention the unknown quantities as x, y, z
• Convert the problem into a mathematical statement.
• Frame Linear Equation in One Variable using the given conditions in the Problem.
• Solve the Equation for Unknown Quantity.

Linear Equations in One Variable Questions

Example 1.
Solve for x, 2x-6=0?
Solution:
Given Linear Equation in One Variable 2x-6=0
Add 6 on both sides
2x-6+6=0+6
2x=6
x=3

Example 2.
Solve 4m-12=8?
Solution:
Given Linear Equation in One Variable 4m-12=8
4m=8+12
4m=20
m=5

Example 3.
The length of the legs of an isosceles triangle is 5 meters more than its base. If the Perimeter of the triangle is 40 meters, find the lengths of the sides of the triangle?
Solution:
Let us assume the base measures the ‘x’ meter. Hence, each of the legs measure y = (x + 5) meters.
The Perimeter of a triangle is the sum of the three sides.
The equations are formed and solved as follows:
x + 2(x + 5) = 40
x + 2x + 10 = 40
3x + 10 = 40-10
3x = 30
3x = 10
x = 30/3
x = 10
The length of the base is solved as 10 meters. Hence, each of the two legs measures 15 meters.

Example 4.
Fifteen years ago, Mohan’s age was one-fourth of what it is now. What is Mohan’s present age?
Solution:
We can write the given information by using a linear equation in one variable. Let Mohan’s present age be x years. Fifteen years ago, Mohan’s age was (x-15) years. According to the given information, x – 15= x/4
4(x – 15)= x
4x – 60= x
4x – x= 60
3x= 60
x= 60/3
x= 20
Therefore the present age of Mohan is 20 years.

In mathematics, Exponents and Indices are tools to rewrite long multiplication sums easily. This topic is covered mainly in algebra concepts. Algebra is one of the important branches in math subject that deals basically with the number theory concept.

Also, it is mainly referred to as the study of mathematical symbols. Superscript is determined as the one that is located above to the right of a number. This is called the exponent and the whole expression is known as exponentiation. Let us understand the formal notation of writing a number with an index at first followed by the laws governing it. So let’s begin!

• Power of a Number
• Laws of Indices
• nth Root of a
• Types of Algebraic Expressions

What is the definition of Exponents and Indices?

Exponentiation is defined as the mathematical operation of raising a quantity to the power of another quantity. Exponential notation, Base, and Power are the three main primary concepts to learn the exponents.  Exponents are often identified as powers or indices.

The definition of Index (Power) is the number that says how many times to use the number in a multiplication. The plural of an index is indices. In maths, Index or Power is formulated as “raising a number to the power of any other number”.

Notation of Exponents (or Index Numbers)

In case, we have written a number in the following form –

x = a^y

Then the number x is said to be equal to the number a raised to the power y. a is called the base and y is called the power or index or exponent of a. Also, it can be evenly taken as –

a^y = a x a x a x …..(y times)

where y can be any real number, a can be any real number for y ∈ Ζ (Integer) and is limited to being a positive real number for fractional values of y.

Exponent Rules | Properties of Exponents & Indices | Laws of Exponents and Indices

Here, you will learn about the three major types of exponential properties to study the indices (or exponents) mathematically.

1. Product Rules of Exponents & Indices:
In maths, two types of product laws are involved and they are applied to multiply a quantity in exponential notation by another quantity in exponential notation.

• a^m x aⁿ = a^m+n
• a^m x b^m = (a x b)^m

2. Quotient Rules of Indices or Exponents:

In mathematics, you will find two types of division laws, and they are utilized to divide a number in exponential form by another number in exponential form.

• \(\frac { a^m}{ aⁿ } \) = a^m-n
• \(\frac { a^m}{ bⁿ } \) = [(latex]\frac { b}{ c } [/latex])^m

3. Power Rules:

You will get to know that there are six types of power rules that aid students to find the value of a variable or number with exponent.

Below is the sharable image on the laws of exponents/indices that helps kids to share with other friends and make them familiar with all properties of indices and exponents.

Exponents of Exponents

An index raised to an exponential number is known as Exponents of Exponents. For instance, let’s solve 3²⁴

In order to solve this expression, first, we calculate the exponent at the top and proceed with the next one;

Start with: 3²⁴ = 2⁴

2⁴ = 2x2x2x2 = 16

3¹⁶ = 3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3 = 43046721

Hence, 3²⁴ is 43046721.

Solved Examples on Indices and Exponents | Laws of Exponents/Indices Questions and Answers

Example 1:
Find the value of the 25³

Solution:
Given that 25³
To calculate the value of the given expression, we have to multiply the base equals to 25 and how many times to do would be stated by the exponent of the number ie., 3
25³ = 25 x 25 x 25 = 15625

Example 2:
Simplify the expression x = y^a-b x y^b-c x y^c-a x y^-a-b

Solution:
Given that x = y^a-b x y^b-c x y^c-a x y^-a-b
By using the first law of exponent/indices, we can simplify this expression;
x = y^a-b x y^b-c x y^c-a x y^-a-b
⇒ x = y^{(a–b)+(b–c)+(c–a)+(−a–b)}
⇒ x = y^−a−b
⇒ x = 1/y^a+b, this is the final simplified expression.

Example 3:

If 2160 = 2^a x 3^b x 5^c, find a, b and c. Hence calculate the value of 5^a x 3^-b x 2^-c.

Solution:
Given that 2160 = 2^a x 3^b x 5^c
2x2x2x2x3x3x3x5 = 2^a x 3^b x 5^c
2⁴ x 3³ x 5¹ = 2^a x 3^b x 5^c
2^a x 3^b x 5^c = 2⁴ x 3³ x 5¹
Now, let’s compare powers of 2, 3 and 5 on both sides of an equation, we have a=4, b=3, c=1
Hence, find the value of 5^a x 3^-b x 2^-c = 5⁴ x 3^-3 x 2^-1
= 5x5x5x5 . 1/3x3x3 . 1/2
= 625 x 1/27 x 1/2
= 625/54.

FAQs on Rules/Laws of Indices with Examples

1. What are the three major rules of exponents?

The list of three major exponent rules in an algebraic form in mathematics are as follows;

• Product rules
• Quotient rules
• Power rules

2. Are indices and exponents the same? 

In mathematics, index or power or exponents are the same. It is a number that raises to a variable or number. It indicated how many times a number has been multiplied by itself.

3. What is the most essential way of using indices and exponents?

The most important approach of using exponents and indices is to write large or small numbers. Scientific notations rely on power or exponents or indices to write such numbers in an easy manner.

Find interesting Factorization Worksheets having multiple problems and make your practice efficient. Have a clear understanding of the topic and perform well in your school exams as well competitive exams. Practice using the Factorization Worksheet PDF and learn the important math skill that is necessary for learning other advanced math concepts. Download the Worksheet on Factorization in PDF Format for free of cost and practice regularly.

Also, See: Miscellaneous Problems on Factorization

Factorization Exercises with Answers

Example 1.
Factorize the expressions of the form a³+b³?
(i)27x³+729y³
(ii)1-216a³

Solution:

(i)27x³+729y³
Given Expression = 27x³+729y³
=(3x)³+(9y)³
As per the Identity a³+b³ =(a+b)(a²-ab+b²)
= (3x+9y)((3x)²-3x.9y+(9y)²)
=(3x+9y)(9x²-27xy+81y²)

(ii)1-216a³
Given Expression = 1-216a³
=(1)³-(6a)³
As per the Identity a³-b³ =(a-b)(a²+ab+b²)
= (1-6a)((1)²+1.6a+(6a)²)
=(1-6a)(1+6a+36a²)

---

Example 2.
Factorize 9a²b+3a²+5b+5b²a?

Solution:

Given Expression = 9a²b+3a²+5b+5b²a
= 3a²(3b+1)+5b(1+ba)

---

Example 3.
Factorie the Algebraic Expression x² – 14x + 49?

Solution:

Given Algebraic Expression = x² – 14x + 49
=x² – 7x-7x + 49
=x(x-7)-7(x-7)
=(x-7)(x-7)
=(x-7)²

---

Example 4.
If a+1/a = 3, find a³+1/a³?

Solution:

Given a+1/a = 3
a³+1/a³  =?
As per the Identity a³+b³ =(a+b)(a²-ab+b²)
Simply rewriting the expression given as per the identity we have a³+1/a³ =(a+1/a )(a²-a.1/a+1/a²)
Substituting the known values we get a³+1/a³ = 3(a²+1/a²-1)
=3((a+1/a)²-3)
=3(3²-3)
=3(9-3)
=3(6)
=18

---

Example 5.
Find the LCM and HCF of
(i)p³-9p and p²+6p+9
(ii)1 – 8x³, 1-x-2x²

Solution:

(i)p³+9p and p²+6p+9
p³+9 = p(p²-9)
=p(p-3)(p+3)
p²+6p+9 = p²+3p+3p+9
=p(p+3)+3(p+3)
=(p+3)(p+3)
By the definition of LCM, LCM of the given expression is p(p-3)(p+3)
By the definition of HCF, the HCF of the given expression is (p+3)
(ii)1 – 8x³, 2x²-x-1
1 – 8x³ = (1)³-(2x)³
=(1-2x)((1)²+1.2x+(2x)²)
=(1-2x)(1+2x+4x²)
=(1-2x)(4x²+2x+1)
2x²-x-1 = 2x²-2x+x-1
=2x(x-1)+1(x-1)
=(2x+1)(x-1)
By the definition of LCM, LCM = (1-2x)(1+2x+4x²)(2x+1)(x-1)
By the definition of HCF, HCF = 1 as it is the only common factor

---

Example 6.
Factorize (2x – y – z)³ + (2y – z – x)³ + (2z – x – y)³

Solution:

Given Expression = (2x – y – z)³ + (2y – z – x)³ + (2z – x – y)³
=3(2x – y – z) . (2y – z – x) (2z – x – y)[Since a³+b³+c³; a+b+c=0 = 3abc]

---

Example 7.
Factorize x²+ 8x + 16

Solution:

Given Expression = x²+ 8x + 16
=x²+ 4x + 4x+16
=x(x+4)+4(x+4)
=(x+4)(x+4)

---

Example 8.
Find the Common Factors of the following terms
(a) 24x²y, 32xy³
(b) 54m³n², 72mn³

Solution:

(a) 24x²y, 32xy³
24x²y = 4*2*3*x*x*y
32xy³=4*4*2*x*y*y*y
Common Factors for both the terms are 8xy
(b) 54m³n², 72mn³
54m³n² =9*6*m*m*m*n*n
72mn³ =9*8*m*n*n*n
Common Factors for both the terms are 9mn²

---

Example 9.
Factorize x² + 9x + 14?

Solution:

Given Expression = x² + 9x + 14
=x² + 7x +2x+ 14
=x(x+7)+2(x+7)
=(x+7)(x+2)

---

Example 10.
Factorize  z² + 6z – 16?

Solution:

Given Expression = z² + 6z – 16
=z² + 8z-2z – 16
=z(z+8)-2(z+8)
=(z-2)(z+8)

---

Here, we will learn completely about the nth root of a number like what is it mean, what is the symbol to express the given context, how to find the nth root, and some solved examples of radical expressions. Students who are pursuing 9th Grade Math should understand this concept and answer all types of questions asked in the examinations from the Exponents and Indices. Practice with the worked-out examples and learn the concept thoroughly for grasping the advanced math topics.

• Power of a Number
• Laws of Indices

nth root of a – Definition

The principal nth root of a is written as \(\sqrt[n]{ a }\), if a is real number with one nth root. \(\sqrt[n]{ a }\) is the variable or number with the same sign as a that when raises to the nth power, equals a. Here, the index of the radical is n.

\(\sqrt[n]{ a }\) expression means nth root of a. So, (\(\sqrt[n]{ a }\))^n = a

Also, (a^1/n)ⁿ = a^{n x 1/n} = a¹ = a

Hence, \(\sqrt[n]{ a }\) = a^1/n

Nth Root Symbol

The symbol applied to define the nth root is \(\sqrt[n]{ a }\). It is a radical symbol utilized for square root with a little n to determine the nth root. When it comes to expression ie., \(\sqrt[n]{ a }\), a is known as a radicand, and n is called as an index.

How to find the nth root of a number?

The calculation of the nth root of a number can be possible by the newton method. Let’s take a look at the below points and understand how to obtain the nth root of a number, A using the Newton method.

Firstly, begin with the initial guess x₀, and then repeat using the recurrence relation.

x_k+1 = \(\frac { 1 }{ n } \)((n-1)x_k + \(\frac { A }{ x_kⁿ⁺¹ } \) ), till the required precision is reached.

Based on the application of nth root, it can be easy to use only the first Newton approximant:

\(\sqrt[n]{ xⁿ + y }\) ≈ x + \(\frac { y }{ nx^n-1 } \)

Rational Exponents

Another method to prove principal nth roots is called Rational exponents. The general form for converting a radical expression to radical symbol with a rational exponent is

a^m/n = (\(\sqrt[n]{ a }\))^m = \(\sqrt[n]{ a^m }\))

Solved Examples on Simplifying Nth Root of A Real Number

Example 1:
Express the given expression in the simplest form without radicals: \(\sqrt[n]{ a ^m}\)

Solution: 
Given that \(\sqrt[n]{ a^m}\)
= a^m^{\(\frac { 1 }{ n } \)}
= a^{m x \(\frac { 1 }{ n } \)}
= a \(\frac { m }{ n } \)

Example 2: 
Simplify the nth root of the given number: \(\sqrt[3]{ 27 }\)

Solution:
Given that, \(\sqrt[3]{ 27 }\)
Let’s find the nth root of it ie.,
\(\sqrt[3]{ 27 }\) = 3
Because cube root of 3 is 3 ie., 3³ = 27
Therefore, the value of \(\sqrt[3]{ 27 }\) is 3.

Example 3:
Simplify 343^{\(\frac { 2 }{ 3 } \)}and write as a radical.

Solution:

Given that 343^2/3
As per the rational exponents a^m/n = (\(\sqrt[n]{ a }\))^m = \(\sqrt[n]{ a^m }\))
So, 343^2/3 = (\(\sqrt[3]{ 343}\))² = \(\sqrt[3]{ 343² }\))
We know that \(\sqrt[3]{ 343}\) = 7 because cube root of 7 is 343
\(\sqrt[3]{ 343² }\)) = 7² =49.

FAQs on How to find the nth root of A without a calculator

1. What is the nth root called?

The nth root is called a radical expression or a radical.

2. How to Solve the nth root of a number?

3. What is the expression of radical A?

The nth root of a is expressed as \(\sqrt[n]{ a }\).

4. How to find the indicated real nth roots of A?

Miscellaneous Problems on Factorization available will give insight on the topic of factorization as well as to acquire knowledge about various types of questions asked on factorization. All the Factorization Questions available with solutions come in handy to revise the concept effectively. Answer the different problems on factorization on a regular basis to become proficient in the topic. Subject Experts have designed the different models of questions on factorization so that students can have enough practice on the same.

Do Refer:

• Problems on Factorization using a^2 – b^2
• Problems on Factorization of Expressions of the Form x² +(a + b)x +ab

Miscellaneous Factoring Problems with Solutions

Example 1.
Factorize the Expression 5x²+14x-3?
Solution:
Given Expression = 5x²+14x-3
=5x²+15x-x-3
=5x(x+3)-1(x+3)
=(5x-1)(x+3)

Example 2.
Factorize 8x³y – 88x²y – 224xy?
Solution:
Given Expression = 8x³y – 88x²y – 224xy
= 8xy(x² – 11x – 26)
=8xy(x² – 13x+2x – 26)
=8xy(x(x-13)+2(x-13))
=8xy(x+2)(x-13)

Example 3.
Factorize (a – b)³ +(b – c)³ + (c – a)³?
Solution:
Given (a – b)³ +(b – c)³ + (c – a)³
=(a – b)³ +(b – c)³ + (c – a)³(Since a+b+c=0)
=3(a-b)(b-c)(c-a)

Example 4.
If x+\(\frac{ 1}{x}\) = \(\sqrt{ 2}\), find x³+1/x³
Solution:
Given x+1/x = \(\sqrt{ 2}\)
x³+1/x³=(x+1/x)(x²-x.1/x+1/x²)
=\(\sqrt{ 2}.\)(x²+1/x²-1)
=\(\sqrt{ 2}.\)(x+1/x)²-3
=\(\sqrt{ 2}.\)((\(\sqrt{ 2}.\))²-3)
=\(\)\sqrt{ 2 *-1}
=\(\)\sqrt{ -2}

Example 5.
Find the LCM and HCF of x² – 4x + 3 and x² + 3x + 2?
Solution:
Factorizing given expressions we have x² – 4x + 3 = x²-3x-x+3
=x(x-3)-1(x-3)
=(x-3)(x-1)
x² – 3x + 2 = x² – 2x -x+ 2
=x(x-2)-1(x-2)
=(x-2)(x-1)

By the definition of LCM, the Least Common Multiple of given expressions is (x-3)(x-1)(x-2)
By the definition of HCF, the Highest Common Factor of given expressions is (x-1)

Example 6.
Factorize the following expressions
(i)6x-42
(ii)10x²-15y²+20z²
(iii)a²+8a+16
(iv)a⁴-2a²b²+b²
Solution:
(i) Given 6x-42
=6(x-7)
(ii) Given 10x²-15y²+20z²
=5(2x²-3y²+4z²)
(iii) Given a²+8a+16
=a²+4a+4a+16
=a(a+4)+4(a+4)
=(a+4)(a+4)
(iv) Given a⁴-2a²b²+b⁴
 = (a²)²-2a²b²+(b²)²
=(a²-b²)²

Example 7.
Factorize  4p² – 4p – 3?
Solution:
Given Expression =  4p² – 4p – 3
=4p² -6p+2p – 3
=2p(2p-3)+1(2p-3)
=(2p+1)(2p-3)

Example 8.
Find the Common Factors of the following terms
(a) 20x²y, 24xy²
(b) 63m³n², 45mn⁴
Solution:
(a) 20x²y, 24xy²
20x²y = 4*5*x*x*y
24xy²=4*6*x*y*y
Common Factors for both the terms are 4xy
(b) 63m³n², 45mn⁴
63m³n² =7*9*m*m*n*n
45mn⁴ =9*5*m*n*n*n*n
Common Factors for both the terms are 9m²n²

Example 9.
Factorize  a³ + b³ – 3ab + 1?
Solution:
Given Expression = a³ + b³ – 3ab + 1
= a³ + b³ + 1³ – 3 ∙ a ∙ b ∙ 1
= (a +b + 1)(a² + b² + 1² – b ∙ 1 – 1 ∙ a – ab)
= (a +b + 1)(a² +b² – b – a – ab + 1)

Example 10.
If a + b + c = 15, a² + b² + c² = 30 and a³ + b³ + c³ = 140, find the value of abc?
Solution:
We know, a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – bc – ca – ab).
Therefore, 140 – 3abc = 15(30 – bc – ca – ab)…………………….. (i)
Now, (a + b + c)² = a² + b² + c² + 2bc + 2ca + 2ab
Therefore, 15² = 30 + 2(bc + ca + ab).
⟹ 2(bc + ca + ab) = 15² – 30
⟹ 2(bc + ca + ab) = 225 – 30
⟹ 2(bc + ca + ab) = 190
Therefore, bc + ca + ab = 190/2 = 95
Putting in (i), we get,
140 – 3abc = 15(30 – 95)
⟹ 140 – 3abc = 450-1425
⟹ 140-3abc = -975
⟹ 3abc = 140+975
3abc=1115
Therefore, abc ~ 371