Prasanna

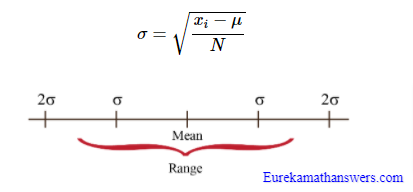
Do you have any difficulty in solving the Problems Based on Recurring Decimals as Rational Numbers? Then, this is the right place for you. We have compiled everything on what is meant by recurring decimal, how to convert recurring decimal to a rational number. Check out the steps listed below that we need to follow while changing between recurring decimal to a rational number. Refer to the solved examples on expressing recurring decimals as rational numbers and apply the related knowledge and score well in your exams.

How to Convert Recurring Decimal into Rational Number?

Have a glance at the simple steps listed below to change between recurring decimals to rational numbers. They are along the lines

• Consider the recurring decimal which we need to change as a rational number to be x.
• Carefully observe the repeating digits in the decimal number.
• Keep the repeating digits on the left side of the decimal point.
• Now put the repeating digits on the right side of the decimal point.
• Subtract both sides of the equation to have equality of equations. Remember that after subtraction differences of both sides are positive.

See Similar Articles:

• Problems on Rational numbers as Decimal Numbers
• Recurring Decimals as Rational Numbers

Recurring Decimal to Rational Numbers Questions and Answers

Example 1.
Convert 2.3333….. into a rational number?
Solution:
Given decimal number = 2.333….
Let us consider the recurring decimal number to be x i.e. x = 2.3333…..
Repeating digit in the recurring decimal is 3.
Move the repeating digits in the decimal number to the left side of the decimal point. We can do so by simply multiplying with 10.
10x = 23.33333…..(1)
Place the repeating digits on the right side of the decimal point.
x= 2.3333…….(2)
Subtract both sides of the equations
10x-x=23.3333……-2.3333….
9x = 21
x=21/9
therefore, the recurring decimal 2.3333…. converted to a rational number is 21/9

Example 2.
Express 10.3454545… as a rational number?
Solution:
Given decimal number = 10.3454545…
Let us consider the recurring decimal number to be x i.e. x = 10.3454545…
Move the repeating digits in the decimal number to the left side of the decimal point. We can do so by simply multiplying with 1000.
1000x = 10345.4545…..(1)
Place the repeating digits on the right side of the decimal point. We need to multiply by 10 to shift so
10x= 103.4545…….(2)
Subtract both sides of the equations
1000x-10x=10345.4545……-103.4545….
990x = 10242
x=10242/990
x=569/55
Therefore, the recurring decimal 10.3454545…. converted to a rational number is 569/55

Example 3.
Convert 123.45757… to rational number?
Solution:
Given decimal number x = 123.45757…
Move the repeating digits in the decimal number to the left side of the decimal point. We can do so by simply multiplying with 1000.
1000x = 123457.5757…..(1)
Place the repeating digits on the right side of the decimal point. We need to multiply by 10 to shift so
10x= 1234.5757…….(2)
Subtract both sides of the equations
1000x-10x=123457.5757……-1234.5757….
990x = 122223
x=122223/990
x=40741/330
Therefore, the recurring decimal 10.3454545…. converted to a rational number is 40741/330

Example 4.
Write 0.5676767….. as a rational number?
Solution:
Given Decimal Number = 0.5676767…..
Move the repeating digits in the decimal number to the left side of the decimal point. We can do so by simply multiplying with 1000.
1000x = 567.6767…..(1)
Place the repeating digits on the right side of the decimal point. We need to multiply by 10 to shift so
x= 5.6767…….(2)
Subtract both sides of the equations
1000x-10x=567.6767……-5.6767….
990x = 562
x=562/990
x=281/495
Therefore, the recurring decimal 10.3454545…. converted to a rational number is 281/495

Rational Numbers can be expressed in the form of Fractions. We can convert the rational numbers to decimal form by simply dividing the numerator with the denominator. In this article, we will help you determine if a rational number is terminating or non-terminating and the formula for telling so. Go through the further sections and find various models of problems on rational numbers as decimal numbers. Get a clear idea of the concept and easily understand the questions present.

How to check if a Rational Number is Terminating or Non-Terminating?

To Identify if a rational number is terminating or not you can use the following formula \(\frac { x }{ 2^m * 5^n } \) where x ∈ Z is the numerator of the given rational fractions and the denominator y can be written in the powers of 2 and 5 where m ∈ W; n ∈ W.

If you can write the rational number in the above form then it is called a terminating decimal. If it can’t be written in the above form it is called a non-terminating decimal.

Do Refer:

• Decimal Representation of Rational Numbers
• Rational Numbers in Terminating and Non-Terminating Decimals
• Recurring Decimals as Rational Numbers

Solved Examples on Expressing Rational Numbers as Decimal Numbers

Example 1.
Check whether \(\frac { 3 }{ 4 } \) is a terminating or non-terminating decimal. Also, convert it to a decimal number?
Solution:
Given Rational Number is \(\frac { 3 }{ 4 } \)
Let us check if it is terminating or not initially, To do so we need to convert the given rational number to the form of \(\frac { x }{ 2^m * 5^n } \)
= \(\frac { 3 }{ 2^2 * 5^0 } \)
Since we can express it in the form of \(\frac { x }{ 2^m * 5^n } \) it is a terminating decimal.
\(\frac { 3 }{ 4 } \) converted to decimal form is 0.75

Example 2.
Check whether \(\frac { 7 }{ 3 } \) is a terminating or non-terminating decimal. Also, change it to decimal number?
Solution:
Given Rational Number is \(\frac { 7 }{ 3 } \)
Let us check if it is terminating or not initially, To do so we need to convert the given rational number to the form of \(\frac { x }{ 2^m * 5^n } \)
Since we can’t express it in the form of \(\frac { x }{ 2^m * 5^n } \) it is a non-terminating decimal.
\(\frac { 7 }{ 3} \) converted to decimal form is 2.333……

Example 3.
Check whether \(\frac { 5 }{ 24 } \) is terminating or non-terminating decimal and express it in decimal form?
Solution:
Given Rational Number is \(\frac { 5 }{ 24 } \)
Let us check if it is terminating or not initially, To do so we need to convert the given rational number to the form of \(\frac { x }{ 2^m * 5^n } \)
= \(\frac { 5 }{ 2^2 * 6^1 } \)
Since we can express it in the form of \(\frac { x }{ 2^m * 5^n } \) it is a terminating decimal.
\(\frac { 5 }{ 24 } \) converted to decimal form is 0.2083

 

A Rational Number is a Real Number that can be denoted in the form of a simple fraction. If you are wondering how to represent Rational Numbers on Number Line then this article is for you. You will know everything about what is a number line and how do we express rational numbers on a number line step by step. Check out solved examples on the representation of the rational numbers on a number line and solve similar kinds of questions easily.

Number Line – Definition

A number Line is a pictorial representation of numbers on a straight line. We can use it as a reference for ordering and comparing numbers. To the right side of the origin, we denote positive values and on the left side of the origin, negative values are expressed.

Do read:

• Use a Number Line
• Expressing Numbers on the Number Line

Rational Numbers – Definition

In Simple Maths, we can define Rational Number as any Number that can be denoted in the form of p/q where p, q are integers and q ≠ 0.

How do you Represent Rational Numbers on a Number Line?

Follow the simple steps listed below for the representation of rational numbers on the number line. They are as such

• Firstly, draw a line and locate a point 0 i.e. origin.
• If the given number is positive mark it on the right side of the origin. if it is negative mark it on the left side of the origin.
• For denoting fractions divide each unit into values equal to the denominator of the fraction.

Rational Number Representation Using Successive Magnification

We can represent the decimal expansion on the number line using the successive magnification process. We know every rational number can be denoted as decimal expansions. Here, 1/3 = 0.33333……..
Step 1: Locate 0.3 on the number line and lies between 0 and 1
Step 2: Now represent 0.33 on the number line. We know 0.33 lies between 0.30 and 0.40

By magnifying numbers between 2 other numbers on the number line, we can represent the decimal expansion of rational numbers easily.

Solved Examples on Representation of Numbers on Number Line

Example 1.
Represent Rational Numbers 3/5 on the Number Line?
Solution:
Given Rational Number is 3/5
We know it is a proper fraction and positive number thus it lies on the right side of the origin. i.e. between 0 and 1.

Split the number line between 0 and 1 into 5 equal parts the number of times the denominator. The third part is the representation of rational number 3/5.

Example 2.
Represent Rational number 9/6 on the number line?
Solution:
Given Rational Number is 9/6
We know it is an improper fraction and a positive number thus it lies on the right side of the origin. i.e. between 0 and 1.
Improper Fraction 9/6 expressed in the mixed fraction is 1 3/6

Example 3.

Represent Rational Number -2/4 on a Number Line?
Solution:
Given Rational Number is -2/4
We know it is a proper fraction but a negative number thus it lies on the left side of the origin. i.e. between 0 and -1.
Proper Fraction -2/4 expressed on the number line is as follows. We will split into 4 equal parts and then the 2nd part between 0 and -1 is -2/4.

 

Range of the Statistical Data: Do you find difficulty when determining the difference between a set of numbers? Calculating the range of their data set is an easy trick. Many of the statisticians, analysts, and mathematicians used this to find the exact variation of a set of numbers.

In this mini range of the statistical data article, we are going to explain the concept of range in statistics. Explore what is the definition of range in statistics, formula, how to find the range of a dataset, what is the rule of thumb to calculate the range and limitations of range.

Do Check:

• Statistics and Statistical Data
• Statistical Variable

What is meant by the Range of Data in Statistics?

In statistics, the spread of your data from the lowest to the highest value in the distribution and also commonly used measure of variability is known as Range of Data. The symbol for range in statistics is R.

The calculation of range is done by subtracting the smallest value from the largest value. This helps them learn & grasp how different and varied the numbers are within the data set. While a small range means low variability, a large range means high variability in a distribution.

Range of the Statistical Data Formula

The formula to calculate the range is as follows:

(Or)

R = H-L

where R = range
H = highest value
L = lowest value

What is the Rule of Thumb?

According to the rule of thumb, the range of data lies within four standard deviations. Two above the mean and two below the mean. The formula for Standard Deviation (σ) is as follows.

How To Calculate Statistical Range with Example?

Calculating the range of statistical data is straightforward. In other words, it just needs to discover the variation between the numbers in a data set. Simply follow the basic steps available to find the range:

1. Firstly, Order all the values in your data set from lowest to highest
2. Find the minimum and maximum numbers which are required to substitute in the formula
3. Then, Subtract the smallest number from the largest number.
4. Finally, note down the range of a given data set.

For Example:
Find the range of the data 15, 3, 7, 87, 4, 33, 45, 32?
Solution:
Given data set is 15, 3, 7, 87, 4, 33, 45, 32
Now, arrange the list in ascending order i.e., 3, 4, 7, 15, 32, 33, 45, 87
By using the ordered set, find the smallest and largest values
Highest Value = 87
Lowest Value = 3
Range(R) = Highest Value – Lowest Value
= 87 – 3
= 84.

Limitations of Range

One of the most convenient metrics to calculate is range. However, it has subsequent conditions.

• It does not notify the number of data points.
• It is not utilized to find mean, median, or mode.
• The range of the statistical data can be changed by extreme values(outliers).
• However, it won’t work for open-ended distribution.

Real-Life Examples of Range in Statistics and Statistical Data

Example 1:
Your data set is the scores of 7 participants.
Participant:  1    2    3    4    5    6    7
Score:        37  18  31  28  21  26  32
Solution:
Given that,
Participant:  1    2    3    4    5    6    7
Score:         37  18  31  28  21  26  32
Firstly, arrange the values from low to high to identify the lowest value (L) and the highest value (H).
18, 21, 26, 28, 31, 32, 37
Now, subtract the lowest from the highest value to find the range:
R = H – L
R = 37 – 18 = 19
Hence, the range of our data set is 19 score.

Example 2: 
The weights (in kg) of the teachers of a school are noted as 53, 60, 65, 63, 70, 65, 62, 65, 63, 64, 80, 60, 68, 58, 62, 65, 63, 65, 64, 60, 62, 63. What is the range of the collection?
Solution:
Given weights of teachers are 53, 60, 65, 63, 70, 65, 62, 65, 63, 64, 80, 60, 68, 58, 62, 65, 63, 65, 64, 60, 62, 63
Here, the least value = 53
the highest value = 80
The formula of Range = Maximum value – Minimum value
= 80 – 53
= 27.

Questions on Range in Statistics

1. Which of the following statements is true about the Range of the Statistical Data?
A. Sensitive only to outlier values
B. Gives equal weight to all observation
C. Gives the difference between the largest and the smallest
D. Most reliable measure of dispersion

2. Which of the following statements is true about the standard deviation of statistical data?
A. The least reliable measure of variability
B. The lower the value the more consistent the data
C. The simplest measure of variability
D. The higher the value the more consistent the data

3. Which of the following statements must be true?
A. The median of a data set must be smaller than its mode.
B. The standard deviation of a data set must be smaller than its mean.
C. The range of a data set must be smaller than its standard deviation.

4. If the lowest value is 15, and the range of the data is 3, what is the highest value?
A. 18
B. 14
C. 8
D. 55

FAQs on Range of Ungrouped Data

1. What is meant by range deviation?

The range deviation is the subtraction of minimum value from the maximum value and it represents the spread of data.

2. What is the formula of range?

The formula of the range is very easy, the difference between the largest value and the smallest value of the data set ie., Range (R) = Maximum Value – Minimum Value.

3. Solve the range of ungrouped data where the marks of a student in 4 tests of the chapter statistics are (out of 10) – 10, 7, 8, and 5. 

Follow the below simple steps and find the range of ungrouped or raw data:

Step-1: Arrange the given marks in ascending order ie., 5, 7, 8, 10
Step-2: Now, take the range of the data formula and substitute the values ie., R = H – L = 10-5 = 5.

4. Can the range be a negative number?

As we know the formula of range, subtracts the lowest number from the highest number, the range is always zero or a positive number. So, it can’t be a negative number.

5. How to obtain the range of a function?

The set of all possible values which it can produce is defined as the range of a function. Hence, irrespective of what value we give to x, the function is always positive. If x is 4, then the function returns x as squared value i.e. 16.

Rational Numbers are the numbers that can be denoted in the form of fraction p/q where p, q are integers and q is a non-zero number. In this article, we will discuss how to find rational numbers between two unequal rational numbers explained in detail. Know the formula for finding rational numbers between two unequal rational numbers, solved examples on finding rational numbers between given two unequal rational numbers mentioned step by step.

How to find Rational Numbers between Two Unequal Rational Numbers?

Go through the below process and learn how to find rational numbers between two unequal rational numbers. They are as under

Let us consider a and b are two unequal rational numbers if we are to find the rational number preset between them we can find so by using the formula (a+b)/2. Rational Numbers are Ordered i.e. given two rational numbers a, b either a >b, a<b, a=b.

We can also say there is an infinite number of rational numbers between two unequal rational numbers.

How to find Rational Numbers between Two Unequal Rational Numbers having Same Denominator?

• Firstly, check the denominators of the given rational numbers.
• For fractions having the same denominators check for the numerators.
• If the numerators differ by a larger value then we can write the rational numbers with increments of one for numerator without changing the value of the denominator.
• If the numerators differ by a lesser value then multiply both the numerators and denominators of rational numbers by multiples of 10.

How to find Rational Numbers between Two Unequal Rational Numbers having Different Denominator?

• In order to find the rational numbers between two unequal rational numbers having different denominators, equate the denominators.
• Equate the denominators using the LCM Method.
• After applying the LCM Method and making the denominators equal apply the rules for finding rational numbers between two unequal rational numbers of the same denominators.

Also, See:

• Comparison between Two Rational Numbers
• Recurring Decimals as Rational Numbers
• Laws of Algebra for Rational Numbers

Solved Examples on How to find a Rational Number Between Two Fractions

Example 1.
Find a Rational Number lying mid-way between 4/3 and 6/7?
Solution:
Given rational numbers are 4/3 and 6/7
We know the formula to find rational number lying midway = (a+b)/2
=(4/3+6/7)/2
=((28+18)/21/2)
=(46*/21)/2
=46/42

Example 2.
Find a rational number lying mid-way between 7/5 and -13/2?
Solution:
Given rational numbers are 7/5 and -13/2
We know the formula to find rational number lying midway = (a+b)/2
=1/2(7/5+-13/2)
=1/2(14-65/10)
=1/2(-51)
=-51/2

Example 3.
Find 5 rational numbers between 3/4 and -7/4?
Solution:
Given rational numbers are 3/4 and -7/4
Here rational numbers are having the same denominators. However, the difference between them is less we will multiply both numerators and denominators with 10.
3/4 = 3*10/4*10  = 30/40
-7/4 = -7*10/4*10 = -70/40
Integers between -70 & 30 are -70<-69<-68<-67<-65<……….28<29<30
Therefore, the 5 rational numbers between 3/4 and -7/4 are -69/40, -68/40, -67/40, -66/40, -65/40.

Example 4.
Find at least 10 Rational Numbers between fractions 1/2 and 5/4?
Solution:
Given rational numbers are 1/2 and 5/4
Here rational numbers are having different denominators. So we will equate the denominators using LCM Method. Doing so we will obtain the fractions as under
LCM(2,4) = 4
1/2 = 1*2/2*2 = 2/4
5/4 =5*1/4*1 = 5/4
Now that we have made Denominators the Same by equating let us apply the further process same as in the process of finding the rational numbers between two unequal rational numbers of same denominators
However, the difference between them is less we will multiply both numerators and denominators with 10.
2/4 = 2*10/4*10  = 20/40
5/4 = 5*10/4*10 = 50/40
Integers between 20 & 50 are 21< 22<23<24<25<26<27…….46<47<48<49<50
Therefore, the 10 rational numbers between 1/2 and 5/4 are 21/40, 22/40, 23/40, 24/40, 25/40, 26/40,27/40,28/40, 29/40,30/40.

 

Do you want to figure out which rational number is greater and smaller among a given set of rational numbers? Then this article is quite handy as it gives you a complete idea of the comparison between two rational numbers. We will discuss all about the classification of rational numbers, common facts about comparing rational numbers, how to compare two rational numbers with enough examples. Step by Step Solutions provided makes it easy for you to understand the concept as well as to improve your problem-solving skills.

Classification of Rational Numbers

Rational Numbers are a type of fractions. They are classified into the following types

Proper Rational Numbers: Proper Rational Numbers are numbers that are less than 1. In these kinds of rational numbers, the denominator is greater than the numerator. Example: 2/4, 5/6, 7/8 are all proper fractions.

Improper Rational Numbers: Improper Rational Numbers are numbers that are greater than 1. In these rational numbers, the numerator is greater than the denominator. Example 4/3, 7/6, 9/10 are all improper rational numbers.

Positive Rational Numbers: In the Case of Positive Rational Numbers both the numerator and denominator are either positive or negative. These are always greater than zero. Example: 3/4, -5/-6, -7/-8 are all Positive Rational Numbers.

Negative Rational Numbers: In this type of rational numbers, either numerator or denominator anyone is negative. These are always less than zero. Example: -3/4, 7/-8, 1/-2 are all Negative Rational Numbers.

Facts about Rational Numbers Comparison

Comparison of Rational Numbers is the same as Comparison of Integers and Fractions. Here is a list of common facts you need to know about Comparing Rational Numbers. They are along the lines

• Every positive rational number is greater than zero.
• Every rational number < 0 is a negative rational number.
• A Positive rational number is greater than a negative rational number.
• Every Rational number denoted by a point on the right of a number line is greater than all rational numbers represented by points on the number line’s left.

Also, See:

• Decimal Representation of Rational Numbers
• Laws of Algebra for Rational Numbers

How do you Compare Two Rational Numbers?

Follow the simple steps listed below to compare two rational numbers. They are as under

• Firstly, identify the rational numbers from the given data.
• Later convert the denominators of the mentioned rational numbers to positive if they aren’t by simply multiplying both numerator and denominator with -1.
• Next, check if the given rational numbers are like rational numbers or unlike rational numbers.
• If the rational numbers are like fractions just check the numerators of the fractions and the one that is higher is the larger rational number. Remember to check if they are positive or negative rational numbers.
• If the rational numbers are unlike fractions calculate the LCM of the Denominators and express the fractions in terms of the common denominator and then compare them.

Let us understand the process better by considering an example.

Example:
Which is greater of the rational numbers -4/8, 5/-12?
Solution:
Given Rational Numbers are -4/8, 5/-12
Since the given rational numbers 5/-12 is having a negative denominator we need to multiply both numerator and denominator with -1 to get the positive denominator.
5/1-12 = 5*(-1)/-12*(-1) = -5/12
Now since the given rational numbers are unlike rational numbers let us calculate the LCM of denominators.
LCM(8, 12) = 24
Expressing the given rational numbers in terms of the common denominator we can rewrite them as
-4/8 = (-4*3)/(8*3) = -12/24
-5/12 = (-5*2)/(12*2) = -10/24
Now let us compare the numerators of both the rational numbers i.e. -12, -10
-10 is greater thus 5/-12 is the greater rational number.

Comparing Rational Numbers Examples

Example 1.
Compare the rational numbers -7/8, -9/10?
Solution:
Given Rational Numbers are -7/8, -9/10
Since the given rational numbers are unlike fractions let us find the LCM of Denominators.
LCM(8,10) = 40
Expressing the given rational numbers in terms of common denominators we have
-7/8 = -(7*5)/(8*5) = -35/40
-9/10 = (-9*4)/(10*4) = -36/40
Now compare the numerators of both the fractions i.e. -35, -36
Thus the fraction with numerator -35 is greater i.e. -7/8

Example 2.
Compare the Rational Numbers 1/3 and -4/3?
Solution:
Given Rational Numbers are 1/3 and -4/3
Here both the fractions are like fractions so we will check the numerators of the fractions and decide which one is greater.
1>-4
Therefore, rational number 1/3 is greater than -4/3

Example 3.
Compare rational numbers 5 and -7?
Solution:
Given Rational Numbers are 5/1 and -7/1
Here both the fractions are like fractions let us check the numerators of the fractions and decide which one os greater.
5>-7
Therefore, rational number 5 is greater than -7.

Word Questions on Mean of Raw Data helps you all to find the mean (or average) of an ungrouped data set where the data is not presented in intervals. Moreover, you can learn more knowledge about the concept by practicing the example problems based on Mean of ungrouped data.

Here, we have explained various styles of word problems on Mean of arrayed data or ungrouped data for your knowledge. Take a look at them and ace up your subject preparation by answering the Mean Deviation for ungrouped data examples and cross-check the solutions here itself.

Check Related Articles:

• Properties Questions on Arithmetic Mean
• Statistical Variable
• Problems Based on Average

Mean of Ungrouped Data Example Problems PDF and Solutions

Example 1:
The monthly salary (in $) of 8 employees in a company are 6000, 8000, 4000, 9000, 5000, 3000, 8000, 6500. Find the mean of ungrouped data?
Solution:
Given salary (in $) for 8 employees are 6000, 8000, 4000, 9000, 5000, 3000, 8000, 6500
Mean of ungrouped data = Sum of the observations / Total number of observations
= 6000+8000+4000+9000+5000+3000+8000+6500 / 8
= 49500 / 8
= 6187.5

Example 2: 
The mean age of ten girls is 25 years. If the ages of nine of them be 10 years, 12 years, 13 years, 15 years and 25 years then find the age of the tenth girl.
Solution:
Let the age of the tenth girl be x years
Now, find the mean age of 10 girls = 10 years +12 years +13 years +15 years + 25 years + x years / 10
⟹ 25 = 75 years + x years / 10 (mean age of 10 girls is 25 years from the question)
⟹ 250 = 75 + x
⟹ x = 250-75
⟹ x = 175
Hence the age of the tenth girl is 175 years.

Example 3:
Find the mean of the first four whole numbers.
Solution:
The first four whole numbers are 0, 1, 2, 3.
Hence, the mean = x1+x2+x3+x4 / 4
= 0+1+2+3/4
= 6/4
= 3/2
= 1.5

Example 4: 
The mean of a sample of 5 numbers is 4. An extra value of 2.5 is added to the sample then find the new mean?
Solution:
Given that Total of original numbers =5×4=20
New total =20+2.5=22.5
The new mean of a sample = 22.5/6
= 3.75
Hence, the new mean of 6 numbers is 3.75.

Example 5: 
The following table gives the points of each player scored in four games:

Player	Game 1	Game 2	Game 3	Game 4
A B C	14 0 8	16 8 11	10 6 Did not play	10 4 13

(i) Find the mean to determine C’s average number of points scored per game.
(ii) Who is the worst performer?

Solution:
(i) Mean Score of C = 8+11+13 / 3
= 32/3
= 10.6
(ii) To calculate who is the worst performer, we have to find the mean score of each player:
Mean score of A = (14 + 16 + 10 + 10) / 4 = 12.5
Mean score of B = (0 + 8 + 6 + 4) / 4 = 18/4 = 4.5
Mean Score of C = 8+11+13 / 3 = 32/3 = 10.6
Therefore, B is the worst performer.

Example 6:
A competitor scored 80%, 90%, 75%, and 60% in four subjects in an entrance test, Calculate the mean percentage of the scores achieved by his/her.
Solution:
Given observations in percentage are x1=80, x2=90, x3=75, x4=60
Hence, their mean A = x1+x2+x3+x4 / 4
= 80+90+74+60 / 4
= 304 / 4
= 76
Hence, the mean percentage of scores achieved by the competitor was 76%.

Rational Numbers are the numbers that can be denoted in the form of p/q where p, q are integers and q is a non-zero number. For understanding the Rational Numbers Laws we have listed all of them explaining step by step. Check out the various general properties or laws that the rational numbers obey such as closure, commutative, associative, distributive, identity & inverse properties, etc. Go through these Algebra Laws for Rational Numbers explained one by one below and have a clear picture of the concept.

Laws of Algebra of Rational Numbers

If a ∈ Q, b ∈ Q, c ∈ Q, where Q is the set of rational numbers then

(i) a + b ∈ Q
(ii) a + b = b + a
(iii) (a + b) + c = a + (b + c)
(iv) a + (-a) = 0, -a being the negative rational of a
(v) a × b ∈ Q
(vi) a × b = b × a
(vii) a × (b × c) = (a × b) × c
(viii) a × (b + c) = a × b + a × c (Distributive law)
(ix) a × b = b × c ⟹ a = 0 or b = c (Cancellation law)

Check Related Articles:

• Rational Numbers in Terminating and Non-Terminating Decimals
• Decimal Representation of Rational Numbers
• Recurring Decimals as Rational Numbers

Properties of Rational Numbers

There are 6 different properties of rational numbers. All of them are explained below with enough examples. They are as under

Closure Property: If we perform addition, subtraction, multiplication operations on two rational numbers say x and y, the result is also a rational number. Thus, we can say that rational numbers are closed under addition, subtraction and multiplication.

Commutative Property: Addition and Multiplication of Rational Numbers are Commutative. Subtraction and Division of Rational Numbers don’t obey the Commutative Property.

Associative Property: Rational Numbers obey the Associative Property for Addition and Multiplication. If x, y, z are rational numbers then for the addition we can write as x+(y+z)=(x+y)+z. In the case of multiplication,  x(yz)=(xy)z

Distributive Property: For three rational numbers a, b, c distributive property states that a x (b+c) = (a x b) + (a x c)

Identity and Inverse Properties: 0 is an additive identity and 1 is a multiplicative identity for rational numbers. For a rational number x/y, the additive inverse is -x/y, and y/x is the multiplicative inverse.

FAQs on Laws of Algebra for Rational Numbers

1. What are the different properties of rational numbers?

The different properties of rational numbers are as such

• Closure Property
• Commutative Property
• Associative Property
• Distributive Property
• Identity Property
• Inverse Property

2. Why is there no closure property for division?

The division doesn’t obey the closure property as division by zero is not defined. We can say that other than ‘0’ all numbers are closed under division.

3. What is the distributive property of rational numbers?

Distributive Property of Rational Numbers state that a x (b+c) = (a x b) + (a x c)

In the earlier articles, we have discussed on what is meant by Rational Number and its representation. Here we will step ahead and discuss the classification of non-terminating decimals i.e. recurring and non-recurring decimals. We will elaborate and explain the definitions of recurring and non-recurring decimals as well as the steps involved in how to turn a recurring decimal into a rational number with enough examples. Go through the article completely and be well versed with the concept.

Recurring Decimals – Definition

Recurring Decimals are the numbers that keep on repeating the same value after the decimal point. These are also called repeating decimals. For Example: 1/3 = 0.3333….
To denote a repeating digit in the recurring decimal we often place a bar over the repeating digit.

Non-Recurring Decimals – Definition

In the case of Non-Recurring Decimals, the numbers don’t repeat after the decimal point. These are also known as Non-Terminating or Non-Repeating Decimals. For Example: √3 = 1.7320508075688772935274463415059……

How to Write Recurring Decimals as Rational Numbers?

Go through the simple steps listed below to convert between recurring decimals to rational numbers. The steps involved are as under

• Firstly, let us assume x to be the recurring decimal we need to change as a rational number.
• Examine the repeating digits carefully in the recurring decimal.
• Place the repeating digit to the left side of the decimal point.
• Next to the above step place the repeating digits on the right of the decimal point.
• Now, subtract both the left-hand sides and right-hand sides accordingly to obtain the rational number.

Shortcut Method for turning a Recurring Decimal into a Rational Number

(The whole number obtained by writing the digits in their order – The whole number made by the nonrecurring digits in order )/(10^The number of digits after the decimal point−10^The number of digits after the decimal point that does not recur)
Let us better understand the method by having a glance at the example.

Example: 
Convert 13.288888…. to a rational number?
Solution:
Given Repeating Decimal Number = 13.288888…….
As per the formula, (The whole number obtained by writing the digits in their order – The whole number made by the nonrecurring digits in order )/(10^The number of digits after the decimal point−10^The number of digits after the decimal point that does not recur)
Here the whole number obtained by writing the digits in order is 1328
The whole number obtained by non-recurring digits in order is 132
The number of digits after the decimal point = 2 (two)
The number of digits after the decimal point that do not recur = 1 (one)
13.288888……. = \(\frac { (1328-132) }{ 10^2 -10^1 } \)
=\(\frac { 1196 }{ 90 } \)
=\(\frac { 598 }{ 45 } \)

See More:  Rational Numbers in Terminating and Non-Terminating Decimals

Solved Examples on Writing Repeating Decimals as Rational Numbers

Example 1.
Convert 0.3333…. to a rational number?
Solution:
Let us assume the recurring decimal as x i.e. x = 0.3333……. (1)
After examining we found the repeating digit is 3
Now let us place the repeating digit on the left side of the decimal point. To do so we need to move the decimal point 1 place to the right. We can do so by multiplying with 10 i.e. 10x =3.3333…..(2)
Subtracting left-hand sides and right-hand sides equations we have
10x-x = 3.3333…..0.333333
9x = 3
x=3/9
Therefore, recurring decimal 0.3333…. converted to a rational number is 3/9

Example 2.
Convert 2.567878….. to a rational number?
Solution:

Let us assume the recurring decimal as x i.e. x = 2.567878……
After examining we found the repeating digit is 78
Now let us place the repeating digit on the left side of the decimal point. To do so we need to move the decimal point 4 place to the right. We can do so by multiplying with 10000 i.e. 10000x =25678.7878…..(1)

Now we need to shift the repeating digits to the left of the decimal point in the original decimal number. To do so we need to multiply the original number by ‘100’.
100x = 256.7878…..(2)
Subtracting left-hand sides and right-hand sides equations we have
10000x-100x = 25678.7878…..-256.7878…..
9900x = 25422
x=25422/9900 = 4237/1650
Therefore, recurring decimal 2.567878….. converted to a rational number is 4237/1650

Mean of Ungrouped Data: Ungrouped data is the type of distribution where individual data is presented in a raw form. The mean of data shows how the data are scattered throughout the central part of the distribution. Hence, the arithmetic numbers are called the measures of central tendencies.

Here, the mean is also known as the arithmetic mean or average of all the observations in the data. In this article, we will be explaining what is the mean of ungrouped data, the formula to find the mean for ungrouped data, steps to calculate mean deviation for raw data, some practice Examples on Mean of Arrayed Data.

Do Check Related Articles:

• Arithmetic Mean
• Properties of Arithmetic Mean
• Word Problems on Arithmetic Mean

Mean of Raw Data or Arrayed Data or Ungrouped Data

In Statistics, Mean is nothing but the measurement of average and it defines the central tendency of a given set of data.

In short, the mean of the given data set is estimated by adding all the observations and then dividing by the total number of observations.

The mean of ungrouped data is denoted by the mathematical symbol or notation ie, \(\overline{x}\)

The mean of the ungrouped data or arrayed data when it is raw can be measured by utilizing the following formula:

The mean of n observations (variables) x₁, x₂, x₃, x₄, ….., x_n is given by the formula:

Mean = (x₁+ x₂ + x₃ + x₄ +…..+ x_{n )} / n = ∑x_i / n

where ∑x_i = x₁+ x₂ + x₃ + x₄ +…..+ x_n

For instance, let’s take the scores of 10 students are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.

Hence, the mean scores of 10 students = ∑x_i / n

= 5+10+15+20+25+30+35+40+45+50 / 10 = 27.5(approx).

Formula for Ungrouped Mean Data

How to Find Assumed Mean of Ungrouped Data?

Want to know more about the assumed mean of ungrouped data? Please have a look at the below stuff and understand the concept of it clearly.

In the method of assumed mean, the values that are taken from the data or not can be used as assumed mean. Yet, it must be centrally positioned in the data so that to determine the mean of the given data via easy calculations.

The formula for the Assumed mean of ungrouped data is A+ sd/N

Where, A is the assumed mean,
sd is the summation of X-A for all figures, and
N is the frequency or the number of elements in the given data.

Apply the formula directly and calculate the assumed mean of the given data with ease and confidence.

Steps to Determine the Mean Deviation for Ungrouped data

The following steps are mainly helpful for all students to calculate the mean for ungrouped data. Simply have a look at them and solve the arithmetic mean of raw data easily.

Let x₁, x₂, x₃, x₄, ….., x_n observations consist in the given set of data.

Step 1: In the first step, we have to find out the mean deviation of the measure of central tendency. Assume that the measure is a.
Step 2: Find the absolute deviation of each variable from the measure of central tendency which is obtained in step 1 ie.,
|x₁ – a|, |x₂ – a|, |x₃ – a|, …., |x_n – a|
Step 3: Estimate the mean of all absolute deviations. At last, it provides the mean absolute deviation (M.A.D) about a for ungrouped data ie.,

If the central tendency measure is mean then the resulted equation can be rewritten as:
Where, \(\overline{x}\) is the mean.

Let’s understand these calculating steps very clearly by practicing with the solved mean of ungrouped data questions with answers.

Mean of Ungrouped Data Example Problems

Example 1:
In the competition of banana eating, the number of bananas consumed by 7 contestants in an hour is as follows: 10, 13, 16, 19, 22, 25, 30. Find the mean deviation from the mean of the given raw data.
Solution:
Given the number of bananas eaten by 7 contestants are 10, 13, 16, 19, 22, 25, 30
Let’s apply the above steps for finding the M.A.D about the mean.
Step 1: The mean of the following data can be given by,
\(\overline{x}\) = \(\frac { 10+13+16+19+22+25+30 }{ 7 } \)
= \(\frac { 135 }{ 7 } \) = 19.2(appox)
Step 2: Now find the absolute deviation around each observation,
|x₁ – \(\overline{x}\)| = |10-19| = 9
|x₂ – \(\overline{x}\)| = |13-19| = 6
|x₃ – \(\overline{x}\)| = |16-19| = 3
|x₄ – \(\overline{x}\)| = |19-19| = 0
|x₅ – \(\overline{x}\)| = |22-19| = 3
|x₆ – \(\overline{x}\)| = |25-19| = 6
|x₇ – \(\overline{x}\)| = |30-19| = 11
Step 3: Finally, calculate the mean deviation for ungrouped data by using the following formula:
M.A.D(x) = ∑ⁿ_i=1|x_i−a| / n
= \(\frac { 9+6+3+0+3+6+11 }{ 7 } \)
= \(\frac { 38 }{ 7 } \) = 5.428

Example 2: 
The mean length of ropes in 20 coils is 12 m. A new coil is added in which the length of the rope is 16 m. What is the mean length of the ropes now?
Solution:
Given that, the mean length of ropes in 20 coils is 12 m. Let’s find the sum of length for each rope using mean formula:
Mean(length) A = x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ / 20
⟹ 12 = x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ / 20
⟹ x₁+ x₂ + x₃ + x₄ +…..+ x_n  = 240 …….(i)
Now, add one coil and find the mean of new coils of rope,
A = x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ + x₂₁ / 21
Here, length of new rope is 16m and use equation (i)
= x₁+ x₂ + x₃ + x₄ +…..+ x₂₀ + x₂₁ / 21
= \(\frac { 240 + 16}{ 21 } \)
= \(\frac { 256 }{ 21 } \)
= 12.19 (Appox)
Hence, the required new mean length is 12.19 m approximately.

Example 3: 
The ages in years of 6 teachers of a school are 32, 28, 54, 40, 65, 20. What is the mean age of these teachers?
Solution:
Mean age of the teachers = \(\frac { Sum of the age of teachers}{ Number of teachers } \)
= \(\frac { (32+28+54+40+65+20) }{ 6 } \)
= \(\frac { 239 }{ 6 } \)
= 39.8 (approx) years.