Prasanna

Diameter, Radius, and Circumference are related to the circle. Let us discuss the relation between diameter radius and circumference of the circle in detail from this page. So, we suggest the students check out the complete article and know the relationship along with the examples. The use of the examples related to the Relation between Diameter Radius and Circumference is that you can know how to solve the problems in different ways using the formulas.

Relation between Diameter Radius and Circumference

The relationship between diameter radius and circumference is that diameter is double the radius and the circumference is slightly more than three times its diameter.
D = 2r
where,
D = diameter of a circle
r = radius of the circle

Formulas on Circle

• Diameter = 2 × radius
• Radius = diameter/2
• Circumference for given radius = πd
• Circumference for given diameter = 2πr

Also, Refer:

• Circumference and Area of Circle
• General Form of the Equation of a Circle

Examples on Relationship between Diameter Radius and Circumference

Example 1.
Find the diameter of a circle whose radius is 2.4 cm?
Solution:
Given that

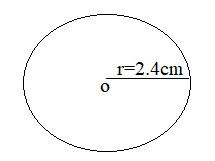
Radius = 2.4 cm
We know that,
Diameter = 2 × radius.
= 2 x 2.4 cm.
4.8 cm.
Therefore, the diameter of the circle = 4.8 cm.

Example 2.
Find the radius of a circle whose diameter is 24 cm.
Solution:
We know that
Radius = Diameter/2

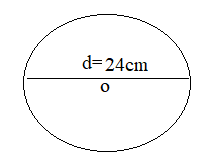
Diameter = 24 cm.
= 24/2 cm.
= 12 cm.
Therefore, the radius of the circle = 12 cm.

Example 3.
What is the circumference of a circle of diameter 20 cm?
Solution:
Given that

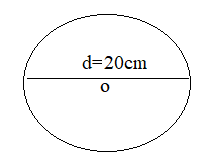
Diameter = 20 cm
We know that
Radius = d/2 = 20/2 = 10
Circumference = 2πr
= 2 × 3.14 × 10
= 62.8
Hence the circumference of the circle is 62.8 cm.

Example 4.
Find the circumference of a circle of radius is 6 cm
Solution:
Given that

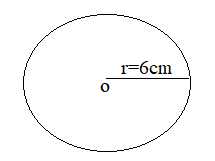
Radius = 6 cm
We know that
Circumference = πd
= 3.14 × 6
= 18.84
Thus the circumference of the circle is 18.84 cm.

Example 5.
What is the circumference of a circle of diameter 34 cm?
Solution:
Given that

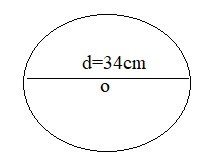
Diameter = 34 cm
We know that
Radius = d/2 = 34/2 = 17
Circumference = 2πr
= 2 × 3.14 × 17
= 106.76
Thus the circumference of the circle is 34 cm.

FAQs on How is Diameter Related to Radius and Circumference

1. How is diameter related to circumference?

The circumference of a circle is related to its diameter. C=πd So, when the circumference C is placed in a ratio with the diameter d.

2. What is the difference between circumference and radius?

The radius of a circle represented by r is the distance from the center of the circle to the outer edge, and the circumference of a circle is the perimeter of the circle that means a measure of the outer round length of the circle.

3. Is a circle a circumference?

In geometry, the circumference is the perimeter of a circle or ellipse.

Are you confused between class, class interval, classmark, and class limits in statistics? Look at this page where we are going to explain complete details about Class Interval Statistics. You can learn what is the definition of the class interval, class interval formula, how to calculate the class interval in frequency distribution along with example problems and solutions.

Do Refer:

• Class Limits
• Class Boundaries

What is Class Interval in Maths?

Class interval refers to the numerical width of any class in a particular distribution. Mathematically, Class Interval is determined as the difference between the upper-class limit and the lower class limit. In statistics, the data is arranged into different classes and the width of such class is known as a class interval.

Class Interval Formula

The formula to calculate the class interval mathematically is as follows:

Class Interval = Upper Class Limit – Lower Class Limit

Let’s see the below example and understand how class intervals can be found with ease.

Class Interval Example: 

Class	0 – 5	5 – 10	10 – 15	15 – 20	20 – 25
Frequency	2	4	0	1	2

Class internal = upper limit − lower limit = 5 − 0 = 5

Similarly, for all classes, 5 – 10, 10 – 15, 15 – 20, 20 – 25.

Class interval = 5 – 10 = 10 – 15 = 15 – 20 = 20 – 25 = 5.

How to find Class Interval in frequency distribution?

A class interval presents the width of each column in a frequency distribution. The following steps help you understand how to calculate class intervals for different frequency distributions:

For instance, let’s consider the following frequency distribution that represents the runs scored by different cricket teams:

Runs	Frequency
20-35	4
35-50	3
50-65	2
65-80	1
80-95	2
95-110	0
110-125	1

Step 1: Firstly, take the class interval formula ie., upper-class limit – lower class limit. Here, the lower class limit and upper-class limit are just the smallest and largest possible values in each class.

Step 2: Now, apply the formula and find the class interval for each class. From the above data, the class interval for the first class is 50 – 35 = 15

Step 3: Here 15 is the size of the class interval of the first class. Repeat step 2 for the remaining classes and calculate the size of the class interval for each class in the frequency distribution.

Hence, for the above example, each class interval has a size of 15.

Solved Examples on Class Interval Statistics

Example 1:
What is the frequency of the class interval 30−40?

Solution:
From the given histogram, the frequency of class interval are as follows:
0−10 is 15
10−20 is 10
20−30 is 20
30−40 is 25
40−50 is 10
50−60 is 5.
Hence, the frequency of the class-interval 20−30 is 25.

Example 2:
If the lower and the upper limits of a class interval are 4 and 10, the class interval is _____
Solution:
The class interval starts from the lower limit and ends at the upper limit.
Hence, Class interval is given by (lower limit − upper limit).
∴ Class-interval for 4 and 10 is 4−10.

Example 3: 
In a frequency distribution with classes (2−9),(10−15),(16−23). What is the class interval?
Solution: 
Class interval = (high − low value +1)
= 9−2+1
= 8.

FAQs on Class Interval

1. What is the size of Class Interval?

The size of the class interval is often selected as 5, 10, 15, or 20, etc.

2. What is Class Interval in grouped data?

The frequency of a class interval in grouped data is the number of data values that come in the range defined by the interval.

3. Define class, class interval, classmark, and class limits in statistics?

In statistics, Class is the subset in which data is grouped, the class interval is the width of that class, classmark is the midpoint of that class, and class limits are upper and lower limits of the class.

Constructing Frequency Distribution Tables: Nowadays, storing and recording data is very important for every firm and sector. A piece of information or any ideas or fact representations is called data. Data collection is maintaining every single piece of information like dates, scores, time, etc. Statistics is defined as the collection, presentation, analysis, organization, and interpretation of observations or data. In order to deal with huge data collection, statistics can be quite helpful.

Statistics and Statistical data collection can be presented in various types like tables, bar graphs, pie charts, histograms, frequency polygons, etc. Here, we are going to discuss data collection through a frequency distribution table and how to draw frequency distribution tables for grouped & ungrouped data with example problems and solutions.

Do Read:

• Frequency Distribution of Ungrouped and Grouped Data
• Class Limits
• Frequency of the Statistical Data
• Class Boundaries

What is Frequency Distribution Table in Statistics?

The general method of representing the organization of raw data of a quantitative variable is the frequency distribution table in statistics. By this table, we can easily find how different values of a variable are distributed and their corresponding frequencies. We can construct two frequency distribution tables in statistics. They are:

(i) Discrete frequency distribution table

(ii) Continuous frequency distribution table

How to Make a Frequency Distribution Table for Grouped Data?

A frequency distribution table can be constructed using tally marks for both discrete and continuous data values. Constructing frequency distribution tables for both discrete and continuous are different from each other.

Here we are learning how to make an ungrouped or raw or discrete frequency distribution table in simple steps along with examples.

For instance, let’s consider the result of a survey from the household on finding out how many bikes they own. The results are 3, 0, 1, 4, 4, 1, 2, 0, 2, 2, 0, 2, 0, 1, 3 now make the table to understand the data easily. Follow the steps carefully and draw a frequency table:

Step 1: Firstly, draw a table with three columns. Now, take the categories in one column (number of bikes):

Number of bikes (x)	Tally	Frequency (f)
0
1
2
3
4

Step 2: In this step, we will use the tally marks approach and tally the numbers in each category. From the above example, the number zero appears four times in the list, so place four tally marks “||||” in the respective row and column.

Number of bikes (x)	Tally	Frequency (f)
0	||||
1	|||
2	||||
3	||
4	||

Step 3: At last, count the tally marks and write down the frequency in the third column. The total tallies is the frequency value placed in the final column. Here, you have four tally marks for 0, thus put 4 in the last column.

Number of bikes (x)	Tally	Frequency (f)
0	||||	4
1	|||	3
2	||||	4
3	||	2
4	||	2

How to Construct a Frequency Distribution Table using Class Limits? (Simple Steps for Ungrouped Data)

Follow the below easy steps to draw a frequency distribution table:

Step 1: Understand how many classes (categories) you require. Follow some of these basic rules about how many classes to select.

• Choose between 5 and 20 classes.
• Ensure that you have a few items in each class. For instance, in case you have 20 items, pick 5 classes (4 items per category), not 20 classes (that would give you only one item per category).

Step 2: Subtract the smallest data value from the highest one and find the range of the statistical data.

Step 3: Now, divide the result get in step 2 by the number of classes you picked in step 1.

Step 4: If you get a decimal result, round the number to the whole number to obtain the class width.

Step 5: Take the least value from the data set.

Step 6: Now, add the class width to step 5 for finding the next lower class limit.

Step 7: Keep on adding your class width to the minimum data values one by one till you create the number of classes you picked in step 1.

Step 8: Note down the upper-class limits. These are the maximum values that can be in the category, thus in such cases, you may subtract 1 from the class width and add that to the least data values.

Step 9: Add a second column for the number of items in each class, and name the column with suited headings.

Step 10: Count the items in each class and place the total in the second column. Thus, the frequency distribution table including classes can be constructed in an easy way.

Check out the detailed explanation of constructing frequency distribution tables using tally marks and classes from the below example problems and solve them on a daily basis for getting a good grip on the concept of how to draw frequency distribution tables.

Steps in Constructing Frequency Distribution Table Example Problems with Solutions PDF

Example 1:
Construct the frequency distribution table for the following runs scored by the 11 players of the Indian cricket team in the match. The scores are 40, 65, 70, 85, 00, 20, 35, 55, 70, 65, 70.
Solution:
The given data is in raw data and this type can represent in the tabular form to understand the data easily and more conveniently.
Thus, the data can be represented in tabular form ie., Frequency Distribution Table (Ungrouped) as follows:

No.of Runs Scored	Tally	Frequency
00	|	1
20	|	1
35	|	1
40	|	1
55	|	1
65	||	2
70	|||	3
85	|	1
		Total: 11

Example 2:
The heights of 45 students, measured to the nearest centimetres, have been found to be as follows:
161, 150, 154, 165, 168, 161, 154, 162, 150, 151, 164, 171, 165, 158, 154, 156, 160, 170, 153, 159, 161, 170, 162, 165, 166, 168, 165, 164, 154, 152, 153, 156, 158, 162, 160, 161, 166, 161, 159, 162, 159, 158, 153, 154, 159.
Explain the data given above by a grouped frequency distribution table, taking the class intervals as 155 – 160, 160 – 165, etc.
Solution:
(i) Let us make the grouped frequency distribution table with classes:
150 – 155, 155 – 160, 160 – 165, 165 – 170, 170 – 175
Class intervals and the corresponding frequencies are tabulated as:

Class intervals	Frequency	Corresponding data values
150 – 155	12	150, 150, 151, 152, 153, 153, 153, 154, 154, 154, 154, 154
155 – 160	9	156, 156, 158, 158, 158, 159, 159, 159, 159
160 – 165	13	160, 160, 161, 161, 161, 161, 161, 162, 162, 162, 162, 164, 164
165 – 170	8	165, 165, 165, 165, 166, 166, 168, 168
170 – 175	3	170, 170, 171
Total	45

Example 3:
Lasya and Tara have a set of playing cards with numbers from 1 to 10. They pick a random card and record the number that comes up. They remain the same process at least 10 times. They get the values like 4, 8, 4, 2, 3, 7, 3, 4, 5, 9. Draw a frequency table to organize the data conveniently.
Solution:
Given values are is 4, 8, 4, 2, 3, 7, 3, 4, 5, 9 out of 1 to 10.
Now, construct the frequency table for ungrouped data:

Values	Frequency
1	0
2	1
3	2
4	3
5	1
6	0
7	1
8	1
9	1
10	0
Total	10

In our earlier articles, we have discussed what is compound interest. Here in this article, we will let you know the formulae for the calculation of compound interest. For your knowledge, we have outlined the various formulae involved in finding the Compound Interest. Also, go through the solved examples on the calculation of compound interest and the amount payable at the principal sum.

Compound Interest Formulas

Below is the list of Compound Interest Formula for different cases. Use them as and when you need them and make the most out of them. They are along the lines

Let us consider the principal sum as ‘P’ i.e. amount taken as loan.
R is the rate of interest for which the principal amount is lent.
T is the Time Duration in which you need to repay the amount.
A is the amount to be paid.

• Formula for Compound Interest Yearly Formula A = P(1+R/100)^T
• Formula for Compound Interest Half-Yearly A = P(1+(R/2)/100)^2T
• Formula for Compound Interest Quarterly A = P(1+(R/4)/100)^4T
• Formula for Compound Interest with Monthly Contributions A = P(1+(R/12)/100)^12T
• When Time is in Fraction A = P(1+R/100)²(1+(R/5)/100)
• If the rate of interest in 1st year, 2nd year, 3rd year,…, nth year are R₁%, R₂%, R₃%,…, R_n% respectively then A = P(1+R₁/100)(1+R₂/100)(1+R₃/100)…(1+R_n/100)
• Present Worth of Rs. X due n years is given by the formula Present Worth = \(\)\frac{1}{1+R/100}[\latex]

Since we are aware of the logic interest is the difference between Amount and Principal i.e. Interest = Amount – Principal

See More:

• Introduction to Compound Interest
• Compound Interest as Repeated Simple Interest

Solved Examples on Compound Interest

Example 1.
A man borrowed $30,000 from a bank at the interest of 5% p.a. compounded annually for 2 years. Calculate the compound amount and interest?
Solution:
Given Interest rate = 5%
Principal amount = $30,000
Time = 2 years
Total interest = ?
Amount = ?
We know that A = P(1+R/100)^T
So, A = 30,000(1+5/100)³
= 30,000(1+0.05)³
= $34728.75
Interest = $34728.75 – $30,000
= $4728.75

Example 2.
If the interest rates for 1st, 2nd, and 3rd are 4%, 8%, and 12% respectively on a sum of $10,000. Then calculate the amount after 3 years?
Solution:
R₁ = 4%
R₂ = 8%
R₃ = 12%
P = $10,000
We know the formula to calculate Amount A = P(1+R₁/100)(1+R₂/100)(1+R₃/100)…(1+R_n/100)
Substituting the input values in the above formula we have
A = $10,000(1+4/100)(1+8/100)(1+12/100)
=$10,000(1+0.04)(1+0.08)(1+0.12)
=$10,000(1.04)(1.08)(1.12)
=$12579.84

Example 3.
Find the compound interest on the amount of $1,00,000 invested at 4% per annum, compounded quarterly for 3 years?
Solution:
Given Interest rate = 4%
Principal amount = $1,00,000
Time = 3 years
Total interest =?
Amount = ?
We know that A = P(1+(R/4)/100)^4T
So, A = $1,00,000(1+(4/4)/100)⁴
= $1,00,000(1+0.01)⁴
= $104060.401
Interest = $104060.401 – $1,00,000
= $4060.401

Example 4.
Find the compound amount of $25,000 if the interest rate is 7% per annum compounded monthly for 2 years. Also, calculate the compound interest?
Solution:
Given Interest rate = 7%
Principal amount = $25,000
Time = 2 years
Total interest =?
Amount = ?
We know that A = P(1+(R/12)/100)^12T
So, A = $25,000(1+(7/12)/100)^12.2
= $25,000(1+0.005833333)²⁴
= $28,745.15
Interest = $28,745.15 – $25,000
= $3745.15

Do you want to calculate Compound Interest? If so, this article is the best place for you to guide you on the concept of Compound Interest as Repeated Simple Interest. We will explain to you everything on how to calculate compound interest as repeated simple interest without using a formula. Check out the Worked-out Examples on Method of Repeated Simple Interest Computation with a Growing Principal and master the concept.

How to Calculate Compound Interest as Repeated Simple Interest?

If you take money under compound interest, the interest earned at the end of the set period is not paid to the moneylender however it is added to the amount lent. Therefore, the sum earned becomes the next period’s principal. The Process is repeated till you determine the latest period’s amount.

Compound Interest is nothing ut the difference between the final amount and the original principal.

Compound Interest = Final Amount – Original Principal

To better understand this concept, let us see a few solved examples and the method of Repeated Simple Interest Computation with a Growing Principal.

See More:

• Introduction to Compound Interest
• To find Rate When Principal Interest and Time are given
• To find Time Principal Interest and Rate are given

Solved Examples on Compound Interest as a Repeated Simple Interest Computation with a Growing Principal

Example 1.
Find the compound interest on $15000 for 2 years at the rate of interest 8% per annum?
Solution:
Interest for the 1st year = \(\frac{15000*1*8}{100}\)
=\(\frac{120000}{100}\)
=$1200
Amount at the end of 1st year= Interest + Amount
=$1200+$15000
=$16200
Interest for 2nd Year = \(\frac{16200*1*8}{100}\)
=$1296
Amount at the end of 2nd Year = Interest + Amount
=  $1296+$16200
= $17496
Therefore, Compound Interest = A – P
=$17496 – $15000
= $2496

Example 2.
Find the compound interest on $45000 for 3 years at the rate of interest of 3% per annum?
Solution:
Interest for the 1st year = \(\frac{45000*1*3}{100}\)
=\(\frac{135000}{100}\)
=$1350
Amount at the end of 1st year= Interest + Amount
=$1350+$45000
=$46350
Interest for 2nd Year = \(\frac{46350*1*3}{100}\)
=$1390.50
Amount at the end of 2nd Year = Interest + Amount
=  $1390.5+$46350
= $47740.5
Interest for 3rd Year = \(\frac{47740.5*1*3}{100}\)
=$1432.215
Amount at the end of 3rd year = Interest + Amount
= $1432.215+$47740.5
=$49172.715
Therefore, Compound Interest = A – P
=$49172.715 – $45000
= $4172.715

Example 3.
Calculate the amount and compound interest on $20000 for 1 year at 5% p.a?
Solution:
Interest for 1st Year = \(\frac{20000*1*5}{100}\)
=$1000
Amount at the end of 1st year = Interest + Amount
=$1000+$20000
= $21000
Therefore, Amount and Compound Interest after 1 Year are $21000 and $1000

Example 4.
Calculate the amount on ₹6000 in 2 years and at 5% compounded annually?
Solution:
Interest at the end of 1st Year = \(\frac{6000*1*5}{100}\)
=₹300
Amount at the end of 1st Year = Interest+Amount
= ₹300+₹6000
=₹6300
Interest at the end of 2nd Year = \(\frac{6300*1*5}{100}\)
=₹315
Amount at the end of 2nd Year = Interest+Amount
=₹315+₹6300
=₹6615
Therefore, amount is ₹6615.

 

Before diving into the topic of Compound Interest let us explain what actually is interest first. For example, you visit a bank and get a loan the amount you bought as a loan is principal. Bank charges a certain percent on this principal amount and it is known as interest. Interest is classified into 2 types namely Simple Interest and Compound Interest.

In this article, we will introduce you to the topic of Compound Interest, Formulas Associated with Compound Interest for different compounding intervals. Along with these concepts, you will learn about Compounding Frequency.

What is meant by Compound Interest?

Compound Interest is the interest calculated on any principal amount borrowed and any previous interest. It is also referred to as interest on interest. The majority of the Banking & Finance Sectors use Compound Interest in their transactions.

Compound Interest Formulae

• Compound Interest Yearly Formula A = P(1+R/100)^T
• When Interest iS Compounded Half-Yearly A = P(1+(R/2)/100)^2T
• When Interest is Compounded Quarterly A = P(1+(R/4)/100)^4T
• When Time is in Fraction A = P(1+R/100)²(1+(R/5)/100)
• If the rate of interest in 1st year, 2nd year, 3rd year,…, nth year are R₁%, R₂%, R₃%,…, R_n% respectively then A = P(1+R₁/100)(1+R₂/100)(1+R₃/100)…(1+R_n/100)

Above Listed Formulae are enough to know the amount to be repaid in case of compound interest.
We know Amount = Principal + Interest
Interest = Amount – Principal

Also, See:

• What is Simple Interest
• To find Rate When Principal Interest and Time are given
• To find Time Principal Interest and Rate are given

Compounding Frequency

Compounding Frequency is the no. of times the accumulated interest is paid on a regular basis. The frequency can be on a yearly, half-yearly, quarterly, weekly, or daily basis till the loan is paid in addition to the interest.

Have a glance at the example listed below to get a clear idea of the concept of compound interest.

Example. A rate of 15% is charged on a principal sum of $20,000. The time given to repay the amount is 3 years. If the interest is compounded annually, then calculate the amount to be repaid and interest charged in three years.

Interest rate = 15%
Principal amount = $20,000
Time = 3 years
Total interest = ?
Amount = ?
We know that A = P(1+R/100)^T
So, A = 20,000(1+15/100)³
= 20,000(1+0.15)³
= $30417.5
Interest = Amount – Principal
= $30,417.5 – $20,000
= $10,417.5

In Mathematics, Frequency is the number that reveals how often a specific item occurs in the data set. For example, two kids like the black color then the frequency is two. But making frequency for the large datasets is not possible sometimes so frequency distribution comes in the frame and helps everyone to solve the huge dataset problems. Learn more about Frequency Distribution its definition, formula, types, table, examples from this page and excel in solving all types of questions in exams.

Do Refer:

• Frequency Distribution of Ungrouped and Grouped Data
• Class Limits
• Frequency of the Statistical Data
• Class Boundaries

What is Frequency Distribution in Statistics?

The representation of data that shows the number of observations that occurred within the given interval is called frequency distribution in statistics. It can be represented in graphical or tabular form for easy understanding to kids. Especially, Frequency distributions help in summarizing large data sets and allocating probabilities.

A few data examples are test scores of students, points scored in a basketball match, temperatures of various towns, etc.

For Example: Let’s consider the following scores of 10 students in the Math MCQ exam: 10, 15, 20, 15, 17, 19, 12, 10, 20, 15. Let’s represent this data in frequency distribution and calculate the number of students who scored the same marks.

Math MCQ Exam Scores	No.of Students
10 12 15 17 19 20	2 1 3 1 1 2

Now, you can see the organized data under two columns ie., MCQ Exam Scores and No.of students. By this, students can easily understand the given data and find out the number of students who obtained the same marks. Hence, frequency distribution in statistics aids everyone to arrange the data in an easy manner to grasp its benefits in one look.

Frequency Distribution Formula

Whenever multiple classes are included in the given data, finding the distribution for ungrouped data will be tough. In such instances, the number of classes can be calculated by using the following frequency distribution formula:

C (no. of classes) = 1 + 3.3 log_n where(log is base 10) or alternatively the square root of frequency distribution formula is written as:

C = √n, where n is the total no. of observations of the data that has been distributed.

Types of Frequency Distribution

We can see four different frequency distribution types in statistics and they are illustrated below:

1. Relative frequency distribution: It represents the proportion of the total number of observations connected with each category.

2. Cumulative frequency distribution: The sum of all frequencies in the frequency distribution is called cumulative frequency distribution. The total sum of all frequencies is the last cumulative frequency.

3. Classified or Grouped frequency distribution: The data is organized or separated into groups called class intervals. Then, the frequency of data of each class interval is calculated and put down in a frequency distribution table. The grouped frequency table shows the distribution of frequencies in class intervals.

For Example: 

Marks Obtained 4 20 30 39 40 45 49 50 65 70 79 80 90 Total

Number of Students 3 7 7 1 3 5 1 9 2 5 1 2 4 50

4. Unclassified or Ungrouped frequency distribution: Representing the frequency of data in each separated data value instead of data value groups is called ungrouped frequency distribution. Look at the below example table to understand it better.

For Example: 

Marks Obtained From 0 to under 20 From 20 to under 40 From 40 to under 60 From 60 to under 80 From 80 to under 100

Number of Students 3 15 (i.e., 7 + 7 + 1) 18 (i.e., 3 + 5 + 1 + 9) 8 (i.e., 2 + 1) 6 (i.e., 2 + 4)

How to Calculate Frequency Distribution in Statistics?

By following some simple steps, we can easily find the frequency distribution in statistics:

1. At first, we have to read the given data properly then make a frequency chart.
2. Initially, take the categories in the first column.
3. Next, use the tally marks in the second column.
4. Later, count the tally to note down the frequency of each category in the third column.
5. Finally, we can find the frequency distribution of the given data set.

Frequency Distribution Table

It is a chart that displays the frequency of each item in a data set. To understand it in a better way, let’s take an instance and grasp how to create a frequency distribution table using tally marks.

Example: A Glass bowl contains various colors of beads ie., red, green, blue, black, red, green, blue, yellow, red, red, green, green, green, yellow, red, green, yellow. To find the exact number of beads of each color, we use the frequency distribution table.

Solution: 

Firstly, we have to classify the beads into categories. Then, we go for the easiest method of finding the number of beads of each color ie., using tally marks. Now, take the beads one after one and enter the tally marks in the particular row and column. Finally, note down the frequency for each item in the table as shown below:

Hence, the obtained table is called a Frequency Distribution Table.

Frequency Distribution Example Problems with Solutions

Example 1:
A blood donation camp is conducted by the school and 30 students’ blood groups were recorded as A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O. Represent this data in the form of a frequency distribution table?
Solution: 
The given data can be shown in a frequency distribution table as follow:

Blood Group	Number of students
A	9
B	6
AB	3
O	12
Total	30

Example 2:
Let’s consider a car survey where people were asked how many cars were registered to their households in each of 15 homes. The outcomes were like this 1, 3, 5, 2, 3, 0, 4, 2, 5, 1, 3, 2, 6, 3, 3. Now, find the maximum number of cars registered by household and also represent this data in Frequency Distribution Table.
Solution:
Firstly, arrange the data along with their frequencies in the frequency distribution table.
Divide the number of cars (x) into intervals, and then count the number of results in each interval (frequency).

Number of Cars	Frequency
0	1
1	2
2	3
3	4
4	1
5	2
6	1
Total	15

Thus, from the above frequency distribution table, it is clear that the 4 household has 3 cars.

We come across compound interest in our day-to-day lives. To know about the calculation of compound interest and how does compound interest works is much essential. To help you with this we have given this article covering everything on What is meant by Compound Interest, Formula for Compound Interest, How to Calculate Compound Interest for various periods of intervals such as monthly, quarterly, half-yearly, yearly, etc. Go through the solved examples on calculating compound interest in our real-life examples and learn how to solve similar kinds of problems.

List of Compound Interest Topics

• Introduction to Compound Interest
• Compound Interest as Repeated Simple Interest
• Formulae for Compound Interest
• Comparison between Simple Interest and Compound Interest
• Worksheet on Compound Interest as Repeated Simple Interest
• Worksheet on Use of Formula for Compound Interest

What is Compound Interest?

Compound Interest is the interest calculated on both principal and interest for regular intervals. For regular intervals, interest obtained is summed with the principal to get the new principal. Usually, we calculate the compound interest for regular intervals like monthly, quarterly, half-yearly, yearly, etc. The majority of the Banks and Financial Organizations calculate their interest on basis of compound interest only.

Compound Interest Formula

The Formula for finding the Compound Interest is given by Compound Interest = Amount- Principal
The amount is given by formula A = (1+r/n)^nt
Where A = Amount
P = Principal
r = rate of interest
n = number of times interest is compounded per year
t = time (in years)
Alternatively, we can write the formula as given below:
CI = A – P
and
\(CI=P\left ( 1+\frac{r}{n} \right )^{nt}-P\)

Also, See:

• What is Simple Interest
• To find Rate When Principal Interest and Time are given
• To find Time Principal Interest and Rate are given

Compound Interest Formula for Different Time Periods

Compound Interest can be found for different intervals using different formulas. The formulas are listed below for your reference

CI Formula – Half Yearly

In the case of calculating compound interest half-yearly we find interest for every 6 months and the amount is compounded twice a year.
Here the rate of interest r is divided by 2 and the time period is doubled.
The formula to calculate the amount when the principal is compounded half-yearly is given by

CI = P(1+\(\frac{r/2}{100}\))^2t – P A= P(1+\(\frac{r/2}{100}\))^2t

CI Formula – Quarterly

In the case of time period calculation on a quarterly basis, we find interest for every 3 months, and the amount is compounded 4 times a year. Compound Interest Formula when Principal is compounded quarterly is

CI = P(1+\(\frac{r/4}{100}\))^4t – P A= P(1+\(\frac{r/4}{100}\))^4t

Monthly Compound Interest Formula

The monthly Compound Interest Formula is the interest calculated for every month i.e n = 12. Monthly Compound Interest can be found using the formula CI = P (1 + r/12)^12t – P

Daily Compound Interest Formula

When the amount compounds daily, it means that the amount compounds 365 times in a year. i.e., n = 365. The daily compound interest formula is expressed as:
CI = P (1 + r/365)^365t – P

Compound Interest Derivation

In order to derive the formula for the compound interest, we use the simplest interest formula. We know the simple interest calculated for 1 year is the same as compound interest calculated for 1 year.
Let, Principal amount = \(P\), Time = \(n\) years, Rate = \(R\)
Simple Interest (SI) for the first year:
\(SI_1\) = \(\frac{P~×~R~×~T}{100}\)
Amount after first year = \(P~+~SI_1\)
= \(P ~+~ \frac{P~×~R~×~T}{100}\)
= \(P \left(1+ \frac{R}{100}\right)\) = \(P_2\)
Simple Interest (SI) for second year:
\(SI_2\) = \(\frac{P_2~×~R~×~T}{100}\)
Amount after second year = \(P_2~+~SI_2\)
= \(P_2 ~+~ \frac{P_2~×~R~×~T}{100}\)
= \(P_2\left(1~+~\frac{R}{100}\right)\)
= \(P\left(1~+~\frac{R}{100}\right) \left(1~+~\frac{R}{100}\right)\)
= \(P \left(1~+~\frac{R}{100}\right)^2\)
Similarly, if we proceed further to \(n\) years, we can deduce:
\(A\) = \(P\left(1~+~\frac{R}{100}\right)^n\)
\(CI\) = \(A~–~P\) = \(P \left[\left(1~+~ \frac{R}{100}\right)^n~ –~ 1\right]\)

Compound Interest Examples

Example 1.
Nazma lends $3000 to Hemanth at an interest rate of 5% per annum, compounded half-yearly for a period of 1 year. Can you help her find out how much amount she gets after a period of 1 year from Hemanth?
Solution:
Given Data Principal P = $3000
Rate of Interest r = 5%
Time Period = 1 Year
We know the formula to find Compound Interest Half-Yearly CI = P(1+\(\frac{r/2}{100}\))^2t – P
Substituting the known values we have
CI =3000(1+\(\frac{5/2}{100}\))^2.1 – 3000
CI = 3151.88-3000
CI = $151.88
Therefore, Compound Interest earned for the given data is $151.88

Example 2.
The price of a radio is Rs. 1500 and it depreciates by 4% per month. Find its value after 6 months?
Solution:
Given Data Price of Radio = Rs.1500
Rate of Depreciation = 4%
Time Interval = 6 months
We know the formula of Depreciation A = P(1 – R/100)ⁿ.
Thus, the price of the radio after 6 months = 1500(1 – 4/100)⁶
= 1500(1 – 0.04)³ = 1500(0.96)³ = Rs. 1327 (Approx.)

Example 3.
A town had 20,000 residents in 2005. Its population declines at a rate of 10% per annum. What will be its total population in 2010?
Solution:
Population in a Town decreases by 10% every year
Depreciation Formula is given by  A = P(1 – R/100)ⁿ
Substituting the known data and calculating the population by the end of 5 years we have 20000(1 – 10/100)⁵
= 20000(1-0.1)⁵
= 20000(0.9)⁵
= 11809 Approximately
Therefore, the total population in 2010 is around 11809 residents.

FAQs on Compound Interest

1. What is the formula for calculating Compound Interest?
Compound Interest can be calculate using the formula CI = A – P Where A = P(1 + r/n)^{nt}P

2. What is meant by Compound Interest?

Compound Interest is the interest calculated on both principal and interest for regular intervals.

3. What is Monthly Compound Interest Formula?

Monthly Compound Interest is given by the Formula CI = P (1 + r/12)^12t – P

Are you wondering how to find and practice problems on the median of raw data? This is the right page for you all as it is holding with the Worksheet on Median of Ungrouped Data. Make use of this statistics median of discrete data worksheet pdf and solve all types of questions with flexibility. Also, you can bridge all your weak areas by answering the questions involved in the worksheet of the median of ungrouped data. Try to memorize all median formulas & tricks from our median of ungrouped data activity sheet pdf and solve the questions effortlessly.

Do Refer:

• Median of Raw Data
• Problems on Median of Ungrouped Data

Activity for Median of Ungrouped Data PDF

Example 1:
The weight of 5 ice bars in grams is 141, 152, 135, 117, 120. Find the median.

Solution:

Given data is 141, 152, 135, 117, 120
Arrange the data in ascending order: 117, 120, 135, 141, 152
The number of observations is 5, which is odd
Median = Middle Number or n+2/2
= 5+1/2
= 6/2
= 3rd observation
= 135
Hence, the median of the weight of 5 ice bars in grams is 135.

---

Example 2:
Find the median of the first 5 prime numbers.

Solution:

The first five prime numbers are 2, 3, 5, 7, 11. It is in an ordered form.
Next, find the number of observations ie., 5 which is odd.
Therefore, the middle value 5 is the median of the first five prime numbers.

---

Example 3:
Find the median of the following:
(i) The first eight even natural numbers
(ii) 8, 0, 2, 4, 3, 4, 6

Solution:

(i) The first eight even natural numbers are 2,4,6,8,10,12,14,16
The total number of observations = 8, which is even.
Therefore, the median is the mean of the 4th and 5th observations, ie.,
Median = Mean {4th + 5th variant}
= 1/2{8 + 10}
= 18/2
= 9
(ii) Given data is 8, 0, 2, 4, 3, 4, 6
Sort them in ordered form (ascending order): 0, 2, 3, 4, 4, 6, 8
Total number of observations = 7, which is odd
Hence median is the middle value( 4th variant) ie., 4.

---

Example 4:
Find the median of 21, 15, 6, 25, 18, 13, 20, 9, 16, 8, 22

Solution:

Given data is 21, 15, 6, 25, 18, 13, 20, 9, 16, 8, 22
First sort the given raw data in ascending order: 6,8,9,13,15,16,18,20,21,22,25
The total number of variants (n) = 11, which is odd.
Hence, median = value of 1/2(n+1)th observation.
= 1/2(11+1)th
= 1/2(12)th
= 6th observation
Therefore, the value of 6th observation is 16.
Hence, the median is 16.

---

Example 5:
Find the median of the following data.
Variates: 10, 11, 12, 13, 14
Frequency: 1, 2, 3, 4, 5

Solution:

First, arrange the variates in ascending order, we get
10, 11, 11, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14, 14
The number of variates = 15, which is odd.
Hence, Median = n+1/2th variate
= 15+1/2th
= 16/2th
= 8th variate
= 13.

---

Example 6:
The marks obtained by 10 students in a class test are given below.

Marks Obtained	Number of Students
10 7 9 5	4 3 2 1

Calculate the median of marks obtained by the students?

Solution:

Given 10, 10, 10, 10, 7, 7, 7, 9, 9, 5
Sorting the variates in ascending order, we get
5, 7, 7, 7, 9, 9, 10, 10, 10, 10
The number of variates = 10, which is even.
Hence, median = mean of 10/2th and (10/2+1)th variate
= mean of 5th and 6th variate
= mean of 9 and 9
= 9+9/2
= 18/2
= 9.

---

Example 7:
Find the median of the first four odd integers. If the fifth odd integer is also included, find the difference of medians in the two cases.

Solution:

Take the first four odd integers in ascending order, we get
1, 3, 5, 7.
The number of variates = 4, which is even.
Hence, median = mean of 2nd and 3rd variate
= 1/2 (3+5)
= 8/2
= 4
When the fifth integer is included, we have (in ascending order)
1, 3, 5, 7, 9
Now, the number of variates = 5, which is odd.
Therefore, median = 5+1/2th
= 6/2th
= 3rd variate
= 5
Hence, the difference of medians in the two cases = 4 – 5 = -1.

---

If you ever feel representing rational numbers on the number line is difficult you will no longer feel the same with our Worksheet on Representation of Rational Numbers on the Number Line. Use the Plotting Rational Numbers on Number Line Worksheet during your practice sessions and learn how to plot rational numbers on number lines.

Questions covered in the Representing Rational Numbers on Number Line include plotting positive, negative rational numbers on the number line. Learn the tips and tricks for representing rational numbers on the number line using our Representing Rational Numbers on the Number Line Worksheets PDF.

See More:

• Representation of Rational Numbers on Number Line
• Problems on Rational numbers as Decimal Numbers
• Problems Based on Recurring Decimals as Rational Numbers

Plotting Rational Numbers on a Number Line Worksheet Answers

Example 1.
Draw the number line and represent the rational 4/5 on the number line?

Solution:

Given Rational Numbers is 4/5
Since the given number is a proper fraction it lies next to 0 on the right side. Split the number line between 0 and 1 into 5 equal parts and the fourth part is the required fraction.

---

Example 2.
Plot the Mixed Number 4 3/4 on the Number Line?

Solution:

Given Mixed Number is 4 3/4
Mixed Fraction 4 3/4 lies between 4 and 5. Split the number line between 4 and 5 into 4 equal parts and the third part of the division is the required fraction.

---

Example 3.
Represent -3/8 on the Number Line?

Solution:

Given Fraction is -3/8
Since it is a negative fraction it lies on the left side of the number line i.e. 0 and -1. Split the number line between 0 and -1 into 8 equal parts. The third part of the division process is the required fraction.

---

Example 4.
Which of the following statements is true or false?

(i) -4/5 lies to the left of 0 on the number line.
(ii) The rational number 21/18 lies to the left of 0 on the number line.
(iii) -13/4 lies to the right of 0 on the number line.

Solution:

(i) -4/5 lies to the left of 0 on the number line.
Since it is a negative number it lies on the left side of the number line. Thus, the given statement is true.
(ii) The rational number 21/18 lies to the left of 0 on the number line.
Given rational number is 21/18. Since it is a positive rational number it lies to the right side of the number line. Thus, the given statement is false.
(iii) -13/4 lies to the right of 0 on the number line.
Given Rational Number is -13/4. Since it is a negative rational number it lies on the left side of the number line. Thus, the given statement is false.

---

Example 5.
Between which two numbers does the Rational Number -12/3 lie?

Solution:

Firstly, change the given improper fraction to a mixed fraction
-12/3 = -3 3/3
Thus, the improper fraction -12/3 lies between -3 and -4.

---

Example 6.
Between which two numbers does the Rational Number 8/5 lie?

Solution:

Firstly, convert the given improper fraction 8/5 to mixed fraction
8/5 = 1 3/5
Therefore, the mixed fraction 8/5 lies between 1 and 2.

---

Example 7.
Plot the Mixed Fraction -1 5/8 on the Number Line?

Solution:

Given Mixed Fraction -1 5/8
Since it is a negative rational number we will place it on the left side of the number line.

---