Tag: Eureka Math Algebra 1 Module 1

Engage NY Eureka Math Algebra 1 Module 1 Lesson 5 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 5 Example Answer Key

Example 1.
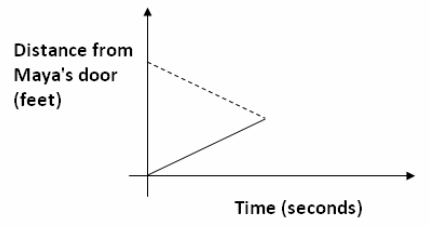
Consider the story:
Maya and Earl live at opposite ends of the hallway in their apartment building. Their doors are 50 ft. apart. Each starts at his or her own door and walks at a steady pace toward each other and stops when they meet.
What would their graphing stories look like if we put them on the same graph? When the two people meet in the hallway, what would be happening on the graph? Sketch a graph that shows their distance from Maya’s door.

Eureka Math Algebra 1 Module 1 Lesson 5 Exercise Answer Key

Exploratory Challenge/Exercises 1–4
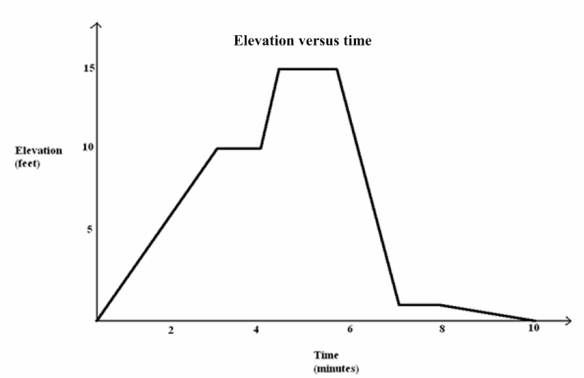
Watch the following graphing story.
http://youtu.be/X956EvmCevI
The video shows a man and a girl walking on the same stairway.

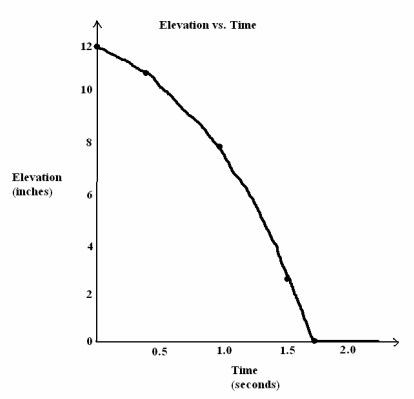
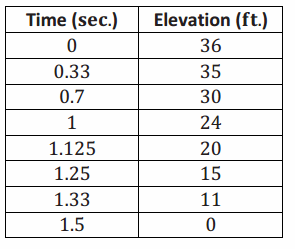
Exercise 1.
Graph the man’s elevation on the stairway versus time in seconds.
Answer:

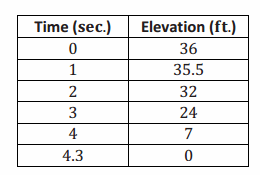
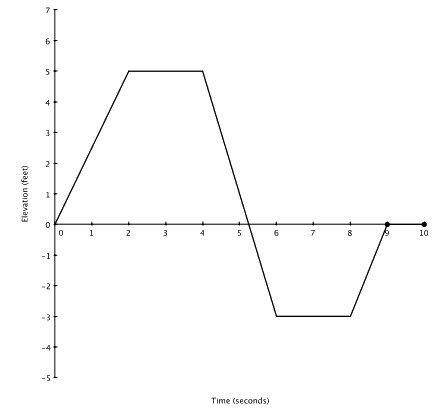
Exercise 2.
Add the girl’s elevation to the same graph. How did you account for the fact that the two people did not start at the same time?
Answer:
Students’ answers should look something like the graph to the right. Student work should also include scales.

Exercise 3.
Suppose the two graphs intersect at the point P(24,4). What is the meaning of this point in this situation?
Answer:
Many students will respond that P is where the two people pass each other on the stairway.

Lead a discussion that highlights these more subtle points before proceeding.
→ We have two elevation-versus-time graphs, one for each of the two people (and that time is being measured in the same way for both people).
→ The point P lies on the elevation-versus-time graph for the first person, and it also lies on the elevation-versus-time graph for the second person.
→ We know the coordinates of the point P. These coordinates mean that since the first person is at an elevation of 4 ft. at 24 sec., the second person is also at an elevation of 4 ft. at 24 sec.

Exercise 4.
Is it possible for two people, walking in stairwells, to produce the same graphs you have been using and not pass each other at time 12 sec.? Explain your reasoning.
Answer:
Yes, they could be walking in separate stairwells. They would still have the same elevation of 4 ft. at time 24 sec. but in different locations.

Give students time to revise their work after discussing this with the entire class.

Example 2/Exercises 5–7 (10 minutes)
Exercise 6 has a similar scenario to Example 1. After students work this exercise in small groups, have each group share their results as time permits. Circulate around the classroom providing assistance to groups as needed. Use the results of the exercises in Example 2 to close this session.

Example 2/Exercises 5–7
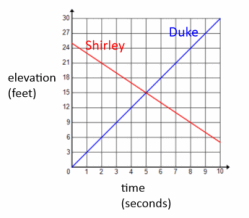
Consider the story:
Duke starts at the base of a ramp and walks up it at a constant rate. His elevation increases by 3 ft. every second. Just as Duke starts walking up the ramp, Shirley starts at the top of the same 25 ft. high ramp and begins walking down the ramp at a constant rate. Her elevation decreases 2 ft. every second.

Exercise 5.
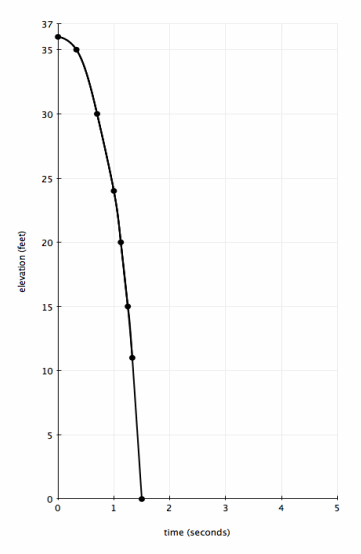
Sketch two graphs on the same set of elevation-versus-time axes to represent Duke’s and Shirley’s motions.
Answer:

Exercise 6.
What are the coordinates of the point of intersection of the two graphs? At what time do Duke and Shirley pass each other?
Answer:
(5,15)
t=5

Exercise 7.
Write down the equation of the line that represents Duke’s motion as he moves up the ramp and the equation of the line that represents Shirley’s motion as she moves down the ramp. Show that the coordinates of the point you found in the question above satisfy both equations.
Answer:
If y represents elevation in feet and t represents time in seconds, then Duke’s elevation is represented by y=3t and Shirley’s elevation is represented by y=25-2t. The lines intersect at (5,15), and this point does indeed lie on both lines.
Duke: 15=3(5) Shirley: 15=25-2(5)

Eureka Math Algebra 1 Module 1 Lesson 5 Problem Set Answer Key

Question 1.
Reread the story about Maya and Earl from Example 1. Suppose that Maya walks at a constant rate of 3 ft. every second and Earl walks at a constant rate of 4 ft. every second starting from 50 ft. away. Create equations for each person’s distance from Maya’s door and determine exactly when they meet in the hallway. How far are they from Maya’s door at this time?
Answer:
Maya’s Equation: y=3t
Earl’s Equation: y=50-4t
Solving the equation 3t=50-4t gives the solution =7 \(\frac{1}{7}\). The two meet at exactly this time at a distance of 3(7 \(\frac{1}{7}\))=21\(\frac{3}{7}\) ft. from Maya’s door.

Question 2.
Consider the story:
May, June, and July were running at the track. May started first and ran at a steady pace of 1 mi. every 11 min. June started 5 min. later than May and ran at a steady pace of 1 mi. every 9 min. July started 2 min. after June and ran at a steady pace, running the first lap (\(\frac{1}{4}\) mi.) in 1.5 min. She maintained this steady pace for 3 more laps and then slowed down to 1 lap every 3 min.
a. Sketch May, June, and July’s distance-versus-time graphs on a coordinate plane.
Answer:

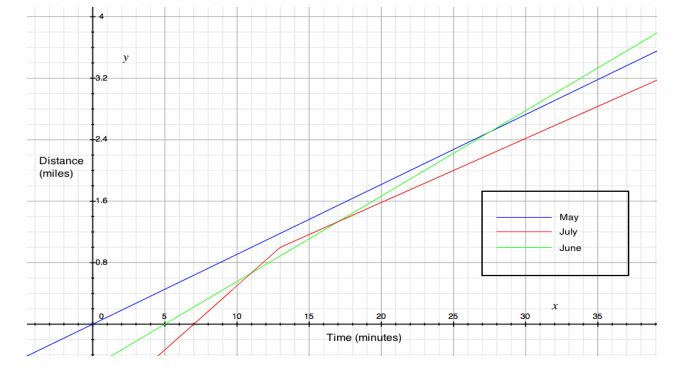
b. Create linear equations that represent each girl’s mileage in terms of time in minutes. You will need two equations for July since her pace changes after 4 laps (1 mi.).
Answer:
Equations for May, June, and July are shown below. Notice that July has two equations since her speed changes after her first mile, which occurs 13 min. after May starts running.
May: d=\(\frac{1}{11}\) t
June: d=\(\frac{1}{9}\)(t-5)
July: d=\(\frac{1}{6}\) (t-7)”,” t≤13 “and” d=\(\frac{1}{12}\) (t-13)+1″,” t>13

c. Who was the first person to run 3 mi.?
Answer:
June at time 32 min.

d. Did June and July pass May on the track? If they did, when and at what mileage?
Answer:
Assuming that they started at the same place, June passes May at time 27.5 min. at the 2.5 mi. marker. July does not pass May.

e. Did July pass June on the track? If she did, when and at what mileage?
Answer:
July passes June at time 11 min. at the \(\frac{2}{3}\) mi. marker.

Question 3.
Suppose two cars are travelling north along a road. Car 1 travels at a constant speed of 50 mph for two hours, then speeds up and drives at a constant speed of 100 mph for the next hour. The car breaks down and the driver has to stop and work on it for two hours. When he gets it running again, he continues driving recklessly at a constant speed of 100 mph. Car 2 starts at the same time that Car 1 starts, but Car 2 starts 100 mi. farther north than Car 1 and travels at a constant speed of 25 mph throughout the trip.
a. Sketch the distance-versus-time graphs for Car 1 and Car 2 on a coordinate plane. Start with time 0 and measure time in hours.
Answer:
A graph is shown below that approximates the two cars traveling north.

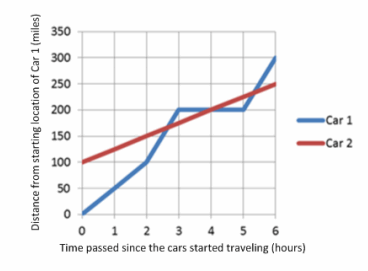
b. Approximately when do the cars pass each other?
Answer:
The cars pass after about 2 \(\frac{1}{2}\) hr., after 4 hr., and after about 5 \(\frac{1}{2}\) hr.

c. Tell the entire story of the graph from the point of view of Car 2. (What does the driver of Car 2 see along the way and when?)
Answer;
The driver of Car 2 is carefully driving along at 25 mph, and he sees Car 1 pass him at 100 mph after about 2 \(\frac{1}{2}\) hr. About 1 \(\frac{1}{2}\) hr. later, he sees Car 1 broken down along the road. After about another 1 \(\frac{1}{2}\) hr., Car 1 whizzes past again.

d. Create linear equations representing each car’s distance in terms of time (in hours). Note that you will need four equations for Car 1 and only one for Car 2. Use these equations to find the exact coordinates of when the cars meet.
Answer:
Using the variables, d for distance (in miles) and t for time (in hours):
Equation for Car 2: d=25t+100
Equations for Car 1:
d=50t, 0≤t≤2
d=100(t-2)+100=100(t-1), 2<t≤3
d=200, 3<t≤5
d=100(t-5)+200=100(t-3), 5<t

Intersection points:
First: solving 100(t-1)=25t+100 gives (\(\frac{200}{75}\), \(\frac{(25)(200)}{75}\)+100)≈(2.7,166.7),
Second: solving 200=25t+100 gives (4,200), and
Third: solving 100(t-3)=25t+100 gives (\(\frac{400}{75}\), \(\frac{(25)(400)}{75}\)+100)≈(5.3,233.3).

Question 4.
Suppose that in Problem 3 above, Car 1 travels at the constant speed of 25 mph the entire time. Sketch the distance-versus-time graphs for the two cars on a graph below. Do the cars ever pass each other? What is the linear equation for Car 1 in this case?
Answer:
A sample graph is shown below. Car 1 never overtakes Car 2, and they are 100 mi. apart the entire time. The equation for Car 1 is y=25t.

Question 5.
Generate six distinct random whole numbers between 2 and 9 inclusive, and fill in the blanks below with the numbers in the order in which they were generated.
A (0 ,_______), B (_______,_______), C (10 ,_______)
D (0 ,_______), E (10 ,_______).

(Link to a random number generator http://www.mathgoodies.com/calculators/random_no_custom.html)

a. On a coordinate plane, plot points A, B, and C. Draw line segments from point A to point B, and from point B to point C.
b. On the same coordinate plane, plot points D and E and draw a line segment from point D to point E.
c. Write a graphing story that describes what is happening in this graph. Include a title, x- and y-axis labels, and scales on your graph that correspond to your story.
Answer:
Answers will vary depending on the random points generated.

Question 6.
The following graph shows the revenue (or income) a company makes from designer coffee mugs and the total cost (including overhead, maintenance of machines, etc.) that the company spends to make the coffee mugs.

a. How are revenue and total cost related to the number of units of coffee mugs produced?
Answer:
Definition: Profit = Revenue – Cost. Revenue is the income from the sales and is directly proportional to the number of coffee mugs actually sold; it does not depend on the units of coffee mugs produced. Total cost is the sum of the fixed costs (overhead, maintaining the machines, rent, etc.) plus the production costs associated with the number of coffee mugs produced; it does not depend on the number of coffee mugs sold.

b. What is the meaning of the point (0,4000) on the total cost line?
Answer:
The overhead costs, the costs incurred regardless of whether 0 or 1,000 coffee mugs are made or sold, is $4,000.

c. What are the coordinates of the intersection point? What is the meaning of this point in this situation?
Answer:
(500,6000). The revenue, $6,000, from selling 500 coffee mugs, is equal to the total cost, $6,000, of producing 500 coffee mugs. This is known as the break-even point. When Revenue = Cost, the Profit is $0. After this point, the more coffee mugs sold, the more the positive profit; before this point, the company loses money.

d. Create linear equations for revenue and total cost in terms of units produced and sold. Verify the coordinates of the intersection point.
Answer:
If u is a whole number for the number of coffee mugs produced and sold, C is the total cost to produce u mugs, and R is the total revenue when u mugs are sold, then
C=4000+4u,
R=12u.
When u=500, both C=4000+4∙500=6000 and R=12∙500=6000.

e. Profit for selling 1,000 units is equal to revenue generated by selling 1,000 units minus the total cost of making 1,000 units. What is the company’s profit if 1,000 units are produced and sold?
Answer:
Profit = Revenue – Total Cost. Hence,
P=R-C=12∙1000-(4000+4∙1000)=12000-8000=4000
The company’s profit is $4,000.

Eureka Math Algebra 1 Module 1 Lesson 5 Exit Ticket Answer Key

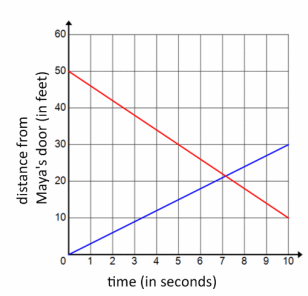
Maya and Earl live at opposite ends of the hallway in their apartment building. Their doors are 50 ft. apart. Each person starts at his or her own door and walks at a steady pace toward the other. They stop walking when they meet.
Suppose:
→ Maya walks at a constant rate of 3 ft. every second.
→ Earl walks at a constant rate of 4 ft. every second.

Answer;

Question 1.
Graph both people’s distance from Maya’s door versus time in seconds.
Answer:
Graphs should be scaled and labeled appropriately. Maya’s graph should start at (0,0) and have a slope of 3, and Earl’s graph should start at (0,50) and have a slope of -4.

Question 2.
According to your graphs, approximately how far will they be from Maya’s door when they meet?
Answer:
The graphs intersect at approximately 7 sec. at a distance of about 21 ft. from Maya’s door.

Engage NY Eureka Math Algebra 1 Module 1 Lesson 4 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 4 Example Answer Key

Example
Direct students to the following graph that appears in their student materials, and ask questions about the kind of data it represents.
→ The title of the graph is “Water Consumption in a Typical School Day.” For what purposes is water used at a school?
→ Primarily through bathroom use.
→ What do you think the numbers along the horizontal axis represent?
→ Time of day.
→ What might the numbers along the vertical axis represent? Do we have any indication of the units being used?
→ Answers will vary. We have no indication of the units being used. We would assume that these numbers are related, in some way, to a volume of water.
→ What could be the reason for the spikes in the graph?
→ Student bathroom use between class periods.
→ What might be the reason for the smaller spikes between the large ones?
→ Some student use during class time.

Example

Now, offer the following further information about the typical school day for the school from which this data was recorded.
→ Regular school day hours: 8:00 a.m.–3:04 p.m.
→ After school activities: 3:15 p.m.–5:15 p.m.
→ Around 10:00 a.m. there is a 13 min. advisory or homeroom period.
Ask students:
→ Can you see features of this information appearing in the graph?
Be sure students notice the large peaks at the times just before 8:00 a.m., near 10:00 a.m., just after 3:00 p.m., and near 5:15 p.m., which can be explained by bathroom use just before and just after activities.
Ask students:
→ Is it possible to deduce the time of lunch at this school?
Students might conjecture that lunch comes in two or three shifts so as to explain the multiple large peaks in the middle of the day.
Now, return to the question of the numbers on the vertical axis:
→ Around 10:00 a.m. the graph indicates a peak of 80 units. What is the number 80 representing?
Students will likely answer “gallons of water used” or “volume of water used.” But what do we mean by used? Lead to the idea that the amount used is measured by the volume of water that drains through the pipes and leaves the school.
Then ask the question:
→ How does one actually measure the amount of water flowing out through the pipes precisely at 10:00 a.m.? What does 80 units of water leaving the school right at 10:00 a.m. mean?
→ The issue to be discussed next is that 80 units of water must take some period of time to flow out through the pipes.

Ask students to think about the bell for the end of class. At this time, they all rise and begin to walk out of the classroom, flowing through the door of the classroom. If there are 25 students in the class, would I say that a volume of 25 students is flowing through the door right at an instant? No, we have instead a flow of 25 students over a short period of time.
Ask students to consider again what the number 80 at the 10:00 a.m. mark might mean.
Now add the following information:
→ The researchers who collected this data watched the school’s water meter during a 12 hr. period. The meter shows the total amount of water (in gallons) that has left the school since the time the meter was last set to zero. Since the researchers did not know when this resetting last occurred, they decided, at each minute mark during the day, to measure how much the meter reading increased over the next minute of time. Thus, the value 80 at the 10:00 a.m. mark on the graph means that 80 gal. of water flowed through the meter and left the school during the period from 10:00 a.m. to 10:01 a.m.
Ask students:
→ What are the units for the numbers on the vertical axis?
→ The units for the numbers on the vertical axis are gallons per minute.
→ Ignoring the large spikes in the graph, what seems to be the typical range of values for water use during the school day?
Help students notice that the value of the graph between the large spikes seems to oscillate between the flow of 0 gal. of water per minute and about 15 gal. of water per minute.
Now have students complete Exercises 1 and 2 independently and then work in pairs or in small groups to discuss approaches and compare answers. Ask students to volunteer their answers to a general class discussion. Discuss any assumptions that were made to arrive at answers.

Eureka Math Algebra 1 Module 1 Lesson 4 Exercise Answer Key

Exercises 1–2

Exercise 1.
The bulk of water usage is due to the flushing of toilets. Each flush uses 2.5 gal. of water. Samson estimates that 2% of the school population uses the bathroom between 10:00 a.m. and 10:01 a.m. right before homeroom. What is a good estimate of the population of the school?
Answer:
We know that 80 gallons of water are used during that minute. This corresponds to \(\frac{80}{2.5}\)=32 flushes. Assuming that each student flushes just once, we can say that 32 students used the bathroom during this time. This represents 2% of the school population, which is one fiftieth of the school population. Thus, there are about 1,600 people at the school.

Exercise 2.
Samson then wonders this: If everyone at the school flushed a toilet at the same time, how much water would go down the drain (if the water pressure of the system allowed)? Are we able to find an answer for Samson?
Answer:
Answers will vary based on assumptions made. If there were enough toilets that everyone could flush a toilet at the same time, and using the estimated school population of 1,600 (there would have to be 1,600 toilets), then 1600×2.5 gal.=4000 gal. of water.

Exercise 3:
Estimation Exercise

a. Make a guess as to how many toilets are at the school.
Answer:
80

b. Make a guess as to how many students are in the school, and what percentage of students might be using the bathroom at break times between classes, just before the start of school, and just after the end of school. Are there enough toilets for the count of students wishing to use them?
Answer:
Of 1,600 students, at any given break time, 20% are using the restroom. That means that during a break time 320 students wish to use the toilet. Since there are only approximately 80 toilets, there are not enough toilets if all of the students go at the same time (say at the beginning of the break).

c. Using the previous two considerations, estimate the number of students using the bathroom during the peak minute of each break.
320 students are using the bathroom during a break, but maybe only \(\frac{1}{4}\) of them at any one minute, so 80 at any one minute.

d. Assuming each flush uses 2.5 gal. of water, estimate the amount of water being used during the peak minute of each break.
Answer:
80 flushes×2.5 \(\frac{\text { gal }}{\text { flush }}\)=200 gal.

e. What time of day do these breaks occur? (If the school schedule varies, consider today’s schedule.)
Answer:
Answers will vary by school; an example: 8:00, 9:45, 11:30, 12:00, 1:45, 3:30

f. Draw a graph that could represent the water consumption in a typical school day of your school.
Answer:

Eureka Math Algebra 1 Module 1 Lesson 4 Exit Ticket Answer Key

Suppose the researchers collecting data for water consumption during a typical school day collected data through the night too.

Question 1.
For the period between the time the last person leaves the building for the evening and the time of the arrival of the first person the next morning, how should the graph of water consumption appear?
Answer:
Since no toilets are being used, the graph should be a horizontal line of constant value zero.

Question 2.
Suppose the researchers see instead, from the time 1:21 a.m. onward, the graph shows a horizontal line of constant value, 4. What might have happened during the night?
Answer:
Perhaps one toilet started to leak at 1:21 a.m., draining water at a rate of 4 gallons per minute.

Eureka Math Algebra 1 Module 1 Lesson 4 Problem Set Answer Key

Question 1.
The following graph shows the temperature (in degrees Fahrenheit) of La Honda, CA in the months of August and September of 2012. Answer the questions following the graph.

a. The graph seems to alternate between peaks and valleys. Explain why.
Answer:
The temperature increases during the day and drops during the night, and the difference between the high and low temperatures can be very large.

b. When do you think it should be the warmest during each day? Circle the peak of each day to determine if the graph matches your guess.
Answer:
The warmest time should be before sunset, a few hours after noon, since heating occurs throughout the day while the sun is up.

c. When do you think it should be the coldest during each day? Draw a dot at the lowest point of each day to determine if the graph matches your guess.
Answer:
Similarly, the coldest temperature should be before sunrise, since cooling occurs throughout the night.

d. Does the graph do anything unexpected such as not following a pattern? What do you notice? Can you explain why it is happening?
Answer:
The graph seems to follow the expected pattern with natural variations, except for the unusually low daytime temperatures on August 31.

Question 2.
The following graph shows the amount of precipitation (rain, snow, or hail) that accumulated over a period of time in La Honda, CA.

a. Tell the complete story of this graph.
Answer:
On August 24, the measurement started with an initial cumulative data of 0.13 in. It stands for the precipitation accumulated before the current measurement. Nothing else happened until August 31, when there was 0.04 in. of precipitation. On September 1, there was 0.01 in. more of precipitation.

b. The term accumulate, in the context of the graph, means to add up the amounts of precipitation over time. The graph starts on August 24. Why didn’t the graph start at 0 in. instead of starting at 0.13 in.?
Answer:
On August 24, the measurement started with an initial cumulative data of 0.13 in. It stands for the precipitation accumulated before the current measurement.

Question 3.
The following graph shows the solar radiation over a period of time in La Honda, CA. Solar radiation is the amount of the sun’s rays that reach the earth’s surface.

a. What happens in La Honda when the graph is flat?
Answer:
This represents time periods during which the solar radiation per unit area is constant. For example, during nighttime, there is no sunlight, and hence there are flat regions on the curve.

b. What do you think is happening when the peaks are very low?
Answer:
It could be an overcast day. Other less common events, such as a solar eclipse, would also cause this.

c. Looking at all three graphs, what do you conclude happened on August 31, 2012 in La Honda, CA?
Answer:
The lower temperature, increase in accumulated precipitation, and the low solar radiation makes me think that August 31, 2012 was overcast and rainy for most of the day.

Question 4.
The following graph shows the velocity (in centimeters per second) and turbidity of the Logan River in Queensland, Australia during a flood. Turbidity refers to the clarity of the water (higher turbidity means murkier water) and is related to the total amount of suspended solids, such as clay, silt, sand, and phytoplankton, present in the water.

a. For recreation, Jill visited the river during the month of January and saw clean and beautiful water. On which day do you think she visited?
Answer:
The fifteenth appears to be the best choice because of the low turbidity. The eighth and tenth are also good choices.

b. What do the negative velocities (below the grey line) that appear periodically at the beginning represent?
Answer:
This shows normal tidal flow, which is disturbed during the flood.

c. The behavior of the river seems to follow a normal pattern at the beginning and at the very end of the time period shown. Approximately when does the flood start? Describe its effects on velocity and turbidity.
Answer:
The flood starts on the eleventh. It increases the velocity so that it is always positive, disturbing the tide, and it increases the turbidity of the water.

Engage NY Eureka Math Algebra 1 Module 1 Lesson 3 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 3 Example Answer Key

Example.
Consider the story:
Darryl lives on the third floor of his apartment building. His bike is locked up outside on the ground floor. At 3:00 p.m., he leaves to go run errands, but as he is walking down the stairs, he realizes he forgot his wallet. He goes back up the stairs to get it and then leaves again. As he tries to unlock his bike, he realizes that he forgot his keys. One last time, he goes back up the stairs to get his keys. He then unlocks his bike, and he is on his way at 3:10 p.m.
Sketch a graph that depicts Darryl’s change in elevation over time.
Answer:
There will be variations in the students’ graphs, but the graph students produce should appear as follows:

Exploratory Challenge
Watch the following graphing story:

The video shows bacteria doubling every second.

Get students started by creating a table of the first few seconds. Stop the video as close as possible to the 0 sec. mark, 1 sec. mark, 2 sec. mark, 3 sec. mark, and so on. Have students count the bacteria at each of those times. Note that some of the bacteria have not fully divided, so expect a discussion on how to count them (guide students to make the choice: approximately the length of a small bacterium). Do not suggest any model just yet as there are some great number sense problems to explore first. Below is a fairly accurate account of the number of bacteria up to the 3 sec. mark:

The 4 sec. mark is already tricky to count (approximately 31 or 32), as well as at the 5 sec. mark (approximately 58–62). Ask students what they might expect to see at time 6 sec. (approximately 116–130). Do not have students count the bacteria at time 6 sec. but instead estimate the number (e.g., the radius of the circular region of bacteria doubles roughly every second).
Students might first produce a graph similar to this:

a. Graph the number of bacteria versus time in seconds. Begin by counting the number of bacteria present at each second and plotting the appropriate points on the set of axes below. Consider how you might handle estimating these counts as the population of the bacteria grows.

Answer:

Ask for, or eventually suggest, the following model to describe the bacteria shown in the video:
→ At time 0 sec., there are 2 bacteria, and the number of bacteria in the Petri dish doubles every second. Stress the point to students that this model does not describe the exact number of bacteria at a given time in the video but that it does reasonably represent an estimate of the number of bacteria at a given time.
Ask students to create a graph that represents bacterial population growth beyond the 6 sec. mark using this model. Two challenges will quickly arise for students: Identifying an appropriate scale for the vertical axis and dealing with the extraordinarily large numbers that arise from this mark onward. Suggest that students first describe the shape of the graph after the 6 sec. mark. To help with larger values, a table can be expanded beyond the 6 sec. mark using scientific notation.
A good question to ask:
→ Will the curve ever be perfectly vertical?
To develop the real-time exponential growth of the bacteria, state:
→ Listen to what the narrator says about the situation, “Just one bacterium, dividing every 20 min. … .”
Then ask:
→ If one bacterium divides once every 20 min., how much real time has passed in what we watched in the time-lapse video?
To help students answer this question, return to the beginning of the video, with two bacteria, and notice how many bacteria there are after 1 sec. There are four. And at the 2 sec. mark, there are eight. Have students conclude that one second of video time matches about 20 min. of real time.
→ We first created a graph with the unit scale for the horizontal axis as seconds. This time scale is according to the video’s clock. How could we change the scale of the horizontal axis so that it represents the real time of bacteria growth?
Students may suggest “crossing out the marks 1 sec., 2 sec., 3 sec., …” on the horizontal axis and replacing them with the numbers “20 min., 40 min., 60 min., … .” While this is acceptable, suggest being careful and deliberate by drawing a table of values akin to the following:

Use this table as a discussion point for justifying the change of scale for the horizontal axis.

Have them sketch a graph of the count of bacteria versus (real) time in minutes for the first five-hour period. Lead students in a discussion to decide on appropriate scales for the vertical and horizontal axes. If needed, encourage the students to extend their tables to determine the number of bacteria at the end of the five-hour period before they decide on the scale. The students’ graphs do not need to match exactly the sample provided below but should accurately depict the points over the first 300 min.

Students may instinctively connect the points with a smooth curve. It is acceptable to use the curve as a model of the reality of the discrete points on the graph; however, encourage students to recognize the difference between the points supported by the context and a continuous curve that is a model of the situation.

b. Graph the number of bacteria versus time in minutes.

Answer:

Now, have students redraw this graph with the unit scale of the horizontal axis as hours.

c. Graph the number of bacteria versus time in hours (for the first five hours).

Answer:

Eureka Math Algebra 1 Module 1 Lesson 3 Problem Set Answer Key

Question 1.
Below are three stories about the population of a city over a period of time and four population-versus-time graphs. Two of the stories each correspond to a graph. Match the two graphs and the two stories. Write stories for the other two graphs, and draw a graph that matches the third story.
Story 1: The population size grows at a constant rate for some time, then doesn’t change for a while, and then grows at a constant rate once again.
Story 2: The population size grows somewhat fast at first, and then the rate of growth slows.
Story 3: The population size declines to zero.

Answer:
Story 1 corresponds to (d), and Story 2 corresponds to (b). For Story 3 answers will vary. The graph can begin at any positive population value and decrease to 0 in any manner.
Sample story for (a): The population starts out at 0 and grows at a constant rate.
Sample story for (c): The population size grows at a constant linear rate for some time, then decreases at a constant linear rate for a while, and then increases at a constant linear rate slower than the original rate of increase.

Question 2.
In the video, the narrator says:
“Just one bacterium, dividing every 20 min., could produce nearly 5,000 billion billion bacteria in one day. That is 5,000,000,000,000,000,000,000 bacteria.”
This seems WAY too big. Could this be correct, or did she make a mistake? (Feel free to experiment with numbers using a calculator.)
Answer:
Yes, this is correct. Do not be too critical of justifications. Accept any explanation that reasonably explains why she is correct.
For the teacher: The function f(t)=\(2^{\left(\frac{t}{20}\right)}\) models the number of bacteria after t minutes starting from a single bacterium. There are 1,440 min. in a 24 hr. period, which means that since the bacteria divide every 20 min., the count of the bacteria will double 72 times during a 24 hr. period. Thus, the answer is f(1440)=2⁷² , which is approximately 4.72×10²¹ . This number is nearly 5,000 billion billion bacteria.

Question 3.
Bacillus cereus is a soil-dwelling bacterium that sometimes causes food poisoning. Each cell divides to form two new cells every 30 min. If a culture starts out with exactly 100 bacterial cells, how many bacteria will be present after 3 hr.?
Answer:
The result is 2⁶ (100)=6400 bacteria. Students can do this by repeated multiplication, without much knowledge of exponential functions.

Question 4.
Create a story to match each graph below:

Answer:
Answers will vary.
Sample story for (a): Bill received his paycheck and did not touch it for a few days. Then, he bought groceries and gas and stopped spending money. After a few more days, he spent almost all of his remaining money on a new jet ski. A few days later he received his paycheck.
Sample story for (b): Mary is riding a Ferris wheel at a theme park.

Question 5.
Consider the following story about skydiving:
Julie gets into an airplane and waits on the tarmac for 2 min. before it takes off. The airplane climbs to 10,000 ft. over the next 15 min. After 2 min. at that constant elevation, Julie jumps from the plane and free falls for 45 sec. until she reaches a height of 5,000 ft. Deploying her chute, she slowly glides back to Earth over the next 7 min. where she lands gently on the ground.
a. Draw an elevation-versus-time graph to represent Julie’s elevation with respect to time.
Answer:
The graph should depict the horizontal line y=0 from 0 min. to 2 min., a linear increase to 10,000 ft. from 2 min. to 17 min., a brief free fall (concave down) curve for 45 sec., and then a leveled out concave up curve for the slow fall at the end.

b. According to your graph, describe the manner in which the plane climbed to its elevation of 10,000 ft.
Answer:
Answers will vary depending on the graph. Example: I assumed that the plane climbed at a constant rate.

c. What assumption(s) did you make about falling after she opened the parachute?
Answer:
Answers may vary. Example: I assumed that her change in elevation slowed down suddenly when she opened her parachute and then was an almost constant rate of change until she reached the ground.

Question 6.
Draw a graph of the number of bacteria versus time for the following story: Dave is doing an experiment with a type of bacteria that he assumes divides in half exactly every 30 min. He begins at 8:00 a.m. with 10 bacteria in a Petri dish and waits for 3 hr. At 11:00 a.m., he decides this is too large of a sample and adds Chemical A to the dish, which kills half of the bacteria almost immediately. The remaining bacteria continue to grow in the same way. At noon, he adds Chemical B to observe its effects. After observing the bacteria for two more hours, he observes that Chemical B seems to have cut the growth rate in half.
Answer:
Answers vary somewhat, but the graph should include the information in the table below connected by some smooth curve. There should be a sudden decrease from 640 to 320 after time 3 (i.e., 3 hr.), say around time 3.01 or sooner, giving a nearly vertical line.

Question 7.
Decide how to label the vertical axis so that you can graph the data set on the axes below. Graph the data set and draw a curve through the data points.

Answer:
(A sample graph is shown above.)

Eureka Math Algebra 1 Module 1 Lesson 3 Exit Ticket Answer Key

Assume that a bacteria population doubles every hour. Which of the following three tables of data, with x representing time in hours and y the count of bacteria, could represent the bacteria population with respect to time? For the chosen table of data, plot the graph of that data. Label the axes appropriately with units.

Answer:
The answer is (b).

Engage NY Eureka Math Algebra 1 Module 1 Lesson 2 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 2 Example Answer Key

Example 1.
Show the video of a ball rolling down a ramp given at http://mbc.sandi.net/library/311612, telling the class that our goal is simply to describe in words the motion of the ball. (If the link does not work, search for “Algebra I, Module 1 Lesson 2 ball rolling down ramp video.”)
After viewing the video, have students share aloud their ideas on describing the motion. Some might speak in terms of speed, distance rolled over time, or change of elevation. All approaches are valid. Help students begin to shape their ideas with language that specifies the names of the quantities being observed and how they are changing over time.
Direct the class to focus on the change of elevation of the ball over time and to begin to put into words specific details linking elevation with time.
→ It first started at the top of the ramp.
→ It rolled down the ramp for about 2 sec.
→ After it hit the bottom of the ramp, it rolled across the floor.
If students do not naturally do so, suggest representing this information on a graph. Display a set of axes on the board.

Begin a discussion that leads students through issues of formalizing the diagram: The labels and units of the axes, a title for the graph, the meaning of a point plotted on the graph, the height at time 0 sec., the time when it reached the bottom of the ramp, etc.
Either individually or in groups of two, have students estimate the general shape of the graph of the elevation-versus-time of the ball rolling down the ramp. At this point, do not worry about engaging students in measuring specific heights and specific times; right now they are just looking for the general shape. Be sure to have students notice the horizontal “tail” of the graph, and ask them to interpret its meaning. (The elevation of the ball does not change as it rolls across the floor.) Some students may draw a curved graph. Others will likely draw a straight line for the graph over the interval 0 to 1.7 sec. Even though this is not correct, allow it at this stage.

After students have created graphs, have them compare their graphs with each other and share with the class. Ask the following questions:
→ Should the change in elevation be decreasing at a constant rate? That is, do you think this graph should be a straight line graph, at least between 0 sec. and about 1.7 sec.?
Some specific questions (below) can help lead to the correct conclusion:
→ Where does the elevation change more slowly? Explain.
→ If it is changing more slowly at the top and more quickly at the bottom, should the graph look the same at those times?
In Exploratory Challenge, students see an elevation-versus-time graph that is clearly not a straight line.

Exploratory Challenge
Plot a graphical representation of change in elevation over time for the following graphing story. It is a video of a man jumping from 36 ft. above ground into 1 ft. of water.
http://www.youtube.com/watch?v=ZCFBC8aXz-g or
http://youtu.be/ZCFBC8aXz-g (If neither link works, search for “OFFICIAL Professor Splash World Record Video!”)

Allow students to analyze the full video, initially giving them as much control as possible (if not full control) in choosing when to pause the video, play it half speed, and so on. Perhaps conduct this part of a class in a computer lab or display the video on an interactive white board. Then direct students to investigate one of the two portions of the clip below, depending on the level of technology you have available:
Portion 1: From time 32 sec. to time 33 sec. Use this to get data for drawing the graph (if they have access to a powerful movie editor that can show each frame).
Portion 2: From time 48 sec. to time 53 sec. Use this for a slow-motion version that can be analyzed easily via YouTube.

Note: In this lesson, keep students’ focus on understanding the relationship between physical measurements and the graph. Students will revisit scenarios like this one in Modules 4 and 5. We know, from physics, that the height function for this example can be modeled by s(t)=36-16t^2 and that in this case, the function models the situation very accurately. For example, the function predicts that he will hit the water at exactly 1.5 sec., which he does. However, quadratic equations and functions are topics for later modules.
Students should start measuring from the top of the man’s jump, which is about 36 ft. high. (He starts at 35.5 ft. and jumps \(\frac{1}{2}\) ft. up before falling.)
Solutions are provided below for each portion.

Give students the opportunity to share their work with the class as a whole or with a partner. Have students articulate and justify any interesting choices they have made. For example, instead of plotting points for every second of footage, some students may wish to plot the time per distance markers (36, 30, 25, 20, 15, etc.). Both methods lead to a graph of a quadratic function.

Students should produce graphs that look similar to the following, according to which clip they used:

Portion 1 Results: If your students used Portion 1, they should get something that looks similar to the table (right) and graph (on the previous page).
The estimates of the heights in the table are based upon the markers in the video. Since the video is taken from the ground, reading height directly from the video can be hampered by the parallax effect. Ideally, for accurate reading, the camera should be at the same height as the jumper at all times so the height reading from the ruler in the background could be accurate. Remind students to make some necessary corrections or adjustments instead of just reading horizontally across the frozen video frame. Regardless, you should not expect your students to have perfect graphs, but their graphs should not be straight lines.Portion 2 Results: If your students used Portion 2 of the video, they should get something that looks similar to the table (below) and graph (right). Have a discussion with them that the results below do not model the actual situation. By specifically talking about film time versus real time, we lay the foundation to talk about transformations of functions. Guide students by asking these questions:
→ What would you need to do to this graph to correctly model the jump with a graph?
→ You need to know how long it took for him to complete the jump.
→ It takes the jumper exactly 1.5 sec. from the top of his jump until he splashes in the water.
→ Then we should shrink the graph horizontally until the t-intercept is at 1.5 sec.
→ Learning how to shrink graphs in this way will be an important topic in Modules 3 and 5.

As an extension, encourage students to try adjusting the graph in this way (shrinking it horizontally such that the t-intercept is at 1.5 sec.), using their intuition to guide them, and compare their results with their peers.

Example 2.
The table below gives the area of a square with sides of whole number lengths. Have students plot the points in the table on a graph and draw the curve that goes through the points.

On the same graph, reflect the curve across the y-axis. This graph is an example of a graph of a quadratic function.

Bring up or ask:
→ On the graph, what do the points between the plotted points from the table represent?
→ Areas of squares with non-whole number side lengths.

Eureka Math Algebra 1 Module 1 Lesson 2 Exit Ticket Answer Key

If you jumped in the air three times, what might the elevation versus time graph of that story look like? Label the axes appropriately.

Answer:
Student answers will vary.
I jump about 1 ft. high every other second.

Eureka Math Algebra 1 Module 1 Lesson 2 Problem Set Answer Key

Question 1.
Here is an elevation-versus-time graph of a ball rolling down a ramp. The first section of the graph is slightly curved.

a. From the time of about 1.7 sec. onward, the graph is a flat horizontal line. If Ken puts his foot on the ball at time 2 sec. to stop the ball from rolling, how will this graph of elevation versus time change?
Answer:
Even if the ball is at rest on the floor, its elevation remains 0 in. and does not change. The elevation-versus-time graph does not change.

b. Estimate the number of inches of change in elevation of the ball from 0 sec. to 0.5 sec. Also estimate the change in elevation of the ball between 1.0 sec. and 1.5 sec.
Answer:
Between 0 and 0.5 sec., the change in elevation was about -2 in. Between 1.0 and 1.5 sec., the change in elevation was about -5.5 in.

c. At what point is the speed of the ball the fastest, near the top of the ramp at the beginning of its journey or near the bottom of the ramp? How does your answer to part (b) support what you say?
Answer:
The speed of the ball is the fastest near the bottom of the ramp. During the \(\frac{1}{2}\) sec. from 1.0 sec. to 1.5 sec., the ball’s change in elevation is greater than the \(\frac{1}{2}\) sec. at the beginning of its journey. It must have traversed a greater length of the ramp during this \(\frac{1}{2}\) sec. and so was traveling faster. Its speed is greater near the bottom of the ramp.

Question 2.
Watch the following graphing story:
Elevation vs. Time #4 [http://www.mrmeyer.com/graphingstories1/graphingstories4.mov. This is the second video under “Download Options” at the site http://blog.mrmeyer.com/?p=213 called “Elevation vs. Time #4.”]
The video is of a man hopping up and down several times at three different heights (first, five medium-sized jumps immediately followed by three large jumps, a slight pause, and then 11 very quick small jumps).
a. What object in the video can be used to estimate the height of the man’s jump? What is your estimate of the object’s height?
Answer:
The stair step. Answers will vary between 4 in. to 8 in.

b. Draw your own graph for this graphing story. Use parts of graphs of quadratic functions to model each of the man’s hops. Label your x-axis and y-axis appropriately and give a title for your graph.
Answer:
Answers will vary but should reflect the estimate made in part (a). See the end of the video for a picture of the graph.

Question 3.
Use the table below to answer the following questions.

a. Plot the points (x,y) in this table on a graph (except when x is 5).
Answer:

b. The y-values in the table follow a regular pattern that can be discovered by computing the differences of consecutive y-values. Find the pattern and use it to find the y-value when x is 5.
Answer:
The y-values have differences that increase by one, suggesting that we next have a y-value of 12+\(\frac{11}{2}\)=\(\frac{35}{2}\) when x is 5.

c. Plot the point you found in part (b). Draw a curve through the points in your graph. Does the graph go through the point you plotted?
Answer:
Yes.

d. How is this graph similar to the graphs you drew in Examples 1 and 2 and the Exploratory Challenge? Different?
Answer:
Answers will vary. This graph is similar to the graphs from Examples 1 and 2 of the Exploratory Challenge in that the curve has the same basic U-shape. (Students may mention that they are all graphs of quadratic functions, although at this point that is not necessary.) This graph is different from the graphs from Example 1 and the Exploratory Challenge because this curve is increasing and the graphs in Example 1 and the Exploratory Challenge are decreasing. This graph is similar to the graph from Example 2 because they are both increasing. However, this graph increases at a slower rate than the one from Example 2. For example, this graph has value 12 when x is 4 (the Example 2 graph had value 16), and this graph has value 24 when x is 6 (the Example 2 graph had value 36).

Question 4.
A ramp is made in the shape of a right triangle using the dimensions described in the picture below. The ramp length is 10 ft. from the top of the ramp to the bottom, and the horizontal width of the ramp is 9.25 ft.

Answer:
A ball is released at the top of the ramp and takes 1.6 sec. to roll from the top of the ramp to the bottom. Find each answer below to the nearest 0.1 \(\frac{\mathrm{ft}}{\mathrm{sec}}\).
a. Find the average speed of the ball over the 1.6 sec.
Answer:
\(\frac{10}{1.6}\) \(\frac{\mathrm{ft}}{\mathrm{sec}}\), or 6.3 \(\frac{\mathrm{ft}}{\mathrm{sec}}\)

b. Find the average rate of horizontal change of the ball over the 1.6 sec.
Answer:
\(\frac{9.25}{1.6}\) \(\frac{\mathrm{ft}}{\mathrm{sec}}\) or 5.8 \(\frac{\mathrm{ft}}{\mathrm{sec}}\)

c. Find the average rate of vertical change of the ball over the 1.6 sec.
Answer:
By the Pythagorean theorem, the vertical length is approximately \(\sqrt{10^{2}-9.25^{2}}\)≈3.8 ft. Hence, the average rate of vertical change is \(\frac{3.8}{1.6}\) \(\frac{\mathrm{ft}}{\mathrm{sec}}\) or 2.4 \(\frac{\mathrm{ft}}{\mathrm{sec}}\).

d. What relationship do you think holds for the values of the three average speeds you found in parts (a), (b), and (c)? (Hint: Use the Pythagorean theorem.)
Answer:
The sum of the squares of the horizontal and vertical rates of change is equal to the square of the speed of the ball.

Engage NY Eureka Math Algebra 1 Module 1 Lesson 1 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 1 Example Answer Key

Example 1.
Here is an elevation-versus-time graph of a person’s motion. Can we describe what the person might have been doing?

Have students discuss this question in pairs or in small groups. It will take some imagination to create a context that matches the shape of the graph, and there will likely be debate.
Additional questions to ask:
→ What is happening in the story when the graph is increasing, decreasing, constant over time?
→ Answers will vary depending on the story: a person is walking up a hill, etc.
→ What does it mean for one part of the graph to be steeper than another?
→ The person is climbing or descending faster than in the other part.
→ How does the slope of each line segment relate to the context of the person’s elevation?
→ The slope gives the average change in elevation per minute.
→ Is it reasonable that a person moving up and down a vertical ladder could have produced this elevation versus time graph?
→ It is unlikely because the speed is too slow: 2.5 \(\frac{\mathrm{ft}}{\mathrm{min}}\). If the same graph had units in seconds then it would be reasonable.
→ Is it possible for someone walking on a hill to produce this elevation-versus-time graph and return to her starting point at the 10 min. mark? If it is, describe what the hill might look like.
→ Yes, the hill could have a long path with a gentle slope that would zigzag back up to the top and then a shorter, slightly steeper path back down to the beginning position.
→ What was the average rate of change of the person’s elevation between time 0 min. and time 4 min.?
→ \(\frac{10}{4}\) \(\frac{\mathrm{ft}}{\mathrm{min}}\), or 2.5 \(\frac{\mathrm{ft}}{\mathrm{min}}\).
These types of questions help students understand that the graph represents only elevation, not speed or horizontal distance from the starting point. This is an important observation.

Eureka Math Algebra 1 Module 1 Lesson 1 Exit Ticket Answer Key

Students may describe the intervals in words. Do not worry about the endpoints of the intervals in this lesson.

The graph in the Exploratory Challenge is made by combining pieces of nine linear functions (it is a piecewise linear function). Each linear function is defined over an interval of time, represented on the horizontal axis. List those nine time intervals.
Answer:
Between 0 and 3 sec.;
between 3 and 5.5 sec.;
between 5.5 and 7 sec.;
between 7 and 8.5 sec.;
between 8.5 and 9 sec.;
between 9 and 11 sec.;
between 11 and 12.7 sec.;
between 12.7 and 13 sec.;
and 13 sec. onward.

Eureka Math Algebra 1 Module 1 Lesson 1 Problem Set Answer Key

Question 1.
Watch the video, “Elevation vs. Time #3” (below).
http://www.mrmeyer.com/graphingstories1/graphingstories3.mov. (This is the third video under “Download Options” at the site http://blog.mrmeyer.com/?p=213 called “Elevation vs. Time #3.”)
It shows a man climbing down a ladder that is 10 ft. high. At time 0 sec., his shoes are at 10 ft. above the floor, and at time 6 sec., his shoes are at 3 ft. From time 6 sec. to the 8.5 sec. mark, he drinks some water on the step 3 ft. off the ground. After drinking the water, he takes 1.5 sec. to descend to the ground, and then he walks into the kitchen. The video ends at the 15 sec. mark.
a. Draw your own graph for this graphing story. Use straight line segments in your graph to model the elevation of the man over different time intervals. Label your x-axis and y-axis appropriately, and give a title for your graph.
Answer:
[See video for one example of a graph of this story.]

b. Your picture is an example of a graph of a piecewise linear function. Each linear function is defined over an interval of time, represented on the horizontal axis. List those time intervals.
Answer:
The intervals are [0,6], (6,8.5], (8.5,10], and (10,15], with the understanding that the inclusion of the endpoints may vary. Students may use any notation they want to describe the intervals.

c. In your graph in part (a), what does a horizontal line segment represent in the graphing story?
Answer:
It is a period of time when he is neither going up nor down.

d. If you measured from the top of the man’s head instead (he is 6.2 ft. tall), how would your graph change?
Answer:
The whole graph would be shifted up 6.2 ft.

e. Suppose the ladder descends into the basement of the apartment. The top of the ladder is at ground level (0 ft.) and the base of the ladder is 10 ft. below ground level. How would your graph change in observing the man following the same motion descending the ladder?
Answer:
The whole graph would be shifted downward 10 ft.

f. What is his average rate of descent between time 0 sec. and time 6 sec.? What was his average rate of descent between time 8.5 sec. and time 10 sec.? Over which interval does he descend faster? Describe how your graph in part (a) can also be used to find the interval during which he is descending fastest.
Answer:
His average rate of descent between 0 and 6 sec. was \(\frac{7}{6}\) \(\frac{\mathrm{ft}}{\mathrm{sec}}\).
His average rate of descent between 8.5 and 10 sec. was 2 \(\frac{\mathrm{ft}}{\mathrm{sec}}\).
He was descending faster from 8.5 to 10 sec.
The interval during which he is descending the fastest corresponds to the line segment with the steepest negative slope.

Question 2.
Create an elevation-versus-time graphing story for the following graph:

Answer:
Answers will vary. A story such as the following fits the graph:
A swimmer climbs a ladder to a waterslide, sits for two seconds at the top of the slide, and then slides down the slide into water. She stays steady at the same position underwater for two seconds before rising to the surface.
Teachers should also accept other contexts, such as interpreting “0 elevation” as the height of a deck 3 ft. above ground.

Question 3.
Draw an elevation-versus-time graphing story of your own, and then create a story for it.
Answer:
Answers will vary. Do not be too critical of their graphs and stories.