Eureka Math Algebra 1 Module 1 Lesson 17 Answer Key

Engage NY Eureka Math Algebra 1 Module 1 Lesson 17 Answer Key

Eureka Math Algebra 1 Module 1 Lesson 17 Example Answer Key

Examples 1–2
Work the two examples as a class.

Example 1.
Solve 2x²-10x=0, for x.
Answer:
{0,5}

Example 2.
Solve x(x-3)+5(x-3)= 0, for x.
Answer:
{-5,3}

Example 3.
Consider the equation (x-2)(2x-3)=(x-2)(x+5). Lulu chooses to multiply through by \(\frac{1}{x-2}\) and gets the
answer x=8. But Poindexter points out that x=2 is also an answer, which Lulu missed.
a. What’s the problem with Lulu’s approach?
Answer:
You cannot multiply by \(\frac{1}{x-2}\) because x-2 could equal 0, which means that you would be dividing by 0.

b. Use factoring to solve the original equation for x.
Answer:
(x-2)(2x-3)-(x-2)(x+5)=0
(x-2)(2x-3-(x+5))=0
(x-2)(x-8)=0
x-2=0 or x-8=0
x=2 or x=8

Work through the responses as a class.
→ Emphasize the idea that multiplying by \(\frac{1}{x-2}\) is a problem when x-2 equals 0.

Eureka Math Algebra 1 Module 1 Lesson 17 Exercise Answer Key

Exercise 1.
Solve each equation for x.
a. x-10=0
Answer:
{10}

b. \(\frac{x}{2}\)+20=0
Answer:
{-40}

c. Demanding Dwight insists that you give him two solutions to the following equation:
(x-10)(\(\frac{x}{2}\)+20)=0
Can you provide him with two solutions?
Answer:
{10,-40}

d. Demanding Dwight now wants FIVE solutions to the following equation:
(x-10)(2x+6)(x²-36)(x²+10)(\(\frac{x}{2}\)+20)=0
Can you provide him with five solutions?
Answer:
{-40,-6,-3,6,10}

Do you think there might be a sixth solution?
Answer:
There are exactly 5 solutions.

Exercise 1 (continued)
Give students a few minutes to complete parts (e) and (f), and elicit student responses.

Consider the equation (x-4)(x+3)=0.

e. Rewrite the equation as a compound statement.
Answer:
x-4=0 or x+3=0

f. Find the two solutions to the equation.
Answer:
{-3,4}

Exercises 2–7
Give students time to work on the problems individually. As students finish, have them work the problems on the board. Answers are below.

Exercises 2–7

Exercise 2.
(x+1)(x+2)=0
Answer:
{-2,-1}

Exercise 3.
(3x-2)(x+12)=0
Answer:
{-12,\(\frac{2}{3}\)}

Exercise 4.
(x-3)(x-3)=0
Answer:
{3}

Exercise 5.
(x+4)(x-6)(x-10)=0
Answer:
{-4,6,10}

Exercise 6.
x²-6x=0
Answer:
{0,6}

Exercise 7.
x(x-5)+4(x-5)=0
Answer:
{-4,5}

Exercises 8–11
Give students time to work on Exercises 8–11 in pairs. Then, elicit student responses. Remind students of the danger of multiplying both sides by a variable expression.

Exercises 8–11

Exercise 8.
Use factoring to solve the equation for x: (x-2)(2x-3)=(x-2)(x+1).
Answer:
{2,4}

Exercise 9.
Solve each of the following for x:
a. x+2=5
Answer:
{3}

b. x²+2x=5x
Answer:
{0,3}

c. x(5x-20)+2(5x-20)=5(5x-20)
Answer:
{3,4}

Exercise 10.
Verify: (a-5)(a+5)=a²-25.
Answer:
a²+5a-5a-25=a²-25
a²-25=a²-25

b. Verify: (x-88)(x+88)= x²-88².
Answer:
x²+88x-88x-88²=x²-88²
x²-88²=x²-88²

c. Verify: A²-B²=(A-B)(A+B).
Answer:
A²-B²=A²+AB-AB-B²
A²-B²=A²-B²

d. Solve for x: x²-9=5(x-3).
Answer:
{2,3}

e. Solve for w: (w+2)(w-5)=w²-4.
Answer:
{-2}

Exercise 11.
A string 60 inches long is to be laid out on a tabletop to make a rectangle of perimeter 60 inches. Write the width of the rectangle as 15+x inches. What is an expression for its length? What is an expression for its area? What value for x gives an area of the largest possible value? Describe the shape of the rectangle for this special value of x.
Answer:
Length: 15-x Area: (15-x)(15+x)
The largest area is when x=0. In this case, the rectangle is a square with length and width both equal to 15.

Eureka Math Algebra 1 Module 1 Lesson 17 Problem Set Answer Key

Question 1.
Find the solution set of each equation:
a. (x-1)(x-2)(x-3)=0
Answer:
{1,2,3}

b. (x-16.5)(x-109)=0
Answer:
{16.5,109}

c. x(x+7)+5(x+7)=0
Answer:
{-7,-5}

d. x²+8x+15=0
Answer:
{-5,-3}

e. (x-3)(x+3)=8x
Answer:
{-1,9}

Question 2.
Solve x²-11x=0, for x.
Answer:
{0,11}

Question 3.
Solve (p+3)(p-5)=2(p+3), for p. What solution do you lose if you simply divide by p+3 to get p-5=2?
Answer:
p=-3 or p=7. The lost solution is p=-3. We assumed p+3 was not zero when we divided by p+3; therefore, our solution was only complete for p values not equal to -3.

Question 4.
The square of a number plus 3 times the number is equal to 4. What is the number?
Answer:
Solve x²+3x=4, for x, to obtain x=-4 or x=1.

Question 5.
In the right triangle shown below, the length of side AB is x, the length of side BC is x+2, and the length of the hypotenuse AC is x+4. Use this information to find the length of each side. (Use the Pythagorean theorem to get an equation, and solve for x.)
Answer:
Use the Pythagorean theorem to get the equation x²+(x+2)²=(x+4)². This is equivalent to x²-4x-12=0, and the solutions are -2 and 6. Choose 6 since x represents a length, and the lengths are

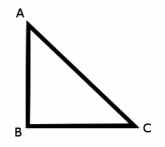
AB: 6
BC: 8
AC: 10

Question 6.
Using what you learned in this lesson, create an equation that has 53 and 22 as its only solutions.
Answer:
(x-22)(x-53)=0

Eureka Math Algebra 1 Module 1 Lesson 17 Exit Ticket Answer Key

Question 1.
Find the solution set to the equation 3x² + 27x = 0.
Answer:
3x(x+9)=0
3x=0 or x+9=0
x=0 or x=-9
Solution set: {-9,0}

Question 2.
Determine if each statement is true or false. If the statement is false, explain why, or show work proving that it is false.
a. If a=5, then ac=5c.
Answer:
True.

b. If ac=5c, then a=5.
Answer:
False. a could equal 5, or c could equal 0.
ac=5c
ac-5c=0
c(a-5)=0
c=0 or a-5=0
c=0 or a=5