Engage NY Eureka Math Algebra 1 Module 1 Lesson 26 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 26 Example Answer Key
Example
Fill in the doubling and adding 5 below:

Answer:

Eureka Math Algebra 1 Module 1 Lesson 26 Exercise Answer Key
Exercise 1.
Complete the tables below for the given starting number.

Answer:

Mathematical Modeling Exercise/Exercise 2
Given a starting number, double it and add 5 to get the result of Round 1. Double the result of Round 1 and add 5, and so on. The goal of the game is to find the smallest starting whole number that produces a result of 100 or greater in three rounds or fewer.
Walk around the class, observe student work, and give advice, such as:
→ Does starting with 10 produce a result of 100 or greater in Round 3?
→ Yes.
→ Why will all numbers greater than 10 work? Can you find a smaller starting number that also works?
→ Do you see any patterns in the tables you have already created?
→ As the starting number increases by 1, the result of Round 3 increases by 8.
→ Yes, 9 works. Is it the smallest?
→ Yes. When I start with 8, I need four rounds to get past 100.
After 8 minutes, show (or have a student show) that 9 is the correct answer by showing the tables:

Invite students to share other methods for finding the answer. For example, some may have worked the problem backward: If 100 is reached in three rounds, then \(\frac{100-5}{2}\)=47.5 must have been reached in two rounds, and
\(\frac{47.5-5}{2}\)=21.25 must been reached after the first round, which means the starting number is greater than
\(\frac{21.25-5}{2}\)=8.125, or the whole number 9.
Tell students that the next goal is to solve the same problem, but find the smallest number that results in 1,000 in three rounds or fewer:
→ Given a starting number, double it and add 5 to get the result of Round 1. Double the result of Round 1 and add 5, and so on. The goal of the game is to find the smallest starting whole number that produces a result of 1,000 or greater in three rounds or fewer.
This problem is not as easy as the starter problem to solve by guess-and-check. To solve this problem, guide students to formulate an equation. But first, you will need to explain how mathematicians create and describe recursive sequences. Let a1 be the number of the result of Round 1. We can also label the result of Round 2 as a2, and so on. Ask, “How could we label the starting number?” Guide them to label the starting number as a0. Then write an equation in terms of a0 and a1 in the table (that is still on the board) like this:
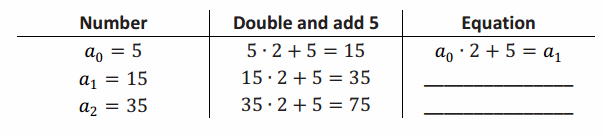
Ask students to help you complete and extend the table as follows:

Highlight on the board that the ordered list of terms 5, 15, 35, 75, … can be described by an initial value, a0=5, and a recurrence relation, ai+1=2ai+5, for i≥0. Written as follows:
a0=5
ai+1=2ai+5, i≥0
Tell them that this is an example of a recursively-defined sequence, or simply, a recursive sequence.
→ Have students mentally use the recurrence relation to find the next term after 75. Is it the double and add 5 rule?
Ask:
→ What other terms have we studied so far that are defined recursively?
→ Algebraic expressions, polynomial expressions, monomials
Teacher note: Terms that are defined recursively often use the term itself in the statement of the definition, but the definition of the term is not considered circular. Circularity does not arise in recursively defined terms because they always start with a well defined set of base examples, and then the definition describes how to generate new examples of the term from those base examples, which, by reiterating further, can then be used to generate all other examples of the term. The base examples prevent the definition from being circular. For recursive sequences, the base example(s) is just the initial value(s). For algebraic expressions, the well defined base examples are numerical symbols and variable symbols.
Exercise 3.
Using a generic initial value, a0, and the recurrence relation, ai+1=2ai+5, for i≥0, find a formula for a1, a2, a3, a4 in terms of a0.
Let students work individually or in pairs. Visit each group and ask questions that lead students to the following:
Answer:
a1=2a0+5,
a2=2a1+5=2(2a0+5)+5=4a0+15,
a3=2a2+5=2(2∙2a0+15)+5=8a0+35,
a4=2a3+5=2(2^3∙a0+35)+5=16a0+75.
Eureka Math Algebra 1 Module 1 Lesson 26 Exit Ticket Answer Key
The following sequence was generated by an initial value a0 and recurrence relation ai+1=2ai+5, for i≥0.
Question 1.
Fill in the blanks in the sequence:
( ___, 29, _______, ____, _______, 539, 1083)
Answer:
(12, 29, 63, 131, 267, 539, 1083)
Question 2.
In the sequence above, what is a0? What is a5?
Answer:
a0=12, a5=539
Eureka Math Algebra 1 Module 1 Lesson 26 Problem Set Answer Key
Question 1.
Write down the first 5 terms of the recursive sequences defined by the initial values and recurrence relations below:
a. a0=0 and ai+1=ai+1, for i≥0,
Answer:
(0,1,2,3,4)
b. a1=1 and ai+1=ai+1, for i≥1,
Answer:
(1,2,3,4,5)
c. a1=2 and ai+1=ai+2, for i≥1,
Answer:
(2,4,6,8,10)
d. a1=3 and ai+1=ai+3, for i≥1,
Answer:
(3,6,9,12,15)
e. a1=2 and ai+1=2ai, for i≥1,
Answer:
(2,4,8,16,32)
f. a1=3 and ai+1=3ai, for i≥1,
Answer:
(3,9,27,81,243)
g. a1=4 and ai+1=4ai, for i≥1,
Answer:
(4,16,64,256,1024)
h. a1=1 and ai+1=(-1)ai, for i≥1,
Answer:
(1,-1,1,-1,1)
i. a1=64 and ai+1=(-\(\frac{1}{2}\)) ai, for i≥1,
Answer:
(64,-32,16,-8,4)
Question 2.
Look at the sequences you created in Problem 1 parts (b)–(d). How would you define a recursive sequence that generates multiples of 31?
Answer:
a1=31 and ai+1=ai+31, for i≥1
Question 3.
Look at the sequences you created in Problem 1 parts (e)–(g). How would you define a recursive sequence that generates powers of 15?
Answer:
a1=15 and ai+1=15ai, for i≥1
Question 4.
The following recursive sequence was generated starting with an initial value of a0 and the recurrence relation ai+1=3ai+1, for i≥0. Fill in the blanks of the sequence.
(___, ___, 94, ___, 850, __)
Answer:
(10, 31, 94, 283, 850, 2551)
Question 5.
For the recursive sequence generated by an initial value of a0 and recurrence relation ai+1=ai+2, for i≥0, find a formula for a1, a2, a3, a4 in terms of a0. Describe in words what this sequence is generating.
Answer:
a1=a0+2,
a2=a0+4,
a3=a0+6,
a4=a0+8
It finds the next consecutive even or odd numbers after a0, depending on whether a0 is even or odd.
Question 6.
For the recursive sequence generated by an initial value of a0 and recurrence relation ai+1=3ai+1, for i≥0, find a formula for a1, a2, a3, a4 in terms of a0.
Answer:
a1=3∙a0+1,
a2=9a0+4,
a3=27a0+13,
a4=81a0+40