Engage NY Eureka Math Algebra 1 Module 1 Lesson 21 Answer Key
Eureka Math Algebra 1 Module 1 Lesson 21 Example Answer Key
Example
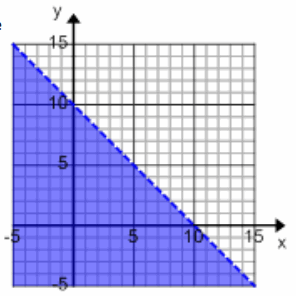
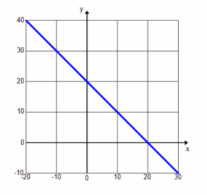
The solution to x+y=20 is shown on the graph below.
a. Graph the solution to x+y≤20.
Answer:
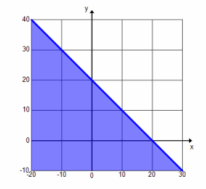
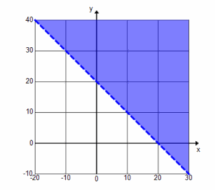
b. Graph the solution to x+y≥20.
Answer:
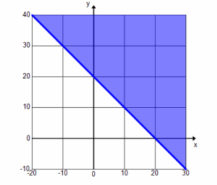
c. Graph the solution to x+y<20.
Answer:
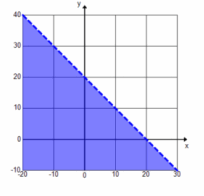
d. Graph the solution to x+y>20.
Answer:
Exercises 3–5
Students will need graph paper for this portion of the lesson. Have students work individually to complete as much of Exercise 3 as they can in 8 minutes, reserving the final 7 minutes for comparing with a neighbor and debating any conflicting answers. Alternatively, differentiate by assigning only a subset of the problems most appropriate for each student or group of students. In any case, make the assignments in pairs so that students have someone with whom to compare answers. Students may struggle as they work on parts (f)–(j), graphing solutions to equations like y=5; allow the students to struggle and discuss with each other. (Exercise 4 will revisit this idea with the entire class.) Students will rely on their experiences in Grade 8 as well as their explorations in Lessons 1–5 of this module to distinguish between the linear and nonlinear inequalities and answer the question that concludes Exercise 3.
Allow students to debate and discuss. Guide them to the correct conclusion, and then review the definition of a half-plane that follows Exercise 3, clarifying for students that a strict inequality does not include the or equal to option. It must be either strictly less than or greater than.
Exercises 3–5
Exercise 3.
Using a separate sheet of graph paper, plot the solution sets to the following equations and inequalities:
a. x-y=10
b. x-y<10 c. y>x-10
d. y≥x
e. x≥y
f. y=5
g. y<5 h. x≥5 i. y≠1 j. x=0 k. x>0
l. y<0
m. x2 -y=0
n. x2 +y2 >0
o. xy≤0
Answer:
Which of the inequalities in this exercise are linear inequalities?
Answer:
Parts (a)–(l) are linear. Parts (m)–(o) are not.
Exercise 4.
Describe in words the half-plane that is the solution to each inequality.
a. y≥0
Answer:
The half-plane lying above the x-axis and including the x-axis.
b. x<-5
Answer:
The half plane to the left of the vertical line x=-5, not including the line x=-5.
c. y≥2x-5
Answer:
The line y=2x-5 and the half-plane lying above it.
d. y<2x-5
Answer:
The half-plane lying below the line y=2x-5.
Exercise 5.
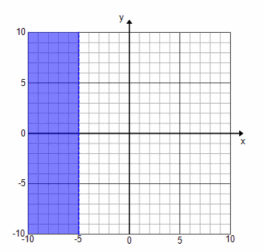
Graph the solution set to x<-5, reading it as an inequality in one variable, and describe the solution set in words. Then graph the solution set to x<-5 again, this time reading it as an inequality in two variables, and describe the solution set in words.
Answer:
Read in one variable: All real numbers less than -5. The graph will have an open circle at the endpoint -5 and extend as a ray to the left of -5 on the number line.
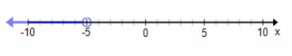
Read in two variables: All ordered pairs (x,y) such that x is less than -5. The graph will be a dashed vertical line through x=-5, and all points to the left of the line will be shaded.
Eureka Math Algebra 1 Module 1 Lesson 21 Exercise Answer Key
Exercises 1–2
Exercise 1.
Circle each ordered pair (x,y) that is a solution to the equation 4x-y≤10.
i. (3,2) (2,3) (-1,-14) (0,0) (1,-6)
Answer:

ii. (5,10) (0,-10) (3,4) (6,0) (4,-1)
Answer:
![]()
b. Plot each solution as a point (x,y) in the coordinate plane.
Answer:

c. Describe the location of the solutions in the coordinate plane.
Answer:
(Students may struggle to describe the points. Here is one possible description.) The points do not all fall on any one line, but if I drew a line through any two of the points, the others are not too far away from that line.
Exercise 2.
Discover as many additional solutions to the inequality 4x-y≤10 as possible. Organize solutions by plotting each as a point (x,y) in the coordinate plane. Be prepared to share the strategies used to find the solutions.
Answer:
(There are an infinite number of correct answers, as well as an infinite number of incorrect answers. Some sample correct answers are shown.)
(1,1), (1,-3), (-2,2), (-5,4)
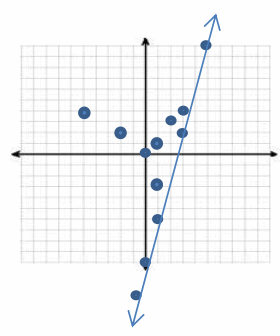
b. Graph the line y=4x-10. What do you notice about the solutions to the inequality 4x-y≤10 and the graph of the line y=4x-10?
Answer:
All of the points are either on the line, to the left of the line, or above the line.
c. Solve the inequality for y.
Answer:
y≥4x-10
d. Complete the following sentence.
If an ordered pair is a solution to 4x-y≤10, then it will be located _____ the line y = 4x – 10
Answer:
If an ordered pair is a solution to 4x-y≤10, then it will be located on, above, or to the left of the line y=4x-10.
Explain how you arrived at your conclusion.
Answer:
I observed that all the points were on one side of the line, and then I tested some points on the other side of the line and found that none of the points I tested from that side of the line were solutions to the inequality.
Next have the groups complete parts (b)–(d). As they work, circulate around the room answering questions and providing support. Make sure that students reversed the inequality symbol when solving for y in part (c). Discuss the following:
→ I noticed some of you wrote that all the points are on the left side of the line and others wrote that all the points are above the line. Are both of those descriptions correct?
→ Now, look at your answer to part (c). When you solved the inequality for y, what does that statement seem to tell you?
→ It tells me that all the y-values have to be greater than or equal to something related to x.
→ Then which description would you say best correlates to the inequality we wrote in part (c)? Points to the left of the line or points above the line? Why?
→ Points above the line because when we solve for y, we are describing where the y-values are in relation to the line, and y-values are plotted on the vertical axis; therefore, the words above and below are the accurate descriptors.
→ How can we depict the entire solution set of ALL the points above the line? When we worked with equations in one variable and graphed our solution set on the number line, how did we show what the solution set was?
→ We colored it darker or shaded it. So we can just shade in the entire area above the line.
→ What about the line itself, is it part of the solution set?
→ Yes.
→ What if it wasn’t? What if the inequality was y>4x-10? How could we show that it is all the points except that line?
→ We traditionally make the line a dashed line instead of a solid line to indicate that the points on the line are not part of the solution set.
Before moving on, make sure students understand that any ordered pair in the solution set will be a point (x,y) that is located on or above the line because that is the portion of the coordinate plane where y is greater than or equal to the difference of 4x and 10.
Eureka Math Algebra 1 Module 1 Lesson 21 Problem Set Answer Key
Question 1.
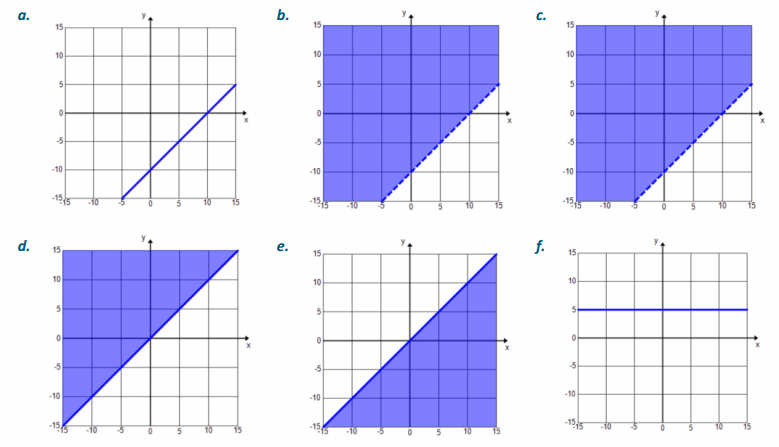
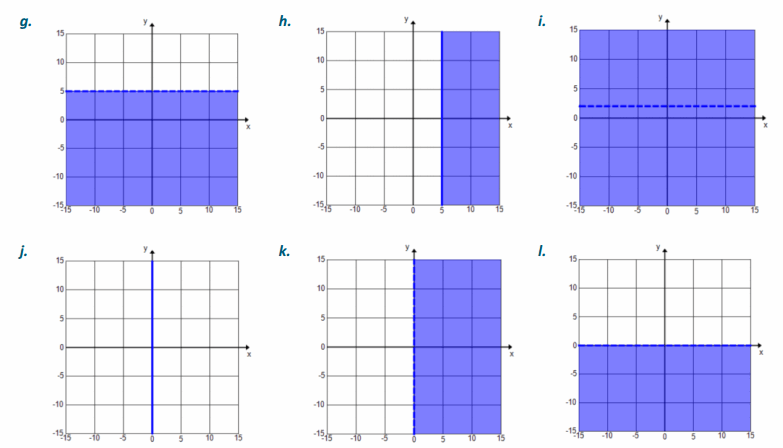
Match each inequality with its graph. Explain your reasoning.
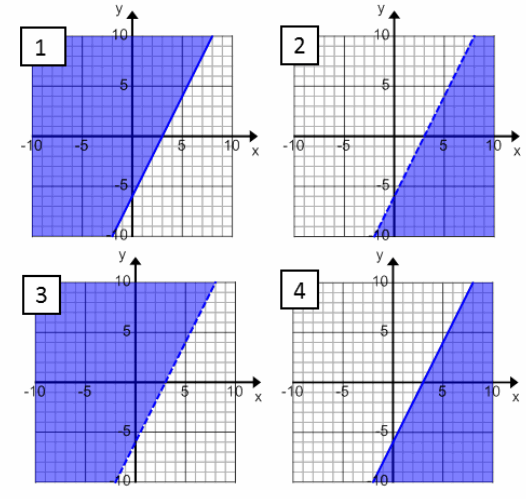
a. 2x-y>6
Answer:
Graph 2
b. y≤2x-6
Answer:
Graph 4
c. 2x<y+6
Answer:
Graph 3
d. 2x-6≤y
Answer:
Graph 1
Answer:
Student explanations will vary. Sample response: I rearranged each equation and found that they were all the same except for the inequality symbol. The strict inequalities are the dashed lines, and the others are solid lines. When solving for y, you can decide the shading. Greater than is shaded above the line, and less than is shaded below the line.
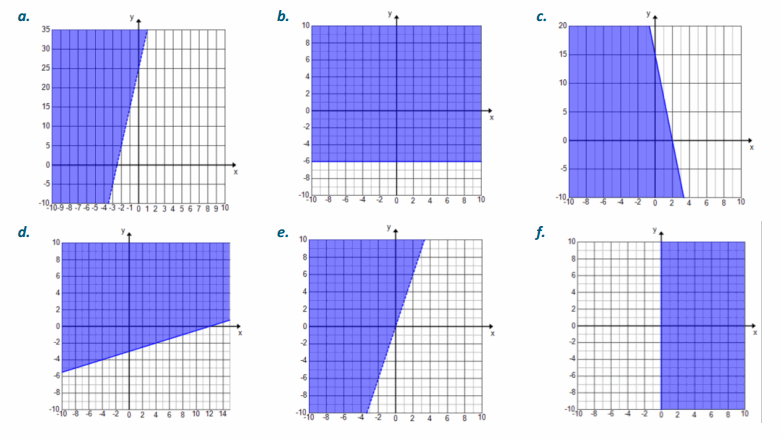
Question 2.
Graph the solution set in the coordinate plane. Support your answer by selecting two ordered pairs in the solution set and verifying that they make the inequality true.
a. -10x+y>25
b. -6≤y
c. y≤-7.5x+15
d. 2x-8y≤24
e. 3x<y
f. 2x>0
Answer:
Question 3.
Marti sells tacos and burritos from a food truck at the farmers market. She sells burritos for $3.50 each and tacos for $2.00 each. She hopes to earn at least $120 at the farmers market this Saturday.
a. Identify three combinations of tacos and burritos that will earn Marti more than $120.
Answer:
Answers will vary but should be solutions to the inequality 3.5x+2y>120.
b. Identify three combinations of tacos and burritos that will earn Marti exactly $120.
Answer:
Answers will vary but should be solutions to the equation 3.5x+2y=120.
c. Identify three combinations of tacos and burritos that will not earn Marti at least $120.
Answer:
Answers will vary but should not be solutions to the inequality or equation.
d. Graph your answers to parts (a)–(c) in the coordinate plane and then shade a half-plane that contains all possible solutions to this problem.
Answer:
The graph shown for part (d) is shown to the right. Answers to part (a) should lie in the shaded half-plane. Answers to part (b) should lie on the line, and answers to part (c) should lie in the un-shaded half-plane.
e. Create a linear inequality that represents the solution to this problem. Let x equal the number of burritos that Marti sells, and let y equal the number of tacos that Marti sells.
Answer:
3.5x+2y≥120
f. Are the points (10,49.5) a solution to the inequality you created in part (e)? Explain your reasoning.
Answer:
The point would not be valid because it would not make sense in this situation to sell a fractional amount of tacos or burritos.
Eureka Math Algebra 1 Module 1 Lesson 21 Exit Ticket Answer Key
What pairs of numbers satisfy the statement: The sum of two numbers is less than 10?
Create an inequality with two variables to represent this situation, and graph the solution set.
Answer:
Let x= one number, and let y= a second number.
Inequality: x+y<10
Graph the line y=-x+10 using a dashed line and shade below the line.