Vinay Pacha

On this page, you have to learn about Plane Figures definitions, types, and examples are here. These figures will demonstrate the shape of objects we see in our daily life. The plane shapes are two-dimensional closed shapes with no thickness and are known as 2-D shapes.

Check the various two-dimensional shapes along with their properties and perimeters to know the complete details. Follow the solved example problems, frequently asked questions of a plane figure. Go through the further modules to know how the shapes are described and how the area and perimeter are calculated.

Also, Read:

• Surface Area of Solids 
• Geometric Objects
• Common Solid Figures

Plane Figures – Definition

A plane figure is defined as a geometric figure it has no thickness. It consists of line segments, curves, or a combination of both line segments and curves. Some examples of plane figures in geometry such as circles, rectangles, triangles, squares, and so on.

A plane in geometry is a flat surface that extends up to infinity in all directions. 2D shapes will be a plane figure which can be drawn on a plane surface or a paper piece. Every 2D shape will have parameters like perimeter and area.

Types of Plane Figures

The following are the different types of plane figures. The plane figures are:

1. Circle
2. Square
3. Rectangle
4. Triangle
5. Pentagon
6. Octagon

1. Circle: The closed 2-Dimensional plane figure which is the set of all points in a plane and equidistant from the given point is known as the “center” (o). The distance from the outer line to the center of the circle is called a radius(R). Some examples of a circle are wheels, orbits, pizzas, etc.

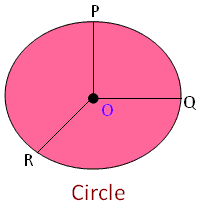
Centre: Centre is a point within the circle, that is equidistant from every point of the curve which encloses the circle. In the above-given figure, O will be the center of the circle.
Radius: The distance between the center to any point situated at the curve closing the circle is called a radius. In the above figure, OP, OQ, and OR are radius. Every radius of a circle has the same length that is all the radius of a circle is equal. Therefore, OP=OQ=OR and the radius is denoted by ‘R’.
Diameter: The line segment passing through the center and joint the two points that occurred at the curve closing the circle is called the diameter. Consider AOB or AB as the diameter of the circle O.
Diameter = Radius + Radius.
Hence, Diamter = 2 x Radius.
Circumference: The curve closing the circle is known as the circumference. In the circumference, every point is equidistant from the center.

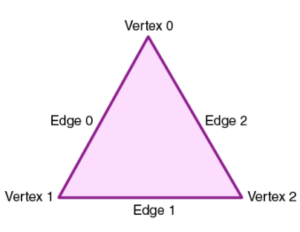
2. Triangle: It is a three-sided polygon with three vertices and edges is known as a triangle. The three angles of a triangle give a sum of 180°. One of the best examples of a triangle is the pyramids. The triangle figure as given below consists of vertex 0, vertex 1, vertex 2, Edge 0, Edge 1, and Edge 2.

 

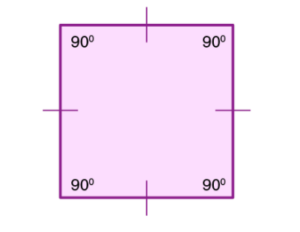
3. Square: A four-sided polygon that has four equal lengths of sides and angles which are equal to 90° is known as a square. A 2-dimensional regular quadrilateral is a square and their diagonals bisect each other at 90 degrees. Some examples of the square are a table, wall, cube, and, etc.

 

4. Rectangle: A 2- dimensional figure with four-sided where the pair of opposite sides are parallel and equal to each other is known as a rectangle. In a rectangle, all the angles are equal to 90 degrees. Examples of rectangles are Cardboard, TV, brick, etc.

 

5. Pentagon: The pentagon is a 2D plane shape. It will be a five-sided polygon, and the pentagon can be regular or irregular. In the regular pentagon, each interior angle is equal to 108 degrees, and each exterior angle measures. This shape has five diagonals. An example of the pentagon is, the US Department of Defence headquarters has the shape Pentagon, it is a perfect example of the pentagon shape.

6. Octagon: An octagon is a polygon with eight sides and can be either regular or irregular. It is a 2D shape with eight angles, and the sum of all interior angles of an octagon is 108 degrees. An example of the octagon is, the stop signboard that you can see on the roadside has an octagon shape.

The plane figures like rectangles, triangles, circles, squares..etc are called two-dimensional (2-D) figures. They have length and breadth.

Perimeter and Area of Plane Figures

2D Shape	Perimeter	Area
Circle	2Πr	Πr²
Square	4(Sides)	Side²
Rectangle	2(Length + Breadth)	Length * Breadth
Triangle	Sum of three sides	1/2 (Base * Height)
Pentagon	4(Side)	1/2 Product of diagonals
Octagon	2(Base + Side)	Base * Height

FAQ’s on Plane Figures

1. What are the examples of plane figures?

The examples of the plane figures are given below,
Plane figures: square, circle, rectangle, triangle, pentagon, octagon, hexagon, etc., are examples of plane figures.

2. Write the difference between 2-Dimensional and 3-Dimensional shapes?

2D shapes do not have thickness or height but 3D shapes have height.

3. What are the real-time examples of 2D shapes?

Examples of 2D shapes are pizza, tiles, brick, rectangular plot, ring, a piece of pizza.

4. What are the plane figures?

A plane figure is a two- dimensional closed figure which has no thickness. A plane in geometry is a flat surface that extends up to infinity in all directions. It has infinite width and length and no thickness (zero thickness).

In this article, you can know about the Midpoint Theorem which is invented by Rene Descartes, the famous mathematician. In geometry, the midpoint theorem benefits to find the missing values of the sides of the triangle. The midpoint theorem is one of the important theorems in the concept of geometry.

The midpoint theorem deals with the properties of triangles. Students can learn about the definition, statement, formula, proof of the Midpoint Theorem, and examples to find the coordinates of the defined points.

Related Articles:

• Similar Triangles
• Congruency of Triangles
• Basic Proportionality Theorem

Midpoint Theorem – Definition

The term midpoint means the ‘center’ of something, it is the midway between the two endpoints. The midpoint theorem expresses that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side of the triangle. A midpoint generally means a point on a line segment that has an equal distance from both endpoints and bisects the line segment.

Statement of Midpoint Theorem

The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side of the triangle and is also half of the length of the third side.”

Proof of Midpoint Theorem

Consider the triangle PQR, as shown in the above figure

Let S and T be the midpoint of the sides PQ and PR. Now, the line ST is said to be parallel to the side QR, where the ST is half of the side QR, i.e.,

ST ∥ QR

ST = (½ × QR)

Now, if you consider the below figure, it is an extended version of the above figure provided.

Construction:

Extend the line segment ST and produce it to point O such that, OT = ST.

In a triangle, PST and TOR,

TR = PT – – (given)

∠RTO = ∠PTD (vertically opposite angles)

∠SPT = ∠TRO (alternate angles)

By ASA congruence criterion,

△TOR ≅ △PST

Therefore,

∠ROT = ∠PST { by c.p.c.t.c}

∠ORT = ∠SPT { by c.p.c.t.c}

and RO = PS { by c.p.c.t.c}

∠ROT and ∠PSE are the alternate interior angles.

Assume OR and PQ  as two lines that are intersected by the transversal SO.

Similarly, ∠ORT and ∠SPT are the alternate interior angles.

Let us again assume that OR and PQ are the two lines that are intersected by the transversal PR.

Therefore, OR ∥ PQ

So, OR ∥ SQ

and OR = SQ (since SQ = SP, it is proved that OR = PS)

Thus, OSQR forms a parallelogram.

By the properties of a parallelogram, we can write

QR ∥ ST

and QR = ST

ST ∥ QR

and ST = (½ × QR)

Hence, the midpoint theorem is proved.

Midpoint Theorem Formula

In geometry, the midpoint theorem describes the midpoint of the line segment. It specifies the coordinate points of the midpoint of the line segment and can be identified by taking the average of the coordinates of the given endpoints. The formula for midpoint is used to identify the midpoint between the two given points.

If (x₁, y₁) and (x₂, y₂) are the coordinates of two given endpoints, then the midpoint formula is as follows

Midpoint (x,y) = [ (x₁+x₂)/2, (y₁+y₂)/2 ]

Here, x₁ and x₂ are coordinates of the x-axis, and y₁ and y₂ are the coordinates of the y-axis.

For example, to find the midpoint of (x,y,z) then the midpoint formula is

(x,y,z) = [ (x₁+x₂)/2, (y₁+y₂)/2 , (z₁+z₂)/2 ]

The coordinates are (x₁,y₁,z₁), (x₂,y₂,z₂).

Examples of Midpoint Theorem

Example 1: 
In triangle PQR, the midpoints of  PQ, RP, QR are S, T, and U respectively. Find the value of ST, if the value of QR = 12 cm.

Solution: 
Given QR = 14 cm
If S is the midpoint of PQ and T is the midpoint of PR then using the midpoint theorem
ST = (½ × QR)
Substituting the value of QR,
ST = (½ × 12)
ST = 6 cm.
Therefore, the value of ST is 6cm.

Example 2:
How do you solve a problem such that the point (1,4) is the midpoint of (2,-4), and at what point is the second coordinate?
Solution: 
The first coordinates are (2,-4).
Let us assume that the other coordinates are (m,n).
Now, the formula for midpoint is
(x,y) = [ (x₁+x₂)/2, (y₁+y₂)/2 ]
Substitute the above given values,
We get,
(1,4) = [(2+m)/2,(-4+n)/2]
⇒ (2+m)/2 = 1 and (-4+n)/2 = 4
⇒ m= 0 and n= 12.
Therefore, the second point has coordinates (0,12).

Example 3:
Find the coordinates of the center of the circle. The endpoints of the triangle are given as (6, 2), and (2, 4).
Solution:
Given coordinates of the triangle are
(6, 2) = (x₁, y₁) and (2, 4) = (x₂, y₂)
Coordinates of the center of the circle (x,y) = [ (x₁+x₂)/2, (y₁+y₂)/2 ]
[ (x₁+x₂)/2, (y₁+y₂)/2 ]
= [ ( 6+2)/2, (2+4)/2 ]
= [ 8/2, 6/2 ]
= (4, 2)
Hence, the coordinates of the center of the circle are (4,2).

FAQs on Midpoint Theorem

1. what does the midpoint theorem says?
The midpoint defines that “the line segment drawn from the midpoint of two sides of the triangle is parallel to the third side of the triangle and it is half of the length of the third side of the triangle”.

2. Why is important to define a midpoint?
The midpoint formula applies when one is needed to find the exact center point between two defined points. A line segment has to use this formula to calculate the exact point that bisects a line segment defined by the two given points.

3. How to prove the midpoint theorem?
To prove the midpoint theorem, we use congruency rules. We draw a triangle outside to the given triangle so that it touches the sides of the triangle. Now, we prove that it is congruent to any one part of the triangle. Here, we use the CPCTC rules to prove the equality between the sides of the triangle.

4. What is the use of the midpoint theorem in everyday life?
The midpoint theorem is basically used to know the specific information regarding the length of the sides of the triangle.

Worksheet on Changing the Subject of a Formula or Equation will help you learn how to change the subject of formula and find the value of a variable easily using the substitution method. Practice the questions in the Changing the Subject in an Equation or Formula Worksheet PDF on a regular basis and improve your subject knowledge of the concept. Download the Changing the Subject of a Formula or Equation Practice Worksheet for free and clear your doubts anytime and anywhere.

See More:

• Worksheet on Changing the Subject of a Formula
• Problem on Change the Subject of a Formula

Changing the Subject of a Formula Worksheet with Answers PDF

I. Discount percentage=Discount/marked price × 100 find discount when discount percent=30 and marked price=1000.

Solution:

Given that,
Discount percentage=Discount/marked price × 100
Discount percentage/100=Discount/marked price
Discount percentage/100 × marked price=Discount
Also given discount percent=30 and marked price=1000.
Discount=Discount percentage/100 × marked price
Discount=30/100 × 1000
=300
Therefore, Discount=Rs 300.

---

II. Area of Trapezium=1/2(a+b).h find h when Area of trapezium is 60 square inches, a=10,b=5.

Solution:

Given that,
Area of Trapezium=1/2(a+b).h
A=1/2(a+b).h
2A=(a+b).h
2A/(a+b)=h
Also given A=60 sq inches,a=10,b=5.
2(60)/(10+5)=h
120/15=h
Therefore, h=8.

---

III. Profit percentage=profit/cp × 100 find profit when cost price is 500 and profit percentage is 20.

Solution:

Given that,
Profit percentage=profit/cp × 100
Profit percentage/100=profit/cp
Profit percentage/100 × cp=profit
Also given cost price is 500 and profit percentage is 20.
20/100 × 500=profit
1/5 × 500=profit
profit=100
Therefore, Profit=Rs 100.

---

IV. Diameter=2 ×  radius Find the radius when diameter=20.

Solution:

Given that,
Diameter=2 ×  radius
radius=Diameter/2
Also given diameter=20
raius=20/2=10.
Therefore, radius=10.

---

V. F=9/5 × c + 32 find c when F=50⁰.

Solution:

Given that,
F=9/5 × c + 32
F-32=9/5 × c
c=(F-32)5/9
Also given F=50⁰
c=(50 – 32)5/9
=18 × 5/9
=10⁰
Therefore,c=10⁰.

---

VI. S=D/T find d when s=80 kmph and time=2 hours.

Solution:

Given that,
S=D/T
D=S × T
Also given s=80 km per hour and time=2 hours.
D=80 × 2
=160
Therefore, distance D=160 km.

---

VII. principal=Amount – Interest. Find Amount when principal=1000 and interest=40.

Solution:

Given that,
principal=Amount – Interest
Amount=principal + Interest
Also given principal=1000 and interest=40.
Amount=1000 + 40
=1040
Therefore, the Amount is Rs 1040.

---

VIII. A=wl find l when A=200 and w=50

Solution:

Given that,
A=wl
A/w=l
Also given A=200 and w=50
200/50=l
l=4
Therefore, l=4.

---

IX. If y=3x+6 find x when y=8

Solution:

Given that,
y=3x+6
y-6=3x
x=y-6/3
Also given y=8
x=8-6/3
=2/3
Therefore, x=2/3.

---

x. v=u+at find a when v=8,u=4,t=2

Solution:

Given that,
v=u+at
v-u=at
v-u/t=a
Also given  v=8,u=4,t=2
8-4/2=a
a=4/2=2
Therefore, a=2.

---

xi. If p=2(l+b) find b when l=5 and p=40.

Solution:

Given that,  p=2(l+b)
p=2l+2b
p-2l=2b
b=p-2l/2
Also given l=5 and p=40.
b=40-2(5)/2
=40-10/2
=30/2=15
Therefore,b=15.

---

xii. Discount=marked price-sales price find marked price when discount=300 and sales price=800.

Solution:

Given that,
Discount=marked price- sales price
marked price=Discount + sales price
Also given discount=300 and sales price=800.
marked price=300 + 800
marked price=1100
Therefore, marked price=1100.

---

 

If you are about to clear your doubts in homework or need an extra bit of practice this is the place for you. Worksheet on Changing the Subject of a Formula gives you ample practice on different kinds of questions framed on the topic. Try the problems over here on your own and then cross-check with the solutions provided to test where you stand in your preparation. Our Changing the Subject of a Formula Worksheet will complement your preparation and help you perform well in your exams.

Read More:

• Problem on Change the Subject of a Formula
• Worksheet on Change of Subject

Changing the Subject of a Formula Worksheet with Answers

Change the subject as indicated in the following formulas
1. Distance= Speed × Time make T as the subject.

Solution:

Given Distance= Speed × Time
Move speed to the left side then,
Distance/Speed=Time
Therefore, Time=Distance/speed.

---

2. p=2(l+b) make l as subject

Solution:

Given p=2(l+b)
Move 2 to the left side and divide it with p.
p/2=l  +b
Subtract b on both sides
p/2-b=l + b – b
p/2-b=l
Therefore, l=p/2-b.

---

3. Profit=Selling Price – Cost Price make selling Price as subject

Solution:

Move Cost Price to the Left,
Profit + Cost Price=Selling Price
Therefore, Selling Price=Profit + Cost Price.

---

4. Y=mx + c make x as a subject.

Solution:

Subtract c on both sides.
y-c=mx + c – c
y-c=mx
Divide m on both sides
(y-c)/m=mx/m
(y-c)/m=x
Therefore, x=(y-c)/m.

---

5. D=b²– 4ac make b as the subject.

Solution:

Given, D = b² – 4ac
Move 4ac to the left side and add it to the D
D + 4ac = b²
By Applying square root on both sides we get,
√(D + 4ac) = √b²
√(D + 4ac) = b
Therefore, b=√(D + 4ac) .
vi) I = (P × R × T)/100 make T as subject
Move 100 to the left side and multiply it with I
I × 100 = PRT
Move RP to the left side and divide it with 100I
100I/RP = T
Therefore, T=100I/RP.

---

6. Profit Margin=Total Income/Net Sales × 100 make Total Income as the subject.

Solution:

Given Profit Margin=Total Income/Net Sales × 100
Move100 to Left and divide by Profit Margin,
Profit Margin/100=Total income/Net Sales
Move Net Sales to the left,
Net Sales × Profit Margin/100=Total Income
Therefore, Total Income= Net Sales × Profit Margin/100.

---

7. Income – Savings=Expenses make Savings as the subject.

Solution:

Given,
Income – Savings=Expenses
Move expenses to the Left and savings to the right,
Income – Expenses= Savings.
Therefore, Savings=Income – Expenses.

---

8. s = mL + r make L the subject by rearranging the formula?

Solution:

Given s=mL + r 
First, Subtract r on both sides
s – r = mL + r -r
s-r=mL
Now, Divide m on both sides
(s – r)/m = L
Therefore, L = (s – r)/m.

---

9. A = 1/2 (l₁ + l₂) h; make l₁ as subject

Solution:

Given that A = 1/2 (l₁ + l₂) h
Move 1/2.h to the left side and divide it with A
2A/h = l₁ + l₂
Move l₂ to the left side and subtract it from 2A/h
2A/h – l₂ = l₁
Therefore, l₁ = 2A/h – l₂.

---

10. h² = p² + b² make p as a subject.

Solution:

Given that h² = p² + b²
Move b² to the left side and subtract it from h²
h² – b² = p²
Apply square root on both sides
√(h² – b²) = √(p²)
√(h² – b²) = p
Therefore, p = √(h² – b²).

---

11. A = P {1 + (Rn/100)}; make R as subject

Solution:

Given that A = P {1 + (Rn/100)}
Move P to the left side and Divide it with A.
A/P = 1 + (Rn/100)
Move 1 to the left side and Subtract it with A/P.
A/P – 1 = Rn/100
Move 100 to the left side and Multiply it with A/P – 1.
100(A/P – 1) = Rn
Move n to the left side and Divide it with 100(A/P – 1).
{100(A/P – 1)}/n = R
Therefore, R={100(A/P – 1)}/n .

---

 

Are you searching for help online to master the concept of Division of Polynomial by Monomial? Then this is the right place as you will get complete information on how to divide a polynomial by a monomial. Worksheet on Dividing Polynomial by Monomial can be great for students to learn the concept of dividing a polynomial by a monomial.  Use this opportunity and practice various questions framed on the topic. Practice the Math Dividing Polynomial by a Monomial Worksheets PDF for free of cost regularly and enhance your math skills.

Also, See:

• Worksheet on Multiplying Monomial and Polynomial
• Worksheet on Multiplying Monomial and Binomial

Dividing Polynomials by Monomials Worksheet PDF

I. Simplify the following polynomial divided by monomial:
(i) 15m³ + 9m² + 6m by 3m
(ii) 5x³ + 30x² + 15x by 5x
(iii) 48x³ – 16x² + 80x by 16x
(iv) -3y⁶ + 6y⁴ + y² + 4 by 2y²
(v) 14a²b – 16ab – 20ab² by 2ab
(vi) 14x³y³ + 21x⁴y² – 49x²y⁴ by -7x²y²

Solution:

(i) Given that,
15m³ + 9m² + 6m by 3m
=15m³ + 9m² + 6m/3m
=15m³/3m + 9m²/3m + 6m/3m
=5m² + 3m + 2
Therefore, By dividing 15m³ + 9m² + 6m by 3m we get  5m² + 3m + 2.
(ii) Given that,
5x³ + 30x² + 15x by 5x
=5x³ + 30x² + 15x/5x
=5x³/5x + 30x²/5x + 15x/5x
=x² + 6x +3
Therefore, By dividing 5x³ + 30x² + 15x by 5x we get  x² + 6x +3.
(iii) Given that, 48x³ – 16x² + 80x by 16x
=48x³ – 16x² + 80x/16x
=48x³/16x -16x²/16x + 80x/16x
=3x²-x +5
Therefore, By dividing 48x³ – 16x² + 80x by 16x we get 3x²-x +5.
(iv) Given that, -3y⁶ + 6y⁴ + y² + 4 by 2y²
=-3y⁶ + 6y⁴ + y² + 4/2y²
=-3y⁶/2y² + 6y⁴/2y² + y²/2y² +4/2y²
=-3/2y⁴ + 3y² + 1/2 +2/y²
Therefore, By dividing -3y⁶ + 6y⁴ + y² + 4 by 2y² we get -3/2y⁴ + 3y² + 1/2 +2/y².
(v) Given that, 14a²b – 16ab – 20ab² by 2ab
=14a²b – 16ab – 20ab²/2ab
=14a²b/2ab – 16ab/2ab – 20ab²/2ab
=7a-8-10b
Therefore, By dividing 14a²b – 16ab – 20ab² by 2ab we get 7a-8-10b.
(vi) Given that, 14x³y³ + 21x⁴y² – 49x²y⁴ by -7x²y²
=14x³y³/-7x²y² + 21x⁴y²/-7x²y²-49x²y⁴/-7x²y²
=-2xy-3x²+7y²
Therefore, By dividing 14x³y³ + 21x⁴y² – 49x²y⁴ by -7x²y² we get -2xy-3x²+7y².

---

II. Solve the following by dividing the polynomial by a monomial:
(i) (x² – 5xy) ÷ 2x
(ii) (3z³ – 6z² + 12z) ÷ 3z
(iii) (4m⁶ – 3m⁵ + 8m⁴) ÷ m²
(iv) (8a⁷ – 6a⁶ + 2a⁴) ÷ a³
(v) (12y⁵ – 21y⁴) ÷ (-3y³)
(vi) (36a⁶ – 72a⁵) ÷ 9a⁵
(vii) (x⁴-3x³+4x²+2x) ÷x²

Solution:

(i) Given that, (x² – 5xy) ÷ 2x
=x²/2x-5xy/2x
=1/2x-5/2y
Therefore, By dividing (x² – 5xy) ÷ 2x we get 1/2x-5/2y.
(ii) Given that, (3z³ – 6z² + 12z) ÷ 3z
=3z³/3z-6z²/3z +12z/3z
=z²-6z+4
Therefore, By dividing 3z³ – 6z² + 12z by 3z we get z²-6z+4.

(iii) Given that, (4m⁶ – 3m⁵ + 8m⁴) ÷ m²
=4m⁶/m²-3m⁵/m² + 8m⁴/m²
=4m⁴-3m³ + 8m²
Therefore, By dividing 4m⁶ – 3m⁵ + 8m⁴ with m² we get 4m⁴-3m³ + 8m².

(iv) Given that, (8a⁷ – 6a⁶ + 2a⁴) ÷ a³
=8a⁷/a³ -6a⁶/a3 + 2a⁴/a³
=8a⁴-6a³+2a
Therefore, By dividing 8a⁷ – 6a⁶ + 2a⁴ with a³ we get 8a⁴-6a³+2a.

(v) Given that, (12y⁵ – 21y⁴) ÷ (-3y³)
=12y⁵ /-3y³ + 21y⁴/3y³
=-4y² +7y
Therefore, By dividing 12y⁵ – 21y⁴ with -3y³ we get -4y² +7y.

(vi) Given that, (36a⁶ – 72a⁵) ÷ 9a⁵
=36a⁶ /9a⁵ – 72a⁵/9a⁵
=4a-8
Therefore, By dividing 36a⁶ – 72a⁵ with 9a⁵ we get 4a-8.
(vii) Given that, (x⁴-3x³+4x²+2x) ÷x
=x⁴/x-3x³/x+4x²/x+2x/x
=x³-3x²+4x+2
Therefore, By dividing x⁴-3x³+4x²+2x by x we get x³-3x²+4x+2.

---

III. Divide the following polynomial by monomial and write the answer in simplest form:
(i) 8a³ – 48a² + 64a by 8a
(ii) 18m²n² – 2mn² + 6mn³ by 2mn
(iii) 8a²b – 4ab² – 20ab by 4ab
(iv) 6x⁴ – 3x³ + (3/2)x² by 3x
(v) x⁴ + 2x² by x²
(vi) 5x³+ 25x²+30x by 5x

Solution:

(i) Given that, 8a³ – 48a² + 64a by 8a
=8a³/8a-48a²/8a + 64a/8a
=a²-6a+8
Therefore, By dividing 8a³ – 48a² + 64a by 8a we get a²-6a+8.
(ii) Given that, 18m²n² – 2mn² + 6mn³ by 2mn
=18m²n²/2mn-2mn²/2mn + 6mn³/2mn
=9mn-n+3n²
Therefore, By dividing 18m²n² – 2mn² + 6mn³ by 2mn we get 9mn-n+3n².
(iii) Given that, 8a²b – 4ab² – 20ab by 4ab
=8a²b/4ab-4ab²/4ab – 20ab/4ab
=2a-b-5
Therefore, By dividing 8a²b – 4ab² – 20ab by 4ab we get 2a-b-5.
(iv) Given that, 6x⁴ – 3x³ + (3/2)x² by 3x
=6x⁴/3x-3x³/3x + (3/2)x²/3x
=2x³ – x² + 1/3x
Therefore, By dividing 6x⁴ – 3x³ + (3/2)x² by 3x we get 2x³ – x² + 1/3x.
(v) Given that, x⁴ + 2x² by x²
=x⁴/x² + 2x²/x²
=x²+2
Therefore, By dividing x⁴ + 2x² by x² we get x²+2.
(vi) Given that, 5x³+ 25x²+30x by 5x
=5x³/5x+25x²/5x + 30x/5x
=x² + 5x + 6
Therefore, By dividing 5x³+ 25x²+30x by 5x we get x² + 5x + 6.

---

 

On this page, you will learn about the properties of natural numbers. Natural numbers are an important part of the number system, it is a set of whole numbers from 1 to infinity. The result of four arithmetic operations on natural numbers referred to Properties of natural numbers.

These numbers are used in our daily activities. Natural numbers come under real numbers, which include only the positive integers i.e., 1, 2, 3, 4, 5,…, and so on, excluding zero, fractions, decimals, and negative numbers. Remember that set of natural numbers does not include negative numbers or zero.

Read Some More Article:

• Prime and Composite Numbers
• Highest Common Factor
• Properties of Whole Numbers

Natural Numbers – Definition

Natural numbers are defined as the numbers which are positive integers and include numbers from 1 to infinity. These natural numbers are countable numbers and are preferred for calculation purposes. A set of natural numbers is denoted by the ‘N’.
N= {1,2,3,4,5,6,7,………..}
Where 1 is the smallest natural number and the sum of natural numbers from 1 to 100 is n(n+1)/2.

Types of Natural Numbers

There are two important types of natural numbers, namely:
1. Even Natural Numbers.
2. Odd Natural Numbers.

Even Natural Numbers: A system of natural numbers, which are divisible by 2 or multiplies of 2 is called a set of even numbers. Even natural number is denoted by ‘E’. Even numbers are infinite.
Therefore, E = {2, 4, 6, 8, 10, 12, 14, …….}.

Odd Natural Numbers: A natural number that is not divisible by 2 or not multiplies of 2 is called a set of odd numbers. An odd natural number is denoted by ‘O’. There are infinite odd natural numbers.
Therefore, O = { 1, 3, 5, 7, 9, 11, 13,…}.

Properties of Natural Numbers

Natural numbers have four important properties, which are as follows,
1. Closure Property
2. Distributive Property
3. Associative Property
4. Commutative Property

1. Closure Property:

A natural number will be closed under addition and multiplication. It means adding or multiplying two natural numbers result will be in a natural number. While, for subtraction and division, natural numbers don’t follow the closure property.
Addition: When x and y are two natural numbers, x+y is also a natural number. Suppose an example, 3+3= 6, 7+4 = 11, and similarly, all the resultants are natural numbers.
Subtraction: When x and y are two natural numbers, but x-y might not result in natural numbers. Consider an example, 4-6 = -2, and 6-4 = 2.
Multiplication: For x and y are two natural numbers, so x*y is also a natural number. For example, 6*3 = 18, similarly all results from multiplication are natural numbers.
Division: For the two national numbers x and y, the division might or might not result in a natural number. For example, 12/3 = 4, and 12/5 =1.222

2. Commutative Property:

These property natural numbers state that the sum or product of two natural numbers remains the same even if you interchange the order of the numbers. Let us check for all four arithmetic operations,
Addition: When two natural numbers x and y,  x + y = y + z is aslo a natural number.
Multiplication: For x, and y are two natural numbers, then x × y = y × x is also a natural number.
Subtraction: When x and y are two natural numbers, but x – y≠ y– x. So x-y and y-z is not natural number.
Division: For two natural numbers x and y, but x ÷ y ≠ x ÷ y (not equal). So these result values are not natural numbers.

Therefore, we can say that the set of natural numbers is commutative property under addition and multiplication but the case is not the same for subtraction and division. So, the commutative property of N is stated as follows: For all x, y ∈ N, x + y = y +x and x × y = y × x.

3. Distributive Property:

Distributive property of natural numbers states that expression with three numbers x, y, and z will be given in the form of X (Y+Z) then it will be resolved as XY+ XZ or X(Y-Z) = XY-XZ, which means that the operand x is distributed among the other two operands, y, and z.

• Multiplication of natural numbers is always distributive over the addition, So it will be expressed as,  x × (y + z) = xy + xz.
• Multiplication of natural numbers is also distributive over subtraction, then the expression is, x × ( y – z) = xy – xz.

4. Associative Property:

The associative property of natural numbers states that the sum or addition and product or multiplication of any three natural numbers remain the same though the grouping of numbers is changed. The three national numbers, say, x, y and z, is x + (y + z) = (x + y) + z and x * (y * z) = (x * y) * z. Whereas, natural numbers do not follow the associative property for multiplication and division.
Addition: For natural numbers x, y and z, addition is associative, i.e. x + (y+z )= (x + y) + z. Consider an example, (12 +1) +1 = 14 = 12 + (1 + 1)
Multiplication: When x and y, z are three natural numbers, multiplication is an associative property, it means x*(y*z) = (x*y)*z. For an example of associative property is, (1*4)*2 = 8 = 1*(4*2).
Subtraction: For three natural numbers, x, y, and z. The subtraction is not an associative property, which means x-(y-z) is not equal to (x-y)-z. Consider an example, (3-7)- 1 = -5 but 3-(7-1) = -3.
Division: For three natural numbers a, b, and c division is not associative property, because x/(y/z) is not equal to (x/y)/z. For example, 2/(3/6) = 4 but (2/3)/6 = 0.11 both values are not equal.

Therefore, we can say that the set of natural numbers is associative under addition and multiplication but the case is not the same for subtraction and division.

FAQ’s on Properties of Natural Numbers

1. What are Natural numbers?

A. Generally, Counting numbers are referred to as Natural numbers. They start with 1 and go on 2, 3, 4, 5, and more. These are ones in which we can do the counting and we will be denoted by ‘N’. The only set of natural numbers are denoted by N. Natural numbers are from 1 to infinity.

2. Is the number 0 a natural number?

A. As we know that 0 is neither positive nor negative, it is however considered a whole number despite not being positive. Hence, it comes under a natural number as well. It will be presented on the number line to identify numbers in a set but we can’t use it to count anything.

3. Write the difference between the natural numbers and whole numbers?

A. Natural numbers only include positive numbers which started from 1 to infinity, whereas whole numbers are the combination of zero, positive numbers(natural numbers), and they start from 0 and end at infinite value.

4. List a few examples of Natural Numbers? 

A. The examples of natural numbers are 2, 5, 7, 9, 13, 15, 18, 98, 117,..etc.

5. State the properties of Natural Numbers?

A. Natural numbers have four properties, which are as follows:

1. Closure Property – The Natural number follows closure property for addition and multiplication but not for the division and subtraction operations.

2. Commutative Property – In this, all the natural numbers follow commutative property only for addition and multiplication operations.

3. Associative Property – The set of natural numbers is associative under addition and multiplication but not subtraction and division.

4. Distributive Property – All given natural numbers, multiplication is distributive under the addition and subtraction operations.

Addition and multiplication are the operations for which a set of natural numbers follows as most of the properties. However, division and subtraction do not follow those properties.

The estimation of Numbers is an integral aspect of mathematics, and we engage in its day-to-day life, approximate value is not good enough occasionally, so we need to know the exact number. 6th Grade Math Students can enhance their math skills by answering the questions from the Estimation Worksheets PDF. Whereas for quick calculation use estimation.

To estimate Sum, Difference, Product, and or Quotient, first, we need to round off the given number to the nearest tens, hundreds, thousand, million, or any other ten multiple numbers, after doing so we need to apply the required mathematical operations. With the help of the Worksheet on Estimation, you can better understand the principles of Estimation. Exercise the Problems in Estimation Worksheet PDF carefully and answer problems fastly in your tests.

Also, Read:

• Worksheet on Estimate 
• Estimating Product and Quotient
• Estimate to nearest Hundreds

Estimation Worksheet with Answers

Problem 1:
Estimate the following values to the nearest ten,
(i) 36+53
(ii) 57- 43

Solution:

The values are given in the question,
Now, we should round off numbers to the nearest ten multiple.
(i) 36 + 53
First, we have to round off 36 to the nearest 10.
In 36, the units digit is 6, which is greater than 5. So, we have to replace zero in the units place and the tens place digit is increased by one.
So, the 36 is rounded off to 40.
Next, the number is 53. In this unit’s place digit, 3 is less than 5, so we need to replace zero in units digit and keep the remaining digits as it is.
The value 53 is rounded off to 50.
Now, find the estimated sum value.
The sum value is 40 + 50 = 90.
Therefore, the sum of the given value is 90.

(ii)57 – 43
Now, we need to find the difference value.
The value 57 is between 50 and 60, compared to 50, 57 is near to 60. So, the value 57 is rounded off to 60.
Next, the value 43 is between 40 and 50, compared to 50, the value 43 is near to 40. So, 43 is rounded off to 40.
After, perform the subtraction operation, the difference value is,
60 – 40 = 20.
Thus, the final difference value is 20.

---

Problem 2:
Estimate the following to nearest tens,
(i) 64÷6
(ii) 23 x 82

Solution:

As given in the question the values.
Now, estimate the given numbers to the nearest tens.
(i) 64÷6
Given the value is 64 and 6.
Now, we have to find the estimating quotient value.
First, round off 64 to the nearest 10 which is 60.
Now, divide 60 by 6.
So, the value is
60 ÷ 6 = 10
Therefore, estimating the quotient of given numbers is 60.

(ii) 23 x 82
The number 23 is between 20 and 30. But the value 23 is near to 20 compared to 30. Therefore, 23 is rounded down to 20.
Next, the number 82 is between 80 and 90. But the value 82 is near 80 compared to 90. Therefore, 82 is rounded up to 80.
Now, Multiply 20 and 80.
20 × 80 = 1600.
Hence, the estimated product value is 1600.

---

Problem 3:
Using the Estimation, find the value to the nearest hundreds. The value is 469+ 972

Solution:

Given the values in the question.
Now, we should round off numbers to the nearest hundreds.
(i) 469 + 972
Now, first, we have to round off 469 to the nearest 100.
In 469, the tens place digit is 6, which is greater than 5. So, we have to replace zero in the units place, tens place, and the hundreds place digit is increased by one.
So, the 469 is rounded off to 500.
Next, the number is 972. In this tens place digit is 7, which is greater than 5. So we need to replace zero in units place digit, tens place digit and increase hundred place digits by one.
The value 972 is rounded off to 1000.
Now, find the estimated sum value.
The sum value is 1000+ 500 = 1500.
Therefore, the sum of the given value is 1500.

---

Problem 4:
Find the estimation difference value of 826- 421 to the nearest hundred?

Solution:

The given values are 826, and 421.
Now, we need to find the difference value using the estimation.
The value 826 is between 800 and 900, compared to 900, 826 is near to 800. So, the value 826 is rounded off to 800.
Next, the value 421 is between 400 and 500, compared to 500, the value 421 is near to 400. So, 421 is rounded off to 400.
After, perform the subtraction operation, the difference value is,
800 – 400 = 400.
Thus, the final difference value of the given numbers is 400.

---

Problem 5:
What is the product value of 1678, 3021 to nearest 1000 using the estimation?

Solution:

As given in the question the values.
Now, we need to find the product value to the nearest 1000’s.
First, the number is 1678 is rounded off to 2000.
Next, the number is 3021, which is rounded off to 3000.
Now, perform the multiplication operation.
The product value is,
2000 x 3000 = 60,00,000
Hence, the estimated product value to the nearest 1000 is 60,00,000.

---

Problem 6:
Using estimation, Find the nearest 100 quotient value of 4210 divided by 3?

Solution:

As given in the question, the values are 4210, and 3.
We have to round off the values and find the quotient value.
The value 4210 is rounded off to 4200, and the dividend value is 3.
Now, divide 4200 by 3.
So, the value is
4200 ÷ 3 = 1400
Therefore, after estimating the quotient of given numbers is 1400.

---

Problem 7:
Sunny spent 876/- on groceries and 582/- on shopping. While discussing the expenditure he says that she approximately spent 880/- on groceries and 580 on shopping. What is the estimated sum of his expenditure?

Solution:

The data is given in the question.
Now, we need to find the estimated sum of his expenditure.
The Actual expenditure on groceries is 876.
876 can be rounded off to 880.
Next, the Actual expenditure on shopping is 582.
582 can be rounded off to 580.
Now, we can easily find the estimated sum value.
So, the sum is, 880 + 580 = 1460.
Thus, the estimated sum value is 1460.

---

Problem 8:
Estimate the products of 23 and 76?

Solution:

As, given in the question the values are 23, 76.
Now, we have to estimate the given numbers to the nearest tens, hundreds, or thousands.
The number 23 is between 20 and 30. But the 23 is near to 20 compared to 30. Therefore, 23 is rounded off to 20.
Next, the number 66 is between 60 and 70. But the 66 is near to 70 compared to 60. Therefore, 66 is rounded up to 70.
So, Multiply 20 and 70.
20 × 70 = 1400.
Hence, the estimated product value is 1400.

---

Problem 9:
Estimate the sum of three digits to the nearest 100. The values are 321 + 216 + 458?

Solution:

The given values are 321, 216, and 458.
Now, we will find the estimated sum value of these numbers.
First, we need to round off the numbers to the nearest 100.
The number 321 tens place digit is 2, which is less than 5. So replace zero in units place digit, and tens place digit, keep the remaining digits as it is.
Next, the number is 216, in this tens place digit is 1, which is less than 5. So replace zero in units place digit, tens place digit, and keep the remaining digit as it is.
In 458, the tens place digit is 5, which is equal to 5. So, replace zero in units place digit, tens place digit, and increase hundreds place digit by one.
After round off, the values are 300, 200, 500.
Now, to perform the addition operation, we get the estimated sum value.
300 + 200 + 500 = 1000
Thus, the estimated sum of the three-digit value is 1000.

---

Problem 10:
Estimate the product of 482 × 826 to the nearest 10. Write the value.

Solution:

Given the numbers are 482 and 826.
Now, we will estimate the given numbers to the nearest tens, hundreds, and thousands.
The number 482 is between 480 and 490. But the 482 is near to 480 compared to 490. Therefore, 482 is rounded down to 480.
Next, the number 826 is between 820 and 830. But the number 826 is near to 830 compared to 820. Therefore, 826 is rounded up to 830.
Now, Multiply 480 and 830.
480 × 830 = 3,98,400
Therefore, the estimated product value is 3,98,400.

---

Practice the Framing Formula Worksheet over here and get acquainted with the concept of how to frame a formula by translating mathematical statements using symbols and literals. Solve the various questions in the Worksheet on Framing a Formula and learn how to approach when given a mathematical statement. Answering the questions over here helps you to improve your math proficiency as well as attempt the exam with utmost confidence.

See More:

• Worksheet on Change of Subject
• Problem on Change the Subject of a Formula

Framing a Formula Worksheet with Solutions

I. Write formulas for the following mathematical statements.
(i) The difference between the cost price and the selling price is Loss.
(ii) Area of the rectangle is the product of length and width.
(iii) The perimeter of a triangle is the sum of the length of the sides of a triangle where a,b,c are sides of a triangle.
(iv) The distance traveled by vehicle is equal to the product of the speed of the vehicle and the time taken to cover the distance.
(v) Discount is calculated as the difference between the marked price and the selling price.
(vi) Area of the parallelogram is defined as the product of the base and height.

Solution:

(i) Given, The difference between the cost price and the selling price is Loss.
The difference between the cost price and the selling price is represented as the Cost price-selling Price.
Therefore, Loss=Cost price-selling Price
(ii) Given, the Area of the rectangle is the product of length and width.
The product of length and width is represented as Length × width.
Therefore, the Area of rectangle=Length × width.
(iii) In a triangle ABC, sides of the triangle are a,b,c.
The perimeter of a triangle is the sum of the length of the sides of a triangle is represented as a+b+c.
Hence,Perimeter of a triangle=a+b+c
(iv) product of the speed of the vehicle and the time taken to cover the distance is represented as = speed × time
Therefore, Distance=speed × time.
(v) The difference between the marked price and the selling price is MP-SP.
Therefore,Discount=MP-SP
(vi)Product of base and height is bh
Therefore, the Area of parallelogram=bh.

---

II. Using math literals and symbols, write the formula for the following mathematical statements.
(i) Three subtracted from a number gives Eight.
(ii) Seven added to a number is 10.
(iii) One-fifth of a number is 20.
(iv) One-third of a number is 6 more than 10.
(v) The sum of five times a number and 2 is 12.
(vi) The sum of three consecutive even numbers is 60.
(vii) The sum of two multiples of 3 is 27.
(viii) One number is 4 less than three times the other, if their sum is increased by 5 the result is 25.
(ix) The difference between m and n is the addition of 15 and p.

Solution:

(i) Given Three subtracted from a number gives Eight.
Let the number be N.
N-3=8
N=8 + 3=11
(ii) Given Seven added to a number is 10.
Let the number be N.
N+7=10
N=10-7
N=3
(iii) Given, One-fifth of a number is 20.
Let the number be N.
1/5(N)=20
N=20 × 5=100
(iv) Given, One-third of a number is 6 more than 10.
Let the number be N.
One-third of a number=1/3(N).
One-third of a number is 6 more than 10 is 1/3(N)=6+10
1/3(N)=16
N=16 × 3=48
(v) Given, The sum of five times a number and 2 is 12.
Let the number be N.
Five times a number is=5N
The sum of five times a number and 2 is 5N +2= 12
5N=12-2
5N=10
N=10/5=2
(vi) Given, The sum of three consecutive even numbers is 42.
Let the three consecutive even numbers be 2x,2x+2,2x+4.
The sum of three consecutive even numbers is 2x+2x+2+2x+4=42
6x+6=42
6x=42-6
6x=36
x=36/6=6
Therefore, the three consecutive even numbers are 6,8, and 10.
(Vii) Given, The sum of two consecutive multiples of 5 is 85.
Let x be the first multiple of 5 and x+5 be the second multiple of 5.
x+x+5=85
2x+5=85
2x=85-5
2x=80
x=80/2=40
Hence, x=40, x+5=40+5=45.
(viii) Given, One number is 4 less than three times the other, if their sum is increased by 5 the result is 25.
Let the first number be x.
Let the second number be y.
One number is 4 less than three times the other i.e. y=3x-4.->eq1
Also given that if their sum is increased by 5 the result is 25.
x+y+5=25
x+y=25-5
x+y=20 ->eq 2
subs y=3x-4 in eq 2.
x + 3x- 4=20
4x=20 + 4
4x=24
x=24/4
=6
Subs x=6 in eq2
6+y=20
y=20-6
y=14
Therefore, x=6,y=14.
(ix) Given, The difference between m and n is the addition of 15 and p.
The difference between the x and y is represented as=m – n
The addition of 15 and z is represented as= 15+ p
The difference between m and n is the addition of 15 and p is m-n=15+p.
Hence, The difference between m and n is the addition of 15 and p is m-n=15+p.

 

---

III. Change the following math statements using expression into statements in the ordinary language.
(i) Age of Ramya is x.  The age of Sravya is 2x.
(ii) Sugar costs Rs x. Wheat costs Rs 20 + x.
(iii) The number of women in a town is ‘n’. The number of men in the town is (1/5)n.
(iv) Arshik is x years old. His mother is (4x – 4) years old.

Solution:

(i) Given, Age of Ramya is x.  The age of Sravya is 2x.
The age of Ramya is x.  The age of Sravya is double the age of Ramya.
(ii) Given, Sugar costs Rs x. Wheat costs Rs 20 + x.
Sugar costs Rs x. Wheat cost is 20 more than sugar.
(iii) Given, The number of women in a town is ‘n’. The number of men in the town is (1/5)n.
The number of women in a town is ‘n’. The number of men in the town is one-fifth of the number of women in the town.
(iv) Given, Arshik is x years old. His mother is (4x – 4) years old.
Arshik is x years old. His mother’s age is 4 less than four times Arshik’s age.

---

IV. Answer the following:
(i) If the present age of a Swapna is x years.

(a) What will her age be after 5 years?
(b) What was her age 3 years ago?
(c)Her father’s age is 3 more than three times her age. Find her father’s age.
(d) Mother is 5 years younger than her father. What is her mother’s age?
Solution:
(a)  Swapna’s age after 5 years is (X+5).
(b) 3 years ago Swapna’s age is (X-3).
(c) Father’s age =(3x+3)
(d) Mother’s age=3x+3-5
=(3x-2) years
(ii) The weight of the apple is 30 g and that of sweet lime is 50 g. Find the total weight of m apples and n sweet limes?
Solution:
The weight of the apple is 30 g.
For m apples, 30mg
The weight of the sweet lime is 50g
For n sweet limes, 50ng
The total weight of m apples and n Sweet limes = 30m+ 50n grams.
(iii) The length of a rectangle is 3m less than thrice its breadth. If the perimeter of the rectangle is 128m find its length and breadth?
Solution:
Let the length is l, breadth = b, and Perimeter = p.
length = 3b – 3
Perimeter p =2(l+b)
=2(3b-3+b)
=2(4b-3)
=8b-6
8b-6=128
8b=128+6
8b=134
b=134/8=16.75
length=3(16.75-3)=41.25
Hence, length of the rectangle=41.25, Breadth=16.75.

---

 

 

 

Worksheet on Word Problems on Unitary Method is prepared by experts keeping in mind the concept and rules associated with it. The Problems available in the Worksheet covers mixed questions on both direct and indirect variation.

Use the Unitary Method Word Problems Worksheet over here as a quick guide and learn the problem-solving approach used. Practice the Question and Answers in the Worksheet for Unitary Method Word Problems on a daily basis and improve your mathematics knowledge.  and you can access them free. Download the handy Worksheet on Unitary Method Word Problems and prepare as and when you want.

Do Refer:

• Worksheet on Inverse Variation Using Unitary Method
• Worksheet on Direct Variation using Unitary Method

Unitary Method Questions with Solutions

I. Jaya types 530 words in half an hour. How many words would she type in 5 minutes?

Solution:

Given that,
Jaya types 530 words in half an hour.
By the unitary method,
In 1 minute, Jaya types 530/30 = 17 words
In 5 minutes Jaya types 17 x 5 = 85 words
Hence, Jaya types 85 words in five minutes.

---

II. A worker is paid Rs.1250 for 5 days of work. If he works for 28 days, how much money will he get?

Solution:

Given that,
A worker is paid money for 5 days of work=Rs 1250
A worker will get money for one day work=1250/5=Rs 250
A worker will get the money for 28 days of work=250 ×28=Rs 7000
Therefore, A Worker will get the money of Rs 7000.

---

III. 3 men or 5 women can earn Rs 500 in a day. Find how much 7 men and 10 women will earn in a day?

Solution:

Given that,
3 men or 5 women can earn money in a day=Rs 500
Let one man earn=x
one woman earn=y
3x=500
x=500/3=166
5y=500
y=500/5=100
7 men and 10 women=7(166) + 10(100)
=1162 + 1000
=Rs 2162
Hence, 7 men and 10 women will earn money in a day is Rs 2162.

---

IV. In a camp, there are provisions for 130 persons for 20 days. If 50 more persons join the camp, find the number of days the provision will last?

Solution:

Given that,
There are provisions for 130 persons for 20 days.
If 50 more students join the camp, the number becomes 180.
The more number of persons, the sooner would the provisions exhaust. Therefore this is the case of inverse proportion.
So, Number of students x Camp days = constant
130 x 20 = 180 x n
n = 14
So, the provisions will last for 14 days.

---

V. A can do a piece of work in 10 days while B can do it in 20 days. With the help of C, they finish the work in 4 days. At what time would C alone do it?

Solution:

Given that,
A can do a piece of work in no.of days=10
B can do a piece of work in no.of days=20
Let “x” be the no. of days taken by C to complete the work.
A’s 1 day work = 1/10
B’s 1 day work = 1/20
C’s 1 day work = 1/x
(A + B + C)’s 1 day work = 1/10 + 1/20 + 1/x
L.C.M of (20, 15, x) = 20x.
Then, we have
(A + B + C)’s 1 day work = (2x/20x) + (x/20x) + (20/20x)
(A + B + C)’s 1 day work = (2x + x + 20)/20x
(A + B + C)’s 1 day work = (3x + 20)/20x ——(1)
Also Given that A, B and C together can do the work in 4 days.
So, we have
(A + B + C)’s 1 day work = 1/4 ——(2)
From (1) and (2), we get
(3x + 20)/20x = 1/4
4(3x + 20) = 1 ⋅ 20x
12x + 80 = 20x
80 = 8x
10 = x
So, C alone can complete the work in 10 Days.

---

VI. A and B together can do a piece of work in 15 days, while A alone can do it in 30 days. How long would B alone take to do it?

Solution:
Given that,
A and B together can do a piece of work in 15 days.
A alone can do it in 30 days
Let “x” be the no. of days taken by B to complete the work.
A’s 1 day work = 1/30
B’s 1 day work = 1/x
(A + B)’s 1 day work = 1/30 + 1/x
L.C.M of (30, x) = 30x.
Then, we have
(A + B)’s 1 day work = (x/30x) + (30/30x)
(A + B)’s 1 day work = (x + 30)/30x ——(1)
Also given, A and B together can do the work in 15 days.
So, we have
(A + B)’s 1-day work = 1/15 ——(2)
From (1) and (2), we get
(x + 30)/30x = 1/15
15(x + 30) = 1 ⋅ 30x
15x + 450 = 30x
450 = 15x
30= x
Hence, B alone can complete the work in 30 Days.

---

VII. A can do 1/3 part of a work in 4 days, while B can do 1/2 part of the work in 3 days. In how many days can both do it together?

Solution:
Given that,
A can-do 1/3 part of a work in 4 days while B can do 1/2 part of the work in 3 days.
A’s 1 day work = (1/3) / 4 = 1/12
B’s 1 day work = (1/2) / 3 = 1/6
(A + B)’s 1 day work = 1/12 + 1/6
L.C.M of (12, 6) = 12.
Then, we have
(A + B)’s 1 day work = 1/12 + 2/12
(A + B)’s 1 day work = 3/12
(A + B)’s 1 day work = 1/4
Hence, A, and B can together finish the work in 4 days.

---

VII. Rakesh goes to the shop to buy some books. The shopkeeper told him that 2 books would cost Rs 50. Can you find the cost of 8 books with the help of the unitary method?

Solution:

Given that,
The cost of two books is=Rs 50
First, we will find the cost of 1 book.
Cost of 1 book =Total cost of books/Total number of books
=50/2
=25.
Now, we will find the cost of 5 books.
Cost of 5 books = Cost of 1 book × Number of books
=25×8=200.
Therefore, the cost of 8 books is Rs 200.

---

VIII. 8 farmers harvest the crops in the field in 16 hours. How many workers are required to do the same amount of work in 12 hours?

Solution:

Given that,
8 farmers harvest the crops in the field in 16 hours.
First, we have to find no. of farmers required to harvest the crop in one hour.
16 hours = 8 farmers
1 hour = 16 x 8 =128 farmers
Now, we have to find the no. of farmers required to complete the work in 12 hours.
1 hour = 128 farmers
12 hours = 128 ÷ 12 =10 farmers.
Hence, 10 farmers are needed to complete the work in 12 hours.

---

IX. The cost of 5 apples is Rs150. Find the number of apples that can be purchased with Rs500.

Solution:

Given that,
The cost of 5 apples =Rs 150.
Hence the cost of 1 apple =Rs 150/5=Rs 30.
Now, the number of apples that can be purchased is Rs 30=1.
The number of apples that can be purchased with Rs 1=1/30.
The number of apples that can be purchased with Rs 500=1/30×500=16 apples.
Hence, the number of apples that can be purchased with Rs 500 is 16 apples.

---

X. A car traveling at a speed of 110kmph covers 330km. How much time will it take to cover 220km?

Solution:

Given that,
A car traveling at a speed of 110kmph covers 330km.
First, we need to find the time required to cover 330km.
Speed=Distance/Time
110=330/T
110 T=330
T=3 hours
Applying the unitary method, we get,
To travel 330km, the time required is 3 hours
So, to travel 1km, the time required is 3/330 hours
To travel 220km, the time required is =3/330×220=2 hours
Hence, to travel 220km by car, the time required is 2 hours.

---

This article helps the students to learn about the construction of parallel lines and perpendicular lines using set squares. 5th Grade students should be aware of drawing types of lines with set squares and compass and protractor. Here, we use set squares to construct the parallel lines. Are you excited to know how to use them? Then, look at this guide without any fail.

On this page, you can find what are parallel lines and the steps followed while constructing parallel lines by using set squares and a few examples to give practical knowledge to children.

Parallel Lines – Definition

Parallel lines are the lines that lie on the same plane and do not meet and never intersect each other and keep the same distance between them are known as parallel lines. They are also known as non-intersecting lines and they meet at infinity. If we have two lines AB and CD of the same length and equidistant to each other then we call them as the line AB is parallel to the line CD. Let us have a small representation of how the parallel lines look as follows:

To represent parallel lines we use the symbol ‘ || ‘and read as the line AB is parallel to the line CD. The distance between the two lines is always the same.

Set Squares

Set squares are of two types and they are named according to their angles. The set squares or pairs of triangles included a right angle and two angles of 45 degrees. It is known as the isosceles triangle. The other with a right angle, one of 60 degrees and another of 30 degrees. It is known as the scalene triangle. Just have a look at set squares as follows

The above figure says that one is 45^o set square and the other is 60^o-30^o set square. Set squares are used for drawing lines like parallel and perpendicular lines.

How to Draw a Parallel Line using Set Square?

There are steps to follow to draw parallel lines using set squares. Here are the steps that are looking for:

Step 1: Draw a straight line by positioning an edge of one of the 45 degrees set squares against a ruler to which we want to draw the parallel lines.

Step 2: Place the 60^o set square that is attached to the 45^o set square, and press it lightly while drawing so it doesn’t move and it fixes the exact position.

Step 3: Now, fix the 60^o– 30^o set square and move the 45^o triangular set square upwards or downwards and draw the required parallel lines.

Do Check: Construction of Perpendicular Lines by using a Protractor

Examples of Drawing Parallel Lines with Set Squares

Example 1:
Draw a parallel line through a point 4 cm by using a ruler and a set square.
Solution: 
We draw parallel lines with the help of set squares by following steps.
Step1:
(i) Draw a line PQ by 45 degrees set square and mark a point A on it.
(ii) Draw AB = 4 cm with the help of a ruler.

Step 2:
(i) Place one set square on the line segment PQ.
(ii) Place another 60 – 30 degrees set square as shown below in the figure.

Step 3:
(i) Press the 60° set square, slide the 45° set square along the other set square till the edge of the square touches point B.
(ii) Through point B, draw a line BC along the edge.
(iii) BC is the line required parallel to PQ through point B.

Here, the line PQ is parallel to the line BC i.e., PQ || BC.

Example 2: 
Draw a parallel line to the given line AB and passes through point X with the help of a ruler and a set square.
Solution: 
Step 1:
(i) Use a set square and draw a parallel line AB and passes through point X.
(ii) Now, place the set square on line AB and place the ruler on the short side of the square.

Step 2:
Just slide the set square along the ruler till the side of the set square touches the point X that was placed against the parallel line AB.

Step 3:
Use the edge of the set square to draw a line through point X as shown below and name the parallel line PQ.

Thus, line AB is parallel to line PQ i.e., AB || PQ.

FAQ’s on How to Draw Parallel Lines with Set Square and Ruler

1. Why set squares are used?
Set squares or triangles are used in technical drawing and in engineering, to furnish a straightedge at a right angle to a baseline.

2. How many set squares are used while drawing?
There are two types of set squares. One set square of 45 degrees and the other is 60-30 degrees set square. The 45 degrees square also has a 90 degrees angles. These set squares are used to draw parallel lines and perpendicular lines.

3. How to find the distance between parallel lines and set squares?

By holding it with one hand and placing a set square with one arm of the right angle corresponding with the edge of the ruler. Now, you can draw the line segment together with the edge of the set square. Later, you are good to measure the distance between parallel lines and set squares.