Vinay Pacha

In this article, you have to learn about how to find the Circumference and Area of a circle. In other words, the circumference of a circle is also known as a Perimeter, it helps to identify the length of the outline of any shape. The circumference and area of a circle are two important parameters of a circle. A circle is made of multiple points arranged equidistant from a single central point and that point is called the center of the circle.

On this page, we will discuss definitions of circumference and area of a circle, formulas, methods to find the circle’s area and circumference with solved example problems, and so on.

Circumference and Area of Circle – Definition

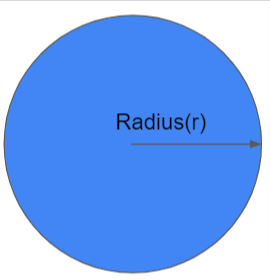
Circumference of Circle: The circumference of a circle is the length of the boundary of the circle. The distance between the center and any point on the circumference is known as the radius of the circle, radius is a constant value. The maximum distance between any two points on the circumference is known as Diameter. It will be twice the radius.

Area of Circle: The area of a circle is defined as the region occupied by the shape in a two-dimensional plane. It means the area of a circle is the total area that is covered by one complete cycle of the radius of the circle on a 2D plane.

Area and Circumference of Circle Formulas

Circumference of a Circle: It is measured in units, centimeters, and etc. The formula for the circumference of a circle is,
Circumference = 2πr = πD
Where r is the radius of the circle and Pi is the constant value i.e. π = 3.14 or 22/7

Area of a Circle: The unit of the area is square units. The area of a circle formula is,
Area of a circle = πr².
Here r is the radius of the circle. π is a constant value that is 22/7 or 3.14

Read More:

• Geometrical Properties of a Square
• Worksheet on Circle
• Worksheet on Circumference and Area of Circle

Circumference and Area of Circle Examples

Example 1:
Find the area and circumference of a circle whose radius is 20 cm. Take the value of π is 3.14?

Solution: 
As given in the question, the radius is 20cm.
Now, we will find the area and circumference of a circle.
We know the formulas of the area and circumference of a circle.
Area of a circle = πr²
Substitute the values in above formula, we get
Area = 3.14x(20)² =  1256 cm²
Next, the Circumference of a circle, C = 2πr
Circumference = 2 × 3.14 × 20  = 125.6 cm
Hence, the area and circumference of a circle are 1256 cm² and 125.6 cm

Example 2:
Find the area of a circle whose circumference is 14.6 cm?

Solution:
Given in the question, the circumference of a circle is 14.6 cm.
Now, to find out the area of a circle value, we must find the radius.
We all know, Area of a circle is πr²
From the circumference, we will calculate the radius.
Circumference = 2πr = 14.6 cm
(2)(3.14)r = 14.6
r = 14.6/(2)(3.14)
r = 4.4 cm
Therefore, the radius of the circle is 4.451 cm.
Now, substitute the given radius value in the area of a circle formula, we get
A = π(4.4)²
A = 3.14 x 19.36
A =  60.790 cm²
Therefore, the area of a circle is 60.790 cm².

Example 3:

The ratio of radii of two circles is 5:9. Find the ratio of their circumferences?

Solution:
In the given question, the values are,
The radii ratio of the two circles is 5:9.
Now, we will find out the ratio of their circumference.
Consider the radius of the first circle be r1 and the radius of the second circle be r2.
We know the formula, circumference of a circle is 2πr.
Let, r1 = 5x and r2 = 9x.
The circumference of a 1st circle is 2πr₁
= 2π5x
= 10πx
Next, the circumference of the 2nd circle is 2πr₂
= 2π9x
= 18πx
Now, the ratio of their circumference
= 10πx/18πx
= 10/18
= 5/9
= 5:9
Therefore, the ratio of their circumference is 5:9.

Example 4:

A circular radar screen has a circumference of 142 cm. Only 80% of its area is effective. Find the value of the effective area of the screen?

Solution:
Given in the question, the values are
The circumference of a circular radar screen is 142 cm.
Where r be the radius of the circular radar screen.
We know the formula, circumference = 2πr
2πr = 142
2 x 22/7 x r = 142
r6.28 = 142
radius of a circle = 142/6.28 = 22.6 cm
Next, find the area of a screen.
Area of a circle = πr²
So, the value is 22/7 x (22.6)²
3.14 x 510.76 = 1604 cm²
But, only 80% of the area of the radar screen is effective.
So, the effective area of the 80% of 1604cm² is, 1604 x 80/100 = 1283.2 cm²

Example 5:

Find the area of a circle of circumference 43 in decimal. Let the π = 3.14?

Solution: 
As given in the question, the circumference of a circle is 43.
Now, we will find the area of a circle value.
We know the formula, Area of a circle is πr². Using circumference, the area of a circle formula is A = C²/4π.
Substitute the given values in the above formula, then the formula is
So, the area is C²/4π.
(43)² /4(3.14) = 1849 / 12.56 = 147.2 cm².
Thus, the area of a circle is 147.2 cm².

FAQ’S on Area and Perimeter of a Circle

1. What are the formulas for calculating the area of a circle? 

A. The area of a circle is calculated by using the below formulas:
In terms of radius, the Area of a circle is πr²,  where r is a radius.
In terms of diameter, the Area of a circle is (π/4) x d², where d is the diameter.
In terms of circumference, the Area of a circle is C²/4π, where c is the circumference.

2. What is the perimeter of a circle? 

A. The perimeter of a circle means that the circumference of a circle, which is equal to twice the product of pi (π) and radius of the circle, i.e., 2πr.

3. If the radius of a circle is given in meters, then what will be the unit of the area of the circle?

A. The radius of a circle is in meters, then the area of a circle unit is square. meters.

The geometrical properties of a square or Perimeter and the area of Square both are the same. A square is a quadrilateral with has four equal sides. There are many square objects around you. Each square shape is characterized by one dimension, which is side length. In this chapter, we will learn about the geometrical properties of a square it means how to find the perimeter and area of a square. A rectangle is also called a square only if all its four sides are equal in length.

Do, Also Read:

• Perimeter and Area of a Plane Figures 
• Worksheet on Area and Perimeter of Squares
• Worksheet on Area and Perimeter of  Triangle

Square – Definition

Square will be a regular quadrilateral, which has all four sides have equal length and the four angles also are equal. The angles of the square are at right-angles or 90 degrees. A square is also defined as a rectangle whose two opposite sides have equal length. The diagonal of the square are equal and bisect each other at 90 degrees.

A Square may be a four-sided polygon that has all sides equal and the measure of the angles are 90 degrees. The shape of the square is, if we cut by a plane from the middle, then both the halves are symmetrical. Each half of the square seems like a rectangle with opposite sides equal.

The above figure represents a square, all sides are equal and each angle equal to 90 degrees.

Properties of a Square:
A few important properties of a square are listed below:

1. All four interior angles are equal to 90 degrees.
2. The opposite sides of a square are parallel to each other.
3. The square has 4 vertices and sides.
4. All four sides of a square are equal to each other.
5. The diagonals of the square bisect one another at 90 degrees.
6. The length of the diagonals is greater than that of the sides of the square.

Geometrical Properties of Square

In the above figure square ABCD,
AB = BC = CD = DA
AC = BD
∠ABC = ∠BCD= ∠CDA = ∠DAB= 90°.
AB and BD will be perpendicular bisectors of each other.
The diagonals are bisect each other at right angles.
OC = OA, OD=OB.
So, the Area of the ∆AOB = Area of the ∆BOC = Area of the ∆COD = Area of the ∆DOA.

Perimeter and Area of Square

The two main properties that outline a square, the properties are Area and Perimeter. Let discuss them one by one:

The perimeter of a Square: Any shape that will be laid on a flat surface is called a two-dimensional object. The length of the side or boundary of any two-dimensional shape is called the perimeter. The perimeter of a square is the sum of all four sides length of a square. Square is one of the 2D shapes having four equal sides and four corners angles are 90 degrees each. The units of the perimeter remain the same as that of the side-length of the square.

So, the perimeter of a square is, a sum of all the sides that is,
Perimeter = Side + Side + Side + Side = 4a.
Let ‘a’ is the side of a square. So, it will be 4a.

Area of a Square: The area of a square is the region covered by it during a two- dimensional plane. The area of a square is adequate to the edges or side squared. It is measured in square units.
So, the Area of a square is side x side
The area of a square is a² sq. unit.
If ‘a’ is that the length of the side of the square.

Length of Diagonal of Square

The length for the diagonals of the square is equal to s√2, where s is the side for the square. As the length for the diagonals is equal to one another, so the diagonal is the hypotenuse and the two sides of the triangle formed by the diagonal of the square, are perpendicular and base.
Since, Hypotenuse² = Base² + Perpendicular²
Hence, Diagonal² = side² + side²
Diagonal = √2side²
d = s√2
Where ‘d ‘ is the length of the diagonal of a square and s is that the side of the square.

Geometric Properties of Square Examples with Solutions

Problem 1: What is the perimeter of a square and also find the cost of fencing a square park of side 150 metres at the rate of Rs 30 per metre.

Solution: 
As given in the question, the data.
To find the cost of fencing a square park we need to find out the length of the boundary of a square park.
Now, we will find out the perimeter of a square.
The perimeter of a square = 4a
The side of the square park is 150 metres then,
The perimeter of a square = 4 x 150 = 600 metres.
Next, the cost of fencing 1 metre is Rs 30.
So, the cost of fencing 600 metres will be 600 x 30  i.e, Rs.18,000
Therefore the cost of fencing a square park of sides 150 metres is Rs 18,000.

Problem 2: If the perimeter of a square is 40m, then what is the side of the square?

Solution:
Given in the question, the values are
The perimeter of a square is 40m.
Now, we will find the side of a square value.
We know that, Perimeter = 4xside
So, side = perimeter/4
Substitute the value in the above formula.
Side = 40/4cm = 10 cm.
Hence, the side of a square value is 10 cm.

Problem 3: A square has a side equal to 5cm. Find the area of a square, perimeter of a square and length of diagonal of a square.

Solution: 
Given in the question, the values are
The Side of the Square, S = 5 cm.
Now, we will find the area, perimeter, and length of the diagonal.
We know that,
The Area of a square is, S^² = 5^² = 25 cm^²
Next, the Perimeter of the square = 4xS= 4 × 5 cm = 20cm.
Length of the diagonal of square = S√2 = 5 × 1.414 = 7.07
Thus, the area, perimeter, and the length of diagonal of a square is 25 cm^², 20cm, 7.07.

Problem 4: Find the area of a square, whose dimensions is 4m 15cm.

Solution:
As given in the question, the value is 4m 15cm.
We know that, 1m = 100cm.
So, 4m 15cm = 4m = 400 cm
400 cm + 15 cm = 415cm.
Now, we have to find out the area of a square.
The area of a square is a^².
Substitute the value in the above formula.
Area of a square = (415 cm)^²= 415 x 415 = 172,225 cm.
Thus, the area of a square is 172,225 sq. cm

FAQ’S on Geometrical Properties of Square

1. What is the formula for the perimeter of a square?

A. All the sides of a square are equal, we need one side to find its perimeter. The perimeter of the square is written as s+s+s+s = 4s
Therefore, the formula of the perimeter of a square is 4x(length of any one of the sides) = 4s.

2. Is square a polygon? 

A. A square is a four-sided polygon, which has all its sides length is equal. It is also a type of Quadrilateral.

3. What are the examples of Square?

A. There are many examples of square shape in real-life such as a square plot or field, a square-shaped ground, square-shaped table cloth, the tiles of the floor in a square shape, etc.

4. What are the five properties of a square? 

A. The following are the five important properties of a square:

• All the four interior angles of a square are equal to 90°.
• The opposite sides of the square are parallel to each other.
• The two diagonals of the square are equal to each other.
• The diagonal of the square is divided into two similar isosceles triangles.
• The length of the diagonals is greater than the sides of the square.

 

This article provides you with the converse of the midpoint theorem. Geometry is the branch of mathematics that deals with triangles, spheres, and planes, etc. Basically, a triangle is the smallest polygon formed by three line segments, the midpoint theorem, and converse of the midpoint theorem uses to find the missing values and the midpoints of the sides of the triangle. It deals with some properties of the triangles.

Midpoint theorem is applied in the field of coordinate geometry, algebra, and calculus. On this page, the converse of midpoint theorem statement, proof, and construction of the theorem is provided. Just dive into this page and gain more knowledge on midpoint theorem concepts.

Related Articles:

• Concept of Parallelogram
• Midpoint Theorem

State and Prove Converse of Mid-Point Theorem

A midpoint is the middle point of a line segment which is equidistant from both the ends. The midpoint theorem works conversely, too because if you draw a line parallel to a side of the triangle over one side’s midpoint, it automatically intersects the midpoint of the other side of the triangle. In the midpoint theorem, four little triangles are created by joining the midpoints that are congruent to one other.

Statement of Converse of Midpoint Theorem

The converse of midpoint theorem states that “If a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side”.

Prove the Theorem:

Consider the above triangle ABC.

Given D is the midpoint of AB. From D a line DE is drawn parallel to BC, intersect AC at E.

We have to prove that E is the midpoint of AC i.e., AE=CE.

Construction:

From the above triangle ABC, construct a line from C a line parallel to AB is drawn which meets DE produced at F.

The above diagram is the constructed version of △ABC to prove the converse of midpoint theorem.

Proof of Converse of the Midpoint Theorem

Since BD is parallel to CF i.e., BD ∥ CF by the construction.

DF is parallel to BC i.e., DF ∥ BC (given)

Hence, BDFC is a parallelogram.

BD = CF and BC = DF (Opposite sides of the parallelogram are equal)

AD=BD (D is the midpoint of AB)

Therefore, AD=CF (because BD=AD and BD=CF)

In the △ADE and △ECF

∠AED = ∠FEC (Vertically opposite angles)

∠DAE = ∠ECF (Alternate interior angles)

AD=FC (It was proved above)

△ADE ≅ △ECF

Therefore, by AAS congruency, triangles are congruent.

Thus, AE = EC by c.p.c.t

Therefore, E is the midpoint of AC.

Hence, the converse of the midpoint theorem is proved.

Do Check:

• Similar Triangles
• Congruency of Triangles

Converse of Midpoint Theorem Questions and Answers

Example 1: 
Consider a triangle PQR, and let S be any point on QR. Let X and Y be the midpoints of PQ and PR respectively. Show that XY bisects PS from the given diagram.

Solution:
Given X and Y are the midpoints of PQ and PR.
By the midpoint theorem, XY || QR.
Now, consider the triangle PQS.
Line XE is parallel to the base QS, and X is the midpoint of PQ.
By the converse of the midpoint theorem, E must be the midpoint of PS.
Hence, XY bisects PS.

Example 2: 
l, m, and n are three parallel lines. P and Q are the transversal intersecting parallel lines at the points A, B, C, D, E, and F as shown in the figure. If AB: BC = 1:1 then find the ratio of DE: EF.

Solution: 
Given AB: BC = 1:1
Join AF, which intersects the line m at point G.
In △ACF
AB: BC = 1:1, which implies B is the midpoint of AC.
BG ∥ CF, from given, the lines m and n are parallel.
By the converse of midpoint theorem, “the line drawn from the midpoint parallel to the other side bisects the third side of the triangle”.
Hence, G is the midpoint of AF.
Thus, AG=GF.
Now, in △AFD
AG=GF (Proved above)
GE ∥ AD as the lines l and m are parallel.
Therefore, by the converse of the midpoint theorem,
E is the midpoint of DF.
Thus, DE=EF.
Therefore, the ratio of DE: EF = 1:1.

FAQ’s for the Converse of the Midpoint Theorem

1. What is the converse of the midpoint theorem states?
The converse of the midpoint theorem states that ” In a triangle, the line drawn through the mid-point of one side of a triangle parallel to the base of a triangle bisects the third side of the triangle”.

2. What is the converse of the theorem in geometry?
The converse of a theorem occurs when the conclusion and hypothesis of a theorem are interchanged. For example, if you have a statement that says “if this and then that”, and the converse theorem says that ” if that and then this”. Logically, the result of reversing its two constituent statements.

3. Is the word converse always false?
The fact of the converse theorem statement is not always the same as the original statement says. The converse defines, however, must always be the truth. If this is not the case, then the definition of converse is not valid.

Test your knowledge on the concept of Area and Perimeter of Triangles in an interesting way by making the most out of our Math Worksheet on Area and Perimeter of Triangle. Find the PDF Formatted Area and Perimeter of Triangle Worksheets for free and resolve all your queries.

Area and Perimeter of Triangles Word Problems Worksheets include questions on the relationship between area and perimeter of triangles, finding areas and perimeters of different triangle types such as isosceles, equilateral, scalene, etc. Kick start your preparation by solving the area and perimeter of triangle questions on a regular basis.

Do Refer:

• Worksheet on Area and Perimeter of Squares
• Worksheet on Area of the Path
• Worksheet on Circumference and Area of Circle

Area and Perimeter of Triangle Worksheet PDF

I. Find the area and perimeter of the triangle whose sides are

i. 4cm, 6cm, 8cm?

ii. 7 cm, 9cm, 11cm?

Solution:

Given sides of the triangle=4cm, 6cm, 8cm
The perimeter of the triangle=a+b+c where a,b, and c are the sides of the triangle.
The perimeter of the triangle=4 cm + 6 cm + 8 cm
=18 cm
Therefore, the perimeter of the triangle is 18 cm.
ii. Given sides of the triangle=7 cm, 9cm, 11cm
We know that the perimeter of the triangle=a+b+c where a,b, and c are the sides of the triangle.
The perimeter of the triangle=7 cm + 9 cm + 11 cm
=27 cm
Therefore, the perimeter of the triangle is 27 cm.

---

II. The three sides of a triangle are in the ratio 3:5:7 and the perimeter 345m. Find its area?

Solution:

Given that,
The three sides of a triangle are in the ratio of 3:5:7.
Perimeter=345 m
Length of first side =3x
Length of second side =5x
Length of third side =7x
The perimeter of the triangle=side1+side2+side3
345 m=3x + 5x + 7x
345 m=15x
x=345 m/15=23 m
Length of first side=3x=3(23 m)=69 m
Length of the second side=5x=5(23 m)=115 m
Length of the third side=7x=7(23 m)=161 m
Area of the triangle=\(\sqrt{ s(s-a)(s-b)(s-c) }\)
S =perimeter of triangle /2 = 345 m/2 =172.5 m
=\(\sqrt{172.5(172.5-69)(172.5-115)(172.5-161) }\)
=\(\sqrt{172.5(103.5)(57.5)(11.5)  }\)
=\(\sqrt{11805792.1875 }\)
=3435.95 sq m
Therefore, Area of the triangle is 3435.95 sq m.

---

III. Find the height of a triangle whose base is 30 cm and whose area is 600 sq cm?

Solution:

Given that,
Base=30 cm, Area=600 sq cm
We know that Area= 1/2 × b × h
600 sq cm=1/2 × 30 cm × h
h=600 × 2 /30
=1200/30
=40 cm
Therefore, the Height is 40 cm.

---

IV. Find the area of an isosceles right-angled triangle of equal sides 12 cm each?

Solution:

We know that area of the triangle=1/2 × b × h
=1/2 × 12 × 12
=72 sq cm
Therefore, the Area of an isosceles right-angled triangle is 72 sq cm.

---

V. The area of the triangle is equal to that of a square whose each side measures 20 cm. Find the base of the triangle whose corresponding altitude is 24 cm?

Solution:

Given that,
The area of the triangle is equal to the area of a square.
Side of a square=20 cm
Area of a square=side × side
=20 × 20=400 sq cm
Therefore, the Area of triangle=400 sq cm.
we know that area of triangle=1/2 × b × corresponding altitude
400=1/2 × b × 24
b=400/12
b=33.33
Therefore, the base of the triangle is 33.33 cm.

---

VI. The sides of a triangle are in the ratio 8: 5: 7, and its perimeter is 600 cm. Find the area. Also, find the altitude corresponding to the smallest side?

Solution:

Given that,
sides of triangle are in ratio of 8:5:7
perimeter of triangle = 600
8x + 5x + 7x = 600
20x = 600
x = 600/20
x = 30
Therefore the sides are
8x = 8 × 30 = 240
5x = 5 × 30 = 150
7x = 7 × 30 = 210
Area of triangle with sides given we use herons formula
area = \(\sqrt{s(s-a)(s-b)(s-c)  }\)
s = (a+b+c)/2 where a, b, c are the sides of triangle
=(240+150+210)/2
=600/2=300
area=\(\sqrt{ 300(300 – 240)(300 – 150)(300 – 210) }\)
=\(\sqrt{300(60)(150)(90)}\)
=\(\sqrt{243000000}\)
=15588.45 sq cm
Altitude corresponding to smallest side is 150
15588.45=1/2 × 150 × h
h=31176.9/150
h=207.84 cm
Hence, height is 207.84 cm.

---

VII. The length of one of the diagonals of a field in the form of a quadrilateral is 84 m. The perpendicular distance of the other two vertices from the diagonal is 15 m and 12 m, find the area of the field?

Solution:

Given that,
The length of diagonal d=84m
The perpendicular distance of the other two vertices from the diagonal h1 = 15 m and
h2=12 m
We know that Area of the quadrilateral=1/2×d(h1+h2)
=1/2× 84(15+12)
=42(27)
=1134 sq m
Hence, the Area of the field is 1134 sq m.

---

VIII. The perimeter of a triangle is 68 cm. The first side is 7 cm shorter than the second side. The third side is 5 cm shorter than four times the length of the first side. What is the length of each side?

Solution:

Given that,
The perimeter of a triangle is= 68 cm
let X = first side
Y = second side
Z = third side
X = Y – 7 (1)
Z = 4X – 5 (2)
68 = X + Y + Z (3)
use (1) (2) into (3)
68 = ( Y – 7 ) + Y + ( 4X – 5 )
68 = Y – 7 + Y + 4X – 5
68 + 7 + 5 = 2Y + 4X
80 = 2(Y + 2X)
y+2x=40
y=40-2x– (4)
substitute (4) to (1)
X = (40 – 2X) – 7
X = 33 – 2X
3X = 33
X = 11 cm
length of first side
use X in (1)
11 = Y – 7 ; Y = 18 cm
use X in (2)
Z = 4(11) -5
Z =39 cm
Hence, x=11cm, y=18 cm,z=39 cm.

---

IX. If the height of a triangle is tripled and the base is doubled then find its area?

Solution:

Let the height of a triangle = h
The base of a triangle = b
∴ The area of a triangle =1/2bh ……. (1)
The new height of a triangle = 3h
The new base of a triangle = 2b
The area of a new triangle=1/2(3h)(2b)
=6(1/2hb)
Using equation (1), we get
= 6 × The area of a triangle
Thus, the area of the triangle becomes “6 times”.

---

X. Find the area of a right-angled triangle whose hypotenuse is 5 cm and one of its sides containing the right angle is 3 cm. Find the length of the other side?

Solution:

Given that,
Hypotenuse AC=5 cm
one of the side containing the right angle BC=3 cm
Let the other side AB be= x cm
By pythagerous theorem,
AC²=AB²+BC²
(x)²+(3)²= (5)²
(x)²+9=25
(x)²=25-9
x= 4 cm
Area of triangle= 1/2×3×4=6 sq cm.

---

XI. A piece of string is 60 cm long. What will be the length of each side of the string is used to form an equilateral triangle and find its area?

Solution:

The string length is the perimeter of the shape.
perimeter=60cm
An equilateral triangle has three equal sides.
Perimeter=3×(side)
∴side=perimeter/3
​=60/3
=20cm
Hence, the length of each side of the string is used to form an equilateral triangle will be 20 cm.
Area=\(\sqrt{ 3}\)a²/4
=\(\sqrt{ 3}\) (20)2/4
=\(\sqrt{ 3}\) 400/4
=100\(\sqrt{ 3}\) sq cm
Therefore, The area of an equilateral triangle is 100\(\sqrt{ 3}\) sq cm.

---

XII. Find the area of a triangle having …………

i. base = 16 cm height = 14 cm

ii. base = 7.5 m height = 8 cm

Solution:
i. Given that,
base = 16 cm height = 14 cm
We know that area of the triangle=1/2bh.
A=1/2(16)(14)
=112
Therefore, the Area of the triangle is 112 sq cm.
ii. Given that,
base = 7.5 m height = 8 cm
we know that 1m=100 cm.
7.5 m=7.5 × 100=750 cm.
We know that area of the triangle=1/2bh.
A=1/2(750)(8)
=3000
Therefore, the Area of the triangle is 3000 sq cm.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Worksheets on finding Circumference and Area of Circle have problems on diameter, radius, and chord of a circle, circumference of a circle, area of a circle, circumference, and area of a circle, distinguishing between circumference and area of a circle, and so on. Area and Circumference of a Circle Worksheet include step-by-step solutions and formulas for all the problems.

Math Worksheet on Circumference and Area of Circle helps students to develop a strong knowledge of geometry and related concepts. Download the PDF Format of easily accessible Area and Circumference of Circle Worksheets and solve the questions for free.

Do Refer:

• General Form of the Equation of a Circle
• Circumference and Area of a Circle

Circumference and Area of Circle Worksheets

I. If the circumference of a circular sheet is 321 m, find its area.

Solution:

Given that,
The circumference of a circular sheet is =321 m
we know that circumference of the circle=2πr
321=2πr
2×22/7×r=321 m
r=321 m×7/22×1/2
=51 m
We know that area=πr²
A=22/7 × 51 × 51
=8174 sq m
Therefore, the Area of the circle is 8174 sq m.

---

II. The area of a circle is 748 cm². Find its circumference.

Solution:

Given that,
The area of a circle is =748 cm²
we know that Area of the circle=πr²
r²=748/22 × 7
=238π
r=\(\sqrt{ 238 }\)
=15.42 cm
circumference=2πr
=2×22/7×15.42 cm
=96.92 cm
Therefore, the Circumference of the circle is 96.92 cm.

---

III. Find the area of a circle whose circumference is the same as the perimeter of the square of the side 11 cm.

Solution:

Given that,
side of the square=11 cm
The circumference of the circle is the same as the perimeter of the square.
we know that the perimeter of the square is 4× side of a square.
=4(11)=44 cm.
2πr=44 cm
2×22/7×r=44 cm
r=44×7/44
r=7 cm
Area of the circle=πr²
=22/7 × 7 × 7
=154 sq cm
Therefore, the Area of the circle=154 sq cm.

---

IV. A circular sheet of radius 5 units is cut out from a circle of radius 10 units. Find the area of the remaining sheet?

Solution:

Given that,
The area of the circular sheet with a 5cm radius is,
A=πr²
A=π×5×5
A=25π
The area of the circular sheet with a 10cm radius is,
A=πr²
A=π×10 × 10
A=100π
Since the circle with a radius of 5cm is removed, then the remaining area is,
A= 100π-25π
A=75π
A=75 × 3.14
A=235.5
Therefore, The remaining area is 235.5 sq cm.

---

V. A thin wire is bent to form a circle. If the length of the wire is 484 meters. What is the area of the circle?

Solution:

Given that,
Length of the wire=484 meters
2πr=484 m
2×22/7×r=484
r=484×7/44
r=77 m
Area of the circle=πr²
=22/7×77×77
=18634 m
Therefore, the Area of the circle is 18634 m.

---

VI. The ratio of the radii of two circles is 3:7. Find the ratio of their circumferences?

Solution:

Given that,
The ratio of the radii of two circles is =3:7
Let the radius of the first circle be r₁ and the radius of the second circle be r₂.
Circumference of a circle = 2πr
r₁ = 3x
r₂ = 7x
Circumference of the 1st wheel= 2πr₁
= 2π3x
= 6πx
Circumference of the 2nd wheel
= 2πr₂
= 2π7x
= 14πx
Now, the ratio of their circumference
= 6πx/14πx
= 6/14
= 3/7
= 3:7
Hence, the ratio of their circumference is 3:7.

---

VII. From a rectangular metal sheet of size 20 cm by 40 cm, a circular sheet as big as possible is cut. Find the area of the remaining sheet?

Solution:

Given that,
Size of the rectangular metal sheet=20 cm by 40 cm
Area of rectangle=l×b=20 cm×40 cm=800 sq cm
Area of circle=πr²
we know that DiameterD=2r
r=D/2
A=π(D/2)2
Diameter of largest circle=length of the smallest side of the rectangle.
Here length of smaller side=20
=π(20/2)2
=314.16 sq cm
Remaining Area=800 sq cm – 314.16 sq cm
= 485.84 sq cm.
Therefore, the Area of the remaining sheet is 485.84 sq cm.

---

VIII. The diameter of the circle is 4.9 cm. What is the circumference of the circle?

Solution:

Given that,
The diameter of the circle is d =4.9 cm
we know that d=2r
r=d/2=4.9/2=2.45
Circumference=2πr
=2 × 22/7 × 2.45
=15.4
Therefore, The circumference of the circle is 15.4.

---

IX. The radius of a cycle wheel is 56 cm. Find the number of turns required to cover a distance of 1680 m?

Solution:

Given that,
The radius of a cycle wheel is= 56 cm
We know that circumference of the circle=2πr
Circumference of the wheel=2 × 22/7 × 56 cm
=352 cm
=3.52 m
In one rotation, the cycle wheel covers a distance of 3.52 m,
So the number of rotations required to cover a distance of 1680 m is,
=1680/3.52=477
Hence, the number of rotations required is 477.

---

X. A well of diameter 180 cm has a stone parapet around it. If the length of the outer edge of the parapet is 840 cm, find the width of the parapet?

Solution:

Given that,
Diameter=180 cm
radius=diameter/2=180/2=90 cm
The outer edge of parapet=840 cm
Let radius and diameter of the parapet is R respectively.
Since the length of the outer edge of the parapet =840 cm.
Therefore, 2πR=840cm
2R=840 cm/π
2R=840 cm × 7/22
=267cm
Therefore, R=133 cm
Now, the width of the parapet=( Radius of parapet – Radius of the well)
=(133-90)
=43 cm
Hence, the Width of the parapet is 43 cm.

---

XI. A storm is expected to hit 5 miles in every direction from a small town. What is the area that the storm will affect?

Solution:

Given that,
Radius=5 miles
We know that A=πr²
A=3.14 ×5miles × 5 miles
=78.5 sq miles
Therefore, the area that the storm will affect is 78.5 sq miles.

---

XII. A semi-circle-shaped rug has a diameter of 4 ft. What is the area of the rug?

Solution:

Given that,
d = 4 ft
radius=d/2=4 ft/2=2
r = 2 ft
Area of circle = 3.14(2 ft) (2 ft)
Area of Circle = 3.14 × 4 sq ft=12.56 sq ft
Area of semi-circle = 12.56 sq ft ÷ 2;
Area of semi-circle = 6.28 sq ft
Hence, Area of the semi circle is 6.28 sq ft.

---

 

Students can use the Worksheet on Area of the Path to learn how to find the area of a path? Subject Experts have designed these Printable Area of the Path Worksheets so that you can use them to self-examine your level of preparation. Solve the different models of questions available in the Area of Path Worksheets and master the topics. Become proficient and enhance your problem-solving skills with the step-by-step solutions provided for all the problems available.

See More: Area of the Path

Area of Path Worksheets PDF with Solutions

I. There is a hall 80 m in length and 40 m in breadth. There is a lawn 7 m wide surrounding the hall on all four sides outside. Find the area of the lawn.

Solution:

First, let us draw the diagram based on the given details.

The hall is a rectangle. The hall and lawns which are outside are a bigger rectangle.
Then length of bigger rectangle = 80 + 7 + 7
= 94 m
Breadth of bigger rectangle = 40 + 7 + 7
= 54 m
Area of hall and Lawns = 94 x 54
= 5076 m2
Area of the hall = 80 x 40= 3200 m²
Area of Lawns = 5076 – 3200= 1876 m²
Therefore, the area of the lawn is 1876 m².

---

II. A square-shaped house is surrounded by a path 20 cm wide around it. If the area of the path is 4000 cm², find the area of the square-shaped house?

Solution:

In the figure,

ABCD is a square-shaped house.
EFGH is the outer boundary of the path.
Let each side of the square shaped house is = x cm
Then, the area of the square shaped houseABCD (x × x) cm² = x² cm²
Now, the side of the square EFGH = (x + 20 + 20) cm = (x + 40) cm
So, the area of square EFGH = (x + 40) (x + 40) cm² = (x + 40)² cm²
Therefore, area of the path = Area of EFGH – Area of ABCD
= [(x + 40)² – x²] cm²
= [x² + 1600 + 80x – x²] cm²
= (80x + 1600) cm²
But the area of path given = 4000 cm²
Therefore, 80x + 1600 = 4000
80x = 4000 – 1600
80x = 2400
x = 2400/80 = 30
side of square shaped house =30 cm
Therefore, the area of the square-shaped house = 30 × 30 cm² = 900 cm².

---

III. Find the area of the shaded portion in the below figure.

Solution:

Area of the shaded portion= Area of rectangle HGFE – Area of rectangle CDBA
Area of rectangle CDBA :
Length (CD) = 100 m
Breadth (BD) = 60 m
Area of rectangle CDBA = Length x width
= 100 x 60
= 6000 m²
Area of rectangle HGFE :
Length (HG) = 120 m
Breadth (GF) = 80 m
Area of rectangle HGFE = Length x width
= 120 x 80
= 9600 m²
Area of the shaded portion
= Area of rectangle HGFE – Area of rectangle CDBA
= 9600 m² – 6000 m²
= 3600 m²
Therefore, the Area of the shaded portion is 3600 m².

---

IV. A rectangular lawn of length 80 m and breadth 20 m is to be surrounded externally by a path that is 5 m wide. Find the cost of turfing the path at the rate of Rs 5 per m²?

Solution:

Length of the lawn = 80 m
Breadth of the lawn = 20 m
Area of the lawn = (80 × 20) m²
= 1600 m²
Length of lawn including the path = [80 + (5 + 5)] m = 90 m
Breadth of the lawn including the path = [20 + (5 + 5)] m = 30 m
Area of the lawn including the path = 90 m × 30 m = 2700 m²
Therefore, area of the path = (2700 – 1600) m² = 1100 m²
For 1 m², the cost of turfing the path = Rs 5
For 1100 m², the cost of turfing the path = Rs 1100 × 5 = Rs 5500.
Therefore, The cost of turfing the path is Rs 5500.

---

V. A square lawn is surrounded by a path 3 m wide. If the area of the path is 360 m², find the area of the lawn?

Solution:

Given that,
Area of the path=360 m²
Let the side of the lawn be a meters.
Area of lawn=a²
Length of outer side=(a+3+3)m=(a+6)m
Area of outer square=(a+6)²
=a²+36+12a
Area of path=Area of outer square-area of lawn
360=a²+36+12a – a²
360 = 12a + 36
12(a+3) = 360
a+3 = 360/12
a+3=30
a=30-3
a= 27 m
The area of the lawn is= 27 × 27=  729 m.

---

VI. Three square flowerbeds each of sides 4 m are dug on a piece of land 15 m long and 5 m wide. Find the area of the remaining portion of the land. Find the cost of leveling this land at the rate of Rs 5 per 100 cm²?

Solution:

Given that,
Sides of flower beds=4m
Length of a dug piece of land=15 m
width of a dug piece of land=5 m
cost=5 per 100 cm²
Area of Three flower beds=area of square=side²
=3 × side²
=3 × 4²
=48 m²
Area of land=Area of Rectangle=l × b
=15 × 5
=75 m²
Remaining portion=area of land – area of four flower beds
=75 m² – 48m²
=27 m²
=27 × 100 × 100 cm²=270000 cm²

Then, the cost of leveling this land at the rate of Rs 5 per 100 cm²,
= 270000 × 5/100
= 2700 × 5
=13500
Therefore, the cost of leveling the land is Rs 13,500.

---

VII. A rectangular field is of dimension 40 m x 20 m. Two paths run parallel to the sides of the rectangle through the center of the field. The width of the longer path is 2m and that of the shorter path is 1 m.
Find (i) the area of the paths
(ii) the area of the remaining portion of the field
(iii) the cost of constructing the roads at the rate of Rs 20 per sq.m.

Solution:

Length of the rectangular field L = 40 m
Breadth B = 20m
Area = L x B
=40 m x 20 m
Area of outer rectangle = 800 m²
Area of inner small rectangle = 39/ 2  x 18/ 2 = 175.5 cm
(i) Area of the path = Area of the outer rectangle – Area of 4 inner small rectangles
= (800 – 4(175.5))m²
= (800 – 702) m²
= 98 m²
Therefore, Area of path=98m²
(ii) Area of the remaining portion of the field = Area of the outer rectangle – Area of the paths
= (800 – 98) m²
= 702 m²
Therefore, the Area of the remaining portion of the field is 702m².
(iii) Cost of constructing 1 m² road = Rs 20
Cost of constructing 98 m² road = Rs 20 x 98
= Rs 1960
Therefore, the cost of constructing the road is Rs 1960.

---

VIII. A grassy plot is 200 m x 80 m. Two cross paths each 7 m wide are constructed at right angles through the center of the field, such that each path is parallel to one of the sides of the rectangle. Find the total area used as a path?

Solution:

 

Given that,
A grassy plot is 200 m x 80 m.
Two cross paths each 7 m wide are constructed at right angles through the center of the field.
Area of the longer path (EFGH) = 200 x 7= 1400
Area of the shorter path (PQRS) = 7 x 80 = 560
Area of the centre field (IJKL) = 7 x 7 = 49
Area of the path = (Area of the longer path + Area of the shorter path – Area of the center field)
=1400 + 560 – 49
= 1960 – 49 = 1911 m².
Hence, The total area used as the path is 1911 m².

---

IX. A floor is 18 m long and 8 m wide. A square carpet of side 8 m is laid on the floor. Find the area of the floor not carpeted?

Solution:

Given that,
Length of the floor=18 m
The breadth of the floor=8 m
Side of the square=8m
Area of the square=side2
=82=64 sq m
Area of the rectangle=length x  breadth
=18 x 8
=144 sq m
The area of floor not carpeted = Area of the floor – Area of carpet
= 144 – 64 = 80 m²
Therefore, the area of the floor not carpeted is 80 m².

---

 

Area and Perimeter are two important properties of two- dimensional shapes. Perimeter is defined as the distance of the boundaries of the shape whereas Area explains the region occupied by it. This article will help you improve your knowledge regarding the concept of finding areas and perimeters for different figures. To make this easy for you we have observed the step-by-step solutions for all the questions.

This will be applicable for any shape and size, whether it is regular or irregular. Each and every shape has its own area and perimeter formula. You will learn about different shapes such as triangle, square, rectangle, circle, sphere, etc. The area and perimeter of plane figures or shapes are discussed here.

Also, Read:

• Word Problems on Area of a Rectangle
• Plane Figures
• Worksheet on Area and Perimeter of Rectangles 

Area and Perimeter – Definitions

Area: Measurement of the plane region is called Area, a part of the plane is enclosed by a simple closed figure is called a plane region. It is measured in square units.

Perimeter: The closed figure’s length of the boundaries is called the Perimeter of the plane figure. The units of Perimeter are the same as that of length that is m, cm, m, mm, and etc.

Perimeter and Area of Plane Figures Formulas

The different plane figures Area and Perimeter formulas are discussed below. The plane figures are circle, square, rectangle, triangle, pentagon, and Hexagon.
Perimeter and Area of a Square: 
The perimeter of a square is 4a.
Let ‘a’ be the length of the sides of a square.
The area of a square is a x a = a².
The length of the diagonal is 2a.
The diagonal of a square is a√2.

Perimeter and Area of a Rectangle:
The perimeter of a rectangle is 2(l+b).
So l is the length of the rectangle and b is the breadth of the rectangle.
The area of a rectangle is length x breadth.
The diagonal of the rectangle is √(l² +b²).
The length of the diagonal is l² +b².

Perimeter and Area of a Circle:
The area of a circle is πr².
The Circumference of a circle is 2πr, which is equal to πd.
We know that the value of π is 3.14 or π = 22/7.
r is the radius of the circle.
d is the diameter of the circle.
The area of the ring is,
Area of the outer circle – Area of the inner circle.

Perimeter and Area of a Triangle:
The area of a triangle is 1/2 (base x height).
The length of the sides is a, b, c. The area of a triangle is s(a+b+c)/2.
The perimeter of a triangle is (a+b+c).

Area of Parallelogram:
The area of a parallelogram is Base x Height (Product of base and height).

Area of a Trapezium:
The area of a trapezium is (1/2)(Sum of all parallel sides) x Height.

The different plane figures perimeter and area formulae are given in the below tabular form:

Perimeter and Area of Plane Figures Questions

Problem 1:
The Length of a rectangular field is 23.7 m and the breadth of its field is 14.5 m respectively.
Find the following,
(i) What is the barbed required wire to fence the field?
(ii) Area of the field.

Solution:
As given in the question the data,
Now, we have to find the solutions to the given questions.
The length of a rectangular field is 23.7 m
The breadth of a rectangular field is 14.5 m
So, the following are
(i) Barbed wire required for fencing the field = perimeter of the field
= 2 (length + breadth)
= 2(23.7m + 14.5m) = 76.4 m
(ii) The Area of the field is, length × breadth
= 23.7 × 14.5 m. square
= 343.65 m. square

Problem 2:
On a square-shaped handkerchief, nine circular designs, each of radius 7 cm, are made. What is the area of the remaining portion of the handkerchief?

Solution:
In the given question,
As the radius of each circular design is 7 cm.
The diameter of each will be 2 × 7 cm = 14 cm
So, the side of the square handkerchief is 3 × 14 cm = 42 cm
Therefore, the area of the square is 42 × 42 cm²
Also, the area of a circle = πr² = 22/7 x 7 x 7 cm² = 154 cm².
Thus, the area of 9 circles is 9 × 154 cm².
Next, the area of the remaining portion of the handkerchief is,
= (42 × 42 – 9 × 154) cm²
= (1764 cm² – 1386 cm²) = 378 cm².
Hence, the area of the remaining portion of the handkerchief is 378 cm².

Problem 3:
If the radius of a circle is 20cm. Find its area and circumference?

Solution:
Given the data, the radius of a circle is 20 cm.
Now, we will find the area and circumference of the circle.
So, the area of a circle is π × r².
A= 22/7 x 20 x 20
A= 1257.14 sq.cm.
The circumference of the circle is, C=2πr
C= 2 x 22/7 x 20 = 125.7 cm
Thus, the area and circumference of a circle are 1257.14 sq. cm, 125.7 cm.

Problem 4:
If the length of the side of a square is 12cm. Find the area of a square and also find the total length of its boundary?

Solution:
Given in the question,
The length of the side of a square is a = 12 cm.
Now, we need to find the area and total length of its boundary.
So, the area is a² = 12² = 144 sq.cm
Next, we will find out the total length of its boundary is,
Perimeter = 4a = 4 x 12 = 48 sq.cm.
Hence the area and total length of the boundary are 144 sq. cm and 48 sq. cm.

FAQ’s on Perimeter and Area of Plane Figures

1. What is the difference between area and perimeter?
The area is the region covered by shape or figure and the units of the area are square units or units² whereas the perimeter is the distance covered by the outer boundary of the shape and the units of the perimeter are the same as the unit.

2. What is the formula for Perimeter?
The perimeter of any polygon is equal to the sum of its all sides.
Perimeter = Sum of all sides.

3. What is the formula for the area of the rectangle? 
The area of the rectangle is equal to the product of its length and breadth (l x b).
So, the area of the rectangle is length x breadth.

4. What is the area and perimeter of a circle?
A circle is a curved shape and its area and perimeter are given by its radius.
So, the area of a circle is πr².
Now, the Perimeter or circumference of a circle is 2πr.

Worksheet on Area and Perimeter of Squares has different questions finding the area and perimeter of squares. Area and Perimeter of Squares Worksheet PDF will help you learn various skills related to squares and evaluate perimeter and area easily. Practice the questions regarding area and perimeter without fail and verify your answers from here. Solve the Area and Perimeter of Squares Questions available in the Area and Perimeter of Square Worksheets with Answers PDF on a regular basis and attempt the exam with confidence.

See More:

• Worksheet on Area and Perimeter of Rectangles
• Area and Perimeter of the Triangle

Perimeter and Area of Square Worksheets PDF

I. Find the perimeter and area of the square, whose dimensions are the following.
(i) 15 cm
(ii) 4.8 m
(iii) 3 m 35 cm
(iv) 80 dm
(v) 25 m

Solution:

i. We know that Area of the square=a²
=(15 cm)²
=225 sq cm
Perimeter=4a
=4(15 cm)
=60 cm
Therefore, the Area and perimeter of a square are 225 sq cm and 60 cm.
ii. We know that Area of the square=a²
=(4.8 m)²
=23.04 square meters
Perimeter=4a
=4(4.8 m)
=19.2m
Therefore, the Area and perimeter of a square are 23.04 square m and 19.2m

iii. Given 3 m 35 cm
we know that 1m=100 cm.

3m 35 cm=3(100) cm
=300 cm
3m 35 cm=300 cm + 35 cm
=335 cm
We know that Area of the square=a²
=(335 cm)²
=112225 sq cm
Perimeter=4a
=4(335 cm)
=1340 cm
Hence, the Area and perimeter of a square are 112225 sq cm and 1340 cm.
iv. We know that Area of the square=a²
=(80 dm)²
=6400 dm²
Perimeter=4a
=4(80 dm)
=320 dm
Hence, The area and perimeter of a square are 6400 dm² and 320 dm.
v. We know that Area of the square=a²
=(25 m)²
=625 m²
Perimeter=4a
=4(25 m)
=100 m
Therefore, The area and perimeter of a square are 625 m² and 100 m.

---

II. Find the perimeter of the squares whose side is:
(i) 10 m
(ii) 23 cm
(iii) 15 cm
(iv) 200 m
(v) 23 cm

Solution:

(i)Given side of a square is 10 m
We know that the perimeter of a square is 4a
=4(10 m)
=40 m
(ii) Given side of a square is 23 cm
We know that the perimeter of a square is 4a
=4(23 cm)
=92 cm
(iii) Given side of a square is 15 cm
We know that the perimeter of a square is 4a
=4(15 cm)
=60 cm
(iv) Given side of a square is 200 m
We know that the perimeter of a square is 4a
=4(200 m)
=800 m
(v) Given side of a square is 23 cm
We know that the perimeter of a square is 4a
=4(23 cm)
=92 cm

---

III. How many square tiles of side 6 cm will be needed to fit in a square floor of a bedroom of side 820 cm. Find the cost of tiling at the rate of Rs50 per tile?

Solution:

Given that,
Side of the square tile=6 cm
Area of the square tile=a²=(6 cm)²=36 cm²
Side of the bedroom=820 cm
Area of the bedroom=(820 cm)²=672400 sq cm.
No. of tiles=672400 sq cm/36 sq cm=18677
Cost of Tiling=18677 * 50=Rs 933850
Therefore, the cost of Tiling the bedroom is Rs 933850.

---

IV. The area of a square field is 64 hectares. Find the cost of fencing the field with a wire at the rate of Rs 5.20 per meter?

Solution:

Given that,
The area of a square field is 64 hectares.
1 hectare = 10000 sq.m.
So, 64 hectare = 640000 sq.m.
So, the Area of square field = 640000 sq.m.
Area of square=side²
side²=640000
side=\(\sqrt{ 640000 }\)
=800
The Perimeter of the square=4 × side
=4 × 800
=3200 m
Cost of fencing for 1m=Rs 5.20
Cost of fencing for 3200 m=3200 × 5.20
=Rs 16640
Therefore, The cost of fencing the field is Rs 16640.

---

V. The areas of a square and rectangle are equal. If the side of the square is 10 cm and the breadth of the rectangle 20 cm, find the length of the rectangle and its perimeter?

Solution:

Given that,
The side of the square is 10 cm and the breadth of the rectangle is 20 cm.
The areas of a square and rectangle are equal.
We know that area of square=a²
area of the rectangle=l*b
10 cm*10 cm=l*20 cm
100 sq cm/20 cm=l
l=5 cm
perimeter of the rectangle=2(l+w)
=2(5 cm+20 cm)
=2(25 cm)
=50 cm
Therefore, The length of the rectangle and perimeter of the rectangle is 5 cm and 50 cm.

---

VI. Raju paid Rs 50,000 to fence his square garden. If the fencing was done at the rate of Rs 20 per meter, what is the length of each side of the square?

Solution:

Given that,
Raju paid Rs 50,000 to fence his square garden.
The fencing was done at the rate of Rs 20 per meter.
we know that cost of fencing is calculated by multiplying the perimeter of the field and the cost per meter.
Therefore, The perimeter of the square garden=50,000/20=2500
we know that perimeter=4a.
4a=2500
a=2500/4=625
side of the square=25 m
Therefore, the length of the side of the square is 25 m.

---

VII. A square garden has a side of 320 meters. To put a wire fencing around this, what is the length of wire required?

Solution:

Given that,
The side of the square garden =320m
perimeter=fencing the garden.
The wire needed =320×4
=1280
Therefore, the wire needed for fencing is 1280m.

---

VIII. A rope length of 3600 m is used to fence a square garden. What is the length of the side of the garden?

Solution:

Given that,
Rope length=3600 m
Therefore, the perimeter of the garden P = 3600 m
We know that perimeter of a square = 4* length of a side
So, 4 *length of a side = 3600
The length of a side = 3600/4
Side length = 900 m
Therefore, the length of the side of the garden is 900 m.

---

IX. A wire is in the shape of a rectangle whose width is 10 cm is bent to form a square of side 15 cm. Find the rectangle length and also find which shape encloses more area.

Solution:

Given that,
rectangle width=10 cm
side of the square=15 cm
The perimeter of rectangle=Perimeter of square
2(l + w) = 4side
2(l + 10) = 4 x 15
2l + 20 = 60
2l=60-20
2l=40
l=40/2=20
Area of square = side²
= 15² = 15 cm x 15 cm
= 225 sq cm
Area of rectangle=20 cm x  10 cm
=20 cm x 10 cm=200 sq cm
Therefore, Square has more area.

---

X. Find the perimeter of a square whose area is 400 m².

Solution:

Given that,
Area of square=400 m²
We know that area=side²
400 m²=side²
side=\(\sqrt{ 400 m² }\)
=20 m
we know that perimeter of a square=4side
p=4 x 20 m
=80 m
Therefore, the perimeter of a square is 80 m.

---

 

Exterior Angles of a Polygon Worksheet will introduce you to Exterior Angles Theorem and help you how to find exterior angles of a regular polygon. The Practice Page on Exterior Angles of a Polygon will help you to apply knowledge of exterior angles while solving questions in your homework. Using Exterior Angles of Polygon Worksheet with Answers you will be able to track measure your progress and achieve their best. Students can build confidence with the personalized learning available for each of them and can start learning at their own pace.

Do Check:

• Worksheet on Interior Angles of a Polygon
• Sum of the Interior Angles of an n-sided Polygon
• Sum of the Exterior Angles of an n-sided Polygon

Questions on Exterior Angles of a Polygon

I. How many sides does a regular polygon have if the measure of an exterior angle is
i.30
ii. 60?

Solution:

i.Given that,
The measure of an exterior angle=30
The sum of all the exterior angles of the regular polygon = 360°
Let the number of sides be = n.
we know that number of sides = Sum of exterior angles / each exterior angle
= 360° / 30°= 12
Thus the regular polygon has 12 sides.
ii. Given that,
The measure of an exterior angle=60
The sum of all the exterior angles of the regular polygon = 360°
Let the number of sides be = n.
we know that number of sides = Sum of exterior angles / each exterior angle
= 360° / 60°= 6
Thus the regular polygon has 6 sides.

---

II. The ratio of the exterior and interior angle of a regular polygon is 2: 9. Find the number of sides in the polygon.

Solution:

Given that,
The ratio of the exterior and interior angle of a regular polygon is 2: 9
Each interior angle of a regular polygon =(n-2)180⁰/n
where n = number of sides of the polygon
Each exterior angle of a regular polygon =360⁰/n
360⁰/n : (n-2)180⁰/n = 2 : 9
360⁰/(n-2)180⁰=2/9
2/n-2=2/9
18=2(n-2)
10=2n-4
2n=14
n=14/2=7
Therefore, The polygon has 7 sides.

---

III. What is the measure of one exterior angle of a regular hexagon (six-sided polygon)?

Solution :

In any polygon, the sum of all exterior angles is 360°.
The given hexagon is a regular polygon.
So, all its exterior angles are of the same measure.
Because hexagon is a six-sided polygon, the measure of each exterior angle is= 360° / 6= 60°
So, the measure of each exterior angle of a regular hexagon is 60°.

---

IV. what is the no. of sides in a regular polygon if the interior angle is equal to its exterior angle?

Solution:

Let interior angle = exterior angle = x°
we know that interior angle. + exterior angle = 180°.
So. x+x=180°.
2.x=180
x = 180°/2= 90°.
But exterior angle =360°/n
90°=360°/n
n= 360°/90°= 4.
Number of sides in a regular polygon = 4.

---

V. Each interior angle of a polygon is nine times the exterior angle of the polygon. Find the number of sides.

Solution:

The Sum of an interior angle and exterior angle of a polygon is 180 degrees.
Let the exterior angle be x.
Interior angle is 9x.
x + 9x = 180°
10x = 180°
x= 180°/10
x=18°
The Sum of all exterior angles of a polygon is 360 degree
So n X x = 360°
n = 360°/18°
n=20
Therefore, The polygon has 20 sides.

---

VI. The sum of all the interior angles of a polygon is two times the sum of its exterior angles.
i. Find the number of sides in the polygon. Also,
ii. find the measure of each exterior angle and each interior angle.

Solution:

Given that,
The sum of all the interior angles of a polygon is two times the sum of its exterior angles.
i. The sum of the exterior angles of a polygon is always equal to 360⁰.
The sum of the interior angles of polygon = 180(n−2)
= 180(n−2)=2×360
=180(n-2)=720
=n-2=720/180
= n−2=4
= n=6
Number of sides in the polygon = 6.
ii. The interior angle of a regular polygon is (n-2) 180/n
By substituting n=6, we get
=(6-2)180/10
=(4)180/10
=72⁰
Exterior angle=180 – interior angle
= 180 – 72
=108⁰
Therefore, the polygon has six sides interior angle is 72⁰ and the exterior angle is 108⁰.

---

VII. The exterior angles of a hexagon are in the ratio 1: 2: 3: 4: 5: 5. Find all the interior angles of the hexagon?

Solution:

Given that,
The exterior angles of a hexagon are in the ratio 1: 2: 3: 4: 5: 5.
Exterior angle sum property of a polygon: 360 degrees
Therefore , x+2x+3x+4x+5x+5x=360
20x=360
x=360/20
x=18
The exterior angles are 18,36,54,72,90,90.
In any polygon, the sum of an interior angle and the sum of an exterior angle is 180.
Therefore, The interior angles are:
180-18=162
180-36=144
180-54=126
180-72=108
180-90=90
By adding them, we get,
162+144+126+108+2(90)=720= interior angle sum property of hexagon
Therefore, The interior angles of the hexagon are 162⁰,144⁰,126⁰,108⁰,90⁰.

---

VIII. What is the measure of each exterior angle of a regular nonagon (nine-sided polygon)?

Solution:

In any polygon, the sum of all exterior angles is 360°.
The given nonagon is a regular polygon.
So, all its exterior angles are of the same measure.
Because nonagon is a nine-sided polygon, the measure of each exterior angle is
= 360° / 9= 40°
The measure of each exterior angle of a regular nonagon is 40°.

---

IX. The ratio between an exterior angle and the interior angle of a regular polygon is 2: 7. Find:
(a) the measure of each exterior angle.
(b) the measure of each interior angle.
(c) the number of sides in the polygon.

Solution:

Given that,
The ratio between an exterior angle and the interior angle of a regular polygon is 2: 7.
We know that measure of an interior angle = (n – 2)(180/n) and the measure of an exterior angle = (360/n).
2/7 = (360/n) / (n – 2)(180/n)
2/7 = (360/n) / n/(n – 2) * 180
2/7 = (360/n) / n(180n – 360)
2/7 = (360)/(180(n – 2))
2/7 = 2/(n – 2)
2(n – 2) = 7 * 2
2n – 4 = 14
2n = 18
n=18/2=9.
Therefore the number of sides in the polygon = 9.
(1) Therefore the measure of each exterior angle = 360/(n)
= 360/9
= 40⁰.
(2) Therefore the measure of each interior angle = 180 – 40
= 140⁰.
Therefore, no. of sides of the polygon is 9, the exterior angle is 40⁰ and the interior angle is 140⁰.

---

x. The measure of the exterior angle of a hexagon is (3x-2),(5x+4),(10x+2),(8x+3),(13x-30),(15x+5).  Find the measure of each angle.

Solution:

Given Exterior angles are (3x-2),(5x+4),(10x+2),(8x+3),(13x-30),(15x+5).
The sum of the exterior angles of any polygon is always equal to 360.
(3x-2)+(5x+4)+(10x+2)+(8x+3)+(13x-30)+(15x+5)=360
54x-18=360
54x=378
x=378/54=7.
Each exterior angle
(3x-2)=(3(7)-2)=21-2=19
(5x+4)=(5(7) +4)=35+4=39
(10x+2)=(10(7) + 2)=70+2=72
(8x+3)=(8(7) + 3)=56+3=59
(13x-30)=(13(7) – 30)=91-30=61
(15x+5)=(15(7) + 5)=105+5=110
Therefore, The measure of exterior angles are 19⁰,39⁰,72⁰,59⁰,61⁰,110⁰.

---

XI. What is the maximum exterior angle possible for a regular polygon?

Solution:

The exterior angle will be maximum when the interior angle is minimal.
Let us consider the interior angle to be 60° since an equilateral triangle is a regular polygon having maximum exterior angle because it consists of the least number of sides.
Exterior angle = 180° – 60°= 120°
Hence, the maximum exterior angle possible for a regular polygon is 120°.

---

 

Try our Worksheet on Interior Angles of a Polygon to solve a variety of problems such as finding the sum of interior angles of a polygon, finding the missing angle in a polygon, etc.  These engaging activities in Interior Angles of a Polygon Worksheet PDFs with regular and irregular polygons are all you need to spruce things up for your learning!

Practice the questions in the Interior Angles of a Polygon Worksheet and enhance your math proficiency in the concept. Printable Interior Angles of a Polygon Worksheet is accessible for free thus making your learning much effective.

See More:

• Sum of the Interior Angles of an n-sided Polygon
• Sum of the Exterior Angles of an n-sided Polygon

Interior Angles of a Polygon Worksheet PDF

Example 1.
Find the sum of interior angles of each polygon

Solution:

i)In the first diagram, no. of sides is 7.
we know that Sum of interior angles of a polygon is (n-2) × 180.
Here n=7
=(7-2) × 180
=5 × 180
=900⁰
Therefore, Sum of interior angles of a polygon is 900⁰.
ii) In the second diagram, no. of sides is
As we know that Sum of interior angles of a polygon is (n-2) × 180.
Here n=4
=(4-2)× 180
=2 × 180
=360⁰
Therefore, Sum of interior angles of a polygon is 360⁰.
iii) In the third diagram, no. of sides is 5.
we know that Sum of interior angles of a polygon is (n-2) × 180.
Here n=5
=(5-2)× 180
=3× 180
=540
Therefore, Sum of interior angles of a polygon is 540⁰.

---

Example 2.
Find the interior angles of a regular heptagon and a regular octagon.
                             

Solution:

The number of sides of a heptagon is 7.
The formula for finding the interior angles of a heptagon is, ((n-2)180°)/n.
Here, ‘n’ or the number of sides is 7.
Interior angles of a heptagon = ((7-2)180°)/8.
=5 ×180°/8
= 900/8
=112.5°
Therefore, the interior angles of a regular heptagon = 112.5° each.
The number of sides of an octagon is 8.
The formula for finding the interior angles of a polygon is, ((n-2)180°)/n.
Here, ‘n’ or the number of sides is 8.
Interior angles of a octagon = ((8-2)180°)/8.
= 6×180°/8
= 1080/8
= 135°
Therefore, the interior angles of a regular octagon = 135° each.

---

Example 3.
The four interior angles of a pentagon are 105⁰,118⁰,75⁰,130⁰. Find the other angle?

Solution:

Given that,
The four interior angles of a pentagon are 105⁰,118⁰,75⁰,130⁰.
We know that sum of angles of the pentagon is 540.
Let the other angle be x.
105+118+75+130+x=540
428+x=540
x=540-428
=112
Therefore, the other angle of a polygon is 112⁰.

---

Example 4.
Find the number of sides in a polygon if the sum of its interior angles is 1080⁰.

Solution:

Given that,
The sum of its interior angles is 1080⁰
Let no. of sides =n
Sum of angles of polygon =1080
(n−2)×180=1080
n−2=1080/180
​n−2=6
n=6+2
n=8
Therefore, no. of sides of the polygon is 8.

---

Example 5.
The interior angle of a polygon is 60 degrees. The other interior angles are all equal to 120 degrees. How many sides does a  polygon have?

Solution:

Given that,
The interior angle of a polygon is 60 degrees
The other interior angles are all equal to 110 degrees.
Let the number of sides be x.
There are x-1 no. of angles,120 degrees.
we know that total interior angles of a polygon=180(sides-2)
180(x-2)=60+120(x-1)
180x-360=60+120x-120
180x-360=-60+120x
60x=-60+360
60x=300
x=300/60=5
Therefore, the polygon has 5 sides.

---

Example 6.
If each interior angle is equal to 120°, then how many sides does a regular polygon have?

Solution:

Given that, each interior angle = 120°
We know that, Interior angle + Exterior angle = 180°
Exterior angle = 180°-120°
Therefore, the exterior angle is 60°
The formula for finding the number of sides of a regular polygon is =360° / Magnitude of each exterior angle
Therefore, the number of sides = 360° / 60° = 6 sides
Hence, the polygon has 6 sides.

---

Example 7.
The three angles of a polygon are 120°, 100°, 140°, and the other two angles are equal. Find the measure of these equal angles?

Solution:

Given that,
The three angles of a polygon are 120°, 100°, 140°.
Here the polygon has six angles. Therefore, it is a hexagon.
The sum of interior angles of a polygon=(n-2)180,n is no. of sides
=(6-2)×180
=4×180
=720
Let x be the measure of three angles that have the same measure.
3x+120+100+140=720
3x+360=720
3x=720-360
3x=360
x=360/3=120⁰
Therefore, the three angles with the same measure have a measurement of 120⁰.

---

Example 8.
The angles of a hexagon are (x – 5)°, (x – 8)°, (2x – 9)°,  x,(2x-6)^0, and (x – 4)°. Find the value of x and the measure of all angles.

Solution:

Given that the angle of a hexagon is (x – 5)°, (x – 8)°, (2x – 9)°,  x, (2x – 6)°, and (x – 4)°.
We know that sum of angles of a hexagon is 720⁰.
Therefore, (x – 5)°+ (x – 8)°+ (2x – 9)°+ (2x – 6)°+ x+ (x – 4)°=720⁰
8x-32=720⁰
8x=752
x=752/8=94⁰
Therefore, x=94⁰
x-5=94-5=89⁰
x-8=94-8=86⁰
2x-9=2(94)-9=179⁰
2x-6=2(94)-6=182⁰
x-4=94-4=90⁰.
Hence, the angles of a hexagon are 94⁰,89⁰,86⁰,179⁰,182⁰,90⁰.

---

Example 9.
The angle of a heptagon is in the ratio 1: 2 : 3: 4: 5: 6: 8. Find the measure of the smallest and the biggest angles.

Solution:

Given that the angles of a heptagon are in the ratio 1: 2 : 3: 4: 5: 6: 8.
Let each angle be of x then,
1=x,
2=2x
3=3x
4=4x
5=5x
6=6x
8=8x
We know that sum of angles of the heptagon is 900⁰.
1x+2x+3x+4x+5x+6x+8x=900⁰
29x=900⁰
x=900⁰/29=31⁰
Here the smallest angle is x=31⁰.
The largest angle is 8x=8(31)=248⁰.
Therefore, the smallest angle and the largest angle are 31⁰,247⁰.

---

Example 10.
The four angles of the pentagon are equal and the fifth angle measure 120°. Find the measure of four equal angles?

Solution:

Given that,
The four angles of the pentagon are equal.
The fifth angle measure= 120°
Let x be the measure of four angles that have the same measure.
We know that the sum of the angles of the pentagon is 360⁰.
4x+120=360⁰
4x=360-120
4x=240
x=240/4=60⁰.
Therefore, the measure of four equal angles is 60⁰.

---

Example 11.
The seven angles of an octagon are 120° each. Find the measure of the eighth angle?

Solution:

Given that,
The seven angles of an octagon are 120° each.
An octagon has 8 sides.
The Sum of angles of an octagon is (n-2)180=(8-2)180
=6(180)
=1080
Let the other angle be x.
x+7(120)=1080
x+840=1080
x=1080-840
x=240
Hence, the measure of eight angles is 240°.

---

Example 12.
If the ratio of the number of sides of two regular polygons is 4:5 and the ratio of the sum of their interior angles is 11:14. Find the number of sides in both the polygons?

Solution:

Given that,
The ratio of the number of sides of two regular polygons = 4:5
Let them be 4X and 5X
The number of sides in the first polygon = 4X
The number of sides in the second polygon = 5X
We know that
The sum of the interior angles in a regular polygon of n sides is (n-2)×180°
The sum of the interior angles in the first polygon of 4X sides = (4X-2)×180°
The sum of the interior angles in the second polygon of 5X sides = (5X-2)×180°
The ratio of the sum of the interior angles of the two polygons = [(4X-2)×180°]:[(5X-2)×180°]
(4X-2) : (5X-2)
According to the given problem
The ratio of the sum of their interior angles = 11:14
=> (4X-2) : (5X-2) = 11:14
=> (4X-2) / (5X-2) = 11 / 14
On applying cross multiplication then
=>14(4X-2) = 11(5X-2)
=> 56X – 28 = 55X – 22
=> 56X – 55X = 28- 22
=> X = 6
So,
The number of sides in the first polygon
= 4(6) = 24.
The number of sides in the second polygon= 5(6) = 30.
Hence, the number of sides of polygons is 24 and 30.

---