Test your knowledge on the concept of Area and Perimeter of Triangles in an interesting way by making the most out of our Math Worksheet on Area and Perimeter of Triangle. Find the PDF Formatted Area and Perimeter of Triangle Worksheets for free and resolve all your queries.
Area and Perimeter of Triangles Word Problems Worksheets include questions on the relationship between area and perimeter of triangles, finding areas and perimeters of different triangle types such as isosceles, equilateral, scalene, etc. Kick start your preparation by solving the area and perimeter of triangle questions on a regular basis.
Do Refer:
- Worksheet on Area and Perimeter of Squares
- Worksheet on Area of the Path
- Worksheet on Circumference and Area of Circle
Area and Perimeter of Triangle Worksheet PDF
I. Find the area and perimeter of the triangle whose sides are
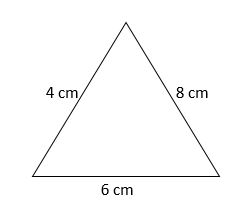
i. 4cm, 6cm, 8cm?
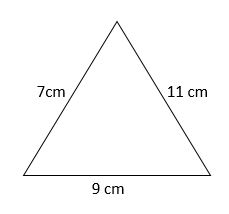
ii. 7 cm, 9cm, 11cm?
Solution:
Given sides of the triangle=4cm, 6cm, 8cm
The perimeter of the triangle=a+b+c where a,b, and c are the sides of the triangle.
The perimeter of the triangle=4 cm + 6 cm + 8 cm
=18 cm
Therefore, the perimeter of the triangle is 18 cm.
ii. Given sides of the triangle=7 cm, 9cm, 11cm
We know that the perimeter of the triangle=a+b+c where a,b, and c are the sides of the triangle.
The perimeter of the triangle=7 cm + 9 cm + 11 cm
=27 cm
Therefore, the perimeter of the triangle is 27 cm.
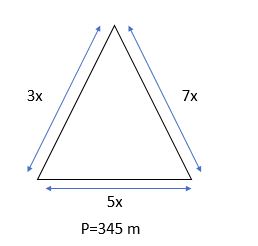
II. The three sides of a triangle are in the ratio 3:5:7 and the perimeter 345m. Find its area?
Solution:
Given that,
The three sides of a triangle are in the ratio of 3:5:7.
Perimeter=345 m
Length of first side =3x
Length of second side =5x
Length of third side =7x
The perimeter of the triangle=side1+side2+side3
345 m=3x + 5x + 7x
345 m=15x
x=345 m/15=23 m
Length of first side=3x=3(23 m)=69 m
Length of the second side=5x=5(23 m)=115 m
Length of the third side=7x=7(23 m)=161 m
Area of the triangle=\(\sqrt{ s(s-a)(s-b)(s-c) }\)
S =perimeter of triangle /2 = 345 m/2 =172.5 m
=\(\sqrt{172.5(172.5-69)(172.5-115)(172.5-161) }\)
=\(\sqrt{172.5(103.5)(57.5)(11.5) }\)
=\(\sqrt{11805792.1875 }\)
=3435.95 sq m
Therefore, Area of the triangle is 3435.95 sq m.
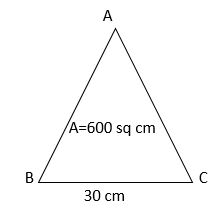
III. Find the height of a triangle whose base is 30 cm and whose area is 600 sq cm?
Solution:
Given that,
Base=30 cm, Area=600 sq cm
We know that Area= 1/2 × b × h
600 sq cm=1/2 × 30 cm × h
h=600 × 2 /30
=1200/30
=40 cm
Therefore, the Height is 40 cm.
IV. Find the area of an isosceles right-angled triangle of equal sides 12 cm each?
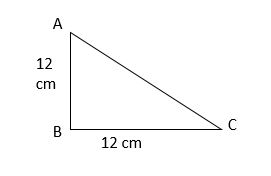
Solution:
We know that area of the triangle=1/2 × b × h
=1/2 × 12 × 12
=72 sq cm
Therefore, the Area of an isosceles right-angled triangle is 72 sq cm.
V. The area of the triangle is equal to that of a square whose each side measures 20 cm. Find the base of the triangle whose corresponding altitude is 24 cm?
Solution:
Given that,
The area of the triangle is equal to the area of a square.
Side of a square=20 cm
Area of a square=side × side
=20 × 20=400 sq cm
Therefore, the Area of triangle=400 sq cm.
we know that area of triangle=1/2 × b × corresponding altitude
400=1/2 × b × 24
b=400/12
b=33.33
Therefore, the base of the triangle is 33.33 cm.
VI. The sides of a triangle are in the ratio 8: 5: 7, and its perimeter is 600 cm. Find the area. Also, find the altitude corresponding to the smallest side?
Solution:
Given that,
sides of triangle are in ratio of 8:5:7
perimeter of triangle = 600
8x + 5x + 7x = 600
20x = 600
x = 600/20
x = 30
Therefore the sides are
8x = 8 × 30 = 240
5x = 5 × 30 = 150
7x = 7 × 30 = 210
Area of triangle with sides given we use herons formula
area = \(\sqrt{s(s-a)(s-b)(s-c) }\)
s = (a+b+c)/2 where a, b, c are the sides of triangle
=(240+150+210)/2
=600/2=300
area=\(\sqrt{ 300(300 – 240)(300 – 150)(300 – 210) }\)
=\(\sqrt{300(60)(150)(90)}\)
=\(\sqrt{243000000}\)
=15588.45 sq cm
Altitude corresponding to smallest side is 150
15588.45=1/2 × 150 × h
h=31176.9/150
h=207.84 cm
Hence, height is 207.84 cm.
VII. The length of one of the diagonals of a field in the form of a quadrilateral is 84 m. The perpendicular distance of the other two vertices from the diagonal is 15 m and 12 m, find the area of the field?
Solution:
Given that,
The length of diagonal d=84m
The perpendicular distance of the other two vertices from the diagonal h1 = 15 m and
h2=12 m
We know that Area of the quadrilateral=1/2×d(h1+h2)
=1/2× 84(15+12)
=42(27)
=1134 sq m
Hence, the Area of the field is 1134 sq m.
VIII. The perimeter of a triangle is 68 cm. The first side is 7 cm shorter than the second side. The third side is 5 cm shorter than four times the length of the first side. What is the length of each side?
Solution:
Given that,
The perimeter of a triangle is= 68 cm
let X = first side
Y = second side
Z = third side
X = Y – 7 (1)
Z = 4X – 5 (2)
68 = X + Y + Z (3)
use (1) (2) into (3)
68 = ( Y – 7 ) + Y + ( 4X – 5 )
68 = Y – 7 + Y + 4X – 5
68 + 7 + 5 = 2Y + 4X
80 = 2(Y + 2X)
y+2x=40
y=40-2x– (4)
substitute (4) to (1)
X = (40 – 2X) – 7
X = 33 – 2X
3X = 33
X = 11 cm
length of first side
use X in (1)
11 = Y – 7 ; Y = 18 cm
use X in (2)
Z = 4(11) -5
Z =39 cm
Hence, x=11cm, y=18 cm,z=39 cm.
IX. If the height of a triangle is tripled and the base is doubled then find its area?
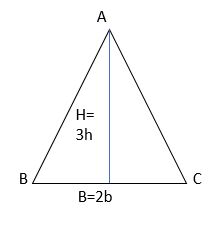
Solution:
Let the height of a triangle = h
The base of a triangle = b
∴ The area of a triangle =1/2bh ……. (1)
The new height of a triangle = 3h
The new base of a triangle = 2b
The area of a new triangle=1/2(3h)(2b)
=6(1/2hb)
Using equation (1), we get
= 6 × The area of a triangle
Thus, the area of the triangle becomes “6 times”.
X. Find the area of a right-angled triangle whose hypotenuse is 5 cm and one of its sides containing the right angle is 3 cm. Find the length of the other side?
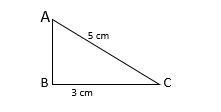
Solution:
Given that,
Hypotenuse AC=5 cm
one of the side containing the right angle BC=3 cm
Let the other side AB be= x cm
By pythagerous theorem,
AC2=AB2+BC2
(x)2+(3)2= (5)2
(x)2+9=25
(x)2=25-9
x= 4 cm
Area of triangle= 1/2×3×4=6 sq cm.
XI. A piece of string is 60 cm long. What will be the length of each side of the string is used to form an equilateral triangle and find its area?
Solution:
The string length is the perimeter of the shape.
perimeter=60cm
An equilateral triangle has three equal sides.
Perimeter=3×(side)
∴side=perimeter/3
=60/3
=20cm
Hence, the length of each side of the string is used to form an equilateral triangle will be 20 cm.
Area=\(\sqrt{ 3}\)a2/4
=\(\sqrt{ 3}\) (20)2/4
=\(\sqrt{ 3}\) 400/4
=100\(\sqrt{ 3}\) sq cm
Therefore, The area of an equilateral triangle is 100\(\sqrt{ 3}\) sq cm.
XII. Find the area of a triangle having …………
i. base = 16 cm height = 14 cm
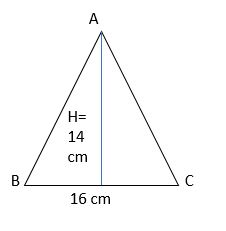
ii. base = 7.5 m height = 8 cm
Solution:
i. Given that,
base = 16 cm height = 14 cm
We know that area of the triangle=1/2bh.
A=1/2(16)(14)
=112
Therefore, the Area of the triangle is 112 sq cm.
ii. Given that,
base = 7.5 m height = 8 cm
we know that 1m=100 cm.
7.5 m=7.5 × 100=750 cm.
We know that area of the triangle=1/2bh.
A=1/2(750)(8)
=3000
Therefore, the Area of the triangle is 3000 sq cm.
