Learn about geometric objects completely by using this page free of cost. In geometry, shapes are the forms of objects which have boundary lines, angles, and surfaces. There are different types of Shapes namely Two-Dimensional and Three-Dimensional. Each geometric object is a set of vertices. Shapes are classified with regard to their regularity or uniformity.
Geometric shapes are the figures which demonstrate the shape of the objects in mathematics. On this page, you will learn the definition of geometry, types, list of geometry shapes, 3D Shapes.
Do Check:
Geometry – Definition
Geometry is a branch of mathematics that deals with the properties, measurements, and relationships of lines, angles, points, coordinates, solids, surfaces.
Geometry is defined as shapes are the figures which represent the forms of different objects. Some figures are two-dimensional shapes, whereas some are three-dimensional shapes. The two-dimensional figures lie on only the x-axis and y-axis, but 3d shapes lie in x, y, and z axes. The z-axis shows the height of the object.
Types of Geometry
Geometry can be divided into,
1. Plane Geometry: It is will be about flat shapes like lines, circles, and triangles.
2. Solid Geometry: It is about three-dimensional objects like cubes, prisms, cylinders, and spheres.
List of Geometry Shapes
Geometry shapes are two types:
- Two-dimensional (2D) shapes.
- Three-dimensional (3D) shapes.
What is meant by 3D Shapes?
The occupying space of shapes is called three-dimensional shapes. Three-dimensional can also be defined as solid shapes having three dimensions length, width, and height. Most of the 3D shapes will be defined as a group of vertices, lines that connect the vertices, and faces enclosed by these lines including obtained interior points. For many three-dimensional shapes, faces are two-dimensional.
Some attributes of Three-dimensional shapes:
1. Edges: If a line segment where the two faces meet is called the edges of 3D shapes.
2. Vertices: A corner point where the edges of the solid figures meet are called vertices.
3. Faces: The flat figures of the solid figures are called the faces of the 3D shapes.
Three-Dimensional Shapes
The three-dimensional objects or shapes of geometry is given below:
Cube
A cube could be a three-dimensional shape formed by two-dimensional 6 square faces. The cube consists of length, breadth, and width. The image of the cube is given below,
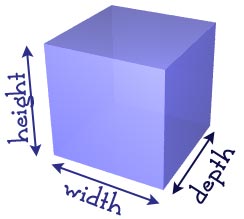
- It has all edges and faces are equal.
- The cube will have 8 vertices, 12 edges, and 6 faces.
- Measures all the angles are 90 degrees.
- The area of a cube formula is A = 6a². where ‘a’ is the length of the edges.
- The volume of a Cube is, V = a3 cubic units.
- An example of the cube is a Puzzle, the image of the Puzzle is given below

Cone
A cone is a solid 3D object that has a circular base connected with a curved surface and has a single vertex is called a cone. The image of the cuboid is given below,
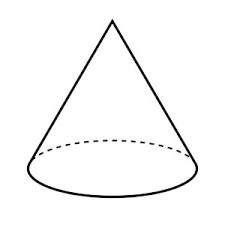
- The cone has one vertex and one edge.
- One flat face is a circle and one curved face, a total of 2 faces.
- Surface Area of a Cone, A = πr (r +√(r2+h2) Square units.
- The volume of a Cone could be V = ⅓ πr2h Cubic units.
- An example of Cone is given below,

Cuboid
A cuboid is a 3D shape formed by two-dimenisoanl rectangular faces. It is also called a rectangular prism. The cuboid image is given below,

- All the angles are 90 degrees.
- The cuboid has 8 vertices, 12 edges, and 6 faces.
- Cuboid opposite faces and edges are equal.
- The surface area of the cuboid is A= 2( lb+ bh+ lh ) square units.
- The volume of a cuboid is V = l x b x h cubic units.
- Brick, book, matchbox, Oven, Eraser, and etc are examples of cuboids. The example image of a cuboid is given below,

Pyramid
A solid shape having its base as any polygon and side face as a triangle with a common vertex is called a pyramid. The pyramid is also known as the polyhedron. The pyramid is the square pyramid because it has four triangular sides face and four square bases. The image of the pyramid is given below,

- The pyramid has 5 vertices, 8 edges, and 5 faces.
- Surface Area of a pyramid, SA = B + L Square units.
- The volume of a pyramid, V = ⅓ Bh Cubic unit.
- The example of the pyramid is given below,

Sphere
A solid three-dimensional shape that is perfectly round in shape and all its points on the surface is equidistant from the center point is called a sphere. The distance between the middle and any point on the surface is termed as the radius of the circle. The imager of the sphere is given below,
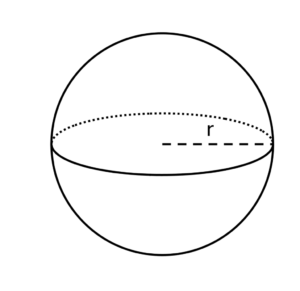
- The sphere has no vertices and no edges.
- It has no flat faces.
- It has only one curved face.
- The volume of a sphere is V = (4 ⁄ 3) π r3.
- The area of a sphere could be, A = 4 π r2.
- The diameter of a sphere is, D = 2r.
- The example image of the sphere is given below,

Prism
A solid 3D shape having its base and top as identical polygons and lateral faces are parallelograms are called prisms. The shape of a prism will not have any curve. The image of the prism is given below,
A prism includes a solid shape consisting of two identical ends (such as triangle, square, rectangle, etc.), flat faces or surfaces, and uniform cross-section across its length. The cross-section seems like a triangle hence called prism. Therefore, a prism can have square, rectangular, pentagonal, and other polygon shapes but not circular shapes.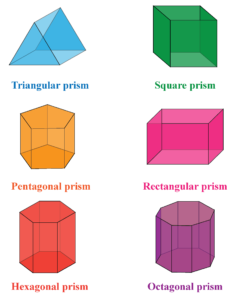
- The prism has 9 edges and 5 faces, 6 vertices.
- 5 faces mean 2 triangles and 3 rectangles.
- The surface area of a prism could be, A = 2( Base Area) + ( Base perimeter x height)
- The volume of a prism will be V = Base Area x Height.
Example Problems on Geometric Objects
Example1: Find the volume and area of a cuboid of l= 9cm, b= 7cm, and h=5cm.
Solution: Given the value of cuboid is,
length = 9cm, breadth = 7cm and height = 5cm
Now, we can find the volume and area of a cuboid,
Volume of a cuboid is, l x b x h
Substitute the given values in above formula, we get
= 9 x 7 x 5 = 315 cm. square.
The area of a cuboid is, A = 2(lb + bh + lh)
Substitute the values, we get
A = 2(63 + 35 + 45) = 2(143) = 188 cm.square.
Example 2: Find the height of the square prism whose volume is 240 cm3 and the base area is 40 cm2.
Solution: Given the values of the square prism is,
The volume of a square prism = 240 cm3
The base area of a square prism = 40 cm2
Now, we can find the height of a prism,
The volume of square prism = Base area x height
Substitute the given values in the above formula, we get
240 = 40 x prism height
So, the height of the prism, h = 240/ 40 = 6cm
Therefore, the height of prism, h = 6 cm.
Example 3: If the value of the side of the cube is 5 cm, then find its surface area and volume.
Solution: Given the side of a cube is 5 cm
Now, we can find the surface area and volume of a cube.
We know the formulas,
Surface Area, A = 6a2
Substitute the given values, we get
A = 6 x 25 = 150 cm2
The volume of a cube is, V = a3
5^3 = 125 cm3
Make your kids even more interested in Math Activities by taking help from our fun-learning Kindergarten Math Curriculum, Worksheets, Activities, Problems, Fun Games
