Engage NY Eureka Math 4th Grade Module 4 Lesson 10 Answer Key
Eureka Math Grade 4 Module 4 Lesson 10 Problem Set Answer Key
Write an equation, and solve for the measure of ∠x. Verify the measurement using a protractor.
Question 1.
∠CBA is a right angle.
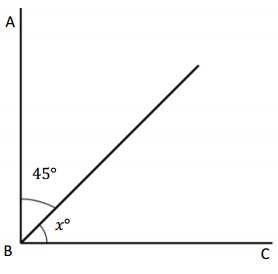
45° + ________ = 90°
x° = __________
Answer:
The value of x is 45°.
Explanation:
Given that <CBA is a right angle and angle B is 45°, so the angle CBA= 90° which is 45°+x= 90°, so the value of x is
x°= 90° – 45°
= 45°
So the value of x° is 45°.
Question 2.
∠GFE is a right angle.
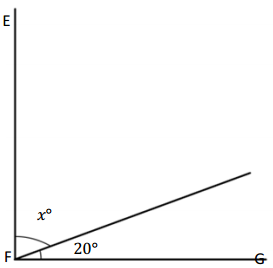
_______ + ________ = _________
x° = __________
Answer:
The value of x is 70°.
Explanation:
Given that <GFE is a right angle which is 90° and another angle is 20°, so the angle GFE= 90° which is 20°+x= 90°, so the value of x is x°= 90° – 20°
= 70°.
So the value of x° is 70°.
Question 3.
∠IJK is a straight angle
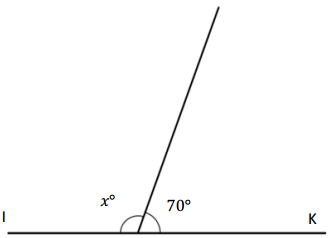
___________ + 70° = 180°
x° = ____________
Answer:
The value of x is 110°
Explanation:
Given that <IJK is a straight angle which is 180° and another angle is 70°, so the angle IJK= 180° which is 70°+x= 180°, so the value of x is
x°= 180° – 70°
= 110°.
So the value of x° is 110°.
Question 4.
∠MNO is a straight angle
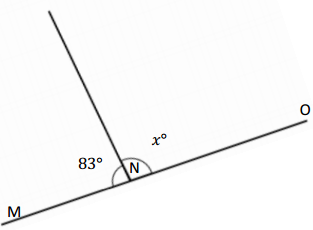
_________ + _________ = __________
x° = ___________
Answer:
The value of x is 97°
Explanation:
Given that <MNO is a straight angle which is 180° and another angle is 83°, so the angle MNO= 180° which is 83°+x= 180°, so the value of x is
x°= 180° – 83°
= 97°.
So the value of x° is 97°.
Solve for the unknown angle measurements. Write an equation to solve.
Question 5.
Solve for the measurement of ∠TRU. ∠QRS is a straight angle.

Answer:
The value of <TRU is 144°.
Explanation:
Given that <QRS is a straight angle which is 180° and another angle is 36°, so the angle MNO= 180° which is 36°+x= 180°, so the value of x is
x°= 180° – 36°
= 144°.
So the value of <TRU is 144°.
Question 6.
Solve for the measurement of ∠ZYV. ∠XYZ is a straight angle.
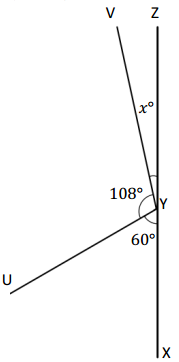
Answer:
The value of <ZYV is 12°.
Explanation:
Given that <XYZ is a straight angle which is 180° and another two angle is 108°+60° which is 168°, so the angle XYZ= 180° which is 168°+x= 180°, so the value of x is
x°= 180° – 168°
= 12°.
So the angle ZYV is 12°.
Question 7.
In the following figure, ACDE ¡s a rectangle. Without using a protractor, determine the measurement of ∠DEB. Write an equation that could be used to solve the problem.
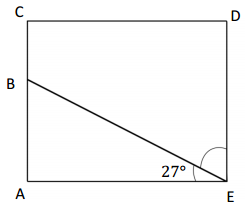
Answer:
The value of x° is 63°.
Explanation:
Here, in the above image we can see that a rectangle where every angle is a right angle, so let’s take one angle as 90° and then we should find out the other angle and the other angle be x. So the equation will be 90°= 27°+x° and the value of x is
x= 90° – 27°
= 63°.
So the value of x° is 63°.
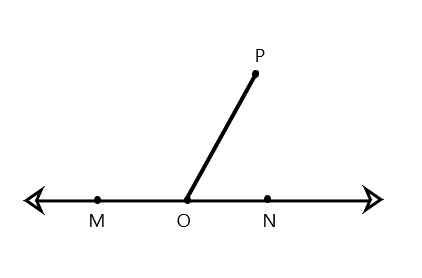
Question 8.
Complete the following directions in the space to the right.
a. Draw 2 points: M and N. Using a straightedge, draw ![]() .
.
b. Plot a point O somewhere between points M and N.
c. Plot a point P, which is not on ![]() .
.
d. Draw \(\overline{O P}\).
e. Find the measure of ∠MOP and ∠NOP.
f. Write an equation to show that the angles add to the measure of a straight angle.
Answer:
The equation of the angles add to the measure of a straight angle is <MOP+<PON= 180°.
Explanation:
Here, we have plotted 2 points which are M and N using a straightedge, and have constructed ![]() .
.
Then we plotted a point O somewhere between points M and N.
Then we need to plot a point P, which is not on ![]() .
.
And now we will construct \(\overline{O P}\).
So, now we need to find the measure of ∠MOP and ∠NOP.
As we have plotted a straight line which is <MON is 180°, which is <MOP+<PON= 180°.
So the equation of the angles add to the measure of a straight angle is <MOP+<PON= 180°.
Eureka Math Grade 4 Module 4 Lesson 10 Exit Ticket Answer Key
Write an equation, and solve for x. ∠TUV is a straight angle.
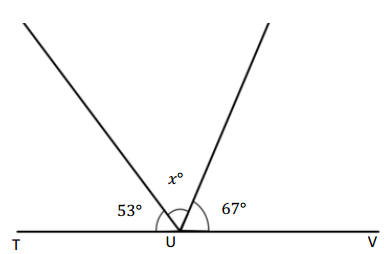
Equation = ______________
x° = ______________
Answer:
The value of x is 60°.
Explanation:
Given that <TUV is a straight angle which is 180° and another two angle is 53°+67° which is 120°, as the angle TUV= 180° which is 168°+x= 180°, so the value of x is
x°= 180° – 120°
= 60°.
So the angle x is 60°.
Write an equation, and solve for the measurement of ∠x. Verify the measurement using a protractor
Question 1.
∠DCB is a right angle
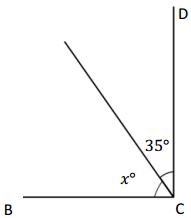
___________ + 35° = 90°
x° = ___________
Answer:
The value of x° is 55°.
Explanation:
Given that <DCB is a right angle and other angle is 35°, so the angle DCB is 90° which is 35°+x= 90°, so the value of x is
x°= 90° – 35°
= 55°
So the value of x° is 55°.
Question 2.
∠HGF is a right angle

___________ + ___________ = ___________
x° = ___________
Answer:
The value of x° is 28°.
Explanation:
Given that <HGF is a right angle and other angle is 62°, so the angle HGF is 90° which is 62°+x= 90°, so the value of x is
x°= 90° – 62°
= 28°
So the value of x° is 28°.
Question 3.
∠JKL is a straight angle.
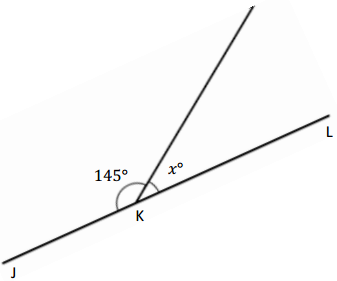
145° + ___________ = 180°
x° = ___________
Answer:
The value of x is 35°.
Explanation:
Given that <JKL is a straight angle which is 180° and another angle is 145° and the angle JKL is 180° which is 145°+ x= 180°, so the value of x is
x°= 180° – 145°
= 35°.
So the angle x is 35°.
Question 4.
∠PQR is a straight angle.
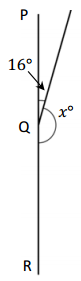
___________ + ___________ = ___________
x° = ___________
Answer:
The value of x is 164°.
Explanation:
Given that <PQR is a straight angle which is 180° and another angle is 16° as the angle PQR is 180° which is 16°+x= 180°, so the value of x is
x°= 180° – 16°
= 164°.
So the angle x is 164°.
Write an equation, and solve for the unknown angle measurements.
Question 5.
Solve for the measurement of ∠USW. ∠RST is a straight angle.
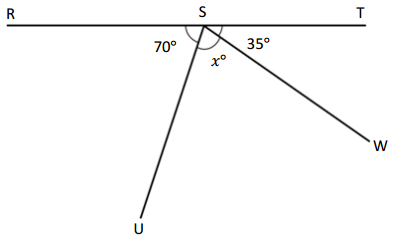
Answer:
The value of x is 75°.
Explanation:
Given that <RST is a straight angle which is 180° and another two angle is 70°+35° which is 105°, as the angle RST= 180° and the equation is 105°+x= 180°, so the value of x is
x°= 180° – 105°
= 75°.
So the angle x is 75°.
Question 6.
Solve for the measurement of ∠OML. ∠LMN is a straight angle.
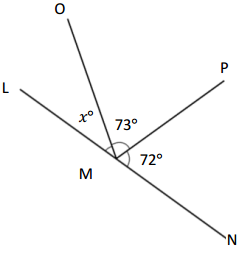
Answer:
The value of <OML is 35°.
Explanation:
Given that <LMN is a straight angle which is 180° and another two angle is 72°+73° which is 145°, as the angle LMN= 180° and the equation is 145°+x= 180°, so the value of x is
x°= 180° – 145°
= 35°.
So the angle <OML is 35°.
Question 7.
In the following figure, DEFH is a rectangle. Without using a protractor, determine the measurement of ∠GEF Write an equation that could be used to solve the problem.

Answer:
The value of x° is 16° and the equation is 90°= 74°+x°.
Explanation:
Here, in the above image we can see that a rectangle where every angle is a right angle, so let’s take one angle as 90° and then we should find out the other angle and the other angle be x. So the equation will be 90°= 74°+x° and the value of x is
x= 90° – 74°
= 16°.
So the value of x° is 16° and the equation is 90°= 74°+x°.
Question 8.
Complete the following directions in the space to the right.
a. Draw 2 points: Q and R. Using a straightedge, draw ![]() .
.
b. Plot a point S somewhere between points Q and R.
c. Plot a point T, which is not on ![]()
d. Draw \(\overline{T S}\).
e. Find the measure of ∠QST and ∠RST.
f. Write an equation to show that the angles add to the measure of a straight angle.
Answer:
The equation of the angles add to the measure of a straight angle is <QST+<STR= 180°.
Explanation:
Here, we need to draw 2 points which is Q and R using a straightedge and then we need to construct ![]() .
.
Then we need to plot a point S somewhere between points Q and R.
And then we need to plot a point T, which is not on ![]()
Then we will construct \(\overline{T S}\).
Then we need to find the measure of ∠QST and ∠RST.
As we have plotted a straight line which is <QSR is 180°, which is <QST+<STR= 180°.
So the equation of the angles add to the measure of a straight angle is <QST+<STR= 180°.