Engage NY Eureka Math 4th Grade Module 4 Lesson 16 Answer Key
Eureka Math Grade 4 Module 4 Lesson 16 Problem Set Answer Key
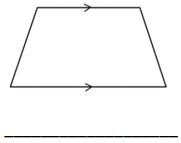
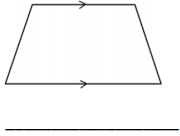
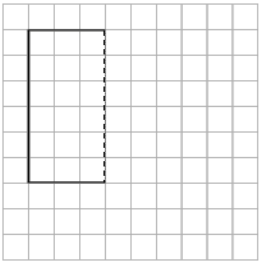
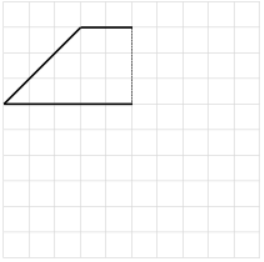
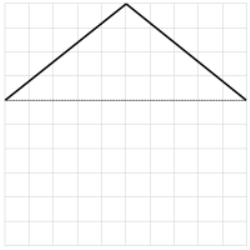
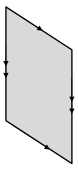
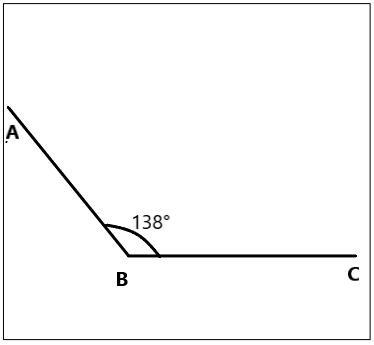
Question 1.
On the grid paper, draw at least one quadrilateral to fit the description. Use the given segment as one segment of the quadrilateral. Name the figure you drew using one of the terms below.
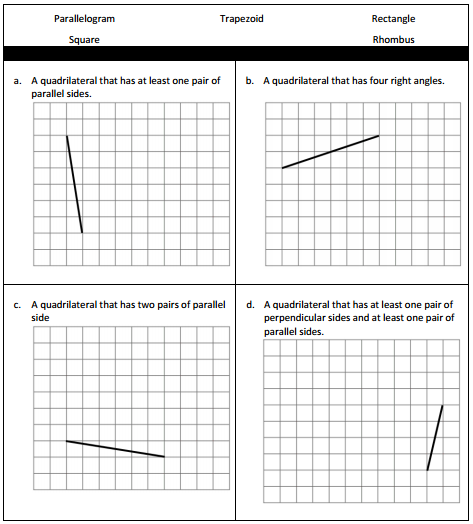
Answer:
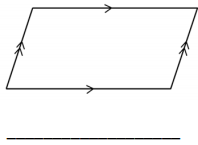
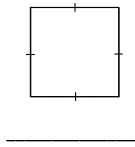
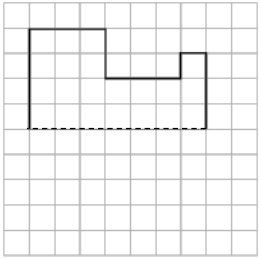
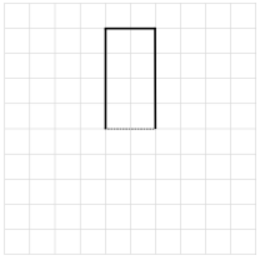
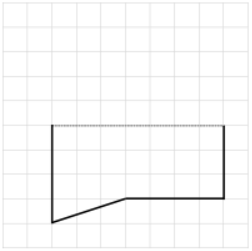
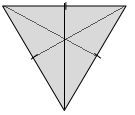
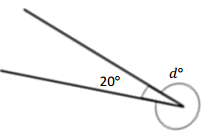
Question 2.
On the grid paper, draw at least one quadrilateral to fit the description. Use the given segment as one segment of the quadrilateral. Name the figure you drew using one of the terms below.

Answer:
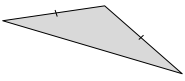
Question 3.
Explain the attributes that make a rhombus different from a rectangle.
Answer:
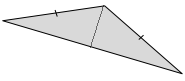
Question 4.
Explain the attribute that makes a square different from a rhombus.
Answer:
Eureka Math Grade 4 Module 4 Lesson 16 Exit Ticket Answer Key
Question 1.
Construct a parallelogram that does not have any right angles on a rectangular grid.

Answer:
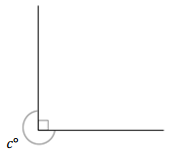
Question 2.
Construct a rectangle on a triangular grid.

Answer:
Eureka Math Grade 4 Module 4 Lesson 16 Homework Answer Key
Use the grid to construct the following. Name the figure you drew using one of the terms in the word box.

Question 1.
Construct a quadrilateral with only one set of parallel sides. Which shape did you create?

Answer:
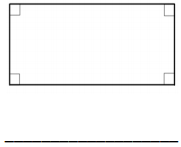
Question 2.
Construct a quadrilateral with one set of parallel sides and two right angles. Which shape did you create?

Answer:
Question 3.
Construct a quadrilateral with two sets of parallel sides. Which shape did you create?

Answer:
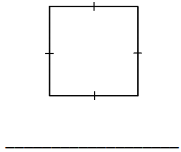
Question 4.
Construct a quadrilateral with all sides of equal length. Which shape did you create?

Answer:
Question 5.
Construct a rectangle with all sides of equal length. Which shape did you create?

Answer: