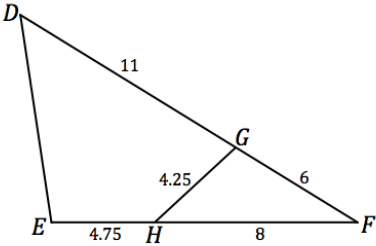
Engage NY Eureka Math Geometry Module 2 Lesson 25 Answer Key
Eureka Math Geometry Module Lesson 25 Exercise Answer Key
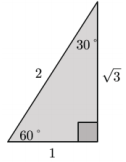
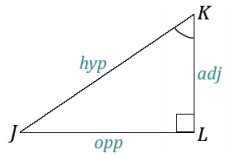
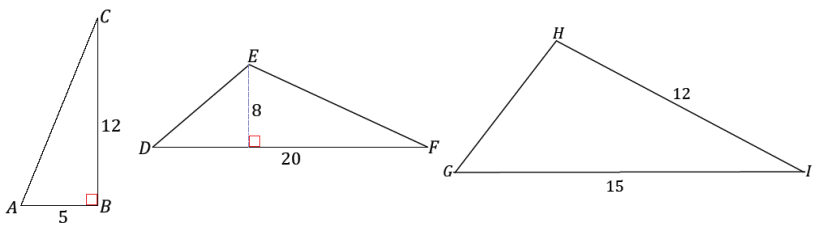
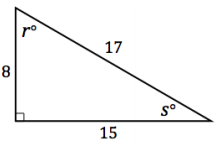
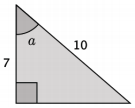
Use the right triangle ∆ ABC to answer Exercises 1 – 3.

Exercise 1.
Name the side of the triangle opposite ∠A.
Answer:
\(\overline{B C}\)
Exercise 2.
Name the side of the triangle opposite ∠B.
Answer:
\(\overline{A C}\)
Exercise 3.
Name the side of the triangle opposite ∠C.
Answer:
\(\overline{A B}\)
For each exercise, label the appropriate sides as adjacent, opposite, and hypotenuse, with respect to the marked acute angle.
Exercise 4.
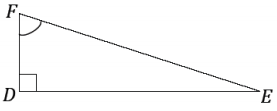
Answer:

Exercise 5.
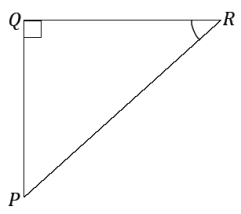
Answer:
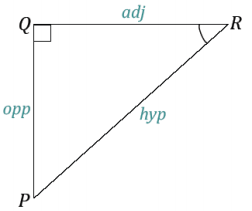
Exercise 6.

Answer:
For each question, round the unknown lengths appropriately. Refer back to your completed chart from the ExploratoryChallenge; each indicated acute angle is the same approximated acute angle measure as in the chart. Set up and label the appropriate length ratios, using the terms app, adj, and hyp in the setup of each ratio.
Exercise 7.
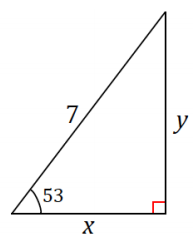
Answer:

Exercise 8.
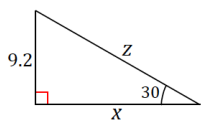
Answer:

Exercise 9.
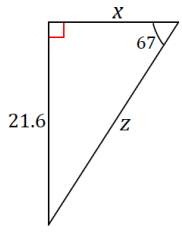
Answer:
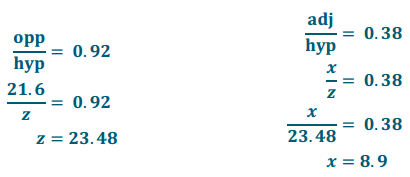
Exercise 10.
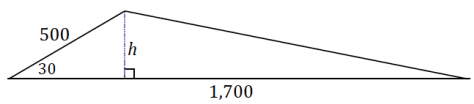
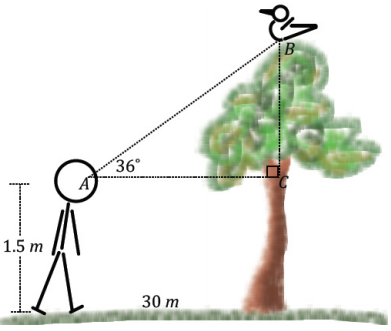
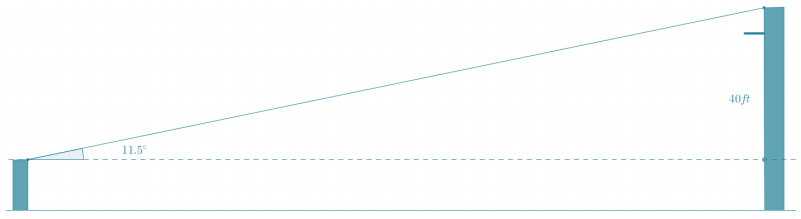
From a point 120 m away from a building, Serena measures the angle between the ground and the top of a building and finds it measures 41°.
What is the height of the building? Round to the nearest meter.
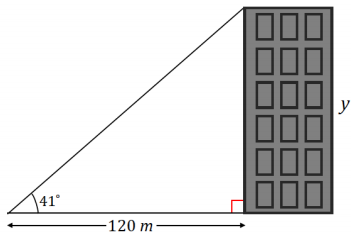
Answer:

The height of the building is approximately 106 meters.
Eureka Math Geometry Module Lesson 25 Problem Set Answer Key
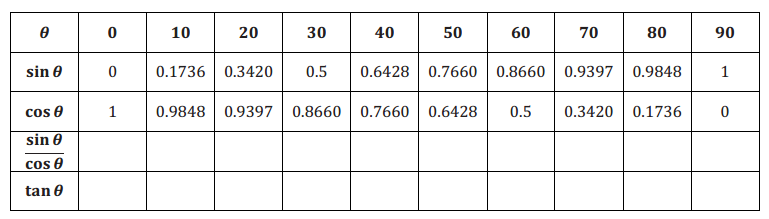
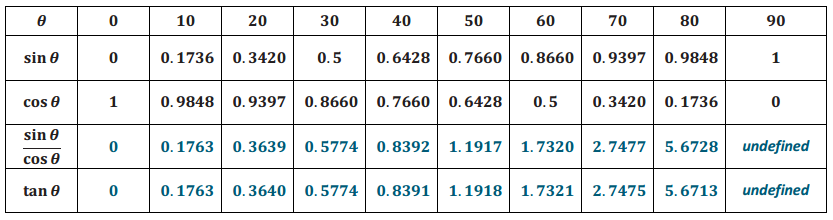
The table below contains the values of the ratios \(\frac{o p p}{h y p}\) and \(\frac{\text { adj }}{\text { hyp }}\) for a variety of right triangles based on a given acute angle, θ, from each triangle. Use the table and the diagram of the right triangle below to complete each problem.
 Answer:
Answer:
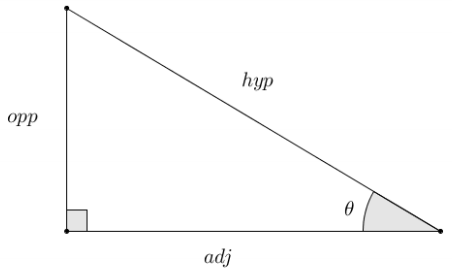
For each problem, approximate the unknown lengths to one decimal place. Write the appropriate length ratios using the terms opp, adj, and hyp in the setup of each ratio.
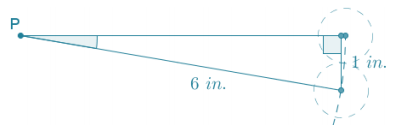
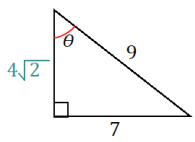
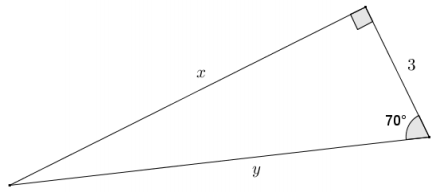
Question 1.
Find the approximate length of the leg opposite the 80° angle.

Answer:
Using the value of the ratio for an \(\frac{\text { opp }}{\text { hyp }}\) 80° angle:
\(\frac{\text { opp }}{24}\) = 0.9848
opp = 23. 6352
The length of the leg opposite the 80° angle is approximately 23.6.
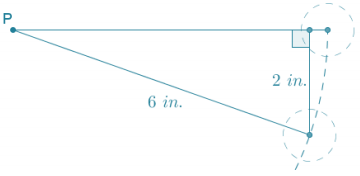
Question 2.
Find the approximate length of the hypotenuse.
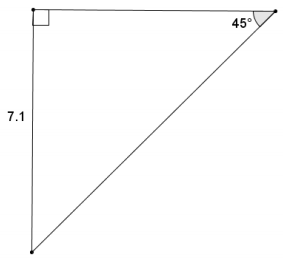
Answer:
Using the value of the ratio \(\frac{\text { opp }}{\text { hyp }}\) for a 45° angle:
\(\frac{7.1}{\text { hyp }}\) = 0.7071
\(\frac{7.1}{0.7071}\) = hyp
10.0410 ≈ hyp
The length of the hypotenuse is approximately 10.0.
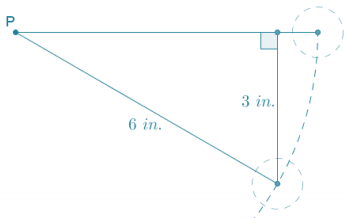
Question 3.
Find the approximate length of the hypotenuse.
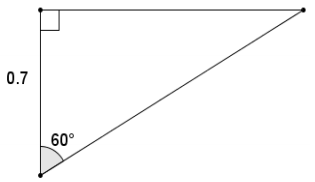
Answer:
adj
Using the value of the ratio \(\frac{\text { adj }}{\text { hyp }}\) for a 60° angle:
\(\frac{0.7}{\text { hyp }}\) = \(\frac{1}{2}\)
\(\frac{0.7}{\frac{1}{2}}\) = hyp
1.4 = hyp
The length of the hypotenuse is 1.4.
Question 4.
Find the approximate length of the leg adjacent to the 40° angle.
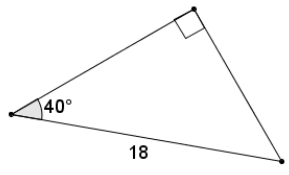
Answer:
Using the value of the ratio \(\frac{\text { adj }}{\text { hyp }}\) for a 40° angle:
\(\frac{\text { adj }}{18}\) = 0.7660
adj = 13. 788
The length of the leg adjacent to the given 40° angle is approximately
13.8.
Question 5.
Find the length of both legs of the right triangle below. Indicate which leg is adjacent and which is opposite the given angle of 30°.
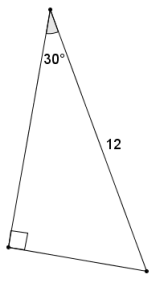
Answer:
Using the value of the ratio \(\frac{\text { opp }}{\text { hyp }}\) for a 30° angle:
\(\frac{\text { opp }}{12}=\frac{1}{2}\)
opp = 6
The length of the leg that is opposite the given 30° angle is 6.
Using the value of the ratio \(\frac{\text { adj }}{\text { hyp }}\) for a 30° angle:
\(\frac{\text { adj }}{12}\) = 0.8660
adj = 10. 392
The length of the leg that is adjacent to the given 30° angle is approximately 10.4.
Question 6.
Three city streets form a right triangle. Main Street and State Street are perpendicular. Laura Street and State Street intersect at a 50° angle. The distance along Laura Street to Main Street is 0.8 mile. If Laura Street is closed between Main Street and State Street for a festival, approximately how far (to the nearest tenth) will someone have to travel to get around the festival if they take only Main Street and State Street?
Answer:
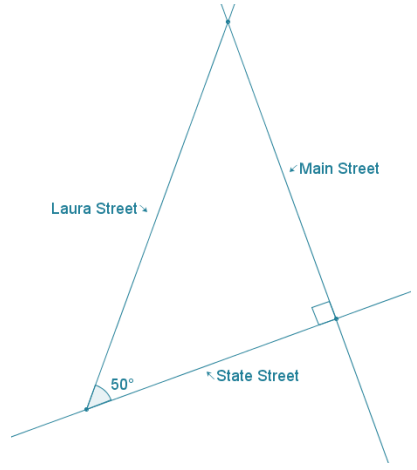
The leg opposite the 50° angle represents the distance along Main Street, the leg adjacent to the 50° angle represents the distance along State Street, and the hypotenuse of the triangle represents the 0.8 mile distance along Laura Street.
Using the ratio \(\frac{\text { opp }}{\text { hyp }}\) for 50°:
0.7660 = \(\frac{\text { opp }}{0.8}\)
0.6128 = opp
Using the ratio \(\frac{\text { adj }}{\text { hyp }}\) for 50°:
0.6428 = \(\frac{\text { adj }}{0.8}\)
0. 51424 = adj
The total distance of the detour:
0.6128 + 0.51424 = 1.12704
The total distance to travel around the festival along State Street and Main Street is approximately 1.1 miles.
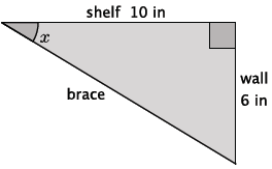
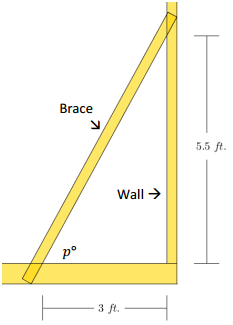
Question 7.
A cable anchors a utility pole to the ground as shown in the picture. The cable forms an angle of 70° with the ground. The distance from the base of the utility pole to the anchor point on the ground is 3.8 meters. Approximately how long is the support cable?
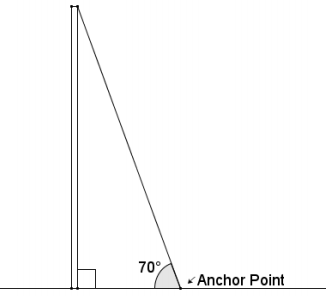
Answer:
The hypotenuse of the triangle represents the length of the support cable in the diagram, and the leg adjacent to the given 70° angIe represents the distance between the anchor point and the base of the utility pole. Using the value of the ratio \(\frac{\text { adj }}{\text { hyp }}\) for 70°:
0.3420 = \(\frac{3.8}{\mathrm{hyp}}\)
hyp = 0. 3420
hyp = 11. 1111
The length of the support cable is approximately 11.1 meters long.
Question 8.
Indy says that the ratio of \(\frac{\text { opp }}{\text { adj }}\) for an angle of 0° has a value of 0 because the opposite side of the triangle has a length of 0. What does she mean?
Answer:
Indy’s triangle is not actually a triangle since the opposite side does not have length, which means that it does not exist. As the degree measure of the angle considered gets closer to 0°, the value of the ratio gets closer to 0.
Eureka Math Geometry Module Lesson 25 Exit Ticket Answer Key
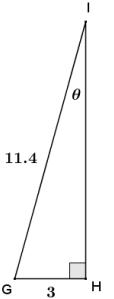
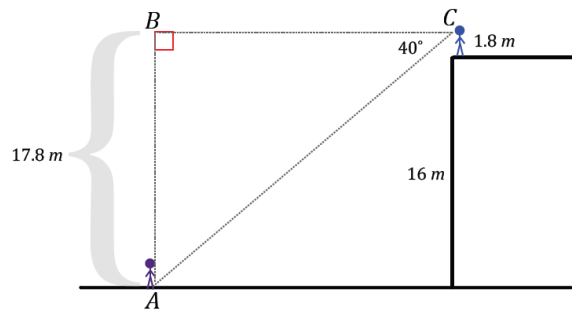
Question 1.
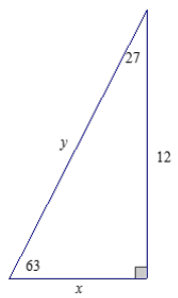
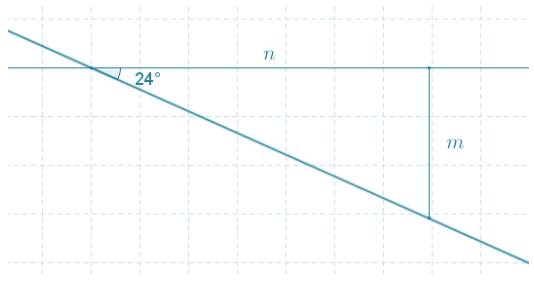
Use the chart from the Exploratory Challenge to approximate the unknown lengths y and z to one decimal place.
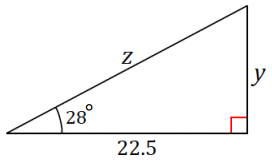
Answer:

Question 2.
Why can we use the chart from the Exploratory Challenge to approximate the unknown lengths?
Answer:
The triangle in Problem 1 is similar to a triangle in the chart from the Exploratory Challenge. Since the triangles are similar, the values of the \(\frac{\text { opp }}{\text { hyp }}\) and \(\frac{\text { adj }}{\text { hyp }}\) ratios in reference to the acute angle of 28° can be used in the equations needed to solve for unknown lengths.
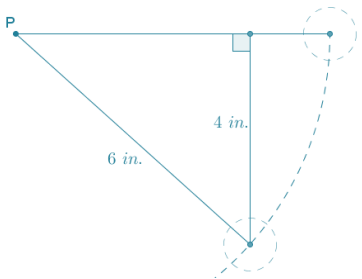
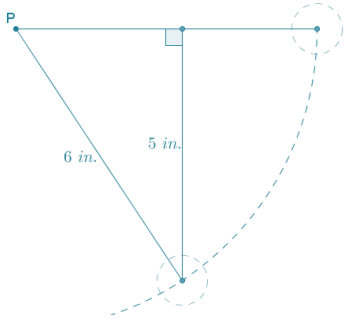
Eureka Math Geometry Module Lesson 25 Exploratory Challenge Ticket Answer Key
Note: Angle measures are approximations.
For each triangle in your set, determine missing angle measurements and side lengths. Side lengths should be measured to one decimal place. Make sure that each of the \(\frac{\text { opp }}{\text { hyp }}\) and \(\frac{\text { adj }}{\text { hyp }}\) ratios are set up and missing values are calculated and rounded appropriately.
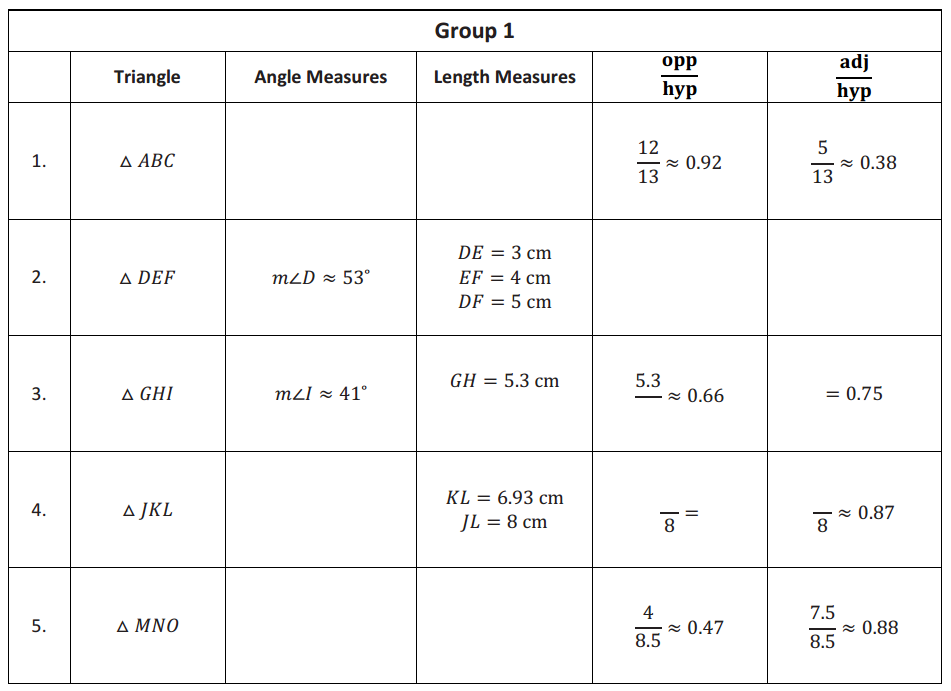
Answer:
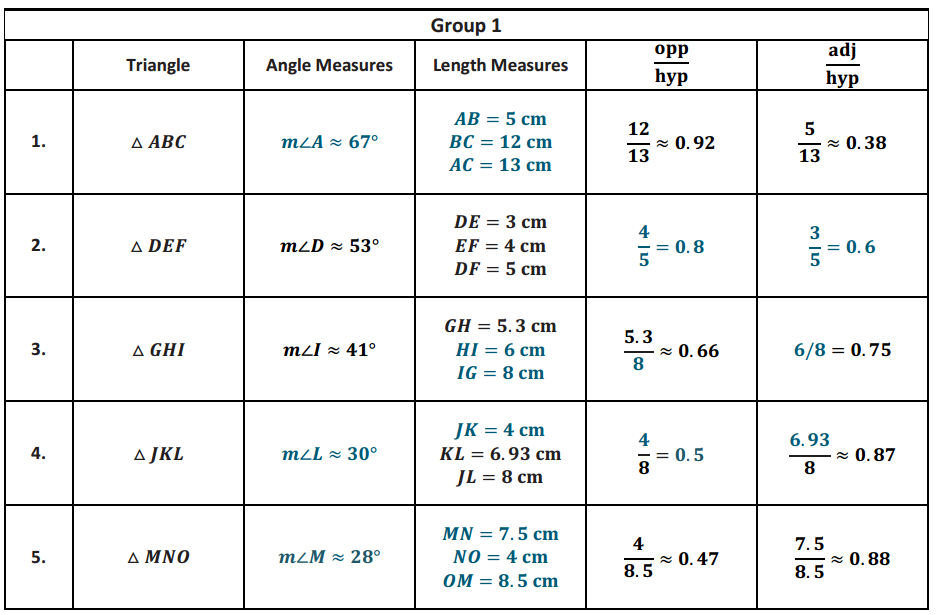
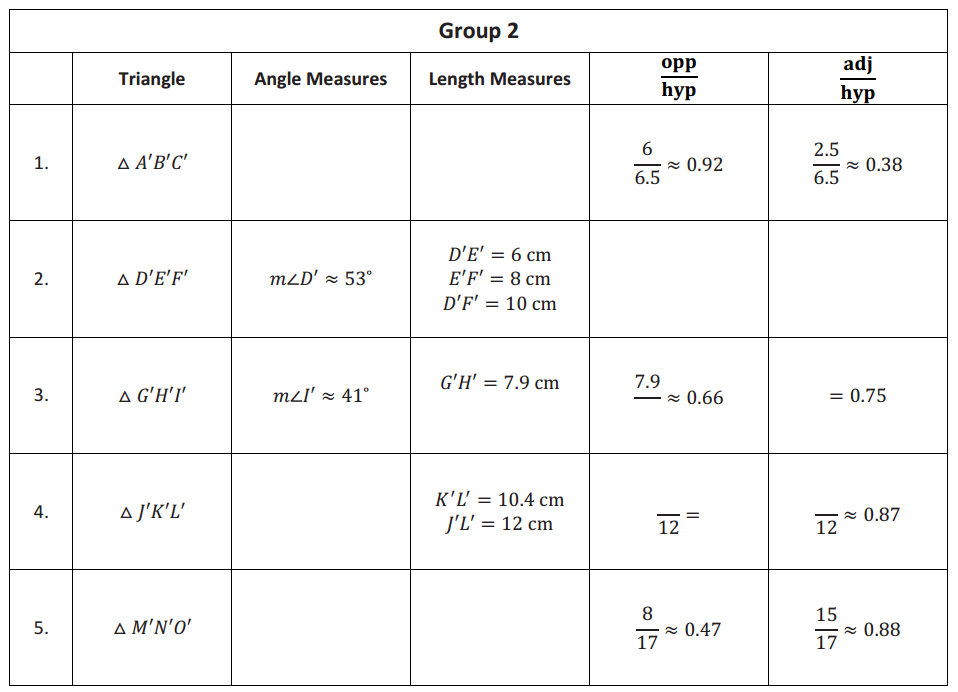
Answer:
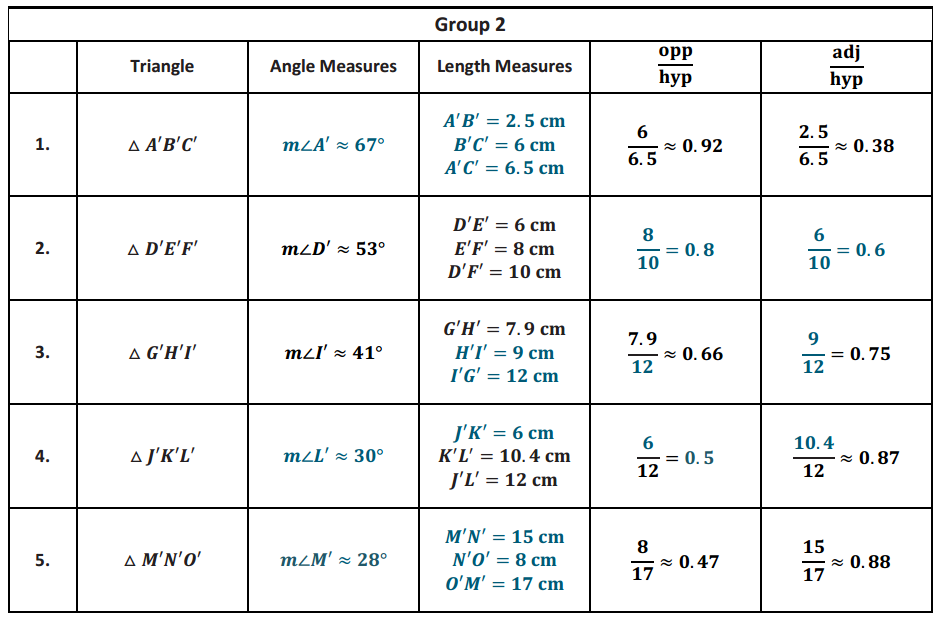
With a partner, discuss what you can conclude about each pair of triangles between the two sets.
Answer:
Each pair of triangles is similar by the AA criterion. The marked acute angle for each pair of corresponding triangles is the same. The values of the \(\frac{\text { opp }}{\text { hyp }}\) and \(\frac{\text { adj }}{\text { hyp }}\) ratios are the same.
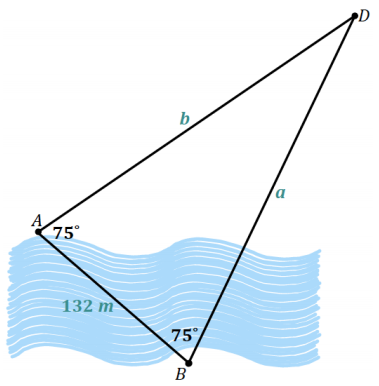
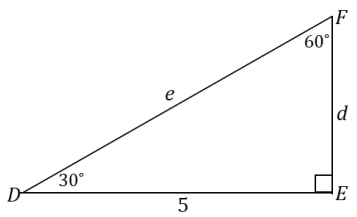

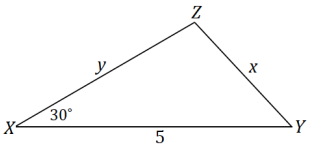
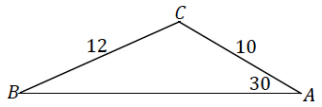
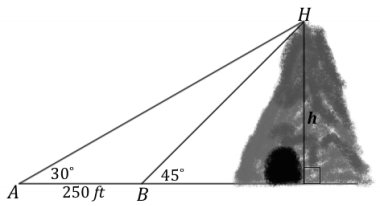
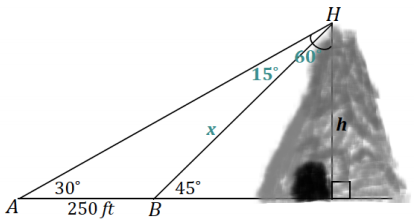
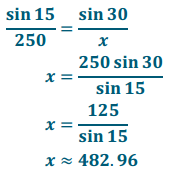
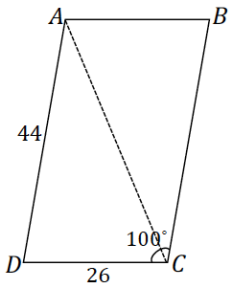

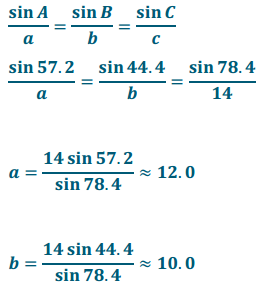
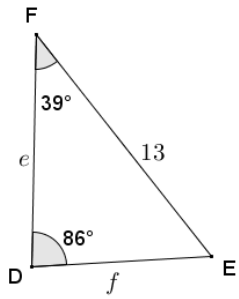
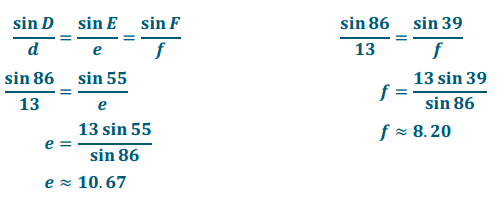
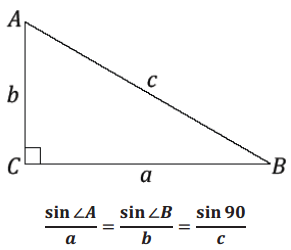

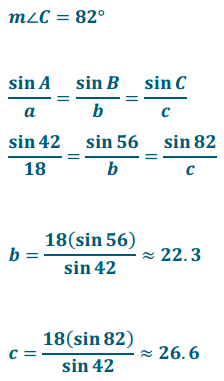
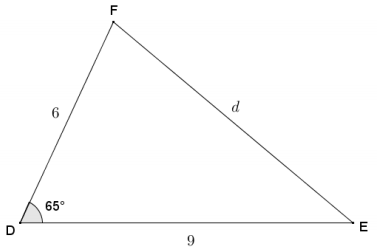
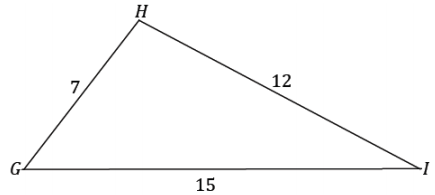
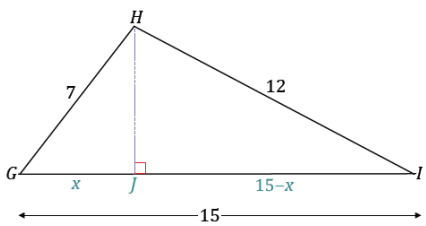













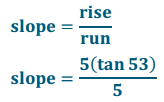
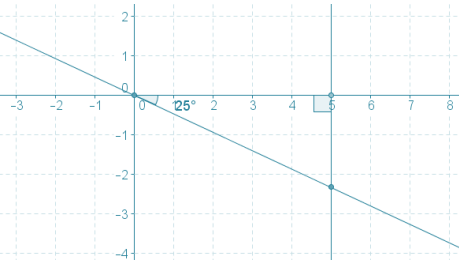
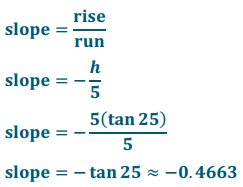
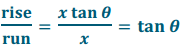



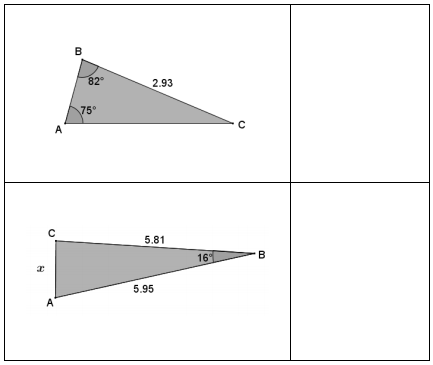
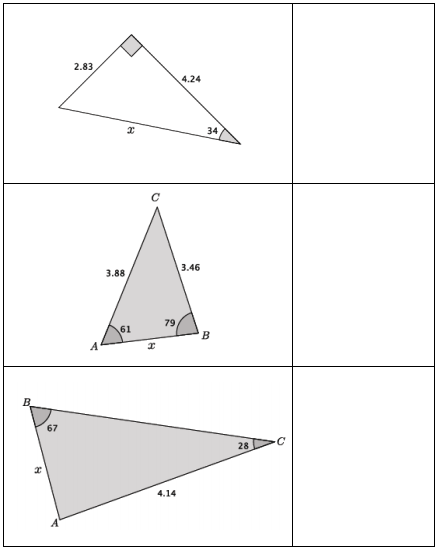
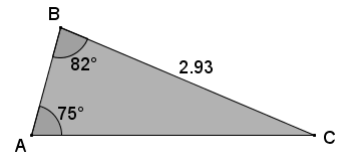 law of sines
law of sines