Engage NY Eureka Math 8th Grade Module 3 Lesson 9 Answer Key
Eureka Math Grade 8 Module 3 Lesson 9 Exploratory Challenge Answer Key
Exploratory Challenge 1.
The goal is to show that if △ABC is similar to △A’ B’ C’, then △A’ B’ C’ is similar to △ABC. Symbolically,
if △ABC~△A’B’C’, then △A’ B’ C’~△ABC.
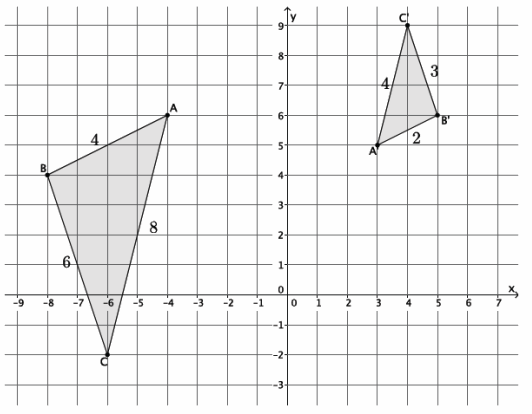
a. First, determine whether or not △ABC is in fact similar to △A’ B’ C’. (If it isn’t, then no further work needs to be done.) Use a protractor to verify that the corresponding angles are congruent and that the ratios of the corresponding sides are equal to some scale factor.
Answer:
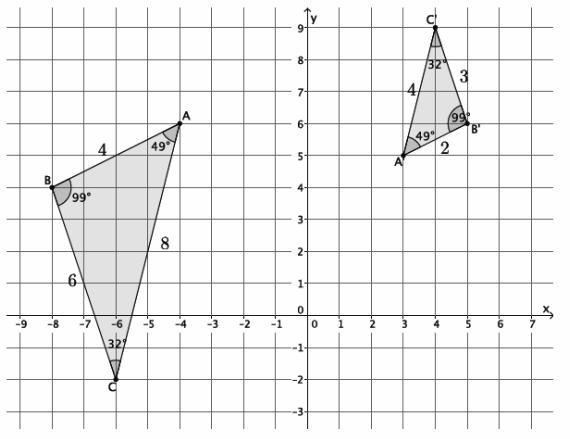
The corresponding angles are congruent: ∠A≅∠A’, ∠B≅∠B’, and ∠C≅∠C’, therefore
|∠A|=|∠A’ |=49°, |∠B|=|∠B’ |=99°, and |∠C|=|∠C’ |=32°.
The ratios of the corresponding sides are equal: \(\frac{4}{8}\)=\(\frac{3}{6}\)=\(\frac{2}{4}\)=r.
b. Describe the sequence of dilation followed by a congruence that proves △ABC~△A’ B’ C’.
Answer:
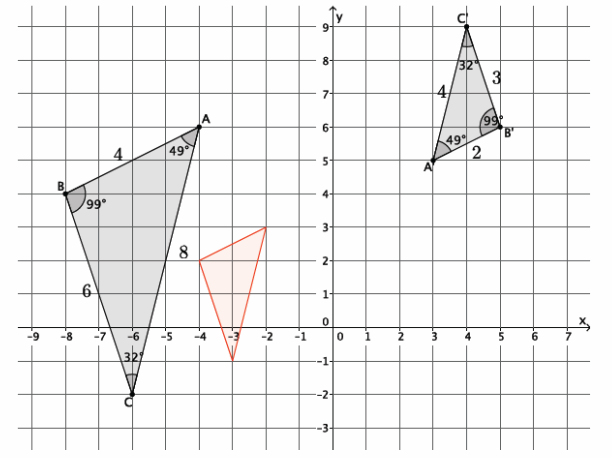
To map △ABC onto △A’ B’ C’, dilate △ABC from center O by scale factor r=\(\frac{1}{2}\), noted in the diagram above by the red triangle. Then, translate the red triangle up two units and five units to the right. Next, rotate the red triangle 180 degrees around point A’ until AC coincides with A’C’.
c. Describe the sequence of dilation followed by a congruence that proves △A’B’C’~△ABC.
Answer:
Note that in the diagram below, both axes have been compressed.
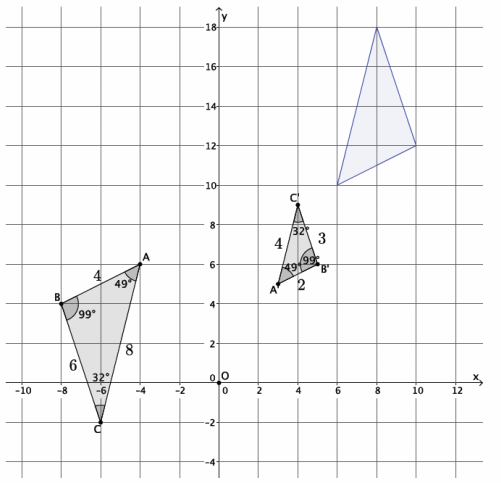
To map △A’B’C’ onto △ABC, dilate △A’B’C’ from center O by scale factor r=2, noted by the blue triangle in the diagram. Then, translate the blue triangle ten units to the left and two units down. Next, rotate the blue triangle 180 degrees around point A until side A’C’ coincides with side AC.
d. Is it true that △ABC~△A’ B’ C’ and △A’ B’ C’~△ABC? Why do you think this is so?
Answer:
Yes, it is true that △ABC~△A’ B’ C’ and △A’ B’ C’~△ABC. I think it is true because when we say figures are similar, it means that they are the same figure, just a different size because one has been dilated by a scale factor. For that reason, if one figure, like △ABC, is similar to another, like △A’ B’ C’, it must mean that △A’ B’ C’~△ABC. However, the sequence you would use to map one of the figures onto the other is different.
Exploratory Challenge 2.
The goal is to show that if △ABC is similar to △A’B’C’ and △A’B’C’ is similar to △A”B”C”, then △ABC is similar to
△A”B”C”. Symbolically, if △ABC~△A’ B’ C’ and △A’B’C’~△A”B”C”, then △ABC~△A”B”C”.
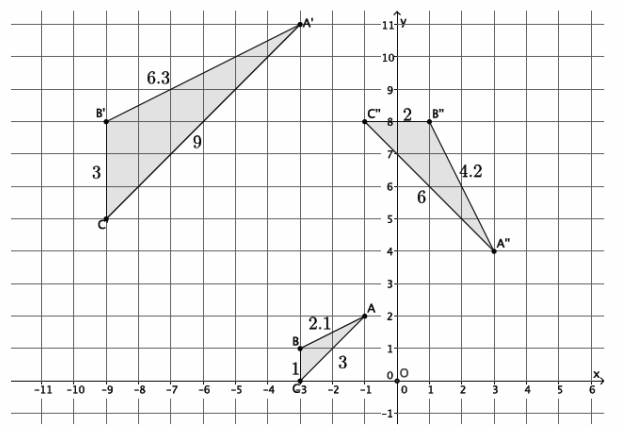
a. Describe the similarity that proves △ABC~△A’B’C’.
Answer:
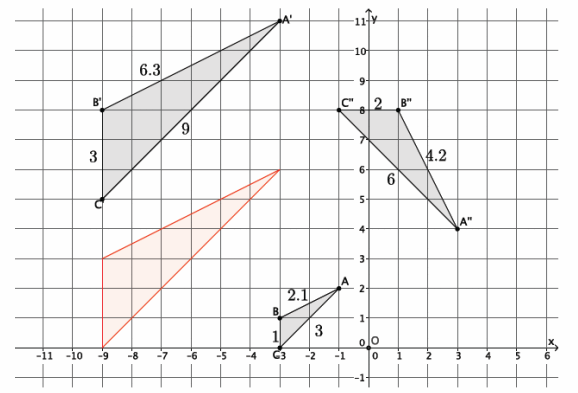
To map △ABC onto △A’B’C’, we need to first determine the scale factor that makes △ABC the same size as △A’ B’ C’. Then, \(\frac{3}{1}\)=\(\frac{6.3}{2.1}\)=\(\frac{9}{3}\)=r. Dilate △ABC from center O by scale factor r=3, shown in red in the diagram. Then, translate the red triangle 5 units up.
b. Describe the similarity that proves △A’B’C’~△A”B”C”.
Answer:
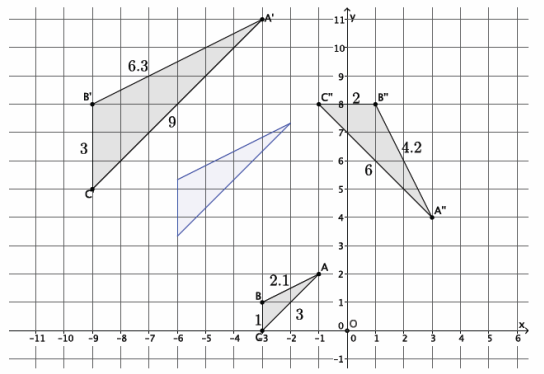
To map △A’B’C’ onto △A”B”C”, we need to first determine the scale factor that makes △A’B’C’ the same size as △A”B”C”. Then, \(\frac{4.2}{6.3}\)=\(\frac{6}{9}\)=\(\frac{2}{3}\)=r. Dilate △A’B’C’ from center O by scale factor r=\(\frac{2}{3}\), shown in blue in the diagram. Then, translate the blue triangle 3.5 units down and 5 units to the right. Next, rotate the blue triangle 90 degrees clockwise around point A” until the blue triangle coincides with
△A”B”C”.
c. Verify that, in fact, △ABC~△A”B”C” by checking corresponding angles and corresponding side lengths. Then, describe the sequence that would prove the similarity △ABC~△A” B” C”.
Answer:
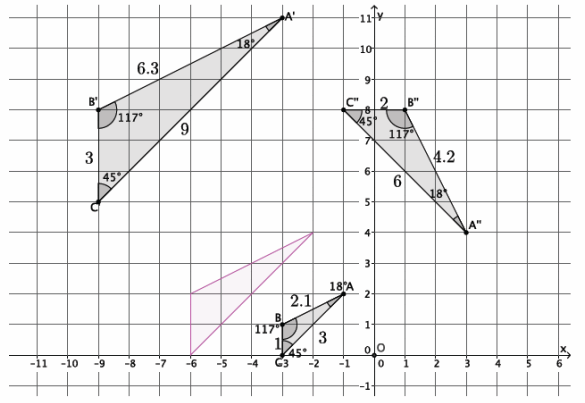
The corresponding angles are congruent: ∠A≅∠A”, ∠B≅∠B”, and ∠C≅∠C”; therefore, |∠A|=|∠A” |=18°, |∠B|=|∠B” |=117°, and |∠C|=|∠C” |=45°. The ratio of the corresponding sides is equal:
\(\frac{4.2}{2.1}\)=\(\frac{6}{3}\)=\(\frac{2}{1}\)=r. Dilate △ABC from center O by scale factor r=2, shown as the pink triangle in the diagram. Then, translate the pink triangle 5 units to the right. Finally, rotate the pink triangle 90 degrees clockwise around point A” until the pink triangle coincides with △A”B”C”.
d. Is it true that if △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”, then △ABC~△A”B”C”? Why do you think this is so?
Answer:
Yes, it is true that if △ABC~△A’ B’ C’ and △A’ B’ C’~△A” B” C”, then △ABC~△A” B” C”. Again, because these figures are similar, it means that they have equal angles and are made different sizes based on a specific scale factor. Since dilations map angles to angles of the same degree, it makes sense that all three figures would have the “same shape.” Also, using the idea that similarity is a symmetric relation, the statement that △ABC~△A’ B’ C’ implies that △A’ B’ C’~△ABC.
Since we know that △A’ B’ C’~△A”B”C”, it is reasonable to conclude that △ABC~△A”B”C”.
Eureka Math Grade 8 Module 3 Lesson 9 Problem Set Answer Key
Question 1.
Would a dilation alone be enough to show that similarity is symmetric? That is, would a dilation alone prove that if △ABC~ △A’B’C’, then △A’ B’ C’~ △ABC? Consider the two examples below.
a. Given △ABC~ △A’ B’ C’, is a dilation enough to show that △A’ B’ C’~ △ABC? Explain.
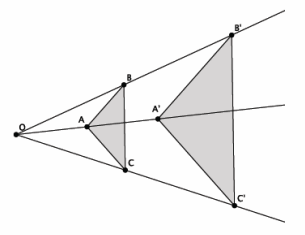
Answer:
For these two triangles, a dilation alone is enough to show that if △ABC~△A’B’C’, then △A’ B’ C’~△ABC. The reason that dilation alone is enough is because both of the triangles have been dilated from the same center. Therefore, to map one onto the other, all that would be required is a dilation.
b. Given △ABC~△A’ B’ C’, is a dilation enough to show that △A’ B’ C’~△ABC? Explain.
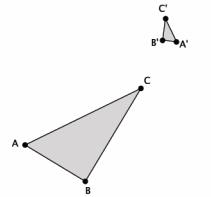
Answer:
For these two triangles, a dilation alone is not enough to show that if △ABC~ △A’ B’ C’, then △A’ B’ C’~
△ABC. The reason is that a dilation would just make them the same size. It would not show that you could map one of the triangles onto the other. To do that, you would need a sequence of basic rigid motions to demonstrate the congruence.
c. In general, is dilation enough to prove that similarity is a symmetric relation? Explain.
Answer:
No, in general, a dilation alone does not prove that similarity is a symmetric relation. In some cases, like part (a), it would be enough, but because we are talking about general cases, we must consider figures that require a sequence of basic rigid motions to map one onto the other. Therefore, in general, to show that there is a symmetric relationship, we must use what we know about similar figures, a dilation followed by a congruence, as opposed to dilation alone.
Question 2.
Would a dilation alone be enough to show that similarity is transitive? That is, would a dilation alone prove that if
△ABC~△A’B’C’, and △A’ B’ C’~△A”B”C”, then △ABC~△A”B”C”? Consider the two examples below.
a. Given △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”, is a dilation enough to show that △ABC~△A”B”C”? Explain.
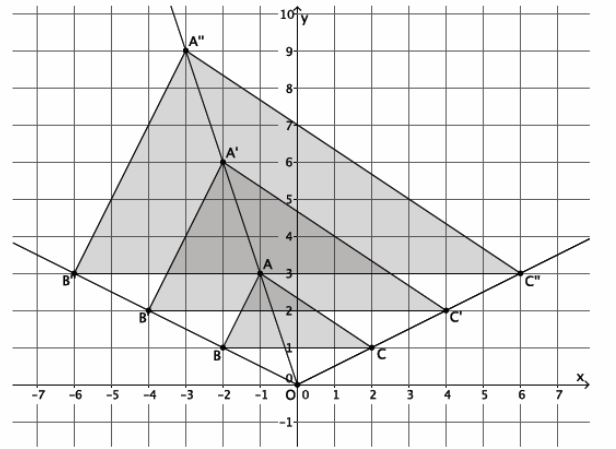
Answer:
Yes, in this case, we could dilate by different scale factors to show that all three triangles are similar to each other.
b. Given △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”, is a dilation enough to show that △ABC~△A”B”C”? Explain.
Answer:
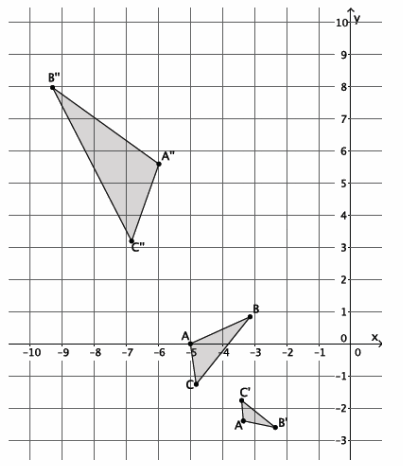
In this case, it would take more than just a dilation to show that all three triangles are similar to one another. Specifically, it would take a dilation followed by a congruence to prove the similarity among the three.
c. In general, is dilation enough to prove that similarity is a transitive relation? Explain.
Answer:
In some cases, it might be enough, but the general case requires the use of dilation and a congruence. Therefore, to prove that similarity is a transitive relation, you must use both a dilation and a congruence.
Question 3.
In the diagram below, △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”. Is △ABC~△A”B”C”? If so, describe the dilation followed by the congruence that demonstrates the similarity.

Answer:
Yes, △ABC~△A”B”C” because similarity is transitive. Since r|AB|=|A”B”|, then r×4=2, which means
r=\(\frac{1}{2}\). Then, a dilation from the origin by scale factor r=\(\frac{1}{2}\) makes △ABC the same size as △A”B”C”. Translate the dilated image of △ABC 6 \(\frac{1}{2}\) units to the left and then reflect across line A”B”. The sequence of the dilation and the congruence map △ABC onto △A” B” C”, demonstrating the similarity.
Eureka Math Grade 8 Module 3 Lesson 9 Exit Ticket Answer Key
Use the diagram below to answer Problems 1 and 2.
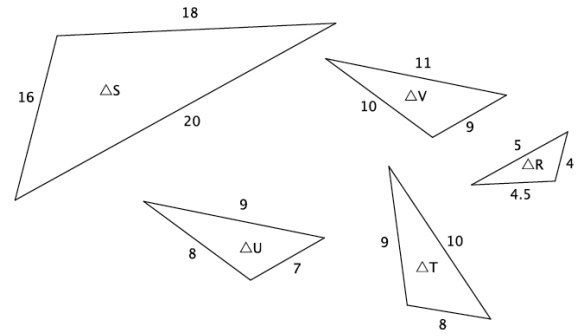
Question 1.
Which two triangles, if any, have similarity that is symmetric?
Answer:
△S~△R and △R~△S
△S~△T and △T~△S
△T~△R and △R~△T
Question 2.
Which three triangles, if any, have similarity that is transitive?
Answer:
One possible solution: Since △S~△R and △R~△T, then △S~△T.
Note that △U and △V are not similar to each other or any other triangles. Therefore, they should not be in any solution.