Tag: Eureka Math Grade 8

Engage NY Eureka Math 8th Grade Module 4 Lesson 4 Answer Key

Eureka Math Grade 8 Module 4 Lesson 4 Exercise Answer Key

For each problem, show your work, and check that your solution is correct.

Exercise 1.
Solve the linear equation x+x+2+x+4+x+6=-28. State the property that justifies your first step and why you chose it.
Answer:
The left side of the equation can be transformed from x+x+2+x+4+x+6 to 4x+12 using the commutative and distributive properties. Using these properties decreases the number of terms of the equation. Now we have the equation:
4x+12=-28
4x+12-12=-28-12
4x=-40
\(\frac{1}{4}\)∙4x=-40∙\(\frac{1}{4}\)
x=-10.
The left side of the equation is equal to (-10)+(-10)+2+(-10)+4+(-10)+6, which is -28. Since the left side is equal to the right side, then x=-10 is the solution to the equation.
Note: Students could use the division property in the last step to get the answer.

Exercise 2.
Solve the linear equation 2(3x+2)=2x-1+x. State the property that justifies your first step and why you chose it.
Answer:
Both sides of equation can be rewritten using the distributive property. I have to use it on the left side to expand the expression. I have to use it on the right side to collect like terms.
The left side is
2(3x+2)=6x+4.
The right side is
2x-1+x=2x+x-1
=3x-1.
The equation is
6x+4=3x-1
6x+4-4=3x-1-4
6x=3x-5
6x-3x=3x-3x-5
(6-3)x=(3-3)x-5
3x=-5
\(\frac{1}{3}\)∙3x=\(\frac{1}{3}\)∙(-5)
x=-\(\frac{5}{3}\).
The left side of the equation is 2(3x+2). Replacing x with –\(\frac{5}{3}\) gives 2(3(-\(\frac{5}{3}\))+2)=2(-5+2)=2(-3)=-6. The right side of the equation is 2x-1+x. Replacing x with –\(\frac{5}{3}\) gives 2(-\(\frac{5}{3}\))-1+(-\(\frac{5}{3}\))=-\(\frac{10}{3}\)-1-\(\frac{5}{3}\)=-6. Since both sides are equal to -6, then x=-\(\frac{5}{3}\) is a solution to 2(3x+2)=2x-1+x.
Note: Students could use the division property in the last step to get the answer.

Exercise 3.
Solve the linear equation x-9=\(\frac{3}{5}\) x. State the property that justifies your first step and why you chose it.
Answer;
I chose to use the subtraction property of equality to get all terms with an x on one side of the equal sign.
x-9=\(\frac{3}{5}\) x
x-x-9=\(\frac{3}{5}\) x-x
(1-1)x-9=(\(\frac{3}{5}\)-1)x
-9=-\(\frac{2}{5}\) x
–\(\frac{5}{2}\)∙(-9)=-\(\frac{5}{2}\)∙-\(\frac{2}{5}\) x
4\(\frac{5}{2}\)=x
The left side of the equation is 4\(\frac{5}{2}\)– \(\frac{18}{2}\)=\(\frac{27}{2}\). The right side is \(\frac{3}{5}\)∙4\(\frac{5}{2}\)=\(\frac{3}{1}\)∙\(\frac{9}{2}\)=\(\frac{27}{2}\). Since both sides are equal to the same number, then x=4\(\frac{5}{2}\) is a solution to x-9=\(\frac{3}{5}\) x.

Exercise 4.
Solve the linear equation 29-3x=5x+5. State the property that justifies your first step and why you chose it.
Answer:
I chose to use the addition property of equality to get all terms with an x on one side of the equal sign.
29-3x=5x+5
29-3x+3x=5x+3x+5
29=8x+5
29-5=8x+5-5
24=8x
\(\frac{1}{8}\)∙24=\(\frac{1}{8}\)∙8x
3=x
The left side of the equal sign is 29-3(3)=29-9=20. The right side is equal to 5(3)+5=15+5=20. Since both sides are equal, x=3 is a solution to 29-3x=5x+5.
Note: Students could use the division property in the last step to get the answer.

Exercise 5.
Solve the linear equation \(\frac{1}{3}\) x-5+171=x. State the property that justifies your first step and why you chose it.
Answer:
I chose to combine the constants -5 and 171. Then, I used the subtraction property of equality to get all terms with an x on one side of the equal sign.
\(\frac{1}{3}\) x-5+171=x
\(\frac{1}{3}\) x+166=x
\(\frac{1}{3}\) x-\(\frac{1}{3}\) x+166=x-\(\frac{1}{3}\) x
166=\(\frac{2}{3}\) x
166∙\(\frac{3}{2}\)=\(\frac{3}{2}\)∙\(\frac{2}{3}\) x
83∙3=x
249=x
The left side of the equation is \(\frac{1}{3}\)∙249-5+171=83-5+171=78+171=249, which is exactly equal to the right side. Therefore, x=249 is a solution to \(\frac{1}{3}\) x-5+171=x.

Eureka Math Grade 8 Module 4 Lesson 4 Exit Ticket Answer Key

Question 6.
Guess a number for x that would make the equation true. Check your solution.
5x-2=8
Answer:
When x=2, the left side of the equation is 8, which is the same as the right side. Therefore, x=2 is the solution to the equation.

Question 7.
Use the properties of equality to solve the equation 7x-4+x=12. State which property justifies your first step and why you chose it. Check your solution.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
7x-4+x=12
7x+x-4=12
(7+1)x-4=12
8x-4=12
8x-4+4=12+4
8x=16
\(\frac{8}{8}\)x=\(\frac{16}{8}\)
x=2
The left side of the equation is 7(2)-4+2=14-4+2=12. The right side is also 12. Since the left side equals the right side, x=2 is the solution to the equation.

Question 8.
Use the properties of equality to solve the equation 3x+2-x=11x+9. State which property justifies your first step and why you chose it. Check your solution.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
3x+2-x=11x+9
3x-x+2=11x+9
(3-1)x+2=11x+9
2x+2=11x+9
2x-2x+2=11x-2x+9
(2-2)x+2=(11-2)x+9
2=9x+9
2-9=9x+9-9
-7=9x
–\(\frac{7}{9}\)=\(\frac{9}{9}\) x
–\(\frac{7}{9}\)=x
The left side of the equation is 3(\(\frac{-7}{9}\))+2-\(\frac{-7}{9}\)=-\(\frac{21}{9}\)+\(\frac{18}{9}\)+\(\frac{7}{9}\)=\(\frac{4}{9}\). The right side is 11(-\(\frac{7}{9}\))+9=\(\frac{-77}{9}\)+\(\frac{81}{9}\)=\(\frac{4}{9}\). Since the left side equals the right side, x=-\(\frac{7}{9}\) is the solution to the equation.

Eureka Math Grade 8 Module 4 Lesson 4 Problem Set Answer Key

Students solve equations using properties of equality.

For each problem, show your work, and check that your solution is correct.

Question 1.
Solve the linear equation x+4+3x=72. State the property that justifies your first step and why you chose it.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
x+4+3x=72
x+3x+4=72
(1+3)x+4=72
4x+4=72
4x+4-4=72-4
4x=68
\(\frac{4}{4}\) x=\(\frac{68}{4}\)
x=17
The left side is equal to 17+4+3(17)=21+51=72, which is equal to the right side. Therefore, x=17 is a solution to the equation x+4+3x=72.

Question 2.
Solve the linear equation x+3+x-8+x=55. State the property that justifies your first step and why you chose it.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
x+3+x-8+x=55
x+x+x+3-8=55
(1+1+1)x+3-8=55
3x-5=55
3x-5+5=55+5
3x=60
\(\frac{3}{3}\) x=\(\frac{60}{3}\)
x=20
The left side is equal to 20+3+20-8+20=43-8+20=35+20=55, which is equal to the right side. Therefore, x=20 is a solution to x+3+x-8+x=55.

Question 3.
Solve the linear equation \(\frac{1}{2}\) x+10=\(\frac{1}{4}\) x+54. State the property that justifies your first step and why you chose it.
Answer;
I chose to use the subtraction property of equality to get all of the constants on one side of the equal sign.
\(\frac{1}{2}\) x+10=\(\frac{1}{4}\) x+54
\(\frac{1}{2}\) x+10-10=\(\frac{1}{4}\) x+54-10
\(\frac{1}{2}\) x=\(\frac{1}{4}\) x+44
\(\frac{1}{2}\) x-\(\frac{1}{4}\) x=\(\frac{1}{4}\) x-\(\frac{1}{4}\) x+44
\(\frac{1}{4}\) x=44
4∙\(\frac{1}{4}\) x=4∙44
x=176
The left side of the equation is \(\frac{1}{2}\) (176)+10=88+10=98. The right side of the equation is
\(\frac{1}{4}\) (176)+54=44+54=98. Since both sides equal 98, x=176 is a solution to the equation
\(\frac{1}{2}\) x+10=\(\frac{1}{4}\) x+54.

Question 4.
Solve the linear equation \(\frac{1}{4}\) x+18=x. State the property that justifies your first step and why you chose it.
I chose to use the subtraction property of equality to get all terms with an x on one side of the equal sign.
\(\frac{1}{4}\) x+18=x
\(\frac{1}{4}\) x-\(\frac{1}{4}\) x+18=x-\(\frac{1}{4}\) x
18=\(\frac{3}{4}\) x
\(\frac{4}{3}\)∙18=\(\frac{4}{3}\)∙\(\frac{3}{4}\) x
24=x
The left side of the equation is \(\frac{1}{4}\) (24)+18=6+18=24, which is what the right side is equal to. Therefore, x=24 is a solution to \(\frac{1}{4}\) x+18=x.

Question 5.
Solve the linear equation 17-x=\(\frac{1}{3}\)∙15+6. State the property that justifies your first step and why you chose it.
Answer:
The right side of the equation can be simplified to 11. Then, the equation is
17-x=11,
and x=6. Both sides of the equation equal 11; therefore, x=6 is a solution to the equation 17-x=\(\frac{1}{3}\)∙15+6. I was able to solve the equation mentally without using the properties of equality.

Question 6.
Solve the linear equation \(\frac{x+x+2}{4}\)=189.5. State the property that justifies your first step and why you chose it.
Answer:
I chose to use the multiplication property of equality to get all terms with an x on one side of the equal sign.
\(\frac{x+x+2}{4}\)=189.5
x+x+2=4(189.5)
2x+2=758
2x+2-2=758-2
2x=756
\(\frac{2}{2}\) x=\(\frac{756}{2}\)
x=378
The left side of the equation is \(\frac{378+378+2}{4}\)=\(\frac{758}{4}\)=189.5, which is equal to the right side of the equation. Therefore, x=378 is a solution to \(\frac{x+x+2}{4}\)=189.5.

Question 7.
Alysha solved the linear equation 2x-3-8x=14+2x-1. Her work is shown below. When she checked her answer, the left side of the equation did not equal the right side. Find and explain Alysha’s error, and then solve the equation correctly.
2x-3-8x=14+2x-1
-6x-3=13+2x
-6x-3+3=13+3+2x
-6x=16+2x
-6x+2x=16
-4x=16
\(\frac{-4}{-4}\) x=\(\frac{16}{-4}\)
x=-4
Answer:
Alysha made a mistake on the fifth line. She added 2x to the left side of the equal sign and subtracted 2x on the right side of the equal sign. To use the property correctly, she should have subtracted 2x on both sides of the equal sign, making the equation at that point:
-6x-2x=16+2x-2x
-8x=16
\(\frac{-8}{-8}\) x=\(\frac{16}{-8}\)
x=-2.

Engage NY Eureka Math 8th Grade Module 4 Lesson 3 Answer Key

Eureka Math Grade 8 Module 4 Lesson 3 Exercise Answer Key

Exercise 1.
Is the equation a true statement when x=-3? In other words, is -3 a solution to the equation 6x+5=5x+8+2x? Explain.
Answer:
If we replace x with the number -3, then the left side of the equation is
6∙(-3)+5=-18+5
=-13″,”
and the right side of the equation is
5∙(-3)+8+2∙(-3)=-15+8-6
=-7-6
=-13.
Since -13=-13, then x=-3 is a solution to the equation 6x+5=5x+8+2x.
Note: Some students may have transformed the equation.

Exercise 2.
Does x=12 satisfy the equation 16-\(\frac{1}{2}\) x=\(\frac{3}{4}\) x+1? Explain.
Answer:
If we replace x with the number 12, then the left side of the equation is
16-\(\frac{1}{2}\) x=16-\(\frac{1}{2}\)∙(12)
=16-6
=10,
and the right side of the equation is
\(\frac{3}{4}\) x+1=\(\frac{3}{4}\)∙(12)+1
=9+1
=10.
Since 10=10, then x=12 is a solution to the equation 16-\(\frac{1}{2}\) x=\(\frac{3}{4}\) x+1.

Exercise 3.
Chad solved the equation 24x+4+2x=3(10x-1) and is claiming that x=2 makes the equation true. Is Chad correct? Explain.
Answer:
If we replace x with the number 2, then the left side of the equation is
24x+4+2x=24∙2+4+2∙2
=48+4+4
=56,
and the right side of the equation is
3(10x-1)=3(10∙2-1)
=3(20-1)
=3(19)
=57.
Since 56≠57, then x=2 is not a solution to the equation 24x+4+2x=3(10x-1), and Chad is not correct.

Exercise 4.
Lisa solved the equation x+6=8+7x and claimed that the solution is x=-\(\frac{1}{3}\). Is she correct? Explain.
Answer:
If we replace x with the number –\(\frac{1}{3}\), then the left side of the equation is
x+6=-\(\frac{1}{3}\)+6
=5 \(\frac{2}{3}\),
and the right side of the equation is
8+7x=8+7∙(-\(\frac{1}{3}\))
=8-\(\frac{7}{3}\)
=\(\frac{24}{3}\)–\(\frac{7}{3}\)
=\(\frac{17}{3}\).
Since 5 \(\frac{2}{3}\)=\(\frac{17}{3}\), then x=-\(\frac{1}{3}\) is a solution to the equation x+6=8+7x, and Lisa is correct.

Exercise 5.
Angel transformed the following equation from 6x+4-x=2(x+1) to 10=2(x+1). He then stated that the solution to the equation is x=4. Is he correct? Explain.
Answer:
No, Angel is not correct. He did not transform the equation correctly. The expression on the left side of the equation 6x+4-x=2(x+1) would transform to
6x+4-x=6x-x+4
=(6-1)x+4
=5x+4.
If we replace x with the number 4, then the left side of the equation is
5x+4=5∙4+4
=20+4
=24,
and the right side of the equation is
2(x+1)=2(4+1)
=2(5)
=10.
Since 24≠10, then x=4 is not a solution to the equation 6x+4-x=2(x+1), and Angel is not correct.

Exercise 6.
Claire was able to verify that x=3 was a solution to her teacher’s linear equation, but the equation got erased from the board. What might the equation have been? Identify as many equations as you can with a solution of x=3.
Answer;
Answers will vary. Ask students to share their equations and justifications as to how they knew x=3 would make a true number sentence.

Exercise 7.
Does an equation always have a solution? Could you come up with an equation that does not have a solution?
Answer:
Answers will vary. Expect students to write equations that are false. Ask students to share their equations and justifications as to how they knew the equation they wrote did not have a solution. The concept of “no solution” is introduced in Lesson 6 and solidified in Lesson 7.

Eureka Math Grade 8 Module 4 Lesson 3 Problem Set Answer Key

Students practice determining whether or not a given number is a solution to the linear equation.

Question 1.
Given that 2x+7=27 and 3x+1=28, does 2x+7=3x+1? Explain.
Answer:
No, because a linear equation is a statement about equality. We are given that 2x+7=27, but 3x+1=28. Since each linear expression is equal to a different number, 2x+7≠3x+1.

Question 2.
Is -5 a solution to the equation 6x+5=5x+8+2x? Explain.
Answer:
If we replace x with the number -5, then the left side of the equation is
6∙(-5)+5=-30+5
=-25,
and the right side of the equation is
5∙(-5)+8+2∙(-5)=-25+8-10
=-17-10
=-27.
Since -25≠-27, then -5 is not a solution of the equation 6x+5=5x+8+2x.
Note: Some students may have transformed the equation.

Question 3.
Does x=1.6 satisfy the equation 6-4x=-\(\frac{x}{4}\)? Explain.
Answer:
If we replace x with the number 1.6, then the left side of the equation is
6-4∙1.6=6-6.4
=-0.4,
and the right side of the equation is
–\(\frac{-1.6}{4}\)=-0.4.
Since -0.4=-0.4, then x=1.6 is a solution of the equation 6-4x=-\(\frac{x}{4}\).

Question 4.
Use the linear equation 3(x+1)=3x+3 to answer parts (a)–(d).
a. Does x=5 satisfy the equation above? Explain.
Answer:
If we replace x with the number 5, then the left side of the equation is
3(5+1)=3(6)
=18,
and the right side of the equation is
3x+3=3∙5+3
=15+3
=18.
Since 18=18, then x=5 is a solution of the equation 3(x+1)=3x+3.

b. Is x=-8 a solution of the equation above? Explain.
Answer:
If we replace x with the number -8, then the left side of the equation is
3(-8+1)=3(-7)
=-21,
and the right side of the equation is
3x+3=3∙(-8)+3
=-24+3
=-21.
Since -21=-21, then x=-8 is a solution of the equation 3(x+1)=3x+3.

c. Is x=\(\frac{1}{2}\) a solution of the equation above? Explain.
Answer:
If we replace x with the number \(\frac{1}{2}\), then the left side of the equation is
3(\(\frac{1}{2}\)+1)=3(\(\frac{1}{2}\)+\(\frac{2}{2}\))
=3(\(\frac{3}{2}\))
=\(\frac{9}{2}\),
and the right side of the equation is
3x+3=3∙(\(\frac{1}{2}\))+3
= \(\frac{3}{2}\)+3
=\(\frac{3}{2}\)+\(\frac{6}{2}\)
=\(\frac{9}{2}\).
Since \(\frac{9}{2}\)=\(\frac{9}{2}\), then x=\(\frac{1}{2}\) is a solution of the equation 3(x+1)=3x+3.

d. What interesting fact about the equation 3(x+1)=3x+3 is illuminated by the answers to parts (a), (b), and (c)? Why do you think this is true?
Answer:
Note to teacher: Ideally, students will notice that the equation 3(x+1)=3x+3 is an identity under the distributive law. The purpose of this problem is to prepare students for the idea that linear equations can have more than one solution, which is a topic of Lesson 7.

Eureka Math Grade 8 Module 4 Lesson 3 Exit Ticket Answer Key

Question 1.
Is 8 a solution to \(\frac{1}{2}\) x+9=13? Explain.
Answer:
If we replace x with the number 8, then the left side is \(\frac{1}{2}\) (8)+9=4+9=13, and the right side is 13. Since 13=13, then x=8 is a solution.

Question 2.
Write three different equations that have x=5 as a solution.
Answer:
Answers will vary. Accept equations where x=5 makes a true number sentence.

Question 3.
Is -3 a solution to the equation 3x-5=4+2x? Explain.
Answer:
If we replace x with the number -3, then the left side is 3(-3)-5=-9-5=-14. The right side is 4+2(-3)=4-6=-2. Since -14≠-2, then -3 is not a solution of the equation.

Engage NY Eureka Math 8th Grade Module 4 Lesson 7 Answer Key

Eureka Math Grade 8 Module 4 Lesson 7 Exercise Answer Key

Exercises
Solve each of the following equations for x.

Exercise 1.
7x-3=5x+5
Answer:
7x-3=5x+5
7x-3+3=5x+5+3
7x=5x+8
7x-5x=5x-5x+8
2x=8
x=4

Exercise 2.
7x-3=7x+5
Answer:
7x-3=7x+5
7x-7x-3=7x-7x+5
-3≠5
This equation has no solution.

Exercise 3.
7x-3=-3+7x
Answer:
7x-3=-3+7x
7x-3+3=-3+3+7x
7x=7x
OR
7x-3=-3+7x
7x-7x-3=-3+7x-7x
-3=-3

Exercises 4–10

Give a brief explanation as to what kind of solution(s) you expect the following linear equations to have. Transform the equations into a simpler form if necessary.

Exercise 4.
11x-2x+15=8+7+9x
Answer:
If I use the distributive property on the left side, I notice that the coefficients of the x are the same, specifically 9, and when I simplify the constants on the right side, I notice that they are the same. Therefore, this equation has infinitely many solutions.

Exercise 5.
3(x-14)+1=-4x+5
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are different. Therefore, the equation has one solution.

Exercise 6.
-3x+32-7x=-2(5x+10)
Answer:
If I use the distributive property on the each side of the equation, I notice that the coefficients of x are the same, but the constants are different. Therefore, this equation has no solutions.

Exercise 7.
\(\frac{1}{2}\) (8x+26)=13+4x
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are the same, specifically 4, and the constants are also the same, 13. Therefore, this equation has infinitely many solutions.

Exercise 8.
Write two equations that have no solutions.
Answer:
Answers will vary. Verify that students have written equations where the coefficients of x on each side of the equal sign are the same and that the constants on each side are unique.

Exercise 9.
Write two equations that have one unique solution each.
Answer:
Answers will vary. Accept equations where the coefficients of x on each side of the equal sign are unique.

Exercise 10.
Write two equations that have infinitely many solutions.
Answer:
Answers will vary. Accept equations where the coefficients of x and the constants on each side of the equal sign are the same.

Eureka Math Grade 8 Module 4 Lesson 7 Problem Set Answer Key

Students apply their knowledge of solutions to linear equations by writing equations with unique solutions, no solutions, and infinitely many solutions.

Question 1.
Give a brief explanation as to what kind of solution(s) you expect for the linear equation 18x+\(\frac{1}{2}\) =6(3x+25). Transform the equation into a simpler form if necessary.
Answer:
If I use the distributive property on the right side of the equation, I notice that the coefficients of x are the same, but the constants are different. Therefore, this equation has no solutions.

Question 2.
Give a brief explanation as to what kind of solution(s) you expect for the linear equation 8-9x=15x+7+3x. Transform the equation into a simpler form if necessary.
Answer:
If I collect the like terms on the right side of the equation, then I notice that the coefficients of x are different, and so are the constants. Therefore, this equation will have a unique solution.

Question 3.
Give a brief explanation as to what kind of solution(s) you expect for the linear equation 5(x+9)=5x+45. Transform the equation into a simpler form if necessary.
Answer:
This is an identity under the distributive property. Therefore, this equation will have infinitely many solutions.

Question 4.
Give three examples of equations where the solution will be unique; that is, only one solution is possible.
Answer:
Accept equations where the coefficients of x on each side of the equal sign are unique.

Question 5.
Solve one of the equations you wrote in Problem 4, and explain why it is the only solution.
Answer:
Verify that students solved one of the equations. They should have an explanation that includes the statement that there is only one possible number that could make the equation true. They may have referenced one of the simpler forms of their transformed equation to make their case.

Question 6.
Give three examples of equations where there will be no solution.
Answer:
Accept equations where the coefficients of x on each side of the equal sign are the same, and the constants on each side are unique.

Question 7.
Attempt to solve one of the equations you wrote in Problem 6, and explain why it has no solution.
Answer:
Verify that students have solved one of the equations. They should have an explanation that includes the statement about getting a false equation (e.g., 6≠10).

Question 8.
Give three examples of equations where there will be infinitely many solutions.
Answer:
Accept equations where the coefficients of x and constants on each side of the equal sign are the same.

Question 9.
Attempt to solve one of the equations you wrote in Problem 8, and explain why it has infinitely many solutions.
Answer:
Verify that students have solved one of the equations. They should have an explanation that includes the statement about the linear expressions being exactly the same, an identity; therefore, any rational number x would make the equation true.

Eureka Math Grade 8 Module 4 Lesson 7 Exit Ticket Answer Key

Give a brief explanation as to what kind of solution(s) you expect the following linear equations to have. Transform the equations into a simpler form if necessary.

Question 1.
3(6x+8)=24+18x
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are the same, and the constants are the same. Therefore, this equation has infinitely many solutions.

Question 2.
12(x+8)=11x-5
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are different, and the constants are different. Therefore, this equation has a unique solution.

Question 3.
5x-8=11-7x+12x
Answer:
If I collect the like terms on the right side, I notice that the coefficients of x are the same, but the constants are different. Therefore, this equation has no solution.

Engage NY Eureka Math 8th Grade Module 4 Lesson 6 Answer Key

Eureka Math Grade 8 Module 4 Lesson 6 Exercise Answer Key

Exercises
Find the value of x that makes the equation true.

Exercise 1.
17-5(2x-9)=-(-6x+10)+4
Answer:
17-5(2x-9)=-(-6x+10)+4
17-10x+45=6x-10+4
62-10x=6x-6
62-10x+10x=6x+10x-6
62=16x-6
62+6=16x-6+6
68=16x
\(\frac{68}{16}\)=\(\frac{16}{16}\) x
\(\frac{68}{16}\) =x
\(\frac{17}{4}\) =x

Exercise 2.
-(x-7)+\(\frac{5}{3}\) =2(x+9)
Answer;
-(x-7)+\(\frac{5}{3}\) =2(x+9)
-x+7+\(\frac{5}{3}\) =2x+18
-x+\(\frac{26}{3}\) =2x+18
-x+x+\(\frac{26}{3}\) =2x+x+18
\(\frac{26}{3}\) =3x+18
\(\frac{26}{3}\) -18=3x+18-18
–\(\frac{28}{3}\) =3x
\(\frac{1}{3}\)∙\(\frac{-28}{3}\) =\(\frac{1}{3}\)∙3x
–\(\frac{28}{9}\) =x

Question 3.
\(\frac{4}{9}\) +4(x-1)=\(\frac{28}{9}\) -(x-7x)+1
Answer;
\(\frac{4}{9}\) +4(x-1)=\(\frac{28}{9}\) -(x-7x)+1
\(\frac{4}{9}\) –\(\frac{4}{9}\) +4(x-1)=\(\frac{28}{9}\) –\(\frac{4}{9}\) -(x-7x)+1
4x-4=2\(\frac{4}{9}\) -x+7x+1
4x-4=\(\frac{33}{9}\) +6x
4x-4+4=\(\frac{33}{9}\) +36/9+6x
4x=\(\frac{69}{9}\) +6x
4x-6x=\(\frac{69}{9}\) +6x-6x
-2x=\(\frac{23}{3}\)
\(\frac{1}{-2}\) ∙-2x=\(\frac{1}{-2}\)∙\(\frac{23}{3}\)
x=-\(\frac{23}{6}\)

Question 4.
5(3x+4)-2x=7x-3(-2x+11)
Answer:
5(3x+4)-2x=7x-3(-2x+11)
15x+20-2x=7x+6x-33
13x+20=13x-33
13x-13x+20=13x-13x-33
20≠-33
This equation has no solution.

Question 5.
7x-(3x+5)-8=\(\frac{1}{2}\) (8x+20)-7x+5
Answer:
7x-(3x+5)-8=\(\frac{1}{2}\) (8x+20)-7x+5
7x-3x-5-8=4x+10-7x+5
4x-13=-3x+15
4x-13+13=-3x+15+13
4x=-3x+28
4x+3x=-3x+3x+28
7x=28
x=4

Question 6.
Write at least three equations that have no solution.
Answer:
Answers will vary. Verify that the equations written have no solution.

Eureka Math Grade 8 Module 4 Lesson 6 Problem Set Answer Key

Students practice using the distributive property to transform equations and solve.

Transform the equation if necessary, and then solve it to find the value of x that makes the equation true.

Question 1.
x-(9x-10)+11=12x+3(-2x+\(\frac{1}{3}\))
x-(9x-10)+11=12x+3(-2x+\(\frac{1}{3}\))
x-9x+10+11=12x-6x+1
-8x+21=6x+1
-8x+8x+21=6x+8x+1
21=14x+1
21-1=14x+1-1
20=14x
\(\frac{20}{14}\)=\(\frac{14}{14}\)
\(\frac{10}{7}\)=x

Question 2.
7x+8(x+\(\frac{1}{4}\) )=3(6x-9)-8
Answer:
7x+8(x+\(\frac{1}{4}\) )=3(6x-9)-8
7x+8x+2=18x-27-8
15x+2=18x-35
15x-15x+2=18x-15x-35
2=3x-35
2+35=3x-35+35
37=3x
\(\frac{37}{3}\) =\(\frac{3}{3}\) x
\(\frac{37}{3}\) =x

Question 3.
-4x-2(8x+1)=-(-2x-10)
Answer:
-4x-2(8x+1)=-(-2x-10)
-4x-16x-2=2x+10
-20x-2=2x+10
-20x+20x-2=2x+20x+10
-2=22x+10
-2-10=22x+10-10
-12=22x
–\(\frac{12}{22}\) =\(\frac{22}{22}\) x
–\(\frac{6}{11}\) =x

Question 4.
11(x+10)=132
Answer:
11(x+10)=132
(\(\frac{1}{11}\) )11(x+10)=(\(\frac{1}{11}\) )132
x+10=12
x+10-10=12-10
x=2

Question 5.
37x+\(\frac{1}{2}\) -(x+\(\frac{1}{4}\) )=9(4x-7)+5
Answer:
37x+\(\frac{1}{2}\) -(x+\(\frac{1}{4}\) )=9(4x-7)+5
37x+\(\frac{1}{2}\) -x-\(\frac{1}{4}\) =36x-63+5
36x+\(\frac{1}{4}\) =36x-58
36x-36x+\(\frac{1}{4}\) =36x-36x-58
\(\frac{1}{4}\) ≠-58
This equation has no solution.

Question 6.
3(2x-14)+x=15-(-9x-5)
Answer:
3(2x-14)+x=15-(-9x-5)
6x-42+x=15+9x+5
7x-42=20+9x
7x-7x-42=20+9x-7x
-42=20+2x
-42-20=20-20+2x
-62=2x
-31=x

Question 7.
8(2x+9)=56
Answer:
8(2x+9)=56
(\(\frac{1}{8}\) )8(2x+9)=(\(\frac{1}{8}\) )56
2x+9=7
2x+9-9=7-9
2x=-2
(\(\frac{1}{2}\) )2x=(\(\frac{1}{2}\) )-2
x=-1

Eureka Math Grade 8 Module 4 Lesson 6 Exit Ticket Answer Key

Transform the equation if necessary, and then solve to find the value of x that makes the equation true.

Question 1.
5x-(x+3)=\(\frac{1}{3}\) (9x+18)-5
Answer:
5x-(x+3)=\(\frac{1}{3}\) (9x+18)-5
5x-x-3=3x+6-5
4x-3=3x+1
4x-3x-3=3x-3x+1
x-3=1
x-3+3=1+3
x=4

Question 2.
5(3x+9)-2x=15x-2(x-5)
Answer:
5(3x+9)-2x=15x-2(x-5)
15x+45-2x=15x-2x+10
13x+45=13x+10
13x-13x+45=13x-13x+10
45≠10
Since 45≠10, the equation has no solution.

Engage NY Eureka Math 8th Grade Module 4 Lesson 5 Answer Key

Eureka Math Grade 8 Module 4 Lesson 5 Example Answer Key

Example 1.
One angle is five degrees less than three times the measure of another angle. Together, the angle measures have a sum of 143°. What is the measure of each angle?

Provide students with time to make sense of the problem and persevere in solving it. They could begin their work by guessing and checking, drawing a diagram, or other methods as appropriate. Then, move to the algebraic method shown below.
→ What do we need to do first to solve this problem?
→ First, we need to define our variable (symbol). Let x be the measure of the first angle in degrees.
→ If x is the measure of the first angle, how do you represent the measure of the second angle?
→ The second angle is 3x-5.
→ What is the equation that represents this situation?
→ The equation is x+3x-5=143.
→ The equation that represents this situation is x+3x-5=143. Solve for x, and then determine the measure of each angle.

As students share their solutions for this and subsequent problems, ask them a variety of questions to reinforce the concepts of the last few lessons. For example, ask students to discuss whether or not this is a linear equation and how they know, to justify their steps and explain why they chose their particular first step, to explain what the solution means, or to justify how they know their answer is correct.
Answer:
x+3x-5=143
(1+3)x-5=143
4x-5=143
4x-5+5=143+5
4x=148
x=37
The measure of the first angle is 37°. The second angle is 3(37°)-5°=111°-5°=106°.

Example 2.
Given a right triangle, find the degree measure of the angles if one angle is ten degrees more than four times the degree measure of the other angle and the third angle is the right angle.

Give students time to work. As they work, walk around and identify students who are writing and solving the problem in different ways. The instructional goal of this example is to make clear that there are different ways to solve a linear equation as opposed to one “right way.” Select students to share their work with the class. If students do not come up with different ways of solving the equation, talk them through the following student work samples.
Again, as students share their solutions, ask them a variety of questions to reinforce the concepts of the last few lessons. For example, ask students to discuss whether or not this is a linear equation and how they know, to justify their steps and explain why they chose their particular first step, to explain what the solution means, or to justify how they know their answer is correct.
Answer:
Solution One
Let x be the measure of the first angle. Then, the second angle is 4x+10. The sum of the measures for the angles for this right triangle is x+4x+10+90=180.
x+4x+10+90=180
(1+4)x+100=180
5x+100=180
5x+100-100=180-100
5x=80
x=16
The measure of the first angle is 16°, the measure of the second angle is 4(16°)+10°=64°+10°=74°, and the measure of the third angle is 90°.

Solution Two
Let x be the measure of the first angle. Then, the second angle is 4x+10. Since we have a right triangle, we already know that one angle is 90°, which means that the sum of the other two angles is 90: x+4x+10=90.
x+4x+10=90
(1+4)x+10=90
5x+10=90
5x+10-10=90-10
5x=80
x=16
The measure of the first angle is 16°, the measure of the second angle is 4(16°)+10°=64°+10°=74°, and the measure of the third angle is 90°.

Solution Three
Let x be the measure of the second angle. Then, the first angle is \(\frac{x-10}{4}\). Since we have a right triangle, we already know that one angle is 90°, which means that the sum of the other two angles is 90: x+\(\frac{x-10}{4}\)=90.
x+\(\frac{x-10}{4}\)=90
4(x+\(\frac{x-10}{4}\)=90)
4x+x-10=360
(4+1)x-10=360
5x-10=360
5x-10+10=360+10
5x=370
x=74
The measure of the second angle is 74°, the measure of the first angle is \(\frac{74^{\circ}-10^{\circ}}{4}\)=\(\frac{64^{\circ}}{4}\)=16°, and the measure of the third angle is 90°.

Solution Four
Let x be the measure of the second angle. Then, the first angle is \(\frac{x-10}{4}\). The sum of the three angles is
x+\(\frac{x-10}{4}\)+90=180.
x+\(\frac{x-10}{4}\)+90=180
x+\(\frac{x-10}{4}\)+90-90=180-90
x+\(\frac{x-10}{4}\)=90
\(\frac{4 x}{4}\)+\(\frac{x-10}{4}\)=90
\(\frac{4 x+x-10}{4}\)=90
4x+x-10=360
5x-10+10=360+10
5x=370
x=74
The measure of the second angle is 74°, the measure of the first angle is \(\frac{74^{\circ}-10^{\circ}}{4}\)=\(\frac{64^{\circ}}{4}\)=16°, and the measure of the third angle is 90°.

Make sure students see at least four different methods of solving the problem. Conclude this example with the statements below.
→ Each method is slightly different either in terms of how the variable is defined or how the properties of equality are used to solve the equation. The way you find the answer may be different from your classmates’ or your teacher’s.
→ As long as you are accurate and do what is mathematically correct, you will find the correct answer.

Eureka Math Grade 8 Module 4 Lesson 5 Exercise Answer Key

Exercises
For each of the following problems, write an equation and solve.

Exercise 1.
A pair of congruent angles are described as follows: The degree measure of one angle is three more than twice a number, and the other angle’s degree measure is 54.5 less than three times the number. Determine the measure of the angles in degrees.
Answer;
Let x be the number. Then, the measure of one angle is 3+2x, and the measure of the other angle is 3x-54.5. Because the angles are congruent, their measures are equal. Therefore,
3+2x=3x-54.5
3+2x-2x=3x-2x-54.5
3=x-54.5
3+54.5=x-54.5+54.5
57.5=x
Replacing x with 57.5 in 3+2x gives 3+2(57.5)=3+115=118; therefore the measure of the angles is 118°.

Exercise 2.
The measure of one angle is described as twelve more than four times a number. Its supplement is twice as large. Find the measure of each angle in degrees.
Answer;
Let x be the number. Then, the measure of one angle is 4x+12. The other angle is 2(4x+12)=8x+24. Since the angles are supplementary, their sum must be 180°.
4x+12+8x+24=180
12x+36=180
12x+36-36=180-36
12x=144
x=12
Replacing x with 12 in 4x+12 gives 4(12)+12=48+12=60. Replacing x with 12 in 2(4x+12) gives 2(4(12)+12)=2(48+12)=2(60)=120. Therefore, the measures of the angles are 60° and 120°.

Exercise 3.
A triangle has angles described as follows: The measure of the first angle is four more than seven times a number, the measure of the second angle is four less than the first, and the measure of the third angle is twice as large as the first. What is the measure of each angle in degrees?
Answer:
Let x be the number. The measure of the first angle is 7x+4. The measure of the second angle is 7x+4-4=7x. The measure of the third angle is 2(7x+4)=14x+8. The sum of the angles of a triangle must be 180°.
7x+4+7x+14x+8=180
28x+12=180
28x+12-12=180-12
28x=168
x=6
Replacing x with 6 in 7x+4 gives 7(6)+4=42+4=46. Replacing x with 6 in 7x gives 7(6)=42. Replacing x with 6 in 14x+8 gives 14(6)+8=84+8=92. Therefore, the measures of the angles are 46°, 42°, and 92°.

Exercise 4.
One angle measures nine more than six times a number. A sequence of rigid motions maps the angle onto another angle that is described as being thirty less than nine times the number. What is the measure of the angle in degrees?
Answer:
Let x be the number. Then, the measure of one angle is 6x+9. The measure of the other angle is 9x-30. Since rigid motions preserve the measures of angles, then the measure of these angles is equal.
6x+9=9x-30
6x+9-9=9x-30-9
6x=9x-39
6x-9x=9x-9x-39
-3x=-39
x=13
Replacing x with 13 in 6x+9 gives 6(13)+9=78+9=87. Therefore, the angle measure is 87°.

Exercise 5.
A right triangle is described as having an angle of measure six less than negative two times a number, another angle measure that is three less than negative one-fourth the number, and a right angle. What are the measures of the angles in degrees?
Answer;
Let x be a number. Then, the measure of one angle is -2x-6. The measure of the other angle is –\(\frac{x}{4}\)-3. The sum of the two angles must be 90°.
-2x-6+(-\(\frac{x}{4}\))-3=90
(-\(\frac{8x}{4}\))+(-\(\frac{x}{4}\))-9=90
(-\(\frac{9x}{4}\))-9+9=90+9
–\(\frac{9x}{4}\)=99
-9x=396
x=-44
Replacing x with -44 gives -2x-6 gives -2(-44)-6=88-6=82. Replacing x with -44 in –\(\frac{x}{4}\)-3 gives 90-82=8. Therefore, the angle measures are 82° and 8°.

Exercise 6.
One angle is one less than six times the measure of another. The two angles are complementary angles. Find the measure of each angle in degrees.
Answer:
Let x be the measure of the first angle. Then, the measure of the second angle is 6x-1. The sum of the measures will be 90 because the angles are complementary.
x+6x-1=90
7x-1=90
7x-1+1=90+1
7x=91
x=13
The first angle is x and therefore measures 13°. Replacing x with 13 in 6x-1 gives 6(13)-1=78-1=77. Therefore, the second angle measure is 77°.

Eureka Math Grade 8 Module 4 Lesson 5 Problem Set Answer Key

Students practice writing and solving linear equations.

For each of the following problems, write an equation and solve.

Question 1.
The measure of one angle is thirteen less than five times the measure of another angle. The sum of the measures of the two angles is 140°. Determine the measure of each angle in degrees.
Answer:
Let x be the measure of the one angle. Then, the measure of the other angle is 5x-13.
x+5x-13=140
6x-13=140
6x-13+13=140+13
6x=153
x=25.5
Since one angle measure is x, it is 25.5°. Replacing x with 25.5 in 5x-13 gives
5(25.5)-13=140-25.5=114.5. Therefore, the other angle measures 114.5°.

Question 2.
An angle measures seventeen more than three times a number. Its supplement is three more than seven times the number. What is the measure of each angle in degrees?
Answer:
Let x be the number. Then, the measure of one angle is 3x+17. The measure of the other angle is 7x+3. Since the angles are supplementary, the sum of their measures will be 180.
3x+17+7x+3=180
10x+20=180
10x+20-20=180-20
10x=160
x=16
Replacing x with 16 in 3x+17 gives 3(16)+17=65. Replacing x with 16 in 7x+3 gives (16)+3= 112+3=115. Therefore, the angle measures are 65° and 115°.

Question 3.
The angles of a triangle are described as follows: ∠A is the largest angle; its measure is twice the measure of ∠B. The measure of ∠C is 2 less than half the measure of ∠B. Find the measures of the three angles in degrees.
Answer:
Let x be the measure of ∠B. Then, the measure of ∠A is 2x, and the measure of ∠C is \(\frac{x}{2}\)-2. The sum of the measures of the angles must be 180°.
x+2x+\(\frac{x}{2}\) -2=180
3x+\(\frac{x}{2}\) -2+2=180+2
3x+\(\frac{x}{2}\) =182
6\(\frac{x}{2}\) +\(\frac{x}{2}\) =182
7\(\frac{x}{2}\) =182
7x=364
x=52
Since x is the measure of ∠B, then ∠B is 52°. Replacing x with 52 in 2x gives 2(52)=104. Therefore, the measure of ∠A is 104°. Replacing x with 52 in \(\frac{x}{2}\) -2 gives \(\frac{52}{2}\)-2=26-2=24. Therefore, the measure of ∠C is 24°.

Question 4.
A pair of corresponding angles are described as follows: The measure of one angle is five less than seven times a number, and the measure of the other angle is eight more than seven times the number. Are the angles congruent? Why or why not?
Answer:
Let x be the number. Then, the measure of one angle is 7x-5, and the measure of the other angle is 7x+8. Assume they are congruent, which means their measures are equal.
7x-5=7x+8
7x-7x-5=7x-7x+8
-5≠8
Since -5≠8, the angles are not congruent.

Question 5.
The measure of one angle is eleven more than four times a number. Another angle is twice the first angle’s measure. The sum of the measures of the angles is 195°. What is the measure of each angle in degrees?
Answer:
Let x be the number. The measure of one angle can be represented with 4x+11, and the other angle’s measure can be represented as 2(4x+11)=8x+22.
4x+11+8x+22=195
12x+33=195
12x+33-33=195-33
12x=162
x=13.5
Replacing x with 13.5 in 4x+11 gives 4(13.5)+11=54+11=65. Replacing x with 13.5 in 2(4x+11) gives 2(4(13.5)+11)=2(54+11)=2(65)=130. Therefore, the measures of the angles are 65° and 130°.

Question 6.
Three angles are described as follows: ∠B is half the size of ∠A. The measure of ∠C is equal to one less than two times the measure of ∠B. The sum of ∠A and ∠B is 114°. Can the three angles form a triangle? Why or why not?
Answer:
Let x represent the measure of ∠A. Then, the measure of ∠B is \(\frac{x}{2}\) , and the measure of ∠C is 2(\(\frac{x}{2}\) )-1=x-1.
The sum of the measures of ∠A and ∠B is 114.
x+\(\frac{x}{2}\) =114
\(\frac{3x}{2}\) =114
3x=228
x=76
Since x is the measure of ∠A, then ∠A is 76°. Replacing x with 76 in \(\frac{x}{2}\) gives \(\frac{76}{2}\)=38; therefore, the measure of ∠B is 38°. Replacing x with 76 in x-1 gives 76-1=75, therefore the measure of ∠C is 75°. The sum of the three angle measures is 76°+38°+75°=189°. Since the sum of the measures of the interior angles of a triangle must equal 180°, these angles do not form a triangle. The sum is too large.

Eureka Math Grade 8 Module 4 Lesson 5 Exit Ticket Answer Key

For each of the following problems, write an equation and solve.

Question 1.
Given a right triangle, find the measures of all of the angles, in degrees, if one angle is a right angle and the measure of the second angle is six less than seven times the measure of the third angle.
Answer:
Let x represent the measure of the third angle. Then, 7x-6 can represent the measure of the second angle. The sum of the two angles in the right triangle will be 90°.
7x-6+x=90
8x-6=90
8x-6+6=90+6
8x=96
\(\frac{8}{8}\) x=\(\frac{96}{8}\)
x=12
The third angle is x and therefore measures 12°. Replacing x with 12 in 7x-6 gives 7(12)-6=84-6=78. Therefore, the measure of the second angle is 78°. The measure of the third angle is 90°.

Question 2.
In a triangle, the measure of the first angle is six times a number. The measure of the second angle is nine less than the first angle. The measure of the third angle is three times the number more than the measure of the first angle. Determine the measure of each angle in degrees.
Answer:
Let x be the number. Then, the measure of the first angle is 6x, the measure of the second angle is 6x-9, and the measure of the third angle is 3x+6x. The sum of the measures of the angles in a triangle is 180°.
6x+6x-9+3x+6x=180
21x-9=180
21x-9+9=180+9
21x=189
\(\frac{21}{21}\) x=\(\frac{189}{21}\)
x=9
Replacing x with 9 in 6x gives 6(9)=54. Replacing x with 9 in 6x-9 gives 6(9)-9=54-9=45. Replacing x with 9 in 3x+6x gives 54+3(9)=54+27=81. Therefore, the angle measures are 54°, 45°, and 81°.

Engage NY Eureka Math 8th Grade Module 7 Lesson 23 Answer Key

Eureka Math Grade 8 Module 7 Lesson 23 Exercise Answer Key

Mathematical Modeling Exercise
A ladder of length L ft. leaning against a wall is sliding down. The ladder starts off being flush with (right up against) the wall. The top of the ladder slides down the vertical wall at a constant speed of v ft. per second. Let the ladder in the position L₁ slide down to position L₂ after 1 second, as shown below.

Will the bottom of the ladder move at a constant rate away from point O?
Answer:
→ Identify what each of the symbols in the diagram represents.
O represents the corner where the floor and the wall intersect.
L₁ represents the position of the ladder after it has slid down the wall.
L₂ represents the position of the ladder after it has slid one second after position L₁ down the wall.
A represents the starting position of the top of the ladder.
A’ represents the position of the top of the ladder after it has slid down the wall for one second.
v represents the distance that the ladder slid down the wall in one second.
B represents the starting position of the bottom of the ladder.
B’ represents the position of the bottom of the ladder after it has slid for one second.
h represents the distance the ladder has moved along the ground after sliding down the wall in one second.

→ The distance from point A to point A’ is v ft. Explain why.
Since the ladder is sliding down the wall at a constant rate of v ft. per second, then after 1 second, the ladder moves v feet. Since we are given that the time it took for the ladder to go from position L₁ to L₂ is one second, then we know the distance between those points must be v feet.

→ The bottom of the ladder then slides on the floor to the left so that in 1 second it moves from B to B’ as shown. Therefore, the average speed of the bottom of the ladder is h ft. per second in this 1-second interval. Will the bottom of the ladder move at a constant rate away from point O? In other words, if the ladder moves at a constant rate, will the distance it has moved (shown as D’ in the image below) coincide with point E where |EO| is the length of the ladder?

Answer:
Provide time for students to discuss the answer to the question in pairs or small groups, and then have students share their reasoning. This question is the essential question of the lesson. The answer to this question is the purpose of the entire investigation.
Consider prompting their thinking with the following questions:

→ Think about the distance the base of the ladder is away from the wall as a function of time t. What do you think the beginning placement of the ladder should be for time t = 0?
→ Flush vertical against the wall
→ How far away from the wall is the base of the ladder then at time t = 0?
→ It is right up against the wall.
→ If we let d represent the distance of the base of the ladder from the wall, we know that at t = 0, d = 0.
→ Can the ladder continue sliding forever? Is there a time at which it must stop sliding?
Yes, it must stop sliding when it lies flat on the floor.
Can we compute at what time that will occur?
Allow students time to struggle with this. They may or may not be able to develop the equation below.
t = \(\frac{L}{v}\)
→ So our question is, is d a linear function of time? That is, does the value of d change by constant amounts over constant time intervals?
Students may suggest modeling the experiment using a note card against a vertical book and observing how the distance changes as the card slides down the book. Students may compare extreme cases where the base of the ladder moves a greater distance in the first second of sliding down the wall as opposed to the last second.

Students should recognize that this situation cannot be described by a linear function. Specifically, if the top of the ladder was v feet from the floor as shown below, it would reach O in one second (because the ladder slides down the wall at a constant rate of v per second). Then after 1 second, the ladder will be flat on the floor, and the foot of the ladder would be at the point where |EO| = L, or the length of the ladder. The discussion points below may be useful if students were unable to determine that the motion is non-linear.

→ If the rate of change could be described by a linear function, then the point D would move to D’ after 1 second, where |D’ D| = h ft . (where h is defined as the length the ladder moved from D to D’ in one second). But this is impossible.

→ Recall that the length of the ladder, L, is |EO|. When the ladder is flat on the floor, then at most, the foot of the ladder will be at point E from point O. If the rate of change of the ladder were linear, then the foot of the ladder would be at D’ because the linear rate of change would move the ladder a distance of h feet every 1 second. From the picture (on the previous page) you can see that D’≠E. Therefore, it is impossible that the rate of change of the ladder could be described by a linear function.

→ Intuitively, if you think about when the top of the ladder, C, is close to the floor (point O), a change in the height of C would produce very little change in the horizontal position of the bottom of the ladder, D.

→ Consider the three right triangles shown below. If we let the length of the ladder be 8 ft., then we can see that a constant change of 1 ft. in the vertical distance produces very little change in the horizontal distance. Specifically, the change from 3 ft. to 2 ft. produces a horizontal change of approximately 0.3 ft., and the change from 2 ft. to 1 ft. produces a horizontal change of approximately 0.2 ft. A change from 1 ft. to 0 ft., meaning that the ladder is flat on the floor, would produce a horizontal change of just 0.1 ft. (the difference between the length of the ladder, 8 ft. and 7.9 ft.)

Consider the three right triangles shown below, specifically the change in the length of the base as the height decreases in increments of 1 ft.

Answer:
→ In particular, when the ladder is flat on the floor so that C = O, then the bottom cannot be further left than the point E because |EO| = L, the length of the ladder. Therefore, the ladder will never reach point D’, and the function that describes the movement of the ladder cannot be linear.

→ We want to show that our intuitive sense of the movement of the ladder is accurate. Our goal is to derive a formula, d, for the function of the distance of the bottom of the ladder from O over time t. Because the top of the ladder slides down the wall at a constant rate of v ft . per second, the top of the ladder is now at point A, which is vt ft. below the vertical height of L feet, and the bottom of the ladder is at point B, as shown below. We want to determine |BO|, which by definition is the formula for the function, d.

Answer:
→ Explain the expression vt. What does it represent?
The expression vt represents the distance the ladder has slid down the wall after t seconds. Since v is the rate at which the ladder slides down the wall, then vt is the distance it slides after t seconds.

→ How can we determine |BO|?
The shape formed by the ladder, wall, and floor is a right triangle, so we can use the Pythagorean theorem to find |BO|.

→ What is the length of |AO|?
|AO| is the length of the ladder L minus the distance the ladder slides down the wall after t seconds (i.e., vt). Therefore, |AO| = L – vt.

→ What is the length of the hypotenuse of the right triangle?
The length of the hypotenuse is the length of the ladder, L.
Use the Pythagorean theorem to write an expression that gives |BO| (i.e., d).
Provide students time to work in pairs to write the expression for |BO|. Give guidance as necessary.
By the Pythagorean theorem,
(L-vt)²+d² = L²
d² = L²-(L-vt)²
\(\sqrt{d^{2}}\) = \(\sqrt{L^{2}-(L-v t)^{2}}\)
d = \(\sqrt{L^{2}-(L-v t)^{2}}\)
Pause after deriving the equation d = \(\sqrt{L^{2}-(L-v t)^{2}}\). Ask students to explain what the equation represents. Students should recognize that the equation gives the distance the foot of the ladder is from the wall, which is |BO|.

→ Let’s return to an earlier question: Will the ladder continue to slide forever?
The goal is for students to conclude that when d = L, the ladder will no longer slide. That is, when
\(\sqrt{L^{2}-(L-v t)^{2}}\) = L, the ladder is finished sliding. If students need convincing, consider the following situation with concrete numbers.
What would happen if t were very large? Suppose the constant rate, v, of the ladder falling down the wall is
2 feet per second, the length of the ladder, L, is 10 feet, and the time t is 100 seconds—what is d equal to?
The value of d is
d = \(\sqrt{L^{2}-(L-v t)^{2}}\)
= \(\sqrt{10^{2}-(10-2(100))^{2}}\)
= \(\sqrt{100-(190)^{2}}\)
= \(\sqrt{100-36,100}\)
= \(\sqrt{-36,000}\)

If the value of t were very large, then the formula would make no sense because the length of |BO| would be equal to the square of a negative number.
For this reason, we can only consider values of t so that the top of the ladder is still above the floor. Symbolically, vt≤L, where vt is the expression that describes the distance the ladder has moved at a specific rate v for a specific time t. We need that distance to be less than or equal to the length of the ladder.

→ What happens when t = \(\frac{L}{v}\)? Substitute \(\frac{L}{v}\) for t in our formula.
Substituting \(\frac{L}{v}\) for t,
d = \(\sqrt{L^{2}-(L-v t)^{2}}\)
= \(\sqrt{L^{2}-\left(L-v\left(\frac{L}{v}\right)\right)^{2}}\)
= \(\sqrt{L^{2}-(L-L)^{2}}\)
= \(\sqrt{L^{2}-0^{2}}\)
= \(\sqrt{L^{2}}\)
= L.
When t = \(\frac{L}{v}\), the top of the ladder will be at the point O, and the ladder will be flat on the floor because d represents the length of |BO|. If that length is equal to L, then the ladder must be on the floor.

→ Back to our original concern: What kind of function describes the rate of change of the movement of the bottom of the ladder on the floor? It should be clear that by the equation d = \(\sqrt{L^{2}-(L-v t)^{2}}\), which represents |BO| for any time t, that the motion (rate of change) is not one of constant speed. Nevertheless, thanks to the concept of a function, we can make predictions about the location of the ladder for any value of t as long as t≤\([latex]\frac{L}{v}\)[/latex]

→ We will use some concrete numbers to compute the average rate of change over different time intervals. Suppose the ladder is 15 feet long, L = 15, and the top of the ladder is sliding down the wall at a constant speed of 1 ft. per second, v = 1. Then, the horizontal distance of the bottom of the ladder from the wall (|BO|) is given by the formula
d = \(\sqrt{15^{2}-(15-1 t)^{2}}\)
= \(\sqrt{225-(15-t)^{2}}\)
Determine the outputs the function would give for the specific inputs. Use a calculator to approximate the lengths. Round to the hundredths place.

Answer:

Make at least three observations about what you notice from the data in the table. Justify your observations mathematically with evidence from the table.
→ Sample observations given below.
The average rate of change between 0 and 1 second is 5.39 feet per second.
\(\frac{5.39-0}{1-0}\) = 5.39
The average rate of change between 3 and 4 seconds is 1.2 feet per second.
\(\frac{10.2-9}{4-3}\) = 1.2
The average rate of change between 7 and 8 seconds is 0.58 feet per second.
\(\frac{13.27-12.69}{8-7}\) = 0.58
The average rate of change between 14 and 15 seconds is 0.03 feet per second.
\(\frac{15-14.97}{15-14}\) = 0.03

→ Now that we have computed the average rate of change over different time intervals, we can make two conclusions: (1) The motion at the bottom of the ladder is not linear, and (2) there is a decrease in the average speeds; that is, the rate of change of the position of the ladder is slowing down as observed in the four 1-second intervals we computed. These conclusions are also supported by the graph of the situation shown on the next page. The data points do not form a line; therefore, the rate of change with respect to the position of the bottom of the ladder is not linear.

Eureka Math Grade 8 Module 7 Lesson 23 Problem Set Answer Key

Question 1.
Suppose the ladder is 10 feet long, and the top of the ladder is sliding down the wall at a rate of 0.8 ft. per second. Compute the average rate of change in the position of the bottom of the ladder over the intervals of time from 0 to 0.5 seconds, 3 to 3.5 seconds, 7 to 7.5 seconds, 9.5 to 10 seconds, and 12 to 12.5 seconds. How do you interpret these numbers?

Answer:

The average rate of change between 0 and 0.5 seconds is 5.6 feet per second.
\(\frac{2.8-0}{0.5-0}\) = \(\frac{2.8}{0.5}\) = 5.6
The average rate of change between 3 and 3.5 seconds is 0.88 feet per second.
\(\frac{6.94-6.5}{3.5-3}\) = \(\frac{0.44}{0.5}\) = 0.88
The average rate of change between 7 and 7.5 seconds is 0.38 feet per second.
\(\frac{9.17-8.98}{7.5-5}\) = \(\frac{0.19}{0.5}\) = 0.38
The average rate of change between 9.5 and 10 seconds is 0.18 feet per second.
\(\frac{9.8-9.71}{10-9.5}\) = \(\frac{0.09}{0.5}\) = 0.18
The average rate of change between 12 and 12.5 seconds is 0.02 feet per second.
\(\frac{10-9.99}{12.5-12}\) = \(\frac{0.01}{0.5}\) = 0.02
The average speeds show that the rate of change in the position of the bottom of the ladder is not linear. Furthermore, it shows that the rate of change in the position at the bottom of the ladder is quick at first, 5.6 feet per second in the first half second of motion, and then slows down to 0.02 feet per second in the half-second interval from 12 to 12.5 seconds.

Question 2.
Will any length of ladder, L, and any constant speed of sliding of the top of the ladder, v ft. per second, ever produce a constant rate of change in the position of the bottom of the ladder? Explain.
Answer:
No, the rate of change in the position at the bottom of the ladder will never be constant. We showed that if the rate were constant, there would be movement in the last second of the ladder sliding down that wall that would place the ladder in an impossible location. That is, if the rate of change were constant, then the bottom of the ladder would be in a location that exceeds the length of the ladder. Also, we determined that the distance that the bottom of the ladder is from the wall over any time period can be found using the formula d = \(\sqrt{L^{2}-(L-v t)^{2}}\), which is a non-linear equation. Since graphs of functions are equal to the graph of a certain equation, the graph of the function represented by the formula d = \(\sqrt{L^{2}-(L-v t)^{2}}\) is not a line, and the rate of change in position at the bottom of the ladder is not constant.

Eureka Math Grade 8 Module 7 Lesson 23 Exit Ticket Answer Key

Question 1.
Suppose a book is 5.5 inches long and leaning on a shelf. The top of the book is sliding down the shelf at a rate of 0.5 in. per second. Complete the table below. Then, compute the average rate of change in the position of the bottom of the book over the intervals of time from 0 to 1 second and 10 to 11 seconds. How do you interpret these numbers?

Answer:

The average rate of change between 0 and 1 second is 2.29 inches per second.
\(\frac{2.29-0}{1-0}\) = \(\frac{2.29}{1}\) = 2.29.
The average rate of change between 10 and 11 seconds is 0.02 inches per second.
\(\frac{5.5-5.48}{11-10}\) = \(\frac{0.02}{1}\) = 0.02.
The average speeds show that the rate of change of the position of the bottom of the book is not linear. Furthermore, it shows that the rate of change of the bottom of the book is quick at first, 2.29 inches per second in the first second of motion, and then slows down to 0.02 inches per second in the one second interval from 10 to 11 seconds.

Engage NY Eureka Math 8th Grade Module 4 Lesson 31 Answer Key

Eureka Math Grade 8 Module 4 Lesson 31 Exercise Answer Key

Exercises

Exercise 1.
Identify two Pythagorean triples using the known triple 3, 4, 5 (other than 6, 8, 10).
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 3, 4, 5.

Exercise 2.
Identify two Pythagorean triples using the known triple 5, 12, 13.
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 5, 12, 13.

Exercise 3.
Identify two triples using either 3, 4, 5 or 5, 12, 13.
Answer:
Answers will vary.

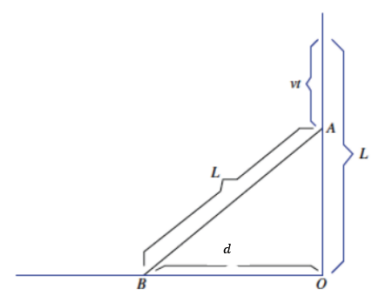
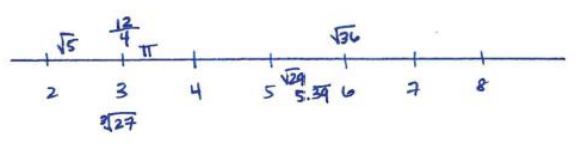
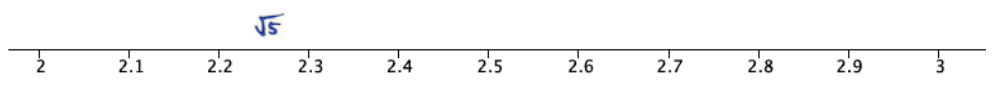
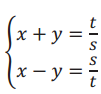Use the system to find Pythagorean triples for the given values of s and t. Recall that the solution in the form of (\(\frac{c}{b}\), \(\frac{a}{b}\)) is the triple a, b, c.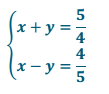
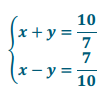
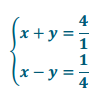
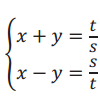Exercise 4.
s = 4, t = 5
Answer:

x + y + x – y = \(\frac{5}{4}\) + \(\frac{4}{5}\)
2x = \(\frac{5}{4}\) + \(\frac{4}{5}\)
2x = \(\frac{41}{20}\)
x = \(\frac{41}{40}\)

\(\frac{41}{40}\) + y = \(\frac{5}{4}\)
y = \(\frac{5}{4}\) – \(\frac{41}{40}\)
y = \(\frac{9}{40}\)

Then the solution is (\(\frac{41}{40}\), \(\frac{9}{40}\)), and the triple is 9, 40, 41.

Exercise 5.
s = 7, t = 10
Answer:

x + y + x – y = \(\frac{10}{7}\) + \(\frac{7}{10}\)
2x = \(\frac{149}{70}\)
x = \(\frac{149}{140}\)

\(\frac{149}{140}\) + y = \(\frac{10}{7}\)
y = \(\frac{10}{7}\) – \(\frac{149}{140}\)
y = \(\frac{51}{140}\)
Then the solution is (\(\frac{149}{140}\), \(\frac{51}{140}\)), and the triple is 51, 140, 149.

Exercise 6.
s = 1, t = 4
Answer:

x + y + x – y = 4 + \(\frac{1}{4}\)
2x = \(\frac{17}{4}\)
x = \(\frac{17}{8}\)

\(\frac{17}{8}\) + y = \(\frac{4}{1}\)
y = 4 – \(\frac{17}{8}\)
y = \(\frac{15}{8}\)
Then the solution is (\(\frac{17}{8}\), \(\frac{15}{8}\)), and the triple is 15, 8, 17.

Exercise 7.
Use a calculator to verify that you found a Pythagorean triple in each of the Exercises 4–6. Show your work below.
Answer:
For the triple 9, 40, 41:
9² + 40² = 41²
81 + 1600 = 1681
1681 = 1681

For the triple 51, 140, 149:
51² + 140² = 149²
2601 + 19600 = 22201
22201 = 22201

For the triple 15, 8, 17:
15² + 8² = 17²
225 + 64 = 289
289 = 289

Eureka Math Grade 8 Module 4 Lesson 31 Problem Set Answer Key

Question 1.
Explain in terms of similar triangles why it is that when you multiply the known Pythagorean triple 3, 4, 5 by 12, it generates a Pythagorean triple.
Answer:
The triangle with lengths 3, 4, 5 is similar to the triangle with lengths 36, 48, 60. They are both right triangles whose corresponding side lengths are equal to the same constant.
\(\frac{36}{3}\) = \(\frac{48}{4}\) = \(\frac{60}{5}\) = 12
Therefore, the triangles are similar, and we can say that there is a dilation from some center with scale factor r = 12 that makes the triangles congruent.

Question 2.
Identify three Pythagorean triples using the known triple 8, 15, 17.
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 8, 15, 17.

Question 3.
Identify three triples (numbers that satisfy a² + b² = c², but a, b, c are not whole numbers) using the triple 8, 15, 17.
Answer:
Answers will vary. Accept any triple that is not a set of whole numbers.

Use the system to find Pythagorean triples for the given values of s and t. Recall that the solution, in the form of (c/b, a/b), is the triple, a, b, c.
Question 4.
s = 2, t = 9
Answer:

x + y + x – y = \(\frac{9}{2}\) + \(\frac{2}{9}\)
2x = \(\frac{85}{18}\)
x = \(\frac{85}{36}\)

\(\frac{85}{36}\) + y = \(\frac{9}{2}\)
y = \(\frac{9}{2}\) – \(\frac{85}{36}\)
y = \(\frac{77}{36}\)
Then the solution is (\(\frac{85}{36}\), \(\frac{77}{36}\)), and the triple is 77, 36, 85.

Question 5.
s = 6, t = 7
Answer:

x + y + x – y = \(\frac{7}{6}\) + 6/7
2x = \(\frac{85}{42}\)
x = \(\frac{85}{84}\)

\(\frac{85}{84}\) + y = \(\frac{7}{6}\)
y = \(\frac{7}{6}\) – \(\frac{85}{84}\)
y = \(\frac{13}{84}\)
Then the solution is (\(\frac{85}{84}\), \(\frac{13}{84}\)), and the triple is 13, 84, 85.

Question 6.
s = 3, t = 4
Answer:

x + y + x – y = \(\frac{4}{3}\) + \(\frac{3}{4}\)
2x = \(\frac{25}{12}\)
x = \(\frac{25}{24}\)

\(\frac{25}{24}\) + y = \(\frac{4}{3}\)
y = \(\frac{4}{3}\) – \(\frac{25}{24}\)
y = \(\frac{7}{24}\)
Then the solution is (\(\frac{25}{24}\), \(\frac{7}{24}\)), and the triple is 7, 24, 25.

Question 7.
Use a calculator to verify that you found a Pythagorean triple in each of the Problems 4–6. Show your work.
Answer:
For the triple 77, 36, 85:
77² + 36² = 85²
5929 + 1296 = 7225
7225 = 7225

For the triple 13, 84, 85:
13² + 84² = 85²
169 + 7056 = 7225
7225 = 7225

For the triple 7, 24, 25:
7² + 24² = 25²
49 + 576 = 625
625 = 625

Eureka Math Grade 8 Module 4 Lesson 31 Exit Ticket Answer Key

Use a calculator to complete Problems 1–3.
Question 1.
Is 7, 20, 21 a Pythagorean triple? Is 1, \(\frac{15}{8}\), \(\frac{17}{8}\) a Pythagorean triple? Explain.
Answer:
The set of numbers 7, 20, 21 is not a Pythagorean triple because 7² + 20² ≠ 21².
The set of numbers 1, \(\frac{15}{8}\), \(\frac{17}{8}\) is not a Pythagorean triple because the numbers \(\frac{15}{8}\) and \(\frac{17}{8}\) are not whole numbers.
But they are a triple because 1² + (\(\frac{15}{8}\))² = (\(\frac{17}{8}\))².

Question 2.
Identify two Pythagorean triples using the known triple 9, 40, 41.
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 9, 40, 41.

Question 3.
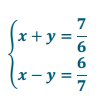
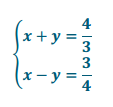
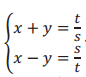Use the system to find Pythagorean triples for the given values of s = 2 and t = 3. Recall that the solution in the form of (\(\frac{c}{b}\), \(\frac{a}{b}\)) is the triple a, b, c. Verify your results.
Answer:

x + y + x – y = \(\frac{3}{2}\) + \(\frac{2}{3}\)
2x = \(\frac{13}{6}\)
x = \(\frac{13}{12}\)

\(\frac{13}{12}\) + y = \(\frac{3}{2}\)
y = \(\frac{3}{2}\) – \(\frac{13}{12}\)
y = \(\frac{5}{12}\)
Then the solution is (\(\frac{13}{12}\), \(\frac{5}{12}\)), and the triple is 5, 12, 13.
5² + 12² = 13²
25 + 144 = 169
169 = 169

Engage NY Eureka Math 8th Grade Module 3 Lesson 9 Answer Key

Eureka Math Grade 8 Module 3 Lesson 9 Exploratory Challenge Answer Key

Exploratory Challenge 1.
The goal is to show that if △ABC is similar to △A’ B’ C’, then △A’ B’ C’ is similar to △ABC. Symbolically,
if △ABC~△A’B’C’, then △A’ B’ C’~△ABC.

a. First, determine whether or not △ABC is in fact similar to △A’ B’ C’. (If it isn’t, then no further work needs to be done.) Use a protractor to verify that the corresponding angles are congruent and that the ratios of the corresponding sides are equal to some scale factor.
Answer:

The corresponding angles are congruent: ∠A≅∠A’, ∠B≅∠B’, and ∠C≅∠C’, therefore
|∠A|=|∠A’ |=49°, |∠B|=|∠B’ |=99°, and |∠C|=|∠C’ |=32°.
The ratios of the corresponding sides are equal: \(\frac{4}{8}\)=\(\frac{3}{6}\)=\(\frac{2}{4}\)=r.

b. Describe the sequence of dilation followed by a congruence that proves △ABC~△A’ B’ C’.
Answer:

To map △ABC onto △A’ B’ C’, dilate △ABC from center O by scale factor r=\(\frac{1}{2}\), noted in the diagram above by the red triangle. Then, translate the red triangle up two units and five units to the right. Next, rotate the red triangle 180 degrees around point A’ until AC coincides with A’C’.

c. Describe the sequence of dilation followed by a congruence that proves △A’B’C’~△ABC.
Answer:
Note that in the diagram below, both axes have been compressed.

To map △A’B’C’ onto △ABC, dilate △A’B’C’ from center O by scale factor r=2, noted by the blue triangle in the diagram. Then, translate the blue triangle ten units to the left and two units down. Next, rotate the blue triangle 180 degrees around point A until side A’C’ coincides with side AC.

d. Is it true that △ABC~△A’ B’ C’ and △A’ B’ C’~△ABC? Why do you think this is so?
Answer:
Yes, it is true that △ABC~△A’ B’ C’ and △A’ B’ C’~△ABC. I think it is true because when we say figures are similar, it means that they are the same figure, just a different size because one has been dilated by a scale factor. For that reason, if one figure, like △ABC, is similar to another, like △A’ B’ C’, it must mean that △A’ B’ C’~△ABC. However, the sequence you would use to map one of the figures onto the other is different.

Exploratory Challenge 2.
The goal is to show that if △ABC is similar to △A’B’C’ and △A’B’C’ is similar to △A”B”C”, then △ABC is similar to
△A”B”C”. Symbolically, if △ABC~△A’ B’ C’ and △A’B’C’~△A”B”C”, then △ABC~△A”B”C”.

a. Describe the similarity that proves △ABC~△A’B’C’.
Answer:

To map △ABC onto △A’B’C’, we need to first determine the scale factor that makes △ABC the same size as △A’ B’ C’. Then, \(\frac{3}{1}\)=\(\frac{6.3}{2.1}\)=\(\frac{9}{3}\)=r. Dilate △ABC from center O by scale factor r=3, shown in red in the diagram. Then, translate the red triangle 5 units up.

b. Describe the similarity that proves △A’B’C’~△A”B”C”.
Answer:

To map △A’B’C’ onto △A”B”C”, we need to first determine the scale factor that makes △A’B’C’ the same size as △A”B”C”. Then, \(\frac{4.2}{6.3}\)=\(\frac{6}{9}\)=\(\frac{2}{3}\)=r. Dilate △A’B’C’ from center O by scale factor r=\(\frac{2}{3}\), shown in blue in the diagram. Then, translate the blue triangle 3.5 units down and 5 units to the right. Next, rotate the blue triangle 90 degrees clockwise around point A” until the blue triangle coincides with
△A”B”C”.

c. Verify that, in fact, △ABC~△A”B”C” by checking corresponding angles and corresponding side lengths. Then, describe the sequence that would prove the similarity △ABC~△A” B” C”.
Answer:

The corresponding angles are congruent: ∠A≅∠A”, ∠B≅∠B”, and ∠C≅∠C”; therefore, |∠A|=|∠A” |=18°, |∠B|=|∠B” |=117°, and |∠C|=|∠C” |=45°. The ratio of the corresponding sides is equal:
\(\frac{4.2}{2.1}\)=\(\frac{6}{3}\)=\(\frac{2}{1}\)=r. Dilate △ABC from center O by scale factor r=2, shown as the pink triangle in the diagram. Then, translate the pink triangle 5 units to the right. Finally, rotate the pink triangle 90 degrees clockwise around point A” until the pink triangle coincides with △A”B”C”.

d. Is it true that if △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”, then △ABC~△A”B”C”? Why do you think this is so?
Answer:
Yes, it is true that if △ABC~△A’ B’ C’ and △A’ B’ C’~△A” B” C”, then △ABC~△A” B” C”. Again, because these figures are similar, it means that they have equal angles and are made different sizes based on a specific scale factor. Since dilations map angles to angles of the same degree, it makes sense that all three figures would have the “same shape.” Also, using the idea that similarity is a symmetric relation, the statement that △ABC~△A’ B’ C’ implies that △A’ B’ C’~△ABC.
Since we know that △A’ B’ C’~△A”B”C”, it is reasonable to conclude that △ABC~△A”B”C”.

Eureka Math Grade 8 Module 3 Lesson 9 Problem Set Answer Key

Question 1.
Would a dilation alone be enough to show that similarity is symmetric? That is, would a dilation alone prove that if △ABC~ △A’B’C’, then △A’ B’ C’~ △ABC? Consider the two examples below.
a. Given △ABC~ △A’ B’ C’, is a dilation enough to show that △A’ B’ C’~ △ABC? Explain.

Answer:
For these two triangles, a dilation alone is enough to show that if △ABC~△A’B’C’, then △A’ B’ C’~△ABC. The reason that dilation alone is enough is because both of the triangles have been dilated from the same center. Therefore, to map one onto the other, all that would be required is a dilation.

b. Given △ABC~△A’ B’ C’, is a dilation enough to show that △A’ B’ C’~△ABC? Explain.

Answer:
For these two triangles, a dilation alone is not enough to show that if △ABC~ △A’ B’ C’, then △A’ B’ C’~
△ABC. The reason is that a dilation would just make them the same size. It would not show that you could map one of the triangles onto the other. To do that, you would need a sequence of basic rigid motions to demonstrate the congruence.

c. In general, is dilation enough to prove that similarity is a symmetric relation? Explain.
Answer:
No, in general, a dilation alone does not prove that similarity is a symmetric relation. In some cases, like part (a), it would be enough, but because we are talking about general cases, we must consider figures that require a sequence of basic rigid motions to map one onto the other. Therefore, in general, to show that there is a symmetric relationship, we must use what we know about similar figures, a dilation followed by a congruence, as opposed to dilation alone.

Question 2.
Would a dilation alone be enough to show that similarity is transitive? That is, would a dilation alone prove that if
△ABC~△A’B’C’, and △A’ B’ C’~△A”B”C”, then △ABC~△A”B”C”? Consider the two examples below.
a. Given △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”, is a dilation enough to show that △ABC~△A”B”C”? Explain.

Answer:
Yes, in this case, we could dilate by different scale factors to show that all three triangles are similar to each other.

b. Given △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”, is a dilation enough to show that △ABC~△A”B”C”? Explain.
Answer:

In this case, it would take more than just a dilation to show that all three triangles are similar to one another. Specifically, it would take a dilation followed by a congruence to prove the similarity among the three.

c. In general, is dilation enough to prove that similarity is a transitive relation? Explain.
Answer:
In some cases, it might be enough, but the general case requires the use of dilation and a congruence. Therefore, to prove that similarity is a transitive relation, you must use both a dilation and a congruence.

Question 3.
In the diagram below, △ABC~△A’ B’ C’ and △A’ B’ C’~△A”B”C”. Is △ABC~△A”B”C”? If so, describe the dilation followed by the congruence that demonstrates the similarity.

Answer:
Yes, △ABC~△A”B”C” because similarity is transitive. Since r|AB|=|A”B”|, then r×4=2, which means
r=\(\frac{1}{2}\). Then, a dilation from the origin by scale factor r=\(\frac{1}{2}\) makes △ABC the same size as △A”B”C”. Translate the dilated image of △ABC 6 \(\frac{1}{2}\) units to the left and then reflect across line A”B”. The sequence of the dilation and the congruence map △ABC onto △A” B” C”, demonstrating the similarity.

Eureka Math Grade 8 Module 3 Lesson 9 Exit Ticket Answer Key

Use the diagram below to answer Problems 1 and 2.

Question 1.
Which two triangles, if any, have similarity that is symmetric?
Answer:
△S~△R and △R~△S
△S~△T and △T~△S
△T~△R and △R~△T

Question 2.
Which three triangles, if any, have similarity that is transitive?
Answer:
One possible solution: Since △S~△R and △R~△T, then △S~△T.
Note that △U and △V are not similar to each other or any other triangles. Therefore, they should not be in any solution.