Engage NY Eureka Math Algebra 1 Module 4 Lesson 20 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 20 Example Answer Key
Example

Answer:
→ Is it possible to shrink or stretch the graph of a function? If so, how might that happen?
→ Yes, since we discovered that adding or subtracting a value to the parts of a parent function shifts its graph horizontally or vertically, it is possible that multiplying or dividing will shrink or stretch a function. Note that students may respond with comments about the points of the graph being pushed together or spread apart.
Eureka Math Algebra 1 Module 4 Lesson 20 Exploratory Challenge Answer Key
Exploratory Challenge
Complete the following to review Module 3 concepts:
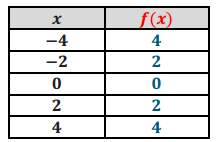
a. Consider the function f(x) = |x|. Complete the table of values for f(x). Then, graph the equation y = f(x) on the coordinate plane provided for part (b).
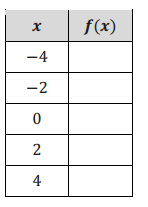
Answer:
b. Complete the following table of values for each transformation of the function f. Then, graph the equations y = g(x), y = h(x), y = j(x), and y = k(x) on the same coordinate plane as the graph of y = f(x). Label each graph.
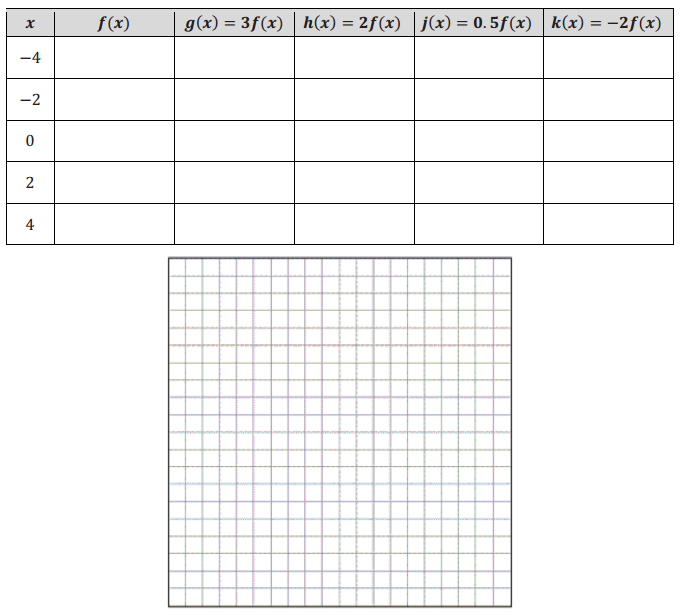
Answer:
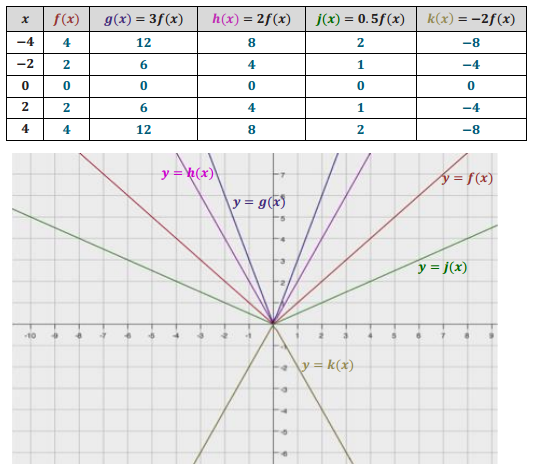
c. Describe how the graph of y = kf(x) relates to the graph of y = f(x) for each case.
i. k > 1
Answer:
The graph is stretched vertically by a factor equal to k.
ii. 0 < k < 1
Answer:
The graph is shrunk vertically by a factor equal to k.
iii. k = – 1
ans;
The graph is reflected across the x – axis.
iv. – 1 < k < 0
Answer:
The graph is reflected across the x – axis and shrunk vertically by a factor equal to |k|.
v. k < – 1
Answer:
The graph is reflected across the x – axis and stretched vertically by a factor equal to |k|.
d. Describe the transformation of the graph of f that results in the graphs of g, h, and k given the following formulas for each function. Then, graph each function and label each graph.
f(x) = x3
g(x) = 2x3
h(x) = 0.5x3
k(x) = – 3x3

Answer:
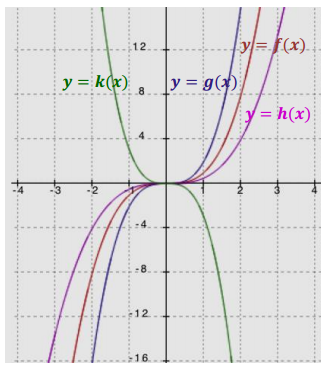
The graph of g shows a vertically stretched graph of f with a scale factor of 2. The graph of h is a vertically shrunk, or compressed, graph of f with a scale factor of 0.5. The graph of k shows a vertically stretched graph of f with a scale factor of 3 and is reflected across the x – axis.
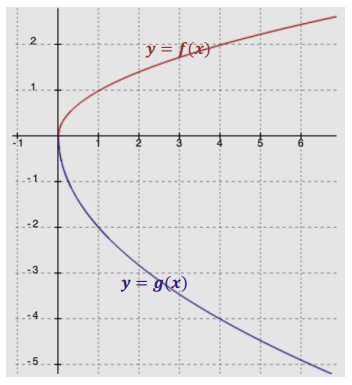
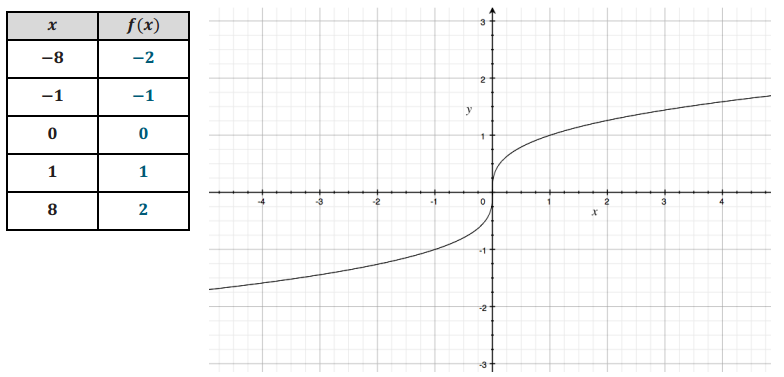
e. Consider the function f(x) = \(\sqrt [ 3 ]{ x }\). Complete the table of values; then graph the equation y = f(x).

Answer:
f. Complete the following table of values, rounding each value to the nearest hundredth. Graph the equations y = g(x), y = h(x), and y = j(x) on the same coordinate plane as your graph of y = f(x) above. Label each graph.
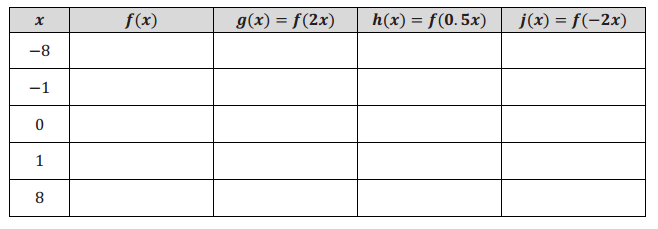
Answer:
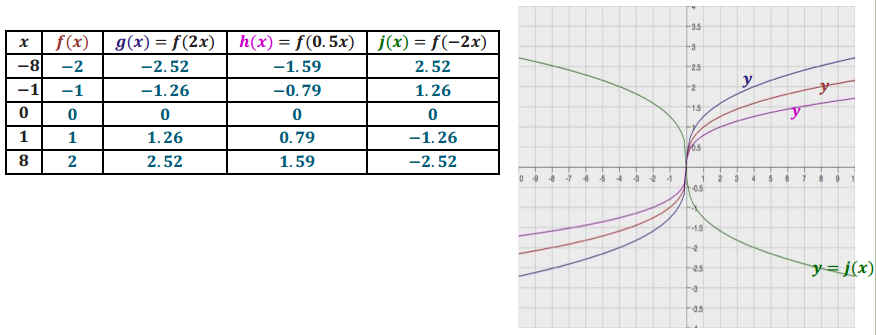
Describe the transformations of the graph of f that result in the graphs of g, h, and j.
When the x – values of f are multiplied by 2, the graph is shrunk horizontally by a factor of 0.5. When the
x – values of f are multiplied by 0.5, the graph is stretched horizontally by a factor of 2. When the x – values of f are multiplied by – 2, the graph is shrunk horizontally by a factor of 0.5 and is reflected about the
y – axis.
f. Describe how the graph of y = f(\(\frac{1}{k}\) x) relates to the graph of y = f(x) for each case.
i. k > 1
Answer:
The graph is stretched horizontally by a factor equal to k.
ii. 0 < k < 1
Answer:
The graph is shrunk horizontally by a factor equal to k.
iii. k = – 1
Answer:
The graph is reflected across the y – axis.
iv. – 1 < k < 0
Answer:
The graph is shrunk horizontally by a factor equal to |k| and is reflected across the y – axis.
v. k < – 1
Answer:
The graph is stretched horizontally by a factor equal to |k| and is reflected across the y – axis.
Eureka Math Algebra 1 Module 4 Lesson 20 Exercise Answer Key
Opening Exercise
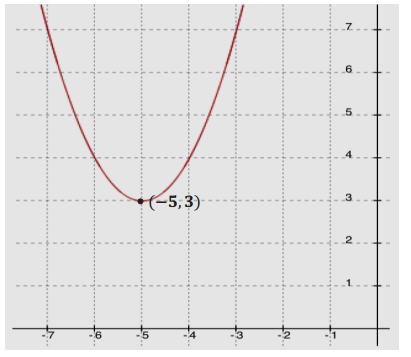
The graph of a quadratic function defined by f(x) = x2 has been translated 5 units to the left and 3 units up. What is the formula for the function, g, depicted by the translated graph?
Answer:
g(x) = (x + 5)2 + 3
Sketch the graph of the equation y = g(x).
Answer:
Exercise 1.
For each set of graphs below, answer the following questions:
What are the parent functions?
How does the transformed graph relate to the graph of the parent function?
Write the formula for the function depicted by the transformed graph.
a.
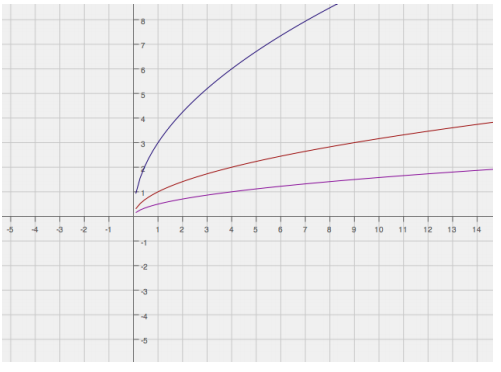
Answer:
The parent function (in red) is f(x) = \(\sqrt{x}\). The graph in blue is a vertical scaling of the graph of f with a scale factor of 3. The function depicted by the blue graph is g(x) = 3\(\sqrt{x}\). The other graph (in pink) is a vertical scaling of the graph of f with a scale factor of 0.5. The function depicted by the graph is h(x) = 0.5\(\sqrt{x}\).
b.
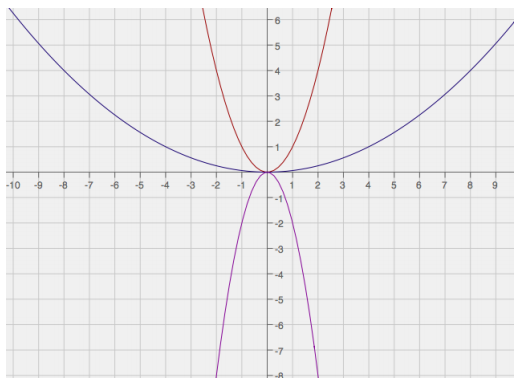
Answer:
The parent function (in red) is f(x) = x2. The graph in blue is a horizontal scaling of the graph of f with a scale factor of 4. The function depicted by the blue graph is g(x) = (\(\frac{1}{4}\) x)2. The other graph (in pink) is a vertical scaling of the graph of f with a scale factor of 2 and is reflected over the x – axis. The function depicted by the graph is h(x) = – 2x2.
Exercise 2.
Graph each set of functions in the same coordinate plane. Do not use a graphing calculator.
a. f(x) = |x|
g(x) = 4|x|
h(x) = |2x|
k(x) = – 2|2x|

Answer:
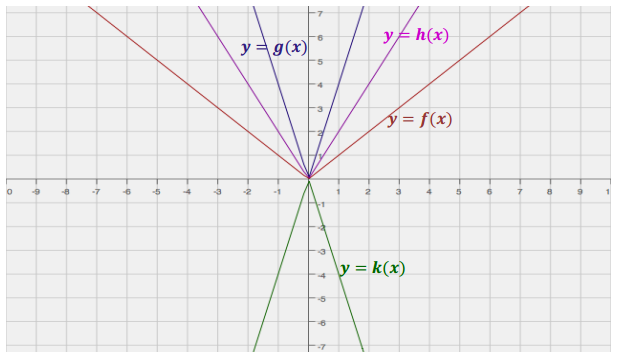
y = f(x) in red
y = g(x) in purple
y = h(x) in pink
y = k(x) in green
b. g(x) = \(\sqrt [ 3 ]{ x }\)
p(x) = 2\(\sqrt [ 3 ]{ x }\)
q(x) = – 2\(\sqrt [ 3 ]{ 2x }\)

Answer:
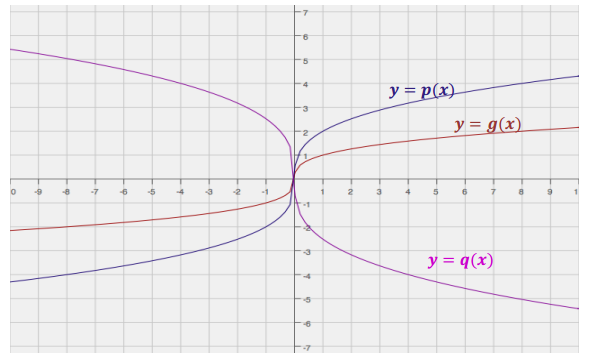
y = g(x) in red
y = p(x) in purple
y = q(x) in pink
Eureka Math Algebra 1 Module 4 Lesson 20 Problem Set Answer Key
Question 1.
Graph the functions in the same coordinate plane. Do not use a graphing calculator.
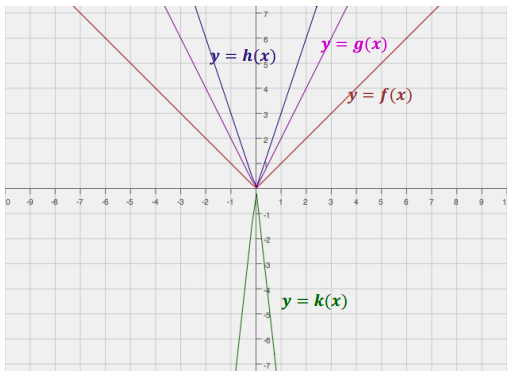
f(x) = |x|
g(x) = 2|x|
h(x) = |3x|
k(x) = – 3|3x|
Answer:
Question 2.
Explain how the graphs of functions j(x) = 3|x| and h(x) = |3x| are related.
Answer:
Each of these transformations of the absolute value functions creates the same graph.
Question 3.
Explain how the graphs of functions q(x) = – 3|x| and r(x) = | – 3x| are related.
Answer:
The two graphs have the same scaling factor of 3, but they are reflections of each other across the x – axis. Multiplying an absolute value by a negative number will reflect it across the x – axis. However, multiplying by a negative number INSIDE the absolute value has the same effect as multiplying by a positive number on the outside.
Question 4.
Write a function, g, in terms of another function, f, such that the graph of g is a vertical shrink of the graph f by a factor of 0.75.
Answer:
g(x) = 0.75 f(x)
Question 5.
A teacher wants the students to write a function based on the parent function f(x) = \(\sqrt [ 3 ]{ x }\). The graph of f is stretched vertically by a factor of 4 and shrunk horizontally by a factor of \(\frac{1}{3}\). Mike wrote g(x) = 4\(\sqrt [ 3 ]{ 3x }\) as the new function, while Lucy wrote h(x) = 3\(\sqrt [ 3 ]{ 4x }\). Which one is correct? Justify your answer.
Answer:
Mike is correct. A vertical stretch by a factor of 4 means multiplying f(x) by 4, and a horizontal shrink by a factor of \(\frac{1}{3}\) means that the x – values of f(x) must be multiplied by 3.
Question 6.
Study the graphs of two different functions below. Which is a parent function? What is the constant value(s) multiplied to the parent function to arrive at the transformed graph? Now write the function defined by the transformed graph.
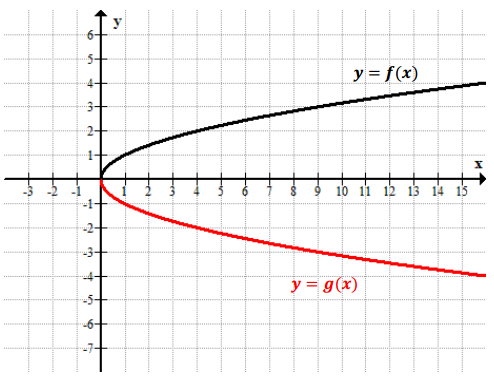
Answer:
The parent function is f(x) = \(\sqrt{x}\). The graph of y = g(x) is the graph of y = f(x) reflected across the x – axis. The function depicted by the transformed graph is g(x) = – \(\sqrt{x}\).
Eureka Math Algebra 1 Module 4 Lesson 20 Exit Ticket Answer Key
Question 1.
How would the graph of f(x) = \(\sqrt{x}\) be affected if it were changed to g(x) = – 2\(\sqrt{x}\)?
Answer:
The graph of f would be stretched vertically by a factor of 2 and reflected across the x – axis.
Question 2.
Sketch and label the graphs of both f and g on the grid below.

Answer: