Learn all the relations of Trigonometrical Ratios of (90° + θ). There are six different trigonometrical ratios depends on the (90° + θ). Let a rotating line OP rotates about O in the anti-clockwise direction, from starting position to ending position. It makes an angle ∠XOP = θ again the same rotating line rotates in the same direction and makes an angle ∠POQ =90°. Therefore, we see that ∠XOQ = 90° + θ.
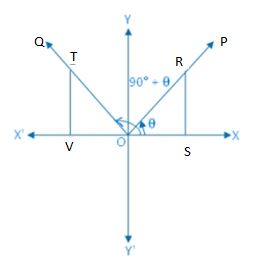
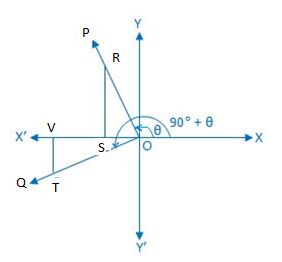
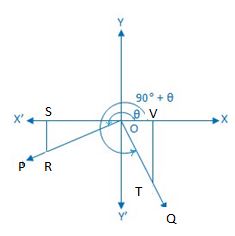
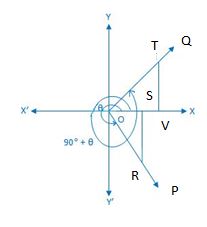
Take a point R on OP and draw RS perpendicular to OX or OX’. Again, take a point T on OQ such that OT = OR and draw TV perpendicular to OX or OX’. From the right-angled ∆ ORS and ∆ OTV, we get,
∠ROS = ∠OTV [since OQ ⊥ OP] and OR = OT.
Therefore, ∆ ORS ≅ ∆ OTV (congruent).
Therefore according to the definition of a trigonometric sign, OV = – SR, VT = OS and OT = OR
We observe that in diagrams 1 and 4 OV and SR are opposite signs and VT, OS are either both positive. Again we observe that in diagrams 2 and 3 OV and SR are opposite signs and TV, OS are both negative.
Check out Worksheet on Trigonometric Identities to learn more about Trig Identities and know the relation between all six quadrants.
Evaluate Trigonometrical Ratios of (90° + θ)
1. Evaluate sin (90° + θ)?
Solution:
To find sin (90° + θ), we need to consider the following important points.
(i) (90° + θ) will present in the IInd quadrant.
(ii) When we have 90°, “sin” will become “cos”.
(iii) In the IInd quadrant, the sign of “sin” is positive.
From the above points, we have sin (90° + θ) = cos θ
sin (90° + θ) = VT/OT
sin (90° + θ) = OS/OR, [VT = OS and OT = OR, since ∆ ORS ≅ ∆ OTV]
sin (90° + θ) = cos θ
2. Evaluate cos (90° + θ)?
Solution:
To find cos (90° + θ), we need to consider the following important points.
(i) (90° + θ) will present in the IInd quadrant.
(ii) When we have 90°, “cos” will become “sin”.
(iii) In the IInd quadrant, the sign of “cos” is negative.
From the above points, we have cos (90° + θ) = – sin θ
cos (90° + θ) = OV/OT
cos (90° + θ) = – SR/OR, [OV = -SR and OT = OR, since ∆ ORS ≅ ∆ OTV]
cos (90° + θ) = – sin θ.
3. Evaluate tan (90° + θ)?
Solution:
To find tan (90° + θ), we need to consider the following important points.
(i) (90° + θ) will present in the IInd quadrant.
(ii) When we have 90°, “tan” will become a “cot”.
(iii) In the IInd quadrant, the sign of “tan” is negative.
From the above points, we have a tan (90° + θ) = – cot θ
tan (90° + θ) = VT/OV
tan (90° + θ) = OS/-SR, [VT = OS and OV = – SR, since ∆ ORS ≅ ∆ OTV]
tan (90° + θ) = – cot θ.
4. Evaluate csc (90° + θ)?
Solution:
To find csc (90° + θ), we need to consider the following important points.
(i) (90° + θ) will present in the IInd quadrant.
(ii) When we have 90°, “csc” will become “sec”.
(iii) In the IInd quadrant, the sign of “csc” is positive.
From the above points, we have csc (90° + θ) = sec θ
csc (90° + θ) = 1/sin(90°+θ)
csc (90° + θ) = 1/cosθ
csc (90° + θ) = sec θ.
5. Evaluate sec (90° + θ)?
Solution:
To find sec (90° + θ), we need to consider the following important points.
(i) (90° + θ) will present in the IInd quadrant.
(ii) When we have 90°, “sec” will become “csc”.
(iii) In the IInd quadrant, the sign of “sec” is negative.
From the above points, we have sec (90° + θ) = – csc θ
sec (90° + θ) = 1/cos(90° + θ)
sec (90° + θ) = 1/-sinθ
sec (90° + θ) = – csc θ.
6. Evaluate cot (90° + θ)?
Solution :
To find cot (90° + θ), we need to consider the following important points.
(i) (90° + θ) will present in the IInd quadrant.
(ii) When we have 90°, “cot” will become “tan”
(iii) In the IInd quadrant, the sign of “cot” is negative.
From the above points, we have cot (90° + θ) = – tan θ
cot (90° + θ) = 1/tan(90° + θ)
cot (90° + θ) = 1/-cotθ
cot (90° + θ) = – tan θ.
Solved Examples on Trigonometrical Ratios of (90° + θ)
1. Find the value of sin 135°?
Solution:
Given value is sin 135°
sin 135° = sin (90 + 55)°
We know that sin (90° + θ) = cos θ
= cos 45°;
The value of cos 45° = 1/√2.
Therefore, the value of sin 135° = 1/√2.
2. Find the value of tan 150°?
Solution:
Given value is tan 150°
tan 150° = tan (90 + 60)°
We know that tan (90° + θ) = – cot θ
= – cot 60°;
The value of -cot 60° = 1/√3.
Therefore, the value of tan 150° = 1/√3.
