Tag: Eureka Math Grade 6

Engage NY Eureka Math Grade 6 Module 5 Lesson 11 Answer Key

Eureka Math Grade 6 Module 5 Lesson 11 Example Answer Key

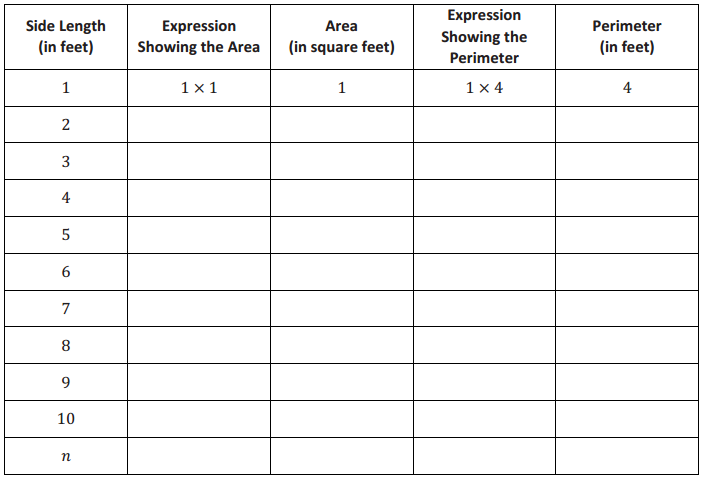
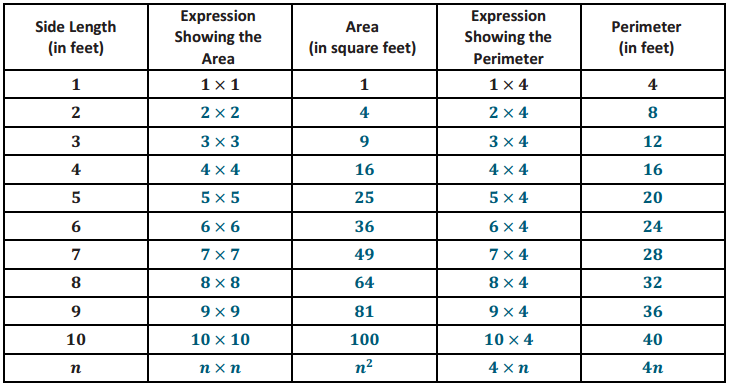
Example 1.
A box with the same dimensions as the prism in the Opening Exercise is used to ship miniature dice whose side lengths have been cut in half. The dice are \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. cubes. How many dice of this size can fit in the box?

Answer:

→ How many cubes could we fit across the length? The width? The height?
Two cubes would fit across a 1-inch length. So, I would need to double the lengths to get the number of cubes. Twenty cubes will fit across the 10-inch length, 8 cubes will fit across the 4 -inch width and 12 cubes will fit across the 6-inch height.

→ How can you use this information to determine the number of \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. cubes it takes to fill the box?
I can multiply the number of cubes in length, width, and height.
20 × 8 × 12 = 1,920, so 1,920 of the smaller cubes will fill the box.

→ How many of these smaller cubes can fit into the 1 in. × 1 in. × 1 in. cube?
Two confits across the length, two across the width, and two for the height. 2 × 2 × 2 = 8. Eight smaller cubes confit in the larger cube.

→ How does the number of cubes in this example compare to the number of cubes that would be needed in the
Opening Exercise?
\(\frac{\text { new }}{\text { old }}=\frac{1,920}{240}=\frac{8}{1}\)
If I fill the same box with cubes that are half the length, I need 8 times as many.

→ How is the volume of the box related to the number of cubes that will fit in it?
The volume of the box is of the number of cubes that will fit in it.

→ What is the volume of 1 cube?
V= \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in.

→ What is the product of the number of cubes and the volume of the cubes? What does this product represent?
1920 × \(\frac{1}{8}\) = 240
The product represents the volume of the original box.

Example 2.
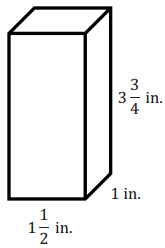
A \(\frac{1}{5}\) in. cube is used to fill the prism. How many in. cubes does it take to fill the prism? What is the volume of the prism? How is the number of cubes related to the volume?

Answer:

→ How would you determine, or find, the number of cubes that fill the prism?
One method would be to determine the number of cubes that will fit across the length, width, and height. Then, I would multiply. 6 will fit across the length, 4 across the width, and 15 across the height. 6 × 4 × 15 = 360, so 360 cubes will fill the prism.

→ How is the number of cubes and the volume related?
The volume is equal to the number of cubes times the volume of one cube.
The volume of one cube is \(\frac{1}{4}\) in. × \(\frac{1}{4}\) in. × \(\frac{1}{4}\) in. = \(\frac{1}{64}\) in³.

360 cubes × \(\frac{1}{64}\) in³ = \(\frac{360}{64}\) in³ = \(\frac{540}{64}\) in³ =5 \(\frac{5}{8}\)in³

→ What other method can be used to determine the volume?
V = l w h
V = (1 \(\frac{1}{2}\) in.) (1 in.) (3 \(\frac{3}{4}\) in.)
V = \(\frac{3}{2}\) in. × \(\frac{1}{1}\) in. × \(\frac{15}{4}\) in.
V = \(\frac{45}{8}\) in³ = 5 \(\frac{5}{8}\) in³

→ Would any other size cubes fit perfectly inside the prism with no space left over?
We would not be able to use cubes with side lengths of \(\frac{1}{2}\) in., \(\frac{1}{3}\) in., or \(\frac{2}{3}\) in. because there would be spaces left over. However, we could use a cube with a side length of \(\frac{1}{8}\) in. without having spaces left over.

Eureka Math Grade 6 Module 5 Lesson 11 Exercise Answer Key

Opening Exercise:

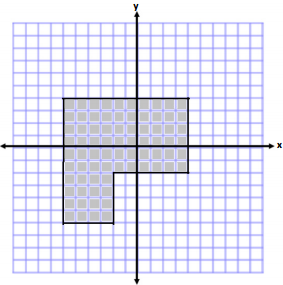
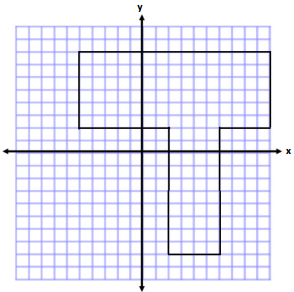
Exercise 1.
Which prism holds more 1 in. × 1 in. × 1 in. cubes? How many more cubes does the prism hold?

Answer:
Students discuss their solutions with a partner.

→ How many 1 in. × 1 in. × 1 in. cubes can fit across the bottom of the first rectangular prism?
Answer:
40 cubes can fit across the bottom.

→ How did you determine this number?
Answer:
Answers will vary. I determined how many cubes could fill the bottom layer of the prism and then decided how many layers were needed.

Students who are English language learners may need a model of what “layers” means in this context.

→ How many layers of 1 in. × 1 in. × 1 in. cubes can fit inside the rectangular prism?
There are 6 inches in the height; therefore, 6 layers of cubes can fit inside.

→ How many 1 in. × 1 in. × 1 in. cubes can fit across the bottom of the second rectangular prism?
40 cubes can fit across the bottom.

→ How many layers do you need?
I need 12 layers because the prism is 12 in. tall.

→ Which rectangular prism can hold more cubes?
The second rectangular prism can holds more cubes.

→ How did you determine this?
Both rectangular prisms hold the same number of cubes in one layer, but the second rectangular prism has more layers.

→ How many more layers does the second rectangular prism hold?
It holds 6 more layers.

→ How many more cubes does the second rectangular prism hold?
The second rectangular prism has 6 more layers than the first, with 40 cubes in each layer.
6 × 40 = 240, so the second rectangular prism holds 240 more cubes than the first.

> What other ways can you determine the volume of a rectangular prism?
We can also use the formula V = l. w . h.

Exercises:

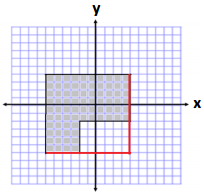
Exercise 1.
Use the prism to answer the following questions.

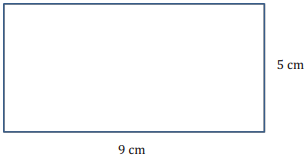
a. Calculate the volume.
Answer:

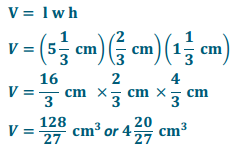
b. If you have to fill the prism with cubes whose side lengths are less than 1 cm, what size would be best?
Answer:
The best choice would be a cube with side lengths of \(\frac{1}{3}\) cm.

c. How many of the cubes would fit in the prism?
Answer:
16 × 2 × 4 = 128, so 128 cubes will fit in the prism.

d. Use the relationship between the number of cubes and the volume to prove that your volume calculation Is correct.
Answer:
The volume of one cube would be \(\frac{1}{3}\) cm × \(\frac{1}{3}\)cm × \(\frac{1}{3}\) cm = \(\frac{1}{27}\) cm³

Since there are 128 cubes, the volume would be 128 × \(\frac{1}{27}\) cm³ = \(\frac{128}{27}\) cm³ or 4\(\frac{20}{27}\) cm³.

Exercise 2.
Calculate the volume of the following rectangular prisms.

a.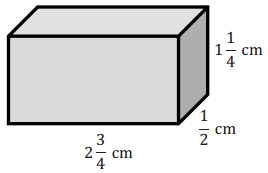
Answer:

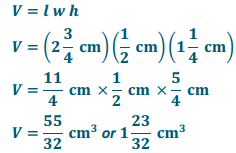
b.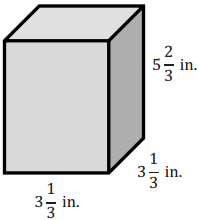
Answer:

Exercise 3.
A toy company is packaging its toys to be shipped. Each small toy is placed inside a cube-shaped box with side lengths of \(\frac{1}{2}\) in. These smaller boxes are then placed into a larger box with dimensions of 12 in. × 4\(\frac{1}{2}\) in. × 3\(\frac{1}{2}\) in.

a. What is the greatest number of small toy boxes that can be packed into the larger box for shipping?
Answer:
24 × 9 × 7 = 1,512, so 1,512 toys can be packed into the larger box.

b. Use the number of small toy boxes that can be shipped in the larger box to help determine the volume of the shipping box.
Answer:
One small box would have a volume of \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. × \(\frac{1}{2}\) in. = \(\frac{1}{8}\) in³.
Now, I multiply the number of cubes by the volume of the cube.
1,512 × \(\frac{1}{8}\) in³ = \(\frac{1512}{8}\) in³ = 189 in³

Exercise 4.
A rectangular prism with a volume of 8 cubic units is filled with cubes twice: once with cubes with side lengths of \(\frac{1}{2}\) unit and once with cubes with side lengths of \(\frac{1}{3}\) unit.

a. How many more of the cubes with \(\frac{1}{3}\) unit side lengths than cubes with \(\frac{1}{2}\) unit side lengths are needed to fill the prism?
Answer:
There are 8 cubes with \(\frac{1}{2}\) unit side lengths in 1 cubic unit because the volume of one cube is \(\frac{1}{8}\) cubic unit. Since we have 8 cubic units, we would have 64 total cubes with \(\frac{1}{2}\) unit side lengths because 8 × 8 = 64.

There are 27 cubes with \(\frac{1}{3}\) unit side lengths in 1 cubic unit because the volume of one cube is \(\frac{1}{27}\) cubic units. Since we have 8 cubic units, we would have 216 total cubes with \(\frac{1}{3}\) unit side lengths because 8 × 27 = 216. 216 – 64 = 152, so 152 more cubes with \(\frac{1}{3}\) unit side lengths are needed to fill the prism.

b. Why does it take more cubes with \(\frac{1}{3}\) unit side lengths to fill the prism than it does with cubes with \(\frac{1}{2}\) unit side lengths?
Answer:
\(\frac{1}{3}\) < \(\frac{1}{2}\). The side length is shorter for the cube with a \(\frac{1}{3}\) unit side length, so it takes more to fill the rectangular prism.

Exercise 5.
Calculate the volume of the rectangular prism. Show two different methods for determining the volume.

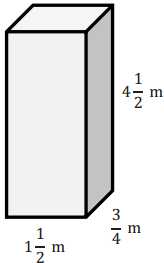
Answer:
Method 1:

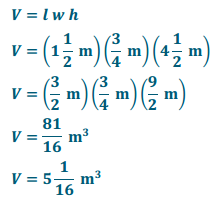
Method 2:
Fill the rectangular prism with cubes that are \(\frac{1}{4}\) m × \(\frac{1}{4}\) m × \(\frac{1}{4}\) m.
The volume of each cube is \(\frac{1}{64}\) m³.
We would have 6 cubes across the length, 3 cubes across the width, and 18 cubes across the height.
6 × 3 × 18 = 324, so the rectangular prism could be filled with 324 cubes with \(\frac{1}{4}\) m side lengths.
324 × \(\frac{1}{64}\) m³ = 5 \(\frac{1}{16}\) m³.

Eureka Math Grade 6 Module 5 Lesson 11 Problem Set Answer Key

Question 1.
Answer the following questions using this rectangular prism:

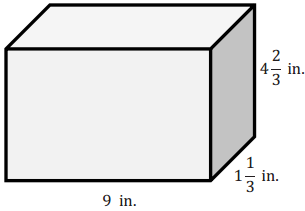
a. What is the volume of the prism?
Answer:
V = l w h
V = (9 in.) (1 \(\frac{1}{3}\) in.) (4 \(\frac{2}{3}\)in.)
V = ( \(\frac{9}{1}\) in.) (\(\frac{4}{3}\) in.) (\(\frac{14}{3}\) in.)
V = \(\frac{504}{9}\) in³
V = 56 in³.

b. Linda fills the rectangular prism with cubes that have side lengths of \(\frac{1}{3}\) in. How many cubes does she need to fill the rectangular prism?
Answer:
She needs 27 across by 4 wide and 14 high.
Number of cubes = 27 × 4 × 14 = 1,512.
Linda needs 512 cubes with \(\frac{1}{3}\) in. side lengths to fill the rectangular prism.

c. How is the number of cubes related to the volume?
Answer:
56 × 27 = 1,512
The number of cubes needed is 27 times larger than the volume.

d. Why is the number of cubes needed different from the volume?
Answer:
Because the cubes are not each 1 in., the volume is different from the number of cubes. However, I could multiply the number of cubes by the volume of one cube and still get the original volume.

e. Should Linda try to fill this rectangular prism with cubes that are \(\frac{1}{2}\) in. long on each side? Why or why not?
Answer:
Because some of the lengths are \(\frac{1}{3}\) in. and some are \(\frac{2}{3}\) in., it would not be possible to use side lengths of \(\frac{1}{2}\) in. to fill the prism.

Question 2.
Calculate the volume of the following prisms.

a.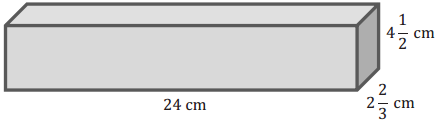
Answer:
V = l w h
V = (24 cm) (2\(\frac{2}{3}\) cm) (4\(\frac{1}{2}\) cm)
V = (24cm) (\(\frac{8}{3}\) cm) (\(\frac{9}{2}\) cm)
V = \(\frac{1728}{6}\) cm³
V = 288 cm³

b.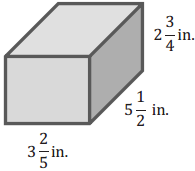
Answer:

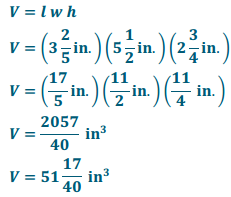
Question 3.
A rectangular prism with a volume of 12 cubic units is filled with cubes twice: once with cubes with \(\frac{1}{2}\) unit side lengths and once with cubes with \(\frac{1}{3}\)-unit side lengths.

a. How many more of the cubes with \(\frac{1}{3}\)-unit side lengths than cubes with \(\frac{1}{2}\)-unit side lengths are needed to fill the prism?
Answer:
There are 8 cubes with \(\frac{1}{2}\)-unit side lengths in 1 cubic unit because the volume of one cube is \(\frac{1}{8}\) cubic unit. Since we have 12 cubic units, we would have 96 total cubes with \(\frac{1}{2}\)-unit side lengths because 12 × 8 = 96.

There are 27 cubes with \(\frac{1}{3}\)-unit side lengths in 1 cubic unit because the volume of one cube is \(\frac{1}{27}\) cubic unit. Since we have 12 cubic units, we would have 324 total cubes with \(\frac{1}{3}\)-unit side lengths because 12 × 27 = 324.

324 – 96 = 228, so there are 228 more cubes with \(\frac{1}{3}\)-unit side lengths needed than there are cubes with \(\frac{1}{2}\)-unit side lengths needed.

b. Finally, the prism is filled with cubes whose side lengths are \(\frac{1}{4}\) unit. How many \(\frac{1}{4}\) unit cubes would it take to fill the prism?
Answer:
There are 64 cubes with \(\frac{1}{4}\)-unit side lengths in 1 cubic unit because the volume of one cube is \(\frac{1}{64}\) cubic unit.
Since there are 12 cubic units, we would have 768 total cubes with side lengths of \(\frac{1}{4}\) unit because 12 × 64 = 768.

Question 4.
A toy company is packaging its toys to be shipped. Each toy is placed inside a cube-shaped box with side lengths of 3\(\frac{1}{2}\) in. These smaller boxes are then packed into a larger box with dimensions of 14 in. × 7 in. × 3\(\frac{1}{2}\) in.

a. What is the greatest number of toy boxes that can be packed into the larger box for shipping?
Answer:
4 × 2 × 1 = 8, so 8 toy boxes can be packed into the larger box for shipping.

b. Use the number of toy boxes that can be shipped in the large box to determine the volume of the shipping box.
Answer:
One small box would haveavolume of 3\(\frac{1}{2}\) in. × 3\(\frac{1}{2}\) in. × 3\(\frac{1}{2}\) in. = 42\(\frac{7}{8}\) in³.
Now, I will multiply the number of cubes by the volume of the cube. 8 × 42\(\frac{7}{8}\) in³ = 343 in³

Question 5.
A rectangular prism has a volume of 34.224 cubic meters. The height of the box is 3. 1 meters, and the length is 2.4 meters.

a. Write an equation that relates the volume to the length, width, and height. Let w represent the width, in meters.
Ans;
34.224 = (3.1) (2. 4)w

b. Solve the equation.
Answer:
34.224 = 7.44 w
w = 4.6
The width is 4.6 m.

Eureka Math Grade 6 Module 5 Lesson 11 Exit Ticket Answer Key

Question 1.
Calculate the volume of the rectangular prism using two different methods. Label your solutions Method 1 and Method 2.

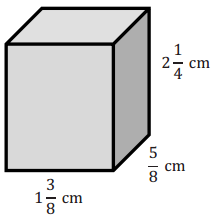
Answer:
Method 1:
V = l w h
V = (1\(\frac{3}{8}\) cm) (\(\frac{5}{8}\) cm) (2\(\frac{1}{4}\) cm)

V = \(\frac{11}{8}\) cm × \(\frac{5}{8}\) cm × \(\frac{9}{4}\) cm

V = \(\frac{495}{256}\) cm³

Method 2:
Fill shape with \(\frac{1}{8}\) cm cubes.
11 × 5 × 18 = 990, so 990 cubes could be used to fill the prism.
Each cube has a volume of \(\frac{1}{8}\) cm × \(\frac{1}{8}\) cm × \(\frac{1}{8}\) cm = \(\frac{1}{512}\) cm³

V = 990 × \(\frac{1}{512}\) cm³ = \(\frac{990}{512}\) cm³ = \(\frac{495}{256}\) cm³

Eureka Math Grade 6 Module 5 Lesson 11 Multiplication of Fractions II Answer Key

Multiplication of Fractions II – Round 1:

Directions: Determine the product of the fractions and simplify.

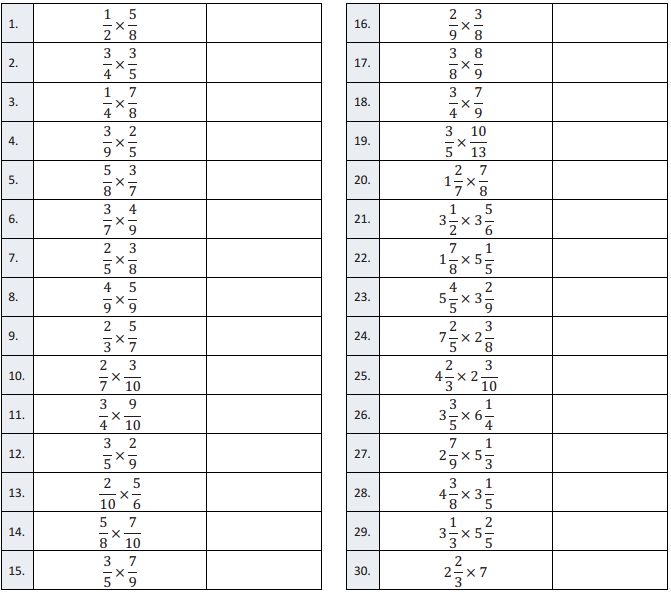
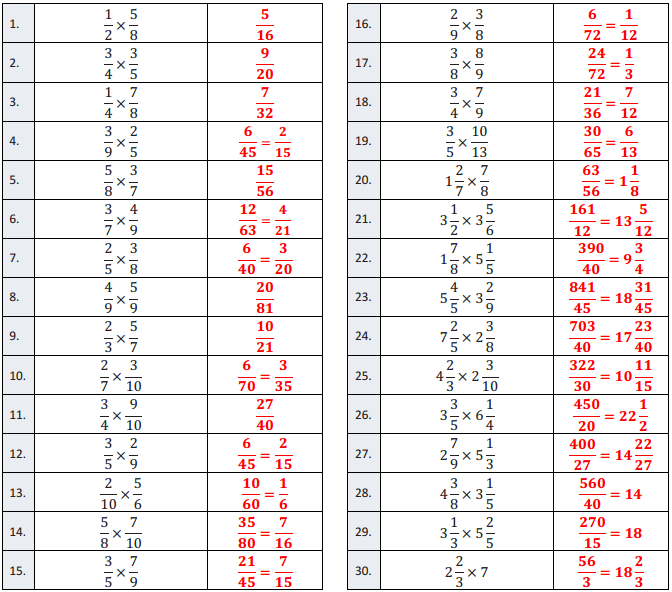
Question 1.
\(\frac{1}{2}\) × \(\frac{5}{8}\)
Answer:
\(\frac{5}{16}\)

Question 2.
\(\frac{3}{4}\) × \(\frac{3}{5}\)
Answer:
\(\frac{9}{20}\)

Question 3.
\(\frac{1}{4}\) × \(\frac{7}{8}\)
Answer:
\(\frac{7}{32}\)

Question 4.
\(\frac{3}{9}\) × \(\frac{2}{5}\)
Answer:
\(\frac{6}{45}\) = \(\frac{2}{15}\)

Question 5.
\(\frac{5}{8}\) × \(\frac{3}{7}\)
Answer:
\(\frac{15}{56}\)

Question 6.
\(\frac{3}{7}\) × \(\frac{4}{9}\)
Answer:
\(\frac{12}{63}\) = \(\frac{4}{21}\)

Question 7.
\(\frac{2}{5}\) × \(\frac{3}{8}\)
Answer:
\(\frac{6}{40}\) = \(\frac{3}{20}\)

Question 8.
\(\frac{4}{9}\) × \(\frac{5}{9}\)
Answer:
\(\frac{20}{81}\)

Question 9.
\(\frac{2}{3}\) × \(\frac{5}{7}\)
Answer:
\(\frac{10}{21}\)

Question 10.
\(\frac{2}{7}\) × \(\frac{3}{10}\)
Answer:
\(\frac{6}{70}\) = \(\frac{3}{35}\)

Question 11.
\(\frac{3}{4}\) × \(\frac{9}{10}\)
Answer:
\(\frac{27}{40}\)

Question 12.
\(\frac{3}{5}\) × \(\frac{2}{9}\)
Answer:
\(\frac{6}{45}\) = \(\frac{2}{15}\)

Question 13.
\(\frac{2}{10}\) × \(\frac{5}{6}\)
Answer:
\(\frac{10}{60}\) = \(\frac{1}{6}\)

Question 14.
\(\frac{5}{8}\) × \(\frac{7}{10}\)
Answer:
\(\frac{35}{80}\) = \(\frac{7}{16}\)

Question 15.
\(\frac{3}{5}\) × \(\frac{7}{9}\)
Answer:
\(\frac{21}{45}\) = \(\frac{7}{15}\)

Question 16.
\(\frac{2}{9}\) × \(\frac{3}{8}\)
Answer:
\(\frac{6}{72}\) = \(\frac{1}{12}\)

Question 17.
\(\frac{3}{8}\) × \(\frac{8}{9}\)
Answer:
\(\frac{24}{72}\) = \(\frac{1}{3}\)

Question 18.
\(\frac{3}{4}\) × \(\frac{7}{9}\)
Answer:
\(\frac{21}{36}\) = \(\frac{7}{12}\)

Question 19.
\(\frac{3}{5}\) × \(\frac{10}{13}\)
Answer:
\(\frac{30}{65}\) = \(\frac{6}{13}\)

Question 20.
1 \(\frac{2}{7}\) × \(\frac{7}{8}\)
Answer:
\(\frac{63}{56}\) = 1 \(\frac{1}{8}\)

Question 21.
3 \(\frac{1}{2}\) × 3 \(\frac{5}{6}\)
Answer:
\(\frac{161}{12}\) = 13 \(\frac{5}{12}\)

Question 22.
\(\frac{1}{4}\) × \(\frac{1}{4}\)
Answer:
\(\frac{1}{4}\)

Question 23.
1 \(\frac{7}{8}\) × 5 \(\frac{1}{5}\)
Answer:
\(\frac{390}{40}\) = 9 \(\frac{3}{4}\)

Question 24.
7 \(\frac{2}{5}\) × 2 \(\frac{3}{8}\)
Answer:
\(\frac{703}{40}\) = 17 \(\frac{23}{40}\)

Question 25.
4 \(\frac{2}{3}\) × 2 \(\frac{3}{10}\)
Answer:
\(\frac{322}{30}\) = 10 \(\frac{11}{15}\)

Question 26.
3 \(\frac{3}{5}\) × 6 \(\frac{1}{4}\)
Answer:
\(\frac{450}{20}\) = 22 \(\frac{1}{2}\)

Question 27.
2 \(\frac{7}{9}\) × 5 \(\frac{1}{3}\)
Answer:
\(\frac{400}{27}\) = 14 \(\frac{22}{27}\)

Question 28.
4 \(\frac{3}{8}\) × 3 \(\frac{1}{5}\)
Answer:
\(\frac{560}{40}\) = 4

Question 29.
3 \(\frac{1}{3}\) × 5 \(\frac{2}{5}\)
Answer:
\(\frac{270}{15}\) = 18 \(\frac{2}{3}\)

Question 30.
2 \(\frac{2}{3}\) × 7
Answer:
\(\frac{56}{3}\) = 18 \(\frac{2}{3}\)

Multiplication of Fractions II – Round 2:

Directions: Determine the product of the fractions and simplify.

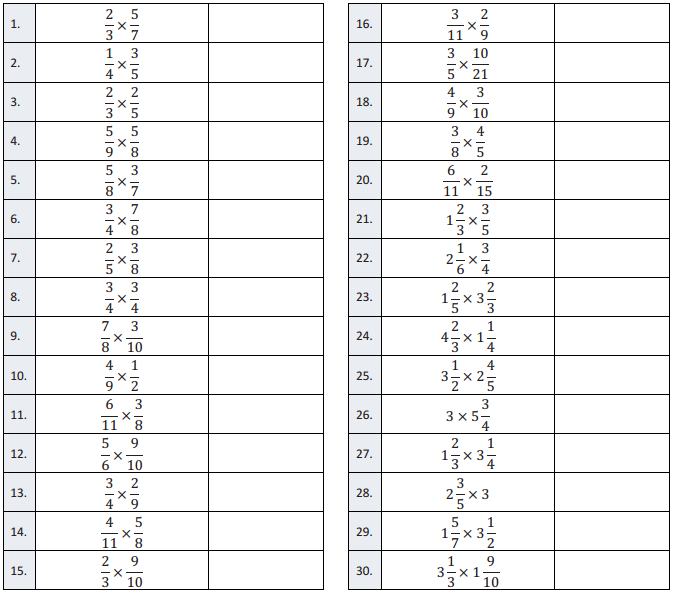
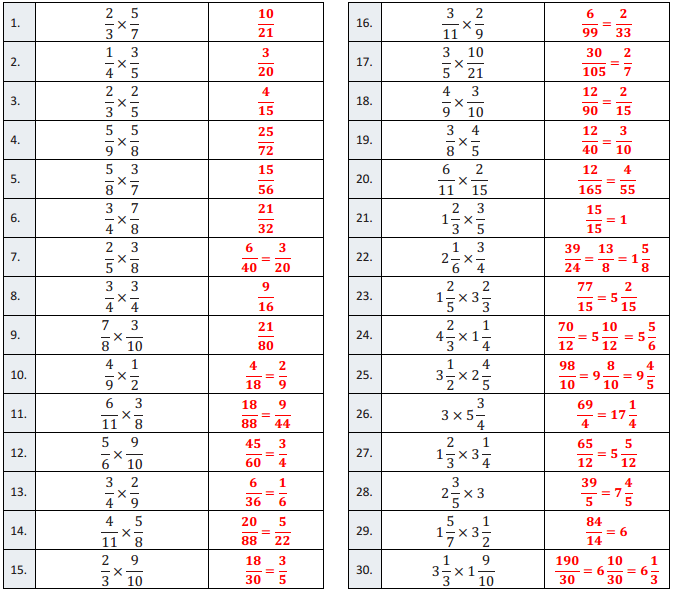
Question 1.
\(\frac{2}{3}\) × \(\frac{5}{7}\)
Answer:
\(\frac{10}{21}\)

Question 2.
\(\frac{1}{4}\) × \(\frac{3}{5}\)
Answer:
\(\frac{3}{20}\)

Question 3.
\(\frac{2}{3}\) × \(\frac{2}{5}\)
Answer:
\(\frac{4}{15}\)

Question 4.
\(\frac{5}{9}\) × \(\frac{5}{8}\)
Answer:
\(\frac{25}{72}\)

Question 5.
\(\frac{5}{8}\) × \(\frac{3}{7}\)
Answer:
\(\frac{15}{56}\)

Question 6.
\(\frac{3}{4}\) × \(\frac{7}{8}\)
Answer:
\(\frac{21}{32}\)

Question 7.
\(\frac{2}{5}\) × \(\frac{3}{8}\)
Answer:
\(\frac{6}{40}\) = \(\frac{3}{20}\)

Question 8.
\(\frac{3}{4}\) × \(\frac{3}{4}\)
Answer:
\(\frac{9}{16}\)

Question 9.
\(\frac{7}{8}\) × \(\frac{3}{10}\)
Answer:
\(\frac{21}{80}\)

Question 10.
\(\frac{4}{9}\) × \(\frac{1}{2}\)
Answer:
\(\frac{4}{18}\) = \(\frac{2}{9}\)

Question 11.
\(\frac{6}{11}\) × \(\frac{3}{8}\)
Answer:
\(\frac{18}{88}\) = \(\frac{9}{44}\)

Question 12.
\(\frac{5}{6}\) × \(\frac{9}{10}\)
Answer:
\(\frac{45}{60}\) = \(\frac{3}{4}\)

Question 13.
\(\frac{3}{4}\) × \(\frac{2}{9}\)
Answer:
\(\frac{6}{36}\) = \(\frac{1}{6}\)

Question 14.
\(\frac{4}{11}\) × \(\frac{5}{8}\)
Answer:
\(\frac{20}{88}\) = \(\frac{5}{22}\)

Question 15.
\(\frac{2}{3}\) × \(\frac{9}{10}\)
Answer:
\(\frac{18}{30}\) = \(\frac{3}{5}\)

Question 16.
\(\frac{3}{11}\) × \(\frac{2}{9}\)
Answer:
\(\frac{6}{99}\) = \(\frac{2}{33}\)

Question 17.
\(\frac{3}{5}\) × \(\frac{10}{21}\)
Answer:
\(\frac{30}{105}\) = \(\frac{2}{7}\)

Question 18.
\(\frac{4}{9}\) × \(\frac{3}{10}\)
Answer:
\(\frac{12}{90}\) = \(\frac{2}{15}\)

Question 19.
\(\frac{3}{8}\) × \(\frac{4}{5}\)
Answer:
\(\frac{12}{40}\) = \(\frac{3}{10}\)

Question 20.
\(\frac{6}{11}\) × \(\frac{2}{15}\)
Answer:
\(\frac{12}{165}\) = \(\frac{4}{55}\)

Question 21.
1 \(\frac{2}{3}\) × \(\frac{3}{5}\)
Answer:
\(\frac{15}{15}\) = 1

Question 22.
2 \(\frac{1}{6}\) × \(\frac{3}{4}\)
Answer:
\(\frac{39}{24}\) = \(\frac{13}{8}\) = 1 \(\frac{5}{8}\)

Question 23.
1 \(\frac{2}{5}\) × 3 \(\frac{2}{3}\)
Answer:
\(\frac{77}{15}\) = 5 \(\frac{2}{15}\)

Question 24.
4 \(\frac{2}{3}\) × 1 \(\frac{1}{4}\)
Answer:
\(\frac{70}{12}\) = 5 \(\frac{10}{12}\) = 5 \(\frac{5}{6}\)

Question 25.
3 \(\frac{1}{2}\) × 2 \(\frac{4}{5}\)
Answer:
\(\frac{98}{10}\) = 9 \(\frac{8}{10}\) = 9 \(\frac{4}{5}\)

Question 26.
3 × 5 \(\frac{3}{4}\)
Answer:
\(\frac{69}{4}\) = 17 \(\frac{1}{4}\)

Question 27.
1 \(\frac{2}{3}\) × 3 \(\frac{1}{4}\)
Answer:
\(\frac{65}{12}\) = 5 \(\frac{5}{12}\)

Question 28.
2 \(\frac{3}{5}\) × 3
Answer:
\(\frac{39}{5}\) = 7 \(\frac{4}{5}\)

Question 29.
1 \(\frac{5}{7}\) × 3 \(\frac{1}{2}\)
Answer:
\(\frac{84}{14}\) = 6

Question 30.
3 \(\frac{1}{3}\) × 1 \(\frac{9}{10}\)
Answer:
\(\frac{190}{30}\) = 6 \(\frac{10}{30}\) = 6 \(\frac{1}{3}\)

Engage NY Eureka Math Grade 6 Module 5 Lesson 10 Answer Key

Eureka Math Grade 6 Module 5 Lesson 10 Exercise Answer Key

Opening Exercise:

Question a.
Find the area and perimeter of this rectangle:

Answer:
A = bh = 9 cm × 5 cm = 45 cm²
P = 9 cm + 9 cm + 5 cm + 5 cm = 28 cm

Question b.
Find the width of this rectangle. The area is 1.2 m², and the length is 1.5 m.

Answer:
A = l × w
1.2 m² = 1.5 m × w
\(\frac{1.2 m^{2}}{1.5 m}\) = \(\frac{1.5 \mathrm{~m} \times \mathrm{w}}{1.5 \mathrm{~m}}\)
0.8 m = w

Eureka Math Grade 6 Module 5 Lesson 10 Example Answer Key

Example: Student Desks or Tables

Question 1.
Measure the dimensions of the top of your desk.
Answer:

Question 2.
How do you find the area of the top of your desk?
Answer:

Question 3.
How do you find the perimeter?
Answer:

Question 4.
Record these on your paper in the appropriate column.
Answer:

Exploratory Challenge:

Question 1.
Estimate and predict the area and perimeter of each object. Then measure each object, and calculate both the area and perimeter of each.

Answer:

Optional Challenge:

Answer:

Eureka Math Grade 6 Module 5 Lesson 10 Problem Set Answer Key

Question 1.
How is the length of the side of a square related to its area and perimeter? The diagram below shows the first four squares stacked on top of each other with their upper left-hand corners lined up. The length of one side of the smallest square is 1 foot.

a. Complete this chart calculating area and perimeter for each square.

Answer:

b. In a square, which numerical value is greater, the area or the perimeter?
Answer:
It depends. For side length less than 4 feet, perimeter is greater; however, for side length greater than 4 feet, area is greater.

c. When is the numerical value of a square’s area (in square units) equal to Its perimeter (in units)?
Answer:
When the side length is exactly 4 feet.

d. Why is this true?
Answer:
n² = 4n is only true when n = 4.

Question 2.
This drawing shows a school pool. The walkway around the pool needs special non skid strips installed but only at the edge of the pool and the outer edges of the walkway.

a. Find the length of nonskid strips that is needed for the job.
Answer:
50 m+ 50 m + 15 m + 15 m + 90 m + 90 m + 25 m + 25 m = 360 m

b. The nonskid strips are sold only in rolls of 50 m. How many rolls need to be purchased for the job?
Answer:
360 m ÷ 50 \(\frac{\mathrm{m}}{\text { roll }}\) = 7.2 rolls
Therefore, 8 rolls need to be purchased.

Question 3.
A homeowner called in a painter to paint the walls and ceiling of one bedroom. His bedroom is 18 ft. long, 12 ft. wide, and 8 ft. high. The room has two doors, each 3 ft. by 7 ft., and three windows each 3 ft. by 5 ft. The doors and windows will not be painted. A gallon of paint can cover 300 ft². A hired painter claims he needs a minimum of 4 gallons. Show that his estimate is too high.
Answer:
Area of 2 long walls:        2(18 ft. × 8 ft.) = 288 ft²
Area of 2 short walls:       2(12 ft. × 8 ft.) = 192 ft²
Area of ceiling:                18 ft. × 12 ft. = 216 ft²
Area of2 doors:                2(3 ft. × 7 ft.) 42 ft²
Area of 3 windows:          3(3 ft. × 5 ft.) = 45 ft²
Area to be painted:          (288 ft² + 192 ft² + 216 ft²) – (42 ft² + 45 ft²2) = 609 ft²
Gallons of point needed:  609 + 300 = 2.03

The painter will need a little more than 2 gallons. The pointer’s estimate for how much paint Is necessary was too high.

Question 4.
Theresa won a gardening contest and was awarded a roll of deer-proof fencing. The fencing is 36 feet long. She and her husband, John, discuss how to best use the fencing to make a rectangular garden. They agree that they should only use whole numbers of feet for the length and width of the garden.

a. What are all of the possible dimensions of the garden?
Answer:

b. Which plan yields the maximum area for the garden? Which plan yields the minimum area?
Answer:

The 9 ft. by 9 ft. garden would have the maximum area (81 ft²), while the 17 ft. by 1 ft. garden would have only 17 ft² of garden space.

Question 5.
Write and then solve the equation to find the missing value below.

Answer:
A = l × w
182 m² = 1.4m × w
\(\frac{1.82 \mathrm{~m}^{2}}{1.4 \mathrm{~m}}\) = w
1.3 m = w

Question 6.
Challenge: This is a drawing of the flag of the Republic of the Congo. The area of this flag is 3\(\frac{3}{4}\) ft².

a. Using the area formula, tell how you would determine the value of the base. This figure is not drawn to scale.
Answer:
A = bh
A ÷ h = b
3\(\frac{3}{4}\) ft² ÷ 1\(\frac{1}{2}\)ft. = b
2\(\frac{1}{2}\) ft. = b

b. Using what you found in part (a), determine the missing value of the base.
Ans:
2\(\frac{1}{2}\) ft. = 1\(\frac{1}{2}\) ft. + x
1 ft. = x

Eureka Math Grade 6 Module 5 Lesson 10 Exit Ticket Answer Key

Question 1.
The local school is building a new playground. This plan shows the part of the playground that needs to be framed with wood for the swing set. The unit of measure is feet. Determine the number of feet of wood needed to frame the area.

Answer:
Perimeter: 10 ft. + 6 ft. + 6 ft. + 3 ft. + 3 ft. + 8 ft. + 8 ft. + 4 ft. = 48 ft.

Question 2.
The school wants to fill the area enclosed with wood with mulch for safety. Determine the number of square feet that needs to be covered by the mulch.
Answer:

Area of Left Rectangle = bh = (6 ft. x 10 ft.) = 60 ft²
Area of Right Rectangle = bh = (8 ft. X 4 ft.) = 32 ft²
Total Area = 60 ft² + 32 ft² = 92 ft²

Engage NY Eureka Math Grade 6 Module 5 Lesson 9 Answer Key

Eureka Math Grade 6 Module 5 Lesson 9 Example Answer Key

Example 1
Jasjeet has made a scale drawing of a vegetable garden she plans to make in her backyard. She needs to determine the perimeter and area to know how much fencing and dirt to purchase. Determine both the perimeter and area.

Answer:

AB = 4 units BC = 7 units CD = 4 units
DE = 6 units EF = 8 units AF = 13 units

Perimeter = 4 units + 7 units + 4 units + 6 units + 8 units + 13 units
Perimeter = 42 units

The area is determined by making a horizontal cut from (1, 1) to point C.
Area of Top
A = lw
A = (4 units)(7 units)
A = 28 units²

Area of Bottom
A = lw
A = (8 units) (6 units)
A = 48 units²

Total Area = 28 units² + 48 units²
Total Area = 76 units²

Example 2:

Calculate the area of the polygon using two different methods. Write two expressions to represent the two methods, and compare the structure of the expressions.

Answer:
Answers will vary. The following are two possible methods. However, students could also break the shape into two
triangles and a rectangle or use another correct method.

Method one:

Method Two:

Area of Triangle 1 and 4
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(3 units)
A = \(\frac{1}{2}\) (12 units²)
A = 6 units2
Since there are 2, we have a total area of 12 units².

Area of Triangle 2 and 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8 units)(3 units)
A = \(\frac{1}{2}\) (24 units²)
A = 12 units2
Since there are 2, we have a total area of 24 units².

A = lw
A = (8 units) (6 units)
A = 48 units²

A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units)(3 units)
A = 3 units²

There are 4 triangles of equivalent base and height.
4(3 units2) = 12 units²

Total Area = 48 units² – 12 units²
Total area = 36 units²

Total Area = 12 units² + 24 units² = 36 units²
Total area = 36 units²

Expressions:
2(\(\frac{1}{2}\)(4)(3)) + 2(\(\frac{1}{2}\)(8)(3)) or (8)(6) – 4(\(\frac{1}{2}\)(2)(3))

The first expression shows terms being added together because I separated the hexagon into smaller pieces and had to add their areas back together.
The second expression shows terms being subtracted because I made a larger outside shape and then had to take away the extra pieces.

Eureka Math Grade 6 Module 5 Lesson 9 Exercise Answer Key

Question 1.
Determine the area of the following shapes.

a.
Answer:

Area of rectangle = lw
A = (10 units) (9 units)
A = 90 units ²

Area of Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (3 units) (3 units)
A = 4.5 units ²

4 triangles with equivalent base and height
4 (4.5 units ²) = 18 units²

Area = 90 units² – 18 units²
Area = 72 units²

Please note the students may also choose to solve by decomposing. Here is another option.

b.
Answer:

Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8 units)(3 units)
A = (4 units)(3 units)
A = 12 units²

Area of Triangles 2 and 4
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units)(3 units)
A = \(\frac{1}{2}\) (15 units²)
A = 7.5 units²

Since triangles 2 and 4 have the same base and height measurements, the combined area is 15 units.

Area of Rectangle 3
A = bh
A = (5 units)(2 units)
A = 10 units²

Total Area = 12 units² + 15 units² + 10 units²
Total Area = 37 units²

Another correct solution might start with the following diagram:

Question 2.
Determine the area and perimeter of the following shapes.

a.
Answer:

Area of Large Square

A = s²
A = (10 units)²
A = 100units²

Removed Piece
A = bh
A = (6 units)(4 units)
A = 24 units²

Area = 100 units² – 24 units²
Area = 76 units²

Perimeter = 10 units + 6 units + 6 units + 4 units + 4 units + 10 units
Perimeter = 40 units

Other correct solutions might start with the following diagrams:

b.
Answer:

Area:

Horizontal Area
A = bh
A = (15 units) (6 units)
A = 90 units²

Vertical Area
A = bh
A = (10 units) (4 units)
A = 40 units²

Total Area = 90 units² + 40 units²
Total Area = 130 units²

Perimeter = 15 units + 6 units + 4 units + 10 units + 4 units + 10 units + 7 units + 6 units
Perimeter = 62 units

Other correct solutions might start with the following diagrams:

Eureka Math Grade 6 Module 5 Lesson 9 Problem Set Answer Key

Question 1.
Determine the area of polygon.

Answer:

Area of Triange 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units)(8 units)
A = \(\frac{1}{2}\) (40 units²)
A = 20 units²

Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (12 units)(8 units)
A = \(\frac{1}{2}\) (96 units²)
A = 48 units²

Area of Tnangle 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (12 units)( 5 units)
A = \(\frac{1}{2}\) (60 units²)
A = 30 units²

Total Area = 20 units² + 48 units² + 30 units²
Total Area = 98 units²

Question 2.
Determine the area and perimeter of the polygon.

Answer:

Area:

Horizontal Rectangle
A = bh
A = (13 units) (5 units)
A = 65 units²

Vertical Rectangle
A = bh
A = (5 units) (9 units)
A = 45 units²

Square
A = S²
A = (2 units)²
A = 4 units²

Total Area = 65 units² + 45 units² +4 units²
Total Area = 114 units²

Perimeter:

Perimeter = 2 units + 2 units + 7 units + 13 units + 14 units + 5 units + 9 units + 6 units
Perimeter = 58 units

Question 3.
Determine the area of the polygon. Then, write an expression that could be used to determine the area.

Answer:

Area of Rectangle on Left
A = lw
A = (8 units) (7 units)
A = 56 units²

Area of Rectangle on Right
A = lw
A = (5 units) (8 units)
A = 40 units²

Area of Triangle on Top
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units)(5 units)
A = 12.5 units²

Total Area = 56 units² + 40 units² + 12.5 units² = 108.5 units²
Expression: (8)(7) + (5)(8) + \(\frac{1}{2}\) (5)(5)

Question 4.
If the length of each square was worth 2 instead of 1, how would the area in Problem 3 change? How would your expression change to represent this area?
Answer:
If each length is twice as long, when they are multiplied, 2l × 2w = 41w. Therefore, the area will be four times larger when the side lengths are doubled.

I could multiply my entire expression by 4 to make it 4 times as big. 4 [(8)(7) + (5)(8) + \(\frac{1}{2}\) (5)(5)]

Question 5.
Determine the area of the polygon. Then, write an expression that represents the area.

Answer:

Area of Outside Rectangle
A = lw
A = (9 units) (16 units)
A = 144 units²

Area of Rectangle on Left
A = lw
A = (4 units) (8 units)
A = 32 units²

Area of Rectangle on Right
A = lw
A = (4 units) (3 units)
A = 12 units²

Total Area = 144 units² – 32 units² – 12 units²
Total Area = 100 units²
Expression: (9)(16) – (4)(8) – (4)(3)

Question 6.
Describe another method you could use to find the area of the polygon in Problem 5. Then, state how the expression for the area would be different than the expression you wrote.
Answer:
I could have broken up the large shape into many smaller rectangles. Then I would need to add all the areas of these rectangles together to determine the total area.

My expression showed subtraction because I created o rectangle that was larger than the original polygon, and then I had to subtract the extra oreos. If I break the shape into pieces, I would need to add the terms together instead of subtracting them to get the total area.

Question 7.
Write one of the letters from your name using rectangles on the coordinate plane. Then, determine the area and perimeter. (For help see Exercise 2(b). This irregular polygon looks sort of like a T.)
Answer:

Answers will vary.

Eureka Math Grade 6 Module 5 Lesson 9 Exit Ticket Answer Key

Question 1.
Determine the area and perimeter of the figure below. Note that each square unit is 1 unit in length.

Answer:

Area:

Area of Large Rectangle
A = bh
A = (11 units)(13 units)
A = 143 units²

Area of Small Square
A = s²
A = (4units)²
A = 16 units²

Area of Irregular Shape
A = 143 units² – 16 units²
A = 127 units²

Perimeter = 13 units + 4 units + 4 units + 4 units + 4 units + 3 units + 13 units + 11 units
Perimeter = 56 units

Other correct solutions might start with the following diagrams:

Eureka Math Grade 6 Module 5 Lesson 9 Addition and Subtraction Equations Answer Key

Addition and Subtraction Equations – Round 1:

Directions: Find the value of m in each equation.

Question 1.
m + 4 = 11
Answer:
m = 7

Question 2.
m + 2 = 5
Answer:
m = 3

Question 3.
m + 5 = 8
Answer:
m = 3

Question 4.
m – 7 = 10
Answer:
m = 17

Question 5.
m – 8 = 1
Answer:
m = 9

Question 6.
m – 4 = 2
Answer:
m = 6

Question 7.
m + 12 = 34
Answer:
m = 22

Question 8.
m + 25 = 45
Answer:
m = 20

Question 9.
m + 43 = 89
Answer:
m = 46

Question 10.
m – 20 = 31
Answer:
m = 51

Question 11.
m – 13 = 34
Answer:
m = 47

Question 12.
m – 45 = 68
Answer:
m = 113

Question 13.
m + 34 = 41
Answer:
m = 7

Question 14.
m + 29 = 52
Answer:
m = 23

Question 15.
m + 37 = 61
Answer:
m = 24

Question 16.
m – 43 = 63
Answer:
m = 106

Question 17.
m – 21 = 40
Answer:
m = 61

Question 18.
m – 54 = 37
Answer:
m = 91

Question 19.
4 + m = 9
Answer:
m = 5

Question 20.
6 + m = 13
Answer:
m = 7

Question 21.
2 + m = 31
Answer:
m = 29

Question 22.
15 = m + 11
Answer:
m = 4

Question 23.
24 = m + 13
Answer:
m = 11

Question 24.
32 = m + 28
Answer:
m = 4

Question 25.
4 = m – 7
Answer:
m = 11

Question 26.
3 = m – 5
Answer:
m = 8

Question 27.
12 = m – 14
Answer:
m = 26

Question 28.
23.6 = m – 7.1
Answer:
m = 30.7

Question 29.
14.2 = m – 33.8
Answer:
m = 48

Question 30.
2.5 = m – 41.8
Answer:
m = 44.3

Question 31.
64.9 = m + 23.4
Answer:
m = 41.5

Question 32.
72.2 = m + 38.7
Answer:
m = 33.5

Question 33.
1.81 = m – 15.13
Answer:
m = 16.94

Question 34.
24.68 = m – 56.82
Answer:
m = 81.5

Addition and Subtraction Equations – Round 1:

Directions: Find the value of m in each equation.

Question 1.
m + 2 = 7
Answer:
m = 5

Question 2.
m + 4 = 10
Answer:
m = 6

Question 3.
m + 8 = 15
Answer:
m = 7

Question 4.
m + 7 = 23
Answer:
m = 16

Question 5.
m + 12 = 16
Answer:
m = 4

Question 6.
m – 5 = 2
Answer:
m = 7

Question 7.
m – 3 = 8
Answer:
m = 11

Question 8.
m – 4 = 12
Answer:
m = 16

Question 9.
m – 14 = 45
Answer:
m = 59

Question 10.
m + 23 = 40
Answer:
m = 17

Question 11.
m + 13 = 31
Answer:
m = 18

Question 12.
m + 23 = 48
Answer: 25
m =

Question 13.
m + 38 = 52
Answer:
m = 14

Question 14.
m – 14 = 27
Answer:
m = 13

Question 15.
m – 23 = 35
Answer:
m = 12

Question 16.
m – 17 = 18
Answer:
m = 35

Question 17.
m – 64 = 1
Answer:
m = 65

Question 18.
6 = m + 3
Answer:
m = 3

Question 19.
12 = m + 7
Answer:
m = 5

Question 20.
24 = m + 16
Answer:
m = 8

Question 21.
13 = m + 9
Answer:
m = 4

Question 21.
32 = m – 3
Answer:
m = 35

Question 23.
22 = m – 12
Answer:
m = 34

Question 24.
34 = m – 10
Answer:
m = 44

Question 25.
48 = m + 29
Answer: 19

Question 26.
21 = m + 17
Answer:
m = 4

Question 27.
52 = m + 37
Answer:
m = 15

Question 28.
\(\frac{6}{7}\) = m + \(\frac{4}{7}\)
Answer:
m = \(\frac{2}{7}\)

Question 29.
\(\frac{2}{3}\) = m – \(\frac{5}{3}\)
Answer:
m = \(\frac{7}{3}\)

Question 30.
\(\frac{1}{4}\) = m – \(\frac{8}{3}\)
Answer:
m = \(\frac{35}{12}\)

Question 31.
\(\frac{5}{6}\) = m – \(\frac{7}{12}\)
Answer:
m = \(\frac{17}{12}\)

Question 32.
\(\frac{7}{8}\) = m – \(\frac{5}{12}\)
Answer:
m = \(\frac{31}{24}\)

Question 33.
\(\frac{7}{6}\) + m = \(\frac{16}{3}\)
Answer:
m = \(\frac{25}{6}\)

Question 34.
\(\frac{1}{3}\) + m = \(\frac{13}{15}\)
Answer:
m = \(\frac{8}{15}\)

Engage NY Eureka Math 6th Grade Module 3 Lesson 17 Answer Key

Eureka Math Grade 6 Module 3 Lesson 17 Example Answer Key

Example 1.
Locate and label the points {(3, 2), (8, 4), (- 3, 8), (- 2, – 9), (0, 6), (- 1, – 2), (10, – 2)) on the grid above.
Answer:

Example 2.
Drawing the Coordinate Plane Using an Increased Number Scale for One Axis
Draw a coordinate plane on the grid below, and then locate and label the following points:
{(- 4, 20), (- 3, 35), (1, – 35), (6, 10), (9, – 40)}.
Answer:

Example 3.
Drawing the Coordinate Plane Using a Decreased Number Scale for One Axis
Draw a coordinate plane on the grid below, and then locate and label the following points:
{(0. 1, 4), (0. 5, 7), (- 0.7, – 5), (- 0.4, 3), (0.8, 1))}.
Answer:

Example 4.
Drawing the Coordinate Plane Using a Different Number Scale for Both Axes
Determine a scale for the x-axis that will allow all x-coordinates to be shown on your grid.
Answer:
The grid is 16 units wide, and the x-coordinates range from – 14 to 14. If I let each grid line represent 2 units, then the x-axis will range from – 16 to 16.

Determine a scale for the y-axis that will allow all y-coordinates to be shown on your grid.
Answer:
The grid is 16 units high, and the y-coordinates range from – 4 to 3. 5. I could let each grid line represent one unit, but if I let each grid line represent \(\frac{1}{2}\) of a unit, the points will be easier to graph.

Draw and label the coordinate plane, and then locate and label the set of points.
{(- 14, 2), (- 4, – 0. 5), (6,- 3. 5), (14, 2. 5), (0, 3.5), (- 8, – 4)}
Answer:

Eureka Math Grade 6 Module 3 Lesson 17 Problem Set Answer Key

Question 1.
Label the coordinate plane, and then locate and label the set of points below.
{(0.3, 0.9), (- 0.1, 0.7), (- 0.5, – 0.1), (- 0.9, 0.3), (0, – 0.4)}
Answer:

Question 2.
Label the coordinate plane, and then locate and label the set of points below.
{(90, 9), (- 110, – 11), (40, 4), (- 60, – 6), (- 80, – 8)}
Answer:

Extension:

Question 3.
Describe the pattern you see in the coordinates In Problem 2 and the pattern you see in the points. Are these patterns consistent for other points too?
Answer:
The x-coordinate for each of the given points is 10 times its y-coordinate. When I graphed the points, they appear to make a straight line. I checked other ordered pairs with the same pattern, such as (- 100, – 10), (20, 2), and even (0, 0), and it appears that these points are also on that line.

Eureka Math Grade 6 Module 3 Lesson 17 Exit Ticket Answer Key

Question 1.
Determine an appropriate scale for the set of points given below. Draw and label the coordinate plane, and then locate and label the set of points.
{(10, 0. 2), (- 25, 0.8), (0, – 0.4), (20, 1), (- 5, – 0. 8)}
Answer:
The x-coordinates range from – 25 to 20. The grid is 10 units wide. If I let each grid line represent 5 units, then the x-axis will range from – 25 to 25.

The y-coordinates range from – 0.8 to 1. The grid is 10 units high. If I let each grid line represent two-tenths of a unit, then the y-axis will range from – 1 to 1.

Eureka Math Grade 6 Module 3 Lesson 17 Opening Exercise Answer Key

Question 1.
Draw all necessary components of the coordinate plane on the blank 20 × 20 grid provided below, placing the origin at the center of the grid and letting each grid line represent 1 unit.

Answer:

Engage NY Eureka Math 6th Grade Module 3 Lesson 18 Answer Key

Eureka Math Grade 6 Module 3 Lesson 18 Example Answer Key

Example 1. The Distance Between Points on an Axis
Consider the points (- 4, 0) and (5, 0).
What do the ordered pairs have in common, and what does that mean about their location in the coordinate plane?
Answer:
Both of their y-coordinates are zero, so each point lies on the x-axis, the horizontal number line.

How did we find the distance between two numbers on the number line?
Answer:
We calculated the absolute values of the numbers, which told us how far the numbers were from zero. If the numbers were located on opposite sides of zero, then we added their absolute values together. If the numbers were located on the same side of zero, then we subtracted their absolute values.

Use the same method to find the distance between (- 4, 0) and (5, 0).
Answer:
|- 4| = 4 and |5| = 5. The numbers are on opposite sides of zero, so the absolute values get combined: 4 + 5 = 9. The distance between (- 4, 0) and (5, 0) is 9 units.

Example 2.
The Length of a Line Segment on an Axis
Consider the line segment with end points (0,- 6) and (0, – 11).
What do the ordered pairs of the end points have in common, and what does that mean about the line segment’s location in the coordinate plane?
Answer:
The x-coordinates of both end points are zero, so the points lie on the y-axis, the vertical number line. If its end points lie on a vertical number line, then the line segment itself must also lie on the vertical line.

Find the length of the line segment described by finding the distance between its end points (0,- 6) and (0, – 11).
Answer:
|- 6| = 6 and |- 11| = 11. The numbers are on the same side of zero, which means the longer distance contains the shorter distance, so the absolute values need to be subtracted: 11 – 6 = 5. The distance between (0, – 6) and (0, – 11) is 5 units, so the length of the line segment with end points (0, – 6) and (0, – 11) is 5 units.

Example 3.
Length of a Horizontal or Vertical Line Segment That Does Not Lie on an Axis
Consider the line segment with end points (- 3, 3) and (- 3, – 5).
What do the end points, which are represented by the ordered pairs, have in common? What does that tell us about the location of the line segment on the coordinate plane?
Answer:
Both end points have x-coordinates of – 3, so the points lie on the vertical line that intersects the x-axis at – 3. This means that the end points of the line segment, and thus the line segment, lie on a vertical line.

Find the length of the line segment by finding the distance between its end points.
Answer:
The end points are on the same vertical line, so we only need to find the distance between 3 and – 5 on the number line.
|3| = 3 and |- 5| = 5, and the numbers are on opposite sides of zero, so the values must be added: 3 + 5 = 8. So, the distance between (- 3, 3) and (- 3, – 5) is 8 units.

Eureka Math Grade 6 Module 3 Lesson 18 Exercise Answer Key

Exercise

Find the lengths of the line segments whose end points are given below. Explain how you determined that the line segments are horizontal or vertical.
a. (- 3, 4) and (- 3, 9)
Answer:
Both end points have x-coordinates of – 3, so the points lie on a vertical line that passes through – 3 on the x-axis. |4| = 4 and |9| = 9, and the numbers are on the same side of zero. By subtraction, 9 – 4 = 5, so the length of the line segment with end points (- 3, 4) and (- 3, 9) is 5 units.

b. (2, – 2) and (- 8, – 2)
Answer:
Both end points have y-coordinates of – 2, so the points lie on a horizontal line that passes through – 2 on the y-axis. |2| = 2 and |- 8| = 8, and the numbers are on opposite sides of zero, so the absolute values must be added. By addition, 8 + 2 = 10, so the length of the line segment with end points (2, – 2) and (- 8, – 2)is 10 units.

c. (- 6, – 6) and (- 6, 1)
Answer:
Both end points hove x-coordinates of – 6, so the points lie on a vertical line. |- 6| = 6 and |1| = 1, and the numbers are on opposite sides of zero, so the absolute values must be added. By addition, 6 + 1 = 7, so the length of the line segment with end points (- 6, – 6) and (- 6, 1) is 7 units.

d. (- 9, 4) and (- 4, 4)
Answer:
Both end points have y-coordinates of 4, so the points lie on a horizontal line. |- 9| = 9 and |- 4| = 4, and the numbers are on the same side of zero. By subtraction, 9 – 4 = 5, so the length of the line segment with end points (- 9, 4) and (- 4, 4) is 5 units.

e. (0, – 11) and (0, 8)
Answer:
Both end points hove x-coordinates of 0, so the points lie on the y-axis. |- 11| = 11 and |8| = 8, and the numbers are on opposite sides of zero, so their absolute values must be added. By addition, 11 + 8 = 19, so the length of the line segment with end points (0, – 11) and (0, 8) is 19 units.

Eureka Math Grade 6 Module 3 Lesson 18 Problem Set Answer Key

Question 1.
Find the length of the line segment with end points (7, 2) and (- 4, 2), and explain how you arrived at your solution.
Answer:
11 units. Both points have the same y-coordinate, so I knew they were on the same horizontal line. I found the
distance between the x-coordinates by counting the number of units on a horizontal number line from – 4 to zero and then from zero to 7, and 4 + 7 = 11.
or
I found the distance between the x-coordinates by finding the absolute value of each coordinate. |7| = 7 and |- 4| = 4. The coordinates lie on opposite sides of zero, so I found the length by adding the absolute values together. Therefore, the length of a line segment with end points (7, 2) and (- 4, 2) is 11 units.

Question 2.
Sarah and Jamal were learning partners in math class and were working independently. They each started at the point (- 2, 5) and moved 3 units vertically in the plane. Each student arrived at a different end point. How is this possible? Explain and list the two different end points.
Answer:
It is possible because Sarah could have counted up and Jamal could have counted down or vice versa. Moving 3 units in either direction vertically would generate the following possible end points: (- 2, 8) or (- 2, 2).

Question 3.
The length of a line segment is 13 units. One end point of the line segment is (- 3,7). Find four points that could be the other end points of the line segment.
Answer:
(- 3, 20), (- 3, – 6), (- 16, 7) or (10, 7)

Eureka Math Grade 6 Module 3 Lesson 18 Exit Ticket Answer Key

Question 1.
Determine whether each given pair of end points lies on the same horizontal or vertical line. If so, find the length of the line segment that joins the pair of points. If not, explain how you know the points are not on the same horizontal or vertical line.

a. (0, – 2) and (0, 9)
Answer:
The end points both have x-coordinates of 0, so they both lie on the y-axis, which is a vertical line. They lie on opposite sides of zero, so their absolute values have to be combined to get the total distance. |- 2| = 2 and |9| = 9, so by addition, 2 + 9 = 11. The length of the line segment with end points (0, – 2) and (0, 9) is 11 units.

b. (11, 4) and (2, 11)
Answer:
The points do not lie on the same horizontal or vertical line because they do not share a common x- or y-coordinate.

c. (3, – 8) and (3, – 1)
Answer:
The end points both have x-coordinates of 3, so the points lie on a vertical line that passes through 3 on the x-axis. The y-coordinates lie on the some side of zero. The distance between the points is determined by subtracting their absolute values, |- 8| = 8 and |- 1| = 1. So, by subtraction, 8 – 1 = 7. The length of the line segment with end points (3, – 8) and (3, – 1) is 7 units.

d. (- 4, – 4) and (5, – 4)
Answer:
The end points have the same y-coordinate of – 4, so they lie on a horizontal line that passes through – 4 on the y-axis. The numbers lie on opposite sides of zero on the number line, so their absolute values must be added to obtain the total distance, |- 4| = 4 and |5| = 5. So, by addition, 4 + 5 = 9. The length of the line segment with endpoints (- 4, – 4) and (5, – 4) is 9 units.

Eureka Math Grade 6 Module 3 Lesson 18 Opening Exercise Answer Key

Four friends are touring on motorcycles. They come to an intersection of two roads; the road they are on continues straight, and the other is perpendicular to it. The sign at the intersection shows the distances to several towns. Draw a map/diagram of the roads, and use it and the information on the sign to answer the following questions:

What is the distance between Albertsville and Dewey Falls?
Answer:
Students draw and use their maps to answer. Albertsville is 8 miles to the left, and Dewey Falls is 6 miles to the right. Since the towns are in opposite directions from the intersection, their distances must be combined by addition, 8 + 6 = 14, so the distance between Albertsville and Dewey Falls is 14 miles.

What is the distance between Blossville and Cheyenne?
Answer:
Blossville and Cheyenne are both straight ahead from the intersection in the direction that they are going. Since they are on the same side of the intersection, Blossville is on the way to Cheyenne, so the distance to Cheyenne includes the 3 miles to Blossville. To find the distance from Blossville to Cheyenne, I have to subtract; 12 – 3 = 9. So, the distance from Blossville to Cheyenne is 9 miles.

On the coordinate plane, what represents the intersection of the two roads?
Answer:
The intersection is represented by the origin.

Engage NY Eureka Math 6th Grade Module 3 Lesson 16 Answer Key

Eureka Math Grade 6 Module 3 Lesson 16 Example Answer Key

Example 1.
Extending Opposite Numbers to the Coordinate Plane
Extending Opposite Numbers to the Coordinates of Points on the Coordinate Plane Locate and label your points on the coordinate plane to the right. For each given pair of points in the table below, record your observations and conjectures in the appropriate cell. Pay attention to the absolute values of the coordinates and where the points lie in reference to each axis.



Answer:

Examples 2 – 3: Navigating the Coordinate Plane

Answer:

Eureka Math Grade 6 Module 3 Lesson 16 Exercise Answer Key

Exercises

In each column, write the coordinates of the points that are related to the given point by the criteria listed in the first column of the table. Point S(5, 3) has been reflected over the x- and y-axes for you as a guide, and its images are shown on the coordinate plane. Use the coordinate grid to help you locate each point and its corresponding coordinates.


Answer:

Exercise 1.
When the coordinates of two points are (x, y) and (- x, y), what line of symmetry do the points share? Explain.
Answer:
They share the y-axis because the y-coordinates are the same and the x-coordinates are opposites, which means the points will be the same distance from the y-axis but on opposite sides.

Exercise 2.
When the coordinates of two points are (x, y) and (x, – y). what line of symmetry do the points share? Explain.
Answer:
They share the x-axis because the x-coordinates are the same and the y-coordinates are opposites, which means the points will be the same distance from the x-axis but on opposite sides.

Eureka Math Grade 6 Module 3 Lesson 16 Problem Set Answer Key

Question 1.
Locate a point In Quadrant IV of the coordinate plane. Label the point A, and write its ordered pair next to it.
Answer:
Answers will vary; Quadrant IV (5, – 3)

a. Reflect point A over an axis so that its image is in Quadrant III. Label the image B, and write its ordered pair next to it. Which axis did you reflect over? What is the only difference in the ordered pairs of points A and B?
Answer:
B(- 5, – 3); reflected over the y-axis
The ordered pairs differ only by the sign of their x-coordinates: A(5, – 3) and B(- 5, – 3).

b. Reflect point B over an axis so that its image is in Quadrant II. Label the image C, and write its ordered pair next to it. Which axis did you reflect over? What is the only difference in the ordered pairs of points B and C? How does the ordered pair of point C relate to the ordered pair of point A?
Answer:
C(- 5, 3); reflected over the x-axis
The ordered pairs differ only by the signs of their y-coordinates: B(- 5, – 3) and C(- 5, 3).
The ordered pair for point C differs from the ordered pair for point A by the signs of both coordinates:
A(5, – 3) and C(- 5, 3).

c. Reflect point C over an axis so that its image is in Quadrant I. Label the image D, and write its ordered pair next to it. Which axis did you reflect over? How does the ordered pair for point D compare to the ordered pair for point C? How does the ordered pair for point D compare to points A and B?
Answer:
D(5, 3); reflected over the y-axis again
Point D differs from point C by only the sign of its x-coordinate: D(5, 3) and C(- 5, 3).
Point D differs from point B by the signs of both coordinates: D(5, 3) and B(- 5, – 3).
Point D differs from point A by only the sign of the y-coordinate: D(5, 3) and A(5, – 3).

Question 2.
Bobbie listened to her teacher’s directions and navigated from the point (- 1,0) to (5, – 3). She knows that she has the correct answer, but she forgot part of the teacher’s directions. Her teacher’s directions included the following:
“Move 7 units down, reflect about the   ?   -axis, move up 4 units, and then move right 4 units.”
Help Bobbie determine the missing axis in the directions, and explain your answer.
Answer:
The missing line is a reflection over the y-axis. The first line would move the location to (- 1, – 7). A reflection over the y-axis would move the location to (1, – 7) in Quadrant IV, which is 4 units left and 4 units down from the end point (5, – 3).

Eureka Math Grade 6 Module 3 Lesson 16 Exit Ticket Answer Key

Question 1.
How are the ordered pairs (4, 9) and (4, – 9) similar, and how are they different? Are the two points related by a reflection over an axis in the coordinate plane? If so, indicate which axis is the line of symmetry between the points. If they are not related by a reflection over an axis in the coordinate plane, explain how you know.
Answer:
The x-coordinates are the same, but the y-coordinates are opposites, meaning they are the same distance from zero on the x-axis and the same distance but on opposite sides of zero on the y-axis. Reflecting about the x-axis interchanges these two points.

Question 2.
Given the point (- 5, 2), write the coordinates of a point that is related by a reflection over the x- or y-axis. Specify which axis is the line of symmetry.
Answer:
Using the x-axis as a line of symmetry, (-3, -2); using the y-axis as a line of symmetry, (5,2)

Eureka Math Grade 6 Module 3 Lesson 16 Opening Exercise Answer Key

Question 1.
Give an example of two opposite numbers, and describe where the numbers lie on the number line. How are opposite numbers similar, and how are they different?
Answer:
Answers may vary. 2 and – 2 are opposites because they are both 2 units from zero on a number line but in opposite directions. Opposites are similar because they have the same absolute value, but they are different because opposites are on opposite sides of zero.

Engage NY Eureka Math 6th Grade Module 3 Lesson 15 Answer Key

Eureka Math Grade 6 Module 3 Lesson 15 Example Answer Key

Example 1. Extending the Axes Beyond Zero
The point below represents zero on the number line. Draw a number line to the right starting at zero. Then, follow directions as provided by the teacher.

Answer:
→ Use a straightedge to extend the x-axis to the left of zero to represent the real number line horizontally, and complete the number line using the same scale as on the right side of zero.
→ Describe the y-axis. What types of numbers should it include?
The y-axis is a vertical number line that includes numbers on both sides of zero (above and below), and so it includes both positive and negative numbers.
→ Use a straightedge to draw a vertical number line above zero.

Provide students with time to draw.
→ Extend the y-axis below zero to represent the real number line vertically, and complete the number line using
the same scale as above zero.

Example 2: Components of the Coordinate Plane
All points on the coordinate plane are described with reference to the origin. What is the origin, and what are its coordinates?
Answer:
The origin is the point where the x- and y-axes intersect. The coordinates of the origin are (0, 0).

To describe locations of points in the coordinate plane, we use _________________________ of numbers. Order is important, so on the coordinate plane, we use the form ( ). The first coordinate represents the point’s location from zero on the ________-axis, and the second coordinate represents the point’s location from zero on the ________-axis.
Answer:
To describe locations of points in the coordinate plane, we use   ordered   pairs of numbers. Order is important, so on the coordinate plane, we use the form (   x, y   ). The first coordinate represents the point’s location from zero on the    x   -axis, and the second coordinate represents the point’s location from zero on the   y   -axis.

Eureka Math Grade 6 Module 3 Lesson 15 Exercise Answer Key

Exercise 1.
Use the coordinate plane below to answer parts (a) – (c).
a. Graph at least five points on the x-axis, and label their coordinates.
Answer:
Points will vary.

b. What do the coordinates of your points have in common?
Answer:
Each point has a y-coordinate of 0.

c. What must be true about any point that lies on the x-axis? Explain.
Answer:
If a point lies on the x-axis, its y-coordinate must be 0 because the point is located 0 units above or below the x-axis. The x-axis intersects the y-axis at 0.

Answer:

Exercise 2.
Use the coordinate plane to answer parts (a) – (c).
a. Graph at least five points on the y-axis, and label their coordinates.
Answer:
Points will wary.

b. What do the coordinates of your points have in common?
Answer:
Each point has an x-coordinate of 0.

c. What must be true about any point that lies on the y-axis? Explain.
Answer:
If a point lies on the y-axis, its x-coordinate must be 0 because the point is located 0 units left or right of the y-axis. The y-axis intersects 0 on the x-axis.

Exercise 3.
If the origin is the only point with 0 for both coordinates, what must be true about the origin?
Answer:
The origin is the only point that is on both the x-axis and the y-axis.

Exercise 4.
Locate and label each point described by the ordered pairs below. Indicate which of the quadrants the points lie in.
a. (7, 2)
Answer:
Quadrant I

b. (3, – 4)
Answer:
Quadrant IV

c. (1, – 5)
Answer:
Quadrant IV

d. (- 3, 8)
Answer:
Quadrant II

e. (- 2, – 1)
Answer:
Quadrant III

Answer:

Exercise 5.
Write the coordinates of at least one other point in each of the four quadrants.
a. Quadrant I
Answer:
Answers will vary, but both numbers must be positive.

b. Quadrant II
Answer:
Answers will vary, but the x-coordinate must be negative, and the y-coordinate must be positive.

c. Quadrant III
Answer:
Answers will vary, but both numbers must be negative.

d. Quadrant IV
Answer:
Answers will vary, but the x-coordinate must be positive, and the y-coordinate must be negative.

Exercise 6.
Do you see any similarities in the points within each quadrant? Explain your reasoning.
Answer:
The ordered pairs describing the points in Quadrant I contain both positive values. The ordered pairs describing the points in Quadrant III contain both negative values. The first coordinates of the ordered pairs describing the points in Quadrant II are negative values, but their second coordinates are positive values. The first coordinates of the ordered pairs describing the points in Quadrant IV are positive values, but their second coordinates are negative values.

Eureka Math Grade 6 Module 3 Lesson 15 Problem Set Answer Key

Question 1.
Name the quadrant in which each of the points lies. If the point does not lie in a quadrant, specify which axis the point lies on.
a. (- 2, 5)
Quadrant II

b. (8, – 4)
Quadrant IV

c. (- 1, – 8)
Quadrant Ill

d. (9. 2, 7)
Quadrant I

e. (0, – 4)
None; the point is not in a quadrant because it lies on the y-axis.

Question 2.
Jackie claims that points with the same x- and y-coordinates must lie in Quadrant I or Quadrant Ill. Do you agree or disagree? Explain your answer.
Answer:
Disagree; most points with the same x- and y-coordinates lie in Quadrant I or Quadrant III, but the origin (o, 0) is on the x- and y-axes, not in any quadrant.

Question 3.
Locate and label each set of points on the coordinate plane. Describe similarities of the ordered pairs in each set, and describe the points on the plane.
a. {(- 2, 5), (- 2, 2), (- 2, 7), (- 2, – 3), (- 2, – 0. 8))
Answer:
The ordered pairs all have x-coordinates of – 2, and the points lie along a vertical line above and below – 2 on the x-axis.

b. {(- 9, 9), (- 4, 4), (- 2, 2), (1, – 1), (3, – 3), (0, 0)}
Answer:
The ordered pairs each have opposite values for their x- and y-coordinates. The points in the plane line up diagonally through Quadrant II, the origin, and Quadrant IV.

c. {(- 7, – 8), (5, – 8), (0, – 8), (10, – 8), (- 3, – 8)}
Answer:
The ordered pairs all have y-coordinates of – 8, and the points lie along a horizontal line to the left and right of – 8 on the y-axis.

Answer:

Question 4.
Locate and label at least five points on the coordinate plane that have an x-coordinate of 6.
a. What is true of the y-coordinates below the x-axis?
Answer:
The y-coordinates are all negative values.

b. What is true of the y-coordinates above the x-axis?
Answer:
The y-coordinates are all positive values.

c. What must be true of the y-coordinates on the x-axis?
Answer:
The y-coordinates on the x-axis must be 0.

Answer:

Eureka Math Grade 6 Module 3 Lesson 15 Exit Ticket Answer Key

Question 1.
Label the second quadrant on the coordinate plane, and then answer the following questions:
a. Write the coordinates of one point that lies in the second quadrant of the coordinate plane.
Answer:
Answers will vary.

b. What must be true about the coordinates of any point that lies in the second quadrant?
Answer:
The x-coordinate must be a negative value, and the y-coordinate must be a positive value.

Answer:

Question 2.
Label the third quadrant on the coordinate plane, and then answer the following questions:
a. Write the coordinates of one point that lies in the third quadrant of the coordinate plane.
Answer:
Answers will vary.

b. What must be true about the coordinates of any point that lies in the third quadrant?
Answer:
The x- and y-coordinates of any point in the third quadrant must both be negative values.

Question 3.
An ordered pair has coordinates that have the same sign. In which quadrant(s) could the point lie? Explain.
Answer:
The point would have to be located either in Quadrant I where both coordinates are positive values or in Quadrant III where both coordinates are negative values.

Question 4.
Another ordered pair has coordinates that are opposites. In which quadrant(s) could the point lie? Explain.
Answer:
The point would have to be located in either Quadrant II or Quadrant IV because those are the two quadrants where the coordinates have opposite signs. The point could also be located at the origin (0, 0) since zero is its own opposite.

Engage NY Eureka Math 6th Grade Module 3 Lesson 14 Answer Key

Eureka Math Grade 6 Module 3 Lesson 14 Example Answer Key

Example 1: The Order in Ordered Pairs
The first number of an ordered pair is called the ___________ .
Answer:
first coordinate.

The second number of an ordered pair is called the ___________ .
Answer:
second coordinate.

Example 2.
Using Ordered Pairs to Name Locations
Describe how the ordered pair is being used in your scenario. Indicate what defines the first coordinate and what defines the second coordinate in your scenario.
Answer:
Ordered pairs are like a set of directions; they indicate where to go in one direction and then indicate where to go in the second direction.
→ Scenario 1: The seats in a college football stadium are arranged into 210 sections, with 144 seats in each
section. Your ticket to the game indicates the location of your seat using the ordered pair of numbers
(123,37). Describe the meaning of each number in the ordered pair and how you would use them to find your seat.

→ Scenario 2: Airline pilots use measurements of longitude and latitude to determine their location and to find airports around the world. Longitude is measured as 0 – 180° east or 0 – 180° west of a line stretching from the North Pole to the South Pole through Greenwich, England, called the prime meridian. Latitude is measured as 0 – 90° north or 0 – 90° south of the earth’s equator. A pilot has the ordered pair (90° west, 30° north). What does each number in the ordered pair describe? How would the pilot locate the airport on a map? Would there be any confusion if a pilot were given the ordered pair (90°, 30°)? Explain.

→ Scenario 3: Each room in a school building is named by an ordered pair of numbers that indicates the number of the floor on which the room lies, followed by the sequential number of the room on the floor from the main staircase. A new student at the school is trying to get to science class in room 4 – 13. Describe to the student what each number means and how she should use the number to find her classroom. Suppose there are classrooms below the main floor. How might these rooms be described?

Eureka Math Grade 6 Module 3 Lesson 14 Exercise Answer Key

The first coordinates of the ordered pairs represent the numbers on the line labeled X, and the second coordinates represent the numbers on the line labeled y.

Exercise 1.
Name the letter from the grid below that corresponds with each ordered pair of numbers below.

a. (1, 4)
Answer:
Point F

b. (0, 5)
Answer:
Point A

c. (4, 1)
Answer:
Point B

d. (8.5, 8)
Answer:
Point L

e. (5, – 2)
Answer:
Point G

f. (5, 4.2)
Answer:
Point H

g. (2,- 1)
Answer:
Point C

h. (0, 9)
Answer:
Point E

Exercise 2.
List the ordered pair of numbers that corresponds with each letter from the grid below.

a. Point M
Answer:
(5, 7)

b. Point S
Answer:
(- 2, 3)

c. Point N
Answer:
(6, 0)

d. Point T
Answer:
(- 3, 2)

e. Point P
Answer:
(0, 6)

f. Point U
Answer:
(7, 5)

g. Point Q
Answer:
(2, 3)

h. Point V
Answer:
(- 1, 6)

I. Point R
Answer:
(0, 3)

Eureka Math Grade 6 Module 3 Lesson 14 Problem Set Answer Key

Question 1.
Use the set of ordered pairs below to answer each question.
{(4, 20), (8, 4), (2, 3), (15, 3), (6, 15), (6, 30), (1, 5), (6, 18), (0, 3)}

a. Write the ordered pair(s) whose first and second coordinate have a greatest common factor of 3.
Answer:
(15, 3) and (6, 15)

b. Write the ordered pair(s) whose first coordinate is a factor of its second coordinate.
Answer:
(4, 20), (6, 30), (1, 5), and (6, 18)

c. Write the ordered pair(s) whose second coordinate is a prime number.
Answer:
(2, 3), (15, 3), (1, 5), and (0, 3)

Question 2.
Write ordered pairs that represent the location of points A, B, C, and D, where the first coordinate represents the horizontal direction, and the second coordinate represents the vertical direction.

Answer:
A (4, 1); B (1, – 3); C (6, 0); D (1, 4)

Extension:

Question 3.
Write ordered pairs of integers that satisfy the criteria in each part below. Remember that the origin is the point whose coordinates are (0, 0). When possible, give ordered pairs such that (i) both coordinates are positive, (ii) both coordinates are negative, and (iii) the coordinates have opposite signs in either order.

a. These points’ vertical distance from the origin Is twice their horizontal distance.
Answer:
Answers will vary; examples are (5, 10), (- 2, 4), (- 5, – 10), (2, – 4).

b. These points’ horizontal distance from the origin Is two units more than the vertical distance.
Answer:
Answers will vary; examples are (3, 1), (- 3, 1), (- 3,- 1), (3, – 1).

c. These points’ horizontal and vertical distances from the origin are equal, but only one coordinate is positive.
Answer:
Answers will vary; examples are (3, – 3), (- 8,8).

Eureka Math Grade 6 Module 3 Lesson 14 Exit Ticket Answer Key

Question 1.
On the map below, the fire department and the hospital have one matching coordinate. Determine the proper order of the ordered pairs In the map, and write the correct ordered pairs for the locations of the fire department and hospital. Indicate which of their coordinates are the same.
Answer:
The order of the numbers is (x, y); fire department: (6, 7) and hospital: (10, 7); they have the same second coordinate.

Answer:

Question 2.
On the map above, locate and label the location of each description below:
a. The local bank has the same first coordinate as the fire department, but its second coordinate is half of the fire department’s second coordinate. What ordered pair describes the location of the bank? Locate and label the bank on the map using point B.
Answer:
(6, 3. 5); see the map image for the correct location of point B.

b. The Village Police Department has the same second coordinate as the bank, but its first coordinate is – 2. What ordered pair describes the location of the Village Police Department? Locate and label the Village Police Department on the map using point P.
Answer:
(- 2, 3.5); see the map image for the correct location of point P.

Engage NY Eureka Math 6th Grade Module 3 Lesson 13 Answer Key

Eureka Math Grade 6 Module 3 Lesson 13 Example Answer Key

Example 1. Ordering Numbers In the Real World
A $25 credit and a $25 charge appear similar, yet they are very different.
Describe what is similar about the two transactions.
Answer:
The transactions look similar because they are described using the same number. Both transactions have the same magnitude (or absolute value) and, therefore, result in a change of $25 to an account balance.

How do the two transactions differ?
Answer:
The credit would cause an increase to an account balance and, therefore, should be represented by 25, while the charge would instead decrease an account balance and should be represented by – 25. The two transactions represent changes that are opposites.

Example 2: Using Absolute Value to Solve Real-World Problems
The captain of a fishing vessel is standing on the deck at 23 feet above sea level. He holds a rope tied to his fishing net that is below him underwater at a depth of 38 feet.

Draw a diagram using a number line, and then use absolute value to compare the lengths of rope in and out of the water.
Answer:

The captain is above the water, and the fishing net is below the water’s surface. Using the water level as reference point zero, I can draw the diagram using a vertical number line. The captain is located at 23, and the fishing net is located at – 38.

|23| = 23 and |- 38| = 38,so there is more rope underwater than above.

38 – 23 = 15
The length of rope below the water’s surface is 15 feet longer than the rope above water.

Example 3: Making Sense of Absolute Value and Statements of Inequality
A recent television commercial asked viewers, “Do you have over $10,000 in credit card debt?”

What types of numbers are associated with the word debt, and why? Write a number that represents the value from the television commercial.
Answer:
Negative numbers; debt describes money that is owed; – 10,000

Give one example of “over $10,000 in credit card debt.” Then, write a rational number that represents your example.
Answer:
Answers will vary, but the number should have a value of less than – 10,000. Credit card debt of $11,000; – 11,000

How do the debts compare, and how do the rational numbers that describe them compare? Explain.
Answer:
The example $11, 000 is greater than $10, 000 from the commercial; however, the rational numbers that represent these debt values have the opposite order because they are negative numbers. – 11,000 < – 10, 000. The absolute values of negative numbers have the opposite order of the negative values themselves.

Eureka Math Grade 6 Module 3 Lesson 13 Exercise Answer Key

Exercise 1.
Scientists are studying temperatures and weather patterns in the Northern Hemisphere. They recorded
temperatures (in degrees Celsius) in the table below as reported in emails from various participants. Represent each reported temperature using a rational number. Order the rational numbers from least to greatest. Explain why the rational numbers that you chose appropriately represent the given temperatures.

Answer:

– 13 < – 8 < – 6 < – 5 < – 4 < 0 < 2 < 12
The words “below zero” refer to negative numbers because they are located below zero on a vertical number line.

Exercise 2.
Jami’s bank account statement shows the transactions below. Represent each transaction as a rational number describing how it changes Jami’s account balance. Then, order the rational numbers from greatest to least. Explain why the rational numbers that you chose appropriately reflect the given transactions.

Answer:

5.5 > 4.08 > – 1.5 > – 3 > – 3.95 > – 12.2 > – 20
The words “debit,” “charge,” and “withdrawal” all describe transactions in which money is taken out of Jami’s account, decreasing its balance. These transactions are represented by negative numbers. The words “credit” and “deposit” describe transactions that will put money into Jami’s account, increasing its balance. These transactions are represented by positive numbers.

Exercise 3.
During the summer, Madison monitors the water level in her parents’ swimming pool to make sure it is not too far above or below normal. The table below shows the numbers she recorded In July and August to represent how the water levels compare to normal. Order the rational numbers from least to greatest. Explain why the rational numbers that you chose appropriately reflect the given water levels.

Answer:

\(-1 \frac{1}{4}<-\frac{3}{4}<-\frac{1}{2}<-\frac{3}{8}<\frac{1}{8}<\frac{1}{4}<\frac{1}{2}\)
The measurements are taken in reference to normal level, which is considered to be 0. The words “above normal” refer to the positive numbers located above zero on a vertical number line, and the words “below normal” refer to the negative numbers located below zero on a vertical number line.

Exercise 4.
Changes in the weather can be predicted by changes in the barometric pressure. Over several weeks, Stephanie recorded changes in barometric pressure seen on her barometer to compare to local weather forecasts. Her observations are recorded In the table below. Use rational numbers to record the indicated changes In the pressure in the second row of the table. Order the rational numbers from least to greatest. Explain why the rational numbers that you chose appropriately represent the given pressure changes.

Answer:

Eureka Math Grade 6 Module 3 Lesson 13 Problem Set Answer Key

Question 1.
Negative air pressure created by an air pump makes a vacuum cleaner able to collect air and dirt into a bag or other container. Below are several readings from a pressure gauge. Write rational numbers to represent each of the readings, and then order the rational numbers from least to greatest.

Answer:

– 13 < – 7.8 < – 6.3 < – 1.9 < 2 < 7.8 < 25

Question 2.
The fuel gauge in Nic’s car says that he has 26 miles to go until his tank is empty. He passed a fuel station 19 miles ago, and a sign says there is a town only 8 miles ahead. If he takes a chance and drives ahead to the town and there isn’t a fuel station there, does he have enough fuel to go back to the last station? Include a diagram along a number line, and use absolute value to find your answer.
Answer:
No, he does not have enough fuel to drive to the town and then back to the fuel station. He needs 8 miles’ worth of fuel to get to the town, which lowers his limit to 18 miles. The total distance between the fuel station and the town is 27 miles; |8| + |- 19| = 8 + 19 = 27. Nic would be9miles short on fuel. It would be safer to go back to the fuel station without going to the town first.

Eureka Math Grade 6 Module 3 Lesson 13 Exit Ticket Answer Key

Question 1.
Loni and Daryl call each other from different sides of Watertown. Their locations are shown on the number line below using miles. Use absolute value to explain who is a farther distance (in miles) from Watertown. How much closer is one than the other?

Answer:

Loni’s location is – 6, and |- 6| = 6 because – 6 is 6 units from 0 on the number line. Daryl’s location is 10, and |10| = 10 because 10 is 10 units from 0 on the number line. We know that 10 > 6, so Daryl is farther from Watertown than Loni.
10 – 6 = 4; Loni is 4 miles closer to Watertown than Daryl.

Question 2.
Claude recently read that no one has ever scuba dived more than 330 meters below sea level. Describe what this means in terms of elevation using sea level as a reference point.
Answer:
330 meters below sea level is an elevation of – 330 feet. “More than 330 meters below sea level” means that no diver has ever had more than 330 meters between himself and sea level when he was below the water’s surface while scuba diving.

Eureka Math Grade 6 Module 3 Lesson 13 Opening Exercise Answer Key

Question 1.
A radio disc jockey reports that the temperature outside his studio has changed 10 degrees since he came on the air this morning. Discuss with your group what listeners can conclude from this report.
Answer:
The report is not specific enough to be conclusive because 10 degrees of change could mean an increase or a decrease in temperature. A listener might assume the report says an increase in temperature; however, the word “changed” is not specific enough to conclude a positive or negative change.

Engage NY Eureka Math 6th Grade Module 3 Lesson 12 Answer Key

Eureka Math Grade 6 Module 3 Lesson 12 Example Answer Key

Example 1: Comparing Order of Integers to the Order of Their Absolute Values
Write an Inequality statement relating the ordered integers from the Opening Exercise. Below each integer, write its absolute value.
Answer:

Circle the absolute values that are in increasing numerical order and their corresponding integers. Describe the circled values.
Answer:

The circled integers are all positive values except zero. The positive integers and their absolute values have the same order.

Rewrite the integers that are not circled in the space below. How do these integers differ from the ones you circled?
Answer:
– 12, – 9, – 5, – 2, – 1
They are all negative integers.

Rewrite the negative integers in ascending order and their absolute values in ascending order below them.
Answer:

Describe how the order of the absolute values compares to the order of the negative integers.
Answer:
The orders of the negative integers and their corresponding absolute values are opposite.

Example 2: The Order of Negative Integers and Their Absolute Values
Draw arrows starting at the dashed line (zero) to represent each of the integers shown on the number line below. The arrows that correspond with 1 and 2 have been modeled for you.

Answer:

As you approach zero from the left on the number line, the integers ___________, but the absolute values of those integers ___________. This means that the order of negative integers is ___________ the order of their absolute values.
Answer:
As you approach zero from the left on the number line, the integers   increase   , but the absolute values of those integers    decrease  . This means that the order of negative integers is   opposite   the order of their absolute values.

Eureka Math Grade 6 Module 3 Lesson 12 Exercise Answer Key

Complete the steps below to order these numbers:

{2.1, – 4\(\frac{1}{2}\), – 6. 0.25, – 1.5, 0, 3.9, – 6.3, – 4, 2\(\frac{3}{4}\), 3.99, – 9\(\frac{1}{4}\)}

a. Separate the set of numbers into positive rational numbers, negative rational numbers, and zero in the top cells below (order does not matter).
Answer:

b. Write the absolute values of the rational numbers (order does not matter) in the bottom cells below.

Answer:

c. Order each subset of absolute values from least to greatest.

Answer:

d. Order each subset of rational numbers from least to greatest.

Answer:

e. Order the whole given set of rational numbers from least to greatest.
Answer:
– 9\(\frac{1}{4,}\), – 6.3, – 6, – 4\(\frac{1}{2}\), – 4, – 1.5, 0, 0.25, 2.1, 2\(\frac{3}{4}\), 3.9, 3.99

Exercise 2.
a. Find a set of four integers such that their order and the order of their absolute values are the same.
Answer:
Answers will vary. An example follows: 4, 6, 8, 10

b. Find a set of four integers such that their order and the order of their absolute values are opposite.
Answer:
Answers will vary. An example follows: – 10, – 8, – 6, – 4

c. Find a set of four non-integer rational numbers such that their order and the order of their absolute values are the same.
Answer:
Answers will vary. An example follows: 2\(\frac{1}{2}\), 3\(\frac{1}{2}\), 4\(\frac{1}{2}\), 5\(\frac{1}{2}\)

d. Find a set of four non-integer rational numbers such that their order and the order of their absolute values are opposite.
Answer:
Answers will vary. An example follows: – 5\(\frac{1}{2}\), – 4\(\frac{1}{2}\), – 3\(\frac{1}{2}\), – 2\(\frac{1}{2}\)

e. Order all of your numbers from parts (a) – (d) in the space below. This means you should be ordering 16 numbers from least to greatest.
Answer:
Answers will vary. An example follows:
– 10, – 8, – 6, – 5\(\frac{1}{2}\), – 4\(\frac{1}{2}\), – 4, – 3\(\frac{1}{2}\), – 2\(\frac{1}{2}\), 2\(\frac{1}{2}\), 3\(\frac{1}{2}\), 4, 4\(\frac{1}{2}\), 5\(\frac{1}{2}\), 6, 8, 10

Eureka Math Grade 6 Module 3 Lesson 12 Problem Set Answer Key

Question 1.
Micah and Joel each have a set of five rational numbers. Although their sets are not the same, their sets of numbers have absolute values that are the same. Show an example of what Micah and Joel could have for numbers. Give the sets in order and the absolute values in order.
Answer:
Examples may vary, If Micah had 1, 2, 3, 4, 5, then his order of absolute values would be the same: 1, 2, 3, 4, 5. If Joel had the numbers – 5, – 4, – 3, -2, -1, then his order of absolute values would also be 1, 2, 3, 4, 5.

Enrichment Extension: Show an example where Micah and Joel both have positive and negative numbers.
Answer:
If Micah had the numbers: – 5, – 3, – 1, 2, 4, his order of absolute values would be 1, 2, 3, 4, 5. If Joel hod the numbers – 4, – 2, 1, 3, 5, then the order of his absolute values would also be 1, 2, 3, 4, 5.

Question 2.
For each pair of rational numbers below, place each number In the Venn diagram based on how it compares to the other.
a. – 4, – 8
b. 4,8
C. 7,- 3
d. – 9,2
e. 6,1
f. – 5,5
g. – 2,0
Answer:

Eureka Math Grade 6 Module 3 Lesson 12 Exit Ticket Answer Key

Question 1.
Bethany writes a set of rational numbers in increasing order. Her teacher asks her to write the absolute values of these numbers in Increasing order. When her teacher checks Bethany’s work, she Is pleased to see that Bethany has not changed the order of her numbers. Why is this?
Answer:
All of Bethany’s rational numbers are positive or 0. The positive rational numbers have the same order as their absolute values. If any of Bethany’s rational numbers are negative, then the order would be different.

Question 2.
Mason was ordering the following rational numbers In math class: – 3. 3, – 15, – 8\(\frac{8}{9}\).
a. Order the numbers from least to greatest.
Answer:
– 15, – 8\(\frac{8}{9}\), – 3.3

b. List the order of their absolute values from least to greatest.
Answer:
3.3, 8\(\frac{8}{9}\), 15

c. Explain why the orderings in parts (a) and (b) are different.
Answer:
Since these are all negative numbers, when I ordered them from least to greatest, the one farthest away from zero (farthest to the left on the number line) came first. This number is – 15. Absolute value is the numbers’ distance from zero, and so the number farthest away from zero has the greatest absolute value, so 15 will be greatest in the list of absolute values, and so on.

Eureka Math Grade 6 Module 3 Lesson 12 Opening Exercise Answer Key

Record your integer values in order from least to greatest in the space below.
Answer:
Sample answer: – 12, – 9, – 5, – 2, – 1, 0, 2, 5, 7, 8