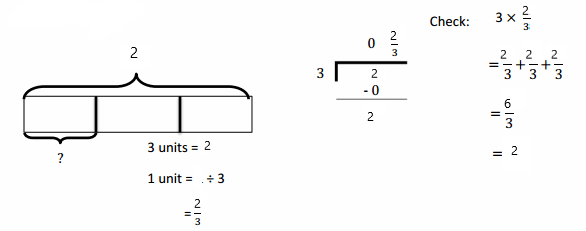Tag: Eureka Math Grade 5 Answer Key

Engage NY Eureka Math 5th Grade Module 4 Lesson 27 Answer Key

Eureka Math Grade 5 Module 4 Lesson 27 Problem Set Answer Key

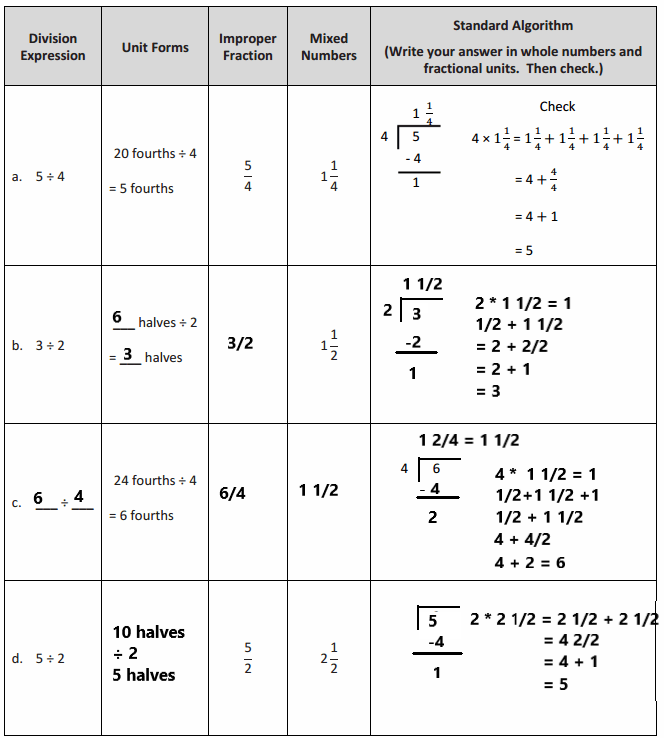
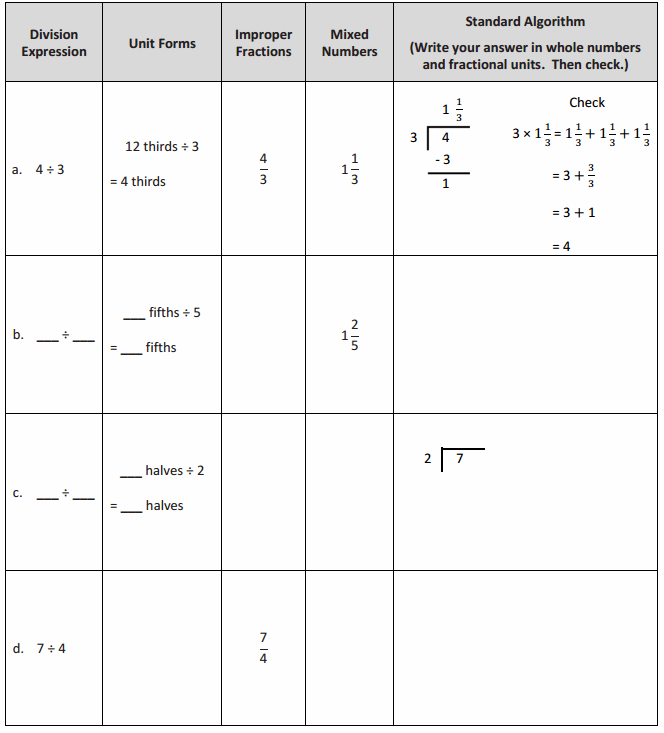
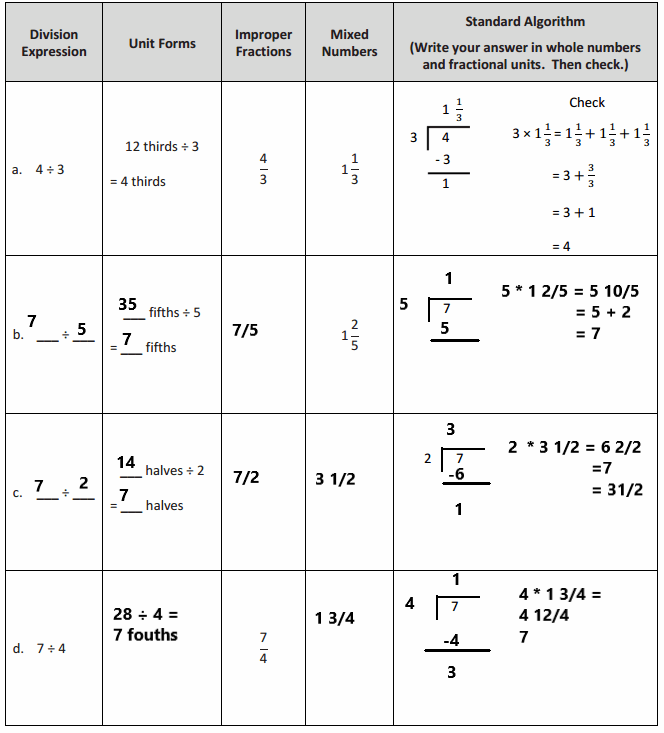
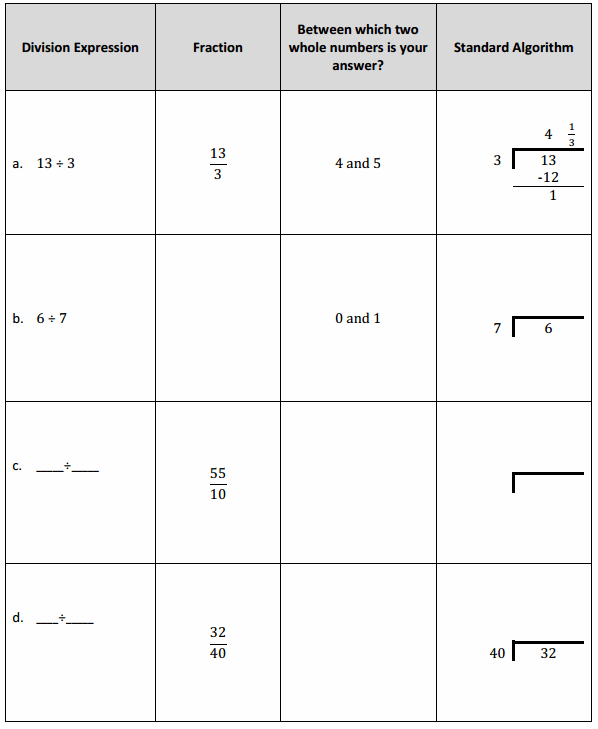
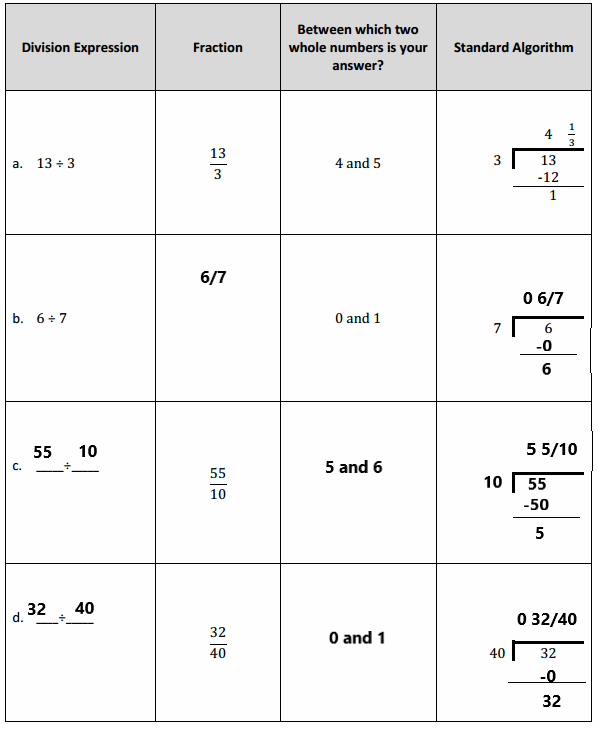
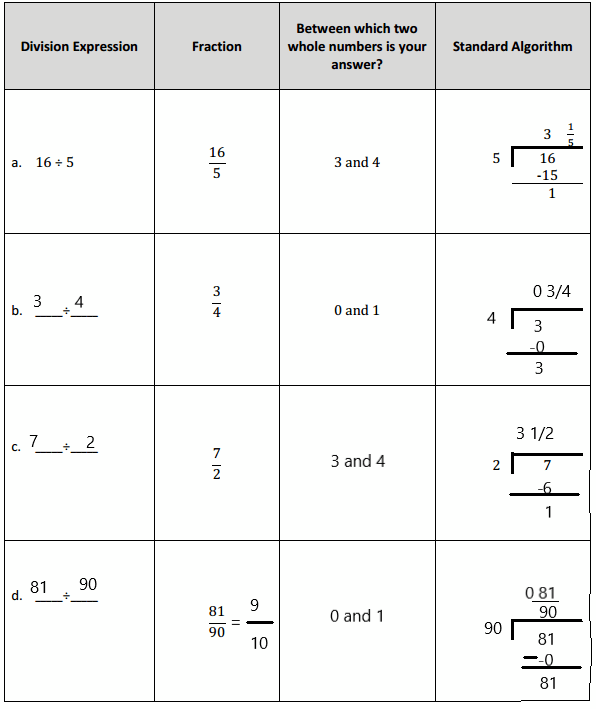
Question 1.
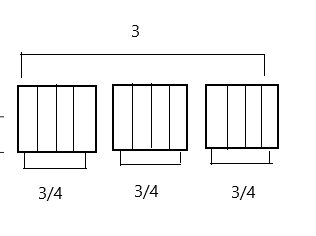
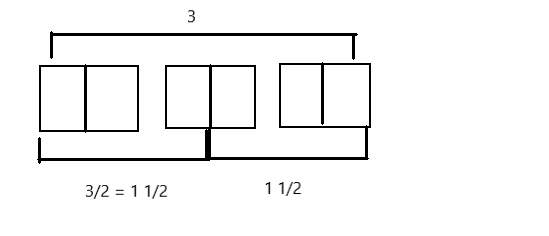
Mrs. Silverstein bought 3 mini cakes for a birthday party. She cuts each cake into quarters and plans to serve each guest 1 quarter of a cake. How many guests can she serve with all her cakes? Draw a picture to support your response.

Answer:
Mrs. Silverstein can serve 12 guests a quarter of the cake.

Explanation:
Here, Mrs. Silverstein bought 3 mini cakes for a birthday party, and she cuts each cake into quarters and plans to serve each guest 1 quarter of a cake, so the number of guests can she serve with all her cakes is 3 ÷ \(\frac{1}{4}\) which is 12, here 4 fourths are 1 whole and 12 fourths are 3 wholes. So Mrs. Silverstein can serve 12 guests a quarter of the cake.

Question 2.
Mr. Pham has \(\frac{1}{4}\) pan of lasagna left in the refrigerator. He wants to cut the lasagna into equal slices so he can have it for dinner for 3 nights. How much lasagna will he eat each night? Draw a picture to support your response.

Answer:
Mr. Pham will eat \(\frac{1}{12}\) of the lasagna each night.

Explanation:
Here, Mr. Pham has \(\frac{1}{4}\) pan of lasagna left in the refrigerator and he wants to cut the lasagna into equal slices so he can have it for dinner for 3 nights, so Mr. Pham will eat \(\frac{1}{4}\) ÷ 3, here 1 fourth ÷ 3 which is 3 twelfths ÷ 3 which is 1 twelfths. So, Mr. Pham will eat \(\frac{1}{12}\) of the lasagna each night.

Question 3.
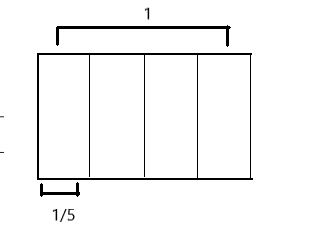
The perimeter of a square is \(\frac{1}{5}\) of a meter.
a. Find the length of each side in meters. Draw a picture to support your response.

Answer:
The length of each side is \(\frac{1}{20}\) meter.

Explanation:
Given the perimeter is \(\frac{1}{5}\) meter and the length of each side is, as the square has four sides and all sides are equal, so \(\frac{1}{5}\) ÷ 4 which is the side length
\(\frac{1}{5}\) ÷ 4 = 1 fifth ÷ 4
= 4 twentieths ÷ 4
= 1 twentieth.
So the length of each side is \(\frac{1}{20}\) meter.

b. How long is each side in centimeters?

Answer:
The length of each side in centimeters is 5 cm.

Explanation:
As the length of each side is \(\frac{1}{20}\) meter, so the length of each side in centimeters is
\(\frac{1}{20}\) meter = \(\frac{1}{20}\) × 100
on solving, we will get the result as 5 cm.
So the length of each side in centimeters is 5 cm.

Question 4.
A pallet holding 5 identical crates weighs \(\frac{1}{4}\) of a ton.
a. How many tons does each crate weigh? Draw a picture to support your response.

Answer:
Each carte weighs is \(\frac{1}{20}\) ton.

Explanation:
Given that a pallet holding 5 identical crates weighs \(\frac{1}{4}\) of a ton, so the number of tons does each crate weigh is \(\frac{1}{4}\) ÷ 5 = 1 fourth ÷ 4
= 5 twentieths ÷ 5
= 1 twentieth.
So each carte weighs is \(\frac{1}{20}\) ton.

b. How many pounds does each crate weigh?

Answer:
The number of pounds does each carte weighs is 100 pounds.

Explanation:
As we know that each carte weighs \(\frac{1}{20}\) ton, so the number of pounds is
\(\frac{1}{20}\) meter = \(\frac{1}{20}\) × 2000 pounds
on solving, we will get the result as 100 pounds.
So the number of pounds does each carte weighs is 100 pounds.

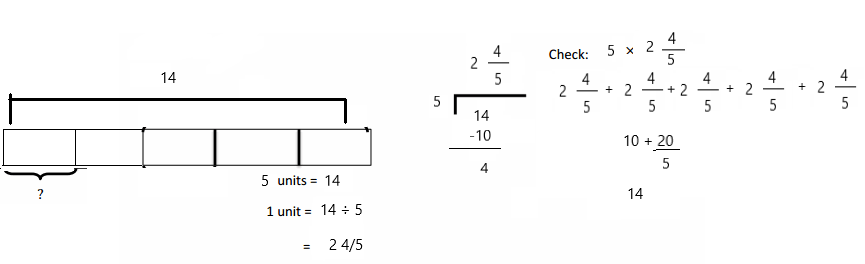
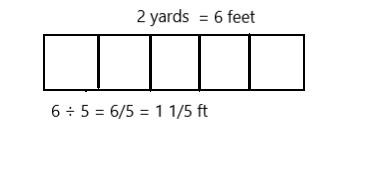
Question 5.
Faye has 5 pieces of ribbon, each 1 yard long. She cuts each ribbon into sixths.
a. How many sixths will she have after cutting all the ribbons?

Answer:
Faye will have 30 sixths after cutting all the ribbons.

Explanation:
Given that Faye has 5 pieces of ribbon and each 1 yard long and then she cuts each ribbon into sixths. So the number of sixths will she have after cutting all the ribbons is
1 ÷ \(\frac{1}{6}\) which is 6
6 sixth in 1-yard and 30 sixths in 5 yards.
So Faye will have 30 sixths after cutting all the ribbons.

b. How long will each of the sixths be in inches?

Answer:
The length of each of the sixths be in inches is 6 in.

Explanation:
As each sixth is \(\frac{1}{6}\) of a yard, so the length of each of the sixths be in inches is
\(\frac{1}{6}\) × 1 yard
= \(\frac{1}{6}\) × 36
on solving, we will get the result as 6 in.
so the length of each of the sixths be in inches is 6 in.

Question 6.
A glass pitcher is filled with water. \(\frac{1}{8}\) of the water is poured equally into 2 glasses.
a. What fraction of the water is in each glass?

Answer:
The fraction of the water is in each glass is \(\frac{1}{16}\).

Explanation:
Given that a glass pitcher is filled with water and \(\frac{1}{8}\) of the water is poured equally into 2 glasses. So the fraction of the water is in each glass is \(\frac{1}{8}\) × \(\frac{1}{2}\) which is \(\frac{1}{16}\).

b. If each glass has 3 fluid ounces of water in it, how many fluid ounces of water were in the full pitcher?

Answer:
There are 48 fluid ounces in the full pitcher.

Explanation:
Given that each glass has 3 fluid ounces of water in it and the fluid ounces of water were in the full pitcher was
3 × 2 = 6,
as 1 unit = 6, so 8 units is 8 × 6 = 48.
So there are 48 fluid ounces in the full pitcher.

c. If \(\frac{1}{4}\) of the remaining water is poured out of the pitcher to water a plant, how many cups of water are left in the pitcher?

Answer:
The number of cups of water is left in the pitcher is 3 \(\frac{15}{16}\) cups

Explanation:
Given that \(\frac{1}{4}\) of the remaining water is poured out of the pitcher to water a plant, so the number of cups of water is left in the pitcher is
\(\frac{3}{4}\) of 42
\(\frac{3}{4}\) × 42, on solving we will get the result as \(\frac{63}{2}\) which is 3 \(\frac{15}{16}\) cups of water left in the pitcher.

Eureka Math Grade 5 Module 4 Lesson 27 Exit Ticket Answer Key

Question 1.
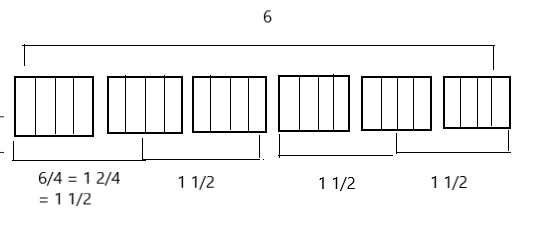
Kevin divides 3 pieces of paper into fourths. How many fourths does he have? Draw a picture to support your response.

Answer:
The number of fourths does he have is 12.

Explanation:
As Kevin divides 3 pieces of paper into fourths and the number of fourths does he have is
Number of fourths = Number pieces of paper ÷ one fourth
= 3 ÷ \(\frac{1}{4}\)
= 3 × 4
= 12.
So, the number of fourths does he have is 12.

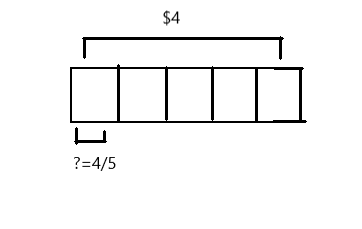
Question 2.
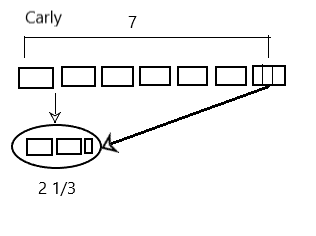
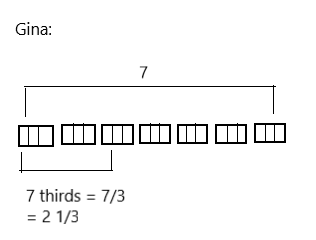
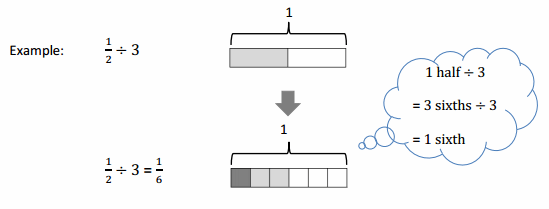
Sybil has \(\frac{1}{2}\) of a pizza leftover. She wants to share the pizza with 3 of her friends. What fraction of the original pizza will Sybil and her 3 friends each receive? Draw a picture to support your response.

Answer:
The fraction of the original pizza will Sybil and her 3 friends each receives is \(\frac{1}{6}\).

Explanation:
Given that Sybil has \(\frac{1}{2}\) of a pizza leftover and she wants to share the pizza with 3 of her friends, so the fraction of the original pizza will Sybil and her 3 friends each receives is \(\frac{1}{2}\) ÷ 3
on solving we will get the result as \(\frac{1}{6}\).

Eureka Math Grade 5 Module 4 Lesson 27 Homework Answer Key

Question 1.
Kelvin ordered four pizzas for a birthday party. The pizzas were cut in eighths. How many slices were there? Draw a picture to support your response.

Answer:
The number of slices were there is 32 slices.

Explanation:
Given that Kelvin ordered four pizzas for a birthday party and he cuts into eighths, so the number of slices were there is
as 1 pizza have 8 slices and for 4 pizza it will be
4 × 8 = 32 slices.

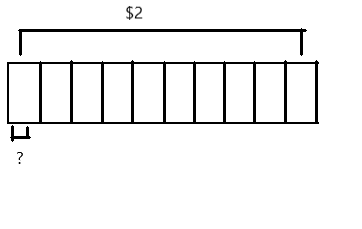
Question 2.
Virgil has \(\frac{1}{6}\) of a birthday cake left over. He wants to share the leftover cake with 3 friends. What fraction of the original cake will each of the 4 people receive? Draw a picture to support your response.

Answer:
The fraction of the original cake will each of the 4 people receives is \(\frac{1}{24}\).

Explanation:
Given that Virgil has \(\frac{1}{6}\) of a birthday cake left over and he share the leftover cake with 3 friends, so the fraction of the original cake will each of the 4 people receives is \(\frac{1}{6}\) ÷ 4
\(\frac{1}{6}\) × \(\frac{1}{4}\) on solving we will get the result as \(\frac{1}{24}\).

Question 3.
A pitcher of water contains \(\frac{1}{4}\) liters of water. The water is poured equally into 5 glasses.
a. How many liters of water are in each glass? Draw a picture to support your response.

Answer:
The number of liters of water are in each glass is \(\frac{1}{20}\) liters.

Explanation:
Given that a pitcher of water contains \(\frac{1}{4}\) liters of water and then he poured equally into 5 glasses, so the number of liters of water are in each glass is \(\frac{1}{4}\) ÷ 5
\(\frac{1}{4}\) × \(\frac{1}{5}\) on solving we will get the result as \(\frac{1}{20}\).

b. Write the amount of water in each glass in milliliters.

Answer:
The amount of water in each glass in milliliters is 50 milliliters.

Explanation:
The number of liters of water are in each glass is \(\frac{1}{20}\) liters, so the amount of water in each glass in milliliters is \(\frac{1}{20}\) × 1000, on solving we will get the result as 50 milliliters.

Question 4.
Drew has 4 pieces of rope 1 meter long each. He cuts each rope into fifths.
a. How many fifths will he have after cutting all the ropes?

Answer:
The number of fifths will he have after cutting all the ropes 20.

Explanation:
Here, we have 4 pieces of rope 1 meter long each and he cuts each rope into fifths, so the number of fifths will he have after cutting all the ropes 5 × 4 = 20.

b. How long will each of the fifths be in centimeters?

Answer:
The length of the each of the fifths be in centimeters is 20 cm.

Explanation:
Here, we have given that each rope is 1 meter long, so the length of fifth part will be equal to \(\frac{1}{5}\) which is 0.2 meters which is 20 cm.

Question 5.
A container is filled with blueberries. \(\frac{1}{6}\) of the blueberries is poured equally into two bowls.
a. What fraction of the blueberries is in each bowl?

b. If each bowl has 6 ounces of blueberries in it, how many ounces of blueberries were in the full container?

c. If \(\frac{1}{5}\) of the remaining blueberries is used to make muffins, how many pounds of blueberries are left in the container?

Answer:
a. The fraction of the blueberries is in each bowl is \(\frac{1}{12}\).

b. The number of ounces of blueberries were in the full container is 36 ounces of blueberries.

c. The number of pounds of blueberries are left in the container is 30 ounces.

Explanation:
a. Given that the container is filled with blueberries and \(\frac{1}{6}\) of the blueberries is poured equally into two bowls, so the fraction of the blueberries is in each bowl is \(\frac{1}{6}\) × \(\frac{1}{2}\) on solving we will get the result as \(\frac{1}{12}\).

b. As the each bowl has 6 ounces of blueberries in it, so the number of ounces of blueberries were in the full container is 6 × 6 which is 36 ounces of blueberries.

c. As there are \(\frac{1}{5}\) of the remaining blueberries is used to make muffins, so the number of pounds of blueberries are left in the container is \(\frac{1}{5}\) × \(\frac{5}{6}\) × 36 on solving we will get the result as \(\frac{180}{30}\) = 30 ounces.

Engage NY Eureka Math 5th Grade Module 4 Lesson 24 Answer Key

Eureka Math Grade 5 Module 4 Lesson 24 Problem Set Answer Key

Question 1.
A vial contains 20 mL of medicine. If each dose is \(\frac{1}{8}\) of the vial, how many mL is each dose? Express your answer as a decimal.

Answer:
Each dose has a 2.5 ml dose.

Explanation:
Here, a vial contains 20 mL of medicine, and if each dose is \(\frac{1}{8}\) of the vial, so each dose has \(\frac{1}{8}\) × 20 ml which is \(\frac{5}{2}\). So each dose has a 2.5 ml dose.

Question 2.
A container holds 0.7 liters of oil and vinegar. \(\frac{3}{4}\) of the mixture is vinegar. How many liters of vinegar are in the container? Express your answer as both a fraction and a decimal.

Answer:
The number of liters of vinegar is in the container is \(\frac{21}{40}\) liters. And in decimals it is 0.75 × 0.7 = 0.525 liters.

Explanation:
Here, a container holds 0.7 liters of oil and vinegar and \(\frac{3}{4}\) of the mixture is vinegar, so the number of liters of vinegar is in the container is \(\frac{3}{4}\) × 0.7
= \(\frac{3}{4}\) × \(\frac{7}{10}\)
= \(\frac{21}{40}\) liters.
and in decimals it is 0.75 × 0.7 = 0.525 liters.

Question 3.
Andres completed a 5-km race in 13.5 minutes. His sister’s time was 1\(\frac{1}{2}\) times longer than his time. How long, in minutes, did it take his sister to run the race?

Answer:
His sister to run the race in 20.25 minutes.

Explanation:
Here, Andres completed a 5-km race in 13.5 minutes, and his sister’s time was 1\(\frac{1}{2}\) times longer than his time. So his sister run the race in \(\frac{1}{2}\) of 13.5 which is 0.5 × 13.5 = 6.75. And his sister to run the race in 13.5 + 6.75 which is 20.25 minutes.

Question 4.
A clothing factory uses 1,275.2 meters of cloth a week to make shirts. How much cloth is needed to make 3\(\frac{3}{5}\) times as many shirts?

Answer:
The cloth needed is 4,509.72 meters.

Explanation:
Here, a clothing factory uses 1,275.2 meters of cloth a week to make shirts which is, and the cloth needed to make shirts are 1,275.2 of 3\(\frac{3}{5}\) which is 1,275.2 × \(\frac{18}{5}\) = 4,509.72 meters.

Question 5.
There are \(\frac{3}{4}\) as many boys as girls in a class of fifth-graders. If there are 35 students in the class, how many are girls?

Answer:
The number of girls is 20 students.

Explanation:
Given that there are \(\frac{3}{4}\) as many boys as girls in a class of fifth-graders and there are 35 students in the class, so the number of girls is, as the total of 7 units are the same as 35 students and for 1 unit it will be 35 ÷ 7 which is 5 students. So the number of girls is 4 × 5 = 20 students and the number of boys is 3 × 5 = 15 students.

Question 6.
Ciro purchased a concert ticket for $56. The cost of the ticket was \(\frac{4}{5}\) the cost of his dinner. The cost of his hotel was 2\(\frac{1}{2}\) times as much as his ticket. How much did Ciro spend altogether for the concert ticket, hotel, and dinner?

Answer:
Ciro spends altogether for the concert ticket, hotel, and dinner is $266.

Explanation:
Given that Ciro purchased a concert ticket for $56 and the cost of the ticket was \(\frac{4}{5}\) the cost of his dinner is, for 4 units it is 56, so for 1 unit it will be \(\frac{56}{4}\) which is 14, and for dinner, it is 5 × 14 = 70. The cost of his hotel was 2\(\frac{1}{2}\) times as much as his ticket, so 2.5 × 56 which is 140. So altogether it will be 140 + 70 + 56 which is 266. Ciro spends altogether for the concert ticket, hotel, and dinner is $266.

Eureka Math Grade 5 Module 4 Lesson 24 Exit Ticket Answer Key

Question 1.
An artist builds a sculpture out of metal and wood that weighs 14.9 kilograms. \(\frac{3}{4}\) of this weight is metal, and the rest is wood. How much does the wood part of the sculpture weigh?

Answer:
The wooden part is 3.725 kilograms.

Explanation:
Given that an artist builds a sculpture out of metal and wood that weighs 14.9 kilograms and \(\frac{3}{4}\) of this weight is metal, and the rest is wood. So the weight of the sculpture is, as metal part is \(\frac{3}{4}\) × 14.9 which is 11.175 kilograms and the wooden part is 14.9 – 11.175 = 3.725 kilograms.

Question 2.
On a boat tour, there are half as many children as there are adults. There are 30 people on the tour. How many children are there?

Answer:
The number of children is 10 children.

Explanation:
The total number of people is 30 and a half as many children as there are adults which means the number of children is \(\frac{1}{2}\). Let the number of adults be X and the equation is
X + X \(\frac{1}{2}\) = 30, now we will multiply both side by 2.
So 2X + X = 60,
3X = 60
X = 20.
So the number of children is \(\frac{1}{2}\) × 20 = 10 children.

Eureka Math Grade 5 Module 4 Lesson 24 Homework Answer Key

Question 1.
Jesse takes his dog and cat for their annual vet visit. Jesse’s dog weighs 23 pounds. The vet tells him his cat’s weight is \(\frac{5}{8}\) as much as his dog’s weight. How much does his cat weigh?

Answer:
The weight of the cat is 14.375 pounds.

Explanation:
Given that Jesse takes his dog and cat for their annual vet visit and Jesse’s dog weighs 23 pounds and the vet tells him his cat’s weight is \(\frac{5}{8}\) as much as his dog’s weight. So the weight of the cat is 23 × \(\frac{5}{8}\) which is 23 × 0.625 = 14.375 pounds.

Question 2.
An image of a snowflake is 1.8 centimeters wide. If the actual snowflake is \(\frac{1}{8}\) the size of the image, what is the width of the actual snowflake? Express your answer as a decimal.

Answer:
The width of the actual snowflake is 0.225 cm.

Explanation:
Given that the image of a snowflake is 1.8 centimeters wide and the actual snowflake is \(\frac{1}{8}\) the size of the image, and the width of the actual snowflake is 1.8 × \(\frac{1}{8}\) which is 0.225 cm.

Question 3.
A community bike ride offers a short 5.7-mile ride for children and families. The short ride is followed by a long ride, 5\(\frac{2}{3}\) times as long as the short ride, for adults. If a woman bikes the short ride with her children and then the long ride with her friends, how many miles does she ride altogether?

Answer:
The adult ride and children ride altogether 38.019 miles.

Explanation:
As a community bike ride offers a short 5.7-mile ride for children and families and the short ride is followed by a long ride, 5\(\frac{2}{3}\) times as long as the short ride, for adults. So if a woman bikes the short ride with her children and then the long ride with her friends, so the adult ride is  5.7 ×  5\(\frac{2}{3}\) which is 5.7 × 5.67 = 32.319. Now we will add the adult ride and children ride altogether, which is 5.7 + 32.319 = 38.019 miles.

Question 4.
Sal bought a house for $78,524.60. Twelve years later he sold the house for 2\(\frac{3}{4}\) times as much. What was the sale price of the house?

Answer:
The sale price of the house is $ 215,942.65.

Explanation:
Here, Sal bought a house for $78,524.60 and twelve years later he sold the house for 2\(\frac{3}{4}\) times as much. So the sale price of the house is 2\(\frac{3}{4}\) × 78,524.60 which is 2.75 × 78,524.60 = $ 215,942.65.

Question 5.
In the fifth grade at Lenape Elementary School, there are \(\frac{4}{5}\) as many students who do not wear glasses as those who do wear glasses. If there are 60 students who wear glasses, how many students are in the fifth grade?

Answer:
The number of students are in fifth grade is 300 students.

Explanation:
Given that there are \(\frac{4}{5}\) as many students who do not wear glasses as those who do wear glasses and the total number of students are equal with one or \(\frac{5}{5}\) which means the proportion of user who wear glasses is \(\frac{5}{5}\) – \(\frac{4}{5}\) which is \(\frac{1}{5}\) and from the information we can process (\(\frac{4}{5}\) ÷ \(\frac{5}{5}\)) × 60 on solving we will get the result as 240. So it means the total number of students in the class is accumulation between students without glasses is 240 + 60 = 300 students.

Question 6.
At a factory, a mechanic earns $17.25 an hour. The president of the company earns 6\(\frac{2}{3}\) times as much for each hour he works. The janitor at the same company earns \(\frac{3}{5}\) as much as the mechanic. How much does the company pay for all three employees’ wages for one hour of work?

Answer:
The company pay for all three employees wages for one hour of work is $142.60.

Explanation:
Given that a factory, a mechanic earns $17.25 an hour and the president of the company earns 6\(\frac{2}{3}\) times as much for each hour he works, so presidents wage is 6\(\frac{2}{3}\) × $17.25 which is $115. And the janitor at the same company earns \(\frac{3}{5}\) as much as the mechanic, so janitor wage is \(\frac{3}{5}\) × $17.25 which is $10.35. So the company pay for all three employees wages for one hour of work is $17.25 + $115 + $10.35 which is $142.60.

Engage NY Eureka Math 5th Grade Module 4 Lesson 23 Answer Key

Eureka Math Grade 5 Module 4 Lesson 23 Problem Set Answer Key

Question 1.
Fill in the blank using one of the following scaling factors to make each number sentence true.

a. 3.4 × _______ = 3.4

Answer:
3.4 × 1.00 = 3.4

b. _______ × 0.21 > 0.21

Answer:
1.021 × 0.21 > 0.21.

c. 8.04 × _______ < 8.04

Answer:
8.04 × 0.989 < 8.04.

Question 2.
a. Sort the following expressions by rewriting them in the table.

The product is less than the boxed number:	The product is greater than the boxed number:
0.3 × 0.069 602 × 0.489 0.2 × 0.1	13.89 × 1.004 0.72 × 1.24 102.03 × 4.015

b. Explain your sorting by writing a sentence that tells what the expressions in each column of the table have in common.

Answer:
Here, in the first column, the boxed number is multiplied by a scaling factor less than 1. So the product will be less than the boxed number. In the second column, the boxed number is multiplied by a scaling factor greater than 1.

Question 3.
Write a statement using one of the following phrases to compare the value of the expressions.
Then, explain how you know.

a. 4 × 0.988 _________________________________ 4

b. 1.05 × 0.8 _________________________________ 0.8

c. 1,725 × 0.013 _________________________________ 1,725

d. 989.001 × 1.003 _________________________________ 1.003

e. 0.002 × 0.911 _________________________________ 0.002

Answer:
a. 4 × 0.988 is less than slightly 4 because 0.988 is slightly less than 1.

b. 1.05 × 0.8 is slightly more than 0.8 because 0.1 is a little more than 1.

c. 1,725 × 0.013 is a lot less than 1,725 because 0.013 is a lot less than 1.

d. 989.001 × 1.003 is a lot more than 1.003 because 989.001 is a lot more than 1.

e. 0.002 × 0.911 is slightly less than 0.002 because 0.911 is a little less than 1.

Question 4.

During science class, Teo, Carson, and Dhakir measure the length of their bean sprouts. Carson’s sprout is 0.9 times the length of Teo’s, and Dhakir’s is 1.08 times the length of Teo’s. Whose bean sprout is the longest? The shortest? Explain your reasoning.

Answer:
Dhakir’s bean sprouts are the longest and Teo’s bean sprouts are the shortest.

Explanation:
Here, Dhakir’s bean sprouts are the longest, because it is slightly more than 1 time. The length of the Teo’s bean sprouts. Carson bean sprout is the shortest because it is a little less than 1 time the length of the Teo’s.

Question 5.
Complete the following statements; then use decimals to give an example of each.
• a × b > a will always be true when b is…

Answer:
It’s true when b is greater than one.

Explanation:
Let’s take an example of a × b > a
3.15 × 1.3 = 4.095 and here 4.095 > 3.15 and it is true when b is greater than one.

• a × b < a will always be true when b is…

Answer:
It’s true when b is less than one.

Explanation:
Let’s take an example of a × b < a
3.15 × 0.7 = 2.205 and here 2.205 < 3.15 and it is true when b is less than one.

Eureka Math Grade 5 Module 4 Lesson 23 Exit Ticket Answer Key

Question 1.
Fill in the blank using one of the following scaling factors to make each number sentence true.

a. 3.06 × _______ < 3.06

b. 5.2 × _______ = 5.2

c. _______ × 0.89 > 0.89

Answer:
a. 3.06 × 0.898 < 3.06.

b. 5.2 × 1.00 = 5.2.

c. 1.009× 0.89 > 0.89.

Question 2.
Will the product of 22.65 × 0.999 be greater than or less than 22.65? Without calculating, explain how you know.

Answer:
It will be less.

Explanation:
It’s a decimal so it’ll be a bit less than 22.65.

Eureka Math Grade 5 Module 4 Lesson 23 Homework Answer Key

Question 1.
Sort the following expressions by rewriting them in the table.

The product is less than the boxed number:	The product is greater than the boxed number:
828 × 0.921 0.05 × 0.1	12.5 × 1.989 0.007 × 1.02 2.16 × 1.11 321.46 × 1.26

b. What do the expressions in each column have in common?

Answer:
Here, in the first column, the boxed number is multiplied by a scaling factor less than 1. So the product will be less than the boxed number. In the second column, the boxed number is multiplied by a scaling factor greater than 1.

Question 2.
Write a statement using one of the following phrases to compare the value of the expressions.
Then, explain how you know.

a. 14 × 0.999 _______________________________ 14

b. 1.01 × 2.06 _______________________________ 2.06

c. 1,955 × 0.019 _______________________________ 1,955

d. Two thousand × 1.0001 _______________________________ two thousand

e. Two-thousandths × 0.911 _______________________________ two-thousandths

Answer:

a. 14 × 0.999 is slightly less than 14.

b. 1.01 × 2.06 is slightly more than 2.06.

c. 1,955 × 0.019 a lot less than 1,955.

d. Two thousand × 1.0001 is slightly more than two thousand.

e. Two-thousandths × 0.911 is slightly less than two-thousandths.

Question 3.
Rachel is 1.5 times as heavy as her cousin, Kayla. Another cousin, Jonathan, weighs 1.25 times as much as Kayla. List the cousins, from lightest to heaviest, and explain your thinking.

Answer:
Kayal, Jonathan, Rachel.

Explanation:
Here, Kayal is the lightest after Kayal Jonathan and then Rachel is the heaviest

Question 4.
Circle your choice.
a. a × b > a

Write two expressions that support your answer. Be sure to include one decimal example.

Answer:
Greater than 1

Explanation:
4.15 × 1.3 = 4.095 and here 5.395 > 4.15 and it is true when b is greater than one.
2.5 × 0.5 = 1.25 and here 1.25 < 2.5 and it is true when b is less than one.

b. a × b < a

Write two expressions that support your answer. Be sure to include one decimal example.

Answer:
It’s true when b is less than one.

Explanation:
Let’s take an example of a × b < a
3.15 × 0.7 = 2.205 and here 2.205 < 3.15 and it is true when b is less than one.
5.2 × 1.6 = 8.32 and here 8.32 > 5.2 and it is true when b is greater than one.

Engage NY Eureka Math 5th Grade Module 4 Lesson 20 Answer Key

Eureka Math Grade 5 Module 4 Lesson 20 Problem Set Answer Key

Question 1.
Convert. Show your work. Express your answer as a mixed number. (Draw a tape diagram if it helps you.) The first one is done for you.

a. 2 \(\frac{2}{3}\) yd = 8 ft
2 \(\frac{2}{3}\) yd = 2 \(\frac{2}{3}\) × 1 yd
= 2 \(\frac{2}{3}\) × 3 ft
= \(\frac{8}{3}\) × 3 ft
= \(\frac{24}{3}\) ft
= 8 ft

b. 1\(\frac{1}{2}\) qt = \(\frac{3}{8}\) gal
1\(\frac{1}{2}\) × 1 qt
= 1 \(\frac{1}{2}\) × \(\frac{1}{4}\) gal
= \(\frac{3}{2}\) × \(\frac{1}{4}\) gal
= \(\frac{3}{8}\) gal.

c. 4 \(\frac{2}{3}\) ft = ______________ in
4 \(\frac{2}{3}\) × 1 ft
= \(\frac{14}{3}\) × 12 in
= \(\frac{168}{3}\) in
= 56 in.

d. 9 \(\frac{1}{2}\) pt = ______________ qt
9 \(\frac{1}{2}\) × 1 pt
=  \(\frac{19}{2}\) × \(\frac{1}{2}\) qt
=  \(\frac{19}{4}\) qt
= 4 \(\frac{3}{4}\) qt.

e. 3 \(\frac{3}{5}\) hr = ______________ min
3 \(\frac{3}{5}\) × 1 hr
= \(\frac{18}{5}\) × 60 min
= \(\frac{1080}{5}\) min
= 216 mins.

f. 3 \(\frac{2}{3}\) ft = ______________ yd
3 \(\frac{2}{3}\) × 1 ft
= \(\frac{11}{3}\) × \(\frac{1}{3}\) yd
= \(\frac{11}{9}\)
= 1 \(\frac{2}{9}\) yd.

Question 2.
Three dump trucks are carrying topsoil to a construction site. Truck A carries 3,545 lb, Truck B carries 1,758 lb, and Truck C carries 3,697 lb. How many tons of topsoil are the 3 trucks carrying altogether?

Answer:
The 3 trucks carrying altogether are 4.5 tons.

Explanation:
Given that there are three dump trucks are carrying topsoil to a construction site and Truck A carries 3,545 lb, Truck B carries 1,758 lb, and Truck C carries 3,697 lb, so the total weight carried altogether is 3,545 + 1,758 + 3,697 = 9,000 lb. As each ton is 2000 pounds, so altogether the trucks are carrying is 9000 × \(\frac{1}{2000}\) which is 4.5 tons.

Question 3.
Melissa buys 3\(\frac{3}{4}\) gallons of iced tea. Denita buys 7 quarts more than Melissa. How much tea do they buy altogether? Express your answer in quarts.

Answer:
The total tea they bought is 37 quarts.

Explanation:
Given that Melissa buys 3\(\frac{3}{4}\) gallons of iced tea, so total iced tea for Melissa is \(\frac{15}{4}\) which is 3.75. And Denita buys 7 quarts more than Melissa, so the total iced tea for Denita is, as 1 quart is 0.25 gallon and for 7 quarts it will be 7 × 0.25 which is 1.75 gallon. so the total iced tea for Denita is 1.75 + 3.75 which is 5.5. Then the total tea they bought is 3.75 + 5.5 = 9.25 gallon which is 9.25 × 4 = 37 quarts.

Question 4.
Marvin buys a hose that is 27\(\frac{3}{4}\) feet long. He already owns a hose at home that is \(\frac{2}{3}\) the length of the new hose. How many total yards of hose does Marvin have now?

Answer:
The total yards of hose does Marvin have now is 15 \(\frac{5}{12}\) yd.

Explanation:
Given that Marvin buys a hose that is 27\(\frac{3}{4}\) feet long and he owns a hose at home that is \(\frac{2}{3}\) the length of the new hose, so \(\frac{2}{3}\) of 27\(\frac{3}{4}\) which is
\(\frac{2}{3}\) × \(\frac{111}{4}\)
= \(\frac{222}{12}\)
= 18 \(\frac{1}{2}\),
So the total yards of hose does Marvin have now is
27\(\frac{3}{4}\) + 18\(\frac{1}{2}\)
= \(\frac{111}{4}\) + \(\frac{37}{2}\)
= \(\frac{185}{4}\)
= 46 \(\frac{1}{4}\).
So total in yards, it will be 46 \(\frac{1}{4}\) × 1 yd
= \(\frac{185}{4}\) × \(\frac{1}{3}\) yd
= \(\frac{185}{12}\)
=15 \(\frac{5}{12}\) yd.

Eureka Math Grade 5 Module 4 Lesson 20 Exit Ticket Answer Key

Convert. Express your answer as a mixed number.

a. 2\(\frac{1}{6}\) ft = ______________ in

Answer:
26 in.

Explanation:
2\(\frac{1}{6}\) ft = \(\frac{13}{6}\) × 1 ft
= \(\frac{13}{6}\) × 12 in
= \(\frac{156}{6}\) in
= 26 in.

b. 3\(\frac{3}{4}\) ft = ______________ yd

Answer:
45 in.

Explanation:
3\(\frac{3}{4}\) ft = \(\frac{15}{4}\) ft × 1 ft
= \(\frac{15}{4}\) × 12 in
= \(\frac{180}{4}\) in
= 45 in.

c. 2\(\frac{1}{2}\)c = ______________ pt

Answer:
1 \(\frac{1}{4}\) pt.

Explanation:
2\(\frac{1}{2}\)c = \(\frac{5}{2}\) × 1 c
= \(\frac{5}{2}\) × \(\frac{1}{2}\) pt
= \(\frac{5}{4}\) pt
= 1 \(\frac{1}{4}\) pt.

d. 3\(\frac{2}{3}\) years = ______________ months

Answer:
44 months.

Explanation:
3\(\frac{2}{3}\) years = \(\frac{11}{3}\) × 1 year
= \(\frac{11}{3}\) × 12 months
= 44 months.

Eureka Math Grade 5 Module 4 Lesson 20 Homework Answer Key

Question 1.
Convert. Show your work. Express your answer as a mixed number. The first one is done for you.
2 \(\frac{2}{3}\) yd = 8 ft
2 \(\frac{2}{3}\) yd = 2 \(\frac{2}{3}\) × 1 yd
= 2 \(\frac{2}{3}\) × 3 ft
= \(\frac{8}{3}\) × 3 ft
= \(\frac{24}{3}\) ft
= 8 ft

b. 1 \(\frac{1}{4}\) ft = \(\frac{5}{12}\) yd
1 \(\frac{1}{4}\) ft = 1 \(\frac{1}{4}\) × 1 ft
= 1 \(\frac{1}{4}\) × \(\frac{1}{3}\) yd
= \(\frac{5}{4}\) × \(\frac{1}{3}\) yd
= \(\frac{5}{12}\) yd.

c. 3\(\frac{5}{6}\) ft = ______________ in

Answer:
46 in.

Explanation:
3\(\frac{5}{6}\) ft = 3\(\frac{5}{6}\) ft × 1 ft
= \(\frac{23}{6}\) × 12 in
= 46 in.

d. 7 \(\frac{1}{2}\) pt = ______________ qt

Answer:
3 \(\frac{3}{4}\) qt.

Explanation:
7 \(\frac{1}{2}\) pt = 7 \(\frac{1}{2}\) pt × 1 pt
= \(\frac{15}{2}\) × \(\frac{1}{2}\) qt
= \(\frac{15}{4}\) qt
= 3 \(\frac{3}{4}\) qt.

e. 4\(\frac{3}{10}\) hr = ______________ min

Answer:
258 mins.

Explanation:
4\(\frac{3}{10}\) hr = 4\(\frac{3}{10}\) × 1 hr
= \(\frac{43}{10}\) × 60 mins
= 258 mins

f. 33 months = ______________ years

Answer:
2 \(\frac{3}{4}\) years.

Explanation:
33 × \(\frac{1}{12}\)
= \(\frac{33}{12}\)
= \(\frac{11}{4}\)
= 2 \(\frac{3}{4}\) years.

Question 2.
Four members of a track team run a relay race in 165 seconds. How many minutes did it take them to run the race?

Answer:
The number of minutes did it take them to run the race is 2 \(\frac{3}{4}\) mins.

Explanation:
Given that there are four members of a track team run a relay race in 165 seconds, so the number of minutes did it take them to run the race is 165 × \(\frac{1}{60}\)
= \(\frac{11}{4}\)
= 2 \(\frac{3}{4}\) mins.

Question 3.
Horace buys 2\(\frac{3}{4}\) pounds of blueberries for a pie. He needs 48 ounces of blueberries for the pie. How many more pounds of blueberries does he need to buy?

Answer:
Horace need more blueberries to buy is 0.25 pounds.

Explanation:
Given that Horace buys 2\(\frac{3}{4}\) pounds of blueberries for a pie and he needs 48 ounces of blueberries for the pie, so the number of pounds of blueberries does he need to buy is, as 1 pound is 16 ounces and 1 ton is 2,200 pounds which is 32,000 ounces. As Horace needs 48 ounces of blueberries for the pie and we need to convert into ounce, so Horace need more blueberries to buy is 3 – 2\(\frac{3}{4}\) which is 3 – \(\frac{11}{4}\) = \(\frac{1}{4}\) = 0.25 pounds.

Question 4.
Tiffany is sending a package that may not exceed 16 pounds. The package contains books that weigh a total of 9\(\frac{3}{8}\) pounds. The other items to be sent weigh \(\frac{3}{5}\) the weight of the books. Will Tiffany be able to send the package?

Answer:
The total package is 15 pounds.

Explanation:
Given that Tiffany is sending a package that may not exceed 16 pounds and the package contains books that weigh a total of 9\(\frac{3}{8}\) pounds and the other items to be sent weigh \(\frac{3}{5}\) the weight of the books. Let the book package be X and let the other package be Y. So from the above problem,
X= 9\(\frac{3}{8}\) which is \(\frac{75}{8}\) and
Y = \(\frac{3}{5}\) X
= \(\frac{3}{5}\) × \(\frac{75}{8}\)
= \(\frac{225}{40}\)
= 5 \(\frac{5}{8}\).
So the total package is
X + Y = 9\(\frac{3}{8}\) + 5 \(\frac{5}{8}\)
= \(\frac{75}{8}\) + \(\frac{225}{40}\)
= \(\frac{600}{40}\)
= 15 pounds.

Engage NY Eureka Math 5th Grade Module 4 Lesson 2 Answer Key

Eureka Math Grade 5 Module 4 Lesson 2 Problem Set Answer Key

Question 1.
Draw a picture to show the division. Write a division expression using the unit form. Then, express your answer as a fraction. The first one is partially done for you.

a. 1 ÷ 5 = 5 fifths ÷ 5 = 1 fifth = \(\frac{1}{5}\)
Answer:
1/5

Explanation:
5 fifths ÷ 5 = 1/5

b. 3 ÷ 4
Answer:
3/4

Explanation:
12 fourths ÷ 4 = 3 fourths = 3/4

c. 6 ÷ 4
Answer:
1 1/2

Explanation:
24 fourths ÷ 4 = 6 fourths = 6/4 = 1 2/4 = 1 1/2

Question 2.
Draw to show how 2 children can equally share 3 cookies. Write an equation, and express your answer as a fraction.
Answer:
1 1/2 cookies.

Explanation:
3 ÷ 2 = 6 halves ÷ 2 = 3 halves
3/2
1 1/2
Each child gets 1 1/2 cookies.

Question 3.
Carly and Gina read the following problem in their math class:
Seven cereal bars were shared equally by 3 children. How much did each child receive?
Carly and Gina solve the problem differently. Carly gives each child 2 whole cereal bars and then divides the remaining cereal bar among the 3 children. Gina divides all the cereal bars into thirds and shares the thirds equally among the 3 children.
a. Illustrate both girls’ solutions.
Answer:
         

b. Explain why they are both right.
Answer:
Both girls are right.

Explanation:
Here they used different strategies to solve the division problem and still ended up with the same answer.
7 ÷ 3 = 7/3 = 2 1/3 this is what carly did.
7 ÷ 3 =21 thirds ÷ 3 = 7 = 7/3 = 2 1/3 thirds that’s what gina did.

Question 4.
Fill in the blanks to make true number sentences.

a. 2 ÷ 3 =
Answer:
2/3

Explanation:
The true number sentence for the given question is 2/3.

b. 15 ÷ 8 =
Answer:
15/8

Explanation:
The true number sentence for the given question is 15/8.

c. 11 ÷ 4 =
Answer:
11/4

Explanation:
The true number sentence for the given question is 11/4.

d. \(\frac{3}{2}\) = _____ ÷ ______
Answer:
3/2

Explanation:
The true number sentence for the given question is 3/2.

e. \(\frac{9}{13}\) = _____ ÷ _____
Answer:
9/13

Explanation:
The true number sentence for the given question is 9/13.

f. 1\(\frac{1}{3}\) = ______ ÷ ____
Answer:
1 1/3 that is 4/3

Explanation:
The true number sentence for the given question is 4/3.

Eureka Math Grade 5 Module 4 Lesson 2 Exit Ticket Answer Key

Question 1.
Draw a picture that shows the division expression. Then, write an equation and solve.

a. 3 ÷ 9
Answer:
3/9

b. 4 ÷ 3
Answer:
4/3

Question 2.
Fill in the blanks to make true number sentences.

a. 21 ÷ 8 =
Answer:
21/8

Explanation:
The true number sentence for the given question is 21/8.

b. \(\frac{7}{4}\) = ______ ÷ ______
Answer:
7/4

Explanation:
The true number sentence for the given question is 7/4.

c. 4 ÷ 9 =
Answer:
4/9

Explanation:
The true number sentence for the given question is 4/9.

d. 1\(\frac{2}{7}\) = ______ ÷ ______
Answer:
1 2/7

Explanation:
The true number sentence for the given question is 9/7.

Eureka Math Grade 5 Module 4 Lesson 2 Homework Answer Key

Question 1.
Draw a picture to show the division. Express your answer as a fraction.

a. 1 ÷ 4
Answer:
1/4

Explanation:

b. 3 ÷ 5
Answer:
3/5

Explanation:
3/5

c. 7 ÷ 4
Answer:
7/4

Explanation:
7 ÷ 4 = 7/4 = 1 3/4

Question 2.
Using a picture, show how six people could share four sandwiches. Then, write an equation and solve.
Answer:
4/6 = 2/3

Explanation:

Question 3.
Fill in the blanks to make true number sentences.

a. 2 ÷ 7 =
Answer:
2/7

Explanation:
The true number sentence for the given question is 2/7.

b. 39 ÷ 5 =
Answer:
39/5

Explanation:
The true number sentence for the given question is 39/5.

c. 13 ÷ 3 =
Answer:
13/3

Explanation:
The true number sentence for the given question is 13/3.

d. \(\frac{9}{5}\) = ______ ÷ ______
Answer:
9/5

Explanation:
The true number sentence for the given question is 9/5.

e. \(\frac{19}{28}\) = ______ ÷ ______
Answer:
19/28

Explanation:
The true number sentence for the given question is 19/28.

f. 1\(\frac{3}{5}\) = ______ ÷ ______
Answer:
1 3/5 = 8/5

Explanation:
The true number sentence for the given question is 8/5.

Engage NY Eureka Math 5th Grade Module 4 Lesson 3 Answer Key

Eureka Math Grade 5 Module 4 Lesson 3 Problem Set Answer Key

Question 1.
Fill in the chart. The first one is done for you.

Answer:
I have filled the chart with the answer which is given below.

Explanation:

Question 2.
A principal evenly distributes 6 reams of copy paper to 8 fifth-grade teachers.
a. How many reams of paper does each fifth-grade teacher receive? Explain how you know using pictures, words, or numbers.
Answers:
3/4 ream of paper

Explanation:
6 reams are divided among 8 teachers.
6 ÷ 8 =6/8 = 3/4
Each Teacher gets 3/4 reams of paper.

b. If there were twice as many reams of paper and half as many teachers, how would the amount each teacher receives change? Explain how you know using pictures, words, or numbers.
Answer:
Each teacher gets 3 reams of paper.

Explanation:
6 reams * 2 = 12 reams
8 Teachers ÷ 2 = 4 Teachers
12 ÷ 4 = 48 fourths ÷ 4 = 12 fourths = 12/4 = 3. Hence each teacher gets 3 reams of paper.

Question 3.
A caterer has prepared 16 trays of hot food for an event. The trays are placed in warming boxes for delivery. Each box can hold 5 trays of food.
a. How many warming boxes are necessary for delivery if the caterer wants to use as few boxes as possible? Explain how you know.
Answer:
16 trays in groups of 5
16 ÷ 5 = 16/5 = 3 1/5

Explanation:
16 trays will require 3 1/5 warming boxes which means that 3 boxes could be full and the 4th box might have just 1 tray. But the caterer will need 4 boxes.

b. If the caterer fills a box completely before filling the next box, what fraction of the last box will be empty?
Answer:
The last box will be 4/5 empty.

Explanation:
3 1/5 boxes are used in this 3 are filled and a filled 1/5

Eureka Math Grade 5 Module 4 Lesson 3 Exit Ticket Answer Key

A baker made 9 cupcakes, each a different type. Four people want to share them equally. How many cupcakes will each person get?
Fill in the chart to show how to solve the problem.
Division Expression Unit Forms Fractions and Mixed numbers Standard Algorithm

Division Expression	Unit Forms	Fractions and Mixed numbers	Standard Algorithm
Draw to show you thinking:

Eureka Math Grade 5 Module 4 Lesson 3 Homework Answer Key

Question 1.
Fill in the chart. The first one is done for you.

Answer:

Question 2.
A coffee shop uses 4 liters of milk every day.
a. If there are 15 liters of milk in the refrigerator, after how many days will more milk need to be purchased? Explain how you know.
Answer:
15 ÷ 4 = 15 /4 =3 3/4

Explanation:
The owner has to shop for after 3 days as it is not enough for the next day.

b. If only half as much milk is used each day, after how many days will more milk need to be purchased?
Answer:
15 ÷ 2 = 15 /2 = 7 1/2

Explanation:
The owner would have to buy milk after seven days. He will need another liter of milk for the next day.

Question 3.
Polly buys 14 cupcakes for a party. The bakery puts them into boxes that hold 4 cupcakes each.
a. How many boxes will be needed for Polly to bring all the cupcakes to the party? Explain how you know.
Answer:
14 ÷ 4 = 14/4 = 3 2/4 = 31/2

Explanation:
Polly needs four boxes more as Polly needs three boxes for 12 cupcakes and one more for 2 cupcakes.

b. If the bakery completely fills as many boxes as possible, what fraction of the last box is empty? How many more cupcakes are needed to fill this box?
Answer:
4/4 – 2/4  = 2/4 = 1/2

Explanation:
The last box will be 1/2 empty. Two more cupcakes are needed to fill it.

Engage NY Eureka Math 5th Grade Module 4 Lesson 16 Answer Key

Eureka Math Grade 5 Module 4 Lesson 16 Problem Set Answer Key

Solve and show your thinking with a tape diagram.

Question 1.
Mrs. Onusko made 60 cookies for a bake sale. She sold \(\frac{2}{3}\) of them and gave \(\frac{3}{4}\) of the remaining cookies to the students working at the sale. How many cookies did she have left?

Answer:
The number of cookies left is 5 cookies.

Explanation:
Given that Mrs. Onusko made 60 cookies for a bake sale and she sold \(\frac{2}{3}\) of them. So the number of cookies did she sold is \(\frac{2}{3}\) × 60 which is 40 cookies. So the remaining cookies are 60 – 40 which is 20 cookies. And Mrs. Onusko gave \(\frac{3}{4}\) of the remaining cookies to the students working at the sale, so \(\frac{3}{4}\) × 20 which is 15 cookies. So the number of cookies left is 20 – 15 = 5 cookies.

Question 2.
Joakim is icing 30 cupcakes. He spreads mint icing on \(\frac{1}{5}\) of the cupcakes and chocolate on \(\frac{1}{2}\) of the remaining cupcakes. The rest will get vanilla icing. How many cupcakes have vanilla icing?

Answer:
The remaining vanilla icing is 9 cupcakes.

Explanation:
Given that Joakim is icing 30 cupcakes and he spreads mint icing on \(\frac{1}{5}\) of the cupcakes and chocolate, so the number of mint icing is 30 × \(\frac{1}{5}\) which is 6 cupcakes. And \(\frac{1}{2}\) of the remaining cupcakes have chocolate icing is 30 × \(\frac{1}{2}\) which is 15 cupcakes. And the remaining vanilla icing is 30 – (15 + 6) which is 30 – 21 = 9 cupcakes.

Question 3.

The Booster Club sells 240 cheeseburgers. \(\frac{1}{4}\) of the cheeseburgers had pickles, \(\frac{1}{2}\) of the remaining burgers had onions, and the rest had tomato. How many cheeseburgers had tomato?

Answer:
90 cheeseburgers had tomato.

Explanation:
Given that the Booster Club sells 240 cheeseburgers and \(\frac{1}{4}\) of the cheeseburgers had pickles which means the number of cheese that had pickle is 240 × \(\frac{1}{4}\) which is 60 burgers. The number of remaining burgers is 240 – 60 which is 180 cheese burgers. And \(\frac{1}{2}\) of the remaining burgers had onions and rest had tomato which means \(\frac{1}{2}\) × 180 which is 90. Therefore 90 cheeseburgers had tomato.

Question 4.
DeSean is sorting his rock collection. \(\frac{2}{3}\) of the rocks are metamorphic, and \(\frac{3}{4}\) of the remainder are igneous rocks. If the 3 rocks left over are sedimentary, how many rocks does DeSean have?

Answer:
The number of rocks that DeSean has are 36.

Explanation:
Given that DeSean is sorting his rock collection and \(\frac{2}{3}\) of the rocks are metamorphic, and \(\frac{3}{4}\) of the remainder are igneous rocks which means \(\frac{1}{3}\) are igneous rocks, and 3 rocks left over are sedimentary, so the number of rocks that DeSean has are
x = \(\frac{2}{3}\)x + \(\frac{3}{4}\) × \(\frac{1}{3}\)x + 3 which is
= \(\frac{8}{12}\)x + \(\frac{3}{12}\)x + 3
= \(\frac{11}{12}\)x + 3
\(\frac{1}{12}\)x = 3
x = 36.
So the number of rocks that DeSean has are 36.

Question 5.
Milan puts \(\frac{1}{4}\) of her lawn-mowing money in savings and uses \(\frac{1}{2}\) of the remaining money to pay back her sister. If she has $15 left, how much did she have at first?

Answer:
The money Milan had at first is $40.

Explanation:
Given that Milan puts \(\frac{1}{4}\) of her lawn-mowing money in savings and uses \(\frac{1}{2}\) of the remaining money to pay back her sister. Let the money that Milan’s has at first be X, the remaining money will be X – \(\frac{1}{4}\) X = \(\frac{3}{4}\) X. Now we are going to calculate the money to pay back her sister, which is \(\frac{1}{2}\) of the remaining money, which is \(\frac{1}{2}\) × \(\frac{3}{4}\) X which is \(\frac{3}{8}\)X. So the total money Milan had at first = money for saving + money for paying back + the amount of money left
X = \(\frac{1}{4}\)X + \(\frac{3}{8}\) X + 15
X – \(\frac{1}{4}\)X – \(\frac{3}{8}\) X = 15
\(\frac{8X – 2X – 3X}{8}\)X = 15
On solving we will get the result as 40.
So, the money Milan had at first is $40.

Question 6.
Parks is wearing several rubber bracelets. \(\frac{1}{3}\) of the bracelets are tie-dye, \(\frac{1}{6}\) are blue, and \(\frac{1}{3}\) of the remainder are camouflage. If Parks wears 2 camouflage bracelets, how many bracelets does he have on?

Answer:
Park has 12 bracelets.

Explanation:
Given that Parks is wearing several rubber bracelets and \(\frac{1}{3}\) of the bracelets are tie-dye, \(\frac{1}{6}\) are blue, and \(\frac{1}{3}\) of the remainder are camouflage and Park wears 2 camouflage bracelets. Let the sum of all braclets be X, and Park wears 2 camouflage bracelets, that is,
\(\frac{1}{3}\) × (1 – \(\frac{1}{3}\) – \(\frac{1}{6}\)) × X = 2
\(\frac{1}{3}\) × (\(\frac{6}{6}\) – \(\frac{2}{6}\) – \(\frac{1}{6}\)) × X = 2
\(\frac{1}{3}\) × \(\frac{3}{6}\) × X = 2
\(\frac{1}{6}\) × X = 2
X = 2 ÷ \(\frac{1}{6}\)
X = 2 × 6
= 12.

Question 7.
Ahmed spent \(\frac{1}{3}\) of his money on a burrito and a water bottle. The burrito cost 2 times as much as the water. The burrito cost $4. How much money does Ahmed have left?

Answer:
Ahmed have left $12.

Explanation:
Given that Ahmed spent \(\frac{1}{3}\) of his money on a burrito and a water bottle and the burrito cost 2 times as much as the water, so the water is the burrito cost divided by 2. So water = \(\frac{4}{2}\) which is $2. And water + burrito is $2 + $4 which is $6. And this $6 is \(\frac{1}{3}\) of the money and Ahmed have left \(\frac{2}{3}\) of the money, so
$6 ÷ \(\frac{1}{3}\) = X ÷ \(\frac{2}{3}\)
X = 6 × (\(\frac{2}{3}\) ÷ \(\frac{1}{3}\), on solving we will get the result as $12. So the Ahmed have left $12.

Eureka Math Grade 5 Module 4 Lesson 16 Exit Ticket Answer Key

Solve and show your thinking with a tape diagram.
Three-quarters of the boats in the marina are white, \(\frac{4}{7}\) of the remaining boats are blue, and the rest are red. If there are 9 red boats, how many boats are in the marina?

Answer:
The total number of boats in the marine is 84.

Explanation:
Let the number of boats in the marina be X, and the number of white boats be \(\frac{3}{4}\)X. Then the remaining boats will be X – \(\frac{3}{4}\)X which is \(\frac{X}{4}\). And now, there are \(\frac{4}{7}\) of the boats are blue, thus the number of blue boats is \(\frac{4}{7}\) × \(\frac{X}{4}\) which is \(\frac{X}{7}\). And the number of red boats is \(\frac{X}{4}\) – \(\frac{X}{7}\) which is \(\frac{3X}{28}\). And if there are 9 red boats, then \(\frac{3X}{28}\) = 9 and
3X = 9 × 28 on solving X = 84.
The total number of boats in the marine is 84.

Eureka Math Grade 5 Module 4 Lesson 16 Homework Answer Key

Solve and show your thinking with a tape diagram.

Question 1.
Anthony bought an 8-foot board. He cut off \(\frac{3}{4}\) of the board to build a shelf and gave \(\frac{1}{3}\) of the rest to his brother for an art project. How many inches long was the piece Anthony gave to his brother?

Answer:
Anthony gave his brother 8 inches board.

Explanation:
Given that Anthony bought an 8-foot board, as 1 foot is 12 inches and 8 feet is 8 × 12 which is 96 inches. Anthony cuts \(\frac{3}{4}\) to build a shelf, so \(\frac{3}{4}\) × 96 which is 72 inches. So the left board after cutting is 96 – 72 which is 24 inches. And Anthony gave \(\frac{1}{3}\) of the leftover of his brother which is \(\frac{1}{3}\) × 24 = 8. So Anthony gave his brother 8 inches board.

Question 2.
Riverside Elementary School is holding a school-wide election to choose a school color. Five-eighths of the votes were for blue, \(\frac{5}{9}\) of the remaining votes were for green, and the remaining 48 votes were for red.
a. How many votes were for blue?

Answer:
The number of blue votes is 180 votes.

Explanation:
Given that Five-eighths of the votes were for blue and \(\frac{5}{9}\) of the remaining votes were for green which means \(\frac{5}{9}\) × \(\frac{3}{8}\) which is \(\frac{5}{24}\). And the number of red is 1 – (\(\frac{5}{8}\) + \(\frac{5}{24}\) which is \(\frac{1}{6}\). So the total amount of people is 48 × 6 which is 288 people. So the number of blue votes is 288 × \(\frac{5}{8}\) which is 180 votes.

b. How many votes were for green?

Answer:
The number of votes were green is 60 votes.

Explanation:
As the total amount of people is 48 × 6 which is 288 people. So the number of green votes is 288 × \(\frac{5}{24}\) which is 60 votes.

c. If every student got one vote, but there were 25 students absent on the day of the vote, how many students are there at Riverside Elementary School?

Answer:
The total number of students are there at Riverside Elementary School is 313 students.

Explanation:
Given that, If every student got one vote, but there were 25 students absent on the day of the vote. So the total number of students are there at Riverside Elementary School is 288 + 25 which is 313 students.

d. Seven-tenths of the votes for blue were made by girls. Did girls who voted for blue make up more than or less than half of all votes? Support your reasoning with a picture.

Answer:

Explanation:
Less than half of all the girls who voted for blue. Because, as Seven-tenths of the votes for blue were made by girls which means \(\frac{7}{10}\) × 180 = 126 which is less than half

e. How many girls voted for blue?

Answer:
The number of girls voted for blue is 126.

Engage NY Eureka Math 5th Grade Module 4 Lesson 28 Answer Key

Eureka Math Grade 5 Module 4 Lesson 28 Problem Set Answer Key

Question 1.
Create and solve a division story problem about 5 meters of rope that is modeled by the tape diagram below.

Answer:
The number of fourths altogether is 20.

Explanation:
Tom has 5 meters of rope. He cuts each meter equally into four parts. How many fourths will he have altogether?
Answer:
As Tom has 5 meters of rope and he cuts each meter equally into four parts, so the number of fourths altogether is
5 ÷ \(\frac{1}{4}\) = 20.

Question 2.
Create and solve a story problem about \(\frac{1}{4}\) pound of almonds that is modeled by the tape diagram below.

Answer:
The number of pounds of almonds is in each bag is \(\frac{1}{20}\) pounds.

Explanation:
Sam bought \(\frac{1}{4}\) pound of almonds. She shares the almonds equally into 5 bags. How many pounds of almonds are in each bag?

Answer:
Here, Sam bought \(\frac{1}{4}\) pound of almonds and she shares the almonds equally into 5 bags. So the number of pounds of almonds are in each bags is
\(\frac{1}{4}\) ÷ 5 which is \(\frac{1}{20}\) pounds in each bag.

Question 3.
Draw a tape diagram and create a word problem for the following expressions, and then solve.
a. 2 ÷ \(\frac{1}{3}\)

Answer:
The number of slices will she have altogether is 6 slices.

Explanation:
Mike bought 2 pizzas. He wants to cut each pizza into thirds. How many slices will she have altogether?

Answer:
Here, Mike bought 2 pizzas and he wants to cut each pizza into thirds, so the number of slices will she have altogether is
2 ÷ \(\frac{1}{3}\) which is 6 slices.

b. \(\frac{1}{3}\) ÷ 4

Answer:
The number of kgs of flour will be in each container is which is \(\frac{1}{12}\) kg of flour.

Explanation:
Kite bought \(\frac{1}{3}\) kg of flour. He poured it equally into 4 containers. How many kg of flour will be in each container?

Answer:
Here, Kite bought \(\frac{1}{3}\) kg of flour and he poured it equally into 4 containers, so the number of kgs of flour will be in each container is \(\frac{1}{3}\) ÷ 4 which is \(\frac{1}{12}\) kg of flour.

c. \(\frac{1}{4}\) ÷ 3

Answer:
The number of pounds of sunflower seeds will she eat each day is \(\frac{1}{12}\).

Explanation:
Ricky bought \(\frac{1}{4}\) pound of sunflower seeds. She wants to share them divide them equally over 3 days as a snack. How many pounds of sunflower seeds will she eat each day?

Answer:
Here, Ricky bought \(\frac{1}{4}\) pound of sunflower seeds and she wants to share them divide them equally over 3 days as a snack, so the number of pounds of sunflower seeds will she eat each day is \(\frac{1}{4}\) ÷ 3 which is \(\frac{1}{12}\).

d. 3 ÷ \(\frac{1}{5}\)

Answer:
The many fifths will he have altogether is 15.

Explanation:
Sean bought 3m of ribbon. He cut each meter into fifths. How many fifths will he have altogether?

Answer:
Here, Sean bought 3m of ribbon and he cut each meter into fifths, so the many fifths will he have altogether is 3 ÷ \(\frac{1}{5}\) which is 15.

Eureka Math Grade 5 Module 4 Lesson 28 Exit Ticket Answer Key

Create a word problem for the following expressions, and then solve.
a. 4 ÷ \(\frac{1}{2}\)

Answer:
Joe share the cake with his friends is 8

Explanation:
Joe has \(\frac{1}{2}\) of a cake and he has to share it with 4 of his friends. How does Joe share the cake with his friends?

Answer:
Here, Joe has \(\frac{1}{2}\) of a cake and he has to share it with 4 of his friends, so Joe share the cake with his friends is
\(\frac{1}{2}\) ÷ 4, on solving we will get the result as \(\frac{1}{8}\).

b. \(\frac{1}{2}\) ÷ 4

Answer:
Ana shares \(\frac{1}{8}\) part of pizza with his friends.

Explanation:
Ana has \(\frac{1}{2}\) of a pizza and she has to share it with 4 of his friends. How does Ana share the pizza with his friends?

Answer:
Here, Ana has \(\frac{1}{2}\) of a pizza and she has to share it with 4 of his friends, so Ana share the cake with his friends is
4 ÷ \(\frac{1}{2}\) on solving we will get the result as \(\frac{1}{8}\).

Eureka Math Grade 5 Module 4 Lesson 28 Homework Answer Key

Question 1.
Create and solve a division story problem about 7 feet of rope that is modeled by the tape diagram below.

Answer:
The number of sevens altogether is 14.

Explanation:
Sian has 7 feet of rope. He cuts each meter equally into seven parts. How many sevens will he have altogether?

Answer:
As Sain has 7 feet of rope and he cuts each meter equally into seven parts, so the number of sevens altogether is
7 ÷ \(\frac{1}{2}\) = 14.

Question 2.
Create and solve a story problem about \(\frac{1}{3}\) pound of flour that is modeled by the tape diagram below.

Answer:
The number of pounds of flour is in each bag is \(\frac{1}{9}\) pounds.

Explanation:
Tim bought \(\frac{1}{3}\) pound of flour. She shares the flour equally into 3 bags. How many pounds of flour is in each bag?

Answer:
Here, Tim bought \(\frac{1}{3}\) pound of flour and she shares the flour equally into 3 bags. So the number of pounds of flour are in each bags is
\(\frac{1}{3}\) ÷ 3 which is \(\frac{1}{9}\) pounds in each bag.

Question 3.
Draw a tape diagram and create a word problem for the following expressions. Then, solve and check.
a. 2 ÷ \(\frac{1}{4}\)

Answer:
The number of pounds of apples will she eat each day is \(\frac{1}{8}\).

Explanation:
Rache bought \(\frac{1}{4}\) pound of apples. She wants to share them divide them equally over 2 days as a snack. How many pounds of apples will she eat each day?

Answer:
Here, Rache bought \(\frac{1}{4}\) pound of apples and she wants to share them divide them equally over 2 days as a snack, so the number of pounds of apples will she eat each day is \(\frac{1}{4}\) ÷ 2 which is \(\frac{1}{8}\).

b. \(\frac{1}{4}\) ÷ 2

Answer:
The number of slices of cake will she eat each day is \(\frac{1}{8}\).

Explanation:
Monica bought \(\frac{1}{4}\) of cake. She wants to share them divide them equally over 2 days as a snack. How many pieces of cake will she eat each day?

Answer:
Here, Monica bought \(\frac{1}{4}\) of cake and she wants to share them divide them equally over 2 days as a snack, so the number of slices of cake will she eat each day is \(\frac{1}{4}\) ÷ 2 which is \(\frac{1}{8}\).

c. \(\frac{1}{3}\) ÷ 5

Answer:
The number of cookies in each bag is \(\frac{1}{15}\).

Explanation:
Park bought \(\frac{1}{3}\) of cookies. He wants to share them divide them equally over 5 bags. How many cookies will he have in each bag?

Answer:
Here, Park bought \(\frac{1}{3}\) of cookies and he wants to share them divide them equally over 5 bags, so the number of cookies in each bag is \(\frac{1}{3}\) ÷ 5 which is \(\frac{1}{15}\).

d. 3 ÷ \(\frac{1}{10}\)

Answer:
The number of toffies in each bag is \(\frac{1}{30}\).

Explanation:
Nancy bought \(\frac{1}{10}\) of toffies. She wants to share them divide them equally over 3 bags. How many toffies will she have in each bag?

Answer:
Here, Nancy bought \(\frac{1}{10}\) of toffies and she wants to share them divide them equally over 3 bags, so the number of cookies in each bag is \(\frac{1}{10}\) ÷ 3 which is \(\frac{1}{30}\).

Engage NY Eureka Math 5th Grade Module 4 Lesson 26 Answer Key

Eureka Math Grade 5 Module 4 Lesson 26 Problem Set Answer Key

Question 1.
Draw a model or tape diagram to solve. Use the thought bubble to show your thinking. Write your quotient in the blank. Use the example to help you.

a. \(\frac{1}{3}\) ÷ 2 = __________

Answer:
\(\frac{1}{3}\) ÷ 2 = \(\frac{1}{6}\).

Explanation:
Given that \(\frac{1}{3}\) ÷ 2.
1 third ÷ 2
= 2 sixth ÷ 2
= 1 sixth.
So \(\frac{1}{3}\) ÷ 2 = \(\frac{1}{6}\).

b. \(\frac{1}{3}\) ÷ 4 = __________

Answer:
\(\frac{1}{3}\) ÷ 4 = \(\frac{1}{12}\).

Explanation:
Given that \(\frac{1}{3}\) ÷ 4.
1 third ÷ 4
= 4 twelths ÷ 4
= 1 twelfth.
So \(\frac{1}{3}\) ÷ 4 = \(\frac{1}{12}\).

c. \(\frac{1}{4}\) ÷ 2 = __________

Answer:
\(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\).

Explanation:
Given that \(\frac{1}{4}\) ÷ 2.
1 fourth ÷ 2
= 2 eighths ÷ 2
= 1 eighth.
So \(\frac{1}{4}\) ÷ 2 = \(\frac{1}{8}\).

d. \(\frac{1}{4}\) ÷ 3 = __________

Answer:
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\).

Explanation:
Given that \(\frac{1}{4}\) ÷ 3.
1 fourth ÷ 3
= 3 twelfths ÷ 3
= 1 twelfth.
So \(\frac{1}{3}\) ÷ 2 = \(\frac{1}{6}\).

Question 2.
Divide. Then, multiply to check.

a. \(\frac{1}{2}\) ÷ 7

Answer:
\(\frac{1}{2}\) ÷ 7 = 14.

Explanation:
Given that \(\frac{1}{2}\) ÷ 7 which is 14. Now we need to check, so
\(\frac{1}{14}\) × 7 which is \(\frac{1}{2}\).

b. \(\frac{1}{3}\) ÷ 6

Answer:
\(\frac{1}{3}\) ÷ 6 = 18.

Explanation:
Given that \(\frac{1}{3}\) ÷ 6 which is 18. Now we need to check, so
\(\frac{1}{18}\) × 6 which is \(\frac{1}{3}\).

c. \(\frac{1}{4}\)÷ 5

Answer:
\(\frac{1}{4}\) ÷ 5 = 20.

Explanation:
Given that \(\frac{1}{4}\) ÷ 5 which is 20. Now we need to check, so
\(\frac{1}{20}\) × 5 which is \(\frac{1}{4}\).

d. \(\frac{1}{5}\) ÷ 4

Answer:
\(\frac{1}{5}\) ÷ 4 = 20.

Explanation:
Given that \(\frac{1}{5}\) ÷ 4 which is 20. Now we need to check, so
\(\frac{1}{20}\) × 4 which is \(\frac{1}{5}\).

e. \(\frac{1}{5}\) ÷ 2

Answer:
\(\frac{1}{5}\) ÷ 2 = 10.

Explanation:
Given that \(\frac{1}{5}\) ÷ 2 which is 10. Now we need to check, so
\(\frac{1}{10}\) × 2 which is \(\frac{1}{5}\).

f. \(\frac{1}{6}\) ÷ 3

Answer:
\(\frac{1}{6}\) ÷ 3 = 18.

Explanation:
Given that \(\frac{1}{6}\) ÷ 3 which is 18. Now we need to check, so
\(\frac{1}{18}\) × 3 which is \(\frac{1}{6}\).

g. \(\frac{1}{8}\) ÷ 2

Answer:
\(\frac{1}{8}\) ÷ 2 = 16.

Explanation:
Given that \(\frac{1}{8}\) ÷ 2 which is 16. Now we need to check, so
\(\frac{1}{16}\) × 2 which is \(\frac{1}{16}\).

h. \(\frac{1}{10}\) ÷ 10

Answer:
\(\frac{1}{10}\) ÷ 10 = 100.

Explanation:
Given that \(\frac{1}{10}\) ÷ 10 which is 1. Now we need to check, so
\(\frac{1}{100}\) × 10 which is \(\frac{1}{10}\).

Question 3.
Tasha eats half her snack and gives the other half to her two best friends for them to share equally. What portion of the whole snack does each friend get? Draw a picture to support your response.

Answer:
Each friend gets \(\frac{1}{4}\) of the snack.

Explanation:
Given that Tasha eats half her snack and gives the other half to her two best friends for them to share equally, so the portion of the whole snack does each friend get is
\(\frac{1}{2}\) ÷ 2 = 1 half ÷ 2
= 2 fourths ÷ 2
= 1 fourth.
So each friend gets \(\frac{1}{4}\) of the snack.

Question 4.
Mrs. Appler used \(\frac{1}{2}\) gallon of olive oil to make 8 identical batches of salad dressing.

a. How many gallons of olive oil did she use in each batch of salad dressing?

Answer:
\(\frac{1}{16}\) gal olive oil in each batch.

Explanation:
Given that a gallons of olive oil did she use in each batch of salad dressing, so
\(\frac{1}{2}\) ÷ 8 = \(\frac{8}{16}\) ÷ 8
= 8 sixteenth ÷ 8
= \(\frac{1}{16}\) gal olive oil in each batch.

b. How many cups of olive oil did she use in each batch of salad dressing?

Answer:
She uses 1 cup of olive in each batch of salad dressing.

Explanation:
The number of cups of olive oil did she use in each batch of salad dressing is
1 gallon = 16 cups and \(\frac{1}{16}\) = 1 cups, so she uses 1 cup of olive in each batch of salad dressing.

Question 5.
Mariano delivers newspapers. He always puts \(\frac{3}{4}\) of his weekly earnings in his savings account and then divides the rest equally into 3 piggy banks for spending at the snack shop, the arcade, and the subway.

a. What fraction of his earnings does Mariano put into each piggy bank?

Answer:
Mariano puts \(\frac{1}{12}\) of his earnings in each piggy bank.

Explanation:
Given that Mariano delivers newspapers and puts \(\frac{3}{4}\) of his weekly earnings in his savings account and then divides the rest equally into 3 piggy banks for spending at the snack shop, the arcade, and the subway. So the fraction of his earnings that Mariano put into each piggy bank is
\(\frac{1}{4}\) ÷ 3 = 1 fourth ÷ 3
= 3 twelfths ÷ 3
= 1 twelfth.
So Mariano puts \(\frac{1}{12}\) of his earnings in each piggy bank.

b. If Mariano adds $2.40 to each piggy bank every week, how much does Mariano earn per week delivering papers?

Answer:
Mariano earns per week delivering papers is $7.20 × 4 which is $28.8.

Explanation:
Given that Mariano adds $2.40 to each piggy bank every week which is $2.40 × 3 = $7.20 , so Mariano earn per week delivering papers is $7.20 × 4 which is $28.8.

Eureka Math Grade 5 Module 4 Lesson 26 Exit Ticket Answer Key

Question 1.
Solve. Support at least one of your answers with a model or tape diagram.

a. \(\frac{1}{2}\) ÷ 4 = ______

Answer:
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).

Explanation:
Given that \(\frac{1}{2}\) ÷ 4.
1 second ÷ 2
= 2 eights ÷ 2
= 1 eights.
So \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).

b. \(\frac{1}{8}\) ÷ 5 = ______

Answer:
\(\frac{1}{8}\) ÷ 5 = \(\frac{1}{40}\).

Explanation:
Given that \(\frac{1}{8}\) ÷ 5.
1 eight ÷ 5
= 5 forty ÷ 5
= 1 forty.
So \(\frac{1}{8}\) ÷ 5 = \(\frac{1}{40}\).

Question 2.
Larry spends half of his workday teaching piano lessons. If he sees 6 students, each for the same amount of time, what fraction of his workday is spent with each student?

Answer:
The fraction of his workday is spent with each student is \(\frac{1}{12}\).

Explanation:
Given that Larry spends half of his workday teaching piano lessons. And the duration of piano lessons is \(\frac{1}{2}\). As he sees 6 students, each for the same amount of time. So,
the duration of teaching each student = duration of teaching piano lessons ÷ Number of students.
= \(\frac{1}{2}\) ÷ 6
= \(\frac{1}{2}\) × 6
= \(\frac{1}{12}\).
So the fraction of his workday is spent with each student is \(\frac{1}{12}\).

Eureka Math Grade 5 Module 4 Lesson 26 Homework Answer Key

Question 1.
Solve and support your answer with a model or tape diagram. Write your quotient in the blank.
a. \(\frac{1}{2}\) ÷ 4 = ______

Answer:
\(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).

Explanation:
Given that \(\frac{1}{2}\) ÷ 4.
1 second ÷ 2
= 2 eights ÷ 2
= 1 eight.
So \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\).

b. \(\frac{1}{3}\) ÷ 6 = ______

Answer:
\(\frac{1}{3}\) ÷ 6 = \(\frac{1}{18}\).

Explanation:
Given that \(\frac{1}{3}\) ÷ 6.
1 third ÷ 6
= 6 eighteens ÷ 6
= 1 eighteen.
So \(\frac{1}{3}\) ÷ 6 = \(\frac{1}{18}\).

c. \(\frac{1}{4}\)÷ 3 = ______

Answer:
\(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\).

Explanation:
Given that \(\frac{1}{4}\) ÷ 3.
1 fourth ÷ 3
= 3 twelfths ÷ 3
= 1 twelfths.
So \(\frac{1}{4}\) ÷ 3 = \(\frac{1}{12}\).

d. \(\frac{1}{5}\) ÷ 2 = ______

Answer:
\(\frac{1}{5}\) ÷ 2 = \(\frac{1}{10}\).

Explanation:
Given that \(\frac{1}{5}\) ÷ 2.
1 fifth ÷ 2
= 2 tens ÷ 2
= 1 ten.
So \(\frac{1}{5}\) ÷ 2 = \(\frac{1}{10}\).

Question 2.
Divide. Then, multiply to check.

a. \(\frac{1}{2}\) ÷ 10

Answer:
\(\frac{1}{2}\) ÷ 10 = 20.

Explanation:
Given that \(\frac{1}{2}\) ÷ 10 which is 20. Now we need to check, so
\(\frac{1}{20}\) × 10 which is \(\frac{1}{2}\).

b. \(\frac{1}{4}\) ÷ 10

Answer:
\(\frac{1}{4}\) ÷ 10 = 40.

Explanation:
Given that \(\frac{1}{4}\) ÷ 10 which is 40. Now we need to check, so
\(\frac{1}{40}\) × 10 which is \(\frac{1}{4}\).

c. \(\frac{1}{3}\)÷ 5

Answer:
\(\frac{1}{3}\) ÷ 5 = 15.

Explanation:
Given that \(\frac{1}{3}\) ÷ 5 which is 15. Now we need to check, so
\(\frac{1}{15}\) × 5 which is \(\frac{1}{3}\).

d. \(\frac{1}{5}\) ÷ 3

Answer:
\(\frac{1}{5}\) ÷ 3 = 15.

Explanation:
Given that \(\frac{1}{5}\) ÷ 3 which is 15. Now we need to check, so
\(\frac{1}{15}\) × 3 which is \(\frac{1}{15}\).

e. \(\frac{1}{8}\) ÷ 4

Answer:
\(\frac{1}{8}\) ÷ 4 = 32.

Explanation:
Given that \(\frac{1}{8}\) ÷ 4 which is 32. Now we need to check, so
\(\frac{1}{32}\) × 4 which is \(\frac{1}{8}\).

f. \(\frac{1}{7}\) ÷ 3

Answer:
\(\frac{1}{7}\) ÷ 3 = 21.

Explanation:
Given that \(\frac{1}{7}\) ÷ 3 which is 21. Now we need to check, so
\(\frac{1}{21}\) × 3 which is \(\frac{1}{7}\).

g. \(\frac{1}{10}\) ÷ 5

Answer:
\(\frac{1}{10}\) ÷ 5 = 50.

Explanation:
Given that \(\frac{1}{10}\) ÷ 5 which is 50. Now we need to check, so
\(\frac{1}{50}\) × 5 which is \(\frac{1}{10}\).

h. \(\frac{1}{5}\) ÷ 20

Answer:
\(\frac{1}{5}\) ÷ 20 = 100.

Explanation:
Given that \(\frac{1}{5}\) ÷ 20 which is 100. Now we need to check, so
\(\frac{1}{100}\) × 20 which is \(\frac{1}{5}\).

Question 3.
Teams of four are competing in a quarter-mile relay race. Each runner must run the same exact distance. What is the distance each teammate runs?

Answer:
Each person will run \(\frac{1}{16}\) miles.

Explanation:
Given that there are teams of four are competing in a quarter-mile relay race and each runner must run the same exact distance, so the distance each teammate runs is,
so each person will run = the total distance ÷ number of persons in a team
= \(\frac{1}{4}\) ÷ 4
= \(\frac{1}{4}\) × \(\frac{1}{4}\)
= \(\frac{1}{16}\).
so each person will run \(\frac{1}{16}\) miles.

Question 4.
Solomon has read \(\frac{1}{3}\) of his book. He finishes the book by reading the same amount each night for 5 nights.

a. What fraction of the book does he read each of the 5 nights?

Answer:
Solomon reads \(\frac{2}{15}\) of the book each night.

Explanation:
Given that Solomon has read \(\frac{1}{3}\) of his book, so 1 – \(\frac{1}{3}\) which is \(\frac{2}{3}\) of the book is left to be read. And we have that, in 5 nights Solomon reads \(\frac{2}{3}\) of the book. So for 1 night he will read \(\frac{2}{3}\) × \(\frac{1}{5}\) which is \(\frac{2}{15}\) of the book.

b. If he reads 14 pages on each of the 5 nights, how long is the book?

Answer:
The total number of pages in the book is 105.

Explanation:
Let the total number of books be X, as he reads 14 pages on each of the 1 night. So he reads 14 × 5 which is 70 pages in 5 nights. So \(\frac{2}{3}\)of the total pages is 70, which is
\(\frac{2}{3}\) X = 70, on solving we will get
X = 105.
So the total number of pages in the book is 105.

Engage NY Eureka Math 5th Grade Module 4 Lesson 4 Answer Key

Eureka Math Grade 5 Module 4 Lesson 4 Problem Set Answer Key

Question 1.
Draw a tape diagram to solve. Express your answer as a fraction. Show the multiplication sentence to check your answer. The first one is done for you.
a. 1 ÷ 3 = \(\frac{1}{3}\)

b. 2 ÷ 3 =
Answer:
2/3

Explanation:

c. 7 ÷ 5 =
Answer:
1 2/5

Explanation:

d. 14 ÷ 5 =
Answer:
2 4/5

Explanation:

Question 2.
Fill in the chart. The first one is done for you.

Answer:

Question 3.
Greg spent $4 on 5 packs of sport cards.
a. How much did Greg spend on each pack?
Answer:
Greg spent $80 on each pack.

Explanation:

5 units = $4
1 unit = $4 ÷ 5 = 4/5
4/5 of $1= $80

b. If Greg spent half as much money and bought twice as many packs of cards, how much did he spend on each pack? Explain your thinking.
Answer:
He spent $20 dollars on each pack.

Explanation:

10 units = $2
1 unit = 2 ÷ 10 = 2/10 = 1/5
1/5 of $1 = $20. Hence he spent $20 on each pack.

Question 4.
Five pounds of birdseed is used to fill 4 identical bird feeders.
a. What fraction of the birdseed will be needed to fill each feeder?
Answer:
1/4

Explanation:
There are 4 identical bird feeders, so 1/4 of the birdseed would be needed to fill each feeder.

b. How many pounds of birdseed are used to fill each feeder? Draw a tape diagram to show your thinking.
Answer:
1 1/4
4 units = 5lb
1 unit = 5lb ÷ 4
= 5/4
= 1 1/4

Explanation:

1 1/4 lb of birdseed is used to fill each feeder.

c. How many ounces of birdseed are used to fill three bird feeders?
Answer:
1 lb = 16 oz
1 1/4 = x
= 1 1/4 * 16 oz
= 16 oz + 4 oz
= 20 oz
1 unit = 20ounces
3 units  = 3*20 = 60 ounces

Explanation:
60 ounces of birdseed are used to fill three birdfeeders.

Eureka Math Grade 5 Module 4 Lesson 4 Exit Ticket Answer Key

Matthew and his 3 siblings are weeding a flower bed with an area of 9 square yards. If they share the job equally, how many square yards of the flower bed will each child need to weed? Use a tape diagram to show your thinking.
Answer:
Each child will need to weed   =2  1/4 square yards

Explanation:
Matthew and his 3 siblings are weeding a flower bed with an area of 9 square yards.
Matthew and his 3 siblings   = 1 + 3 = 4
The Total area given is = 9  square yards.
Hence, Each child will need to weed   = 9/4  square  yards
                                                = 2  1/4 square yards

Eureka Math Grade 5 Module 4 Lesson 4 Homework Answer Key

Question 1.
Draw a tape diagram to solve. Express your answer as a fraction. Show the addition sentence to support your answer. The first one is done for you.
a. 1 ÷ 4 = \(\frac{1}{4}\)

b. 4 ÷ 5 =
Answer:

c. 8 ÷ 5 =
Answer:
8/5 = 1 3/8

Explanation:

d. 14 ÷ 3 =
Answer:
2 4/5

Explanation:

Question 2.
Fill in the chart. The first one is done for you.

Answer:

Question 3.
Jackie cut a 2-yard spool into 5 equal lengths of ribbon.
a. What is the length of each ribbon in yards? Draw a tape diagram to show your thinking.
Answer:
2/5 yard

Explanation:
2 ÷ 5 = 2/5 yards

b. What is the length of each ribbon in feet? Draw a tape diagram to show your thinking.
Answer:
1 1/5 ft

Explanation:

1 yd * 0.4 / 3ft * 0.4 = 2/5 yard / ? feet
3 * 2/5 = 6/5 = 1 1/5

Question 4.
Baa Baa, the black sheep, had 7 pounds of wool. If he separated the wool equally into 3 bags, how much wool would be in 2 bags?
Answer:
4 2/3 pounds
Explanation:

2 bags = 2 1/3 + 2 1/3
= 4 2/3 pounds

Question 5.
An adult sweater is made from 2 pounds of wool. This is 3 times as much wool as it takes to make a baby sweater. How much wool does it take to make a baby sweater? Use a tape diagram to solve.
Answer:
2 lbs

Explanation: