Irrational numbers are one type of number in mathematics that cannot be expressed as a fraction. A number line is a straight line with numbers placed at equal intervals along its length. On this page, you can learn the simple way to represent a square root number on the number line using the Pythagoras theorem. Check more details like how to represent irrational numbers on the number line and problems on it.
Representing Irrational Numbers on The Number Line
We use a simple concept called the Pythagoras theorem for the representation of irrational numbers on the number line. We already know that, irrational number can never be written in the form of \(\frac { a }{ b } \). Some of the examples are √2, √5, √7, and so on.
Let us take a right-angled triangle ABC with AB, BC, CA as perpendicular, base, hypotenuse sides and AB = x units, BC = y units, the hypotenuse AC = √(x² + y²). Following are the steps that are helpful to point the irrational number on the number line.
- Draw a number line and mark the centre point as zero.
- Mark the right side of zero as positive numbers and the left side as negative numbers.
- Decide to take the left side or right side based on the given irrational number.
- Draw a perpendicular line to the real number such that the new line has a length of 1 unit.
- Join the point (0) and the end of a new line of unity length to form a right-angled triangle.
- Name perpendicular side as AB, base as BC, and hypotenuse as AC of the right-angled triangle ABC.
- The length of hypotenuse AC can be calculated by applying Pythagoras theorem.
- Now take AC as the radius, C as the centre and cut an arc on the same number line and name that point as D.
- Since AC is the radius of the arc and CD is the length of the irrational number.
- Hence, D is the representation of an irrational number on the number line.
More Related Articles:
Questions on Representation of Irrational Numbers on The Number Line
Question 1:
Represent √2 on the number line.
Solution:
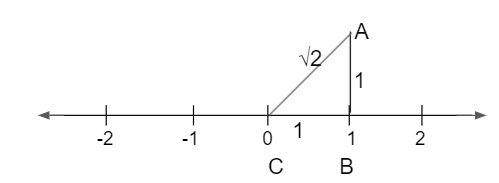
To represent √2 on the number line, draw a number line.
Draw a line perpendicular to point 1 and its length should be 1 unit.
Join points 0, end of the new line and that right-angle triangle.
Using the Pythagorean theorem,
AC² = AB² + BC²
= 1² + 1² = 2
AC = √2
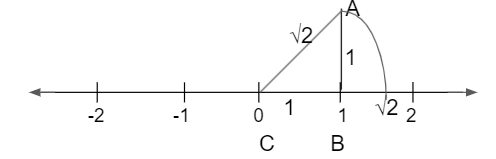
Take 0 as centre C, with AC as radius, cut the number line at point D which is √2
Question 2:
Represent √5 on the number line.
Solution:
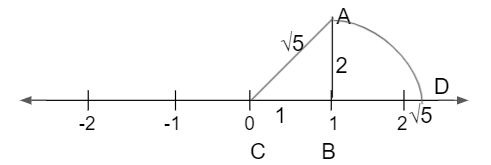
To represent √5 on the number line, draw a number line.
Draw a line perpendicular to point 1 and its length should be 2 units.
Join points 0, end of the new line and that right-angle triangle.
Using the Pythagorean theorem,
AC² = AB² + BC²
= 2² + 1² = 5
AC = √5
Take 0 as centre C, with AC as radius, cut the number line at point D which is √5.
Question 3:
How to represent √3 on the number line?
Solution:
To represent √3 on a number line, we have to represent √2 on it.
At √2 on the number line, draw a line that is perpendicular to AB from point A such that the new line has unit length and a new point is E.
Join C and E. Using Pythagoras theorem,
AE² + Ac² = EC²
EC² = 1² + (√2)² = 1 + 2 = 3
EC = √3
With C as centre and EC as radius, cut the number line at F which is √3.

