Relations are one of the main topics of the set theory. Sets, relations, and functions are interrelated. Sets are the collection of ordered elements. Relation means the connection between the two sets. Have a look at the definition of Relations in Math definition, types of relations, and solved example questions in the below sections of this page.
Also, Read: Worksheet on Math Relation
Relation in Math – Definition
A relation in math defines the relationship between two or more different sets. A set of ordered pairs is also defined as the relation. Let us take two sets, if there is a relation between them that will be established, then there is a connection between the elements of the two sets. Mapping represents the relation.
Example:
Let two sets are A = {10, 20, 30, 45, 50}, B = {a, b, c, d}
The relation from set A into B is a subset of A x B.
A x B = {10, 20, 30, 45, 50} x {a, b, c, d}
= {(10, a), (10, b) (10, c), (10, d), (20, a), (20, b), (20, c), (20, d), (30, a), (30, b), (30, c), (30, d), (45, a), (45, b), (45, c), (45, d), (50, a), (50, b), (50, c), (50, d)}
The ordered pairs (10, c), (20, b), (30, d), (50, b)
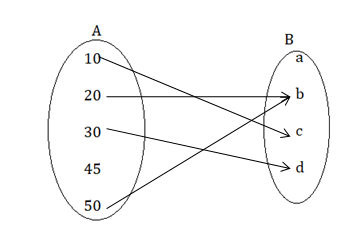
The first set A {10, 20, 30, 45, 50} represents the domain.
The second set B {a, b, c, d} represents the range.
Representation of Relation in Math
In general, the relation is denoted by R. The relation in math from set A to set B is represented in any of three ways.
- Set Builder Form
- Roster Form
- Arrow Diagram
Set Builder Form:
In the set-builder form, the relation R from setA to set B is R = {(a, b): ∈ A, b ∈ B, a . . b}, the blank space is replaced by the rule which associates a and b.
Example:
A = {2, 4, 5, 6, 8}, B = {4, 6, 8, 9}
Let R = {(2, 4), (4, 6), (6, 8), (8, 10)}
The set builder form of R = {(a, b): ∈ A, b ∈ B a is 2 less than b}
Roster Form:
The roster form of the relation R from set A to set B is represented as the set of ordered pairs. In every ordered pair, 1st component is collected from set A, and 2nd component is collected from set B.
Example:
If A = {1, 8, 5}, B = {p, q, r}
then R = {(1, ), (8, p), (5, r)}
Hence, R ⊆ A × B
Arrow Diagram:
You need to draw two circles to represent two sets. Write elements in their corresponding sets. Draw arrows from set A to B which satisfy the relation and indicate the ordered pairs.
Example:
If A = {2, 4, 5, 6, 8} and B = {4, 6, 8, 9}
Then the relation from set A to set B is R = {(2, 4), (4, 6), (4, 8), (5, 8), (6, 9)}
Draw a diagram to represent the relation.

Types of Relations
There are 8 types of relations. They are along the lines.
1. Empty Relation:
It is also known as void relation. If there is no relation between any elements of a set, then it is an empty relation. The representation is R = Φ ⊂ A x A.
2. Transitive Relation:
In a transitive relation, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R. The representation is aRb and bRc ⇒ aRc such that a, b, c ∈ A.
3. Identity Relation:
Identity relation means every element of a set is related to itself only. The representation is i = {(a, a), a ∈ A}
4. Inverse Relation:
If a set has elements that are inverse pairs of another set, then it is called inverse relation. The representation is R-1 = {(b, a): (a, b) ∈ R}
5. Universal Relation:
In universal relation, every element of a set is related to each other. The representation is R = A x A.
6. Reflexive Relation:
In reflexive relation, every element maps to itself. The representation is (a, a) ∈ R.
7. Symmetric Relation:
If a = b is true then b = a is also true in a symmetric relation. The representation is aRb ⇒ bRa, such that a, b ∈ A.
8. Equivalence Relation:
If a relation is reflexive, symmetric, and transitive at the same time then it called the equivalence relation.
Frequently Asked Questions on Relation in Math
1. What is a relation in math?
A relation between two sets is a collection of ordered pairs having one object from each set. If the element x is from the first set and element y is from the second set, then the elements are said to be related if the ordered pair (x, y) is in the relation.
2. What are the example of relation in math?
Let us take two sets as A = {a, b, c, d}, B = {x, y, z}. Then the relation from set A to set b is R = {(a, x), (b, y), (d, z), (c, y)}
3. What is a domain and range?
In any relation, the first set is called the domain and the second set is called the range.
