A puzzle is a game or toy or question that test’s your knowledge. We have different types of puzzles. In general, puzzles are created for entertainment but they can also form mathematical and logical problems. For solving puzzles, students have to recognize patterns and adherence to a particular kind of order. Get to know more details about the mathematical puzzles and the solved questions in the following sections.
Puzzle Meaning
A puzzle is defined as a game or toy or problem that tests a person’s knowledge. An example of a puzzle is New York Times Cross Word.
Types of Puzzles
The different types of puzzles are cryptic puzzles, logic puzzles, math puzzles, mechanical puzzles, number puzzles, trivia puzzles, word puzzles, pattern guessing, riddles, and so on.
More Related Articles:
Benefits of Playing Puzzles
The benefits of solving the math puzzles are listed here.
- Students who practice solving puzzle questions gain more knowledge and improve problem-solving skills
- Solving number puzzles is helpful for the students at every stage.
- During primary school, every student has to solve math puzzles to create interest in mathematics.
- It not only develops kid’s mathematical skills but also logical thinking.
How to Solve Math Puzzles?
The following are basic tips & tricks to solve the math puzzles.
- Observe the given question carefully.
- Check the numbers, patterns of the puzzle.
- Imagine the concept of the puzzle and the way of the puzzle theme is given.
- Apply the arithmetic operations i.e., addition, subtractions, multiplication, division, and also square roots, etc., and the chances to the given conditions of the number puzzle.
- The operation that satisfies the given conditions is the answer to the puzzle.
Puzzle Questions and Answers
Question 1:
Ramu has to distribute 19 sheep among 3 brothers in such a way that the eldest gets half of all the cows, the middle brother gets one fourth and the youngest one gets fifth. But no sheep should be left.
Solution:
Ramu has to borrow one sheep from any one person.
The total number of sheep becomes 19 + 1 = 20
As, stated eldest brother gets 1/2 of 20 sheep = 10 sheep
Middle brother gets 1/4 of total sheep = 1/4 x 20 = 5 sheep
Youngest brother gets 1/5 of total sheep = 1/5 of 20 = 4 sheep
The total number of sheep distributed = 10 + 5 + 4
= 19 sheep
The remaining one sheep is returned. So, no sheep has remained.
Question 2:
Write the next three numbers in the series
(i) 10, 20, 30, _, _, _
(ii) 10, 9, 8, _, _, _
(iii) 1, 3, 5, 7, 9, _, _, _
Solution:
(i) The given series is 10, 20, 30, _, _, _
The series is multiple of 10 and the list is natural numbers.
1 x 10 = 10
2 x 10 = 20
3 x 10 = 30
So, 4 x 10 = 40
5 x 10 = 50
6 x 10 = 6
The next three numbers in the series are 40, 50, 60
(ii) The given series is 10, 9, 8, _, _, _
The series in the reverse order of natural numbers starting from 10
10 – 9 = 1
9 – 8 = 1
8 – 7 = 1
7 – 6 = 1
6 – 5 = 1
Therefore, the next three numbers in the series are 7, 6, 5.
(iii) The given series is 1, 3, 5, 7, 9, _, _, _
The numbers in the series are prime numbers.
Prime numbers are the numbers that are divisible by 1 and the number itself.
The next 3 prime numbers are 11, 13, 17
Question 3:
Write a 3 x 3 magic square that has numbers from 1 to 9 and sum of rows or columns or diagonals is 15.
Solution:
Given that,
The list of numbers in the 3 x 3 square should be 1, 2, 3, 4, 5, 6, 7, 8, 9
The sum of numbers in every row = 15
The sum of numbers in every column = 15
The sum of numbers in every diagonal = 15
The possibility of the arrangement of numbers is given below.
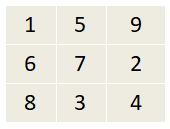
Check the condition:
The sum of numbers in 1st row = 1 + 5 + 9 = 15
The sum of numbers in 2nd row = 6 + 7 + 2 = 15
The sum of numbers in 3rd row = 8 + 3 + 4 = 15
The sum of numbers in 1st column = 1 + 6 + 8 = 15
The sum of numbers in 2nd column = 5 + 7 + 3 = 15
The sum of numbers in 3rd column = 9 + 2 + 4 = 15
The sum of numbers in one diagonal = 1 + 7 + 4 = 15
The sum of numbers in second diagonal = 9 + 7 + 8 = 15
