Students may feel difficult and confusing to solve triangle congruence problems. No need to worry we are here to give the complete information regarding the Congruency of Triangles that helps to solve the questions easily. If two triangles have three angles, three sides of equal measure, then they are called congruent triangles.
Solve the triangles congruency problems by referring to the six different conditions for the congruency of triangles. In the following sections, students can see the techniques and criteria applied while solving the triangles congruency problems.
Also, Check
Problems on Congruency of Triangles With Answers
Students who want to be perfect in the geometry and measurement chapter can check the below modules and solve the questions. These different solving techniques are helpful to prepare well for the exam.
Problem 1:
In the given figures, prove that two triangles are congruent.
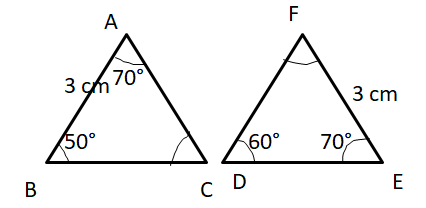
Solution:
In ∆ABC, ∠BAC + ∠ABC + ∠BCA = 180°
70° + 50° + ∠BCA = 180°
120° + ∠BCA = 180°
∠BCA = 180° – 120° = 60°
In ∆ABC and ∆DEF,
AB = EF = 3 cm
∠BAC = ∠FED = 70°, ∠BCA = ∠FDE = 60°
Therefore, by AAS (Angle-Side-Angle) criterion the two triangles are congruent.
Problem 2:
In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ≅ ∆CBD.
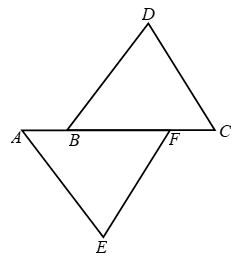
Solution:
Given that,
AB = CF
So, AB + BF = BF + CF
AF = BC
Corresponding sides are EF = BD, AF = BC
Corresponding angle is ∠AFE = ∠DBC
Therefore, by SAS (Side-Angle-Side) criterion the two triangles are congruent.
Problem 3:
In the given figure PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.
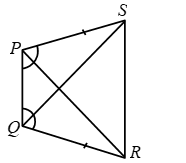
Solution:
Given that,
PS = QR and ∠SPQ = ∠RQP
In both triangles ∆PQS, ∆PQR, PQ is the common side. So, PQ = PQ
Corresponding sides are PS = QR, PQ = PQ
The corresponding angle is ∠SPQ = ∠RQP
By SAS congruence criteria ∆PQS ≅ ∆PQR
So, PR = QS and ∠QPR = ∠PQS.
Problem 4:
PQR and XYZ are two triangles in which PQ = XY and ∠PRQ = 90°, ∠PQR = 50°, ∠XYZ = 40°, and ∠YXZ = 50°. Prove that the two triangles are congruent.
Solution:
In a triangle, the sum of three angles is 180°.
Therefore, in ∆XYZ, ∠XYZ + ∠YXZ + ∠YZX = 180°
40° + 50° + ∠YZX = 180°
90° + ∠YZX = 180°
∠YZX = 180° – 90°
∠YZX = 90°
In ∆PQR and ∆XYZ,
PQ = XZ, ∠PRQ = ∠XZY = 90° and ∠PQR = ∠YXZ = 50°.
Therefore, by AAS (Angle-Angle-Side) criterion, the two triangles are congruent.
Problem 5:
Prove the following triangles are congruent using RHS Criterion. If M is the midpoint of the line.
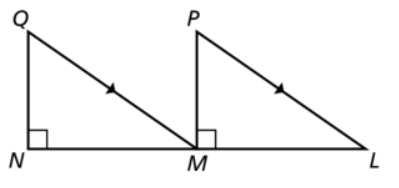
Solution:
Given that,
M is the midpoint of the line NL.
So, MN = ML
QM = PL
∠QNM = ∠PML
Congruent hypotenuse QM = PL
Congruent side NM = ML
Congruent angle ∠QNM = ∠PML = 90°
Therefore, by RHS (Right-angled Hypotenuse Side) criterion, the two triangles are congruent.
Problem 6:
Check if the given triangles below are congruent and state the criterion test for congruence in triangles.
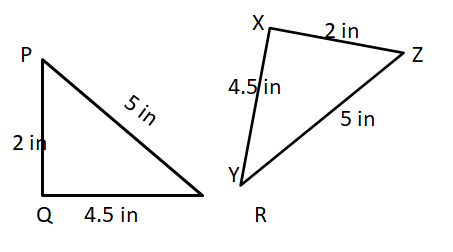
Solution:
By observing both triangles.
Congruent sides are PQ = XZ = 2 in
PR = YZ = 5 in
QR = XY = 4.5 in
Therefore, by SSS (Side-Side-Side) criterion, the two triangles are congruent.
