Do you want to know What is linear pair of angles? Linear Pair of Angles are similar to adjacent angles but only the difference is adding two angles we get 180º in linear angles. Linear Pair of Angles will also have a common vertex, common arm like adjacent angles. Their interiors will also do not overlap. Remember that all adjacent angles may not form a linear pair. Learn all the Lines and Angles concepts in one place on our website.
Properties of Linear Pair of Angles
Check the below Linear Pair of Angles properties listed below.
- They have a common vertex.
- They have a common arm.
- Also, they do not overlap.
- The sum of the angles is 180°.
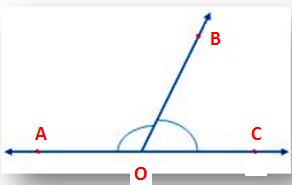
From the above figure, AO and OC are two opposite rays and ∠AOB and ∠BOC are the adjacent angles. Therefore, ∠AOB and ∠BOC form a linear pair.
Explanation for Linear Pair of Angles
The angle between the two straight lines is 180° and they form a straight angle. The line segment is the portion of a line that consists of two endpoints. Also, a line with one endpoint is known as a ray. If you consider a line mn and the middle point is o. A ray OP dividing the two lines MO and ON. The complete angle MOP and angle PON becomes 180º to form a linear pair of angles.
∠MOP + ∠PON = ∠MON = 180°
We have also given Lines and Angles concepts and problems for free of cost on our website.
Axioms
Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.

From the above figure, there are different line segments available that are passing through point O. From the figure, we can say that Angle BOD and Angle BOC are Linear Pair of Angles.
Linear Pair of Angles Examples
In the given figure, ∠AOC and ∠ BOC form a linear pair if x – y = 50°, find the value of x and y.
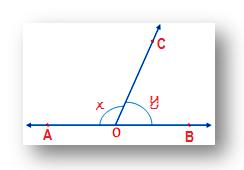
Solution:
Given x – y = 50° ………… (i)
We know that, x + y = 180° ………… (ii)
Adding (i) and (ii)
x – y + x + y = 180° + 50°
2x = 230°
x = 240°/2
Therefore, x = 115°
Since, x – y = 50°
or, 115° – y = 50°
or, 115° – 115° – y = 50° – 115°
or, -y = -65°
Therefore, y = 65°
The final answer is x = 115° and y = 65°.