Quick and easy learning is possible with Go Math Grade 7 Answer Key Chapter 7 Writing and Solving One-Step Inequalities. The answers in Go Math Grade 7 are prepared by the concerned subject experts. Go Math Answer Key helps the students of 7th grade to prove their best in the exams. So, Download Go Math Grade 7 Answer Key Chapter 7 Writing and Solving One-Step Inequalities and kickstart your preparation.
Go Math Grade 7 Answer Key Chapter 7 Writing and Solving One-Step Inequalities
It is important to gain knowledge along with the marks. Go Math Answer Key team’s main aim is to provide quality education for students of all grades. You can learn the basics of Writing and Solving One-Step Inequalities in Go Math Grade 7 Chapter 7 Answer key. Check out the topics before you start practicing. Only practice will help you to score the best marks in the exams. Refer to our Go Math Grade 7 Answer Key Chapter 7 Writing and Solving One-Step Inequalities while doing your homework and also during exam preparation. You can know how to draw the number line with the help of Go Math 7th Grade Chapter 7 Writing and Solving One-Step Inequalities.
Chapter 7 – Lesson 1:
Chapter 7 – Lesson: 2
Chapter 7 – Lesson: 3
Chapter 7 – Writing and Solving One-Step Inequalities Lesson: 4
Chapter 7 – Lesson: 5
Chapter 7 – Performance Tasks
Guided Practice – Page No. 208
Write the resulting inequality.
Question 1.
−5 ≤ −2; Add 7 to both sides
Type below:
___________
Answer: 2 ≤ 5
Explanation:
Add 7 to both sides of the inequality.
-5 + 7 ≤ -2 + 7
2 ≤ 5
Question 2.
−6 < −3; Divide both sides by -3
Type below:
___________
Answer: 2 > 1
Explanation:
Divide both sides by -3. switch the inequality sign since you are dividing by a negative number.
-6/-3 > -3/-3
2 > 1
Question 3.
7 > −4; Subtract 7 from both sides
Type below:
___________
Answer: 0 > -11
Explanation:
7 – 7 > -4 – 7
Subtract 7 from both sides
0 > -11
Question 4.
−1 ≥ −8; Multiply both sides by -2
Type below:
___________
Answer: 2 ≤ 16
Explanation:
Multiply both sides by -2 switch the inequality sign since you are multiplying by a negative number.
-1(-2) ≤ -8(-2)
2 ≤ 16
Solve each inequality. Graph and check the solution.
Question 5.
n−5 ≥ −2
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
Solve the inequality first:
n – 5 ≥ -2
n – 5 + 5 ≥ -2 + 5
n ≥ 3
The number opposite the variable is 3, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would look like the one below:
Question 6.
3 + x < 7
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
Solve the inequality first:
3 + x < 7
3 – 3 + x < 7 – 3
x < 4
The number opposite the variable is 4, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would look like the one below:
Question 7.
−7y ≤ 14
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
Solve the inequality first:
−7y ≤ 14
-7y/-7 ≤ 14/-7
y ≥ -2
The number opposite the variable is -2, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would look like the one below:
Question 8.
\(\frac{b}{5}\) > −1
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
Solve the inequality first:
\(\frac{b}{5}\) > −1
Multiply 5 on both sides.
(5)\(\frac{b}{5}\) > −1(5)
b > -5
The number opposite the variable is -5, we look for this in the number line. Since the inequality is >, we use a hollow dot and shade the line going to the right. Its graph would look like the one below:
Question 9.
For a scientific experiment, a physicist must make sure that the temperature of a metal at 0 °C gets no colder than -80 °C. The physicist changes the metal’s temperature at a steady rate of -4 °C per hour. For how long can the physicist change the temperature?
a. Let t represent the temperature in degrees Celsius. Write an inequality. Use the fact that the rate of change in temperature times the number of hours equals the final temperature.
Type below:
___________
Answer:
We need to use the fact that the final temperature is equal to the rate of change in temperature times the number of hours.
We are given that the rate of change is -4°C per hour so the final temperature is -4 times the number of hours.
Let t represent the number of hours. The final temperature is then -4t degrees Celsius after t hours.
If the temperature must be no colder than -80°C, then the final temperature must be greater than or equal to -80.
The inequality is then -4t ≥ -80.
Question 9.
b. Solve the inequality in part a. How long can the physicist change the temperature of the metal?
Type below:
___________
Answer:
To solve the inequality for t, we need to divide both sides by -4. Remember to switch the inequality symbol since you are dividing by a negative number.
Dividing both sides by -4 then gives:
-4t/-4 ≤ -80/-4
t ≤ 20
The number of hours that the physicist can change the temperature of the metal is then at most 20 hours.
Question 9.
c. The physicist has to repeat the experiment if the metal gets cooler than -80 °C. How many hours would the physicist have to cool the metal for this to happen?
Type below:
___________
Answer:
From part (b), we know that the physicist can change the temperature for at most 20 hours to keep the temperature no colder than -80°C. This means the temperature will reach a temperature cooler than -80°C if he cools the metal for more than 20 hours.
Essential Question Check-In
Question 10.
Suppose you are solving an inequality. Under what circumstances do you reverse the inequality symbol?
Type below:
___________
Answer: You must reverse the inequality sign any time you multiply or divide both sides of the inequality by a negative number.
Page No. 209
In 11–16, solve each inequality. Graph and check the solution.
Question 11.
x − 35 > 15
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
x − 35 > 15
Add 35 on both sides
x – 35 + 35 > 15 + 35
x > 50
The number opposite the variable is 50, we look for this in the number line. Since the inequality is >, we use a hollow dot and shade the line going to the right. Its graph would like the one below:
Question 12.
193 + y ≥ 201
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
193 + y ≥ 201
193 + y – 193 ≥ 201 – 193
y ≥ 8
The number opposite the variable is 8, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would like the one below:
Question 13.
−\(\frac{q}{7}\) ≥ −1
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
−\(\frac{q}{7}\) ≥ −1
Multiply both sides by -7
(-7)−\(\frac{q}{7}\) ≥ −1(-7)
q ≤ 7
The number opposite the variable is 7, we look for this in the number line. Since the inequality is ≤, we use a closed dot and shade the line going to the left. Its graph would like the one below:
Question 14.
−12x < 60
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
−12x < 60
Divide both sides by -12
-12x/12 < 60/-12
x > -5
The number opposite the variable is -5, we look for this in the number line. Since the inequality is >, we use a hollow dot and shade the line going to the right. Its graph would like the one below:
Question 15.
5 > z − 3
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
5 > z − 3
Add both sides by 3
5 + 3 > z – 3 + 3
8 > z
z < 8
The number opposite the variable is 8, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would like the one below:
Question 16.
0.5 ≤ \(\frac{y}{8}\)
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
0.5 ≤ \(\frac{y}{8}\)
Multiply both sides by 8
(8)0.5 ≤ \(\frac{y}{8}\)(8)
4 ≤ y
y ≥ 4
The number opposite the variable is 4, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would like the one below:
Question 17.
The vet says that Lena’s puppy will grow to be at most 28 inches tall. Lena’s puppy is currently 1 foot tall. How many more inches will the puppy grow?
Type below:
___________
Answer: not more than 16 inches
Explanation:
Let x be the additional inches the puppy can grow remember 1 foot is 12 inches so the height of the puppy is 12 + x
12 + x ≤ 28
x ≤ 16
Question 18.
In a litter of 7 kittens, each kitten weighs less than 3.5 ounces. Find all the possible values of the combined weights of the kittens.
Type below:
___________
Answer:
All of the kittens must weigh more than 0 ounces so the smallest combined weight is more than 0 ounces. Since there are 7 kittens, each kitten weights less than 3.5 ounces, and 7 × 3.5 = 24.5, then the combined weights of the kittens must be less than 24.5 ounces.
This gives the inequality 0 < w < 24.5
where w is the combined weight of the kittens in ounces.
Question 19.
Geometry
The sides of the hexagon shown are equal in length. The perimeter of the hexagon is at most 42 inches. Find the possible side lengths of the hexagon.

Type below:
___________
Answer: 0 < s ≤ 7
Explanation:
Let s be the side lengths of the hexagon since its sides are all equal in length.
The side lengths of the hexagon must be greater than 0 since lengths can’t be negative or 0 so s > 0.
The perimeter of the figure is the sum of its side lengths so the perimeter of the hexagon must be 6s since it has 6 sides that are all s inches long.
The perimeter is at most 42 inches so 6s ≤ 42.
Dividing both sides by 6 then gives s ≤ 7.
Combining the inequalities s > 0 and s ≤ 7 then gives possible side lengths of 0 < s ≤ 7.
Question 20.
To get a free meal at his favorite restaurant, Tom needs to spend $50 or more at the restaurant. He has already spent $30.25. How much more does Tom need to spend to get his free meal?
Type below:
___________
Answer: at least $ 19.75
Explanation:
Let x be the additional amount he needs to spend. subtract 30.25 on both sides to solve for x.
x + 30.25 ≥ 50
x ≥ 19.75
Question 21.
To cover a rectangular region of her yard, Penny needs at least 170.5 square feet of sod. The length of the region is 15.5 feet. What are the possible widths of the region?
Type below:
___________
Answer: at least 11 feet
Explanation:
Area is the length times width so let w be the width.
Divide both sides by 15.5 to solve for w.
15.5w ≥ 170.5
w ≥ 11
Question 22.
Draw Conclusions
A submarine descends from sea level to the entrance of an underwater cave. The elevation of the entrance is -120 feet. The rate of change in the submarine’s elevation is no greater than -12 feet per second. Can the submarine reach the entrance to the cave in less than 10 seconds? Explain.
Type below:
___________
Answer:
No. Since the rate of descent is less than -12 feet per second and the submarine is descending for less than 10 seconds, the submarine elevation will still be greater than -120. The submarine would have to descend at a rate greater than -12 feet per second to reach the entrance in less than 10 seconds or descend for more than 10 seconds at a rate less than -12 feet per second to reach the entrance.
Page No. 210
The sign shows some prices at a produce stand.

Question 23.
Selena has $10. What is the greatest amount of spinach she can buy?
Type below:
___________
Answer: 3 \(\frac{1}{3}\) pounds
Explanation:
Let x be the number of pounds of spinach. divide both sides by 3 to solve for x.
3x ≤ 10
x ≤ \(\frac{10}{3}\)
x ≤ 3 \(\frac{1}{3}\) pounds
Question 24.
Gary has enough money to buy at most 5.5 pounds of potatoes. How much money does Gary have?
Type below:
___________
Answer: $2.75
Explanation:
Let x be the amount of money he has
Multiply the price per pound of potatoes by the number of pounds.
5.5(0.50) ≤ x
2.75 ≤ x
Question 25.
Florence wants to spend no more than $3 on onions. Will she be able to buy 2.5 pounds of onions? Explain.
Type below:
___________
Answer:
Since each pound of onions costs $1.25, then 2.5 pounds of onions cost $1.25 × 2.5 ≈ 3.13.
Since $3.13 is greater than $3, she will not have enough money if she wants to spend no more than $3.
H.O.T.
Focus on Higher Order Thinking
Question 26.
Counterexamples
John says that if one side of an inequality is 0, you don’t have to reverse the inequality symbol when you multiply or divide both sides by a negative number. Find an inequality that you can use to disprove John’s statement. Explain your thinking.
Type below:
___________
Answer:
A possible counterexample is -2x ≤ 0. Solving this correctly gives x ≥ 0 which means the inequality is true for all non-negative values. If you don’t switch the inequality sign you would get x ≤ 0 which means the inequality would be true for all non-positive numbers
x = -3 is a possible value for x ≤ 0 but -2x = -2(-3) = 6 which is not less than or equal to 0.
Question 27.
Look for a Pattern
Solve x + 1 > 10, x + 11 > 20, and x + 21 > 30. Describe a pattern. Then use the pattern to predict the solution of x + 9,991 > 10,000.
Type below:
___________
Answer:
x + 1 > 10
x > 9
Subtract both sides by 11
x + 11 > 20
x > 9
Subtract both sides by 21.
x + 21 > 30
x > 9
The pattern is that when the number on the left side of the inequality is 9 less than the number on the right side of the inequality, the answer is x > 9.
Since 9991 is 9 less than 10000, x + 9991 > 10,000 ha the solution x > 9
Question 28.
Persevere in Problem Solving
The base of a rectangular prism has a length of 13 inches and a width of \(\frac{1}{2}\) inch. The volume of the prism is less than 65 cubic inches. Find all possible heights of the prism. Show your work.
Type below:
___________
Answer: 0 < h < 10
Explanation:
Let h be the height of the prism. It is given that the prism has a length of 13 inches and a width of 1/2 inches.
Using the formula v = lbh
13(1/2) h< 65
Multiply 2/13 on both sides
2/13 (13/2)h< 2/13 × 65
h < 2 × 5
h < 10
Since the height must be a positive number, then h > 0. Combining h > 0 and h < 10 then gives the final answer of 0 < h < 10.
Guided Practice – Page No. 214
Draw algebra tiles to model each two-step inequality.
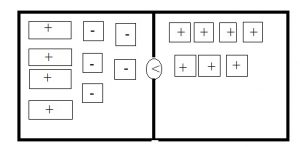
Question 1.
4x − 5 < 7
Type below:
___________
Answer:
On the left side, draw 4 positive rectangles to model 4x and 5 negative squares to represent -5. On the right side, draw 7 positive squares to represent 7. then draw < in the middle.
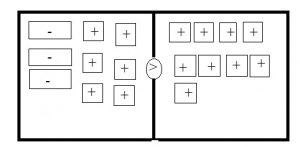
Question 2.
−3x + 6 > 9
Type below:
___________
Answer:
On the left side, draw 3 negative rectangles to model -3x and 6 positive squares to represent 6. On the right side, draw 9 positive squares to represent 9. then draw > in the middle.
Question 3.
The booster club needs to raise at least $7,000 for new football uniforms. So far, they have raised $1,250. Write an inequality to find the average amounts each of the 92 members can raise to meet the club’s objective.
Type below:
___________
Answer: 1250 + 92a ≥ 7000
Explanation:
The amount to be raised is $7000. The amount already raised is $1250. The number of members is 92.
The inequality is then of the form: amount already raised + number of members × amount each member raises ≥ target amount.
The inequality is then:
1250 + 92a ≥ 7000
Question 4.
Analyze what each part of 7x − 18 ≤ 32 means mathematically.
Type below:
___________
Answer:
x is the variable so it is the solution. 7x is the solution multiplied by 7. -18 means 7x is subtracted by 18. ≤ 32 means the result is no more than 32.
Question 5.
Write a real-world problem to represent 7x − 18 ≤ 32.
Type below:
___________
Answer:
A real-world problem could be: The temperature of a metal is currently at -18°C. A scientist will warm the metal at a rate of 7°C per hour until the temperature is 32°C. How many hours will it take to warm up the metal?
Essential Question Check-In
Question 6.
Describe the steps you would follow to write a two-step inequality you can use to solve a real-world problem.
Type below:
___________
Answer:
The first step is to translate the words into an algebraic expression.
The next step is to determine the target amount.
The third step is to determine what inequality sign to use by determining if you need to be greater than, greater than or equal to, less than, less than, or equal to the target amount to write the inequality. Then solve the inequality sign, and target amount to write the inequality.
Then solve the inequality for the unknown value. Finally, interpret the solution in the context of the problem.
Independent Practice – Page No. 215
Question 7.
Three friends earned more than $200 washing cars. They paid their parents $28 for supplies and divided the rest of the money equally. Write an inequality to find possible amounts each friend earned. Identify what your variable represents.
Type below:
___________
Answer: 3x + 28 > 200
Explanation:
Let x be the amount each friend received. Since there are 3 friends, then 3x is the amount of money they split evenly.
The amount of money they split evenly was the amount left over after paying their parent’s $28.
Therefore 3x + 28 is the total amount they earned.
3x + 28 > 200
Question 8.
Nick has $7.00. Bagels cost $0.75 each, and a small container of cream cheese costs $1.29. Write an inequality to find the numbers of bagels Nick can buy. Identify what your variable represents.
Type below:
___________
Answer: 0.75x + 1.29 ≤ 7
Explanation:
Let x represent the number of bagels he can buy.
Then 0.75x is the total cost of the bagels and 0.75x + 1.29 is the total cost of his purchase.
Question 9.
Chet needs to buy 4 work shirts, all costing the same amount. After he uses a $25 gift certificate, he can spend no more than $75. Write an inequality to find the possible costs for a shirt. Identify what your variable represents.
Type below:
___________
Answer: 4x – 25 ≤ 75
Explanation:
Let x represent the cost of each skirt the 4x is the total costs of the shirts. Since he has a $25 gift card, the total amount he is spending is 4x – 25.
4x – 25 ≤ 75
Question 10.
Due to fire laws, no more than 720 people may attend a performance at Metro Auditorium. The balcony holds 120 people. There are 32 rows on the ground floor, each with the same number of seats. Write an inequality to find the numbers of people that can sit in a ground-floor row if the balcony is full. Identify what your variable represents.
Type below:
___________
Answer: 32x + 120 ≤ 720
Explanation:
Let x represent the number of people that can sit in each ground floor row. then 32x is the total number of people sitting in the ground floor.
Since 120 people are sitting in the balcony, the total number of people is 32x + 120.
Question 11.
Liz earns a salary of $2,100 per month, plus a commission of 5% of her sales. She wants to earn at least $2,400 this month. Write an inequality to find amounts of sales that will meet her goal. Identify what your variable represents.
Type below:
___________
Answer: 2100 + 0.05x ≥ 2400
Explanation:
Let x represent the number of sales then 0.05x is the amount she earns in commission and 2100 + 0.05x is her total earnings.
2100 + 0.05x ≥ 2400
Question 12.
Lincoln Middle School plans to collect more than 2,000 cans of food in a food drive. So far, 668 cans have been collected. Write an inequality to find numbers of cans the school can collect on each of the final 7 days of the drive to meet this goal. Identify what your variable represents.
Type below:
___________
Answer: 7x + 668 > 2000
Explanation:
Let x represent the number of cans collected each day. Then 7x is the total number of cans collected on the final 7 days of the drive.
Since they have collected 668 cans already, the total number of cans collected is 7x + 668.
They want to collect more than 2000 cans, so the inequality is:
7x + 668 > 2000
Question 13.
Joanna joins a CD club. She pays $7 per month plus $10 for each CD that she orders. Write an inequality to find how many CDs she can purchase in a month if she spends no more than $100. Identify what your variable represents.
Type below:
___________
Answer: 7 + 10x ≤ 100
Explanation:
Let x represent the number of CDs then 10x is the total amount spent on CDs and 7 + 10x is the total purchase amount for the month.
7 + 10x ≤ 100
Question 14.
Lionel wants to buy a belt that costs $22. He also wants to buy some shirts that are on sale for $17 each. He has $80. What inequality can you write to find the number of shirts he can buy? Identify what your variable represents.
Type below:
___________
Answer: 22 + 17x ≤ 80
Explanation:
Let x represent the number of shirts he can buy then 17x is the total cost of the shirts and 22 + 17x is the total cost
22 + 17x ≤ 80
Page No. 216
Question 15.
Write a situation for 15x − 20 ≤ 130 and solve.
Type below:
___________
Answer:
You are given in the inequality 15x − 20 ≤ 130 and need to write a situation that is represented by this inequality. A possible situation could be:
You are going shopping to buy some shirts. The shirts cost $15 each. You have a $20 gift card and $130 in cash. How many shirts can you buy?
This solution is modeled by the inequality 15x − 20 ≤ 130 because if we let x be the number of shirts you buy, then 15x is the cost of the shirts before you use the gift card since each shirt is $15. The total cost after using the $20 gift card would then be 15x – 20 dollars. Since you have $130 in cash, you can spend at most $130 so the total cost of 15x – 20 must then be less than or equal to 130.
Therefore, 15x − 20 ≤ 130.
Solving this gives:
15x − 20 ≤ 130
Add 20 on both sides
15x ≤ 130
Divide both sides by 15.
x ≤ 10
Analyze Relationships
Write >, <, ≥, or ≤ in the blank to express the given relationship.
Question 16.
m is at least 25
______
Answer: m ≥ 25
Explanation:
m is at least 25 means m ≥ 25 since at least means it can equal or needs to be bigger.
Question 17.
k is no greater than 9
______
Answer: k ≤ 9
Explanation:
k is no greater than 9 means k ≤ 9 since no greater means it can equal or must be smaller.
Question 18.
p is less than 48
______
Answer: p < 48
Explanation:
p is less than 48 means p < 48 since the < symbol in words is “less than”.
Question 19.
b is no more than -5
______
Answer: b ≤ -5
Explanation:
b is no more than -5 means b ≤ -5 since no more means it can equal or must be smaller.
Question 20.
h is at most 56
______
Answer: h ≤ 56
Explanation:
h is at most 56 means h ≤ 56 since at most means it can equal or must be smaller.
Question 21.
w is no less than 0
______
Answer: w ≥ 0
Explanation:
w is no less than 0 means w ≥ 0 since no less than means it can equal or is bigger.
Question 22.
Critical Thinking
Marie scored 95, 86, and 89 on three science tests. She wants her average score for 6 tests to be at least 90. What inequality can you write to find the average scores that she can get on her next three tests to meet this goal? Use s to represent the lowest average score.
Type below:
______
Answer: (95 + 86 + 89 + 3s)/6 ≥ 90
Explanation:
Let s be the average score on the remaining 3 tests. Then 3s is the sum of these 3 remaining tests. Since averages are found by adding up all the members, which gives 95 + 86 + 89 + 3s, and dividing by the total amount of numbers, which is 6, the inequality to the left can be used to find the lowest average she can get to have minimum total average of 90.
(95 + 86 + 89 + 3s)/6 ≥ 90
H.O.T.
Focus on Higher Order Thinking
Question 23.
Communicate Mathematical Ideas
Write an inequality that expresses the reason the lengths 5 feet, 10 feet, and 20 feet could not be used to make a triangle. Explain how inequality demonstrates that fact.
Type below:
__________
Answer:
A side of a triangle must be greater than the difference of the other two sides and smaller than the sum of the other two sides.
Since 20 > 5 +10, the side with length 20 is not less than the sum of the other two sides.
Question 24.
Analyze Relationships
The number m satisfies the relationship m < 0. Write an inequality expressing the relationship between -m and 0. Explain your reasoning.
Type below:
__________
Answer: Multiplying both sides of m < 0 by -1 gives -m > 0 since you must switch the inequality sign when you multiply by a negative number.
Question 25.
Analyze Relationships The number n satisfies the relationship n > 0. Write three inequalities to express the relationship between n and \(\frac{1}{n}\).
Type below:
__________
Answer: 0 < n < 1: n < \(\frac{1}{n}\), n = 1: n = \(\frac{1}{n}\), n > 1: n > \(\frac{1}{n}\)
Explanation:
Since n is positive, there are three cases for the value of n to consider when comparing n and \(\frac{1}{n}\).
0 < n < 1: In case, n is a fraction smaller than 1 such as \(\frac{1}{4}\). Its reciprocal is the n bigger than 1, such as 1/\(\frac{1}{4}\) = 4.
Therefore, n < \(\frac{1}{n}\)
n = 1: If n = 1, then the reciprocal is also 1 so n = \(\frac{1}{n}\)
n > 1: If n is a value greater than 1, such as \(\frac{3}{2}\), then the reciprocal is smaller than 1, such as 1/\(\frac{3}{2}\) = \(\frac{2}{3}\).
Therefore n > \(\frac{1}{n}\)
Page No. 220
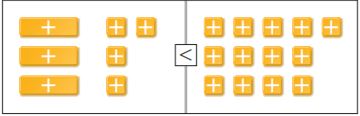
Question 1.
Describe how to solve the inequality 3x + 4 < 13 using algebra tiles.
Type below:
__________
Answer:
First, remove 4 positive squares from each side. This leaves 9 positive squares on the right side.
Then divide each side into 3 equal groups.
Each group would then have 3 positive squares on the left side. since the rectangles on the left are positive, the answer would be x < 3.
Solve each inequality. Graph and check the solution.
Question 2.
5d − 13 < 32
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
5d − 13 < 32
Add 13 on both sides
5d – 13 + 13 < 32 + 13
5d < 45
Divide 5 on both sides
5d/5 < 45/5
d < 9
The number opposite to the variable is 9, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would like the one below:
Question 3.
−4b + 9 ≤ −7
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
−4b + 9 ≤ −7
Subtract 9 on both sides
-4b + 9 – 9 ≤ −7 – 9
-4b ≤ −16
Divide -4 by both sides
-4b/-4 ≤ −16/-4
b ≥ 4
The number opposite to the variable is 4, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would like the one below:
Circle any given values that make the inequality true.
Question 4.
2m + 18 > −4
m = −12; m = −11; m = −10
Type below:
__________
Answer: m = -10
Explanation:
m = -12
2m + 18 > −4
2(-12) + 18 = -24 + 18 = -6 > -4 not true
m = -11
2m + 18 > −4
2(-11) + 18 > -4
-22 + 18 > -4
-4 > -4 not true
m = -10
2m + 18 > −4
2(-10) + 18 > -4
-20 + 18 > -4
-2 > -4 true
Question 5.
−6y + 3 ≥ 0
y = 1; y = \(\frac{1}{2}\); y = 0
Type below:
__________
Answer: y = \(\frac{1}{2}\); y = 0
Explanation:
y = 1
−6y + 3 ≥ 0
-6(1) + 3 ≥ 0
-6 + 3 ≥ 0 not true
y = \(\frac{1}{2}\)
−6y + 3 ≥ 0
−6(\(\frac{1}{2}\)) + 3 ≥ 0
-3 + 3 ≥ 0
0 ≥ 0 true
y = 0
−6y + 3 ≥ 0
-6(0) + 3 ≥ 0
3 ≥ 0 true
Question 6.
Lizzy has 6.5 hours to tutor 4 students and spend 1.5 hours in a lab. She plans to tutor each student the same amount of time. The inequality 6.5 − 4t ≥ 1.5 can be used to find t, the amount of time in hours Lizzy could spend with each student. Solve the inequality. Graph and interpret the solution. Can Lizzy tutor each student for 1.5 hours? Explain.
Type below:
__________
Answer:
6.5 − 4t ≥ 1.5
Subtract both sides by 6.5
6.5 − 4t – 6.5 ≥ 1.5 – 6.5
− 4t ≥ 1.5
Divide both sides by -4 remember to switch the inequality sign since you are dividing by a negative number.
t ≤ 1.25
Since the inequality sign has an equal sign, draw a closed circle at 1.25. Since the inequality is less than, draw an arrow to the left the interpretation of this problem is that she can tutor each student no more than 1.25 hours.
Since 1.5 hours is more than 1.25 hours, she cannot tutor each student for 1.5 hours.
Essential Question Check-In
Question 7.
How do you solve a two-step inequality?
Type below:
__________
Answer:
To solve a two-step inequality you must use inverse operations.
Use subtraction to get rid of addition, and addition to get rid of subtraction for any terms that are being added or subtracted to the term that contains the variable. Use multiplication to get rid of any coefficient on the variable if it is a fraction and use division to get rid of any coefficient on the variable if its an integer. If the coefficient is negative, make sure to switch the inequality sign if you multiply or divide by a negative number.
Independent Practice – Page No. 221
Solve each inequality. Graph and check the solution.
Question 8.
2s + 5 ≥ 49
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
2s + 5 ≥ 49
Subtract 5 on both sides
2s + 5 – 5 ≥ 49 – 5
2s ≥ 44
Divide both sides by 2.
s ≥ 22
The number opposite to the variable is 22, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would like the one below:
Question 9.
−3t + 9 ≥ −21
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
−3t + 9 ≥ −21
Subtract 9 on both sides
-3t + 9 – 9 ≥ −21 – 9
-3t ≥ −30
Divide by -3 on both sides
t ≤ 10
The number opposite to the variable is 10, we look for this in the number line. Since the inequality is ≤, we use a closed dot and shade the line going to the left. Its graph would like the one below:
Question 10.
55 > −7v + 6
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
55 > −7v + 6
Subtract 6 on both sides
55 – 6 > −7v + 6 – 6
49 > -7v
Divide -7 on both sides
-7 < v
v > -7
The number opposite to the variable is -7, we look for this in the number line. Since the inequality is >, we use a hollow dot and shade the line going to the right. Its graph would like the one below:
Question 11.
41 > 6m − 7
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
41 > 6m − 7
Add 7 on both sides
41 + 7 > 6m – 7 + 7
48 > 6m
Divide by 6 on both sides
8 > m
m < 8
The number opposite to the variable is 8, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would like the one below:
Question 12.
\(\frac{a}{-8}\) + 15 > 23
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
\(\frac{a}{-8}\) + 15 > 23
Subtract 15 on both sides
\(\frac{a}{-8}\) + 15 – 15 > 23 – 15
(-8)\(\frac{a}{-8}\) > (8)(-8)
a < -64
The number opposite to the variable is -64, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would like the one below:
Question 13.
\(\frac{f}{2}\) − 22 < 48
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
\(\frac{f}{2}\) − 22 < 48
Add 22 on both sides
\(\frac{f}{2}\) − 22 + 22 < 48 + 22
\(\frac{f}{2}\) < 70
Multiply 2 on both sides
(2)\(\frac{f}{2}\) < 70(2)
f < 140
The number opposite to the variable is 140, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would like the one below:
Question 14.
−25 + \(\frac{t}{2}\) ≥ 50
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
−25 + \(\frac{t}{2}\) ≥ 50
Add 25 on both sides
−25 + \(\frac{t}{2}\) + 25 ≥ 50 + 25
\(\frac{t}{2}\) ≥ 75
Multiply 2 on both sides
(2)\(\frac{t}{2}\) ≥ 75 (2)
t ≥ 150
The number opposite to the variable is 150, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would like the one below:
Question 15.
10 + \(\frac{g}{-9}\) > 12
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
10 + \(\frac{g}{-9}\) > 12
Subtract 10 on both sides
10 + \(\frac{g}{-9}\) -10 > 12 – 10
\(\frac{g}{-9}\) > 2
Divide both sides by -9
g < -18
The number opposite to the variable is -18, we look for this in the number line. Since the inequality is <, we use a hollow dot and shade the line going to the left. Its graph would like the one below:
Question 16.
25.2 ≤ − 1.5y + 1.2
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
25.2 ≤ − 1.5y + 1.2
Subtract 1.2 on both sides
25.2 – 1.2 ≤ − 1.5y + 1.2 – 1.2
24 ≤ -1.5y
Divide both sides by 1.5
-16 ≥ y
y ≤ -16
The number opposite to the variable is -16, we look for this in the number line. Since the inequality is ≤, we use a closed dot and shade the line going to the left. Its graph would like the one below:
Question 17.
−3.6 ≥ −0.3a + 1.2
Type below:
__________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
−3.6 ≥ −0.3a + 1.2
Subtract 1.2 on both sides
−3.6 – 1.2 ≥ −0.3a + 1.2 – 1.2
-4.8 ≥ −0.3a
Divide both sides by -0.3
16 ≤ a
a ≥ 16
The number opposite to the variable is 16, we look for this in the number line. Since the inequality is ≥, we use a closed dot and shade the line going to the right. Its graph would like the one below:
Question 18.
What If?
The perimeter of a rectangle is at most 80 inches. The length of the rectangle is 25 inches. The inequality 80 − 2w ≥ 50 can be used to find w, the width of the rectangle in inches. Solve the inequality and interpret the solution. How will the solution change if the width must be at least 10 inches and a whole number?
Type below:
__________
Answer:
The perimeter of a rectangle is at most 80 inches. The length of the rectangle is 25 inches. The inequality 80 − 2w ≥ 50 can be used to find w, the width of the rectangle in inches.
Subtract 80 on both sides
-2w ≥ -30
Divide -2 on both sides
w ≤ 15
The interpretation of this solution is that width must be a positive real number that is at most 15 inches.
If the width must be at least 10 inches and a whole number, then the solution would be the whole number lengths such that 10 ≤ w ≤ 15 which is 10, 11, 12, 13, 14 or 15 inches.
Page No. 222
Question 19.
Interpret the Answer
Grace earns $7 for each car she washes. She always saves $25 of her weekly earnings. This week, she wants to have at least $65 in spending money. How many cars must she wash? Write and solve an inequality to represent this situation. Interpret the solution in context.
Type below:
__________
Answer:
Let x represent the number of cars she must wash then 7x is the total amount she makes from washing cars. Since she is saving $25 of her earnings, 7x – 25 is the amount of earnings she will have to spend.
7x – 25 ≥ 65
Add 25 on both sides
7x – 25 + 25 ≥ 65 + 25
7x ≥ 90
Divide both sides by 7.
x ≥ 90/7 ≈ 13
H.O.T.
Focus on Higher Order Thinking
Question 20.
Critical Thinking
Is there any value of x with the property that x < x – 1? Explain your reasoning.
Type below:
__________
Answer:
Subtracting x on both sides of x < x – 1 gives x – x < x – 1 -x
0 < -1.
Since this not a true statement, inequality is not true for any value of x.
Question 21.
Analyze Relationships A compound inequality consists of two simple equalities joined by the word “and” or “or.” Graph the solution sets of each of these compound inequalities. a. x > 2 and x < 7
Type below:
__________
Answer: Since the two inequalities are joined by “and”, we need to satisfy both inequalities. Therefore, we need all values greater than 2 but also we need values less than 7. Hence we can place a hollow dot on 2 and shade the line going to the right until another hollow dot on 7.
Question 21.
b. x < 2 or x > 7
Type below:
__________
Answer: Since the two inequalities are joined by “or”, we need to satisfy either of the inequalities. Therefore, we need all values less than 2 but also we need to graph the values greater than 7. Hence we can place a hollow dot on 2 and shade the line going to the left and another hollow dot on 7 and shade the line going to the right.
Question 21.
c. Describe the solution set of the compound inequality x < 2 and x > 7.
Type below:
__________
Answer: The solution set for x > 2 and x < 7 sould be 2 < x < 7.
Question 21.
d. Describe the solution set of the compound inequality x > 2 or x < 7.
Type below:
__________
Answer: The solution set for x < 2 and x > 7 sould be (-∞, 2) ∪ (7, ∞).
Question 22.
Communicate Mathematical Ideas
Joseph used the problem-solving strategy Work Backward to solve the inequality 2n + 5 < 13. Shawnee solved the inequality using the algebraic method you used in this lesson. Compare the two methods.
Type below:
__________
Answer: Both involve using the same operations. The only difference is that working backward is done mostly mentally while algebraically is done on paper. It is easier to determine which direction the inequality is pointing when using the algebraic method.
7.1 Writing and Solving One-Step Inequalities – Page No. 223
Solve each inequality.
Question 1.
n + 7 < −3
Type below:
__________
Answer: n < -10
Explanation:
Subtract 7 on both sides
n + 7 – 7 < −3 – 7
n < -10
Question 2.
5p ≥ −30
Type below:
__________
Answer: p ≥ -6
Explanation:
5p ≥ −30
Divide by 5 on both sides
p ≥ -6
Question 3.
14 < k + 11
Type below:
__________
Answer: 3 < k
Explanation:
14 < k + 11
Subtract 11 on both sides
14 – 11 < k + 11 – 11
3 < k
Question 4.
\(\frac{d}{-3}\) ≤ −6
Type below:
__________
Answer: d ≥ 18
Explanation:
\(\frac{d}{-3}\) ≤ −6
Multiply both sides by -3 remember to switch the inequality sign since you are multiplying both sides by a negative number.
d ≥ 18
Question 5.
c − 2.5 ≤ 2.5
Type below:
__________
Answer: c ≤ 5
Explanation:
c − 2.5 ≤ 2.5
Add 2.5 on both sides
c − 2.5 + 2.5 ≤ 2.5 + 2.5
c ≤ 5
Question 6.
12 ≥ −3b
Type below:
__________
Answer: -4 ≤ b
Explanation:
12 ≥ −3b
Divide by -3 on both sides
-4 ≤ b
Question 7.
Jose has scored 562 points on his math tests so far this semester. To get an A for the semester, he must score at least 650 points. Write and solve an inequality to find the minimum number of points he must score on the remaining tests in order to get an A.
Type below:
__________
Answer: x + 562 ≥ 650
Explanation:
Let x represent the score he must receive on the remaining tests. Then x + 562 is his total score for the semester.
x + 562 ≥ 650
Subtract 562 on both sides
x ≥ 88
7.2 Writing Two-Step Inequalities
Question 8.
During a scuba dive, Lainey descended to a point 20 feet below the ocean surface. She continued her descent at a rate of 20 feet per minute. Write an inequality you could solve to find the number of minutes she can continue to descend if she does not want to reach a point more than 100 feet below the ocean surface.
Type below:
__________
Answer:
Let x represent the number of minutes. Since she is descending 20 feet per minute, then -20x represents her altitude. It is negative since descending means her altitude is decreasing.
Since she started at 20 feet below the ocean surface, she started at -20 feet. Its negative since an altitude below the ocean surface must be represented by a negative number.
Her ending position is the sum of how far she has descended and her initial position so her ending position is -20 + (-20x) = -20 – 20x
She doesn’t want to travel more than 100 feet below the ocean surface so she needs to be higher than -100 feet.
The inequality is then -20 -20x ≥ -100.
7.3 Solving Two-Step Inequalities
Solve.
Question 9.
2s + 3 > 15
Type below:
__________
Answer: s > 6
Explanation:
2s + 3 > 15
Subtract 3 on both sides
2s + 3 – 3 > 15 – 3
2s > 12
Divide by 2 on both sides
s > 6
Question 10.
−\(\frac{d}{12}\) − 6 < 1
Type below:
__________
Answer: d > -84
Explanation:
−\(\frac{d}{12}\) − 6 < 1
Add 6 on both sides
−\(\frac{d}{12}\) − 6 + 6 < 1 + 6
d > -84
Question 11.
−6w − 18 ≥ 36
Type below:
__________
Answer: w ≤ -9
Explanation:
−6w − 18 ≥ 36
Add 18 on both sides
−6w − 18 + 18 ≥ 36 + 18
-6w ≥ 54
Divide by -6
w ≤ -9
Question 12.
\(\frac{z}{4}\) + 22 ≤ 38
Type below:
__________
Answer: z ≤ 64
Explanation:
Subtract 22 on both sides
\(\frac{z}{4}\) + 22 – 22 ≤ 38 – 22
\(\frac{z}{4}\) ≤ 16
z ≤ 64
Question 13.
\(\frac{b}{9}\) − 34 < −36
Type below:
__________
Answer: b < -18
Explanation:
\(\frac{b}{9}\) − 34 < −36
Add 34 on both sides
\(\frac{b}{9}\) − 34 + 34 < −36 + 34
\(\frac{b}{9}\) < -2
b < -18
Question 14.
−2p + 12 > 8
Type below:
__________
Answer: p < 2
Explanation:
−2p + 12 > 8
Subtract 12 on both sides
-2p + 12 – 12 > 8 – 12
-2p > -4
p < 2
Essential Question
Question 15.
How can you recognize whether a real-world situation should be represented by an equation or an inequality?
Type below:
__________
Answer:
You use an equation when the situation involves finding an exact answer. You use an inequality when the solution can have more than one value. Problems that require the use of inequalities have phrases in them such as “at least”, “no more”, “at most” and “no less than”.
Selected Response – Page No. 224
Question 1.
Which graph models the solution of the inequality −6 ≤ −3x?
Options:
a. ![]()
b. ![]()
c. ![]()
d. ![]()
Answer: ![]()
Dividing both sides of −6 ≤ −3x by -3 gives 2 ≥ x.
Rewriting this so x is on the left side gives x ≤ 2. The graph must have a closed circle at 2 since the inequality has an equal sign and must be shaded to the left since its <.
Thus the correct answer is option C.
Question 2.
A taxi cab costs $1.75 for the first mile and $0.75 for each additional mile. You have $20 to spend on your ride. Which inequality could be solved to find how many miles you can travel, if n is the number of additional miles?
Options:
a. 1.75n + 0.75 ≥ 20
b. 1.75n + 0.75 ≤ 20
c. 0.75n + 1.75 ≥ 20
d. 0.75n + 1.75 ≤ 20
Answer: 1.75n + 0.75 ≤ 20
Explanation:
Let n represent the number of additional miles. Then 0.75n is the cost of the additional miles which gives a total cost of 1.75 + 0.75n. You can spend a maximum of $20 so the inequality is ≤.
Thus the correct answer is option B.
Question 3.
The inequality \(\frac{9}{5}\)C + 32 < −40 can be used to find Celsius temperatures that are less than -40° Fahrenheit. What is the solution of the inequality?
Options:
a. C < 40
b. C < −\(\frac{40}{9}\)
c. C < −40
d. C < −\(\frac{72}{5}\)
Answer: C < −40
Explanation:
\(\frac{9}{5}\)C + 32 < −40
Subtract 32 on both sides.
\(\frac{9}{5}\)C + 32 – 32 < −40 – 32
\(\frac{9}{5}\)C < -72
c < -40
Thus the correct answer is option C.
Question 4.
The 30 members of a choir are trying to raise at least $1,500 to cover travel costs to a singing camp. They have already raised $600. Which inequality could you solve to find the average amounts each member can raise that will at least meet the goal?
Options:
a. 30x + 600 > 1,500
b. 30x + 600 ≥ 1,500
c. 30x + 600 < 1,500
d. 30x + 600 ≤ 1,500
Answer: 30x + 600 ≥ 1,500
Explanation:
Given,
The 30 members of a choir are trying to raise at least $1,500 to cover travel costs to a singing camp. They have already raised $600.
Let x represent the average amount each member raises.
There are 30 members so the members raise a combined amount of 30x.
Since they have already raised $600, the total amount raised 30x + 600 they need to raise at least $1500 so the inequality is ≥.
Thus the correct answer is option B.
Question 5.
Which represents the solution for the inequality 3x − 7 > 5?
Options:
a. x < 4
b. x ≤ 4
c. x > 4
d. x ≥ 4
Answer: x > 4
Explanation:
Add 7 on both sides
3x − 7 > 5
3x − 7 + 7> 5 + 7
3x > 12
x > 4
Thus the correct answer is option C.
Question 6.
Which inequality has the following graphed solution?
![]()
Options:
a. 3x + 8 ≤ 2
b. 4x + 12 < 4
c. 2x + 5 ≤ 1
d. 3x + 6 < 3
Answer: 4x + 12 < 4
Explanation:
4x + 12 < 4
Subtract 12 on both sides
4x + 12 – 12 < 4 – 12
4x < -8
x < -2
Thus the correct answer is option B.
Question 7.
Divide: −36 ÷ 6.
Options:
a. 30
b. 6
c. -6
d. -30
Answer: -6
Explanation:
6 divides 36 six times
−36 ÷ 6 = -6
Thus the correct answer is option C.
Question 8.
Eleni bought 2 pounds of grapes at a cost of $3.49 per pound. She paid with a $10 bill. How much change did she get back?
Options:
a. $3.02
b. $4.51
c. $6.51
d. $6.98
Answer: $3.02
Explanation:
Given,
Eleni bought 2 pounds of grapes at a cost of $3.49 per pound. She paid with a $10 bill.
We have to find the total amount paid for the grapes
2 × 3.49 = 6.98
10 – 6.98 = 3.02
Thus the correct answer is option A.
Question 9.
In golf, the lower your score, the better. Negative scores are best of all. Teri scored +1 on each of the first three holes at a nine-hole miniature golf course. Her goal is a total score of -9 or better after she has completed the final six holes.
a. Let h represent the score Teri must average on each of the last six holes in order to meet her goal. Write a two-step inequality you can solve to find h.
Type below:
_____________
Answer: 3 +6h ≤ -9
Explanation:
If h is her average score for the last 6 holes, then 6h is her total score for the last 6 holes.
She currently has a score of 3 so ger total score for all 9 holes is 3 + 6h.
She wants a score of -9 or better and since smaller scores are better, the inequality is ≤.
Question 9.
b. Solve the inequality.
Type below:
_____________
Answer: h ≤ -2
Explanation:
6h ≤ -12
Divide by 6 on both sides
h ≤ -2
EXERCISES – Page No. 226
Simplify each expression.
Question 1.
\(\left(2 x+3 \frac{2}{5}\right)+\left(5 x-\frac{4}{5}\right)\)
Type below:
_____________
Answer: 7x + 2 \(\frac{3}{5}\)
Explanation:
We are given the expression,
\(\left(2 x+3 \frac{2}{5}\right)+\left(5 x-\frac{4}{5}\right)\)
Group the like terms
(2x + 5x) + (3\(\frac{2}{5}\) – \(\frac{4}{5}\))
7x + 2 \(\frac{3}{5}\)
Question 2.
(−0.5x − 4) − (1.5x + 2.3)
Type below:
_____________
Answer: -2x – 6.3
Explanation:
(−0.5x − 4) − (1.5x + 2.3)
(−0.5x − 4) − 1.5x – 2.3
Combine the lilke terms
-0.5x – 1.5x – 4 – 2.3
-2x – 6.3
Question 3.
9(3t + 4b)
Type below:
_____________
Answer: 27t + 36b
Explanation:
9(3t + 4b)
9 × 3t + 9 × 4b
27t + 36b
Question 4.
0.7(5a − 13p)
Type below:
_____________
Answer: 3.5a – 9.1p
Explanation:
0.7(5a − 13p)
0.7 × 5a – 0.7 × 13p
3.5a – 9.1p
Factor each expression.
Question 5.
8x + 56
Type below:
_____________
Answer: 8(x + 7)
Explanation:
Since 56 ÷ 8 = 7 and 8 ÷ 8 = 1, factor out 8 from both terms
8x + 56 = 8(x + 7)
Question 6.
3x + 57
Type below:
_____________
Answer: 3(x + 19)
Explanation:
Since 3 ÷ 3 = 1 and 57 ÷ 3 = 19 factor out 3 from both terms.
3x + 57 = 3(x + 19)
Question 7.
1.6 + y = −7.3
_______
Answer: y = -8.9
Explanation:
subtract 1.6 on both sides
1.6 + y – 1.6 = -7.3 – 1.6
y = -8.9
Question 8.
−\(\frac{2}{3}\) n = 12
_______
Answer: n = -18
Explanation:
−\(\frac{2}{3}\) n = 12
n = −\(\frac{3}{2}\)(12)
n = -3 × 6
n = -18
Question 9.
The cost of a ticket to an amusement park is $42 per person. For groups of up to 8 people, the cost per ticket decreases by $3 for each person in the group. Marcos’s ticket cost $30. Write and solve an equation to find the number of people in Marcos’s group.
_______ people
Answer: 4
Explanation:
Given that,
The cost of a ticket to an amusement park is $42 per person.
For groups of up to 8 people, the cost per ticket decreases by $3 for each person in the group. Marcos’s ticket cost $30.
Let x represent the number of people in his group then the ticket price has changed by -3x dollars.
The original price is $42 so the discount price is 42 – 3x
42 – 3x = 30
-3x = 30 – 42
-3x = -12
Divide both sides by -3
x = 4
Thus there are 4 people in Marcos’s group.
Question 10.
8x − 28 = 44
_______
Answer:
To plot a point, starting from 0, count the number of units going to the left or right.
Given equation is
8x − 28 = 44
Add 28 on both sides
8x – 28 + 28 = 44 + 28
8x = 72
Divide by 8 on both sides
x = 9
To plot 9 on a number line, from 0, we move 9 units to the right.
Question 11.
−5z + 4 = 34
_______
Answer:
To plot a point, starting from 0, count the number of units going to the left or right.
Given equation is
−5z + 4 = 34
Subtract 4 on both sides
-5z + 4 – 4 = 34 – 4
-5z = 30
Divide both sides by -5
z = -6
To plot -6 on the number line, from 0, we move 6 units to the left.
EXERCISES – Page No. 227
Question 1.
Prudie needs $90 or more to be able to take her family out to dinner. She has already saved $30 and wants to take her family out to eat in 4 days.
a. Suppose that Prudie earns the same each day. Write an inequality to find how much she needs to earn each day.
Type below:
___________
Answer:
Let x be the amount she makes each day then 4x is the amount she will make in the 4 days before she takes her family out to eat and 4x + 30 is the total amount she will have saved.
4x + 30 ≥ 90
Question 1.
b. Suppose that Prudie earns $18 each day. Will she have enough money to take her family to dinner in 4 days? Explain.
_______
Answer:
4(18) + 30 = 72 + 30 = 102
She will have saved $102 in total if she earns $18 each day so she will have enough money.
Solve each inequality. Graph and check the solution.
Question 2.
11 − 5y < −19
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
11 − 5y < −19
Subtract 11 on both sides
11 – 5y – 11 < −19 – 11
-5y < -30
Divide by -5 on both sides
y > 6
The number opposite to the variable is 6, we look for this in the number line. Since the inequality is >, we use a hollow dot and shade the line going to the right. Its graph would like the one below:
Question 3.
7x − 2 ≤ 61
Type below:
___________
Answer:
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
From here, shade the line going to the left if the inequality is either ≤ or < and shade the line going to the right if the inequality is either ≥ or >.
First, solve the inequality:
7x − 2 ≤ 61
Add 2 on both sides
7x – 2 + 2 ≤ 61 + 2
7x ≤ 63
Divide by 7 into both sides
x ≤ 9
The number opposite to the variable is 9, we look for this in the number line. Since the inequality is ≤, we use a closed dot and shade the line going to the left. Its graph would like the one below:
Unit 3 Performance Tasks – Page No. 228
Question 1.
Mechanical Engineer
A mechanical engineer is testing the amount of force needed to make a spring stretch by a given amount. The force y is measured in units called Newtons, abbreviated N. The stretch x is measured in centimeters. Her results are shown in the graph.
a. Write an equation for the line. Explain, using the graph and then using the equation, why the relationship is proportional.
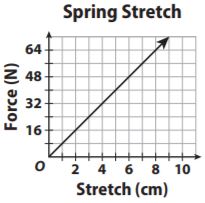
Type below:
___________
Answer: The graph is linear and passes through the origin so the relationship is proportional. find k by using the formula k = y/x where (x, y) is a point on the line then plug k into the equation of a line y = kx.
Question 1.
b. Identify the rate of change and the constant of proportionality.
Type below:
___________
Answer: k = 8
Explanation:
Observe part a the units N/cm since the units for y are N and the units for x are cm and the units for k must be the units for y divided by the units for x.
8 N/ cm
k = 8
Question 1.
c. What is the meaning of the constant of proportionality in the context of the problem?
Type below:
___________
Answer:
Since the rate of change is 8 N/ cm this means that for every 1 cm stretch in the spring, the force required in Newton increases by 8 N.
Question 1.
d. The engineer applies a force of 41.6 Newtons to the spring. Write and solve an equation to find the corresponding stretch in the spring.
______ cm
Answer:
y = 8x
41.6 = 8x
x = 41.6/8
x = 5.2 cm
Question 2.
A math tutor charges $30 for a consultation, and then $25 per hour. An online tutoring service charges $30 per hour.
a. Does either service represent a proportional relationship? Explain.
Type below:
___________
Answer:
The math tutor charges $30 initially but has a constant rate of $25 per hour after. This means that it still is a proportional relationship. The online tutoring charges a constant rate of $30 per hour and thus is also a proportional relationship.
Question 2.
b. Write an equation for the cost c of h hours of tutoring for either service. Which service charges less for 4 hours of tutoring? Show your work.
Type below:
___________
Answer:
Using y as the total cost and x as the number of hours, we can represent each tutoring service. For Math tutor, we can write this as y = 30 + 25x while for the online tutoring, we can write this as y = 30x.
Substituting x = 4, we can see that:
For Math tutor:
y = 30 + 25x
y = 30 + 25(4)
y = 30 + 100
y = 130
For Online tutoring:
y = 30x
y = 30(4)
y = 120
Therefore, the online tutoring service charge less at $120.
Selected Response – Page No. 229
Question 1.
Which expression is equivalent to (9x − 3 \(\frac{1}{8}\)) − (7x + 1 \(\frac{3}{8}\))?
Options:
a. 2x − 4 \(\frac{1}{2}\)
b. 16x−4 \(\frac{1}{2}\)
c. 2x − 1 \(\frac{3}{4}\)
d. 16x − 1 \(\frac{3}{4}\)
Answer: 2x − 4 \(\frac{1}{2}\)
Explanation:
(9x − 3 \(\frac{1}{8}\)) − (7x + 1 \(\frac{3}{8}\))
9x − 3 \(\frac{1}{8}\)− 7x – 1 \(\frac{3}{8}\)
Combine the lilke terms
2x – 4 \(\frac{1}{2}\)
Thus the correct answer is option A.
Question 2.
Timothy began the week with $35. He bought lunch at school, paying $2.25 for each meal. Let x be the number of meals he bought at school and y be the amount of money he had left at the end of the week. Which equation represents the relationship in the situation?
Options:
a. y = 2.25x + 35
b. y = 35 − 2.25x
c. x = 35 − 2.25y
d. y = 2.25x − 35
Answer: y = 35 − 2.25x
Explanation:
Let x be the number of meals he buys means 2.25x is the amount of money he has spent on meals. The money he has left is then 35 – 2.25x
The expression is y = 35 – 2.25x
Thus the correct answer is option B.
Question 3.
Which expression factors to 8(x + 2)?
Options:
a. 8x + 2
b. 8x + 10
c. 16x
d. 8x + 16
Answer: 8x + 16
Explanation:
Given the expression
8(x + 2)
8x + 8(2)
8x + 16
Thus the correcr answer is option D.
Question 4.
Ramón’s toll pass account has a value of $32. Each time he uses the toll road, $1.25 is deducted from the account. When the value drops below $10, he must add value to the toll pass. Which inequality represents how many times Ramón can use the toll road without having to add value to the toll pass?
Options:
a. 10 − 1.25t ≥ 0
b. −1.25t + 32 < 10
c. 32 − 1.25t ≥ 10
d. 32 − 10t ≥ 1.25
Answer: 32 − 1.25t ≥ 10
Explanation:
Let t represent the number of times he uses the toll road then 1.25t is the amount deducted from his account. the remaining balance is then 32 – 1.25t.
Since his balance must be at least $10 for him to not have to add value, the inequality sign is ≥
Thus the correct answer is option C.
Question 5.
A taxi costs $1.65 for the first mile and $0.85 for each additional mile. Which equation could be solved to find the number x of additional miles traveled in a taxi given that the total cost of the trip is $20?
Options:
a. 1.65x + 0.85 = 20
b. 0.85x + 1.65 = 20
c. 1.65x − 0.85 = 20
d. 0.85x − 1.65 = 20
Answer: 0.85x + 1.65 = 20
Explanation:
Let x be the number of additional miles means 0.85x is the cost of the additional miles the total cost is then 1.65 + 0.85x
1.65 + 0.85x = 20
Thus the correct answer is option B.
Question 6.
A sales tax of 6% is added to the price of an item. If Marisa buys an item, which expression indicates how much she will pay in all?
Options:
a. n + 0.06
b. 0.06n
c. n + 0.06n
d. 0.06 + 0.06n
Answer: n + 0.06n
Explanation:
The total cost she will pay is the cost of the item n plus the cost of tax 0.06n.
The expression is n + 0.06n
Thus the correct answer is option C.
Question 7.
Which equation has the solution x = 12?
Options:
a. 4x + 3 = 45
b. 3x + 6 = 42
c. 2x − 5 = 29
d. 5x −8 = 68
Answer: 3x + 6 = 42
Explanation:
a. 4x + 3 = 45
Substitute x = 12 in the above equation.
4(12) + 3 = 45
48 + 3 = 45
51 ≠ 45
b. 3x + 6 = 42
Substitute x = 12 in the above equation.
3(12) + 6 = 42
36 + 6 = 42
42 = 42
c. 2x − 5 = 29
Substitute x = 12 in the above equation.
2(12) – 5 = 29
24 – 5 = 29
19 ≠ 29
d. 5x −8 = 68
Substitute x = 12 in the above equation.
5(12) – 8 = 68
60 – 8 = 68
52 ≠ 68
Thus the correct answer is option B.
Question 8.
The 23 members of the school jazz band are trying to raise at least $1,800 to cover the cost of traveling to a competition. The members have already raised $750. Which inequality could you solve to find the amount that each member should raise to meet the goal?
Options:
a. 23x + 750 > 1,800
b. 23x + 750 ≥ 1,800
c. 23x + 750 < 1,800
d. 23x + 750 ≤ 1,800
Answer: 23x + 750 ≥ 1,800
Explanation:
Let x represent the amount each member raises means 23x is the amount the members raise individually.
The total amount raised is then 23x + 750 since they have already raised $750.
Since they are trying to raise at least $1800, the inequality is ≥
Thus the correct answer is option B.
Page No. 230
Question 9.
What is the solution of the inequality 2x − 9 < 7?
Options:
a. x < 8
b. x ≤ 8
c. x > 8
d. x ≥ 8
Answer: x < 8
Explanation:
Given the inequality 2x − 9 < 7
Add 9 on both sides 2x – 9 + 9 < 7 + 9
2x < 16
Divide by 2 on both sides
2x/2 < 16/2
x < 8
Thus the correct answer is option A.
Question 10.
Which inequality has the solution n < 5?
Options:
a. 4n + 11 > −9
b. 4n + 11 < −9
c. −4n + 11 < −9
d. −4n + 11 > −9
Answer: −4n + 11 > −9
Explanation:
Given the inequality n < 5
To graph inequalities, locate the number opposite the variable of the inequality on a number line. If the inequality is either a ≤ or a ≥, we use a closed dot, meaning the number is a solution as well. If the inequality is either a > or a <, use an open dot, indicating that the number is not a solution.
a. 4n + 11 > −9
4n + 11 – 11 > -9 – 11
4n/4 > -20/4
n -5
b. 4n + 11 < −9
4n + 11 – 11 < -9 – 11
4n < -20
4n/4 < -20/4
n < -5
c. −4n + 11 < −9
-4n + 11 – 11 < -9 – 11
-4n < -20
-4n/-4 < -20/-4
n > 5
d. −4n + 11 > −9
-4n + 11 – 11 > -9 – 11
-4n > -20
-4n/-4 > -20/-4
n < 5
Thus the correct answer is option D.
Question 11.
Which inequality has the solution shown?
![]()
Options:
a. 3x + 5 < 2
b. 4x + 12 < 4
c. 2x + 5 ≤ 1
d. 3x + 6 ≤ 3
Answer: 3x + 6 ≤ 3
Explanation:
The graph shows the inequality x ≤ -1 so the possible answers are C and D since A and B have < as the inequality signs. Solve C and D for x to see which one has x ≤ -1 as the solution.
c. 2x + 5 ≤ 1
2x + 5 – 5 ≤ 1 – 5
2x ≤ -4
x ≤ -2
d. 3x + 6 ≤ 3
3x + 6 – 6 ≤ 3 – 6
3x ≤ -3
x ≤ -1
Thus the correct answer is option D.
Question 12.
On a 4 \(\frac{1}{2}\) hour trip, Leslie drove \(\frac{2}{3}\) of the time. For how many hours did Leslie drive?
Options:
a. 3 hours
b. 3 \(\frac{1}{2}\) hours
c. 3 \(\frac{2}{3}\) hours
d. 3 \(\frac{5}{6}\) hours
Answer: 3 hours
Explanation:
Given that,
On a 4 \(\frac{1}{2}\) hour trip, Leslie drove \(\frac{2}{3}\) of the time.
Multiply the two fractions by first writing 4 \(\frac{1}{2}\) as an improper fraction then cancel the 2s and then simplifying the division.
4 \(\frac{1}{2}\)(\(\frac{2}{3}\)) = \(\frac{9}{2}\) × \(\frac{2}{3}\) = 3
Thus the correct answer is option A.
Question 13.
During a sale, the price of a sweater was changed from $20 to $16. What was the percent of decrease in the price of the sweater?
Options:
a. 4%
b. 20%
c. 25%
d. 40%
Answer:
Mini-Task
Question 14.
Max wants to buy some shorts that are priced at $8 each. He decided to buy a pair of sneakers for $39, but the total cost of the shorts and the sneakers must be less than $75.
a. Write an inequality to find out how many pairs of shorts Max can buy.
Type below:
____________
Answer: 39 + 8x < 75
Explanation:
Let x be the number of shorts he buys then 8x is the total cost of the shorts and 8x + 39 is the total cost of the shorts and sneakers his total must be less than $75 so the inequality is <.
39 + 8x < 75
Question 14.
b. Suppose that Max wants to buy 6 pairs of shorts. Will he have enough money? Explain.
______
Answer: No
Explanation:
Find the total amount he will spend buying 6 pairs of shorts this is more than the $75 he has so he will not have enough.
39 + 8(6) = 39 + 48 = 87
Question 14.
c. Solve the inequality to find the greatest number of pairs of shorts that Max can buy. Show your work.
______ pairs of shoes
Answer: 4 pairs of shoes
Explanation:
Use the above inequality,
39 + 8x < 75
Subtract 39 on both sides and then divide both sides by 8. Since you can’t buy a fraction of a pair of shorts the most pairs he can buy is 4.
39 + 8x – 39 < 75 – 39
8x < 36
x < 4.5
Summary:
We wish the solutions given in this article are satisfactory for all the students of the 7th class. This Go Math Answer Key of Grade 7 helps teachers to know the easy tricks to explain the problems to the students. Feel free to clarify your doubts by posting your questions in the below comment box. We will answer them as early as possible.