Engage NY Eureka Math Precalculus Module 5 Lesson 4 Answer Key
Eureka Math Precalculus Module 5 Lesson 4 Exercise Answer Key
Exercises 1–6
Exercise 1.
A high school is planning to put on the musical West Side Story. There are 20 singers auditioning for the musical. The director is looking for two singers who could sing a good duet. In how many ways can the director choose two singers from the 20 singers?
Indicate if this question involves a permutation or a combination. Give a reason for your answer.
Answer:
Combination; the order that the singers are selected is not important.
Exercise 2.
The director is also interested in the number of ways to choose a lead singer and a backup singer. In how many ways can the director choose a lead singer and then a backup singer?
Indicate if this question involves a permutation or a combination. Give a reason for your answer.
Answer:
Permutation; the order is important; the lead is “chosen first,” and then the backup singer is chosen.
Exercise 3.
For each of the following, indicate if it is a problem involving permutations, combinations, or neither, and then answer the question posed. Explain your reasoning.
a. How many groups of five songs can be chosen from a list of 35 songs?
Answer:
Combination; the order of the songs is not important; 35C5 = 324 632
b. How many ways can a person choose three different desserts from a dessert tray of eight desserts?
Answer:
Combination; the order of the desserts is not important; 8C3 = 56
c. How many ways can a manager of a baseball team choose the lead-off batter and second batter from a baseball team of nine players?
Answer:
Permutation; the order of the batters is important; 9P2 = 72
d. How many ways are there to place seven distinct pieces of art in a row?
Answer:
Permutation; the order of each piece of art is important; 7P7 or 7! = 5040
e. How many ways are there to randomly select four balls without replacement from a container of 15 balls numbered 1 to 15?
Answer:
Combination; the order of the balls is not important; 15C4 = 1365
Exercise 4.
The manager of a large store that sells TV sets wants to set up a display of all the different TV sets that they sell. The manager has seven different TVs that have screen sizes between 37 and 43 inches, nine that have screen sizes between 46 and 52 inches, and twelve that have screen sizes of 55 inches or greater.
a. In how many ways can the manager arrange the 37- to 43-inch TV sets?
Answer:
7! = 5040
b. In how many ways can the manager arrange the 55-inch or greater TV sets?
Answer:
12! = 479 001 600
c. In how many ways can the manager arrange all the TV sets if he is concerned about the order they were placed in?
Answer:
28! or 28P28 ≈ 3.0∙1029
Exercise 5.
Seven slips of paper with the digits 1 to 7 are placed in a large jar. After thoroughly mixing the slips of paper, two slips are picked without replacement.
a. Explain the difference between 7P2 and 7C2 in terms of the digits selected.
Answer:
7P2 is the number of permutations of picking two slips from the seven slips of paper. The value of 7P2 is the number of ways that the two slips can be picked from the seven slips of paper in which the order of the digits is important. For example, if the digit 2 is picked first and the digit 1 is picked second, then 21 is considered a different outcome than if 1 is picked first and 2 is picked second, or 12. 7C2 is the combination of picking two slips from the seven slips. It represents the total number of ways two digits can be selected in which order does not matter. Therefore, 21 and 12 are not counted as different outcomes.
b. Describe a situation in which 7P2 is the total number of outcomes.
Answer:
Answers will vary. One example could be similar to the following: Seven students from your school are eligible to participate in a tennis competition; however, only one student can compete, with one other student designated as a backup. (The backup will compete if the first student is injured or unable to attend.) 7P4 represents how many different pairings of the seven students could be selected for the competition.
c. Describe a situation in which 7C2 is the total number of outcomes.
Answer:
Answers will vary. One example that could be developed by students is the following: Two students from seven eligible students will receive a prize. Each person is assigned a number from 1 to 7 (with no duplicates). Their numbers are placed in the jar. Two slips are drawn. The students assigned to the selected digits are the winners and will receive the prizes. 7C2 represents the number of ways two people from the group of seven students could win the prizes.
d. What is the relationship between 7P2 and 7C2?
Answer:
7C2 = \(\left(\frac{{ }_{7} P_{2}}{2 !}\right)\)
Exercise 6.
If you know nCk, and you also know the value of n and k, how could you find the value of nPk? Explain your answer.
Answer:
The following steps show the relation to be the value of the combination and the permutation:
Recall that nCk = \(\frac{n !}{k !(n-k) !}\).
Multiply each side of the above equation by k!, or
k! nCk = \(\frac{n !}{(n-k) !}\).
\(\frac{\boldsymbol{n} !}{(\boldsymbol{n}-\boldsymbol{k}) !}\) is nPk, therefore:
k!nCk = nPk.
Exercises 7–9
Exercise 7.
A high school is planning to put on the musical West Side Story. There are 20 singers auditioning for the musical. The director is looking for two singers who could sing a good duet.
a. What is the probability that Alicia and Juan are the two singers who are selected by the director? How did you get your answer?
Answer:
\(\frac{1}{{ }_{20} C_{2}}\) ≈ 0.005
This question involves a combination because the order of the two students selected does not matter. The probability of one of the selections (Alicia and Juan) would be 1 divided by the combination.
b. The director is also interested in the number of ways to choose a lead singer and a backup singer. What is the probability that Alicia is selected the lead singer and Juan is selected the backup singer? How did you get your answer?
Answer:
\(\frac{1}{{ }_{20} C_{2}}\) ≈ 0.0026
This question involves a permutation because the order of the two singers matters. The probability of one of these selections (Alicia as the lead singer and Juan as the backup) would be 1 divided by the permutation.
Exercise 8.
For many computer tablets, the owner can set a 4-digit pass code to lock the device.
a. How many different 4-digit pass codes are possible if the digits cannot be repeated? How did you get your answer?
Answer:
10P4 = 5040
I used a permutation because order matters.
b. If the digits of a pass code are chosen at random and without replacement from the digits 0, 1, …, 9, what is the probability that the pass code is 1234? How did you get your answer?
Answer:
\(\frac{1}{5040}\) ≈ 1.98∙10-4 ≈ 0 .000 198
The pass code 1234 is 1 out of the total number of possible pass codes. Therefore, the probability would be 1 divided by the permutation representing the total number of pass codes.
c. What is the probability that two people, who both chose a pass code by selecting digits at random and without replacement, both have a pass code of 1234? Explain your answer.
Answer:
\(\frac{1}{5040}\) ∙\(\frac{1}{5040}\) ≈ 3.9∙10-8 ≈ 0.000 000 039
I multiplied the probability of the first person getting this pass code by the probability of a second person getting this pass code.
Exercise 9.
A chili recipe calls for ground beef, beans, green pepper, onion, chili powder, crushed tomatoes, salt, and pepper. You have lost the directions about the order in which to add the ingredients, so you decide to add them in a random order.
a. How many different ways are there to add the ingredients? How did you get this answer?
Answer:
8P8 or 8! = 40320
This problem indicates that the order of adding the ingredients is important. The total number of ways of adding the eight ingredients in which order is important is the permutation indicated.
b. What is the probability that the first ingredient that you add is crushed tomatoes? How did you get your answer?
Answer:
\(\frac{1}{8}\) = 0.125
There are eight ingredients to pick for my first pick. The probability of selecting crushed tomatoes would be the probability of selecting one of the eight ingredients, or \(\frac{1}{8}\).
c. What is the probability that the ingredients are added in the exact order listed above? How did you get your answer?
Answer:
\(\frac{1}{40320}\) ≈ 2.5∙10-5 ≈ 0.000 025
The exact order of adding the ingredients represents 1 of the total number of permutations of the eight ingredients. The probability of selecting this 1 selection would be 1 divided by the total number of permutations.
Exercises 10–11
Exercise 10.
There are nine golf balls numbered from 1 to 9 in a bag. Three balls are randomly selected without replacement to form a 3-digit number.
a. How many 3-digit numbers can be formed? Explain your answer.
Answer:
9P3 = 504
Order is important. As a result, I formed the permutation of selecting three golf balls from the nine golf balls.
b. How many 3-digit numbers start with the digit 1? Explain how you got your answer.
Answer:
1∙8P2 = 1∙8∙7 = 56
If I select the digit 1 first, then there are 8 digits left for the other two digits. The number of ways of picking two of the remaining eight digits would be how many 3-digit numbers are formed with the digit 1 in the first position.
c. What is the probability that the 3-digit number formed is less than 200? Explain your answer.
Answer:
\(\frac{{ }_{8} P_{3}}{{ }_{9} P_{3}}\) ≈ 0.111
The probability of a 3-digit number formed that is less than 200 would be the probability formed by the number of 3-digit numbers that start with 1 (my answer to part (b)) divided by the total number of 3-digit numbers (my answer to part (a)).
Exercise 11.
There are eleven seniors and five juniors who are sprinters on the high school track team. The coach must select four sprinters to run the 800-meter relay race.
a. How many 4-sprinter relay teams can be formed from the group of 16 sprinters?
Answer:
16C4 = 1820
b. In how many ways can two seniors be chosen to be part of the relay team?
Answer:
11C2 = 55
c. In how many ways can two juniors be chosen to be part of the relay team?
Answer:
5C2 = 10
d. In how many ways can two seniors and two juniors be chosen to be part of the relay team?
Answer:
11C2∙5C2 = 550
e. What is the probability that two seniors and two juniors will be chosen for the relay team?
Answer:
\(\frac{{ }_{11} C_{2} \cdot{ }_{5} C_{2}}{{ }_{16} C_{4}}\) = \(\frac{550}{1820}\) ≈ 0.302
Eureka Math Precalculus Module 5 Lesson 4 Problem Set Answer Key
Question 1.
For each of the following, indicate whether it is a question that involves permutations, combinations, or neither, and then answer the question posed. Explain your reasoning.
a. How many ways can a coach choose two co-captains from 16 players in the basketball team?
Answer:
Combination; order does not matter; 16C2 = 120
b. In how many ways can seven questions out of ten be chosen on an examination?
Answer:
Combination; the order of the questions does not matter; 10C7 = 120
c. Find the number of ways that 10 women in the finals of the skateboard street competition can finish first, second, and third in the X Games final.
Answer:
Permutation; the order of the women is important in determining first, second, and third place; 10P3 = 720
d. A postal zip code contains five digits. How many different zip codes can be made with the digits 0–9? Assume a digit can be repeated.
Answer:
Neither; the digits can repeat; 105 = 100 000
Question 2.
Four pieces of candy are drawn at random from a bag containing five orange pieces and seven brown pieces.
a. How many different ways can four pieces be selected from the 12 colored pieces?
Answer:
12C4 = 495
b. How many different ways can two orange pieces be selected from five orange pieces?
Answer:
5C2 = 10
c. How many different ways can two brown pieces be selected from seven brown pieces?
Answer:
7C2 = 21
Question 3.
Consider the following:
a. A game was advertised as having a probability of 0.4 of winning. You know that the game involved five cards with a different digit on each card. Describe a possible game involving the cards that would have a probability of 0.4 of winning.
Answer:
Answers will vary. One possible answer would be to have the numbers 1, 2, 3, 4, 5 on the cards. A card is selected at random. If the number is even, you win the game.
b. A second game involving the same five cards was advertised as having a winning probability of 0.05. Describe a possible game that would have a probability of 0.05 or close to 0.05 of winning.
Answer:
Answers will again vary. Given that this probability is considerably less than the probability in Exercise 3, part (a), students would be expected to consider games in which more than one card is randomly selected, and the numbers formed from the selections would be involved in winning the game. If they randomly select two cards from the five possible cards, the probability of picking one of the possible 2-digit numbers without replacement is \(\frac{1}{{ }_{5} P_{2}}\), or 0.05. Encourage students to experiment with their suggestions by approximating the winning probabilities.
Question 4.
You have five people who are your friends on a certain social network. You are related to two of the people, but you do not recall who of the five people are your relatives. You are going to invite two of the five people to a special meeting. If you randomly select two of the five people to invite, explain how you would derive the probability of inviting your relatives to this meeting.
Answer:
The number of ways of picking two people does not involve order. There is only one way I could pick the two relatives, and that would be if my pick involved both relatives. I would divide 1 by the total number of ways I could pick two people from five people, or the combination of picking two out of five.
Question 5.
Charlotte is picking out her class ring. She can select from a ruby, an emerald, or an opal stone, and she can also select silver or gold for the metal.
a. How many different combinations of one stone and one type of metal can she choose? Explain how you got your answer.
Answer:
6; I multiplied the number of different stones by the number of different metals.
b. If Charlotte selects a stone and a metal at random, what is the probability that she would select a ring with a ruby stone and gold metal?
Answer:
\(\frac{1}{6}\)
Question 6.
In a lottery, three numbers are chosen from 0 to 9. You win if the three numbers you pick match the three numbers selected by the lottery machine.
a. What is the probability of winning this lottery if the numbers cannot be repeated?
Answer:
\(\frac{1}{{ }_{10} C_{2}}\) ≈ 0.008
b. What is the probability of winning this lottery if the numbers can be repeated?
Answer:
\(\frac{1}{10^{3}}\) = 0.001
c. What is the probability of winning this lottery if you must match the exact order that the lottery machine picked the numbers?
Answer:
\(\frac{1}{{ }_{10} P_{3}}\) ≈ 0.0014
Question 7.
The store at your school wants to stock T-shirts that come in five sizes (small, medium, large, XL, XXL) and in two colors (orange and black).
a. How many different type T-shirts will the store have to stock?
Answer:
10
b. At the next basketball game, the cheerleaders plan to have a T-shirt toss. If they have one T-shirt of each type in a box and select a shirt at random, what is the probability that the first randomly selected T-shirt is a large orange T-shirt?
Answer:
\(\frac{1}{10}\)
Question 8.
There are 10 balls in a bag numbered from 1 to 10. Three balls are selected at random without replacement.
a. How many different ways are there of selecting the three balls?
Answer:
10C3 = 120
b. What is the probability that one of the balls selected is the number 5?
Answer:
\(\frac{{ }_{9} C_{2}}{{ }_{10} C_{3}}\) = 0.3
Question 9.
There are nine slips of paper numbered from 1 to 9 in a bag. Four slips are randomly selected without replacement to form a 4-digit number.
a. How many 4-digit numbers can be formed?
Answer:
9P4 = 3024
b. How many 4-digit numbers start with the digit 1?
Answer:
8P3 = 336
Question 10.
There are fourteen juniors and twenty-three seniors in the Service Club. The club is to send four representatives to the state conference.
a. How many different ways are there to select a group of four students to attend the conference from the 37 Service Club members?
Answer:
37C4 = 66045
b. How many ways are there to select exactly two juniors?
Answer:
14C2 = 91
c. How many ways are there to select exactly two seniors?
Answer:
23C2 = 253
d. If the members of the club decide to send two juniors and two seniors, how many different groupings are possible?
Answer:
14C2∙23C2 = 23023
e. What is the probability that two juniors and two seniors are selected to attend the conference?
Answer:
\(\frac{{ }_{14} C_{2} \cdot{ }_{23} C_{2}}{{ }_{37} C_{4}}\) = \(\frac{23023}{66045}\) ≈ 0.349
Question 11.
A basketball team of 16 players consists of 6 guards, 7 forwards, and 3 centers. The coach decides to randomly select 5 players to start the game. What is the probability of 2 guards, 2 forwards, and 1 center starting the game?
Answer:
\(\frac{{ }_{6} C_{2} \cdot{ }_{7} C_{2} \cdot{ }_{3} C_{1}}{{ }_{16} C_{5}}\) ≈ 0.216
Question 12.
A research study was conducted to estimate the number of white perch (a type of fish) in a Midwestern lake. 300 perch were captured and tagged. After they were tagged, the perch were released back into the lake. A scientist involved in the research estimates there are 1,000 perch in this lake. Several days after tagging and releasing the fish, the scientist caught 50 perch of which 20 were tagged. If this scientist’s estimate about the number of fish in the lake is correct, do you think it was likely to get 20 perch out of 50 with a tag? Explain your answer.
Answer:
Assume the total number of fish was 1,000 perch. The probability of getting 20 of 50 perch tagged would be based on the number of ways to get 20 perch from the 300 tagged fish, multiplied by the number of ways of getting 30 perch from the 700 fish that are not tagged, divided by the number of ways of picking 50 fish from 1,000 fish. This result is the requested probability, or
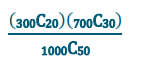
The above probability is approximately 0.04. This is a small probability and not likely to occur.
Eureka Math Precalculus Module 5 Lesson 4 Exit Ticket Answer Key
Question 1.
An ice cream shop has 25 different flavors of ice cream. For each of the following, indicate whether it is a problem that involves permutations, combinations, or neither.
a. What is the number of different 3-scoop ice cream cones that are possible if all three scoops are different flavors, and a cone with vanilla, strawberry, and chocolate is different from a cone with vanilla, chocolate, and strawberry?
Answer:
Permutation
b. What is the number of different 3-scoop ice cream cones that are possible if all three scoops are different flavors, and a cone with vanilla, strawberry, and chocolate is considered the same as a cone with vanilla, chocolate, and strawberry?
Answer:
Combination
c. What is the number of different ice cream cones if all three scoops could be the same, and the order of the flavors is important?
Answer:
Neither; 253 = 15625
Question 2.
A train consists of an engine at the front, a caboose at the rear, and 27 boxcars that are numbered from 1 to 27.
a. How many different orders are there for cars that make up the train?
Answer:
1∙27!∙1 ≈ 1.1∙1028
b. If the cars are attached to the train in a random order, what is the probability that the boxcars are in numerical order from 1 to 27?
Answer:
\(\frac{1}{27!}\) ≈ 9.2∙10-29
Question 3.
The dance club at school has 22 members. The dance coach wants to send four members to a special training on new dance routines.
a. The dance coach will select four dancers to go to the special training. Is the number of ways to select four dancers a permutation, a combination, or neither? Explain your answer.
Answer:
The order of the dancers is not important; therefore, the number of ways of selecting four dancers would be a combination of four dancers from 22 possible dancers.
b. If the dance coach chooses at random, how would you determine the probability of selecting dancers Laura, Matthew, Lakiesha, and Santos?
Answer:
The probability of selecting one of the combinations would be 1 divided by the total number of combinations.