Engage NY Eureka Math Precalculus Module 5 Lesson 1 Answer Key
Eureka Math Precalculus Module 5 Lesson 1 Exercise Answer Key
Example 1: Independent Events
Do you remember when breakfast cereal companies placed prizes in boxes of cereal? Possibly you recall that when a certain prize or toy was particularly special to children, it increased their interest in trying to get that toy. How many boxes of cereal would a customer have to buy to get that toy? Companies used this strategy to sell their cereal.
One of these companies put one of the following toys in its cereal boxes: a block (B), a toy watch (W), a toy ring (R), and a toy airplane (A). A machine that placed the toy in the box was programmed to select a toy by drawing a random number of 1 to 4. If a 1 was selected, the block (or B) was placed in the box; if a 2 was selected, a watch (or W) was placed in the box; if a 3 was selected, a ring (or R) was placed in the box; and if a 4 was selected, an airplane (or A) was placed in the box. When this promotion was launched, young children were especially interested in getting the toy airplane.

Exercises 1–8
Exercise 1.
If you bought one box of cereal, what is your estimate of the probability of getting the toy airplane? Explain how you got your answer.
Answer:
The probability is \(\frac{1}{4}\). I got this answer based on a sample space of {B,W,R,A}. Each outcome has the same chance of occurring. Therefore, the probability of getting the airplane is \(\frac{1}{4}\).
Exercise 2.
If you bought a second box of cereal, what is your estimate of the probability of getting the toy airplane in the second box? Explain how you got your answer.
Answer:
The probability is again \(\frac{1}{4}\). Since the machine that places a toy in the box picks a random number from 1 to 4, the probability that the second toy will be an airplane will again be \(\frac{1}{4}\).
Exercise 3.
If you bought two boxes of cereal, does your chance of getting at least one airplane increase or decrease? Explain your answer.
Answer:
The probability of getting at least one airplane increases because the possible outcomes include the following: an airplane in the first box but not the second box, an airplane in the second box but not the first box, and an airplane in both the first and second boxes.
Exercise 4.
Do you think the probability of getting at least one airplane from two boxes is greater than 0.5? Again, explain your answer.
Answer:
I think the probability is less than 0.5 as there are many more outcomes that I can describe that do not include the airplane. For example, you could get a watch and a block, a watch and a watch, a watch and a ring, and so on.
Exercise 5.
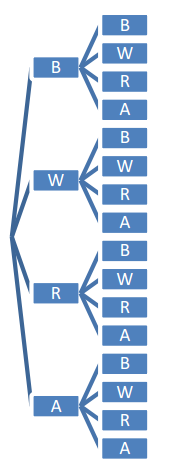
List all of the possibilities of getting two toys from two boxes of cereal. (Hint: Think of the possible outcomes as ordered pairs. For example, BA would represent a block from the first box and an airplane from the second box.)
Answer:
Consider the following ways students might create their lists using the notation:
B for block, W for watch, R for ring, and A for airplane.
The first letter represents the toy found in the first box, and the second letter represents the toy found in the second box. The first column represents getting the block in the first box, followed by each one of the other toys. The second column represents getting the watch in the first box, followed by each one of the other toys. The third column is developed with the ring in the first box, and the fourth column is developed with the airplane in the first box.
BB WB RB AB
BW WW RW AW
BR WR RR AR
BA WA RA AA
The following represents a tree diagram to form the lists:
Exercise 6.
Based on the list you created, what do you think is the probability of each of the following outcomes if two cereal boxes are purchased?
a. One (and only one) airplane
Answer:
\(\frac{6}{16}\) or \(\frac{3}{8}\)
b. At least one airplane
Answer:
\(\frac{7}{16}\)
c. No airplanes
Answer:
\(\frac{9}{16}\)
Exercise 7.
Consider the purchase of two cereal boxes.
a. What is the probability of getting an airplane in the first cereal box? Explain your answer.
Answer:
The probability is \(\frac{1}{4}\) because there are 4 possible toys, and each is equally likely to be in the box.
b. What is the probability of getting an airplane in the second cereal box?
Answer:
Again, the probability is \(\frac{1}{4}\) because there are 4 possible toys, and each is equally likely to be in the box.
c. What is the probability of getting airplanes in both cereal boxes?
Answer:
The probability is \(\frac{1}{16}\) because there is 1 pair in the list (AA) out of the 16 that fits this description.
P(A and B) is the probability that events A and B both occur and is the probability of the intersection of A and B. The probability of the intersection of events A and B is sometimes also denoted by P(A ∩ B).
Multiplication Rule for Independent Events
If A and B are independent events, P(A and B) = P(A) ∙ P(B).
This rule generalizes to more than two independent events. For example:
P(A and B and C) or P(A intersect B intersect C) = P(A) ∙ P(B) ∙ P(C).
Exercise 8.
Based on the multiplication rule for independent events, what is the probability of getting an airplane in both boxes? Explain your answer.
Answer:
The probability would be \(\frac{1}{16}\) as I would multiply the probability of getting an airplane in the first box (\(\frac{1}{4}\)) by the probability of getting an airplane in the second box, which is also \(\frac{1}{4}\).
Example 2: Dependent Events
Do you remember the famous line, “Life is like a box of chocolates,” from the movie Forrest Gump? When you take a piece of chocolate from a box, you never quite know what the chocolate will be filled with. Suppose a box of chocolates contains 15 identical-looking pieces. The 15 are filled in this manner: 3 caramel, 2 cherry cream, 2 coconut, 4 chocolate whip, and 4 fudge.
Exercises 9–14
Exercise 9.
If you randomly select one of the pieces of chocolate from the box, what is the probability that the piece will be filled with fudge?
Answer:
\(\frac{4}{15}\) ≈ 0.2667
Exercise 10.
If you randomly select a second piece of chocolate (after you have eaten the first one, which was filled with fudge), what is the probability that the piece will be filled with caramel?
Answer:
\(\frac{3}{14}\) ≈ 0.2143
The events, picking a fudge-filled piece on the first selection and picking a caramel-filled piece on the second selection, are called dependent events.
Two events are dependent if knowing that one has occurred changes the probability that the other occurs.
Multiplication Rule for Dependent Events
P(A and B) = P(A) ∙ P(B|A)
Recall from your previous work with probability in Algebra II that P(B|A) is the conditional probability of event B given that event A occurred. If event A is picking a fudge-filled piece on the first selection and event B is picking a caramel-filled piece on the second selection, then P(B|A) represents the probability of picking a caramel-filled piece second knowing that a fudge-filled piece was selected first.
Exercise 11.
If A1 is the event picking a fudge-filled piece on the first selection and B2 is the event picking a caramel-filled piece on the second selection, what does P(A1 and B2) represent? Find P(A1 and B2).
Answer:
P(A1 and B2) represents the probability of picking a fudge-filled piece first and a caramel-filled piece second:
\(\frac{4}{15}\) ∙ \(\frac{3}{14}\) ≈ 0.057
Exercise 12.
What does P(B1 and A2) represent? Calculate this probability.
Answer:
P(B1 and A2) represents the probability of picking a caramel-filled piece first and a fudge-filled piece second:
\(\frac{3}{15}\) ∙ \(\frac{4}{14}\) ≈ 0.057
Exercise 13.
If C represents selecting a coconut-filled piece of chocolate, what does P(A1 and C2) represent? Find this probability.
Answer:
P(A1 and C2) represents the probability of picking a fudge-filled piece first and a coconut-filled piece second:
\(\frac{4}{15}\) ∙ \(\frac{2}{14}\) ≈ 0.038
Exercise 14.
Find the probability that both the first and second pieces selected are filled with chocolate whip.
Answer:
\(\frac{4}{15}\) ∙ \(\frac{3}{14}\) ≈ 0.057
Exercises 15–17
Exercise 15.
For each of the following, write the probability as the intersection of two events. Then, indicate whether the two events are independent or dependent, and calculate the probability of the intersection of the two events occurring.
a. The probability of selecting a 6 from the first draw and a 7 on the second draw when two balls are selected without replacement from a container with 10 balls numbered 1 to 10
Answer:
Dependent
P(6 first and 7 second) = P(6 first) ∙ P(7 second│6 first) = \(\frac{1}{10}\) ∙ \(\frac{1}{9}\) = \(\frac{1}{90}\) ≈ 0.011
b. The probability of selecting a 6 on the first draw and a 7 on the second draw when two balls are selected with replacement from a container with 10 balls numbered 1 to 10
Answer:
Independent
P(6 first and 7 second) = P(6 first) ∙ P(7 second) = \(\frac{1}{10}\) ∙ \(\frac{1}{10}\) = \(\frac{1}{100}\) = 0.01
c. The probability that two people selected at random in a shopping mall on a very busy Saturday both have a birthday in the month of June. Assume that all 365 birthdays are equally likely, and ignore the possibility of a February 29 leap-year birthday.
Answer:
Independent
P(first person June birthday and second person June birthday) =
P(first person June birthday) ∙ P(second person June birthday) =
\(\frac{30}{365}\) ∙ \(\frac{30}{365}\) = 0.0068
d. The probability that two socks selected at random from a drawer containing 10 black socks and 6 white socks will both be black
Answer:
Dependent
P(first sock black and second sock black) =
P(first sock black) ∙ P(second sock black │first sock black)
= \(\frac{10}{16}\) ∙ \(\frac{9}{15}\)
= 0.375
Exercise 16.
A gumball machine has gumballs of 4 different flavors: sour apple (A), grape (G), orange (O), and cherry (C). There are six gumballs of each flavor. When 50¢ is put into the machine, two random gumballs come out. The event C1 means a cherry gumball came out first, the event C2 means a cherry gumball came out second, the event A1 means a sour apple gumball came out first, and the event G2 means a grape gumball came out second.
a. What does P(C2|C1) mean in this context?
Answer:
The probability of the second gumball being cherry knowing the first gumball was cherry
b. Find P(C1 and C2).
Answer:
\(\frac{6}{24}\) ∙ \(\frac{5}{23}\) ≈ 0.0543
c. Find P(A1 and G2).
Answer:
\(\frac{6}{24}\) ∙ \(\frac{6}{23}\) ≈ 0.0652
Exercise 17.
Below are the approximate percentages of the different blood types for people in the United States.
Type O 44%
Type A 42%
Type B 10%
Type AB 4%
Consider a group of 100 people with a distribution of blood types consistent with these percentages. If two people are randomly selected with replacement from this group, what is the probability that
a. Both people have type O blood?
Answer:
0.44 ∙ 0.44 = 0.1936
b. The first person has type A blood and the second person has type AB blood?
Answer:
0.42 ∙ 0.04 = 0.0168
Eureka Math Precalculus Module 5 Lesson 1 Problem Set Answer Key
Question 1.
In a game using the spinner below, a participant spins the spinner twice. If the spinner lands on red both times, the participant is a winner.
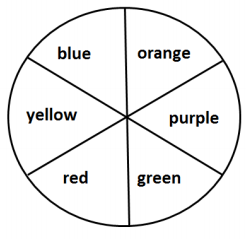
a. The event participant is a winner can be thought of as the intersection of two events. List the two events.
Answer:
The first spin lands on red, and the second spin lands on red.
b. Are the two events independent? Explain.
Answer:
Independent—knowing the first spin landed on red does not change the probability of the second spin landing on red.
c. Find the probability that a participant wins the game.
Answer:
\(\frac{1}{6}\) ∙ \(\frac{1}{6}\) ≈ 0.0278
Question 2.
The overall probability of winning a prize in a weekly lottery is \(\frac{1}{32}\). What is the probability of winning a prize in this lottery three weeks in a row?
Answer:
\(\frac{1}{32}\) ∙ \(\frac{1}{32}\) ∙ \(\frac{1}{32}\) ≈ 0.00003
Question 3.
A Gallup poll reported that 28% of adults (age 18 and older) eat at a fast food restaurant about once a week. Find the probability that two randomly selected adults would both say they eat at a fast food restaurant about once a week.
Answer:
0.28⋅0.28 = 0.0784
Question 4.
In the game Scrabble, there are a total of 100 tiles. Of the 100 tiles, 42 tiles have the vowels A, E, I, O, and U printed on them, 56 tiles have the consonants printed on them, and 2 tiles are left blank.
a. If tiles are selected at random, what is the probability that the first tile drawn from the pile of 100 tiles is a vowel?
\(\frac{42}{100}\) = 0.42
b. If tiles drawn are not replaced, what is the probability that the first two tiles selected are both vowels?
Answer:
\(\frac{42}{100}\) ∙ \(\frac{41}{99}\) ≈ 0.174
c. Event A is drawing a vowel, event B is drawing a consonant, and event C is drawing a blank tile. A1 means a vowel is drawn on the first selection, B2 means a consonant is drawn on the second selection, and C2 means a blank tile is drawn on the second selection. Tiles are selected at random and without replacement.
i. Find P(A1 and B2).
Answer:
= \(\frac{42}{100}\) ∙ \(\frac{56}{99}\) ≈ 0.238
ii. Find P(A1 and C2).
Answer:
= \(\frac{42}{100}\) ∙ \(\frac{2}{99}\) ≈ 0.008
iii. Find P(B1 and C2).
Answer:
= \(\frac{56}{100}\) ∙ \(\frac{2}{99}\) ≈ 0.011
Question 5.
To prevent a flooded basement, a homeowner has installed two special pumps that work automatically and independently to pump water if the water level gets too high. One pump is rather old and does not work 28% of the time, and the second pump is newer and does not work 9% of the time. Find the probability that both pumps will fail to work at the same time.
Answer:
0.28 ∙ 0.09 ≈ 0.025
Question 6.
According to a recent survey, approximately 77% of Americans get to work by driving alone. Other methods for getting to work are listed in the table below.
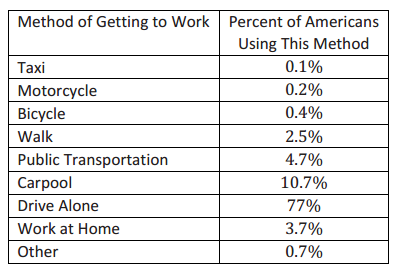
a. What is the probability that a randomly selected worker drives to work alone?
Answer:
0.77
b. What is the probability that two workers selected at random with replacement both drive to work alone?
Answer:
Assume independent 0.77 ∙ 0.77 ≈ 0.593
Question 7.
A bag of M&Ms contains the following distribution of colors:
9 blue
6 orange
5 brown
5 green
4 red
3 yellow
Three M&Ms are randomly selected without replacement. Find the probabilities of the following events.
a. All three are blue.
Answer:
\(\frac{9}{32}\) ∙ \(\frac{8}{31}\) ∙ \(\frac{7}{30}\) ≈ 0.017
b. The first one selected is blue, the second one selected is orange, and the third one selected is red.
Answer:
\(\frac{9}{32}\) ∙ \(\frac{6}{31}\) ∙ \(\frac{4}{30}\) ≈ 0.007
c. The first two selected are red, and the third one selected is yellow.
Answer:
\(\frac{4}{32}\) ∙ \(\frac{3}{31}\) ∙ \(\frac{3}{30}\) ≈ 0.001
Question 8.
Suppose in a certain breed of dog, the color of fur can either be tan or black. Eighty-five percent of the time, a puppy will be born with tan fur, while 15% of the time, the puppy will have black fur. Suppose in a future litter, six puppies will be born.
a. Are the events having tan fur and having black fur independent? Explain.
Answer:
Yes. Knowing the color of fur for one puppy doesn’t affect the probability of fur color for another puppy.
b. What is the probability that one puppy in the litter will have black fur and another puppy will have tan fur?
Answer:
0.15 ∙ 0.85 = 0.1275
c. What is the probability that all six puppies will have tan fur?
Answer:
0.85 ∙ 0.85 ∙ 0.85 ∙ 0.85 ∙ 0.85 ∙ 0.85 ≈ 0.377
d. Is it likely for three out of the six puppies to be born with black fur? Justify mathematically.
Answer:
0.15 ∙ 0.15 ∙ 0.15 = 0.003 375
No. The probability of three puppies being born with black fur is 0.003 375. This is not likely to happen.
Question 9.
Suppose that in the litter of six puppies from Exercise 8, five puppies are born with tan fur, and one puppy is born with black fur.
a. You randomly pick up one puppy. What is the probability that puppy will have black fur?
Answer:
\(\frac{1}{6}\) ≈ 0.167
b. You randomly pick up one puppy, put it down, and randomly pick up a puppy again. What is the probability that both puppies will have black fur?
Answer:
\(\frac{1}{6}\) ∙ \(\frac{1}{6}\) ≈ 0.028
c. You randomly pick up two puppies, one in each hand. What is the probability that both puppies will have black fur?
Answer:
0; this outcome can never happen since there is only one black puppy.
d. You randomly pick up two puppies, one in each hand. What is the probability that both puppies will have tan fur?
Answer:
\(\frac{5}{6}\) ∙ \(\frac{4}{5}\) ≈ 0.667
Eureka Math Precalculus Module 5 Lesson 1 Exit Ticket Answer Key
Question 1.
Serena is in a math class of 20 students. Each day for a week (Monday to Friday), a student in Serena’s class is randomly selected by the teacher to explain a homework problem. Once a student’s name is selected, that student is not eligible to be selected again that week.
a. What is the probability that Serena is selected on Monday?
Answer:
\(\frac{1}{20}\) = 0.05
b. What is the probability that Serena is selected on Tuesday given that she was not selected on Monday?
Answer:
\(\frac{1}{19}\) ≈ 0.0526
c. What is the probability that she will be selected on Friday given that she was not selected on any of the other days?
Answer:
\(\frac{1}{16}\) = 0.0625
Question 2.
Suppose A represents Serena being selected, and B represents Dominic (another student in class) being selected. The event A1 means Serena was selected on Monday, and the event B2 means Dominic was selected on Tuesday. The event B1 means Dominic was selected on Monday, and the event A2 means Serena was selected on Tuesday.
a. Explain in words what P(A1 and B2) represents, and then calculate this probability.
Answer:
It is the probability that Serena is selected on Monday and Dominic is selected on Tuesday.
P(A1 and B2) = \(\frac{1}{20}\) ∙ \(\frac{1}{19}\) ≈ 0.0026
b. Explain in words what P(B1 and A2) represents, and then calculate this probability.
Answer:
It is the probability that Dominic is selected on Monday and Serena is selected on Tuesday.
P(B1 and A2) = \(\frac{1}{20}\) ∙ \(\frac{1}{19}\) ≈ 0.0026