Engage NY Eureka Math Precalculus Module 4 Lesson 7 Answer Key
Eureka Math Precalculus Module 4 Lesson 7 Exploratory Challenge/Exercise Answer Key
Exploratory Challenge/Exercises 1–6: Triangles in Circles
In this Exploratory Challenge, you will find the area of triangles with base along the positive x-axis and a third point on the graph of the circle x2 + y2 = 25.
Exercise 1.
Find the area of each triangle shown below. Show work to support your answer.
a.

Answer:
The base is given by the measure of \(\overline{A C}\), which is 5 units. The height is the vertical distance from B to the horizontal axis, which is 4 units.
\(\frac{1}{2}\) (5)(4) = 10
The area is 10 square units.
b.
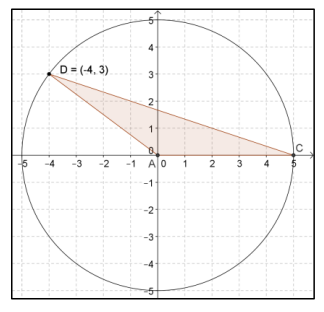
Answer:
The base is 5 units and the height is 3 units.
\(\frac{1}{2}\) (5)(3) = 7.5
The area is 7.5 square units.
Exercise 2.
Find the area of each of the triangles shown below. Show work to support your answer.
a.
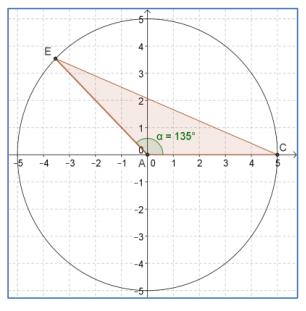
Answer:
Draw a perpendicular line from E to the horizontal axis. The distance from E to the horizontal axis is a leg of a 45°-45°-90° right triangle whose sides are in a ratio a:a:a[/latex] \(\sqrt{2}\). Since EA = 5, the height of the triangle will be the solution to the equation a\(\sqrt{2}\) = 5. Thus, the height of triangle AEC is \(\frac{5}{\sqrt{2}}\) or \(\frac{5}{2}\) \(\sqrt{2}\) units.
\(\frac{1}{2}\) (5)(\(\frac{5}{2}\) \(\sqrt{2}\)) = \(\frac{25}{4}\) \(\sqrt{2}\)
The area is \(\frac{25}{4}\) \(\sqrt{2}\) square units.
b.
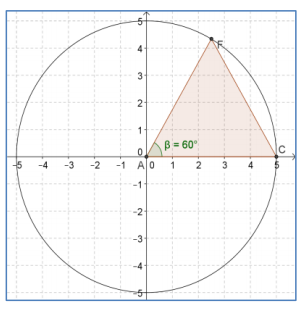
Answer:
Draw a perpendicular line from F to the horizontal axis. The height of the triangle is a leg of a 30°-60°-90° right triangle whose sides are the ratio a:a\(\sqrt{3}\) :2a. Since AF = 5 units, the shorter leg will be \(\frac{5}{2}\) units and the longer leg will be \(\frac{5}{2}\) \(\sqrt{3}\) units. Thus, the height of the triangle is \(\frac{5}{2}\) \(\sqrt{3}\) units.
\(\frac{1}{2}\) (5)(\(\frac{5}{2}\) \(\sqrt{3}\)) = \(\frac{25}{4}\) \(\sqrt{3}\)
The area is \(\frac{25}{4}\) \(\sqrt{3}\) square units.
Exercise 3.
Joni said that the area of triangle AFC in Exercise 2 part (b) can be found using the definition of the sine function.
a. What are the coordinates of point F in terms of the cosine and sine functions? Explain how you know.
Answer:
The coordinates are the point on the unit circle given by (cos(θ), sin(θ) ), where θ is the rotation of a ray from its initial position to its terminal position. This circle has a radius of 5 units so each point on this circle is a dilation by a factor of 5 of the points on the unit circle; thus, the coordinates are (5 cos(θ), 5 sin(θ) ).
b. Explain why the y-coordinate of point F is equal to the height of the triangle.
Answer:
If \(\overline{A C}\) is the base of the triangle, then the height of the triangle is on a line perpendicular to the base that contains point F. The y-coordinate of any point in the Cartesian plane represents the distance from that point to the horizontal axis. Thus, the y-coordinate is equal to the height of this triangle.
c. Write the area of triangle AFC in terms of the sine function.
Answer:
The height is the y-coordinate of a point on the circle of radius 5 units. This y-coordinate is 5 sin(\(\frac{\pi}{3}\)). Thus, the area in square units is given by
Area = \(\frac{1}{2}\) (5)(5 sin(\(\frac{\pi}{3}\)) )
= \(\frac{5}{2}\) (\(\frac{5 \sqrt{3}}{2}\))
= \(\frac{25}{4}\) \(\sqrt{3}\)
d. Does this method work for the area of triangle AEC?
Answer:
Yes. The angle 135° corresponds to a rotation of \(3\frac{\pi}{4}\) radians. In square units, the area of triangle AEC is given by
Area = \(\frac{1}{2}\) (5)(5 sin(\(3\frac{\pi}{4}\)) )
= \(\frac{5}{2}\) (\(\frac{5 \sqrt{2}}{2}\))
= \(\frac{25}{4}\) \(\sqrt{2}\)
Exercise 4.
Find the area of the following triangles.
a.
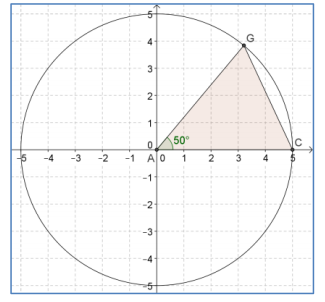
Answer:
The base is 5 units, and if we draw a perpendicular line from point G to side \(\overline{A C}\), then the distance from G to \(\overline{A C}\) is given by 5 sin(50°).
\(\frac{1}{2}\) (5)(5 sin(50°) ) ≈ 9.58
The area is approximately 9.58 square units.
b.

Answer:
Drawing a perpendicular line from point G to the horizontal axis gives a height for this triangle that is equal to 5 sin(115°).
\(\frac{1}{2}\) (5)(5 sin(115°)) 11.33
The area is approximately 11.33 square units.
Exercise 5.
Write a formula that will give the area of any triangle with vertices located at A(0,0), C(5,0), and B(x,y) a point on the graph of x2 + y2 = 25 such that y > 0.
Answer:
Area = \(\frac{25}{2}\) sin(θ), where θ is the counterclockwise rotation of B from C about the origin.
Exercise 6.
For what value of θ will this triangle have maximum area? Explain your reasoning.
Answer:
The triangle has maximum area when θ = \(\frac{\pi}{2}\) because the height is the greatest for this rotation since that is the rotation value when the height of the triangle is equal to the radius of the circle. For all other rotations, given that y > 0, the height is less than the radius.
Exploratory Challenge/Exercises 7–10: Triangles in Circles
Exercise 7.
Find the area of the following triangle.
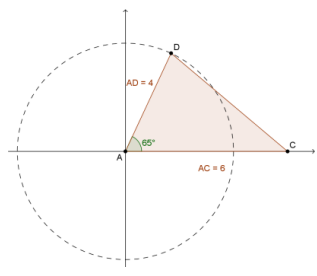
Answer:
The height is 4 sin(65°) units, and the base is 6 units.
\(\frac{1}{2}\) (6)(4 sin(65°) ) ≈ 10.88
The area is approximately 10.88 square units.
Exercise 8.
Prove that the area of any oblique triangle is given by the formula
Area = \(\frac{1}{2}\) absin(C)
where a and b are adjacent sides of △ABC and C is the measure of the angle between them.
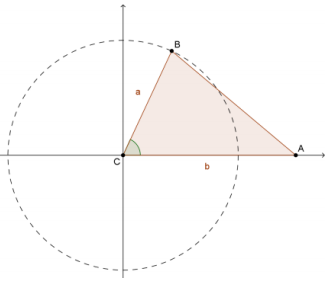
Answer:
If we take B to be a point on a circle of radius a units centered at C, then the coordinates of B are given by (a cos(C), a sin(C)) where C is the measure of ∠BCA. Construct the height of △ABC from point B to side \(\overline{A C}\).
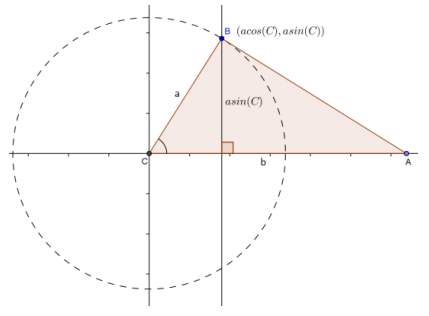
This height corresponds to the y-coordinate of B, which is a sin(C). The base is b units, and thus, the area is as follows:
Area = \(\frac{1}{2}\) (base)(height)
= \(\frac{1}{2}\) (b)(a sin(C) )
= \(\frac{1}{2}\) ab sin(C).
Exercise 9.
Use the area formula from Exercise 8 to calculate the area of the following triangles.
a.
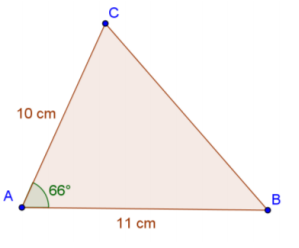
Answer:
Area = \(\frac{1}{2}\)(10)(11)sin(66°)
Area = 55 sin(66°)
Area ≈ 50.25
The area is 50.25 cm2.
b.
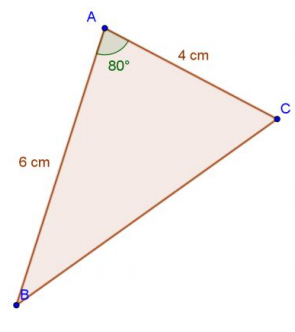
Answer:
Area = \(\frac{1}{2}\) (6)(4) sin(80°)
Area = 12 sin(80°)
Area ≈ 11.82
The area is 11.82 cm2.
c. A quilter is making an applique design with triangular pieces like the one shown below. How much fabric is used in each piece?
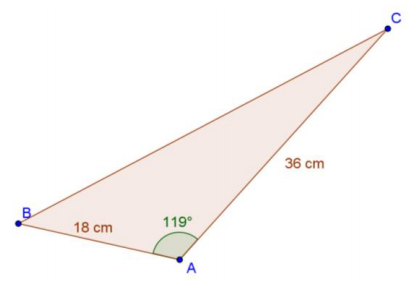
Answer:
Area = \(\frac{1}{2}\)(18)(36)sin(119°)
Area = 182 sin(119°)
Area ≈ 283.38
Each triangular piece is 283.38 cm2 of fabric.
Exercise 10.
Calculate the area of the following regular polygons inscribed in a unit circle by dividing the polygon into congruent triangles where one of the triangles has a base along the positive x-axis.
a.
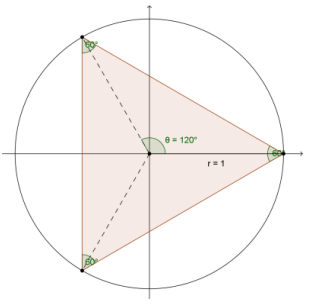
Answer:
3(\(\frac{1}{2}\))(1)(1 ∙ sin(120°) ) ≈ 1.30
The area is approximately 1.30 square units.
b.

Answer:
4(\(\frac{1}{2}\))(1)(1 ∙ sin(90°) ) ≈ 2
The area is approximately 2 square units.
c.
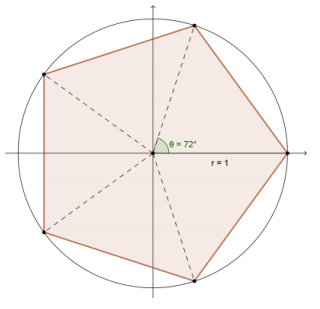
Answer:
5(\(\frac{1}{2}\))(1)(1 ∙ sin(72°) ) ≈ 2.38
The area is approximately 2.38 square units.
d. Sketch a regular hexagon inscribed in a unit circle with one vertex at (1,0), and find the area of this hexagon.
Answer:
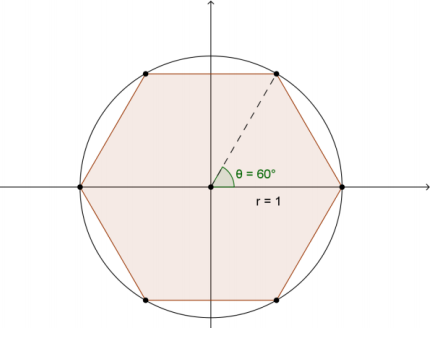
6(\(\frac{1}{2}\))(1)(1 ∙ sin(60°) ) ≈ 2.59
The area is approximately 2.59 square units.
e. Write a formula that gives the area of a regular polygon with n sides inscribed in a unit circle if one vertex is at (1,0) and θ is the angle formed by the positive x-axis and the segment connecting the origin to the point on the polygon that lies in the first quadrant.
Answer:
Area = \(\frac{n}{2}\) sin(\(\frac{360^{\circ}}{n}\))
f. Use a calculator to explore the area of this regular polygon for large values of n. What does the area of this polygon appear to be approaching as the value of n increases?
Answer:
If we select n = 10, the area is 2.94 square units.
If we select n = 30, the area is 3.12 square units.
If we select n = 100, the area is 3.139 525 square units.
The area appears to be approaching π.
Eureka Math Precalculus Module 4 Lesson 7 Problem Set Answer Key
Question 1.
Find the area of the triangle ABC shown to the right, with the following data:
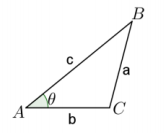
a. θ = \(\frac{\pi}{6}\), b = 3, and c = 6.
Answer:
\(\frac{1}{2}\) (b ∙ c ∙ sin(\(\frac{\pi}{6}\))) = \(\frac{1}{2}\) (18 ∙ \(\frac{1}{2}\)) = \(\frac{9}{2}\)
The area is \(\frac{9}{2}\) square units.
b. θ = \(\frac{\pi}{3}\), b = 4, and c = 8.
Answer:
\(\frac{1}{2}\) (b ∙ c ∙ sin(\(\frac{\pi}{3}\))) = \(\frac{1}{2}\) (32 ∙ \(\frac{\sqrt{3}}{2}\)) = 8\(\sqrt{3}\)
The area is 8\(\sqrt{3}\) square units.
c. θ = \(\frac{\pi}{4}\), b = 5, and c = 10.
Answer:
\(\frac{1}{2}\) (b ∙ c ∙ sin(\(\frac{\pi}{4}\))) = \(\frac{1}{2}\) (50 ∙ \(\frac{\sqrt{2}}{2}\)) = \(\frac{25 \sqrt{2}}{2}\)
The area is \(\frac{25 \sqrt{2}}{2}\) square units.
Question 2.
Find the area of the triangle ABC shown to the right, with the following data:
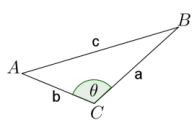
a. θ = \(\frac{3\pi}{4}\), a = 6, and b = 4.
Answer:
\(\frac{1}{2}\) (a ∙ b ∙ sin(\(\frac{\pi}{4}\))) = \(\frac{1}{2}\) (24 ∙ \(\frac{\sqrt{2}}{2}\)) = 6\(\sqrt{2}\)
The area is 6\(\sqrt{2}\) square units.
b. θ = \(\frac{5\pi}{6}\), a = 4, and b = 3.
Answer:
\(\frac{1}{2}\) (a ∙ b ∙ sin(\(\frac{\pi}{6}\))) = \(\frac{1}{2}\) (12 ∙ \(\frac{1}{2}\)) = 3
The area is 3 square units.
Question 3.
Find the area of each triangle shown below. State the area to the nearest tenth of a square centimeter.
a.

Answer:
A = \(\frac{1}{2}\)⋅4⋅7.5⋅sin(99°) ≈ 14.8
The area is approximately 14.8 sq.cm.
b.

Answer:
A = \(\frac{1}{2}\)⋅40⋅50⋅sin(50°) ≈ 766.0
The area is approximately 766 sq.cm.
Question 4.
The diameter of the circle O in the figure shown to the right is EB = 10.
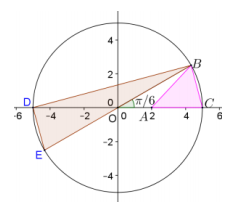
a. Find the area of the triangle OBA.
Answer:
\(\frac{1}{2}\) (2 ∙ 5 ∙ sin(\(\frac{\pi}{6}\))) = \(\frac{1}{2}\) (2 ∙ 5 ∙ \(\frac{1}{2}\)) = \(\frac{5}{2}\)
The area is \(\frac{5}{2}\) square units.
b. Find the area of the triangle ABC.
Answer:
\(\frac{1}{2}\) (bh) = \(\frac{1}{2}\) (3 ∙ \(\frac{5}{2}\)) = \(\frac{15}{4}\)
The area is \(\frac{15}{4}\) square units.
c. Find the area of the triangle DBO.
Answer:
\(\frac{1}{2}\) (bh) = \(\frac{1}{2}\) (5 ∙ \(\frac{5}{2}\)) = \(\frac{25}{4}\)
The area is \(\frac{25}{4}\) square units.
d. Find the area of the triangle DBE.
Answer:
The area of triangle DBE is the sum of the areas of triangles DBO, OBA, and ABC.
\(\frac{25}{4}\) + \(\frac{15}{4}\) + \(\frac{5}{2}\) = \(\frac{50}{4}\)
The area of triangle DBE is \(\frac{50}{4}\) square units.
Question 6.
Find the area of the equilateral triangle ABC inscribed in a circle with a radius of 6.
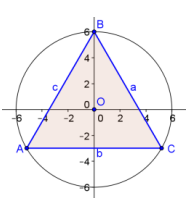
3 ∙ \(\frac{1}{2}\) (6 ∙ 6 ∙ sin(\(\frac{2 \pi}{3}\))) = \(\frac{54 \sqrt{3}}{2}\)
The area is \(\frac{54 \sqrt{3}}{2}\) square units.
Question 7.
Find the shaded area in the diagram below.
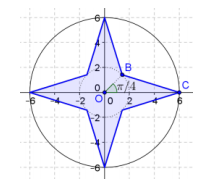
Answer:
8 ∙ \(\frac{1}{2}\) (6 ∙ 2 ∙ sin(\(\frac{\pi}{4}\))) = 24\(\sqrt{2}\)
The area is 24\(\sqrt{2}\) square units.
Question 7.
Find the shaded area in the diagram below. The radius of the outer circle is 5; the length of the line segment OB is 2.
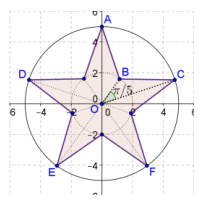
Answer:
10 ∙ \(\frac{1}{2}\) (5 ∙ 2 ∙ sin(\(\frac{\pi}{5}\))) ≈ 29.389
The area is 29.289 square units
Question 8.
Find the shaded area in the diagram below. The radius of the outer circle is 5.

Answer:
5 ∙ \(\frac{1}{2}\) (5 ∙ 5 ∙ sin(\(\frac{2\pi}{5}\))) = \(\frac{125}{2}\) sin(\(\frac{2\pi}{5}\)) = 59.441
The area of the pentagon is 59.441 square units. From Problem 7, we have the area of the star is 29.389. The shaded area is the area of the pentagon minus the area of the star.
The shaded area is 30.052 square units.
Question 9.
Find the area of the regular hexagon inscribed in a circle if one vertex is at (2,0).
Answer:
6 ∙ \(\frac{1}{2}\) (2 ∙ 2 ∙ sin(\(\frac{2\pi}{6}\))) = 12 ∙ sin(\(\frac{\pi}{3}\)) = 12 ∙ \(\frac{\sqrt{3}}{2}\) = 6\(\sqrt{3}\)
The area is 6\(\sqrt{3}\) square units.
Question 10.
Find the area of the regular dodecagon inscribed in a circle if one vertex is at (3,0).
Answer:
12 ∙ \(\frac{1}{2}\) (3 ∙ 3 ∙ sin(\(\frac{2\pi}{12}\))) = 54 ∙ sin(\(\frac{\pi}{6}\)) = 54 ∙ \(\frac{1}{2}\) = 27
The area is 27 square units.
Question 11.
A horse rancher wants to add on to existing fencing to create a triangular pasture for colts and fillies. She has 1,000 feet of fence to construct the additional two sides of the pasture.
a. What angle between the two new sides would produce the greatest area?
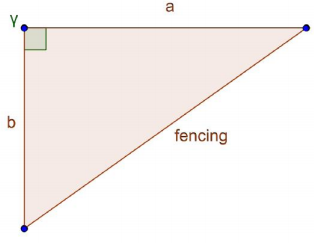
Answer:
Our formula is A = \(\frac{1}{2}\) ab sin(γ). When a and b are constant, the equation is maximized when sin(γ) is maximized, which occurs at γ = 90°. Thus, the greatest area would be when the angle is a 90° angle.
b. What is the area of her pasture if she decides to make two sides of 500 ft. each and uses the angle you found in part (a)?
Answer:
A = \(\frac{1}{2}\)⋅250 000⋅1 = 125 000
The area would be 125,000 sq.ft.
c. Due to property constraints, she ends up using sides of 100 ft. and 900 ft. with an angle of 30° between them. What is the area of the new pasture?
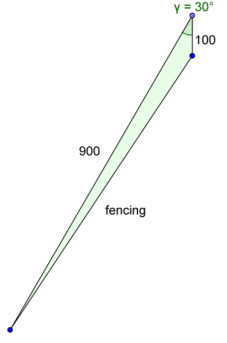
Answer:
A = \(\frac{1}{2}\)⋅90000⋅sin(30°)
= 45000⋅\(\frac{1}{2}\)
= 22500
The area would be 22,500 sq.ft.
Question 12.
An enthusiast of Egyptian history wants to make a life-size version of the Great Pyramid using modern building materials. The base of each side of the Great Pyramid was measured to be 756 ft. long, and the angle of elevation is about 52°.
a. How much material will go into the creation of the sides of the structure (the triangular faces of the pyramid)?

Answer:
According to these measurements, each side of the Great Pyramid has a base of 756 ft. The Great Pyramid’s height is in the middle of the triangle, so we can construct a right triangle of side \(\frac{756}{2}\) = 378 and the height of the pyramid, and use the cosine function.
cos(52°) = \(\frac{378}{h}\)
h = \(\frac{378}{\cos \left(52^{\circ}\right)}\)
h ≈ 614
Area of one side: \(\frac{1}{2}\)⋅614⋅756 ≈ 232 092. For four sides, the area is 928,368 sq.ft.
b. If the price of plywood for the sides is $0.75 per square foot, what is the cost of just the plywood for the sides?
Answer:
The total price would be about $696,276 for just the plywood going into the sides.
Question 13.
Depending on which side you choose to be the “base,” there are three possible ways to write the area of an oblique triangle, one being A = \(\frac{1}{2}\) ab sin(γ).
a. Write the other two possibilities using sin(α) and sin(β).
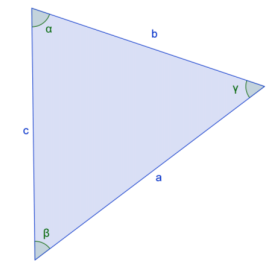
Answer:
\(\frac{1}{2}\) bc sin(α)
and
\(\frac{1}{2}\) ac sin(β)
b. Are all three equal?
Answer:
Yes, since each expression is equal to the area of the triangle, they are all equal to each other.
c. Find \(\frac{2A}{abc}\) for all three possibilities.
Answer:
\(\frac{2A}{abc}\) = \(\frac{\sin (\alpha)}{a}\) = \(\frac{\sin (\beta)}{b}\) = \(\frac{\sin (\gamma)}{c}\)
d. Is the relationship you found in part (c) true for all triangles?
Answer:
There was nothing special about the triangle we picked, so it should be true for all triangles.
Eureka Math Precalculus Module 4 Lesson 7 Exit Ticket Answer Key
Question 1.
Find the area of △ABC.
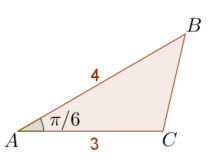
Answer:
Area = \(\frac{1}{2}\) (3)(4) sin(\(\frac{\pi}{6}\)) = 3
The area is 3 square units.
Question 2.
Explain why \(\frac{1}{2}\) ab sin(θ) gives the area of a triangle with sides a and b and included angle θ.
Answer:
In the diagram below, the height is the perpendicular line segment from point B to the base b. The length of this line segment is a sin(θ), which is the y-coordinate of point B, a point on a circle of radius a with center at C as shown.
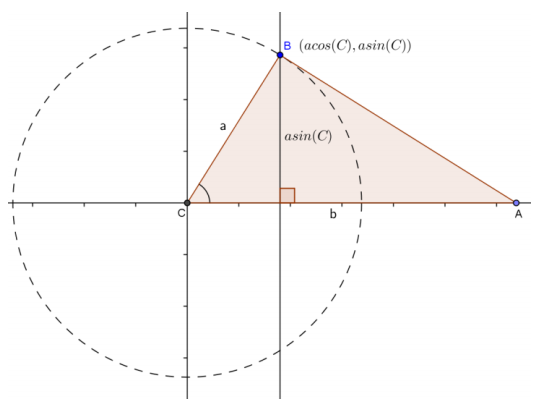
The area of a triangle is one-half the product of one side (the base) and the height to that side. If we let b be the base, then
Area = \(\frac{1}{2}\) b ∙ a sin(θ)
= \(\frac{1}{2}\) ab sin(θ).