Engage NY Eureka Math Precalculus Module 4 Lesson 4 Answer Key
Eureka Math Precalculus Module 4 Lesson 4 Exercise Answer Key
Exercises
Exercise 1.
Derive formulas for the following:
a. sin(2θ)
Answer:
sin(2θ) = sin(θ + θ)
= sin(θ)cos(θ) + cos(θ)sin(θ)
= 2sin(θ)cos(θ)
b. cos(2θ)
Answer:
cos(2θ) = cos(θ + θ)
= cos(θ)cos(θ) – sin(θ)sin(θ)
= cos2 (θ) – sin2 (θ)
Exercise 2.
Use the double – angle formulas for sine and cosine to verify these identities:
a. tan(2θ) = \(\frac{2 \tan (\theta)}{1 – \tan ^{2}(\theta)}\)
Answer:
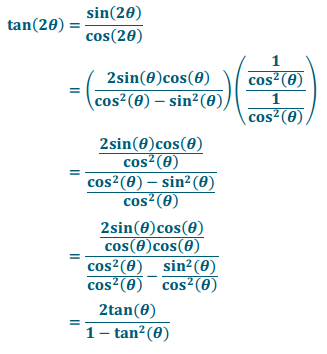
b. sin2 (θ) = (1 – cos(2θ))/2
Answer:
\(\frac{1 – \cos (2 \theta)}{2}\) = \(\frac{1 – \left(1 – 2 \sin ^{2}(\theta)\right)}{2}\) = \(\frac{2 \sin ^{2}(\theta)}{2}\) = sin2 (θ)
c. sin(3θ) = – 4sin3 (θ) + 3sin(θ)
Answer:
sin(3θ) = sin(2θ + θ)
= sin(2θ)cos(θ) + cos(2θ)sin(θ)
= 2sin(θ)(cos(θ))(cos(θ)) + (1 – 2sin2 (θ))(sin(θ))
= 2sin(θ) cos2 (θ) + sin(θ) – 2sin3 (θ)
= 2sin(θ)(1 – sin2 (θ)) + sin(θ) – 2sin3 (θ)
= 2sin(θ) – 2sin3 (θ) + sin(θ) – 2sin3 (θ)
= – 4sin3 (θ) + 3sin(θ)
Exercise 3.
Suppose that the position of a rider on the unit circle carousel is (0.8, – 0.6) for a rotation θ. What is the position of the rider after rotation by 2θ?
Answer:
x2θ = cos(2θ) = cos2(θ) – sin2 (θ) = 0.82 – ( – 0.6)2 = 0.64 – 0.36 = 0.28
y2θ = sin(2θ) = 2sin(θ)cos(θ) = 2( – 0.6)(0.8) = – 0.96
The rider’s position is (0.28, – 0.96).
Exercise 4.
Use the double – angle formula for cosine to establish the identity cos(\(\frac{\theta}{2}\)) = ±\(\sqrt{\frac{\cos (\theta) + 1}{2}}\)
Answer:
Since θ = 2(\(\frac{\theta}{2}\)), the double – angle formula gives cos(2(\(\frac{\theta}{2}\))) = 2cos2 (\(\frac{\theta}{2}\)) – 1. Then we have
cos(θ) = 2cos2 (\(\frac{\theta}{2}\)) – 1
1 + cos(θ) = 2cos2 (\(\frac{\theta}{2}\))
\(\frac{1 + \cos (\theta)}{2}\) = cos2 (\(\frac{\theta}{2}\))
cos(\(\frac{\theta}{2}\)) = ±\(\sqrt{\frac{\cos (\theta) + 1}{2}}\)
Exercise 5.
Use the double – angle formulas to verify these identities:
a. sin(\(\frac{\theta}{2}\)) = ±\(\sqrt{\frac{1 – \cos (\theta)}{2}}\)
Answer:
Since θ = 2(\(\frac{\theta}{2}\)), the double – ange formulas give cos(2(\(\frac{\theta}{2}\))) = 1 – 2sin2 (\(\frac{\theta}{2}\)).
Then we have
cos(θ) = 1 – 2sin2 (\(\frac{\theta}{2}\))
1 – cos(θ) = 2sin2 (\(\frac{\theta}{2}\))
\(\frac{1 – \cos (\theta)}{2}\) = sin2 (\(\frac{\theta}{2}\))
sin(\(\frac{\theta}{2}\)) = ±\(\sqrt{\frac{1 – \cos (\theta)}{2}}\)
b. tan(\(\frac{\theta}{2}\)) = ±\(\)
Answer:
tan(\(\frac{\theta}{2}\)) = \(\frac{\sin \left(\frac{\theta}{2}\right)}{\cos \left(\frac{\theta}{2}\right)}\) = \(\frac{\pm \sqrt{\frac{1 – \cos (\theta)}{2}}}{\pm \sqrt{\frac{\cos (\theta) + 1}{2}}}\) = ±\(\sqrt{\frac{1 – \cos (\theta)}{1 + \cos (\theta)}}\)
Exercise 6.
The position of a rider on the unit circle carousel is (0.8, – 0.6) after a rotation by θ where 0 ≤ θ < 2π. What is the position of the rider after rotation by \(\frac{\theta}{2}\)?
Answer:
Given that cos(θ) is positive and sin(θ) is negative, the rider is located in Quadrant IV after rotation by θ, so
\(\frac{3\pi}{2}\) < θ < 2π. This means that \(\frac{3\pi}{4}\) < \(\frac{\theta}{2}\) < π, which is in Quadrant II, so cos(\(\frac{\theta}{2}\)) is negative and sin(\(\frac{\theta}{2}\)) is positive.
x(\(\frac{\theta}{2}\)) = cos(\(\frac{\theta}{2}\)) = ±\(\sqrt{\frac{\cos (\theta) + 1}{2}}\) = – \(\sqrt{\frac{0.8 + 1}{2}}\) ≈ – 0.95
y(\(\frac{\theta}{2}\)) = sin(\(\frac{\theta}{2}\)) = ±\(\sqrt{\frac{1 – \cos (\theta)}{2}}\) = \(\sqrt{\frac{1 – 0.8}{2}}\) ≈ 0.32
The rider’s position is approximately ( – 0.95,0.32) after rotation by \(\frac{\theta}{2}\).
Exercise 7.
Evaluate the following trigonometric expressions.
a. sin(\(\frac{3\pi}{8}\))
Answer:
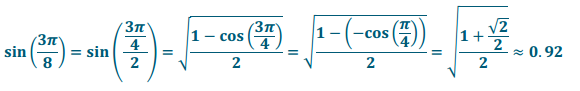
b. tan(\(\frac{\pi}{24}\))
Answer:
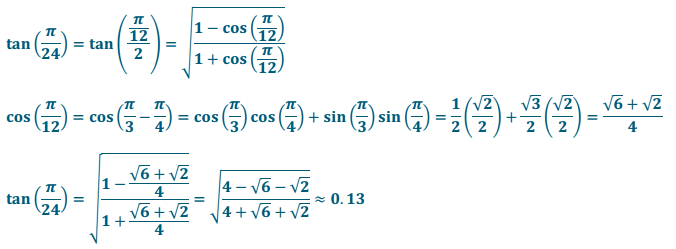
Eureka Math Precalculus Module 4 Lesson 4 Problem Set Answer Key
Question 1.
Evaluate the following trigonometric expressions.
a. 2 sin(\(\frac{\pi}{8}\))cos(\(\frac{\pi}{8}\))
Answer:
sin(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\)
b. \(\frac{1}{2}\) sin(\(\frac{\pi}{12}\))cos(\(\frac{\pi}{12}\))
Answer:
\(\frac{1}{4}\) (sin(\(\frac{\pi}{6}\))) = \(\frac{1}{8}\)
c. 4 sin( – \(\frac{5\pi}{12}\))cos( – \(\frac{5\pi}{12}\))
Answer:
2 sin(\(\frac{ – 5\pi}{6}\)) = – 2sin(\(\frac{\pi}{6}\)) = – 2(\(\frac{1}{2}\)) = – 1
d.cos2 (\(\frac{3\pi}{8}\)) – sin2 (\(\frac{3\pi}{8}\))
Answer:
cos(\(\frac{3\pi}{4}\)) = – cos(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\)
e. 2 cos2 (\(\frac{\pi}{12}\)) – 1
Answer:
cos(\(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{2}\)
f. 1 – 2sin2 ( – \(\frac{\pi}{8}\))
Answer:
cos( – \(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\)
g. cos2 ( – \(\frac{11\pi}{12}\)) – 2
Answer:
\(\frac{1}{2}\) (2 cos2 ( – \(\frac{11\pi}{12}\)) – 1) – \(\frac{3}{2}\) = \(\frac{1}{2}\) (cos(\(\frac{ – 11\pi}{12}\))) – \(\frac{3}{2}\) = \(\frac{1}{2}\) (cos(\(\frac{\pi}{6}\))) – \(\frac{3}{2}\) = \(\frac{1}{2}\) (\(\frac{\sqrt{3}}{2}\)) – \(\frac{3}{2}\) = \(\frac{\sqrt{3}}{4}\) – \(\frac{3}{2}\)
h. \(\frac{2 \tan \left(\frac{\pi}{8}\right)}{1 – \tan ^{2}\left(\frac{\pi}{8}\right)}\)
tan(\(\frac{\pi}{4}\)) = 1
i. \(\frac{2 \tan \left( – \frac{5 \pi}{12}\right)}{1 – \tan ^{2}\left( – \frac{5 \pi}{12}\right)}\)
Answer:
tan( – \(\frac{5\pi}{6}\)) = tan(\(\frac{\pi}{6}\)) = \(\frac{1}{\sqrt{3}}\) = \(\frac{\sqrt{2}}{3}\)
j. cos2 (\(\frac{\pi}{8}\))
Answer:
cos2 (\(\frac{\pi}{8}\)) = \(\frac{1 + \cos \left(\frac{\pi}{4}\right)}{2}\) = \(\frac{1 + \frac{\sqrt{2}}{2}}{2}\) = \(\frac{1}{2}\) + \(\frac{\sqrt{2}}{4}\)
k. cos(\(\frac{\pi}{8}\))
Answer:
Rotation by θ = \(\frac{\pi}{8}\) terminates in Quadrant I; therefore, cos(\(\frac{\pi}{8}\)) has a positive value.
cos(\(\frac{\pi}{8}\)) = \(\sqrt{\frac{1 + \cos \left(\frac{\pi}{4}\right)}{2}}\) = \(\sqrt{\frac{1}{2} + \frac{\sqrt{2}}{4}}\) = \(\frac{\sqrt{2 + \sqrt{2}}}{2}\)
l. cos( – \(\frac{9\pi}{8}\))
Answer:
Rotation by θ = – \(\frac{9\pi}{8}\) terminates in Quadrant II; therefore, cos( – \(\frac{9\pi}{8}\)) has a negative value.

m. sin2(\(\frac{\pi}{12}\))
Answer:
sin2(\(\frac{\pi}{12}\)) = \(\frac{1 – \cos \left(\frac{\pi}{6}\right)}{2}\) = \(\frac{1 – \frac{\sqrt{3}}{2}}{2}\) = \(\frac{1}{2}\) – \(\frac{\sqrt{3}}{4}\)
n. sin(\(\frac{\pi}{12}\))
Answer:
Rotation by θ = \(\frac{\pi}{12}\) terminates in Quadrant I; therefore, sin(\(\frac{\pi}{12}\)) has a positive value.
sin(\(\frac{\pi}{12}\)) = \(\sqrt{\frac{1 – \cos \left(\frac{\pi}{6}\right)}{2}}\) = \(\sqrt{\frac{1}{2} + \frac{\sqrt{3}}{4}}\) = \(\frac{\sqrt{2 + \sqrt{3}}}{2}\)
o. sin( – 5\(\frac{\pi}{12}\))
Answer:
Rotation by θ = – 5\(\frac{\pi}{12}\) terminates in Quadrant IV; therefore, sin( – 5\(\frac{\pi}{12}\)) has a negative value.

p. tan(\(\frac{\pi}{8}\))
Answer:
Rotation by θ = \(\frac{\pi}{8}\) terminates in Quadrant I; therefore, tan(\(\frac{\pi}{8}\)) has a positive value.
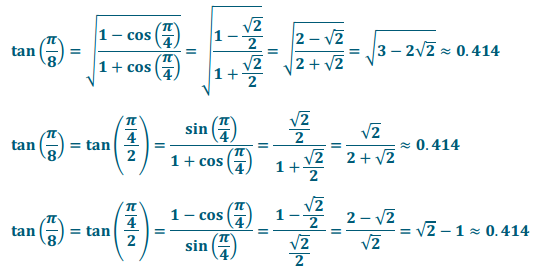
q. tan(\(\frac{\pi}{12}\))
Answer:

r. tan( – \(\frac{3\pi}{8}\))
Answer:
Rotation by θ = – \(\frac{3\pi}{8}\) terminates in Quadrant IV; therefore, tan( – \(\frac{3\pi}{8}\)) has a negative value.
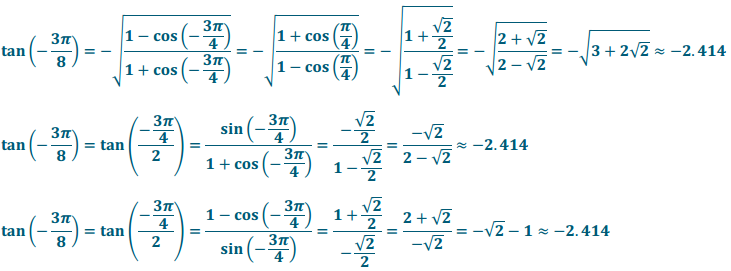
Question 2.
Show that sin(3x) = 3sin(x)cos2 (x) – sin3 (x). (Hint: Use sin(2x) = 2sin(x)cos(x) and the sine sum formula.)
Answer:
sin(3x) = sin(x + (2x))
= sin(x)cos(2x) + cos(x)sin(2x)
= sin(x)[cos2 (x) – sin2 (x)] + cos(x)[2sin(x)cos(x)]
= sin(x)cos2 (x) – sin3 (x) + 2sin(x)cos2 (x)
= 3sin(x)cos2 (x) – sin3 (x)
Question 3.
Show that cos(3x) = cos3 (x) – 3sin2 (x)cos(x). (Hint: Use cos(2x) = cos2 (x) – sin2 (x) and the cosine sum formula.)
Answer:
cos(3x) = cos(x + (2x))
= cos(x)cos(2x) – sin(x)sin(2x)
= cos(x)[cos2 (x) – sin2 (x)] – sin(x)[2sin(x)cos(x)]
= cos3 (x) – cos(x)sin2 (x) – 2cos(x)sin2 (x)
= cos3 (x) – 3cos(x)sin2 (x)
Question 4.
Use cos(2x) = cos2 (x) – sin2 (x) to establish the following formulas.
a. cos2 (x) = \(\frac{1 + \cos (2 x)}{2}\)
Answer:
cos(2x) = cos2 (x) – sin2 (x)
= cos2 (x) – (1 – cos2 (x))
= 2cos2 (x) – 1
Therefore, cos2 (x) = \(\frac{1 + \cos (2 x)}{2}\)
b. sin2 (x) = \(\frac{1 – \cos (2 x)}{2}\)
Answer:
cos(2x) = cos2 (x) – sin2 (x)
= (1 – sin2 (x)) – sin2 (x)
= 1 – 2sin2 (x)
Therefore, sin2 (x) = \(\frac{1 – \cos (2 x)}{2}\)
Question 5.
Jamia says that because sine is an odd function, sin(\(\frac{\theta}{2}\)) is always negative if θ is negative. That is, she says that for negative values of sin(\(\frac{\theta}{2}\)) = – \(\sqrt{\frac{1 – \cos (\theta)}{2}}\). Is she correct? Explain how you know.
Answer:
Jamia is not correct. Consider θ = – \(\frac{7\pi}{3}\). In this case, \(\frac{\theta}{2}\) = – \(\frac{7\pi}{6}\), and rotation by – \(\frac{7\pi}{6}\) terminates in Quadrant II. Thus, sin( – \(\frac{7\pi}{6}\)) is positive.
Question 6.
Ginger says that the only way to calculate sin(\(\frac{\pi}{12}\)) is using the difference formula for sine since \(\frac{\pi}{12}\) = \(\frac{\pi}{3}\) – \(\frac{\pi}{4}\). Fred says that there is another way to calculate sin(\(\frac{\pi}{12}\)). Who is correct and why?
Answer:
Fred is correct. We can use the half – angle formula with θ = \(\frac{\pi}{6}\) to calculate sin(\(\frac{\pi}{12}\)).
Question 7.
Henry says that by repeatedly applying the half – angle formula for sine we can create a formula for sin(\(\frac{\theta}{n}\)) for any positive integer n. Is he correct? Explain how you know.
Answer:
Henry is not correct. Repeating this process will only give us formulas for sin(\(\frac{\theta}{2^{k}}\)) for positive integers k. There is no way to derive a formula for quantities such as sin(\(\frac{\theta}{5}\)) using this method.
Eureka Math Precalculus Module 4 Lesson 4 Exit Ticket Answer Key
Question 1.
Show that cos(3θ) = 4cos3 (θ) – 3cos(θ).
Answer:
cos(3θ) = cos(2θ + θ) = cos(2θ)cos(θ) – sin(2θ)sin(θ)
= (2cos2 (θ) – 1)(cos(θ)) – 2sin(θ)cos(θ)(sin(θ))
= 2cos3 (θ) – cos(θ) – 2sin2 (θ)cos(θ)
= 2cos3 (θ) – cos(θ) – 2(1 – cos2 (θ))(cos(θ))
= 2cos3 (θ) – cos(θ) – 2cos(θ) + 2cos3 (θ)
= 4cos3 (θ) – 3cos(θ)
Question 2.
Evaluate cos(\(\frac{7\pi}{12}\)) using the half – angle formula, and then verify your solution using a different formula.
Answer: