Engage NY Eureka Math Precalculus Module 3 Lesson 7 Answer Key
Eureka Math Precalculus Module 3 Lesson 7 Exercise Answer Key
Exercise
Points F and G are located at (0, 3) and (0, – 3). Let P(x, y) be a point such that PF + PG = 8. Use this information to show that the equation of the ellipse is \(\frac{x^{2}}{7} + \frac{y^{2}}{16}\) = 1.
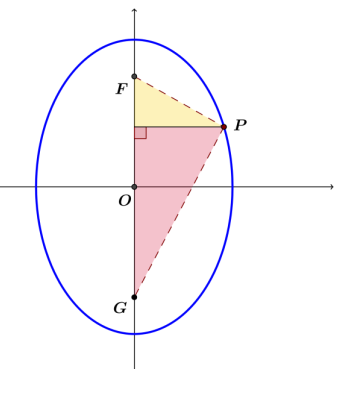
Answer:
The distance from the x – axis to point F and to point G is 3. The distance from the x – axis to point P is x; that means the vertical distance from F to P is 3 – y, and the vertical distance from G to P is 3 + y.
PF + PG = \(\sqrt{x^{2} + (3 – y)^{2}}\) + \(\sqrt{x^{2} + (y + 3)^{2}}\) = 8
\(\sqrt{x^{2} + (3 – y)^{2}}\) = 8 – \(\sqrt{x^{2} + (y + 3)^{2}}\)
x2 + (3 – y)2 = 64 – 16\(\sqrt{x^{2} + (y + 3)^{2}}\) + x2 + (y + 3)2
y2 – 6y + 9 = 64 – 16\(\sqrt{x^{2} + (y + 3)^{2}}\) + y2 + 6y + 9
16\(\sqrt{x^{2} + (y + 3)^{2}}\) = 64 + 12y
256[x2 + (y + 3)2 ] = 4096 + 1536y + 144y2
256[x2 + y2 + 6y + 9] = 4096 + 1536y + 144y2
256x2 + 256y2 + 1536y + 2304 = 4096 + 1536y + 144y2
256x2 + 112y2 = 1792
\(\frac{x^{2}}{7} + \frac{y^{2}}{16}\) = 1
Eureka Math Precalculus Module 3 Lesson 7 Problem Set Answer Key
Question 1.
Derive the equation of the ellipse with the given foci F and G that passes through point P. Write your answer in standard form: \(\) = 1.
a. The foci are F( – 2, 0) and G(2, 0), and point P(x, y) satisfies the condition PF + PG = 5.
Answer:
\(\frac{x^{2}}{\frac{25}{4}}\) + \(\frac{y^{2}}{\frac{9}{4}}\) = 1
\(\frac{4 x^{2}}{25}\) + \(\frac{4 y^{2}}{9}\)
b. The foci are F( – 1, 0) and G(1, 0), and point P(x, y) satisfies the condition PF + PG = 5.
Answer:
\(\frac{x^{2}}{\frac{25}{4}}\) + \(\frac{y^{2}}{\frac{21}{4}}\) = 1
\(\frac{4 x^{2}}{25}\) + \(\frac{4 y^{2}}{21}\)
c. The foci are F(0, – 1) and G(0, 1), and point P(x, y) satisfies the condition PF + PG = 4.
Answer:
\(\frac{x^{2}}{3}\) + \(\frac{y^{2}}{4}\) = 1
d. The foci are F( – \(\frac{2}{3}\), 0) and G(\(\frac{2}{3}\), 0), and point P(x, y) satisfies the condition PF + PG = 3.
Answer:
\(\frac{x^{2}}{\frac{9}{4}}\) + \(\frac{y^{2}}{\frac{65}{36}}\) = 1
\(\frac{4x^{2}}{9}\) + \(\frac{36y^{2}}{65}\) = 1
e. The foci are F(0, – 5) and G(0, 5), and point P(x, y) satisfies the condition PF + PG = 12.
Answer:
\(\frac{x^{2}}{11}\) + \(\frac{y^{2}}{36}\) = 1
f. The foci are F( – 6, 0) and G(6, 0), and point P(x, y) satisfies the condition PF + PG = 20.
Answer:
\(\frac{x^{2}}{100}\) + \(\frac{y^{2}}{64}\) = 1
Question 2.
Recall from Lesson 6 that the semi – major axes of an ellipse are the segments from the center to the farthest vertices, and the semi – minor axes are the segments from the center to the closest vertices. For each of the ellipses in Problem 1, find the lengths a and b of the semi – major axes.
Answer:
a. a = \(\frac{5}{2}\), b = \(\frac{3}{2}\)
b. a = \(\frac{5}{2}\), b = \(\frac{\sqrt{21}}{2}\)
c. a = \(\sqrt{3}\), b = 2
d. a = \(\frac{3}{2}\), b = \(\frac{\sqrt{65}}{6}\)
e. a = \(\sqrt{11}\), b = 6
f. a = 10, b = 8
Question 3.
Summarize what you know about equations of ellipses centered at the origin with vertices (a, 0), ( – a, 0), (0, b), and (0, – b).
Answer:
For ellipses centered at the origin, the equation is always \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1, where a is the positive x – value of the
x – intercepts and b is the positive y – value of the y – intercepts. If we know the x – and y – intercepts, then we know the equation of the ellipse.
Question 4.
Use your answer to Problem 3 to find the equation of the ellipse for each of the situations below.
a. An ellipse centered at the origin with x – intercepts ( – 2, 0), (2, 0) and y – intercepts (0, 8), (0, – 8)
Answer:
\(\frac{x^{2}}{4}\) + \(\frac{y^{2}}{64}\) = 1
b. An ellipse centered at the origin with x – intercepts ( – \(\sqrt{5}\), 0), (\(\sqrt{5}\), 0) and y – intercepts (0, 3), (0, – 3)
Answer:
\(\frac{x^{2}}{5}\) + \(\frac{y^{2}}{9}\) = 1
Question 5.
Examine the ellipses and the equations of the ellipses you have worked with, and describe the ellipses with equation \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 in the three cases a > b, a = b, and b > a.
Answer:
If a > b, then the foci are on the x – axis and the ellipse is oriented horizontally, and if b > a, the foci are on the y – axis and the ellipse is oriented vertically. If a = b, then the ellipse is a circle with radius a.
Question 6.
Is it possible for \(\frac{x^{2}}{4}\) + \(\frac{y^{2}}{9}\) = 1 to have foci at ( – c, 0) and (c, 0) for some real number c?
Answer:
No. Since 9 > 4, the foci must be along the y – axis.
Question 7.
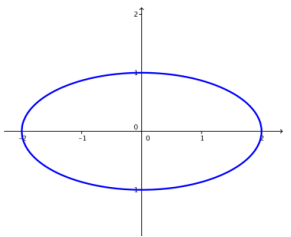
For each value of k specified in parts (a)–(e), plot the set of points in the plane that satisfy the equation
\(\frac{x^{2}}{4}\) + y2 = k.
a. k = 1
Answer:
b. k = \(\frac{1}{4}\)
Answer:

c. k = \(\frac{1}{9}\)
Answer:
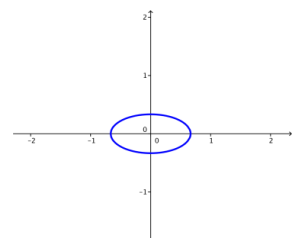
d. k = \(\frac{1}{16}\)
Answer:
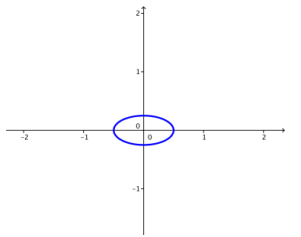
e. k = \(\frac{1}{25}\)
Answer:
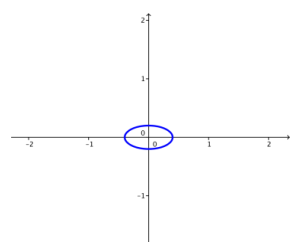
f. k = \(\frac{1}{100}\)
Answer:

g. Make a conjecture: Which points in the plane satisfy the equation \(\frac{x^{2}}{4}\) + y2 = 0?
Answer:
As k is getting smaller, the ellipse is shrinking. It seems that the only point that lies on the curve given by \(\frac{x^{2}}{4}\) + y2 = 0 would be the single point (0, 0).
h. Explain why your conjecture in part (g) makes sense algebraically.
Answer:
Both \(\frac{x^{2}}{4}\) and y2 are nonnegative numbers, and the only way to sum two nonnegative numbers and get zero would be if they were both zero. Thus, \(\frac{x^{2}}{4}\) = 0 and y2 = 0, which means that (x, y) is (0, 0).
i. Which points in the plane satisfy the equation \(\frac{x^{2}}{4}\) + y2 = – 1?
Answer:
There are no points in the plane that satisfy the equation x2 + y2 = – 1 because \(\frac{x^{2}}{4}\) + y2 ≥ 0 for all real numbers x and y.
Question 8.
For each value of k specified in parts (a)–(e), plot the set of points in the plane that satisfy the equation
\(\frac{x^{2}}{k}\) + y2 = 1.
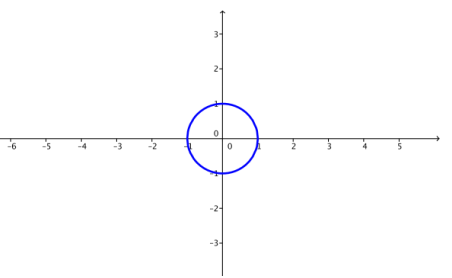
a. k = 1
Answer:
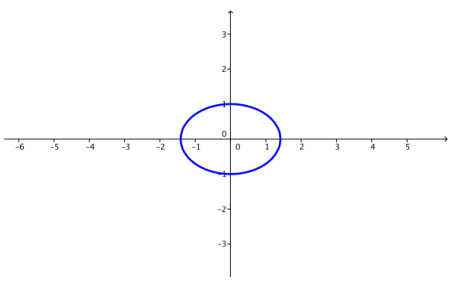
b. k = 2
Answer:
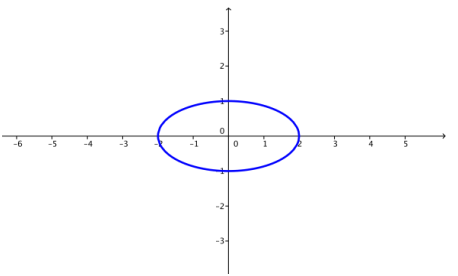
c. k = 4
Answer:
d. k = 10
Answer:
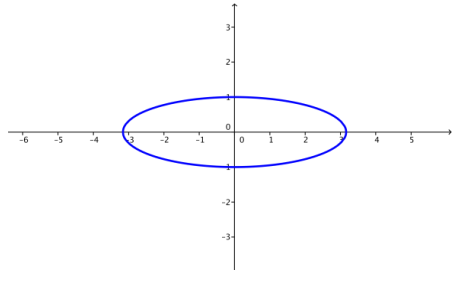
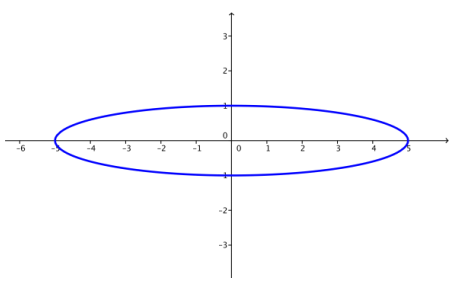
e. k = 25
Answer:
f. Describe what happens to the graph of \(\frac{x^{2}}{k}\) + y2 = 1 as k→∞.
Answer:
As k gets larger and larger, the ellipse stretches more and more horizontally, while not changing vertically. The vertices are ( – \(\sqrt{k}\), 0), (\(\sqrt{k}\), 0), (0, – 1), and (0, 1).
Question 9.
For each value of k specified in parts (a)–(e), plot the set of points in the plane that satisfy the equation
x2 + \(\frac{y^{2}}{k}\) = 1.
a. k = 1
Answer:
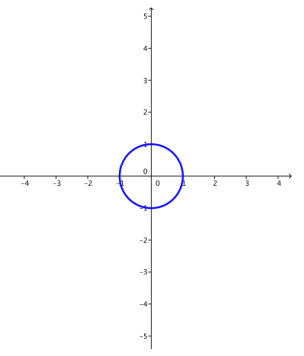
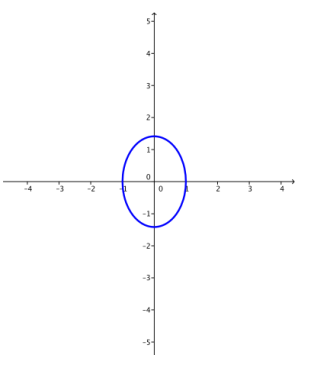
b. k = 2
Answer:
c. k = 4
Answer:
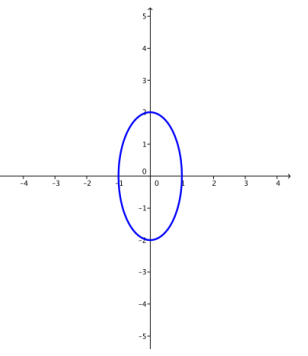
d. k = 10
Answer:
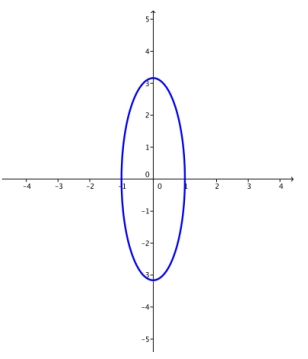
e. k = 25
Answer:
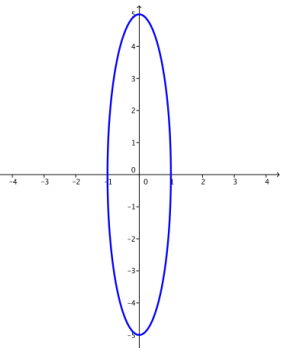
f. Describe what happens to the graph of x2 + \(\frac{y^{2}}{k}\) = 1 as k → ∞.
Answer:
As k gets larger and larger, the ellipse stretches more and more vertically, while not changing horizontally. The vertices are ( – 1, 0), (1, 0), (0, – \(\sqrt{k}\)), and (0, \(\sqrt{k}\)).
Eureka Math Precalculus Module 3 Lesson 7 Exit Ticket Answer Key
Question 1.
Suppose that the foci of an ellipse are F( – 1, 0) and G(1, 0) and that the point P(x, y) satisfies the condition
PF + PG = 4.
a. Derive an equation of an ellipse with foci F and G that passes through P. Write your answer in standard form: \(\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}\) = 1.
Answer:
PF + PG = 4
\(\sqrt{(x – 1)^{2} + y^{2}}\) + \(\sqrt{(x + 1)^{2} + y^{2}}\) = 4
(x – 1)2 + y2 = 16 – 8\(\sqrt{(x + 1)^{2} + y^{2}}\) + (x + 1)2 + y2
(x – 1)2 – (x + 1)2 – 16 = – 8\(\sqrt{(x + 1)^{2} + y^{2}}\)
x2 – 2x + 1 – (x2 + 2x + 1) – 16 = – 8\(\sqrt{(x + 1)^{2} + y^{2}}\)
– 4x – 16 = – 8\(\sqrt{(x + 1)^{2} + y^{2}}\)
x + 4 = 2\(\sqrt{(x + 1)^{2} + y^{2}}\)
x2 + 8x + 16 = 4(x2 + 2x + 1 + y2 )
x2 + 8x + 16 = 4x2 + 8x + 4 + 4y2
– 3x2 – 4y2 = – 12
\(\frac{x^{2}}{4} + \frac{y^{2}}{3}\) = 1
b. Sketch the graph of the ellipse defined above.
Answer:
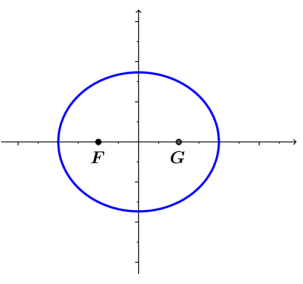
c. Verify that the x – intercepts of the graph satisfy the condition PF + PG = 4.
Answer:
For the x – intercepts (2, 0) and ( – 2, 0), we have PF + PG = 1 + 3 = 4 and PF + PG = 3 + 1 = 4.
d. Verify that the y – intercepts of the graph satisfy the condition PF + PG = 4.
Answer:
For the y – intercepts (0, \(\sqrt{3}\)) and (0, – \(\sqrt{3}\)), we have \(\sqrt{\sqrt{3}^{2} + ( – 1)^{2}}\) + \(\sqrt{\sqrt{3}^{2} + 1^{2}}\) = 2 + 2 = 4 and \(\sqrt{( – \sqrt{3})^{2} + ( – 1)^{2}}\) + \(\sqrt{( – \sqrt{3})^{2} + 1^{2}}\) = 2 + 2 = 4.