Eureka Math Precalculus Module 2 Lesson 9 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 9 Answer Key

Eureka Math Precalculus Module 2 Lesson 9 Exercise Answer Key

Opening Exercise
Recall from Problem 1, part (d), of the Problem Set of Lesson 7 that if you know what a linear transformation does to the three points (1,0,0), (0,1,0), and (0,0,1), you can find the matrix of the transformation. How do the images of these three points lead to the matrix of the transformation?
a. Suppose that a linear transformation L₁ rotates the unit cube by 90° counterclockwise about the z-axis. Find the matrix A₁ of the transformation L₁.
Answer:
Since this transformation rotates by 90° counterclockwise in the xy-plane, a vector along the positive x-axis will be transformed to lie along the positive y-axis, a vector along the positive y-axis will be transformed to lie along the negative x-axis, and a vector along the z-axis will be left alone. Thus,

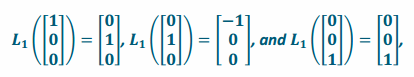
so the matrix of the transformation is A₁=\(\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] .\)

b. Suppose that a linear transformation L₂ rotates the unit cube by 90° counterclockwise about the y-axis. Find the matrix A₂ of the transformation L₂.
Answer:
Since this transformation rotates by 90° counterclockwise in the xz-plane, a vector along the positive x-axis will be transformed to lie along the positive z-axis, a vector along the y-axis will be left alone, and a vector along the positive z-axis will be transformed to lie along the negative x-axis. Thus,

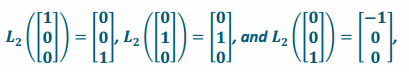
so the matrix of the transformation is A₂=\(\left[\begin{array}{ccc}
0 & 0 & -1 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{array}\right]\).

c. Suppose that a linear transformation L₃ scales by 2 in the x-direction, scales by 3 in the y-direction, and scales by 4 in the z-direction. Find the matrix A₃ of the transformation L₃.
Answer:
Since this transformation scales by 2 in the x-direction, by 3 in the y-direction, and by 4 in the z-direction, a vector along the x-axis will be multiplied by 2, a vector along the y-axis will be multiplied by 3, and a vector along the z-axis will be multiplied by 4. Thus,

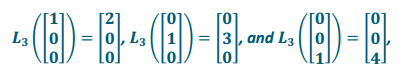
so the matrix of the transformation is A₃=\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 4
\end{array}\right]\).

d. Suppose that a linear transformation L₄ projects onto the xy-plane. Find the matrix A₄ of the transformation L₄.
Answer:
Since this transformation projects onto the xy-plane, a vector along the x-axis will be left alone, a vector along the y-axis will be left alone, and a vector along the z-axis will be transformed into the zero vector. Thus,

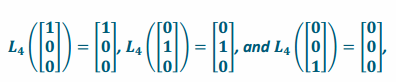
so the matrix of the transformation is A₄=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]\).

e. Suppose that a linear transformation L₅ projects onto the xz-plane. Find the matrix A₅ of the transformation L₅.
Answer:
Since this transformation projects onto the xz-plane, a vector along the x-axis will be left alone, a vector along the y-axis will be transformed into the zero vector, and a vector along the z-axis will be left alone. Thus,

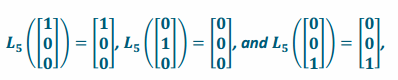
so the matrix of the transformation is A₅=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\).

f. Suppose that a linear transformation L₆ reflects across the plane with equation y=x. Find the matrix A₆ of the transformation L₆.
Answer:
Since this transformation reflects across the plane y=x, a vector along the positive x-axis will be transformed into a vector along the positive y-axis with the same length, a vector along the positive y-axis will be transformed into a vector along the positive x-axis, and a vector along the z-axis will be left alone. Thus,

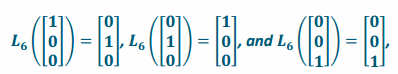
so the matrix of the transformation is A₆=\(\left[\begin{array}{lll}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\).

g. Suppose that a linear transformation L₇ satisfies 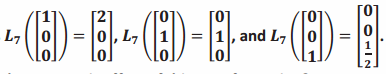Find the matrix A₇ of the transformation L₇. What is the geometric effect of this transformation?
Answer:
The matrix of this transformation is 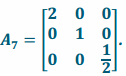. The geometric effect of L₇ is to stretch by a factor of 2 in the x-direction and scale by a factor of \(\frac{1}{2}\) in the z-direction.

h. Suppose that a linear transformation L₈ satisfies 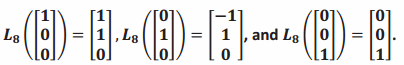. Find the matrix of the transformation L₈. What is the geometric effect of this transformation?
Answer:
The matrix of this transformation is 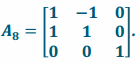. The geometric effect of L₈ is to rotate by 45° in the xy-plane, to scale by \(\sqrt{2}\) in both the x and y directions, and to not change in the z-direction.

Eureka Math Precalculus Module 2 Lesson 9 Exploratory Challenge Answer Key

Exploratory Challenge 1
Transformations L₁–L₈ refer to the linear transformations from the Opening Exercise. For each pair:
i. Make a conjecture to predict the geometric effect of performing the two transformations in the order specified.
ii. Find the product of the corresponding matrices in the order that corresponds to the indicated order of composition. Remember that if we perform a transformation L_B with matrix B and then L_A with matrix A, the matrix that corresponds to the composition L_A∘L_B is AB. That is, L_B is applied first, but matrix B is written second.
iii. Use the GeoGebra applet TransformCubes.ggb to draw the image of the unit cube under the transformation induced by the matrix product in part (ii). Was your conjecture in part (i) correct?

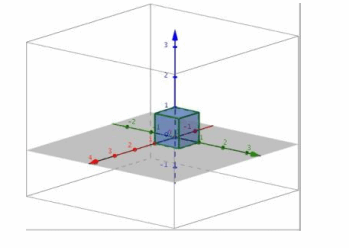
a. Perform L₆ and then L₆.
Answer:
i. Since L₆ reflects across the plane through y=x that is perpendicular to the xy-plane, performing L₆ twice in succession will result in the identity transformation.
ii. A₆⋅A₆=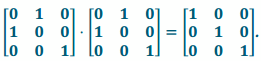. Since A₆⋅A₆ is the identity matrix, we know that
L₆∘L₆ is the identity transformation.
iii. The conjecture was correct.

b. Perform L₁ and then L₂.
Answer:
i. Sample student response: Since L₁ rotates 90° about the z-axis and L₂ rotates 90° about the y-axis, the composition L₂∘L₁ should rotate 180° about the line y=-x in the xy-plane.
ii.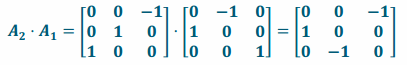
iii. The conjecture in part (i) is not correct. While it appears that the composition L₂∘L₁ is a rotation by 180° about the line y=-x, it is not because, for example, point (0,1,0) is transformed to point (0,0,-1) and does not remain on the y-axis after the transformation. Thus, this cannot be a rotation around the y-axis.

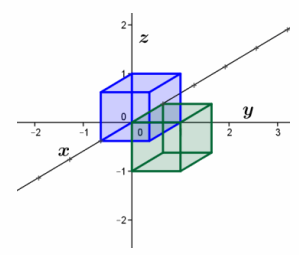
c. Perform L₄ and then L₅.
Answer:
i. Since L₄ projects onto the xy-plane and L₅ projects onto the xz-plane, the composition L₅∘L₄ will project onto the x-axis.
ii.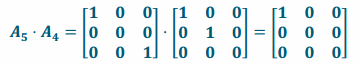
iii. The conjecture in part (i) is correct. The cube is first transformed to a square in the xy-plane and then transformed onto a segment on the x-axis.

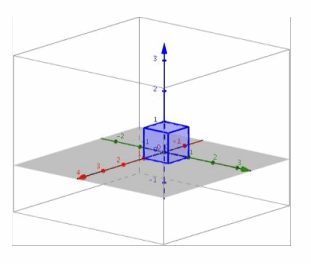
d. Perform L₄ and then L₃.
Answer:
i. Since L₄ projects onto the xy-plane and L₃ scales in the x, y, and z directions, the composition L₃∘L₄ will project onto the xy-plane and scale in the x and y directions.
ii.
iii. The conjecture in part (i) is correct.

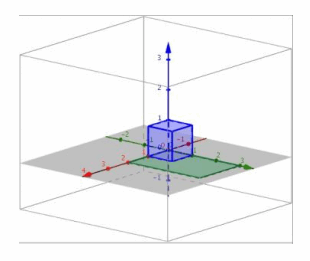
e. Perform L₃ and then L₇.
Answer:
i. Since L₃ scales in the x, y, and z directions and so does L₇, the composition will be a transformation that also scales in all three directions but with different scale factors.
ii.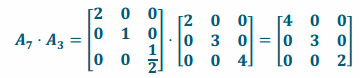
iii. The conjecture from (i) is correct.

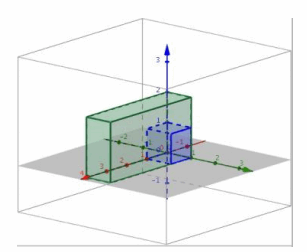
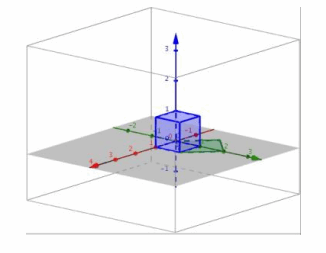
f. Perform L₈ and then L₄.
Answer:
i. Transformation L₈ rotates the unit cube by 45° about the z-axis and stretches by a factor of \(\sqrt{2}\) in both the x and y directions, while L₄ projects the image onto the xy-plane. The composition will transform the unit cube into a larger square that has been rotated 45° in the xy-plane.
ii.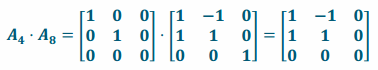
iii. The conjecture from part (i) is correct.

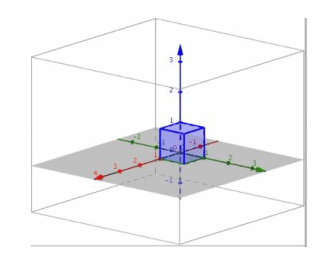
g. Perform L₄ and then L₆.
Answer:
i. Transformation L₄ projects onto the xy-plane, and transformation L₆ reflects across the plane through the line y=x in the xy-plane and is perpendicular to the xy-plane, so the composition L₆∘L₄ will appear to be the reflection in the xy-plane across the line y=x.
ii.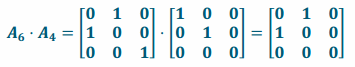
iii. The conjecture in part (i) is correct.

h. Perform L₂ and then L₇.
Answer:
i. Since L₂ rotates 90° around the y-axis and L₇ scales in the x and z directions, the composition L₇∘L₂ will rotate and scale simultaneously.
ii.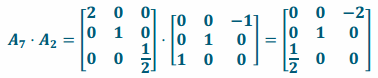
iii. The conjecture in part (i) is correct.

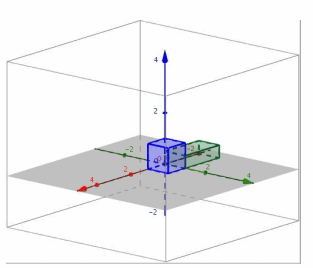
i. Perform L₈ and then L₈.
Answer:
i. Since L₈ rotates by 45° about the z-axis and scales by \(\sqrt{2}\) in the x and y directions, performing this transformation twice will rotate by 90° about the z-axis and scale by 2 in the x and y directions.
ii.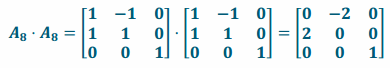
iii. The conjecture in part (i) is correct.

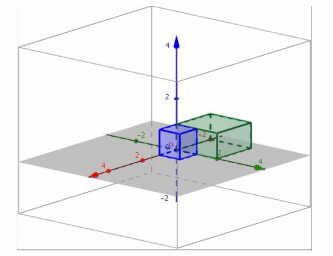
Exploratory Challenge 2
Transformations L₁–L₈ refer to the transformations from the Opening Exercise. For each of the following pairs of matrices A and B below, compare the transformations L_A∘L_B and L_B∘L_A.
a. L₄ and L₅
Answer:
Transformation L₄∘L₅ has matrix representation A₄⋅A₅= 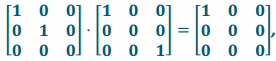and transformation L₅∘L₄ has matrix representation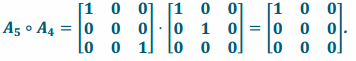
Since the two transformations have the same matrix representation, they are the same transformation:
L₅∘L₄=L₄∘L₅

b. L₂ and L₅
Answer:
Transformation L₂ \(\text { o }\) L₅ has matrix representation 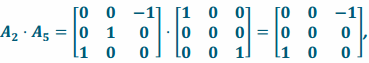and
transformation L₅ \(\text { o }\) L₂ has matrix representation A₅∙A₂ =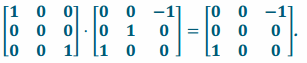
Since the two transformations have the same matrix representation, they are the same transformation:
L₂ \(\text { o }\)L₅ = L₅ \(\text { o }\) L₂

c. L₃ and L₇
Answer:
Transformation L₃∘L₇ has matrix representation 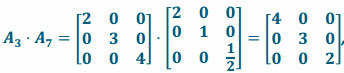and transformation as matrix representation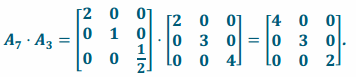
Since the two transformations have the same matrix representation, they are the same transformation:
L₃\(\text { o }\)L₇=L₇\(\text { o }\)L₃

d. L₃ and L₆
Answer:
Transformation L₃\(\text { o }\)L₆ has matrix representation 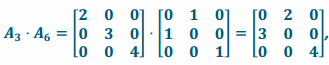and transformation L₆\(\text { o }\)L₃ has matrix representation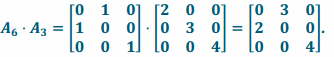
Since the two transformations have different matrix representations, they are not the same transformation: L₃∘L₆≠L₆∘L₃

e. L₇ and L₁
Answer:
Transformation L₇\(\text { o }\)L₁ has matrix representation 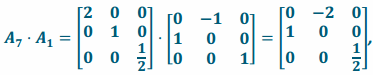and transformation L₁∘L₇ has matrix representation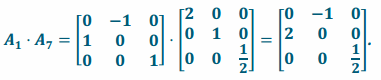
Since the two transformations have different matrix representations, they are not the same transformation: L₁∘L₇≠L₇∘L₁

f. What can you conclude about the order in which you compose two linear transformations?
Answer:
In some cases, the order of composition of two linear transformations matters. For two matrices A and B, the transformation L_A∘L_B is not always the same transformation as L_B∘L_A.

Eureka Math Precalculus Module 2 Lesson 9 Problem Set Answer Key

Question 1.
Let A be the matrix representing a dilation of \(\frac{1}{2}\), and let B be the matrix representing a reflection across the
yz-plane.
a. Write A and B.
Answer:

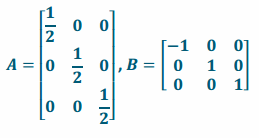
b. Evaluate AB. What does this matrix represent?
Answer:

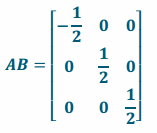
AB is a reflection across the yz-plane followed by a dilation of \(\frac{1}{2}\).

c. Let x=\(\left[\begin{array}{l}
5 \\
6 \\
4
\end{array}\right]\), y=\(\left[\begin{array}{l}
-1 \\
3 \\
2
\end{array}\right]\), and z=\(\left[\begin{array}{l}
8 \\
-2 \\
-4
\end{array}\right]\). Find (AB)x, (AB)y, and (AB)z.
Answer:

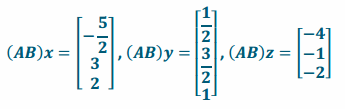
Question 2.
Let A be the matrix representing a rotation of 30° about the x-axis, and let B be the matrix representing a dilation of 5.
a. Write A and B.
Answer:

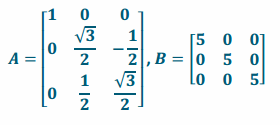
b. Evaluate AB. What does this matrix represent?
Answer:

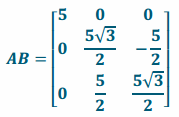
AB is a dilation of 5 followed by a rotation of 30° about the x-axis.

c. Let x=\(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\), y=\(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\), z=\(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\). Find (AB)x, (AB)y, and (AB)z.
Answer:

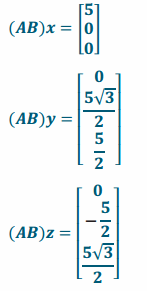
Question 3.
Let A be the matrix representing a dilation of 3, and let B be the matrix representing a reflection across the plane y=x.
a. Write A and B.
Answer:

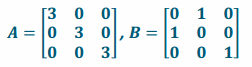
b. Evaluate AB. What does this matrix represent?
Answer:
AB=\(\left[\begin{array}{lll}
0 & 3 & 0 \\
3 & 0 & 0 \\
0 & 0 & 3
\end{array}\right]\)
AB is a reflection across the y=x plane followed by a dilation of 3.

c. Let x=\(\left[\begin{array}{c}
-2 \\
7 \\
3
\end{array}\right]\). Find (AB)x.
Answer:
(AB)x=\(\left[\begin{array}{c}
21 \\
-6 \\
9
\end{array}\right]\)

Question 4.
Let A=\(\left[\begin{array}{lll}
3 & 0 & 0 \\
3 & 3 & 0 \\
0 & 0 & 1
\end{array}\right]\), B=\(\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{ccc}
0 & -3 & 0 \\
3 & -3 & 0 \\
0 & 0 & 1
\end{array}\right]\)

b. Let x=\(\left[\begin{array}{c}
-2 \\
2 \\
5
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
-6 \\
-12 \\
5
\end{array}\right]\)

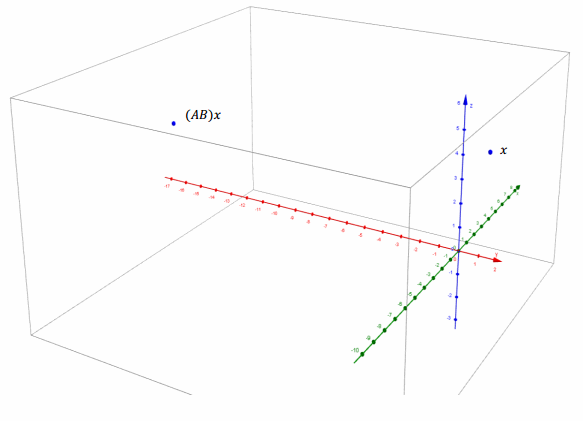
c. Graph x and (AB)x.
Answer:

Question 5.
Let A=\(\left[\begin{array}{lll}
\frac{1}{3} & 0 & 0 \\
0 & 1 & 0 \\
2 & 0 & \frac{1}{3}
\end{array}\right]\), B=\(\left[\begin{array}{ccc}
3 & 1 & 0 \\
1 & -3 & 0 \\
0 & 0 & 1
\end{array}\right]\)

a. Evaluate AB.
Answer:
\(\left[\begin{array}{ccc}
1 & \frac{1}{3} & 0 \\
1 & -3 & 0 \\
6 & 2 & \frac{1}{3}
\end{array}\right]\)

b. Let x=\(\left[\begin{array}{l}
\mathbf{0} \\
3 \\
2
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
1 \\
-9 \\
\frac{20}{3}
\end{array}\right]\)

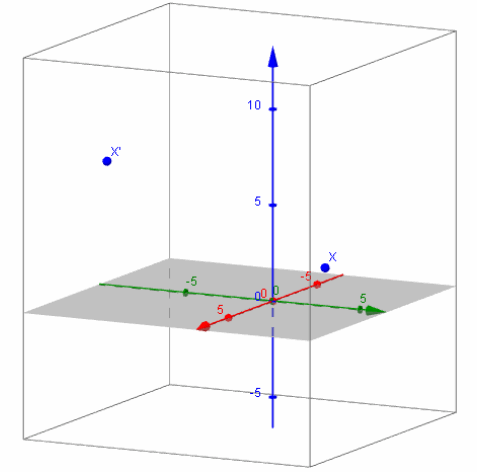
c. Graph x and (AB)x.
Answer:

Question 6.
Let A=\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 8
\end{array}\right]\), B=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 0
\end{array}\right]\)

b. Let x=\(\left[\begin{array}{c}
1 \\
-2 \\
4
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
2 \\
-6 \\
0
\end{array}\right]\)

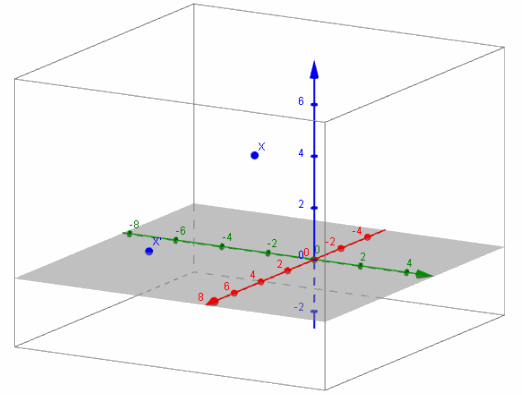
c. Graph x and (AB)x.
Answer:

d. What does AB represent geometrically?
Answer:
AB represents a projection onto the xy-plane, and a dilation of 2 in the x-direction and 3 in the y-direction.

Question 7.
Let A, B, C be 3×3 matrices representing linear transformations.
a. What does A(BC) represent?
Answer:
The linear transformation of applying the linear transformation that C represents followed by the transformation that B represents followed by the transformation that A represents

b. Will the pattern established in part (a) be true no matter how many matrices are multiplied on the left?
Answer:
Yes, in general. When you multiply by a matrix on the left, you are applying a linear transformation after all linear transformations to the right have been applied.

c. Does (AB)C represent something different from A(BC)? Explain.
Answer:
No, it does not. This is the linear transformation obtained by applying C and then AB, which is B followed by A.

Question 8.
Let AB represent any composition of linear transformations in R³. What is the value of (AB)x where x=\(\left[\begin{array}{l}
\mathbf{0} \\
\mathbf{0} \\
\mathbf{0}
\end{array}\right]\)?
Answer:
Since a composition of linear transformations in R³ is also a linear transformation, we know that applying it to the origin will result in no change.

Eureka Math Precalculus Module 2 Lesson 9 Exit Ticket Answer Key

Let A be the matrix representing a rotation about the z-axis of 45° and B be the matrix representing a dilation of 2.
a. Write down A and B.
Answer:

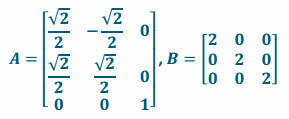
b. Let x=\(\left[\begin{array}{c}
3 \\
-1 \\
2
\end{array}\right]\). Find the matrix representing a dilation of x by 2 followed by a rotation about the z-axis of 45°.
Answer:
AB=\(\left[\begin{array}{ccc}
\sqrt{2} & -\sqrt{2} & 0 \\
\sqrt{2} & \sqrt{2} & 0 \\
0 & 0 & 2
\end{array}\right]\)

c. Do your best to sketch a picture of x, x after the first transformation, and x after both transformations. You may use technology to help you.
Answer: